Формула матрица: Единичная матрица: формула, примеры, свойства

Функция МОПРЕД

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование MDETERM  в Microsoft Excel.

Описание

Возвращает определитель матрицы (матрица хранится в массиве).

Синтаксис

МОПРЕД(массив)

Аргументы функции МОПРЕД описаны ниже.

Замечания

• Массив может быть задан как интервал ячеек, например A1:C3, как массив констант, например {1;2;3:4;5;6:7;8;9}, как имя для интервала или массива.

• Функция МОПРЕД возвращает значение ошибки #ЗНАЧ! в случаях, указанных ниже.

• Определитель матрицы — это число, вычисляемое на основе значений элементов массива. Для массива A1:C3, состоящего из трех строк и трех столбцов, определитель вычисляется следующим образом:

МОПРЕД(A1:C3)
равно A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)

• Определители матриц обычно используются при решении систем уравнений с несколькими неизвестными.

• org/ListItem»>

  Функция МОПРЕД производит вычисления с точностью примерно 16 значащих цифр, что может в некоторых случаях приводить к незначительным ошибкам. Например, определитель сингулярной матрицы отличается от нуля на 1E-16.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Данные	Данные	Данные
1	3	8	5
1	3	6	1
1	1	1	0
7	3	10	2
Формула	Описание	Результат
=МОПРЕД(A2:D5)	Определитель приведенной выше матрицы.	88
=МОПРЕД({3;6;1:1;1;0:3;10;2})	Определитель матрицы, представленной в виде массива констант.	1
=МОПРЕД({3;6:1;1})	Определитель матрицы в массиве констант.	-3
=МОПРЕД({1;3;8;5:1;3;6;1})	Возвращает сообщение об ошибке, так как массив имеет разное количество строк и столбцов.	#ЗНАЧ!

Матрица производной формулы — Русские Блоги

Оригинальный адрес:Матрица производной формулы [очередь]Автор:Сан Инь

Получил формулу сегодня и обнаружил, что на самом деле есть производная матрицы, Хан — вовсе нет. К счастью, кто-то подвел итоги онлайн. Рёв, поторопись и собери резервную копию.

Основная формула:
Y = A * X —> DY/DX = A’
Y = X * A —> DY/DX = A
Y = A’ * X * B —> DY/DX = A * B’
Y = A’ * X’ * B —> DY/DX = B * A’

1. Матрица Y является производной от скаляра x:

Это эквивалентно транспонированию каждого элемента после производной. Обратите внимание, что матрица M × N становится N × M после производной.

Y = [y(ij)] —> dY/dx = [dy(ji)/dx]

2. Скалярный y дифференцирует вектор столбца X:

Обратите внимание, что это отличается от приведенного выше. На этот раз квадратные скобки относятся к частным производным и не транспонируются. После производной вектора N × 1 он по-прежнему является вектором N × 1.

y = f(x1,x2,..,xn) —> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)’

3. Вектор строки Y ‘дифференцирует вектор столбца X:

Обратите внимание, что вектор 1 × M дифференцирует вектор N × 1 в матрицу N × M.

Выведите каждый столбец Y против X и сформируйте каждую матрицу в матрицу.

Важные выводы:

dX’/dX = I

d(AX)’/dX = A’

4. Вектор столбца Y отличается от вектора строки X ’:

Он преобразуется в производную вектора Y строки в вектор X столбцов и затем транспонируется.

Обратите внимание, что производная вектора 1 × N по вектору M × 1 является матрицей M × N.

dY/dX’ = (dY’/dX)’

5. Алгоритм производного векторного произведения для вектора столбца X:

Обратите внимание, что это немного отличается от скалярной производной.

d(UV’)/dX = (dU/dX)V’ + U(dV’/dX)

d(U’V)/dX = (dU’/dX)V + (dV’/dX)U’

Важные выводы:

d(X’A)/dX = (dX’/dX)A + (dA/dX)X’ = IA + 0X’ = A

d(AX)/dX’ = (d(X’A’)/dX)’ = (A’)’ = A

d(X’AX)/dX = (dX’/dX)AX + (d(AX)’/dX)X = AX + A’X

6. Матрица Y дифференцирует вектор столбца X:

Частичная производная Y по каждому компоненту X образует супервектор.

Обратите внимание, что каждый элемент вектора является матрицей.

7. Правило производного матричного произведения для векторов столбцов:

d(uV)/dX = (du/dX)V + u(dV/dX)

d(UV)/dX = (dU/dX)V + U(dV/dX)

Важные выводы:

d(X’A)/dX = (dX’/dX)A + X'(dA/dX) = IA + X’0 = A

8. Производная от скаляра y до матрицы X:

Аналогично производной скаляра y по вектору X столбца,

Частично получить y для каждого элемента X без транспонирования.

dy/dX = [ Dy/Dx(ij) ]

Важные выводы:

y = U’XV ​​= ΣΣu (i) x (ij) v (j), тогда dy / dX = [u (i) v (j)] = UV ‘

y = U’X’XU, затем dy / dX = 2XUU ‘

y = (XU-V) ‘(XU-V), затем dy / dX = d (U’X’XU-2V’XU + V’V) / dX = 2XUU’-2VU’ + 0 = 2 (XU-V U ‘

9. Производная матрицы Y по матрице X:

Продифференцируйте каждый элемент Y от X, а затем расположите их вместе, чтобы сформировать суперматрицу.

 

10. Производная продукта

d(f*g)/dx=(df’/dx)g+(dg/dx)f’

вывод

d (x’Ax) = (d (x ») / dx) Ax + (d (Ax) / dx) (x ») = Ax + A’x (Примечание: « означает два транспонирования)

 

 

Более подробные пункты следующие:

 

 

 

 

http://lzh31cen.blog.163.com/blog/static/145880136201051113615571/

http://hi.baidu.com/wangwen926/blog/item/eb189bf6b0fb702b720eec94.html

 

Другие ссылки:

 

Contents

• Notation
• Derivatives of Linear Products
• Derivatives of Quadratic Products

Notation

• d/dx (y) is a vector whose (i) element is dy(i)/dx
• d/dx (y) is a vector whose (i) element is dy/dx(i)
• d/dx (yT) is a matrix whose (i,j) element is dy(j)/dx(i)
• d/dx (Y) is a matrix whose (i,j) element is dy(i,j)/dx
• d/dX (y) is a matrix whose (i,j) element is dy/dx(i,j)

Note that the Hermitian transpose is not used because complex conjugates are not analytic.

In the expressions below matrices and vectors A

, B, C do not depend on X.

Derivatives of Linear Products

• d/dx (AYB) =A * d/dx (Y) * B
• • d/dx (Ay) =A * d/dx (y)
• d/dx (xTA) =A
• • d/dx (xT) =I
  • d/dx (xTa) = d/dx (aTx) = a
• d/dX (aTXb) = abT
• • d/dX  (aTXa) = d/dX (aTXTa) = aaT
• d/dX (aTXTb) = baT
• d/dx (YZ) =Y * d/dx (Z) + d/dx (Y) * Z

Derivatives of Quadratic Products

• d/dx (Ax+b)TC(Dx+e) = ATC(Dx+e) + DTCT(Ax+b)
• • d/dx (xTCx) = (C+CT)x
  • • [C: symmetric]: d/dx (xTCx) = 2Cx
    • d/dx (xTx) = 2x
  • d/dx (Ax+b)T (Dx+e) = AT (Dx+e) + DT (Ax+b)
  • • d/dx (Ax+b)T (Ax+b) = 2AT (Ax+b)
  • [C: symmetric]: d/dx (Ax+b)TC(Ax+b) = 2ATC(Ax+b)
• d/dX (aTX TXb) = X(abT + baT)
• • d/dX (aTXTXa) = 2XaaT
• d/dX (aTXTCXb) = CTXabT + CXbaT
• • d/dX (aTXTCXa) = (C + CT)XaaT
  • [C:Symmetric] d/dX (aTXTCXa) = 2CXaaT
• d/dX ((Xa+b)TC(Xa+b)) = (C+CT)(Xa+b)aT

Derivatives of Cubic Products

• d/dx (xTAxxT) = (A+AT)xxT+xTAxI

Derivatives of Inverses

• d/dx (Y-1) = -Y-1d/dx (Y)Y-1

Derivative of Trace

Note: matrix dimensions must result in an n*n argument for tr().

• d/dX (tr(X)) = I
• d/dX (tr(Xk)) =k(Xk-1)T
• d/dX (tr(AXk)) = SUMr=0:k-1(XrAXk-r-1)T
• d/dX (tr(AX-1B)) = -(X-1BAX-1)T
  • d/dX (tr(AX-1)) =d/dX (tr(X-1A)) = -X—TATX—T
• d/dX (tr(ATXBT)) = d/dX (tr(BXTA)) = AB
  • d/dX (tr(XAT)) = d/dX (tr(ATX)) =d/dX (tr(XTA)) = d/dX (tr(AXT)) = A
• d/dX (tr(AXBXT)) = ATXBT + AXB
  • d/dX (tr(XAXT)) = X(A+AT)
  • d/dX (tr(XTAX)) = XT(A+AT)
  • d/dX (tr(AXTX)) = (A+AT)X
• d/dX (tr(AXBX)) = ATXTBT + BTXTAT
• [C:symmetric] d/dX (tr((XTCX)-1A) = d/dX (tr(A (XTCX)-1) = -(CX(XTCX)-1)(A+AT)(XTCX)-1
• [B,C:symmetric] d/dX (tr((XTCX)-1(XTBX)) = d/dX (tr( (XTBX)(XTCX)-1) = -2(CX(XTCX)-1)XTBX(XTCX)-1 + 2BX(XTCX)-1

Derivative of Determinant

Note: matrix dimensions must result in an n*n argument for det().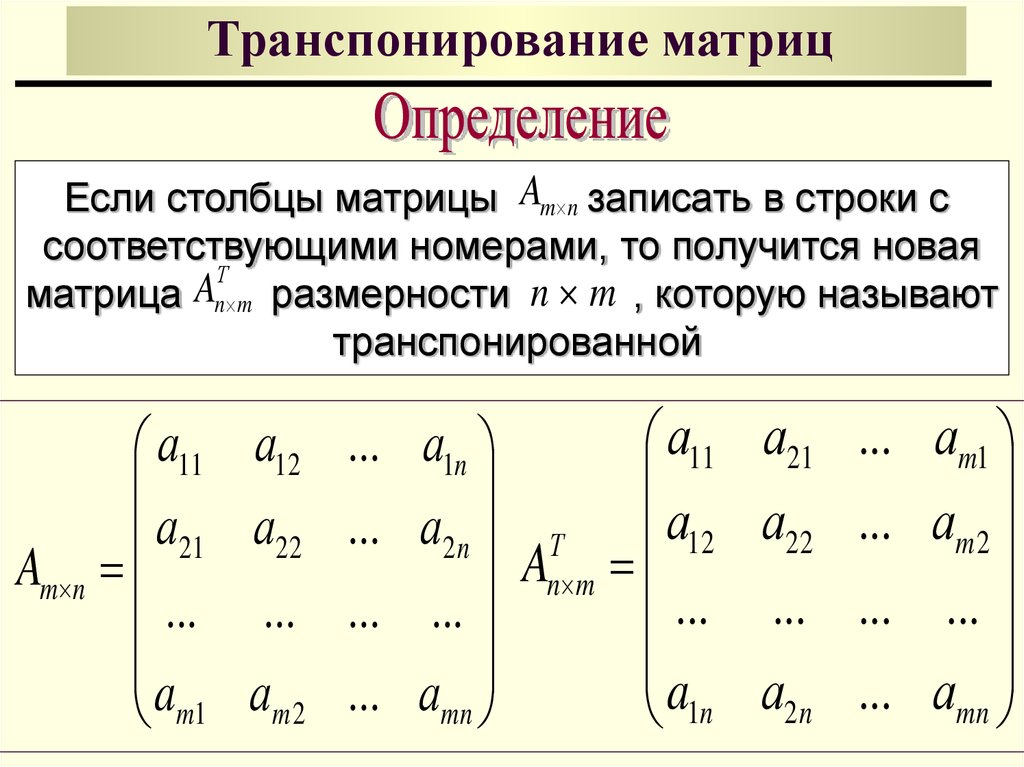

• d/dX (det(X)) = d/dX (det(XT)) = det(X)*X—T
• • d/dX (det(AXB)) = det(AXB)*X—T
  • d/dX (ln(det(AXB))) = X—T
• d/dX (det(Xk)) = k*det(Xk)*X—T
  • d/dX (ln(det(Xk))) = kX—T
• [Real] d/dX (det(XTCX)) = det(XTCX)*(C+CT)X(XTCX)-1
• • [C: Real,Symmetric] d/dX (det(XTCX)) = 2det(XTCX)* CX(XTCX)-1
• [C: Real,Symmetricc] d/dX (ln(det(XTCX))) = 2CX(XTCX)-1

If y is a function of x, then dyT/dx is the Jacobian matrix of y with respect to x.

Its determinant, |dyT/dx|, is the Jacobian of y with respect to x and represents the ratio of the hyper-volumes dy and dx. The Jacobian occurs when changing variables in an integration: Integral(f(y)dy)=Integral(f(y(x)) |dyT/dx| dx).

Hessian matrix

If f is a function of x then the symmetric matrix d2f/dx2 = d/dxT(df/dx) is the Hessian matrix of f(x). A value of x for which df/dx = 0 corresponds to a minimum, maximum or saddle point according to whether the Hessian is positive definite, negative definite or indefinite.

• d2/dx2 (aTx) = 0
• d2/dx2 (Ax+b)TC(Dx+e) = ATCD + DTCTA
• • d2/dx2 (xTCx) = C+CT
  • • d2/dx2 (xTx) = 2I
  • d2/dx2 (Ax+b)T (Dx+e) = ATD + DTA
  • • d2/dx2 (Ax+b)T (Ax+b) = 2ATA
  • [C: symmetric]: d2/dx2 (Ax+b)TC(Ax+b) = 2ATCA  

http://www. psi.toronto.edu/matrix/calculus.html

http://www.stanford.edu/~dattorro/matrixcalc.pdf

http://www.colorado.edu/engineering/CAS/courses.d/IFEM.d/IFEM.AppD.d/IFEM.AppD.pdf

http://www4.ncsu.edu/~pfackler/MatCalc.pdf

http://center.uvt.nl/staff/magnus/wip12.pdf

——————— Эта статья из блога CSDN Time Broken, пожалуйста, нажмите здесь: https://blog.csdn.net/u013289254/article/ details / 69055876? utm_source = copy

Матрица в математике — примеры с решением, теоремы и доказательства

Содержание:

1. Понятие матрицы. Основные определения
2. Действия над матрицами и их свойства. Определим основные действия над матрицами
3. Сложение матриц
4. Произведение матриц

 

Понятие матрицы. Основные определения

Матрицей размерности называется прямоугольная таблица чисел, содержащая строк и столбцов. Для записи матрицы применяются либо сдвоенные черточки, либо круглые скобки:

или

Сокращенно матрица записывается также в виде

либо ,

где указывает номер строки а — номер столбца.

Числа , образующие матрицу называются ее элементами.

Две матрицы называются равными, если они имеют одинаковую размерность и их соответствующие элементы совпадают.

Иначе говоря, если и — матрицы одинаковой размерности, то

для всех и .

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Матрица размерности (соответственно, ) называется вектор-столбцом (соответственно, вектор-строкой).

Матрица, все элементы которой равны нулю, называется нулевой и обозначается через О:

Матрица называется противоположной матрице

Матрица, полученная из данной матрицы заменой местами строк и столбцов с сохранением порядка их следования, называется транспонированной к матрице и обозначается через А(или ). Итак, если — матрица размерности , то транспонированная матрица

имеет размерность .

Нетрудно заметить, что, транспонируя транспонированную матрицу, возвращаемся к исходной матрице, т. е.

Матрица , у которой число строк равно числу столбцов:, называется квадратной матрицей порядка . В квадратной матрице

диагональ , идущая из левого верхнего угла в правый нижний угол, называется главной диагональю матрицы . Побочной диагональю той же матрицы называется другая диагональ: , идущая из левого нижнего угла в правый верхний угол.

Возможно вам будут полезны данные страницы:

Признак Даламбера: пример решения

Исследовать сходимость ряда по признаку Даламбера

Собственные числа матрицы

Собственные векторы матрицы

Квадратная матрица , называется верхней треугольной {нижней треугольной), если все элементы этой матрицы, стоящие ниже (выше) главной диагонали, равны нулю. Итак, верхняя треугольная матрица имеет вид

а нижняя треугольная матрица — вид

Квадратная матрица , называется диагональной, если все элементы этой матрицы, расположенные вне главной диагонали, равны нулю: для всех . Если в диагональной матрице

все элементы главной диагонали равны единице: , то эта матрица называется единичной и обычно обозначается через . Итак, иначе говоря, где

Действия над матрицами и их свойства. 

Определим основные действия над матрицами

Сложение матриц

Суммой двух матриц и одинаковой размерности , называется матрица той же размерности , элементы которой определяются равенством

В этом случае пишут

Точно так же определяется понятие разности двух матриц одной и той же размерности. Итак, по определению

Из определения суммы двух матриц (см. формулу (1.4)) следует, что операция сложения матриц обладает такими же свойствами, что и операция сложения действительных чисел:

Теорема 1. 1. Операция сложения матриц обладает следующими основными свойствами:

1) коммутативность:

2) ассоциативность:

3) существование нулевого вектора:

4) существование противоположной матрицы:

где А, В и С — произвольные матрицы одной и той же размерности, а О — нулевая матрица.

Умножение матрицы на число

Произведением матрицы размерности на число называется матрица той же размерности , элементы которой определяются равенством:

В этом случае пишут или . Итак, по определению

Теорема 1.2. Умножение матрицы на число обладает следующими основными свойствами:

1) ассоциативность:

2) дистрибутивность относительно суммы матриц:

3) дистрибутивность относительно суммы чисел:

4) нормированность:

где Л и В — произвольные матрицы одной и той же размерности, а и — произвольные числа.

Доказательства перечисленных в теореме свойств непосредственно следуют из формул (1. 4) и (1.10).

Произведение матриц

Пусть — матрица размерности , а — матрица размерности , т. е. предполагаем, что число столбцов матрицы А равно числу строк матрицы В.

Произведением матрицы на матрицу называется матрица размерности , элементы которой определяются равенством:

где . То есть, элемент -й строки и -го столбца матрицы произведения С равен сумме произведений элементов -й строки матрицы А на соответствующие элементы -го столбца матрицы В.

Для обозначения произведения матрицы А на В используют запись или .

Если применить указанное правило умножения матриц к квадратным матрицам второго порядка, получим

Теорема 1.3. Произведение матриц обладает следующими основными свойствами:

1) ассоциативность:

2) дистрибутивность относительно суммы матриц:

3) однородность:

если, конечно, указанные суммы и произведения матриц имеют смысл.

Доказательство.

Свойства (1.19) и (1.20) непосредственно следуют из формул (1.4), (1.10) и (1.16).

Докажем свойство (1.18). Пусть — матрица размерности , — матрица размерности , а матрица размерности . Тогда, согласно (1.16), элемент произведения вычисляется по формуле

а элемент произведения — по формуле

Теперь заметим, что { в силу правомерности изменения порядка суммирования относительно и .

Теорема доказана.

Замечание 1.1. Пусть А и В — квадратные матрицы одинакового порядка. Тогда имеет смысл ставить вопрос о свойстве коммутативности произведения матриц.

Следующий простой пример показывает, что произведение квадратных матриц одинакового порядка, вообще говоря, не обладает свойством коммутативности .

В самом деле, пусть

Тогда

и, значит,

Однако верно утверждение: для произвольной квадратной матрицы порядка справедливы равенства

где — единичная матрица, а — нулевая матрица того же порядка .

Справедливость формулы (1.22) очевидна.

Докажем формулу (1.21). Пусть , а , где , если , и , если (см. (1.3)). Тогда, в силу (1.16), для элемента произведения получаем

т. е. . Точно так же имеем: . Итак, формула (1.21) доказана.

Matrix Formula — Что такое Matrix Formula? Примеры

Матрица – это упорядоченное расположение чисел, выражений и даже символов в строках и столбцах. Если две матрицы имеют одинаковый размер (относительно их строк и столбцов), то их можно складывать, вычитать и умножать поэлементно. Давайте изучим матричные формулы вместе с несколькими решенными примерами.

Что такое формула матрицы?

Матрица – это массив чисел, разделенный на строки и столбцы и представленный в квадратных скобках. Если вы видите матрицу 2 × 2, это означает, что матрица имеет 2 строки и 2 столбца. Матричные формулы используются для вычисления коэффициента вариации, сопряженной матрицы, определителя матрицы и обратной матрицы. Матричная формула особенно полезна в тех случаях, когда нам нужно сравнить результаты двух разных опросов с разными значениями.

Матричные формулы

Формула 1: Формула коэффициента вариации может быть представлена ​​как

\(M=\begin{bmatrix} m_{11} & m_{12}\\ m_{21} & m_ {22} \end{bmatrix}\)

Формула 2:  Сопряженная формула матрицы 2 × 2 задается как

\( adj(M)=\begin{bmatrix} m_{22} & — m_{12}\\ -m_{21} & m_{11} \end{bmatrix}\)

Формула 3:  Обратная формула матрицы 2×2 задается как

9T\) =A’= \(\begin{bmatrix}a&d\\b&e\\c&f\end{bmatrix}\)

Формула 6: Матричная формула для сложения:

A= \(\begin{bmatrix }a&b&c\\d&e&f\\g&h&i\end{bmatrix}\)
B=  \(\begin{bmatrix}j&k&l\\m&n&o\\p&q&r\end{bmatrix}\)

A+B=  \(\begin{bmatrix}a+j&b+k&c+l\\d+m&e+n&f +o\\g+p&h+q&i+r\end{bmatrix}\)

Формула 7:  Матричная формула для вычитания:

A = \(\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\)
B=  \(\begin{bmatrix}j&k&l\\m&n&o\\p&q&r\end{bmatrix}\)

A-B=  \(\begin{bmatrix}a-j&b-k&c-l\\d-m&e-n&f-o \\g-p&h-q&i-r\end{bmatrix}\)

Формула 8: Матричная формула для умножения:

A= \(\begin{bmatrix}a&b&c\\d&e&f\end{bmatrix}\)
B = \(\begin{bmatrix}g&h\\i&j\\k&l\end{bmatrix}\)

AB= \(\begin{bmatrix}ag+bi+ck&ah+bj+cl\\dg+ei+fk&dh+ej+fl\end{bmatrix}\)

Формула 9: Для ортогональной матрицы произведение матрицы и ее транспонирования дает единичную матрицу. M × M ^T  = I

M × M ^T  = \(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) × \(\begin{bmatrix}a&c\\b&d\end{ bmatrix}\) = \(\begin{bmatrix}1&0\\0&1\end{bmatrix}\)

Применение матричных формул 

Матричные формулы обычно используются для нахождения решений линейных уравнений и исчисления, оптики, квантовой механики, и другие математические функции.

Давайте посмотрим, как использовать матричную формулу в следующем разделе решенных примеров.

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, зачем нужна математика, с нашими сертифицированными экспертами

Закажите бесплатный пробный урок

Примеры с использованием матричной формулы

Пример 1: Используя матричную формулу, определите определитель данной матрицы.

\(\begin{bmatrix} 3 и 4 \\ 4 и 8 \end{bmatrix}\)

Решение: 

Найти: Определитель матрицы.
\(m_{11}\) = 3, \(m_{12}\) = 4, \(m_{21}\) = 4 и,   \(m_{22}\) = 8(данные)

Используя матричную формулу для определителя,

|M| = \(m_{11}\)\(m_{22}\)–\(m_{12}\)\(m_{21}\)

= (3)(8) — (4)(4)

= 24 — 16
= 8

Ответ: определитель данной матрицы равен 8.

Пример 2 : Определите сопряжение данной матрицы 2 x 2.

\(\begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}\)

Решение:

Найти:  примыкание к заданной матрице 2 x 2

Дано: \( m_{11}= 5, m_{12} = 6, m_{21} = 7 и, m_{22} = 8\)(дано)  

Используя матричную формулу для сопряженной матрицы,

\ ( adj(M)=\begin{bmatrix} m_{22} & -m_{12}\\ -m_{21} & m_{11} \end{bmatrix}\)

Поместите все значения,

\ ( adj(M)=\begin{bmatrix} 8 & — 6\\ — 7 & 5 \end{bmatrix}\)

Ответ: Сопряженная матрица равна \(\begin{bmatrix} 8 & — 6\\ — 7 & 5 \end{bmatrix}\).

Пример 3: Используйте матричную формулу для определения определителя матрицы:

\(\begin{bmatrix} 2 & 4 \\ 6 & 5 \end{bmatrix}\)

Решение:

3

Найти: Определитель матрицы.
\(m_{11}\)= 2, \(m_{12}\) = 4, \(m_{21}\) = 6 и, 90 109   \(m_{22}\) = 5 (дано) 90 109

Использование матричной формулы для определителя,

|M| = \(m_{11}\)\(m_{22}\)–\(m_{12}\)\(m_{21}\)

= (2)(5) — (4)(6)

= 10 — 24
= -14

Ответ: Определитель данной матрицы равен -14.

Часто задаваемые вопросы о матричной формуле

Что такое матричная формула в алгебре?

Матричные формулы используются для вычисления коэффициента вариации, сопряженного к матрице, определителя матрицы и обратной матрицы.

9{-1}=\frac{1}{|M|}\times adj(M)\)

Определитель задается как |M| = \(м_{11}м_{22} – м_{12}м_{21}\)

Что такое формула матрицы идентичности?

Индивидуальная матрица – это квадратная матрица, состоящая из всех элементов главной диагонали, обозначенных единицами, и всех остальных элементов, обозначенных нулями.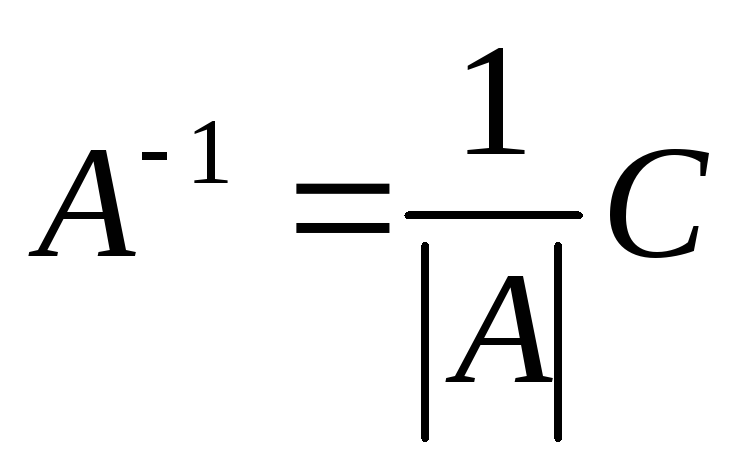 Она называется единичной матрицей, также известной как единичная матрица или элементарная матрица. Для любой единичной матрицы A×I _n×n = A, где A — любая квадратная матрица порядка n×n.

Что такое формула ортогональной матрицы?

Для ортогональной матрицы произведение матрицы и ее транспонирования дает значение идентичности. Если M — матрица, M ^T — ее транспонирование. Их произведение представляет собой единичную матрицу со значениями на ведущих диагоналях, равными 1.

 Формула ортогональной матрицы M × M ^T  = I

Каковы применения матричной формулы?

Матричные формулы находят применение во многих областях

• поиск решений линейных уравнений
• в исчислении,
• в оптике,
• в квантовой механике
• в других математических функциях.

2.3: Матричные уравнения — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

70188

• Дэн Маргалит и Джозеф Рабинофф
• Технологический институт Джорджии

Цели

1. Понять эквивалентность между системой линейных уравнений, расширенной матрицей, векторным уравнением и матричным уравнением.
2. Охарактеризуйте векторы \(b\) так, что \(Ax=b\) непротиворечиво, в терминах диапазона столбцов \(A\).
3. Охарактеризуйте матрицы \(A\) так, что \(Ax=b\) непротиворечиво для всех векторов \(b\).
4. Рецепт: умножить вектор на матрицу (два способа).
5. Picture: множество всех векторов \(b\) таких, что \(Ax=b\) непротиворечиво.
6. Словарь: матричное уравнение .

Матричное уравнение \(Ax=b\)

В этом разделе мы вводим очень краткий способ записи системы линейных уравнений: \(Ax=b\). Здесь \(A\) — матрица, а \(x,b\) — векторы (обычно разных размеров), поэтому сначала мы должны объяснить, как умножать матрицу на вектор.

Примечание \(\PageIndex{1}\)

Когда мы говорим, что \(A\) является матрицей \(m\x n\)», мы имеем в виду, что \(A\) имеет \(m\) строк и \(n\) столбцов.

Примечание

В этой книге мы делаем , а не , резервируя буквы \(m\) и \(n\) для номеров строк и столбцов матрицы. Если мы напишем «\(A\) — матрица \(n\times m\)», то \(n\) — количество строк матрицы \(A\), а \(m\) — количество столбцов .

Определение \(\PageIndex{1}\): Продукт

Пусть \(A\) будет матрицей \(m\times n\) со столбцами \(v_1,v_2,\ldots,v_n\text{:} \) 9м\).

Пример \(\PageIndex{1}\)

\[\left(\begin{array}{ccc}4&5&6 \\ 7&8&9\end{array}\right)\:\left(\begin{array}{ c}1\\2\\3\end{массив}\right) =1\left(\begin{массив}{c}4\\7\end{массив}\right) +2\left(\begin{ array}{c}5\\8\end{array}\right)+3\left(\begin{array}{c}6\\9\end{array}\right)=\left(\begin{array }{c}32\\50\end{массив}\right).\nonumber\]

Чтобы \(Ax\) имело смысл, число элементов \(x\) должно быть одинаковым в качестве количества столбцов \(A\text{:}\) мы используем записи \(x\) в качестве коэффициентов столбцов \(A\) в линейной комбинации. Результирующий вектор имеет то же количество элементов, что и число 9.m\text{,}\) и \(x\) — вектор, коэффициенты которого \(x_1,x_2,\ldots,x_n\) неизвестны. 2-1=0\) для \(x\). Второй вопрос, возможно, является новой концепцией для вас. Теорема 2.9м\). Рассмотрим векторное уравнение

\[ x_1v_1 + x_2v_2 + \cdots + x_nv_n = b. \nonumber \]

Это эквивалентно матричному уравнению \(Ax=b\text{,}\), где

\[A=\left(\begin{array}{cccc}|&|&\quad & | \\ v_1 &v_2 &\cdots &v_n \\ |&|&\quad &|\end{массив}\right)\quad\text{and}\quad x=\left(\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right).\nonumber \]

Наоборот, если \(A\) является любой матрицей \(m\times n\), то \(Ax= б\) эквивалентно векторному уравнению 93\).

Решение

Пусть \(A\) будет матрицей со столбцами \(v_1,v_2,v_3\text{,}\), а \(x\) будет вектором с элементами \(2,3,-4 \). Затем

\[Ax=\left(\begin{array}{ccc}|&|&| \\ v_1 & v_2 & v_3 \\ |&|&|\end{array}\right)\:\left( \begin{array}{c}2\\3\\-4\end{array}\right) = 2v_1 +3v_2 -4v_3, \nonumber\]

, поэтому векторное уравнение эквивалентно матричному уравнению \(Ax =\left(\begin{массив}{c}7\\2\\1\end{массив}\right)\).

Примечание \(\PageIndex{4}\): четыре способа записи линейной системы

Теперь у нас есть четыре эквивалентных способа записи (и обдумывания) системы линейных уравнений:

1. В виде системы уравнений:
   \[\left\{\begin{array}{rrrrrrr} 2x_1 &+ & 3x_2 &-& 2x_3 &=& 7\\ x_1 &-& x_2 &-& 3x_3 &=& 5\end{массив}\right.\nonnumber\]
2. В виде расширенной матрицы:
   \[\left(\begin{array}{ccc|c} 2&3&-2&7 \\ 1&-1&-3&5\end{array}\right)\nonumber\]
3. В виде векторного уравнения (\(x_1v_1 + x_2v_2 + \cdots + x_nv_n = b\)):
   \[x_{1}\left(\begin{array}{c}2\\1\end{array}\ вправо)+x_2\влево(\begin{массив}{c}3\\-1\конец{массив}\вправо)+x_3\влево(\begin{массив}{c}-2\\-3\конец{ массив}\справа)=\слева(\начало{массив}{с}7\\5\конец{массив}\справа)\номер\]
4. В виде матричного уравнения (\(Ax=b\)):
   \[\left(\begin{array}{ccc}2&3&-2 \\ 1&-1&-3\end{array}\right)\:\ влево(\begin{массив}{c}x_1 \\ x_2 \\ x_3\end{массив}\right)=\left(\begin{массив}{c}7\\5\end{массив}\right). \номер\]

В частности, все четыре имеют одинаковый набор решений .

Примечание \(\PageIndex{5}\)

Мы будем свободно перемещаться между четырьмя способами записи линейной системы снова и снова до конца книги.

Другой способ вычисления \(Ax\)

Приведенное выше определение продукта, определение \(\PageIndex{1}\), – полезный способ определения произведения матрицы на вектор, когда дело доходит до понимания связь между матричными уравнениями и векторными уравнениями. Здесь мы даем определение, которое лучше подходит для ручных вычислений.

Определение \(\PageIndex{3}\): вектор-строка

Вектор-строка представляет собой матрицу с одной строкой. Произведение вектора-строки длины \(n\) и вектора (столбца) длины \(n\) равно

\[\left(\begin{array}{cccc}a_1 &a_2 &\ cdots a_n \end{массив}\right)\:\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{массив}\right) =a_1 x_1 + a_2 x_2 +\ cdots + a_n x_n .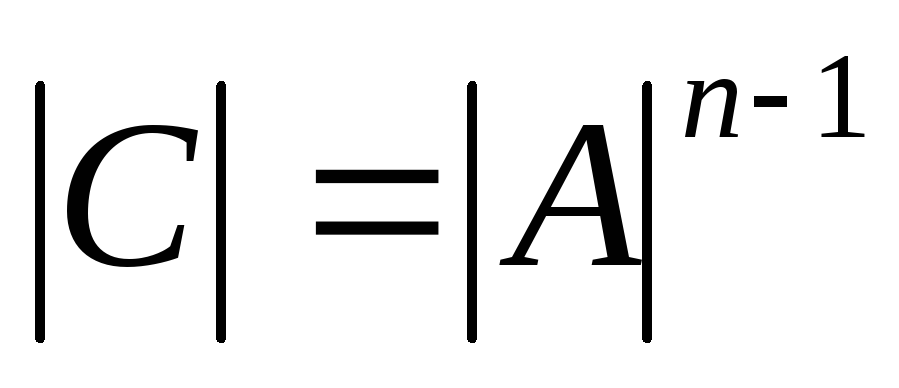 \nonumber\]

Это скаляр.

Рецепт: Правило строки-столбца для умножения матрицы на вектор 9n\text{,}\) then

\[Ax=\left(\begin{array}{c} — r_1 — \\ —r_2 — \\ \vdots \\ — r_m —\end{array}\right ) x=\left(\begin{array}{c} r_1 x \\ r_2 x \\ \vdots \\ r_m x\end{array}\right).\nonumber\]

Пример \(\PageIndex{3 }\)

\[\left(\begin{array}{ccc}4&5&6 \\ 7&8&9\end{массив}\right)\:\left(\begin{array}{c}1\\2\\3 \end{массив}\right)=\left(\begin{array}{cc}{\left(\begin{array}{c}4&5&6\end{массив}\right)}&{\left(\begin{ array}{c}1\\2\\3\end{массив}\right)}\\{\left(\begin{array}{ccc}7&8&9\end{массив}\right)}&{\left(\begin{array}{c}1\\2\\3\end{массив}\right)}\end{массив}\right) =\left( \begin{array}{ccccccccccc} 4 & \cdot &1&+&5 &\cdot & 2&+& 6& \cdot & 3 \\ 7 &\cdot & 1&+&8 & \cdot & 2&+&9 & \cdot &3\end {array}\right)=\left(\begin{array}{c} 32\\50\end{array}\right).\nonumber\]

Это тот же ответ, что и раньше:

\[\ влево(\begin{массив}{ccc}4&5&6 \\ 7&8&9\end{массив}\right)\:\left(\begin{массив}{c}1\\2\\3\end{массив}\right) =1\left(\begin{массив}{c}4\\7\end{массив}\right)+2\left(\begin{массив}{c}5\\8\end{массив}\right) +3\влево(\begin{массив}{с}6\\9\end{массив}\right)=\left(\begin{array}{cccccccccc} 1 & \cdot & 4&+& 2& \cdot &5&+&3& \cdot &6 \\ 1 & \cdot &7&+& 2& \cdot &8& +&3& \cdot &9\end{массив}\right)=\left(\begin{array}{c}32\\50\end{массив}\right). \nonumber\]

Диапазоны и согласованность

Let \(A\) — матрица со столбцами \(v_1,v_2,\ldots,v_n\text{:}\)

\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots & v_n \\ |&|&\quad &|\end{массив}\right).\nonumber\]

Тогда

\[ \begin{split} Ax=b&\text{ имеет решение} \\ &\iff \text{существуют $x_1,x_2,\ldots,x_n$ такие, что } A\left(\ begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right) = b \\ &\iff \text{существуют $x_1,x_2,\ldots,x_n$ такие, что } x_1v_1 + x_2v_2 + \cdots + x_nv_n = b \\ &\iff \text{$b$ является линейной комбинацией } v_1,v_2,\ldots,v_n \\ &\iff \text{$b$ находится в диапазон столбцов $A$}. \end{split} \nonumber \]

Примечание \(\PageIndex{6}\): диапазоны и согласованность

Матричное уравнение \(Ax=b\) имеет решение тогда и только тогда, когда \(b\) находится в диапазоне столбцов \(A\).

Это дает эквивалентность между алгебраическим утверждением (\(Ax=b\) непротиворечиво) и геометрическим утверждением (\(b\) находится в диапазоне столбцов \(A\)) .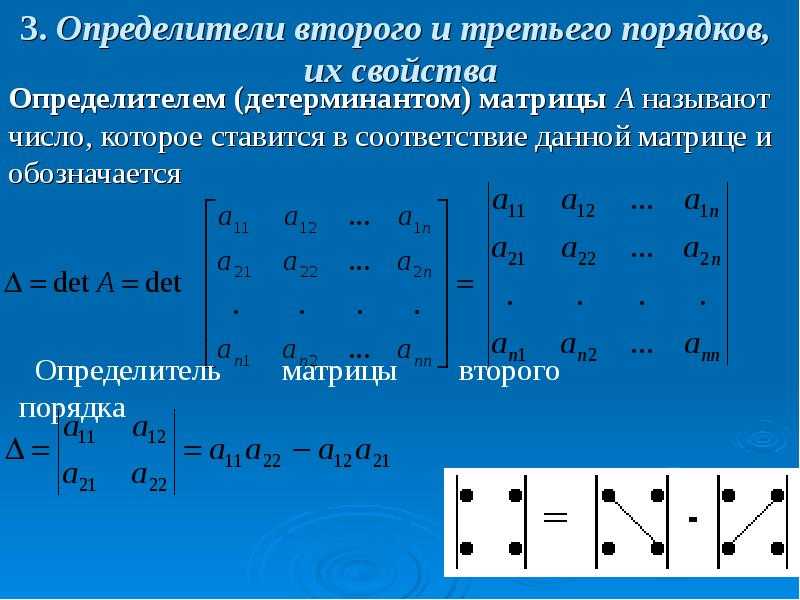

Пример \(\PageIndex{4}\): несовместимая система

Пусть \(A=\left(\begin{array}{cc}2&1\\ -1&0 \\ 1&-1\end{array}\ Правильно)\). Имеет ли уравнение \(Ax=\left(\begin{array}{c}0\\2\\2\end{array}\right)\) решение?

Решение

Сначала ответим на вопрос геометрически. Столбцы \(A\) равны

\[\color{Red}{v_1 =\left(\begin{array}{c}2\\-1\\1\end{array}\right)}\ quad\color{black}{\text{and}}\quad\color{blue}{v_2 =\left(\begin{array}{c}1\\0\\-1\end{array}\right) }\color{black}{,}\nonumber\]

, а целевой вектор (в правой части уравнения) равен \(\color{Green}{w=\left(\begin{array}{) c}0\\2\\2\конец{массив}\справа)}\). Уравнение \(Ax=w\) непротиворечиво тогда и только тогда, когда \(w\) содержится в промежутке столбцов \(A\). Итак рисуем картинку:

Рисунок \(\PageIndex{1}\)

 Похоже, что \(w\) не лежит в \(\text{Span}\{v_1,v_2\},\), поэтому уравнение несовместимо .

Рисунок \(\PageIndex{2}\): Вектор \(w\) не содержится в \(\text{Span}\{v_1,v_2\}\text{,}\), поэтому уравнение \ (Ax=b\) противоречиво. (Попробуйте переместить ползунки, чтобы решить уравнение.)

Давайте проверим наш геометрический ответ, решив матричное уравнение, используя сокращение строк. Помещаем систему в расширенную матрицу и уменьшаем строку:

\[\left(\begin{array}{cc|c} 2&1&0 \\ -1&0&2 \\ 1&-1&2\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left (\begin{array}{cc|c} 1&0&0 \\ 0&1&0 \\ 0&0&1\end{array}\right).\nonumber\]

Последнее уравнение равно \(0=1\text{,}\), поэтому система действительно противоречива, и матричное уравнение

\[\left(\begin{array}{cc}2&1\\-1&0\\1&-1\end{array}\right)x=\left(\begin {массив}{с}0\\2\\2\конец{массив}\справа)\номер\]

не имеет решения.

Пример \(\PageIndex{5}\): согласованная система

Пусть \(A=\left(\begin{array}{cc}2&1\\-1&0\\1&-1\end{array}\ Правильно)\). Имеет ли уравнение \(Ax=\left(\begin{array}{c}1\\-1\\2\end{array}\right)\) решение?

Решение

Сначала ответим на вопрос геометрически. Столбцы \(A\) равны

\[\color{Red}{v_1=\left(\begin{array}{c}2\\-1\\1\end{array}\right)}\ quad\color{black}{\text{and}}\quad\color{blue}{v_2 =\left(\begin{array}{c}1\\0\\-1\end{array}\right) },\номер\]

, а целевой вектор (в правой части уравнения) равен \(\color{Green}{w=\left(\begin{array}{c}1\\-1\\2\end{ массив}\справа)}\). Уравнение \(Ax=w\) непротиворечиво тогда и только тогда, когда \(w\) содержится в промежутке столбцов \(A\). Итак, мы рисуем картинку:

Рисунок \(\PageIndex{3}\)

Похоже, что \(w\) действительно содержится в диапазоне столбцов \(A\text{;}\) на самом деле мы можем видеть

\[ w = v_1 — v_2 \ подразумевает x = \left(\begin{array}{c}1\\-1\end{array}\right). \номер\]

Рисунок \(\PageIndex{4}\): Вектор \(w\) содержится в \(\text{Span}\{v_1,v_2\}\text{,}\), поэтому уравнение \( Ах=b\) непротиворечиво. (Двигайте ползунки, чтобы решить уравнение.)

Давайте проверим наш геометрический ответ, решив матричное уравнение с помощью редукции строк. Мы помещаем систему в расширенную матрицу и уменьшаем строку:

\[\left(\begin{array}{cc|c}2&1&1\\-1&0&-1\\1&-1&2\end{array}\right) \ quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&0&1 \\ 0&1&-1 \\ 0&0&0\end{массив}\right).\nonumber\]

Это дает нам \(x=1\) и \(y=-1\text{,}\), что соответствует картинке:

\[1\left(\begin{array}{c}2 \\-1\\1\конец{массив}\справа)-1\слева(\начало{массив}{с}1\\0\\-1\конец{массив}\справа)=\слева(\начало {массив} {c} 1\\-1\\2\end{массив}\right)\quad\text{or}\quad A\left(\begin{array}{c}1\\-1\end {array}\right)=\left(\begin{array}{c}1\\-1\\2\end{array}\right). \nonnumber\]

Когда решения всегда существуют.

Опираясь на примечание \(\PageIndex{6}\): промежутки и согласованность, у нас есть следующий критерий, когда \(Ax=b\) непротиворечив для 9м\).

Теперь покажем, что 1 и 3 эквивалентны. (Поскольку мы знаем, что 1 и 2 эквивалентны, отсюда следует, что 2 и 3 также эквивалентны.) Если \(A\) имеет точку опоры в каждой строке, то его сокращенная ступенчатая форма строки выглядит следующим образом:

\[\left(\begin{array}{ccccc}1&0&\star &0&\star \\ 0&1&\star &0&\star \\ 0&0&0&1&\star \end{array}\right),\nonumber\]

и, следовательно, \(\left(\begin{array}{c|c}A&b\end{array}\right)\) сводится к этому:

\[\left(\begin{array}{ccccc|c} 1&0&\star &0&\star &\star \\ 0&1&\star &0&\star &\star \\ 0&0&0&1&\star &\star\end{array}\ справа).\номер\]

Нет \(b\), что делает его несовместимым, поэтому всегда есть решение. Наоборот, если \(A\) не имеет стержня в каждой строке, то его сокращенная ступенчатая форма строки выглядит так:

\[\left(\begin{array}{ccccc}1&0&\star &0&\star \\ 0&1&\star &0&\star \\ 0&0&0&0&0\end{array}\right),\nonumber\]

, что может привести к несогласованности системы после добавления \(b\text{:}\)

\[\left(\begin{array}{ccccc|c} 1&0&\star &0&\star &0 \\ 0&1&\star &0&\star &0 \\ 0&0&0&0&0&16\end{array}\right). \nonumber\]

Напомним, что эквивалентно означает, что для любой заданной матрицы \(A\text{,}\) либо все условий приведенной выше теоремы, \(\PageIndex{1}\), выполняются , либо все они ложны.

Примечание \(\PageIndex{7}\)

Будьте внимательны при чтении формулировки приведенной выше теоремы \(\PageIndex{1}\). Первые два условия очень похожи на это примечание \(\PageIndex{6}\): диапазоны и согласованность, но логически они совершенно разные из-за квантификатора « для всех \(b\)».

Пример \(\PageIndex{6}\): Интерактивный: Соблюдены критерии теоремы

Рисунок \(\PageIndex{5}\): Пример, в котором критерии приведенной выше теоремы \(\PageIndex{ 1}\) удовлетворены. Фиолетовая область — это диапазон столбцов \(v_1,v_2,v_3\) массива \(A\text{,}\), который совпадает с набором всех \(b\), таких что \(Ax=b \) имеет решение. Если вы перетащите \(b\text{,}\), демо решит за вас \(Ax=b\) и переместит \(x\). m\), когда \(A\) имеет \ (м\) повороты.

---

Эта страница под названием 2.3: Матричные уравнения распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, переработана и/или курирована Дэном Маргалитом и Джозефом Рабинофф через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дэн Маргалит и Джозеф Рабинофф

   Лицензия

   ГНУ ФДЛ

   Версия лицензии

   1,3

2. Теги

   1. источник@https://textbooks. math.gatech.edu/ila

матрица | Определение, типы и факты

Ключевые люди:

Артур Кэли Нильс Фабиан Хельге фон Кох

Похожие темы:

магический квадрат определитель квадратная матрица нулевая матрица элемент

Просмотреть весь связанный контент →

Резюме

Прочтите краткий обзор этой темы

матрица , набор чисел, расположенных в строках и столбцах так, чтобы образовать прямоугольный массив. Числа называются элементами или элементами матрицы. Матрицы имеют широкое применение в технике, физике, экономике и статистике, а также в различных разделах математики. Матрицы также имеют важные приложения в компьютерной графике, где они использовались для представления поворотов и других преобразований изображений.

Исторически сложилось так, что первой была распознана не матрица, а определенное число, связанное с квадратным массивом чисел, называемое определителем. Лишь постепенно возникло представление о матрице как об алгебраической сущности. Термин матрица был введен английским математиком 19-го века Джеймсом Сильвестром, но именно его друг, математик Артур Кэли, разработал алгебраический аспект матриц в двух статьях в 1850-х годах. Кейли впервые применил их к изучению систем линейных уравнений, где они до сих пор очень полезны. Они важны еще и потому, что, как признал Кейли, определенные наборы матриц образуют алгебраические системы, в которых справедливы многие обычные законы арифметики (например, ассоциативный и распределительный законы), но в которых другие законы (например, коммутативный закон) справедливы. недействительный.

Britannica Quiz

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.

Если имеется 90 274 ​​м 90 275 строк и 90 274 ​​n 90 275 столбцов, матрица называется «90 274 ​​м 90 275 на 90 274 ​​n 90 275» и записывается как «90 274 ​​м 90 275 × 90 274 ​​n 90 275». Например,

— это матрица 2 × 3. Матрица с n строк и n столбцов называется квадратной матрицей порядка n . Обычное число можно рассматривать как матрицу 1 × 1; таким образом, 3 можно рассматривать как матрицу [3]. Матрица только с одной строкой и 90 274 ​​n 90 275 столбцов называется вектором-строкой, а матрица только с одним столбцом и 90 274 ​​n 90 275 строк называется вектором-столбцом.

В общепринятых обозначениях заглавная буква обозначает матрицу, а соответствующая строчная буква с двойным нижним индексом описывает элемент матрицы. Таким образом, a _ij элемент в i -й строке и j -м столбце матрицы A . If A is the 2 × 3 matrix shown above, then a ₁₁ = 1, a ₁₂ = 3, a ₁₃ = 8, a ₂₁ = 2, a ₂₂ = −4 и a ₂₃ = 5. При определенных условиях матрицы можно складывать и умножать как отдельные объекты, что приводит к важным математическим системам, известным как матричные алгебры.

Матрицы встречаются естественным образом в системах одновременных уравнений. В следующей системе для неизвестных x и y массив чисел представляет собой матрицу, элементами которой являются коэффициенты неизвестных. Решение уравнений полностью зависит от этих чисел и от их конкретного расположения. Если бы 3 и 4 поменять местами, решение было бы другим.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Две матрицы A и B равны друг другу, если они имеют одинаковое количество строк и одинаковое количество столбцов и если a _ij = b 17 ij для 9 902 каждый i и каждый j . Если A и B — это две матрицы размером m × n , то их сумма S = A + B равна m × элементам0274 с _ij = a _ij + b _ij . То есть каждый элемент S равен сумме элементов в соответствующих позициях A и B .

Матрицу A можно умножить на обычное число c , которое называется скаляром. Произведение обозначается cA или Ac и представляет собой матрицу, элементы которой равны 9.0274 ca _ij .

Умножение матрицы A на матрицу B для получения матрицы C определяется только тогда, когда количество столбцов первой матрицы A равно количеству строк второй матрицы B . Для определения элемента c _ij , который находится в i -й строке и j -м столбце произведения, первый элемент в i -я строка A умножается на первый элемент в j -й столбец B , второй элемент в строке на второй элемент в столбце, и так далее, пока последний элемент в строке не будет умножается на последний элемент столбца; сумма всех этих произведений дает элемент c _ij . В символах, для случая, когда A имеет m столбцов, а B имеет m строк, матрица C имеет столько же строк, сколько A и столько же столбцов, сколько B .

В отличие от умножения обычных чисел a и b , в котором ab всегда равно ba , умножение матриц A и B не является коммутативным. Однако он является ассоциативным и дистрибутивным по сравнению с сложением. То есть, когда операции возможны, всегда выполняются следующие уравнения: A ( BC ) = ( AB ) C , A ( B + C ) = AB + AC , and ( B + C ) A = BA + СА . Если матрицу 2 × 2 A , строками которой являются (2, 3) и (4, 5), умножить саму на себя, то произведение, обычно записываемое как A ² , имеет строки (16, 21) и ( 28, 37).

Матрица O , все элементы которой равны 0, называется нулевой или нулевой матрицей. Квадратная матрица Число с единицами на главной диагонали (слева вверху и справа внизу) и нулями повсюду в остальных местах называется единичной или единичной матрицей. Его обозначают I или I _n , чтобы показать, что его порядок равен n . Если B — любая квадратная матрица, а I и O — единичная и нулевая матрицы одного порядка, всегда верно, что B + O = O + B = B и БИ = БИ = Б . Следовательно, O и I ведут себя как 0 и 1 в обычной арифметике. (На самом деле обычная арифметика — это частный случай матричной арифметики, в которой все матрицы имеют размер 1 × 1.)

Квадратная матрица A , в которой элементы a _ij отличны от нуля только тогда, когда i = j называется диагональной матрицей. Диагональные матрицы обладают тем особым свойством, что их умножение коммутативно; то есть для двух диагональных матриц А и Б , АВ = ВА . След квадратной матрицы представляет собой сумму элементов на главной диагонали.

С каждой квадратной матрицей A связано число, известное как определитель A , обозначаемый det A . Например, для матрицы 2 × 2 det A = ad − bc . Квадратная матрица B называется невырожденной, если det B ≠ 0. Если B невырожденна, существует матрица, обратная B , обозначаемый B ^-1 , такой, что BB ^-1 = B ^-1 B = I 90. Уравнение AX = B , в котором A и B — известные матрицы, а X — неизвестная матрица, решается однозначно, если A — невырожденная матрица, тогда A −1 существует, и обе части уравнения можно умножить на него слева: А ^-1 ( АХ ) = А ^-1 В . Теперь A ⁻¹ ( AX ) = ( A ⁻¹ A ) X = IX = X 9; следовательно, решение X = A ⁻¹ B . Система из 90 274 ​​m 90 275 линейных уравнений с 90 274 ​​n 90 275 неизвестными всегда может быть выражена в виде матричного уравнения 90 274 ​​AX = B 90 275, в котором 90 274 ​​A — m × n матрица коэффициентов неизвестных, X — n × 1 матрица неизвестных, B — n × 1 матрица, содержащая числа на правая часть уравнения.

Проблема большого значения во многих областях науки состоит в следующем: по квадратной матрице A порядка n, найти n × 1 матрицу X, называемую n -мерный вектор, такой что AX = cX . Здесь c — число, называемое собственным значением, а X — собственный вектор. Существование собственного вектора X с собственным значением c означает, что некоторое преобразование пространства, связанное с матрицей A , растягивает пространство в направлении вектора X в c раз.