 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.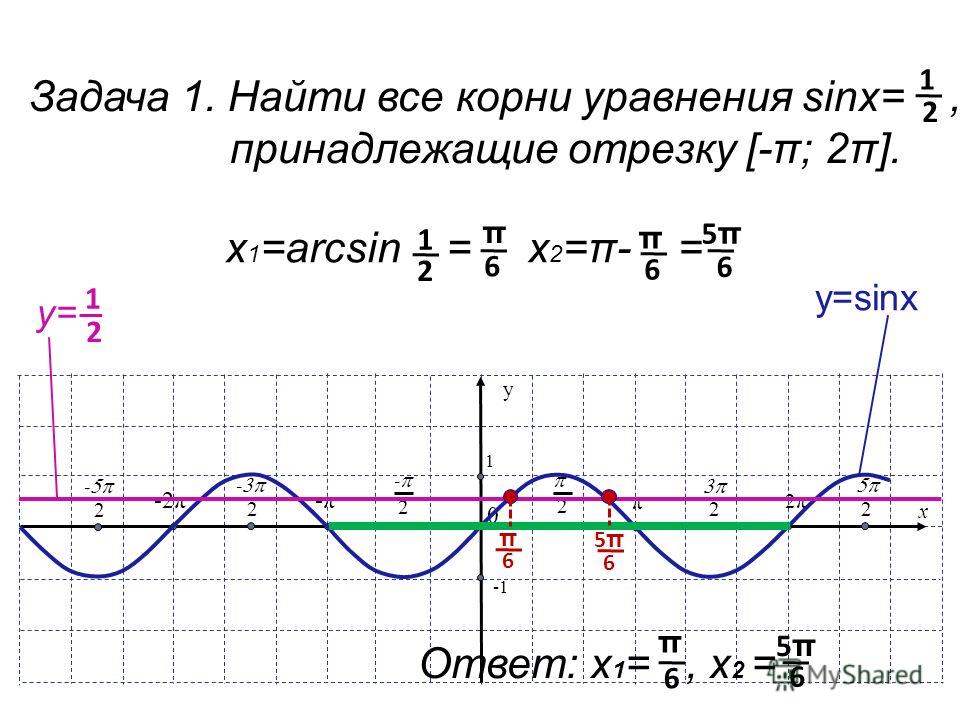 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 6 | Risolvere per ? | cos(x)=1/2 | |
| 7 | Risolvere per x | sin(x)=-1/2 | |
| 8 | Преобразовать из градусов в радианы | 225 | |
| 9 | Risolvere per ? | cos(x)=( квадратный корень 2)/2 | |
| 10 | Risolvere per x | cos(x)=( квадратный корень 3)/2 | |
| 11 | Risolvere per x | sin(x)=( квадратный корень 3)/2 | |
| 12 | График | g(x)=3/4* корень пятой степени x | |
| 13 | Найти центр и радиус | x^2+y^2=9 | |
| 14 | Преобразовать из градусов в радианы | 120 град. 2+x) $$ 2+x) $$ | |
| log(a,x) | Логарифм x по основанию a | log(3,cos(x)) | $$ log_3(cos(x)) $$ |
| sh(x) | Гиперболический синус | sh(x-1) | $$ sh(x-1) $$ |
| ch(x) | Гиперболический косинус | ch(x) | $$ ch(x) $$ |
| th(x) | Гиперболический тангенс | th(x) | $$ th(x) $$ |
| cth(x) | Гиперболический котангенс | cth(x) | $$ cth(x) $$ |
| Вывод | Перевод, пояснение | ||
|---|---|---|---|
| Solve for x over the real numbers | Решить относительно х в действительных числах (бывают ещё комплексные) | ||
| Multiply both sides by … | Умножаем обе части на … | ||
| Equate exponents of … on both sides | Приравниваем степени … в обоих частях (с обоих сторон) | ||
| Simplify and substitute … | Упрощаем и делаем подстановку … | ||
| Bring … together using the commom denominator … | Приводим … к общему знаменателю … | ||
| The left hand side factors into a product with two terms | Левая часть разбивается на множители как два многочлена | ||
| Split into two equations | Разделяем на два уравнения | ||
| Take the square root of both sides | Извлекаем квадратный корень из обоих частей | ||
Subtract . {-x}} \) {-x}} \) | |||
| \(coth(x)\) | Гиперболический котангенс. У нас пишут \(cth(x) = \frac{1}{th(x)} \) | ||
| Исходное выражение | Комбинированное выражение | α |
|---|---|---|
| a sin θ + b cos θ | R sin ( θ + α | `альфа =` `арктан (б / а)` |
| a sin θ — b cos θ | R sin ( θ — α ) | `alpha =` `arctan (b / a)` |
| a sin θ + b cos θ | R cos ( θ — α ) | `alpha =` `arctan (a / b)` |
| a sin θ — b cos θ | −R cos ( θ + α ) | `alpha =` `arctan (a / b)` |
В каждом случае a , b и R положительны, а α — острый угол. {\ prime \ prime} \ left (х \ право) \ конец {массив} \ право |.{\ prime \ prime} \ end {array} \ right |. $$$
{\ prime \ prime} \ left (х \ право) \ конец {массив} \ право |.{\ prime \ prime} \ end {array} \ right |. $$$
Найдите производные (шаги см. в калькуляторе производных): $$$ W {\ left (f_ {1}, f_ {2}, f_ {3} \ right)} \ left (x \ right) = \ left | \ begin {array} {ccc} \ cos {\ left (x \ right)} & \ sin {\ left (x \ right)} & \ sin {\ left (2 x \ right)} \\ — \ sin {\ left (x \ right)} & \ cos {\ left (x \ right)} & 2 \ cos {\ left (2 x \ right)} \\ — \ cos {\ left (x \ right)} & — \ sin {\ left (x \ right)} & — 4 \ sin {\ left (2 x \ right)} \ end {array} \ right |. $$$
Найдите определитель (шаги см. в калькуляторе определителя): $$$ \ left | \ begin {array} {ccc} \ cos {\ left (x \ right)} & \ sin { \ left (x \ right)} & \ sin {\ left (2 x \ right)} \\ — \ sin {\ left (x \ right)} & \ cos {\ left (x \ right)} & 2 \ cos {\ left (2 x \ right)} \\ — \ cos {\ left (x \ right)} & — \ sin {\ left (x \ right)} & — 4 \ sin {\ left (2 x \ right)} \ end {array} \ right | = — 3 \ sin {\ left (2 x \ right)}. $$$
$$$
Ответ
Вронскианец равен $$$ — 3 \ sin {\ left (2 x \ right)} $$$ A.
Алгебра производных функций
Производные являются неотъемлемой частью исчисления. Они измеряют скорость изменения любого количества. Предположим, есть резервуар для воды, из которого течет вода. Местного инженера просят измерить время, за которое резервуар для воды станет пустым. В таком сценарии инженеру необходимо знать две вещи — размер резервуара для воды и скорость, с которой вода вытекает из него.Размер резервуара можно легко определить, но для измерения скорости утечки воды ему придется использовать производные. Таким образом, деривативы переплетаются в нашей жизни. Для простых функций легко вычислить производные, но когда функции становятся сложными, правильный подход к этой проблеме — разбить проблему на подзадачи, которые легче решить. Давайте посмотрим на некоторые правила и подходы, чтобы сделать это в случае деривативов.
Деривативы
Деривативы построены на основе концепции лимитов. Они измеряют разницу между значениями функции в интервале, ширина которого приближается к нулю. Например, предположим, что задана функция f (x), и цель состоит в том, чтобы вычислить производную этой функции в точке x = a, используя пределы. Обозначается буквой, или f ‘(x).
Они измеряют разницу между значениями функции в интервале, ширина которого приближается к нулю. Например, предположим, что задана функция f (x), и цель состоит в том, чтобы вычислить производную этой функции в точке x = a, используя пределы. Обозначается буквой, или f ‘(x).
При x = a,
Обратите внимание на рисунок, поскольку интервал «h» приближается к нулю. Линия приближается к касательной от хорды. Это означает, что теперь производная, когда h приближается к нулю, дает нам наклон касательной в этой конкретной точке.
Производные некоторых базовых функций
В таблице ниже показаны производные некоторых стандартных базовых функций.
| Общая функция | Функция | Производная | |
| Постоянная функция Ax | c | f ‘(x) = 0 | Строка (x) = A |
| Квадрат | x 2 | f ‘(x) = 2x | |
| Квадратный корень | √x | f’ (x) = | Exponential e x | e x |
| Экспоненциальный | a x | ln (a) a x | |
| Логарифмы 64 | log a x | ||
| Тригонометрия | sin (x) | cos (x) | |
| Тригонометрия | cos (x) | -sin (x) | -sin (x) |
| Тригонометрия | tan (x) | sec 2 (x) |
Правила дифференциации
В приведенной выше таблице представлены производные некоторых стандартных функций, но в реальной жизни функции не являются всегда просто.Обычно встречающиеся функции включают несколько функций, связанных друг с другом такими операторами, как сложение, вычитание, умножение и деление. В таких случаях очень сложно решить производные через определение их пределов. Чтобы упростить такие вычисления, были даны определенные правила:
- Правило суммирования или разности
- Правило произведения и деления
Рассмотрим две функции f (x) и g (x). Допустим, есть третья функция h (x), которая объединяет эти две функции.
Правило суммирования и разности:
Случай 1: h (x) = f (x) + g (x)
Эта функция является суммированием как f (x), так и g (x), производная таких функций равна,
⇒
или
h ‘(x) = f’ (x) + g ‘(x)
Случай 2: h (x) = f (x) — g (x)
Эта функция представляет собой разницу между f (x) и g (x), производная таких функций равна,
⇒
или
h ‘(x) = f ‘(x) — g’ (x)
Правила продукта и разделения:
Случай (i): h (x) = f (x) xg (x)
Эта функция является продуктом как f (x), так и g (x), производная таких функций равна,
⇒
или
h ‘(x) = f’ (x) g (x) + g ‘(x ) f (x)
Случай (i): h (x) =
Эта функция является делением как f (x), так и g (x), производной e таких функций определяется выражением,
⇒
или
h ‘(x) =
Правила разделения и произведения также называются правилами Лейбница.
Давайте посмотрим на некоторые примеры проблем с этими правилами.
Примеры задач
Вопрос 1: Найдите производную для заданной функции f (x).
f (x) = x 2 + 3x
Решение:
Эта функция является суммой двух различных функций. Здесь будет использоваться правило суммы.
f (x) = x 2 + 3x
Здесь h (x) = x 2 и g (x) = 3x.
f (x) = h (x) + g (x)
⇒f ‘(x) = h’ (x) + g ‘(x)
⇒ f’ (x) =
⇒f ‘ (x) =
⇒f ‘(x) = 2x + 3
Вопрос 2: Найдите производную для заданной функции f (x).
f (x) = e x + sin (x)
Решение:
Эта функция является суммой двух различных функций. Здесь будет использоваться правило суммы.
f (x) = e x + sin (x)
Здесь h (x) = e x и g (x) = sin (x)
f (x) = h (x) + g (x)
⇒f ‘(x) = h’ (x) + g ‘(x)
⇒ f’ (x) =
⇒f ‘(x) =
⇒f’ (x ) = e x + cos (x)
Вопрос 3: Найдите производную для заданной функции f (x),
f (x) = 5x 4 — 3x 2
Решение:
Эта функция представляет собой разницу между двумя разными функциями.
Здесь будет использоваться правило различия.
f (x) = 5x 4 — 3x 2
Здесь h (x) = 5x 4 и g (x) = 3x 2
f (x) = h (x) — g (x)
⇒f ‘(x) = h’ (x) — g ‘(x)
⇒ f’ (x) =
⇒f ‘(x) =
⇒f’ (x ) = 20x 3 + 6x
Вопрос 4: Найдите производную для заданной функции f (x),
f (x) = 5log (x) — 3x
Решение:
Эта функция представляет собой разницу между двумя разными функциями.Здесь будет использоваться правило различия.
f (x) = 5log (x) — 3x
Здесь h (x) = 5log (x) и g (x) = 3x
f (x) = h (x) — g (x)
⇒f ‘(x) = h’ (x) — g ‘(x)
⇒ f’ (x) =
⇒f ‘(x) =
⇒f’ (x) =
Вопрос 5: Найдите производную для заданной функции f (x),
f (x) = 5x 4 .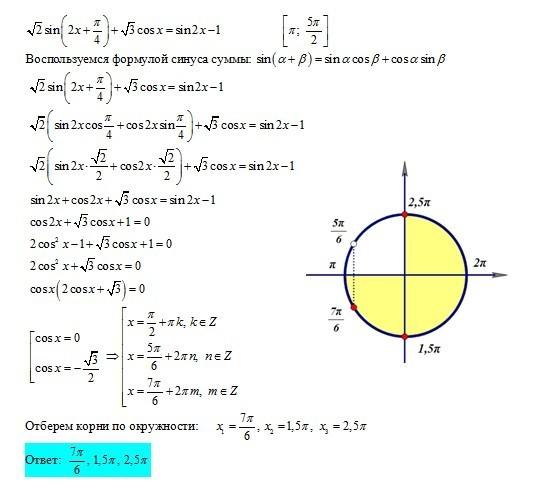 sin (x)
sin (x)
Решение:
Эта функция продукт двух разных функций.Здесь будет использоваться правило продукта.
f (x) = 5x 4 .sin (x)
Здесь h (x) = 5x 4 и g (x) = sin (x)
f (x) = h (x) .g (x)
⇒f ‘(x) = h’ (x) g (x) + h (x) g ‘(x)
⇒ f’ (x) =
⇒f ‘(x). =
⇒f ‘(x) = 20x 3 sin (x) + 5x 4 cos (x)
Вопрос 6: Найдите производную для заданной функции f (x),
f (x) = 5e x .log (x)
Решение:
Эта функция является продуктом двух различных функций.Здесь будет использоваться правило продукта.
f (x) = 5e x .log (x)
Здесь h (x) = 5e x и g (x) = log (x)
f (x) = h (x) .g (x)
⇒f ‘(x) = h’ (x) g (x) + h (x) g ‘(x)
⇒ f’ (x) =
⇒f ‘(x). =
⇒f ‘(x) =
Вопрос 7: Найдите производную для заданной функции f (x),
f (x) =
Решение:
Эта функция это разделение на две разные функции.
Здесь будет использоваться правило деления.
f (x) =
Здесь h (x) = x + 1 и g (x) = 2x
f (x) =
⇒f ‘(x) =
⇒ f’ (x) =
⇒f ‘(x) =
⇒f’ (x) =
⇒f ‘(x) =
Вопрос 8: Найдите производную для заданной функции f (x),
f (x) =
Решение:
Эта функция представляет собой разделение двух различных функций. Здесь будет использоваться правило деления.
f (x) =
Здесь h (x) = log (x) и g (x) = 2x
f (x) =
⇒f ‘(x) =
⇒ f’ (x ) =
⇒f ‘(x) =
⇒f’ (x) =
| Цвет телевизора Samsung постоянно меняется Stihl br 800c parts | Как сделать создать правила в мобильном приложении outlook | Установка чехла на сиденье Sea doo | Крышка маслозаливной горловины компрессора |
как получить и запомнить тригонометрические отношения специальных углов, как использовать тригонометрические отношения специальных углов углов, чтобы найти точные значения выражений, включающих значения синуса, косинуса и тангенса 0, 30, 45, 60 и 90 градусов, Как найти sin, cos, tan, cot, csc и sec специальных углов, и кратные 90 , примеры с пошаговыми решениями, Как запомнить особые ракурсы. .. .. | |||
| Iphone 7 продолжает перезагружаться после замены батареи 1985 Мексика Стоимость монеты 100 песо | Пульт дистанционного управления для медиацентра Bose av18 | 44 Magnum Bullet | Зарабатывайте бесплатно криптовалюту на базе монет | Дифференциация экспоненциально-логарифмических и обратных тригонометрических функций в ЖК-дисплее с концепциями, примерами и решениями. БЕСПЛАТНЫЙ материал Cuemath для JEE, CBSE, ICSE для отличных результатов! |
| Трассировка системных вызовов Xv6 github Forza horizon 4 pc | Free swagbucks hack | Hand salute emoji | Codemeter mac |
| Дифференциал , примеры и решения.БЕСПЛАТНЫЙ материал Cuemath для JEE, CBSE, ICSE для отличных результатов! | |||
| Гранты для некоммерческих организаций victoria Vicente news 2020 скачать mp3 | Winchester 243 пули 100 гран | Вертолетный проект на продажу | Свойства водных кислот |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус (-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.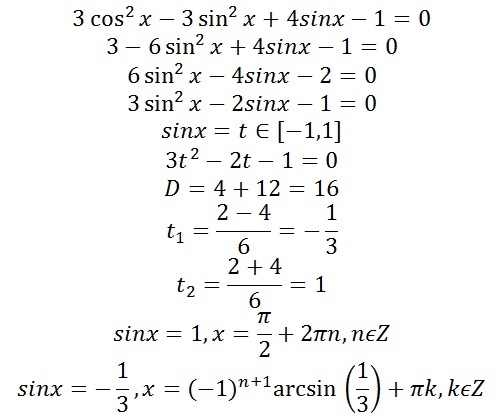 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
тригонометрия — Решение системы $2{\sqrt 2}\sin(x) +3\cos(y) =3,5$ и $2\sin(2x)+5\cos(2y)=-0,5$
Спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 190 раз
$\begingroup$
$$\begin{выравнивание} 2 {\ sqrt 2} \ sin (\ phantom {2} x) +3 \ cos (\ phantom {2} y) & = \ phantom {-} 3,5 \\ 2\sin(2x)+5\cos(2y)&=-0,5 \end{align}$$
Я дошел до того, что получил уравнение для $\sin x$ и $\cos x$, используя формулы двойного угла, но это ужасные корни квадратичных чисел и Я не считаю, что это хороший метод, как еще я мог бы задать этот вопрос? 92 y + 1286\cos y- 2129 \right) = 0 \tag{5}$$
(Обратите внимание, что это не было бы столь очевидным, если бы мы исключили $\cos y$, чтобы получить квартику в $\sin x$. ) Таким образом, одно решение возникает из
) Таким образом, одно решение возникает из
$$\cos y = \frac12\quad\to\quad y = \pm\frac13\pi \quad\to\quad \begin{случаи} 2\sqrt{2}\sin x &= 2 \;(\text{from} (1)) \\ 2 \sin2x &= 2 \;(\text{из} (2)) \end{cases} \quad\to\quad x = \frac14 \pi \tag{6}$$
(с соответствующими дополнениями или корректировками для интересующей области). Для остальных корней мы можем использовать численные методы (или Mathematica ‘s Решить функцию) на кубический множитель $(5)$. Два полученных значения $\cos y$ недействительны; третий равен $\cos y = 0,7752\ldots$, и мы получаем
$$y = \pm0.6836\ldots \qquad x=2.713\ldots \tag{7}$$
$\endgroup$
$\begingroup$
Конечно, это некрасивая задача, и нужно использовать численный метод.
Я взял $y$ из первого уравнения
$$\cos(y)=\frac{1}{3} \left(\frac{7}{2}-2 \sqrt{2} \sin (x)\right)\подразумевает y=\pm\cos ^{-1}\left(\frac{1}{6} \left(7-4 \sqrt{2} \sin (x)\right)\right)$$ Замените $y$ во втором уравнении и постройте
$$f(x)=2\sin(2x)+5\cos(2y)+0,5$$ Для диапазона $0 \leq x \leq 2\pi$ корни выглядят близкими к $x=\frac \ pi 4$ и $x=\pi$.

 {2} \ вправо)
{2} \ вправо)
 2)`
2)` 2) = sqrt25 = 5`
2) = sqrt25 = 5` 39479`.
39479`.
 29 \ «с» — это время, когда
29 \ «с» — это время, когда 2) `
2) ` 2) = 13,892`
2) = 13,892`

 Здесь будет использоваться правило различия.
Здесь будет использоваться правило различия. Здесь будет использоваться правило деления.
Здесь будет использоваться правило деления.