Медиана (Median) · Loginom Wiki
Синонимы: Медиана статистическая, Непараметрическая средняя
Разделы: Метрики
Медиана (от лат. mediana — средина, срединный) — статистическая характеристика распределения случайной величины. Наряду с модой и математическим ожиданием медиана определяет центр распределения, т.е. область, в которой его значения наиболее вероятны.
На практике это означает, что если признак некоторого объекта принимает значение, близкое к медианному, то оно является типичным для данной выборки. Если же значение оказывается далёким от медианы (как говорят, расположено в «хвосте» распределения), то у аналитика возникает повод задуматься о том, какими закономерностями исследуемого процесса вызвано такое отклонение и не является ли оно выбросом или аномальным значением.
Если определять медиану в контексте распределения случайной величины, то она представляет собой значение, которое делит площадь под кривой функции распределения на две равные части.
M_{e})»>P(x<Me)=P(x>Me),
где x — случайная величина, Me — медиана.
Если распределение симметричное, то мода, математическое ожидание и медиана совпадают. Если симметрия распределения нарушается, то медиана смещается от моды в сторону более длинного «хвоста». При этом медиана всегда меньше математического ожидания.
Медиана относится к классу непараметрических статистик, поскольку для её определения не требуется каких-либо предположений о распределении случайной величины, для которой она вычисляется. Медиана имеет смысл только для упорядочиваемых данных, значения которых могут быть ранжированы.
Если случайная величина x задана не функцией распределения вероятности P(x), а набором выборочных значений признака (дискретным рядом), то медиана вычисляется следующим образом:
Упорядочить (расположить в порядке неубывания) значения набора данных: x1≤x2≤⋯≤x(n−1)≤xn, где n — количество элементов выборки.

Определить номер медианного элемента выборки по формуле NME=(n+1)/2.
Полученное значение будет точно показывать, где находится элемент ряда, значение которого является медианным.
Например, пусть задана последовательность [7, 14, 10, 12, 16, 9, 11]. Для вычисления медианы упорядочим её: [7, 9, 10, 11, 12, 14, 16]. Тогда номер медианного элемента NME=(7+1)/2=4, следовательно, медиана равна 11.
Если n чётное, то номер медианного элемента оказывается дробным. Например, при n=8 номер медианного элемента окажется NME=(7+1)/2=4.5. В этом случае берут значения 4-го и 5-го элементов и вычисляют их среднее. Т.е. медиана в случае нечётного размера выборки определяется как среднее двух срединных значений ряда её ранжированных элементов. Легко увидеть, что номер первого усредняемого значения при чётном n будет NME+0.5, а второго NME−0.5.
В анализе данных медиана может использоваться как альтернатива среднего значения, устойчивая к выбросам и аномальным значениям. Действительно, из-за ранжирования аномально большие и аномально низкие значения всегда будут оказываться в начале или конце ряда и никогда не станут медианными.
Действительно, из-за ранжирования аномально большие и аномально низкие значения всегда будут оказываться в начале или конце ряда и никогда не станут медианными.
Медиана является порядковой статистикой распределения и может быть выражена через другие порядковые статистики (т.е. получаемые при ранжировании). Она является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.
В Loginom существует специализированный обработчик группировка, который позволяет объединять записи избранных полей в группы, а для оставшихся полей вычислять статистические показатели (медиану, сумму, среднее, минимум и т.д.). А также визуализаторы статистика и качество данных, в перечень показателей которых включена медиана.
Среднее арифметическое, мода и медиана в математической статистики с примерами
- Предмет, цели и методы математической статистики
- Метод выборочных исследований
- Средняя арифметическая, простая и взвешенная
- Мода и медиана
- Примеры
Предмет, цели и методы математической статистики
Начиная с XVIII века, в общем направлении статистических исследований начинает активно формироваться математическая статистика.
Математическая статистика – раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений.
В зависимости от предмета исследований математическая статистика делится на:
- статистику чисел;
- многомерный статистический анализ;
- анализ функций (процессов) и временных рядов;
- статистику объектов с нечисловыми характеристиками.
В зависимости от цели и методов исследований математическая статистика делится на: описательную статистику; теорию оценивания; теорию проверки гипотез.
| Описательная статистика | Теория оценивания | Теория проверки гипотез | |
| Цель | Обработка и систематизация эмпирических данных | Оценивание ненаблюдаемых данных и сигналов от объектов наблюдения на основе наблюдаемых данных | Обоснование предположений о виде распределения и свойствах случайной величины |
| Методы | 1. 2. Количественное описание с помощью статистических показателей. | 1. Параметрические методы (наименьших квадратов, максимального правдоподобия и др.). 2. Непараметрические методы. | 1. Последовательный анализ. 2. Статистические критерии. |
Метод выборочных исследований
Статистика получила признание в различных областях человеческой деятельности благодаря заметной экономии времени и прочих ресурсов. Её основная идея: не нужно измерять всё, измерьте только часть всего и сделайте предположение об остальном.
«Всё» в статистике называется генеральной совокупностью.
«Часть всего», которую мы тщательно исследуем, называется выборкой.
Метод выборочных исследований – способ определения свойств группы объектов (генеральной совокупности) на основании статистического исследования её части (выборки).
Например, чтобы оценить средние размеры апельсина, который продаётся в магазине в декабре, необязательно денно и нощно мерить все апельсины во всех ящиках (сколько же для этого нужно времени и людей?!). K n_i , i = \overline{1,K} $$
K n_i , i = \overline{1,K} $$
где K – количество групп с повторяющимися вариантами, $x_i$ — значение варианты в -й группе, $n_i$ – частота варианты $x_i$.
Например:
Рассматриваем тот же ряд оценок: 5,4,3,5,4,4,5,4,3,5,5,4,3,5,4,4 и составляем таблицу:
x_i
3
4
5
Σ
n_i
3
7
6
16
x_i n_i
9
28
30
67
$$ x_cp = \frac{3\cdot3+4\cdot7+5\cdot6}{3+7+6} ≈ 4,2 $$
Вычисления заметно упростились.
Мода и медиана
Мода дискретного вариационного ряда – это варианта с максимальной частотой. Мод может быть несколько. Тогда говорят, что ряд мультимодальный.
В примере с оценками по алгебре мода $M_0 = 4$ — эта оценка встречается чаще всего, её частота равна 7.
В примере с оценками по алгебре N = 16 — четное. $m = \frac{N}{2} = 8 $.
Сортируем ряд оценок по возрастанию: 3,3,3,4,4,4,4, 4,4, 4,5,5,5,5,5,5
$$ x_8 = 4, x_9 = 4 \Rightarrow M_e = \frac{4+4}{2} = 4 $$
Примеры
Пример 1. В исследовании месячных доходов десяти человек были получены следующие данные: 200,100,300,300,1000,5000,100,200, 300,400 (дол.).
В исследовании месячных доходов десяти человек были получены следующие данные: 200,100,300,300,1000,5000,100,200, 300,400 (дол.).
Найдите выборочную среднюю, моду и медиану.
Почему при оценке доходов мода и медиана предпочтительней выборочной средней?
Составим таблицу:
$x_i$, дол.
100
200
300
400
1000
5000
$\sum$
$n_i$, чел.
2
2
3
1
1
1
10
$x_i n_i$
200
400
900
1000
5000
7900
Выборочная средняя:$ x_{cp} = \frac{7900}{10} = 790$ (дол.)
Мода: $M_o$ = 300 (дол.) – максимальная частота 3
Медиана:
100, 100, 200, 200, 300, 300, 300, 400, 1000, 5000
$$ m = \frac{10}{2} = 5, x_5 = x_6 = 300, M_e = \frac{300+300}{2} = 300 (дол.) $$
Выборочная средняя не отражает доходов большей части людей в выборке, поскольку даже один человек с большими доходами может резко сместить оценку вправо. Мода и медиана хорошо отражают доходы большей части людей в выборке.
Мода и медиана хорошо отражают доходы большей части людей в выборке.
Пример 2. Исследовалось время решения задачи. В исследовании принимало участие 20 человек, из них двое задачу не решили. Время решения остальных участников:
$x_i$, мин
10
15
20
25
30
n_i, чел
2
5
5
4
2
Найдите выборочную среднюю, моду и медиану.
При подборе задач для контрольной работы, сколько времени следует отвести на решение подобной задачи?
Проведём вычисления:
$x_i$
10
15
20
25
30
$\sum$
$n_i$, чел
2
5
5
4
2
18
$x_i n_i$
20
75
100
100
60
355
$$x_cp = \frac{355}{18} ≈ 19,7 мин $$
В выборке 2 моды: $M_{o1}$ = 15 мин, $M_{o2}$ = 20 мин
Положение медианы: $m = \frac{N}{2} = \frac{18}{2} = 9, x_9 = x_10 = 20, Me = 20$ мин
Средняя, одна из мод и медиана равны 20 мин.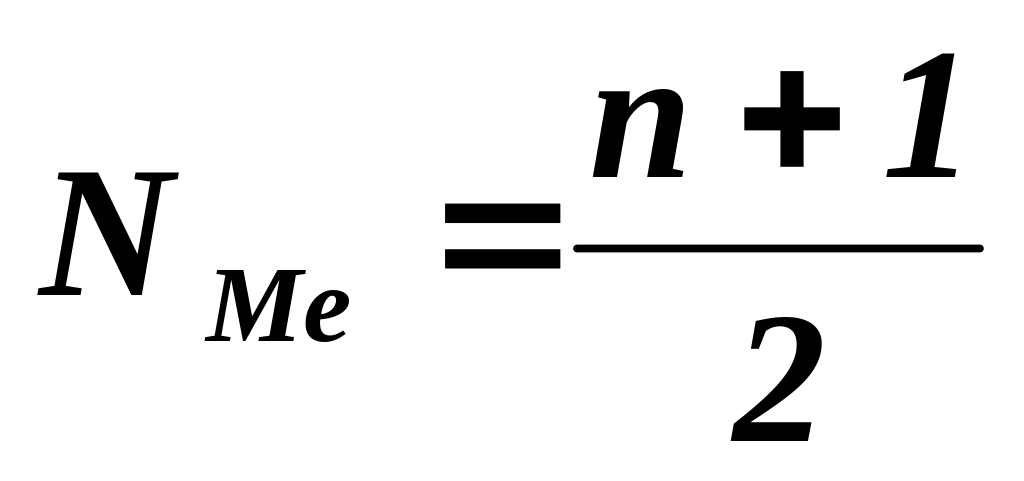 Поэтому при составлении контрольной следует отвести на подобную задачу 20 мин.
Поэтому при составлении контрольной следует отвести на подобную задачу 20 мин.
Пример 3. работа по геометрии показала следующие результаты:
$x_i$
2
3
4
5
$n_i$, чел
5
22
10
2
Найдите выборочную среднюю, моду и медиану.
Что вы можете сказать об уровне понимания материала?
Проведём вычисления:
$x_i$
2
3
4
5
$\sum$
$n_i$
5
22
10
2
39
$x_i n_i$
10
66
40
10
126
$$x_cp = \frac{126}{39} ≈ 3,2$$
Мода: $M_o$ = 3 — эта оценка получена 22 раза
Положение медианы: $m = ⌈ \frac{N}{2}⌉ = ⌈\frac{39}{2}⌉ = 20, x_{20} = 3, Me = 3$
Средняя, мода и медиана равны 3.
Уровень понимания удовлетворительный, «на троечку».
Медианные понятия и определения
По вашему доходу вы входите в верхнюю половину всех получателей дохода? Вы можете найти ответ, сравнив свой доход со средним доходом.
Но что такое медиана? Это «среднее значение» в группе после того, как все наблюдения расположены в порядке возрастания, т. е. от меньшего к большему. По крайней мере половина наблюдений равна или меньше медианы, и по крайней мере половина измерений равна или больше медианы. Медиана отделяет нижнюю половину наблюдений от верхней половины.
Как найти медиану?
Шаг 1: Имея набор данных (например, заработную плату), расположите числа в порядке возрастания , т. е. от меньшего к большему.
Шаг 2:
Если число наблюдений нечетное , число в середине списка является медианой. Это можно найти, взяв значение (n+1)/2 -го члена, где n — количество наблюдений. В противном случае, если количество наблюдений равно даже , то медиана представляет собой простое среднее двух средних чисел.
В расчетах медиана представляет собой простое среднее n/2 -го и (n/2 + 1) -го членов.
Поскольку имеется четыре наблюдения (т. е. четное число), медиана представляет собой простое среднее 2-го и 3-го самых низких заработных плат людей. Следовательно,
Медиана = ½ (заработная плата лица D + заработная плата лица C)
= ½ (3400 + 5000) = 4200 долларов США.
Пример 1: Кто посередине? (Нечетное число наблюдений)
Чтобы сравнить возрастной профиль своих сотрудников с возрастным профилем других компаний отрасли, ваша компания Middle World Co. попросила вас рассчитать средний возраст ваших коллег по работе.
Каков средний возраст этих девяти рабочих?
Решение: Поскольку число наблюдений нечетное, а возраст расположен от самого младшего к самому старшему (т. не нанимает новых рабочих и рабочие не увольняются, возраст Люциуса всегда будет средним, независимо от того, сколько лет прошло.
Пример 2: Сравнение заработной платы (четное число наблюдений)
Предположим, у нас есть месячная заработная плата 10 сотрудников компании. Как бы вы нашли медианную заработную плату?
Решение: Обратите внимание, что мы расположили их заработную плату от самой низкой к самой высокой. Этот рейтинг поможет нам определить медиану. Используя метод, введенный ранее, медиана вычисляется путем взятия простого среднего из (n/2)-го = (10/2)-го = 5-го и (n/2 + 1)-го = (10/2+). 1)-е = 6-е наблюдения.
Следовательно, медиана равна
Чем медиана отличается от среднего?
Обратите внимание, что среднее значение составляет 7 214 долларов США, что намного выше среднего значения. Эта разница в значениях показывает, что на медиану не влияет небольшое количество экстремальных значений. (Экстремальные значения здесь, или выбросы, составляют 20 000 и 25 000 долларов США. )
)
Что это такое и как его рассчитать, с примерами
Что такое медиана?
Медиана — это среднее число в отсортированном, восходящем или нисходящем списке чисел, и оно может быть более информативным для этого набора данных, чем среднее значение. Это точка, выше и ниже которой падает половина (50%) наблюдаемых данных, и, таким образом, она представляет собой среднюю точку данных.
Медиану часто сравнивают с другими описательными статистическими данными, такими как среднее (среднее), мода и стандартное отклонение.
Ключевые выводы
- Медиана — это среднее число в отсортированном списке чисел, которое может быть более информативным для этого набора данных, чем среднее значение.
- Медиана иногда используется вместо среднего, когда в последовательности есть выбросы, которые могут исказить среднее значение значений.
- Если имеется нечетное количество чисел, медианное значение — это число, которое находится в середине, с одинаковым количеством чисел ниже и выше.

- Если в списке четное количество чисел, необходимо определить среднюю пару, сложить ее и разделить на два, чтобы найти медианное значение.
- В нормальном распределении медиана совпадает со средним значением и модой.
Понимание медианы
Медиана — это среднее число в отсортированном списке чисел. Чтобы определить среднее значение в последовательности чисел, числа должны быть сначала отсортированы или расположены в порядке значений от наименьшего к наибольшему или от наибольшего к наименьшему. Медиану можно использовать для определения приблизительного среднего или среднего значения, но ее не следует путать с фактическим средним значением.
- Если имеется нечетное количество чисел, медианным значением является число, которое находится в середине, с одинаковым количеством чисел ниже и выше.
- Если в списке четное количество чисел, необходимо определить среднюю пару, сложить ее и разделить на два, чтобы найти медианное значение.

Медиана иногда используется вместо среднего, когда в последовательности есть выбросы, которые могут исказить среднее значение. Медиана последовательности может меньше зависеть от выбросов, чем среднее значение.
Пример медианы
Чтобы найти медианное значение в списке с нечетными числами, нужно найти число, которое находится в середине с одинаковым количеством чисел по обе стороны от медианы. Чтобы найти медиану, сначала расположите числа по порядку, обычно от меньшего к большему.
Например, в наборе данных {3, 13, 2, 34, 11, 26, 47} порядок сортировки становится {2, 3, 11, 13, 26, 34, 47}. Медиана — это число в середине {2, 3, 11, 13 , 26, 34, 47}, что в данном случае равно 13, поскольку с каждой стороны по три числа.
Чтобы найти медианное значение в списке из даже чисел, нужно определить среднюю пару, сложить их и разделить на два. Опять же, расположите числа в порядке от меньшего к большему.
Например, в наборе данных {3, 13, 2, 34, 11, 17, 27, 47} порядок сортировки становится {2, 3, 11, 13, 17, 27, 34, 47}. Медиана — это среднее двух чисел в середине {2, 3, 11, 13 , 17 , 26 34, 47}, что в данном случае равно пятнадцати {(13 + 17) ÷ 2 = 15}.
Медиана тесно связана с квартилями или делением наблюдаемых данных на четыре равные части. Медиана будет центральной точкой, при этом первые два квартиля окажутся ниже нее, а вторые два выше нее. Другие способы группировки данных включают квинтиль (в пяти разделах) и децили (в 10 разделах).
Как рассчитать медиану?
Медиана — это среднее значение в наборе данных. Во-первых, организуйте и упорядочите данные от меньшего к большему. Чтобы найти среднее значение, разделите количество наблюдений на два. Если имеется нечетное количество наблюдений, округлите это число в большую сторону, и значение в этой позиции будет медианой.


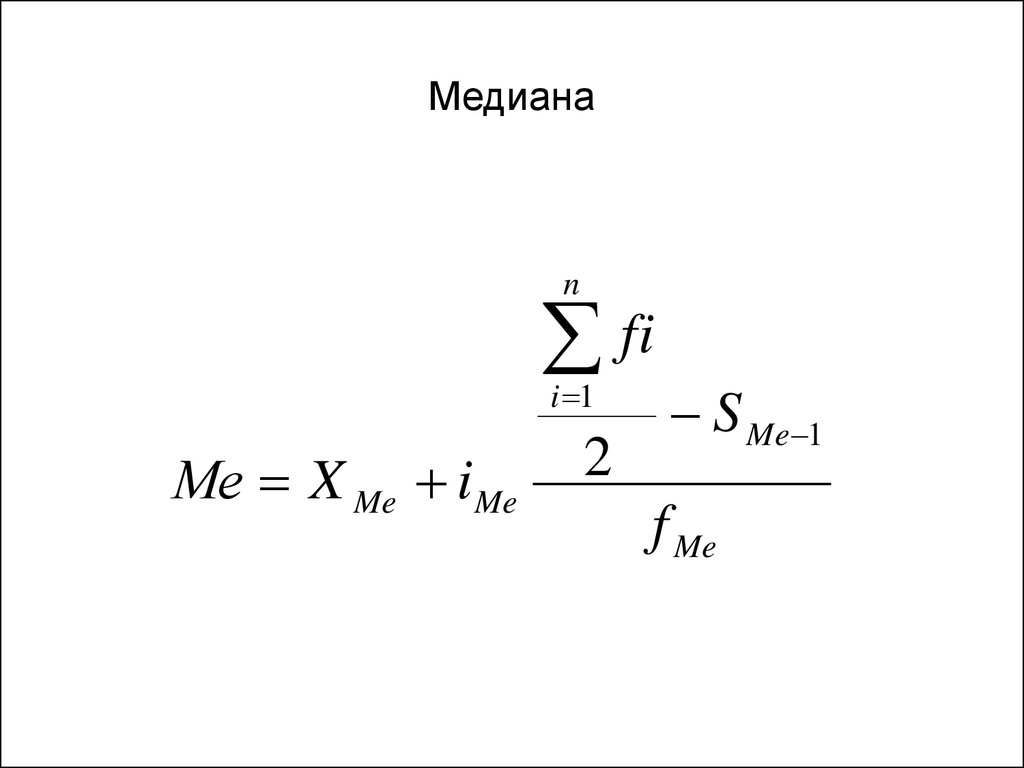 Наглядное представление в форме графиков и таблиц.
Наглядное представление в форме графиков и таблиц. В расчетах медиана представляет собой простое среднее n/2 -го и (n/2 + 1) -го членов.
В расчетах медиана представляет собой простое среднее n/2 -го и (n/2 + 1) -го членов.
