Тангенс 6 градусов: Тангенс 6 равен чему? tg(6) = ?

alexxlab / / Разное

Содержание

Тангенс — что это такое? Таблица тангенсов и котангенсов

Тангенс (tg) — это отношение синуса к косинусу (tgα = sinα / cosα). Либо отношение противолежащего катета (дальнего/противоположного) к прилежащему (который находится рядом с углом).

В этом треугольнике тангенс угла вычисляется по этой формуле:

Обратите внимание, что в вычислении принимают участие только катеты, гипотенузы здесь нет (противолежащий делится на прилежащий — это тангенс острого угла прямоугольного треугольника).

Например:

Вычислите длину стороны BC, зная, что tan α = 0,4:

tan α = противолежащий катет / прилежащий катет = BC / AB = x / 15 <=>

<=> x / 15 = 0,4 <=> x = 15 * 0,4 <=> x = 6

Ответ: BC = 6 см.

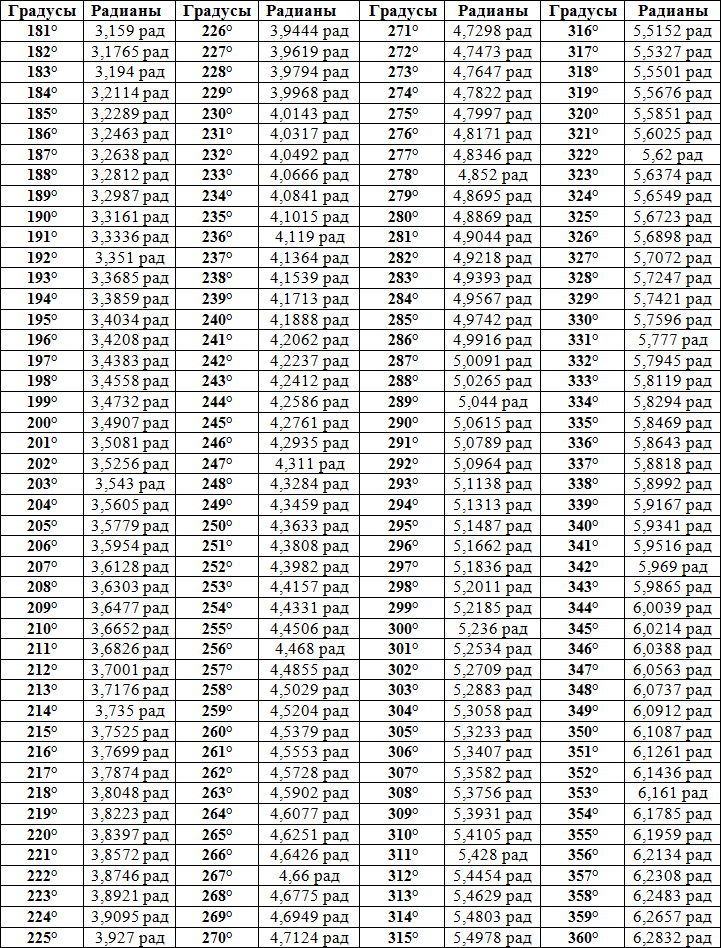
Таблица тангенсов и котангенсов (главных углов от 0° до 360°)

α градусов0°30°45°60°
90°		180°270°360°
α радиан0π/6π/4π/3π/2π3π/22π
tg α0√3/31√3–0–0
ctg α–√31√3/30–0–

Основные тригонометрические тождества

Что такое синус?

Синус угла (sin) — это отношение противолежащего катета (который находится напротив угла) к гипотенузе (самой длинной стороне, находится напротив прямого угла).

В нашем примере sin α = BC/AC.

Что такое косинус?

Косинус угла (cos) — это отношение прилежащего катета (находится рядом с углом) к гипотенузе (самой длинной стороне, находится напротив прямого угла). В нашем примере cos α = AB/AC.

Что такое котангенс?

Котангенс угла (ctg) — это отношение прилежащего катета (который находится рядом с углом) к противолежащему (напротив угла). В нашем примере ctg α = AB / BC. Обратите внимание, что котангенс — это как «тангенс наоборот» (прилежащий делится на противолежащий), т. е. ctg α = AB / BC, а tg α = BC / AB (противолежащий делится на прилежащий).

Что такое секанс?

Секанс (sec или sec x) — это отношение гипотенузы (самой длинной стороны, напротив прямого угла) к прилежащему катету (рядом с углом) острого угла в прямоугольном треугольнике. Ещё секанс определяется формулой:

Что такое гипотенуза и катет?

Гипотенуза — это та сторона, которая находится напротив прямого угла (она самая длинная), в нашем треугольнике это сторона AC.

Катеты — это две другие стороны, которые находятся рядом с прямым углом, в нашем треугольнике это стороны BC и AB:

Узнайте про Теорему Пифагора, Теорему косинусов и Гиперболу в математике

Дата обновления 08/10/2020.

Другие значения и понятия, которые могут вас заинтересовать

  • Гипотенуза
  • Теорема Пифагора
  • Теорема косинусов
  • Аксиома
  • Производная
  • Интеграл
  • Антонимы
  • Гипербола в математике
  • Трансцендентность
  • Магнитное поле

Узнай Что Такое: узнайте значения, понятия и определения.

ПоследниеПопулярныеКонтактыПолитика КонфиденциальностиО нас

2018 — 2023 © 7Graus

Вычислить и найти тангенс онлайн

Пример решили: 79359 раз Сегодня решили: 0 раз

Введите градусы или радианы

Угол Градусы (°)Радианы (rad)


Вычисление тангенса

Скачать решение в PDF

Порекомендуйте наш сервис друзьям

Вконтакте

Facebook

Twitter

Одноклассники

Google+

В прямоугольном треугольнике с острым углом α справедливо следующее соотношение:

тангенс угла α равен отношению противолежащего катета к прилежащему.

Формула вычисления тангенса:

$$ tg \, \color{red}{ \alpha } = { b \over a} $$

График функции y = tan(x):

Примеры решений

  1. Один из катетов прямоугольного треугольника равен 25 см. Вычислите длину второго катета, если прилежащий к известному катету угол равен 36º. {\circ} $$.

    Ответ:

    $$ tg \alpha = 1 $$

Попробуйте другие сервисы

  • Перевод градусов в радианы

  • Вычисление косинуса

  • Вычисление синуса

  • Вычисление котангенса

  • Вычисление секанса

История решений

    Тан 6 градусов — Найдите значение Тан 6 градусов

    LearnPracticeDownload

    Значение Тан 6 градусов равно 0,1051042. . . . Тангенс 6 градусов в радианах записывается как тангенс (6° × π/180°), то есть тангенс (π/30) или тангенс (0,104719…). В этой статье мы обсудим методы определения значения тангенса 6 градусов на примерах.

    • Tan 6° в десятичном формате: 0,1051042. . .
    • Тан (-6 градусов): -0,1051042. . .
    • Tan 6° в радианах: tan (π/30) или tan (0,1047197 . . .)

    Сколько стоит Тан 6 градусов?

    Значение тангенса 6 градусов в десятичной системе равно 0,105104235. . .. Tan 6 градусов также можно выразить, используя эквивалент данного угла (6 градусов) в радианах (0,10471 . . .)

    Мы знаем, используя преобразование градусов в радианы, θ в радианах = θ в градусах × (пи/ 180°)

    ⇒ 6 градусов = 6° × (π/180°) рад = π/30 или 0,1047. . .
    ∴ тангенс 6° = тангенс (0,1047) = 0,1051042. . .

    Объяснение:

    Для тангенса 6 градусов угол 6° лежит между 0° и 90° (первый квадрант). Поскольку функция тангенса положительна в первом квадранте, значение тангенса 6° = 0,1051042. . .
    Поскольку функция тангенса является периодической функцией, мы можем представить тангенс 6° как тангенс 6 градусов = тангенс (6° + n × 180°), n ∈ Z.
    ⇒ тангенс 6° = тангенс 186° = тангенс 366° и так далее.
    Примечание: Поскольку тангенс является нечетной функцией, значение тангенса (-6°) = -тангенса (6°).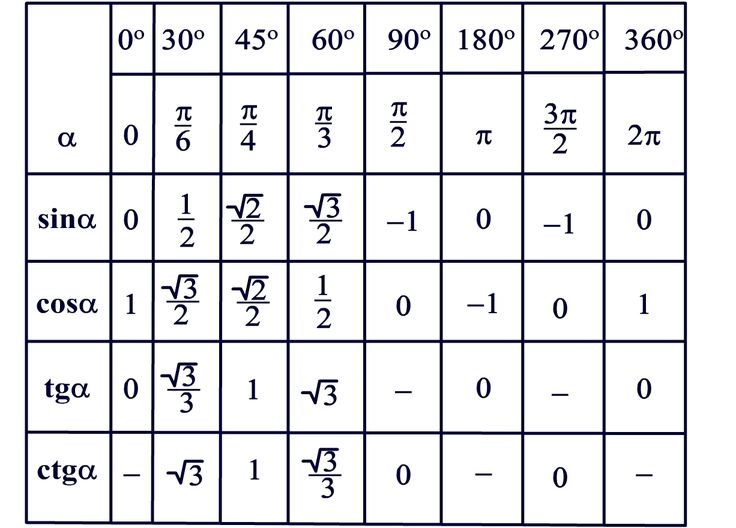

    Методы определения значения Tan 6 градусов

    Функция тангенса положительна в 1-м квадранте. Значение тангенса 6° составляет 0,10510. . .. Мы можем найти значение тангенса 6 градусов по:

    • Используя единичный круг
    • Использование тригонометрических функций

    Tan 6 градусов с помощью единичной окружности

    Чтобы найти значение tan 6 градусов с помощью единичной окружности:

    • Поверните ‘r’ против часовой стрелки, чтобы образовать угол 6° с положительной осью x.
    • Тангенс 6 градусов равен координате y (0,1045), деленной на координату x (0,9945) точки пересечения (0,9945, 0,1045) единичной окружности и r.

    Следовательно, значение тангенса 6° = y/x = 0,1051 (приблизительно).

    Тангенс 6° в терминах тригонометрических функций

    Используя формулы тригонометрии, мы можем представить тангенс 6° как:

    • sin(6°)/cos(6°)
    • ± sin 6°/√(1 — sin²(6°))
    • ± √(1 — cos²(6°))/cos 6°
    • ± 1/√(косек²(6°) — 1)
    • ± √(сек²(6°) — 1)
    • 1/кровать 6°

    Примечание. Поскольку 6° лежит в 1-м квадранте, окончательное значение тангенса 6° будет положительным.

    Мы можем использовать тригонометрические тождества для представления tan 6° как

    • cot(90° — 6°) = cot 84°
    • -кроватка(90° + 6°) = -кроватка 96°
    • -тангенс (180° — 6°) = -тангенс 174°

    ☛ Также проверьте:

    • загар 30 градусов
    • загар 0 градусов
    • загар 270 градусов
    • загар 67 градусов
    • загар 130 градусов
    • загар 73 градуса

    Примеры использования Tan 6 градусов

    1. Пример 1. Найдите значение тангенса 2 (6°)/тангенса 3 (174°).

      Решение:

      Используя тригонометрические тождества, мы знаем, что tan(6°) = -tan(180° — 6°) = -tan 174°.
      ⇒ тангенс (6°) = -тангенс (174°)
      ⇒ Значение тангенса 2 (6°)/тангенса 3 (174°) = -2/3

    2. Пример 2: Используя значение тангенса 6°, найдите: (sec²(6°) — 1).

      Решение:

      Мы знаем, (sec²(6°) — 1) = (tan²(6°)) = 0,011
      ⇒ (сек²(6°) — 1) = 0,011

    3. Пример 3: Найдите значение tan 6°, если cot 6° равно 9,5143.

      Решение:

      Так как tan 6° = 1/cot 6°
      ⇒ тангенс 6° = 1/9,5143 = 0,1051

    перейти к слайдуперейти к слайдуперейти к слайду

     

    Готовы увидеть мир глазами математика?

    Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

    Запишитесь на бесплатный пробный урок

    Часто задаваемые вопросы о Tan 6 Degrees

    Что такое Tan 6 Degrees?

    Тангенс 6 градусов — значение тангенса тригонометрической функции для угла, равного 6 градусам. Значение тангенса 6° составляет 0,1051 (приблизительно).

    Как найти тангенс 6° в терминах других тригонометрических функций?

    Используя формулу тригонометрии, значение тангенса 6° может быть выражено через другие тригонометрические функции следующим образом:

    • sin(6°)/cos(6°)
    • ± sin 6°/√(1 — sin²(6°))
    • ± √(1 — cos²(6°))/cos 6°
    • ± 1/√(cosec²(6°) — 1)
    • ± √(сек²(6°) — 1)
    • 1/кровать 6°

    ☛ Также проверьте: тригонометрическую таблицу

    Каково значение Tan 6° в пересчете на Cosec 6°?

    Поскольку функция тангенса может быть представлена ​​с помощью функции косеканса, мы можем записать тангенс 6° как 1/√(cosec²(6°) — 1). Значение cosec 6° равно 9,56677.

    Как найти значение Тан 6 градусов?

    Значение тангенса 6 градусов можно рассчитать, построив угол 6° с осью x, а затем найдя координаты соответствующей точки (0,9945, 0,1045) на единичной окружности. Значение tan 6° равно координате y (0,1045), деленной на координату x (0,9945). ∴ тангенс 6° = 0,1051

    Каково значение тангенса 6 градусов с точки зрения Cos 6°?

    Мы знаем, что, используя тригонометрические тождества, мы можем записать тангенс 6° как √(1 — cos²(6°))/cos 6°. Здесь значение cos 6° равно 0,994521.

     

    Скачать БЕСПЛАТНЫЕ учебные материалы

    Тригонометрия

    Рабочие листы по математике и
    наглядный учебный план

    Калькулятор — tan(0.6) — Solumaths

    Тан, расчет онлайн

    Резюме:

    Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

    загар онлайн

    Описание:

    Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить желтовато-коричневый , синус и косинус угла через одноименные функции.

    Тангенс тригонометрической функции отметил тангенс , позволяет вычислить тангенс угла онлайн , можно использовать разные угловые единицы:

    • радиан, который является угловой единицей по умолчанию,
    • градусов или
    • град.

    1. Расчет касательной

      2. Тангенс, вычисляющий угол в радианах

      Калькулятор тангенса позволяет через функцию загара вычислить онлайн тангенс угла в радианах, вы должны сначала выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.

      Чтобы вычислить тангенс онлайн от `pi/6`, введите tan(`pi/6`), после вычисления результат `sqrt(3)/3` возвращается.

      Обратите внимание, что функция касательной может распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.

      Вычисление тангенса угла в градусах

      Чтобы вычислить тангенс угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

      Чтобы вычислить тангенс 60, введите tan(60), после вычисления Возвращается результат `sqrt(3)`.

      Вычисление тангенса угла в градусах

      Чтобы вычислить тангенс угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

      Чтобы вычислить тангенс 50, введите tan(50), после вычисления, возвращается результат `1`.

      Обратите внимание, что функция касательной может распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.

    2. Специальные значения тангенса

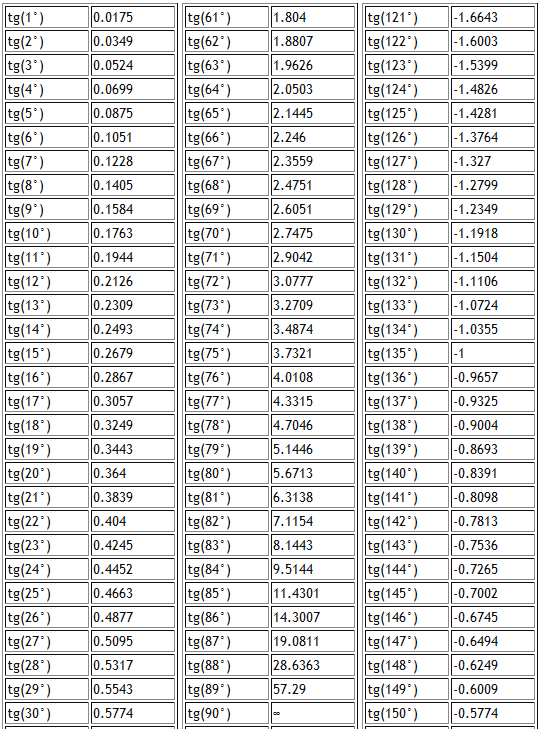
      3. Тангенс допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список специальные значения тангенса :

      903 03
      tan(`2*pi`) `0`
      tan(`pi`) `0`
      tan(`pi/4` ) `1`
      tan(`pi/3`) `sqrt(3)`
      tan(`pi/6`) `sqrt(3)/3`
      tan(`2*pi/3`) `-sqrt(3)`
      желтовато-коричневый( `3*pi/4`) `-1`
      tan(`5*pi/6`) `-sqrt(3)/3`
      tan(`-2*pi `) `0`
      tan(`-pi`) `0`
      tan(`-pi/4`) `-1` 903 05
      желтовато-коричневый(`- пи/3`) `-sqrt(3)`
      tan(`-pi/6`) `sqrt(3)/3`
      tan(`-2*pi/3`) `sqrt(3)`
      tan( ` -3*pi/4`) `1`
      tan(`-5*pi/6`) `sqrt(3)/3`

    3. Основные свойства

      4. `AA x в RR, k в ZZ`,

    • `tan(-x)= -tan(x)`
    • `tan(x+k*pi)=tan(x)`
    • `tan(pi-x)=-tan(x)`
    • `tan(pi+x)=tan(x)`
    • 2`.

    • Первообразная касательной

      • Первообразная касательной равна `-ln(cos(x))`.

    • Свойства функции касательной

      • Функция тангенса является нечетной функцией, для каждого действительного x `tan(-x)=-tan(x)`. Следствием для кривой, представляющей функцию тангенса, является то, что она допускает начало отсчета как точку симметрии.

      Синтаксис:

      tan(x), где x — мера угла в градусах, радианах или градах. 92`

      Тангенс первообразной :

      Калькулятор начальных производных позволяет вычислить первообразную функции тангенса.

      Первопроизводная tan(x) есть первопроизводная(`tan(x)`)=`-ln(cos(x))`

      Предельный тангенс :
      касательная функция.

      Предел tan(x) is limit(`tan(x)`)

      Тангенс обратной функции:

      обратная функция тангенса — функция арктангенса, отмеченная как arctan.

      Графический тангенс :

      Графический калькулятор может отображать функцию тангенса в заданном интервале.

      Свойство тангенса функции:

      Касательная функция является нечетной функцией.

      Расчет онлайн с тангенсом (тангенсом)

      См. также

      Список связанных калькуляторов:

      • Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
      • Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
      • Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
      • Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
      • Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
      • Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
      • Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
      • Тригонометрическое расширение: expand_trigo.

        No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *