Формула нахождения середины отрезка: Найдите координаты середины отрезка AB если A(6;5) B (3;6)

Математика: Справ. материалы

Математика: Справ. материалы

Гусев В. А., Мордкович А. Г. Математика: Справ. материалы: Кн. для учащихся.— М.: Просвещение, 1988.— 416 с. В книге дано краткое изложение основных разделов школьных курсов алгебры и начал анализа, геометрии. Книга окажет помощь в систематизации и обобщении знаний по математике. Оглавление СЛОВО К УЧАЩИМСЯ ГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел. 8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами. 30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. 47. Отыскание комплексных корней уравнений. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49. 3. 112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени. 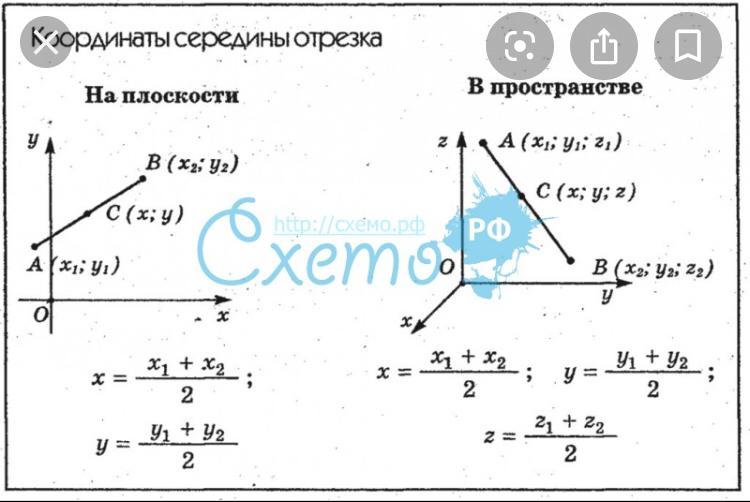130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения. 149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными. 169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188. Неравенства и системы неравенств с двумя переменными. § 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21. 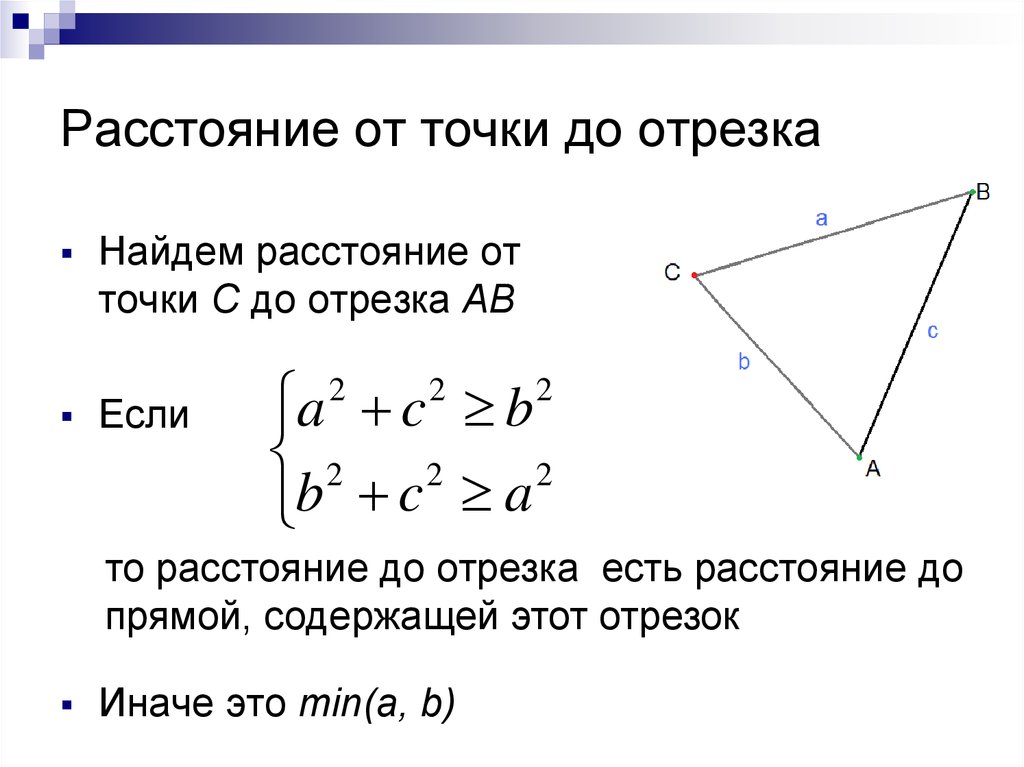Производная и ее применения 209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226. Правила вычисления первообразных. 227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости 22. Простейшие задачи на построение. 23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники. 49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76. Понятие движения. § 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ

Нахождение координат середины отрезка. Нахождение координат точки, делящей отрезок в данном отношении.

1. Матрицы, виды, действия над ними.

2. Произведение матриц, свойства, элементарные преобразования матриц.

3. Определитель квадратной матрицы. Вычисление определителя 2-го порядка. Вычисление определителя 3-го порядка. Правило Саррюса.

4. Свойства определителей не связанные с понятием алгебраического дополнения.

5. Минор и алгебраическое дополнение. Разложение определителя по строке.

6)Вырожденные и невырожденные матрицы. Обратная матрица( свойства, вычисление).

7)Ранг матрицы. Вычисление ранга матрицы.

8) СЛАУ, совместная система, определенная система, понятие «решить систему», общее и частное решение СЛАУ. Матричная форма записи СЛАУ. Решение СЛАУ с помощью обратной матрицы.

Метод обратной матрицы (Матричный метод) решения систем линейных алгебраических уравнений с ненулевым определителем основной матрицы состоит в поиске матрицы, обратной к основной матрице, и умножению ее на матрицу свободных членов.

При решении систем уравнений методом обратной матрицы используются вычисления определителя матрицы (Для вычисления матрицы, обратной к основной матрице системы уравнений). Для того, чтобы матрица имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля, тоесть матрица должна быть невырожденной.

9) СЛАУ с квадратной невырожденной матрицей. Формулы Крамера.

Невырожденная матрица (система) — квадратная матрица (система),определитель которой D=detА не равен нулю.

Квадратная матрица — матрица, у которой число строк равно числу столбцов.

10) Метод Гаусса для решения СЛАУ.

11) Совместность СЛАУ. Теорема Кронекера-Капелли. Критерий определенности СЛАУ.

12) Однородная система линейных уравнений.

13) Понятие вектора. (длина, единичный,нуль- вектор). Равные, противоположные, орт-вектор)

14) Коллинеарные векоры (сонаправленные, противоположнонаправленные) Признак коллинеарности, компланарные вектора.

Признаком коллинеарности двух векторов является пропорциональность их координат

15. Сложение векторов. (правило треугольника, параллелограмма, многоугольника). Разность векторов, умножение вектора на число.

15. Базис векторного пространства. Разложения вектора по ортам координатных осей. Понятие координат вектора.

Называется такая система векторов,которая:

1. Задана в определенном порядке

2. Линейно не зависима

3. Любой вектор пространства является линейной комбинацией данной системы векторов.

Числа стоящие перед базисными векторами называются координатами вектора в данном базисе.

Определение. Базисом векторного пространства   называется любая упорядоченная тройка некомпланарных векторов (т.е. не лежащих в одной плоскости) пространства  .

                         

                                      рис.2.

– базис  .

Замечание. Базис векторного пространства не может содержать нулевого вектора: в пространстве   по определению, в пространстве   двавектора будут коллинеарные, если хотя бы один из них нулевой, впространстве   три вектора будут компланарные, т.е будут лежать в одной плоскости, если хотя бы один из трех векторов будет нулевой.

15. Координаты и Модуль вектора,заданные координатами начала и конца. Действия над векторами,заданными своими координатами (сложение, вычитание, умножение на число, равенство, коллинеарность).

15. Направляющие косинусы векторов. Равенство их связывающее.

15. Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты.

15. Угол между векторами. Признак перпендикулярности векторов.

15. Векторное произведение векторов и его свойство. Выражение векторного произведения через координаты. Геометрические приложения векторного произведения.

15. Смешанное произведение векторов и его свойство. Выражение смешанного произведения через координаты. Геометрические приложения смешанного произведения.

15. Прямоугольная декартова система координат. Понятие линии. Полярная система координат. Выражение полярных координат через прямоугольные и наоборот.

15. Понятие ГМТ плоскости, примеры.

Геометрическое место точек — это множество всех точек, удовлетворяющих определённым заданным условиям.

Пример 1. Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO AB и AO = OB:

Пример 2. Окружность — это геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра (одна из этих точек — А).

Координаты середины отрезка в пространстве

Есть две произвольные точки A1(x1;y1;z1) и A2(x2;y2;z2). Тогда серединой отрезка A1A2 будет точка С с координатами x, y, z, где 

26) Каноническое уравнение прямой (вывод). Параметрическое задание прямой. Уравнение прямой через две точки (вывод).

Каноническое уравнение прямой в пространстве:

где   — координаты некоторой фиксированной точки M₀, лежащей на прямой;   — координаты вектора, коллинеарного этой прямой.

Параметрическое уравнение прямой в пространстве:

27)

Общее уравнение прямой и его частные случаи. Условия параллельности и перпендикулярности прямых заданных в общем виде. Направляющий и нормальный вектор прямой. Нахождение их координат из общего уравнения прямой.

Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     (9)

Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ = 0.     

 Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором.

 Найти уравнение прямой с направляющим вектором  (1, -1) и проходящей через точку А(1, 2).

 

Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

 

1 * A + (-1) * B = 0, т.е. А = В.

28) Уравнение прямой в отрезках (вывод) Уравнение прямой с угловым коэфицентом. Геометрический смысл углового коэффицента прямой.

29) Уравнение прямой через точку с данным угловым коэффициентом. Условия параллельности и перпендикулярности прямых, заданных с угловым коэффициентом.

Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂

В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

30) Уравнение прямой в полярной системе координат. Уравнение прямой через точку с данным нормальным вектором.

31) Нормальное уравнение прямой. Приведение общего уравнения прямой к нормальному виду. Расстояние от точки до прямой. Расстояние между двумя параллельными прямыми.

Расстоянием между параллельными прямыми называется часть перпендикуляра к этим параллельным прямым заключенная между ними

32) Определение и каноническое уравнение эллипса. Свойства эллипса.

Свойства:

1. точки пересечения эллипса с осями,называются вершинами.

(большая ось- фокальная и малая ось)

2. из канонического уравнения следует что

Эллипс лежит внутри прямоугольника со сторонами 2a и 2b.

3.Т.к. уравнение эллипса содержит только квадраты переменных то, если точка с координатами (x;y) принадл. Э, то точка с коорд.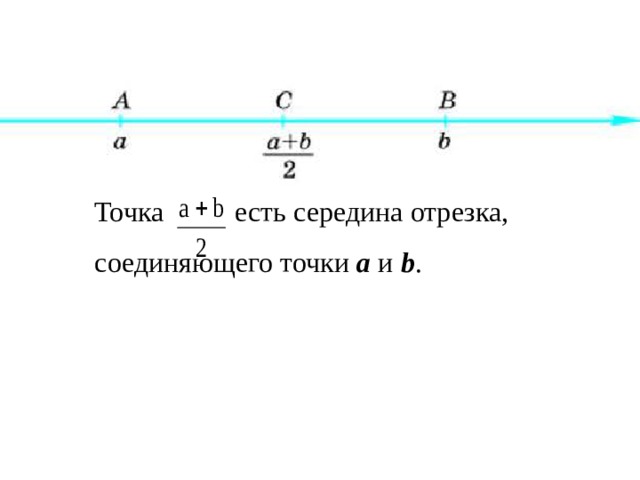 2

4. Директрисы эллипса.

Это прямые которые перпендикулярны фокальной оси и находятся на расстоянии a/E от ее центра x= +/- a/E

R1+R2=2a

R1,R2- фокальные радиусы

Для фокальных радиусов имеют место формулы

5. Основное свойство.

Отношение расстояния от произвольной точки эллипса до фокуса к расстоянию до соответствующей директрисы есть величина постоянная равная ексцентриситету.

33) Определение и каноническое уравнение гиперболы. Свойства гиперболы. Асимптоты гиперболы.

Свойства :

Гипербола лежит вне прямоугольника со сторонами 2a и 2b.

4. Эксцентриситет гиперболы.

E=c/a E>1

B^2=c^2-a^2

Чем меньше E тем меньше отношение е полуосей,тем больше вытягивается прямоугольник, ветви приближаются к осям,сжаты.

5.

Директрисы

6. Основное свойство.

34) Определение и каноническое уравнение параболы. Свойства параболы.

35) Основное свойство кривой второго порядка.

36) Понятие функции. Область определения и область значения. График функции.

37) Основные свойства функции. (четность/ нечетность, монотонность, периодичность, ограниченность). Обратная функция. Сложная функция.

38. Основные элементарные функции и их графики.

38. Понятие окрестности точки. Предел функции (по Коши). Основные теоремы о пределах.

Окре́стность точки — множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней. 

Пусть ε > 0 произвольное фиксированное число.

Окрестностью точки x₀ на числовой прямой (иногда говорят ε-окрестностью) называется множество точек, удаленных от x₀ не более чем на ε, т.е. O_ε(x₀) = {x: | x − x₀ | < ε}.

Середина сегмента линии

Для любых двух точек A и B средней точкой линии является точка M, расположенная посередине между точками A и B.

(Изображение будет загружено в ближайшее время)

Обратите внимание, что точка M равноудалена из точек A и B.

Середина линии может быть найдена только в сегменте линии. Линия или луч не могут иметь середины, поскольку линия неопределенна и может бесконечно продолжаться в обоих направлениях, тогда как у луча есть только один конец.

Давайте теперь узнаем, что такое середина отрезка?

Что такое линейный сегмент?

Отрезок — это часть линии, соединяющая две разные точки.

Это кратчайшее расстояние между двумя точками определенной длины, которое можно измерить.

Отрезок прямой с двумя конечными точками XY записывается как \[\overline{XY}\].

Определить середину сегмента линии?

Середина отрезка — это точка на отрезке, которая делит отрезок пополам на два конгруэнтных отрезка.

Середина отрезка — это точка отрезка, которая находится на том же расстоянии или посередине между двумя конечными точками.

(Изображение будет загружено в ближайшее время)

Середина формулы отрезка линии

Пусть (a ₁ , b ₁ ) и (a ₂ , b ₂ ) будут конечной точкой отрезок. Формула середины отрезка, соединяющего эти две точки, имеет следующий вид: \frac{b_{1} + b_{2}}{2})\]

Пример:

Предположим, у нас есть две точки 9и 5 на числовой прямой, середина прямой будет вычисляться как:

\[\frac{9 + 5}{2} = \frac{14}{2} = 7\]

Давайте научимся найти середину отрезка, соединенного конечными точками (-3, 3) и (5, 3).

Пусть (-3, 3) будет первой конечной точкой, поэтому a ₁ = -3 и b ₁ = 3. Точно так же пусть (5, 3) будет второй конечной точкой, поэтому a ₂ = 5 и b ₂ = 3. Подставьте эти точки в формулу средней точки, приведенную ниже, и упростите, чтобы получить середину отрезка прямой.

Используя формулу средней точки, получаем:

\[(\frac{a_{1} + a_{2}}{2}, \frac{b_{1} + b_{2}}{2}) = (\frac{-3 + 5}{2}, \frac{3 + 3}{2}) = (\frac{2}{2}, \frac{6}{2} = (1, 3)\ ]

Теорема о средней точке

Утверждение теоремы о средней точке гласит, что отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне треугольника и равен ее половине. Рассмотрим △ABC, приведенный ниже .Пусть точки D и E будут серединами AB и AC. Предположим, что вы соедините точки D и E.

(Изображение скоро будет загружено)

Теорема о средней точке утверждает, что прямая DE параллельна ВС и равна ровно половине ВС.

Как найти середину отрезка?

Середину отрезка можно определить с помощью этих двух разных методов. Это:

1. Метод подсчета.

2. Использование средней точки формулы отрезка прямой.

Метод подсчета

Если отрезок прямой или горизонтальный, вы можете найти середину отрезка, разделив длину отрезка на 2 и посчитав это значение от любой из двух конечных точек.

Метод формулы средней точки

Середину отрезка, лежащего по диагонали через ось координат, можно найти с помощью формулы средней точки.

Середины (x,y) отрезков с конечной точкой A (x ₁ , y ₁ ) и B(x ₂ , y ₂ ) можно найти, используя следующую формулу средней точки.

\[(x, y) = (a, b) = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2} )\]

Пример:

Найдите середину отрезка AB, где координаты точек A и B равны (-3, 3) (1, 4) соответственно.

Решение:

Используя формулу средней точки, получаем

\[(\frac{-3 + 1}{2}, \frac{-3 + 4}{2}) = (\frac{-2} {2}, \frac{1}{2}) = (-1, \frac{1}{2})\]

Следовательно, середина отрезка AB равна (-1, ½).

Середина отрезка Пример с решениями

1. Указанный ниже диаметр окружности имеет две конечные точки (2, 3) и (-6, 5). Определите координаты центра окружности, приведенной ниже.

Решение:

Центр окружности делит диаметр на две равные части. Следовательно, координаты центра являются серединами окружности.

Пусть (2, 3) будет первой конечной точкой, поэтому a ₁ = 2 и  b ₁ = 3. Точно так же пусть (-6, 5) будет второй конечной точкой, поэтому a ₂ = -6 и b ₂ = 5. Подставьте эти точки в формулу средней точки, приведенную ниже, и упростите, чтобы получить середину отрезка прямой.

Используя формулу средней точки, получаем:

\[(\frac{a_{1} + a_{2}}{2}, \frac{b_{1} + b_{2}}{2}) = (\frac{2 + (-6)}{2}, \frac{-3 + 3}{2}) = (\frac{-4}{2}, \frac{2}{2}) = ( -2, 1)\]

Следовательно, координаты центра окружности равны (-2, 1).

2. Если (3, -2) — середина прямой, соединяющей точки (1, x) и (5, 7). Найдите значение х.

Решение:

Пусть (1, h) будет первой конечной точкой, поэтому a ₁ = 1 и b ₁ = h. Точно так же пусть (5, 7) будет второй конечной точкой, поэтому a ₂ = 5 и b ₂ = 7. Подставьте эти точки в формулу средней точки, приведенную ниже, и упростите, чтобы получить середину отрезка.

Используя формулу средней точки, получаем:

\[(\frac{a_{1} + a_{2}}{2}, \frac{b_{1} + b_{2}}{2}) = (3, -2)\]

\[(\frac{1 + 5}{2}, \frac{h + 7}{2}) = (3, -2)\]

\[\frac {7 + h}{2} = -2 = 7 + h = -4\]

\[h= -11\]

Следовательно, значение h равно -11.

Расстояние и середины: определение, формула и пример

Вы когда-нибудь задумывались, как мы можем определить расстояние между двумя точками, даже если они не являются строго горизонтальными или вертикальными? Или как найти середину между двумя точками на любом расстоянии? В этой статье будет объяснено понятие середины и расстояния в геометрии.

Расстояние и середины: определение

Отрезок — это часть линии, соединяющая две разные точки. Это всего лишь отрезок линии, поскольку линии бесконечно длинны.

Середина отрезка, соединяющего две точки, является средней точкой, лежащей на отрезке.

Отрезок AB с серединой C — StudySmarter Originals

Приведенный выше отрезок AB соединяет точки A и B. Точка C лежит в средней точке прямой, поэтому она является серединой прямой.

Расстояние между двумя точками — это длина отрезка, соединяющего точки вместе.

Отрезок линии AB — StudySmarter Originals

Расстояние между точкой A и точкой B выше — это длина синей линии, которая представляет собой отрезок линии, соединяющий две точки.

Расстояние и средние точки на координатной плоскости

На координатной плоскости точки определяются координатой и координатой, которые указывают, насколько далеко поперек и насколько вверх по координатной плоскости расположена линия, соответственно. Координаты точек записываются в виде .

График, показывающий точки (2, 1) и (4, 3) — StudySmarter Originals

На рисунке выше показаны координаты точек и . Проведем между ними отрезок на следующем рисунке:

Отрезок, соединяющий точки (2, 1) и (4, 3) — StudySmarter Originals

Средняя точка на этом отрезке является серединой, а длина сегмента линии описывает расстояние между двумя точками. Как мы можем определить среднюю точку на линии и расстояние между двумя точками? Существуют формулы, которые могут помочь нам разобраться в этих деталях. Давайте посмотрим на них.

Расстояние и середины: Формула

В этом разделе мы рассмотрим две формулы:

• Формула для середины отрезка
• Формула для расстояния между двумя точками

Формула для середины прямой сегмент

Мы знаем, что средняя точка находится на полпути между двумя точками. Это означает, что его координата x находится посередине между координатами x точек, а его координата y находится посередине между координатами y точек.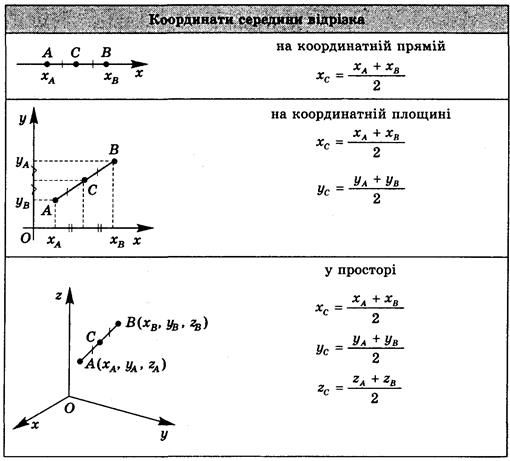 Итак, если мы знаем координаты x и координаты y для обеих точек, как мы можем найти среднюю точку, расположенную посередине между ними?

Для отрезка, соединяющего точки и , середина: .

На рисунке ниже показаны точки и на координатной плоскости со средней точкой . Остановимся подробнее на том, как находится середина.

Середина отрезка, соединяющего точки (2, 1) и (4, 3) — StudySmarter Originals

Формула средней точки, приведенная выше, позволяет нам найти среднее координат x точек и среднее координат y точек. Чтобы найти среднее значение для координат x наших точек, мы должны сложить два значения координат x. (), а затем разделить на два (). Это дает нам координату x средней точки, 3. Затем мы добавляем две координаты y () и делим на два (), чтобы найти среднее значение координат y наших точек, которое является координатой y средней точки.

Формула расстояния между двумя точками

Когда мы вычисляем расстояние между двумя точками, мы находим длину отрезка между ними. Как определить эту длину?

Расстояние между двумя точками и определяется по формуле: .

Следовательно, если мы знаем координаты x и y обеих точек, мы можем применить эту формулу. Вам может быть интересно, откуда взялась эта формула. Формула расстояния между точками рассматривает отрезок, соединяющий точки, как если бы он был гипотенузой прямоугольного треугольника, что означает, что применяется теорема Пифагора, заданная . Гипотенуза a и соответствующие длины сторон b и c показаны на рисунке ниже.

График, показывающий, как с помощью теоремы Пифагора можно вычислить расстояние между двумя точками на координатной плоскости — StudySmarter Originals

Формула также учитывает разницу между координатами x и y точек, которую можно получить, вычитая меньшие координаты от больших в этом случае. На приведенном выше графике расстояние между координатами x и равно . Это означает, что длина стороны нашего воображаемого треугольника равна 2! Точно так же расстояние между координатами y равно , что дает длину стороны второго треугольника 2,9. 0003

А гипотенуза треугольника? Когда мы применяем теорему Пифагора, мы получаем длину гипотенузы созданного нами треугольника, которая будет отрезком прямой между двумя точками:

Теперь, когда мы поняли происхождение формулы, давайте применим ее. в задаче-примере.

Нахождение средних точек и расстояний с примерами

Используя приведенные выше формулы, мы можем найти расстояние и средние точки между двумя точками, заданными на координатной плоскости.

Найдите середину отрезка, соединяющего точки и

Решение:

Если нам известны координаты двух точек, мы можем использовать формулу середины для определения середины отрезка, соединяющего их. . Формула средней точки задается как , поэтому мы подставляем наши известные координаты в формулу, чтобы получить среднюю точку.

Для координаты x средней точки =. Здесь мы сложили значения координат x и разделили на два.

Для координаты y средней точки.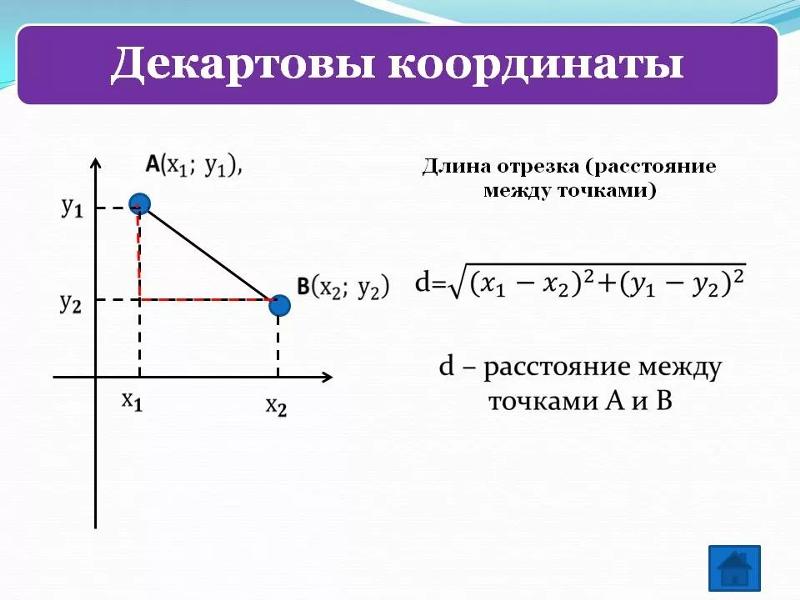 Здесь мы добавили значения координат y каждой из точек. Помните, что добавление отрицательного числа — это то же самое, что и вычитание, и любое число над самим собой можно упростить до единицы.

Теперь, когда у нас есть координаты x и y средней точки, мы можем записать их в типичной форме (x, y).

Найдите точное расстояние между точками и

Решение:

Мы можем применить формулу расстояния, чтобы найти расстояние между двумя точками. Формула расстояния задается формулой . Подставляем наши координаты в формулу, чтобы получить расстояние. Неважно, в каком порядке мы вычитаем координаты друг из друга (какая точка считается 1 или 2). Важно то, что мы остаемся последовательными при вычитании координаты x из другой координаты x и при вычитании координаты y из другой координаты y. Это связано с тем, что когда мы возводим значения в квадрат, он избавляется от отрицательного знака и в итоге получается одно и то же значение в любом случае.

Здесь мы подставили координаты x и y каждой точки в формулу расстояния, чтобы получить расстояние между ними. Вопрос задавался о точном расстоянии, поэтому мы оставляем наш результат как иррациональное число.

Применение формулы средней точки и расстояния

Середины и расстояния имеют множество математических приложений. В этом разделе мы приводим несколько примеров того, как можно применять рассмотренные нами формулы.

Использование формулы середины для нахождения серединного перпендикуляра

Вы можете использовать формулу средней точки, чтобы найти серединный перпендикуляр к отрезку. Биссектриса — это прямая, которая пересекается с отрезком в его середине под прямым углом, разрезая его на две половины.

Мы можем найти биссектрису, найдя середину и наклон отрезка, а также отрицательную обратную величину его наклона. Затем мы подставляем эти значения в формулу, используя координаты середины и отрицательную обратную величину наклона отрезка.

Использование формулы расстояния для определения форм и объектов

Мы знаем, что можем использовать формулу расстояния для нахождения длин отрезков, если знаем точки, в которых отрезок начинается и заканчивается. Например, если бы у нас была лестница, которая упиралась в стену, и лестница касалась стены и пола в точках, мы могли бы использовать формулу расстояния для определения длины лестницы.

Мы также можем доказать, что отрезки, соединяющие точки на координатной плоскости, работают вместе, образуя определенную форму. Например, если три отрезка, соединяющие 3 точки, имеют равные расстояния, мы можем показать, что отрезки образуют равносторонний треугольник, поскольку равносторонние треугольники имеют 3 равные длины сторон.

Лестница упирается в стену в плоскости xy, причем ось x представляет собой пол, а ось y представляет собой стену. Он касается пола в точке и касается стены в точке. Найдите длину лестницы с точностью до 2 знаков после запятой.