ОГЭ 2023 Ященко 1 вариант ФИПИ школе полный разбор! смотреть онлайн видео от Просто-понятно! Математика с Виктором Осиповым. в хорошем качестве.
12+
15 часов назад
Просто-понятно! Математика с Виктором Осиповым.
Решаем 1 вариант Ященко ОГЭ 2023 года сборника ФИПИ школе 36 вариантов. Разбор всех заданий. Готовимся к ОГЭ по математике! Разбор заданий ОГЭ из сборника Ященко за 2023 год ФИПИ школе 36 вариантов.
Помочь проекту: https://mathlesson.ru/donate
ОГЭ по математике; ОГЭ математика 2022; ОГЭ 2023 Ященко; Ященко 36 типовых вариантов; Математика 9 класс; Подготовка к ОГЭ 2023; ОГЭ; Сдать ОГЭ по математике; ОГЭ алгебра; ОГЭ геометрия;
группа ВК: https://vk.com/mr.mathlesson
сайт: https://mathlesson.ru/oge2023fipi-yashenko36var-1var
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
Тайминг:
00:00:00 — приветствие
0:0:15 — Найдите высоту теплицы PQ в метрах
0:3:0 — Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке — 6 штук?
0:5:27 — Найдите ширину центральной грядки, если она в 1,2 раза больше ширины узкой грядки.
2 больше 4
0:20:28 — В амфитеатре 24 ряда, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 27 мест, а в седьмом ряду 31 место. Сколько мест в последнем ряду амфитеатра?.
0:22:29 — В треугольнике ABC известно, что AB=14, BC = 5, sin ABC=6/7. Найдите площадь треугольника ABC.
0:23:2 — Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=18, DK=9, BC =16. Найдите AD.
0:24:47 — В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
0:26:8 — На клетчатой бумаге с размером клетки 1 x 1 отмечены три точки: A, B и C. Найдите расстояние от точки A до отрезка BC.
0:26:35 — Какое из следующих утверждений верно?
1) Если две стороны одного треугольника соответственно другого треугольника, то такие треугольники равны.
2) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
3) Диагонали ромба точкой пересечения делятся пополам.
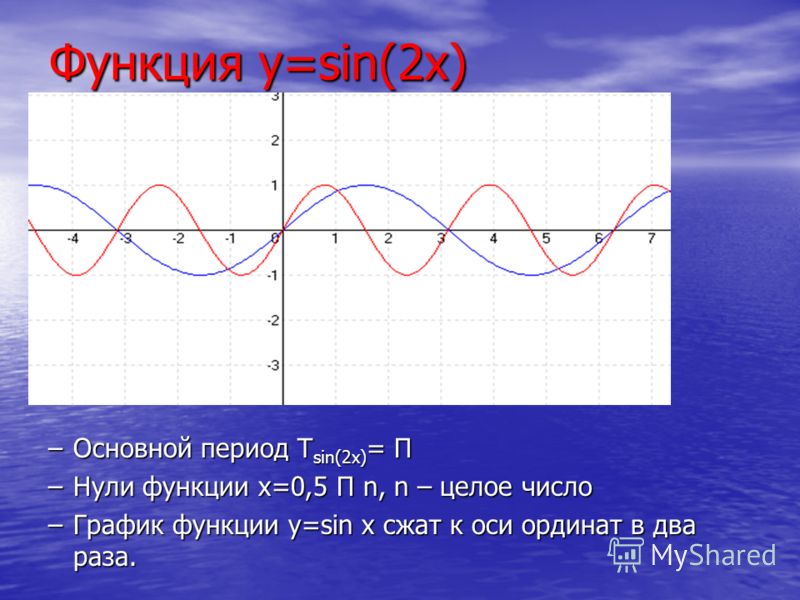
Заполните приведенную ниже таблицу до 2 знаков после запятой для графика y = sin x и y = 2sin (x-30) для диапазона
1 Ответ
0 голосов
ответил к анонимный-
xº -180 -150 -120 -90 -60 -30 0 30 60 90 120 150 180 Sin xº 0 -0.5 -0.87 -1.0 -0.87 -0.5 0 0.5 0.87 1.0 0.87 0.5 0.0 2 Sin (x – 30)º 1 0 -1.0 -1.73 -2.0 0 -1 0 1.0 1.73 2.0 1.73 1,0 - Используя свой график
- Укажите амплитуду и период графика y = 2 sin (x-30)0
y = 2sin(x-30º) Период = 1 ед. - Решите уравнение
Sin xº = 2 sin (x-30)º
SinX = 2Sin (x – 30º)
X = -126º cr 51,50 ±1º - Полностью опишите преобразование, которое преобразует y = 2sin (x- 30)0 на y = sin x
+30
0 Перевод
- Укажите амплитуду и период графика y = 2 sin (x-30)0
Похожие вопросы
Составьте таблицу и нарисуйте график y=sinx–cosx для x в диапазоне 0°≤x≤360°, со значениями y до 2dp и интервалами x в 30°
спросил
2 августа 2021 г.
по математике 3 класс
к
анонимность
- тригонометрия
На рисунке ниже показан треугольник PQR, в котором PQ=8 см, угол QPR=1000 и угол PQR=350. Рассчитайте длину QR с точностью до 2 знаков после запятой и, следовательно, площадь треугольника PQR с точностью до 2 знаков после запятой.
- тригонометрия
В таблице ниже показаны некоторые значения кривой y = 2cos x и y= 3 sin x.
спросил 21 июля 2021 г. по математике 3 класс к анонимный
- тригонометрия
Стороны треугольника были измерены и записаны как 4 см, 6,2 см и 9,50 см. Рассчитайте процентную ошибку в его периметре с точностью до 2 знаков после запятой.
спросил 21 июля 2021 г. по математике 3 класс к аноним
- тригонометрия
- приближение и ошибки
Треугольник ABC таков, что AB = 8 см, BC = 11 см и AC = 15 см.
рассчитать правильно до 2 знаков после запятой; Угол ABC Радиус описанной окружности
спросил 30 июня 2021 г. по математике 3 класс к анонимный
- тригонометрия
Категории
- Все категории
- Математика
(544)
- Математика Форма 1 (236)
- Математика Форма 2 (151)
- Математика Форма 3 (137)
- Математика Форма 4 (20)
- Английский (259)
- суахили (505)
- Химия (581)
- Физика (578)
- Биология (587)
- География (514)
- История (541)
- КРЭ (327)
- ИРЭ (51)
- сельское хозяйство (494)
- Бизнес-исследования (349)
- Компьютерные исследования (14)
- Домашняя наука (60)
- Общие вопросы (79)
период-амплитуда-фазовый сдвиг — Googlesuche
AlleBilderVideosBücherMapsNewsShopping
suchoptionen
Нахождение амплитуды, периода и фазового сдвига функции вида A × sin(Bx — C) + D или A × cos( Bx — C) + D получается следующим образом: Амплитуда равна A ; Период равен 2π/B; и.
Фазовый сдвиг равен C/B.
30. Дез. 2022
Калькулятор фазового сдвига
www.omnicalculator.com › математика › фазовый сдвиг
Hervorgehobene Snippets
Амплитуда, период, фазовый сдвиг и частота — Math is Fun
www.mathsisfun.com › алгебра › амплитуда-период-…
амплитуда A = 2 · период 2π/B = 2π/4 = π/2 · фазовый сдвиг = −0,5 (или 0,5 вправо) · вертикальный сдвиг D = 3.
Ähnliche Fragen
Как влияет фазовый сдвиг амплитуда?
Какова формула фазового сдвига?
Как узнать сдвиг фазы влево или вправо?
Амплитуда, период, фазовый сдвиг и вертикальный сдвиг тригонометрического… · Амплитуда записывается как A. Период равен 2π/B. Фазовый сдвиг равен C. Если +C, сдвигается влево. Если фазовый сдвиг – C, …
Как найти период амплитуды и фазовый сдвиг синуса — YouTube
www.youtube.com › смотреть
25.01.2017 · Узнайте, как построить график синусоидальной функции.
Чтобы построить график функции синуса, мы сначала определяем амплитуду…
Dauer: 3:03
Прислан: 25.01.2017
Амплитуда, период и фазовый сдвиг — одна математическая кошка
www.onemathematicalcat.org › Precalculus_obj › a…
Для синусоидальных и косинусоидальных кривых: АМПЛИТУДА – расстояние по вертикали от оси x до самой высокой/низшей точки; ПЕРИОД – продолжительность одного полного цикла; ФАЗОВЫЙ СДВИГ …
Bilder
Alle anzeigen
Alle anzeigen
Примеры тригонометрии | Амплитуда, период и фазовый сдвиг — Mathway
www.mathway.com › примеры › тригонометрия › a…
Примеры тригонометрии. Пошаговые примеры · Тригонометрия · Графики тригонометрических функций. Найдите амплитуду, период и фазовый сдвиг.
Предварительный расчет: амплитуда, период, фазовый сдвиг триггерной функции
www.varsitytutors.com › precalculus-help › amplitu…
Уравнение будет иметь вид \displaystyle y = A \cdot \cos (f (x — h)) + k, где A – амплитуда, f – частота, h – сдвиг по горизонтали, а k .