Формула определения площади круга: Формулы, как найти площадь круга

Содержание

Площадь круга все формулы и примеры расчета

Площадь круга – это размер области внутри окружности, определенный в квадратных единицах измерения. Определять площадь круга можно по формулам, которые давно известны и использовались еще в Древнем мире для определения необходимого количества строительных материалов при построения зданий, амфитеатра и других архитектурных сооружений. В современном мире, с его быстрыми изменениями в архитектуре и в строительстве – определять площадь круга не менее важно. И в задачах алгебры и геометрии это умение пригодится.

Содержание

Формулы площади круга

Площадь круга через радиус

В геометрии используются следующая формула для определения площади круга через радиус круга:

Здесь – площадь круга, – радиус круга.

В формуле фигурирует – это постоянная величина, которая называется “число ” – это постоянная величина, которая часто используется в геометрии и в тригонометрии и означает отношение длины окружности к ее диаметру. Значение этого отношение получается постоянным, но не точным, и до сегодняшнего дня ученые стараются уточнить это значение. Приближенно “число ” равно 3,14. Хотя после цифры “4” еще бесконечное количество цифр:

Площадь круга измеряется в квадратных единицах длины: см², м², дм², мм², кв.ед. Однако, в физике площадь круга будет рассчитываться в СИ: м². Иногда в задачах сразу указывается – в каких единицах следует рассчитать площадь круга.

Площадь круга через диаметр

Давайте получим формулу площади круга через диаметр.

Так как диаметр – это два радиуса, то, следовательно, радиус – это половина диаметра:

– диаметр круга.

Подставим это выражение для радиуса в формулу площади круга, получим:

Таким образом, нами получена формула площади круга через диаметр круга:

Площадь круга через длину окружности

Окружность – это граница круга. Зная длину этой границы мы можем рассчитать площадь круга. Итак, формула длины окружности: , тогда определим радиус и подставим его в формулу (1):

И формула площади круга через длину окружности:

Примеры решения задач

Задача 1

Найдите площадь круга, если известен его радиус см.

Решение: Для определения площади круга используем формулу (1):

см². Сейчас мы имеем точное значение площади круга. Но если мы возьмем вместо число 3,14, то получим приближенное значение площади круга:

см².

Ответ: 78,5 см².

Задача 2

Найдите площадь земельного участка, если известно, что форма участка – круг, а диаметр участка составляет 50 м.

Решение: Чтобы найти площадь земельного участка, мы должны рассчитать площадь круга с диаметром 50 м. Используем формулу (2):

м².

Ответ: м².

Задача 3

Длина границы земельного участка круглой формы равна 64 м. Найдите площадь участка.

Решение: граница участка круглой формы – это окружность. Тогда длина этой границы – это длина окружности. Площадь участка – площадь круга, которую мы определим по формуле (3) через длину окружности:

м².

Ответ: м².

Для того, чтобы определять площадь круга в задачах по геометрии вам нужно определить с тем, какие данные вам известны и использовать те формулы для определения площади круга, которые больше всего подходят.

Формула площади круга

В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность, а в том случае, если длина радиуса равна нулю, круг вырождается в точку.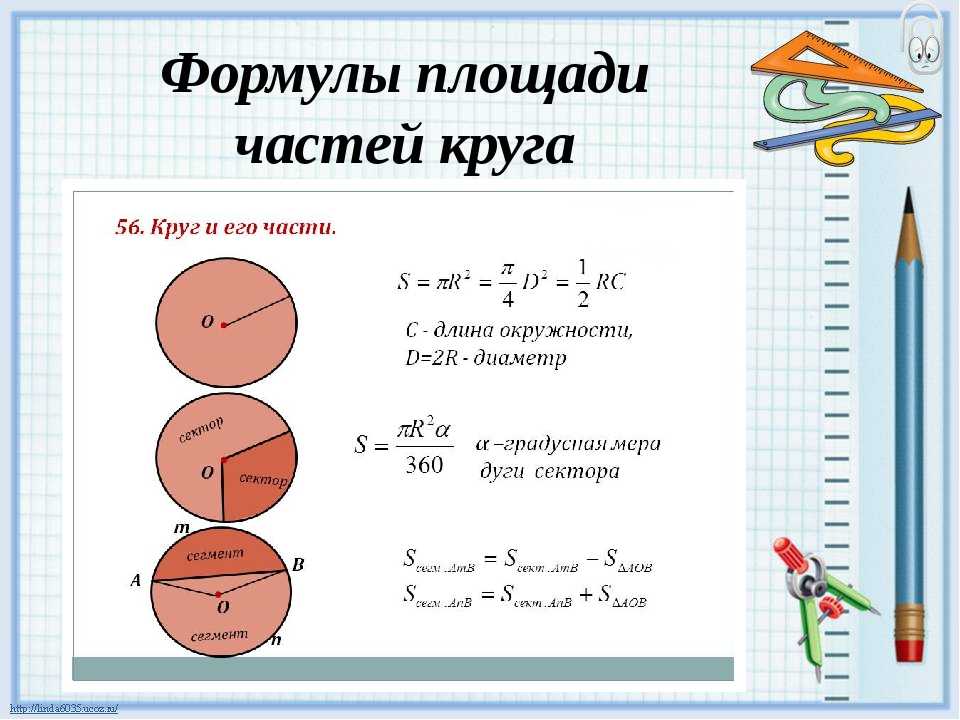

Определение площади круга

При необходимости площадь круга можно вычислить по формуле:

πr²

D²

r – радиус круга

D – диаметр круга

S – площадь круга

π –

3.14

Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг. К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг. Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.

Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму

круга, а впервые они стали строиться еще во времена античности. Само слово «circus» в переводе с латинского языка означает «круг». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.

Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.

Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол», которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.

Калькулятор окружности и площади круга

Создано Luis Hoyos

Отзыв от Wojciech Sas, PhD

Последнее обновление: 11 октября 2022 г.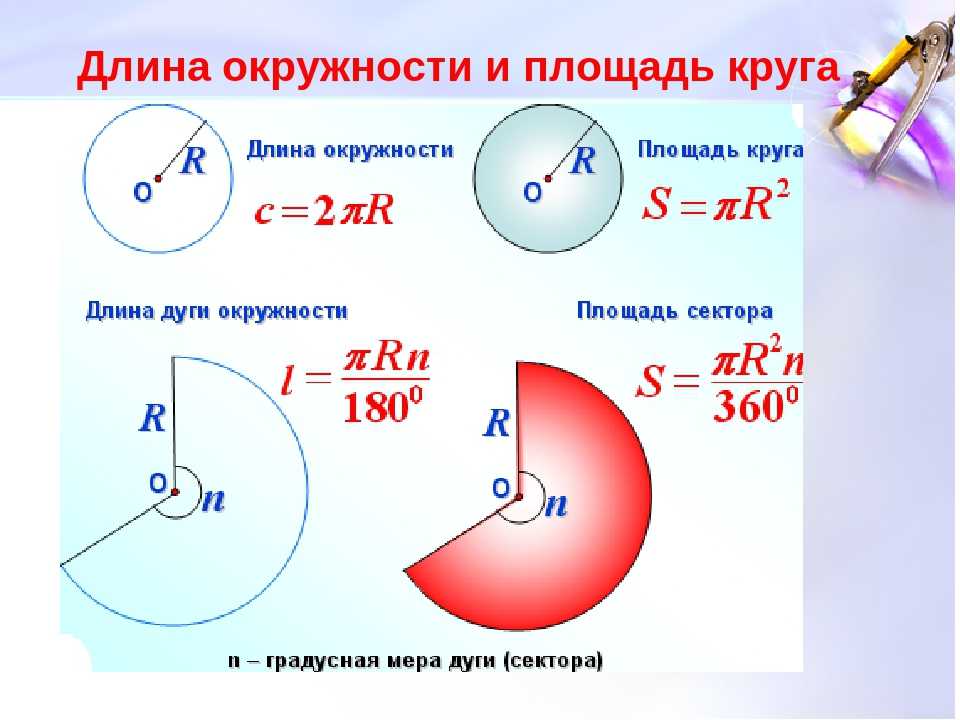

Содержание:

Формула для расчета длины окружности и площади круга
0 Как найти длину окружности и площадь круга?
Другие удивительные калькуляторы Omni
Часто задаваемые вопросы

Вас интересует вычисление площади и длины окружности и формула для этого? Это идеальный инструмент.

Круги присутствуют во многих местах . Монеты, пицца и виниловые диски являются примерами круглых объектов, и площадь является важным их аспектом.

Читайте дальше, если вам интересно:

Как найти площадь и длину окружности.
Как соотносятся длина окружности и площадь круга.
Как найти площадь четверти круга.

💡 Знаете ли вы, что

Диаметр и, следовательно, площадь пиццы имеют решающее значение при определении оптимального размера пиццы для вашего бюджета и вкуса. На самом деле, у нас есть калькулятор сравнения стоимости пиццы для вашего удовольствия.

Формула для вычисления длины окружности и площади круга

Это формулы для вычисления длины окружности и площади круга:

c = 2πr
A = πr² = πd²/4

, где:

c обозначает длину окружности;
r для радиуса; и
d для диаметра круга.

π — константа, приблизительно равная 3,14159265359 и, среди прочего, представляет отношение длины окружности к диаметру любой окружности .

Как найти длину окружности и площадь круга?

Предположим, вы хотите узнать, как найти длину окружности и площадь круга с радиусом 8 см . В этом случае необходимо выполнить следующие шаги:

Используйте формулы для вычисления длины окружности и площади: c = 2πr и A = πr² .
Окружность должна равняться c = 2π × 8 см = 50,265 см .
Площадь должна равняться A = π × (8 см)² = 201,06 см² .
Чтобы проверить результаты , введите диаметр 8 см в калькулятор. Результаты также должны быть 50,265 см и 201,06 см².

Другие удивительные Omni-калькуляторы

Освоив процесс вычисления длины окружности и площади круга, вы можете посмотреть на эти другие инструменты и продолжать совершенствовать свои навыки:

Расчет круга: найти c, d, a, r;
Калькулятор измерения окружности;
Калькулятор формулы круга;
Калькулятор радиуса окружности;
Калькулятор длины окружности;
Окружность к диаметру;
Калькулятор диаметра круга;

Калькулятор периметра круга;
Квадратные метры кругового калькулятора; и
Квадратный дюйм калькулятора круга.

Часто задаваемые вопросы

Как связаны длина окружности и площадь круга?

Они связаны друг с другом следующей формулой: c = 2√(πA) . Уравнение говорит, что длина окружности пропорциональна квадратному корню из площади , поэтому чем больше размер окружности, тем больше длина окружности.

Какова площадь 9-дюймового круга?

63,617 дюйма² . Чтобы найти площадь любого круга, зная его диаметр:

Умножьте π (пи) на квадрат диаметра: π × (9 дюймов)² = 254,47 дюйма² .
Разделите полученный результат на четыре:
254,47 дюйма²/4 = 63,617 дюйма² .
Теперь вы знаете, какова площадь 9-дюймового круга ✔️

Как найти площадь четверти круга?

Чтобы получить площадь четверти круга:

Возьмем формулу площади обычного круга: A = πr² .
Разделите эту формулу на четыре.
После выполнения этих шагов мы можем заметить, что площадь четверти круга равна A = πr²/4 .

Luis Hoyos

Radius (r)

Diameter (d)

Circumference (c)

Area (A)

Check out 23 similar 2d geometry calculators 📏

AreaArea of a rectangleArea of crescent… 20 подробнее

Площадь круга: формулы и примеры

Давайте научимся определять площадь круга .

Окружность — это фигура, содержащая набор точек, равноудаленных от заданной точки. Точка называется центр , а расстояние от центра до любой точки окружности называется радиусом .

Удвоенная длина радиуса называется диаметром — это отрезок, который проходит через центр и имеет свои концы на самой окружности. Итак, если у вас есть радиус, вы можете умножить его на 2, чтобы получить диаметр,
, представленный формулой d=2r . Или, если вы знаете диаметр и вам нужен радиус, вы можете разделить d на 2, что представлено выражением r=d/2 . Наконец, расстояние по окружности называется окружностью , которая называется периметром в многоугольнике.

Дополнительная информация: Периметр прямоугольника – формулы и примеры

Наиболее распространенными единицами измерения расстояния, используемыми в окружности, являются миллиметры (мм), сантиметры (см), метры (м) и километры (км). . Область — это пространство, заключенное внутри круга. Измеряется в квадратных единицах, таких как мм ² , см ² , м ² , и км ² . Чтобы найти площадь круга, умножьте число пи, равное примерно 3,14, на квадрат радиуса.

Формула площади круга:

A = πr ² Перед вычислением площади убедитесь, что единицы измерения совпадают.

Пример 1: Найдите площадь круга, зная радиус

Найдите площадь круга ниже.

Решение для примера 1:

Запишите данное измерение, которое является радиусом (r = 10 м) , и подставьте его в формулу для площади .

Помните, что формула для площади такова: A = πr ²

Подставьте 3,14 вместо pi и 2 r 10m вместо .

A = 3,14 (10 м) ²

Упрощение.

А = 3,14 (100 м ² )

A = 314 м ²

Следовательно, площадь круга равна 314 м ² 8 .

Пример 2: Найдите площадь круга, зная диаметр

Найдите площадь круга ниже.

Решение для примера 2:

Запишите данное измерение, которое является диаметром (d = 50 м) .

Помните, что формула для области , A = πr ² , требуется радиус, а не диаметр. Итак, давайте найдем радиус, используя заданный диаметр.

Вы, наверное, помните, что диаметр в два раза больше радиуса, что выражается формулой d=2r . Следовательно, чтобы получить радиус, замените d на

50 м .

d = 2r

50m = 2r

Упростите уравнение, разделив уравнение на 2.0021 р = 25м .

Следовательно, радиус равен 25 м. Теперь, когда у нас есть это, давайте вычислим площадь .

Подставить 3.14 вместо pi и 25m вместо r в формуле для площади .

A = πr ²

A = 3,14 (25 м) ²

Упростить.

А = 3,14 (625 м ² )

А = 1962,5 м ²

Следовательно, площадь круга равна 1962,5 м ² .