Квадратичная функция, ее график.
1º. Функция, заданная формулой , гдеx, y– переменные,a, b, c– действительные числа, причема ≠ 0, называетсяквадратичной.
2º. Графиком функции является парабола – кривая, симметричная относительно прямой, проходящей через вершину параболы.
Координаты вершины параболы определяются по формулам:
.
Если квадратичную функцию путем выделения полного квадрата привести к виду, то точка (x0;y0) – вершина параболы.
График квадратичной функции получается из графика функциис помощью параллельного переноса.
3º. Если коэффициент a > 0, ветви параболы направлены вверх, еслиa < 0– вниз.
При
парабола пересекает ось абсцисс в двух
точках, приD=0– в одной (т.
Пример 3. Построим график функции .
Выполним следующие преобразования (называемые «выделением полного квадрата»):
График функции получается из графика функциипараллельным переносом на 2 единицы влево и на две единицы вниз.
Уравнения, содержащие переменную под знаком модуля.
1º. Модуль (абсолютная величина)числааопределяется следующим образом:
.
Геометрический смысл модуля: |a| есть расстояние от точки числовой оси, изображающей данное числоа, до начала отсчета — точки О, а |x—a| есть расстояние между точками числовой оси, соответствующими числамхиа.
2º. Уравнения вида можно решать геометрически.
Рассмотрим аналитические способы решения уравнений, содержащих переменную под знаком модуля, на примерах.
При решении уравнений важно уметь в соответствии с определением модуля освободиться от вертикальных скобок.
Например, , еслиa≥ 5;
, еслиa< 5.
Пример 4. Решим уравнение , используя определение модуля числа.
Решение: Уравнение имеет решение, если x+1≥0, т.е.x≥-1.
.
Условие x≥-1 выполняется в обоих случаях.
Ответ: 4; 2/3.
Пример 5. Решим уравнение , используя свойство модулей («модули противоположных чисел равны»).
Решение:
.
|2
|2x+1|-3=-4 => |2x+1|=-1 – нет решений.
Ответ: 3; -4.
Пример 6.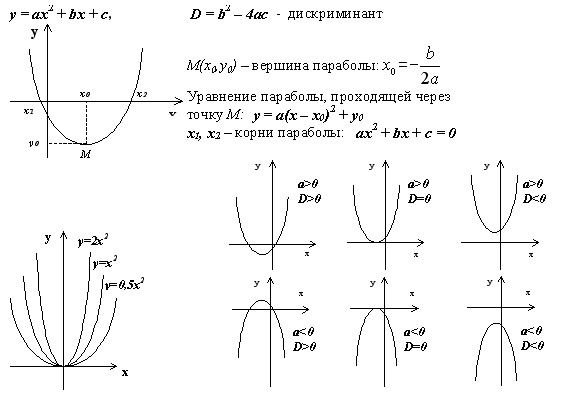 Решим уравнение
,
рассматривая решения на интервалах.
Решим уравнение
,
рассматривая решения на интервалах.
Решение: Найдем нули модулей, т.е. такие значения x, при которыхи: .
Рассмотрим уравнение на интервалах (-∞; -2), [-2; -1), [-1; +∞).
а) Для уравнение примет вид:
-(x+1)-(x+2)=2; —x-1-x-2=2; -2x=5; x=-2,5;=>x=-2,5– корень уравнения.
б) Для уравнение примет вид:
-(x+1)+(x+2)=2; —x-1+x+2=2; 0·x=1- нет корней.
в) Для уравнение примет вид:
x+1+x+2=2; 2x=-1; x=-0,5;=> x=-0,5– корень уравнения.
Ответ: -2,5; -0,5.
Дидактический материал.
Решите уравнения, сводящиеся к линейным:
1. ; 2.; 3.;
4. ; 5.;
6. ; 7.;
8. ; 9.;
10. ; 11..
Решите квадратные уравнения:
12. ; 13.;
14. ; 15.;
16. .
Разложите на линейные множители:
17. ; 18.; 19.;
; 18.; 19.;
20. ; 21..
Сократите дроби:
22. ; 23.; 24.;
25. ; 26.; 27..
Упростите выражение:
28. ; 29..
Найдите среднее арифметическое всех действительных корней уравнения:
30. ; 31.;
32. ; 33.;
34. ; 35.;
36. .
Найдите расстояние от вершины параболы до точки М:
37. ; 38.;
39. ; 39..
Постройте график функции:
40. ; 41.; 42.;
43. ; 44.; 45.;
46. ; 47.; 48.;
49. ; 50.; 51..
52. По графику квадратичной функции определить знаки ее коэффициентов и их суммы:
Найдите рациональные корни уравнения:
53. ; 54.; 55.;
56. ; 57.; 58.;
59. ; 60.; 61..
Решите уравнения:
62. ; 63.; 64.;
65. ; 66.; 67.;
68. ; 69.;
70. ; 71.; 72..
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
Хотите купить новую квартиру и уже нашли несколько подходящих под ваш бюджет вариантов? Не забудьте добавить к стоимости жилья ряд дополнительных расходов, которые вам придется оплатить при покупке недвижимости в Казахстане.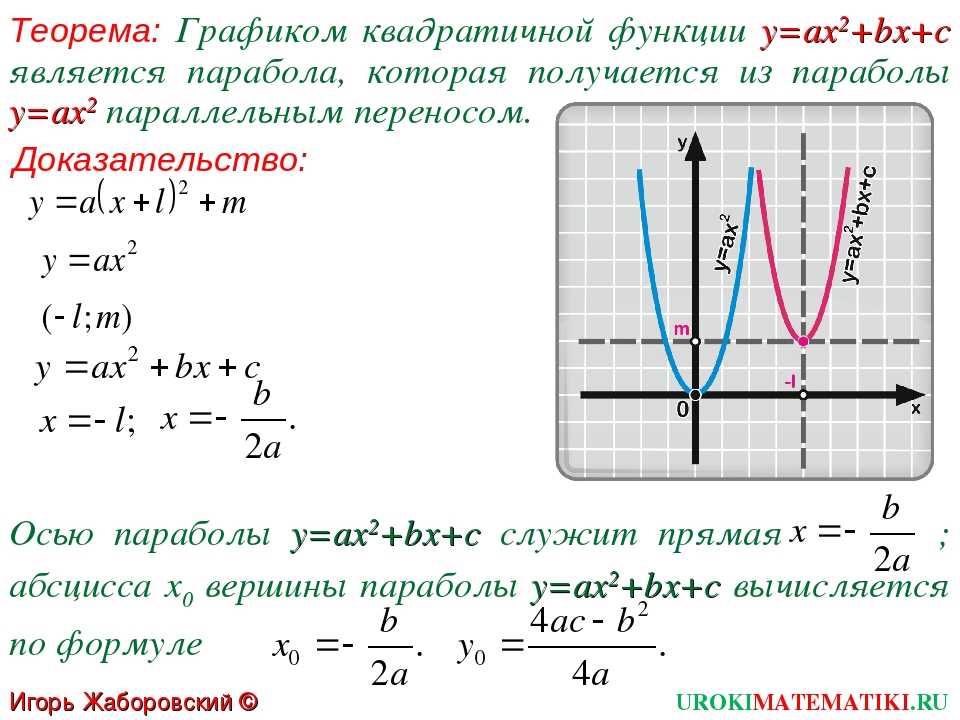 Квартиры в Астане и квартиры в Алматы можно посмотреть на korter.kz, где с помощью фильтров можно максимально точно подобрать желаемые варианты.
Квартиры в Астане и квартиры в Алматы можно посмотреть на korter.kz, где с помощью фильтров можно максимально точно подобрать желаемые варианты.
Договор купли-продажи недвижимости включает в себя ряд обязательных платежей, независимо от того, где было куплено жилье — на вторичном рынке или в новостройке. Определенную часть расходов должен погасить покупатель. Сумма платежей рассчитывается в зависимости от особенностей сделки и может достигать значительных размеров, поэтому важно перед покупкой подсчитать все расходы.
Дополнительные платежи покупателя при оформлении права собственности:
- услуги нотариуса;
- оплата госпошлины за регистрацию.
Нотариальное оформление договора купли-продажи не является обязательной процедурой, но специалисты рынка недвижимости советуют не пренебрегать услугами нотариуса. Нотариус проверяет стороны сделки, контролирует процесс заключения договора и выступает гарантом безопасности.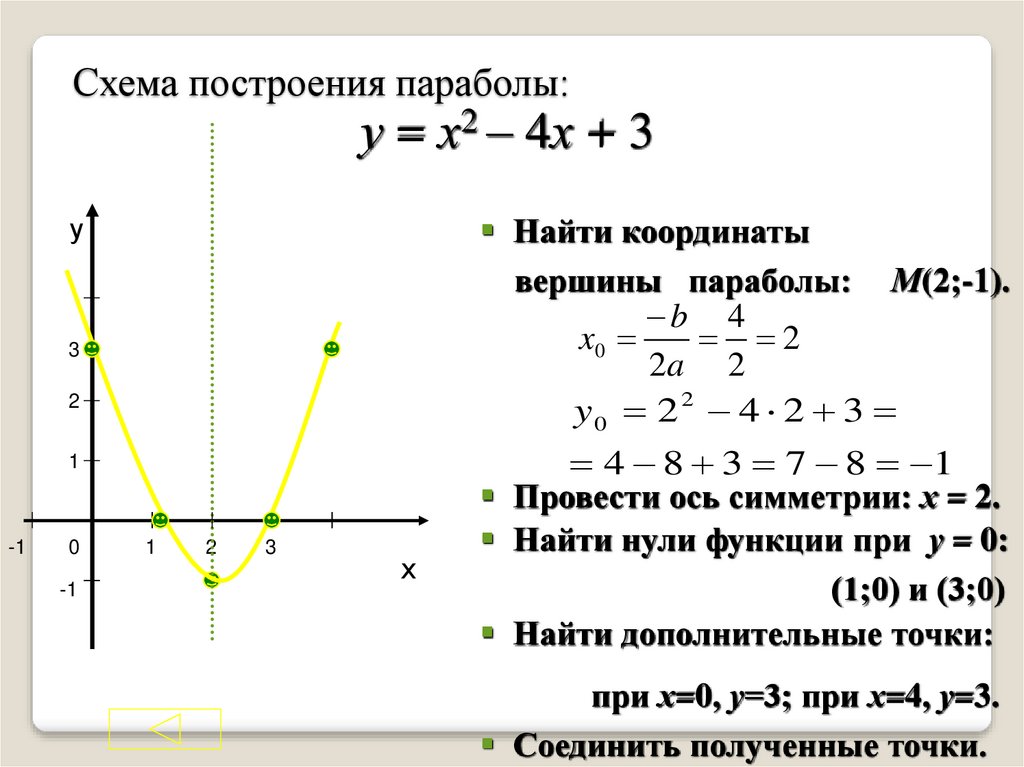
Нотариальные услуги имеют фиксированную стоимость. Средняя стоимость нотариального оформления объекта недвижимости в 2023 году составляет 12 МРП, т.е. около 37000 тг. Следует обращать внимание на то, что сумма платы зависит от того, кто является участниками сделки. Если сделка заключается с близким родственником – сумма уменьшается, если с юридическим лицом – увеличивается.
Как правило, участники сделки делят расходы на оформление поровну. Однако, лучше заранее согласовать этот момент с продавцом недвижимости.
Прямые сделки также предусматривают дополнительные расходы, например, оформление задатка.
Регистрация прав на имуществоПри покупке недвижимости покупатель обязуется оплатить государственную пошлину за регистрацию своих прав на имущество в ЦОН. Процедура оформления занимает до 3 рабочих дней. Стоимость данной услуги — 1 073,7 тг.
Покупатель может заказать услугу ускоренной регистрации права собственности. Процесс внесения информации в реестр займет 1 день. Стоимость ускоренной регистрации — 5000 тг.
Стоимость ускоренной регистрации — 5000 тг.
Зачастую дополнительных трат требуют услуги опытных специалистов: риелторов, оценщиков, юристов. Однако в зависимости от типа сделки могут появиться и другие дополнительные издержки:
- Ипотечный налог. Если вы покупаете квартиру в ипотеку, вы должны совершить платеж, размер которого зависит от условий кредитования, налоговых вычетов и т.д.
- Банковские услуги. Плата за совершение операций, использование банковской ячейки, аренда сейфа, страховка и т.д.
- Увеличение фактической площади. Это относится к покупке квартиры в новостройке. Когда конечная площадь жилья превышает предусмотренную проектом.
- Оплата коммунальных. Управляющая компания жилого комплекса может взимать оплату своих услуги наперед.
Следовательно, в понятие конечной стоимости жилья входит не только цена квадратных метров, но ряд дополнительных расходов, сумма которых может составлять около 10% стоимости самого объекта.
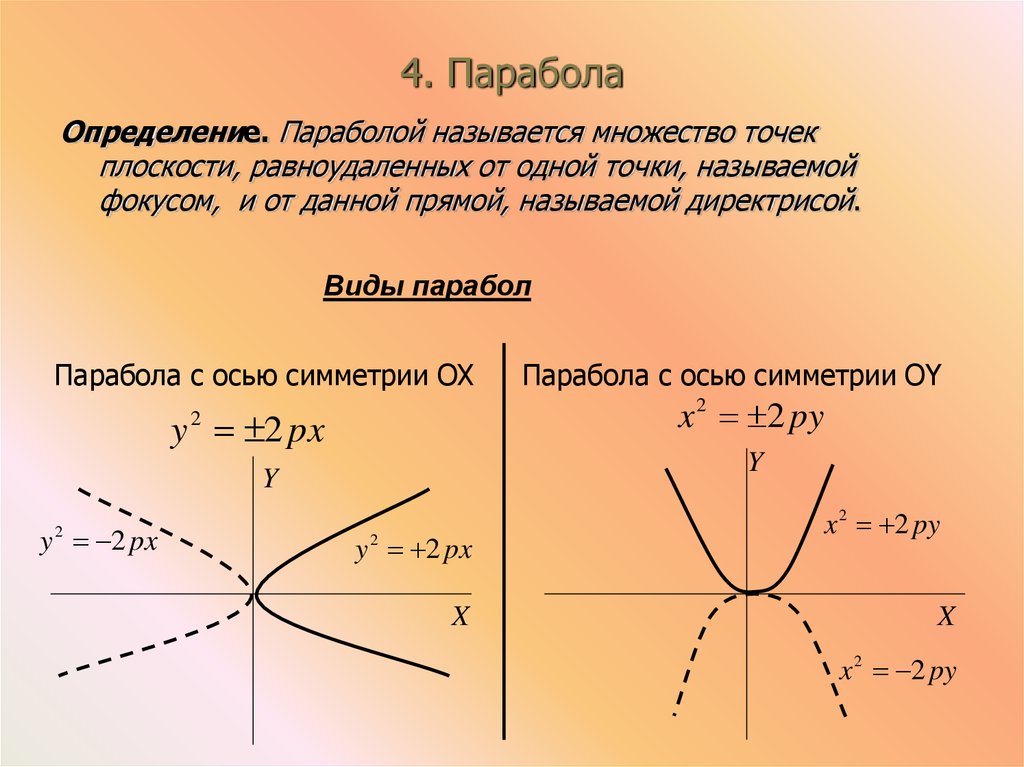
Как найти точку поворота параболы?
Когда квадратное уравнение представлено графически в виде буквы U, оно называется параболой. Парабола также может быть определена как плоская кривая, где любая точка на этой кривой равноудалена от фиксированной точки, фокуса. Точка поворота любой кривой или параболы — это точка, в которой ее направление меняется с восходящего на нисходящее или наоборот. Точка поворота параболы называется вершиной. Стандартная форма параболы: y = ax 2 + бх + в. Форма вершины параболы с вершиной (h, k) равна y = a(x – h) 2 + k.
Точка поворота параболы
Чтобы получить точку поворота или вершину (h, k) параболы, мы можем преобразовать это уравнение в форму вершины параболы: y = a(x – h) 2 + к. Мы можем сделать это, используя метод «Завершение квадратов».
- Вычтите c из левой и правой сторон.
y – c = ax 2 + bx
- Возьмем «a» в качестве общего множителя в правой части.
y – c = a(x 2 + (b/a)x)
- Добавьте член a(b / 2a) 2 как к правой, так и к левой стороне.
y – c + (b 2 /4a) = a(x 2 + (b/a)x + (b/2a) 2 )
- Теперь уравнение на RHS имеет вид форма (м + п) 2 .
у – (с + (б 2 /4а)) = а(х + (б/2а) 2 )
Сравнивая это уравнение с вершинной формой параболы, мы можем наблюдать следующую связь между значениями a, b, c и h, k.
Вершина (h, k) = (-b/2a, c – (b 2 /4a))
Примеры задач
Задача 1. Найти точку поворота параболы, определяемой уравнение y = 5x 2 + 3x + 2.
Решение:
Дано, y = 5x 2 + 3x + 2: a = 5 b = 3 c = 2
Используя приведенную выше формулу, (h, k) = (-b/2a, c – (b 2 /4a))
⇒ h = -3/(2 × 5) = -3/10 = 0,3
⇒ k = 2 – (3 × 3)/(4 × 5) = 2 – (9/20) = 1,55
Итак, (h, k) = (0,3, 1,55)
Задача 2 : Учитывая функцию F(x) = 7x 2 + 5x + 8, найдите значение x, при котором оно увеличивается.
Решение:
Уравнение 7x 2 + 5x + 8 имеет форму параболы.
Где, a = 7, b = 5 и c = 8
Мы знаем, что при a > 0 парабола имеет восходящее или возрастающее направление при x > h.
Используя приведенную выше формулу, (h, k) = (-b/2a, c – (b 2 /4a))
⇒ h = -5/(2 × 7) = -5/14 = -0,357
Итак, функция возрастает при (x > -0,357)
Задача 3: Каково минимальное значение функции y = 3x 2 + 8x + 1?
Решение:
Уравнение y = 3x 2 + 8x + 1 имеет форму параболы.
Где, a = 3, b = 8 и c = 1
Мы знаем, что при a > 0 парабола имеет минимальное значение в своей вершине.
Используя приведенную выше формулу, вершина V (h, k) = (-b/2a, c – (b 2 /4a))
⇒ h = -8/(2 × 3) = -8/ 6 = -1,33
⇒ k = 1 – (8 × 8/(4 × 3)) = 1 – (64/12) = -4,33
Следовательно, минимальное значение функции находится при (-1,33, — 4.
33).
Задача 4. Найти точку поворота параболы, заданной уравнением y = 1x 2 + 2x + 3.
Решение:
Дано, y = 90 2 9 0 3x 1 3,
a = 1
b = 2
c = 3
Используя приведенную выше формулу, точка поворота или вершина равна
(h, k) = (-b/2a, c – ( b 2 /4a))
⇒ h = -2/(2 × 1) = -1
⇒ k = 3 – (2 × 2/4) = 2
Итак, (h, k) = (-1, 2)
Задача 5. Для заданной функции F(x) = -2x 2 + 2x + 1 найти значение x, для которого она уменьшение.
Решение:
Уравнение -2x 2 + 2x + 1 имеет форму параболы.
Где, a = -2, b = 2 и c = 1
Мы знаем, что при a < 0 парабола имеет нисходящее или убывающее направление при x > h.
Используя приведенную выше формулу,
(h, k) = (-b/2a, c – (b 2 /4a))
⇒ h = -2/(2 × (-2)) = 1/2 = 0,5
Итак , функция возрастает при (x > 0,5).
Задача 6: какова вершина параболы Y = -8x 2 + 8x + 1.
Решение:
Учитывает Y = -8x 2 + 8x + 1:
a = -8
b = 8
c = 1
Используя приведенную выше формулу, (h, k) = (-b/2a, c – (b 2 /4a))
⇒ h = -8/(2 × (-8)) = 1/2 = 0,5
⇒ k = 1 – (8 × 8/(4 × (-8)) = 1 + (64/32) = 3
Итак, (h, k) = (0,5, 3)
Задача 7. Для заданной функции y = -9x 2 + 2x + 5 найти максимум точка кривой.
Решение:
Уравнение y = -9x 2 + 2x + 5 имеет форму параболы.
Где, a = -9, b = 2 и c = 5
Мы знаем, что при a < 0 точка максимума параболы находится в точке (h, k).
Используя приведенную выше формулу, (h, k) = (-b/2a, c – (b 2 /4a))
⇒ h = -2/(2 × (-9)) = 1/ 9 = 0,11
Итак, функция возрастает для (x > 0,5)
Как построить параболу за 3 простых шага — Mashup Math
Предварительный просмотр руководства: Как построить параболу.
В алгебре важно понимать поведение квадратичных функций и их графики. В этом кратком руководстве рассматриваются следующие ключевые понятия (включая примеры):
Как построить параболу?
Как нарисовать параболу в стандартной форме?
Построение параболы на координатной плоскости
92+bx+c (обратите внимание, что в этом руководстве мы будем использовать f(x)= и y= взаимозаменяемо). Построение графика параболы на координатной плоскости с использованием ее формулы является важным навыком алгебры, и это руководство научит вас простому 3-этапному процессу, который вы можете использовать для построения графика параболы практически в любом сценарии. Шаг 1: Найдите координаты точки вершины
Шаг 2: Создайте таблицу функций и «постройте» две точки на каждой стороне вершины
Шаг 3: Нанесите точки и постройте кривую (параболу)
Шаг B: Введите значение координаты x из шага A в функцию, чтобы найти значение координаты y.
Теперь, когда вы знаете, что значение координаты x для вершины равно x=-3, вы можете ввести x=-3 в функцию, чтобы найти значение координаты y следующим образом: 92 -6(-3) + 5 → f(2) = 4 — 8 + 5 = -4 → y=-4
Прежде чем вы научитесь строить параболы в стандартной форме, давайте рассмотрим некоторые ключевые понятия и словарный запас, связанные с квадратичными функциями и их графиками, прежде чем перейти к нескольким примерам графических парабол. 92 -4x + 5, a=1, b=-4 и c=5
92 -4x + 5, a=1, b=-4 и c=5
График функции представляет собой параболу — U-образную плоскую кривую, симметричную относительно линии симметрии, проходящей через вершинная точка. Парабола симметрична и образует зеркальное отражение самой себя по разные стороны от линии симметрии, проходящей через точку вершины.
На рисунке 01 ниже показаны примеры квадратичных функций в стандартной форме вместе с соответствующим графиком. Обратите внимание на U-образную параболу для каждого графика вместе с точкой вершины. Также обратите внимание, что парабола может открываться вверх (U-образная форма) или открываться вниз (перевернутая U-образная форма).
Рисунок 01: Как построить параболу: примеры построения параболы на координатной плоскости
Теперь, когда вы знаете, как выглядит график квадратичной функции в стандартной форме, давайте еще раз посмотрим, что такое вершина параболы.
Вершина параболы — это координатная точка (x,y), в которой пересекаются парабола и ее ось симметрии.
В Рисунок 01 выше вершина параболы помечена, а осью симметрии является горизонтальная пунктирная линия, проходящая через нее.
Проще говоря, что является вершиной параболы? Вершина — это точка в самом низу кривой для парабол, открывающихся вверх, или в самом верху кривой для парабол, открывающихся вниз.
Если вы можете найти вершину параболы, то вы можете легко научиться рисовать параболу на координатной плоскости, поэтому важно понять, что такое вершина параболы и как ее найти. К счастью, найти вершину параболы несложно, если выполнить два простых шага:2-4х+5 равно (2,1).
График этой функции, включая точку вершины, показан на координатной плоскости Рисунок 03 .
Теперь, когда вы знаете, как найти точку вершины параболы, вы готовы выполнить несколько пошаговых примеров того, как изобразить параболу на координатной плоскости, используя 3 простых шага (первый из которых определить, что является вершиной параболы).
92 + 6x + 5
Теперь вы готовы начать рисовать параболу на координатной плоскости, используя простой трехэтапный метод:
Теперь давайте продолжим и применим эти три шага к этому первому примеру: 92 + 6x + 5, мы будем использовать тот же процесс, показанный в Рисунок 02 выше, следующим образом:
Поскольку b=6 и a=1, x=-b/2a → x= -6 / 2(1) → x = -6/2 → x = -3
Итак, координаты вершины парабола (-3,-4)
Как построить параболу: используйте таблицу функций.
Шаг 2: Создайте таблицу функций и «постройте» две точки на каждой стороне вершины
Как только вы определите координаты точки вершины, вы можете построить таблицу функций, как показано на рисунке 9.0067 Рисунок 04 . Ваша таблица функций должна включать столбец с координатами x и столбец с координатами y, а также строки не менее чем для пяти точек на графике.
Поскольку вершина представляет собой «точку поворота» U-образной параболы, координаты вершины должны быть помещены в середину таблицы функций.
Затем пришло время «построить» точки по обе стороны от точки вершины, введя значения x, которые меньше -3 и больше 3, в исходную функцию и выводят значения.
Опять же, поскольку координата x точки вершины равна -3, мы выберем два значения x меньше -3 (-4 и -5 в этом примере) и два значения x больше — 3 (-2 и -1 в этом примере).
Затем возьмите каждое значение x и введите его в функцию, чтобы найти соответствующее значение y. Например, чтобы найти значение координаты y при x=-5, просто оцените значение f(-5), как показано на Рисунок 04 ниже.
Например, чтобы найти значение координаты y при x=-5, просто оцените значение f(-5), как показано на Рисунок 04 ниже.
Рисунок 05: Заполненная таблица функций
Шаг 3: Нанесите точки и постройте кривую (параболу)
Третий и последний шаг — нанесение всех пяти точек таблицы функций на координатную плоскость. Вы должны заметить, что точки следуют симметричной U-образной форме с точкой поворота вокруг точки вершины, которая в этом примере (-3,-4).
Обратите внимание, что точки в заполненной таблице функций: (-5,0), (-4,-3), (-3,-4), (-2,-3) и (-1,0) .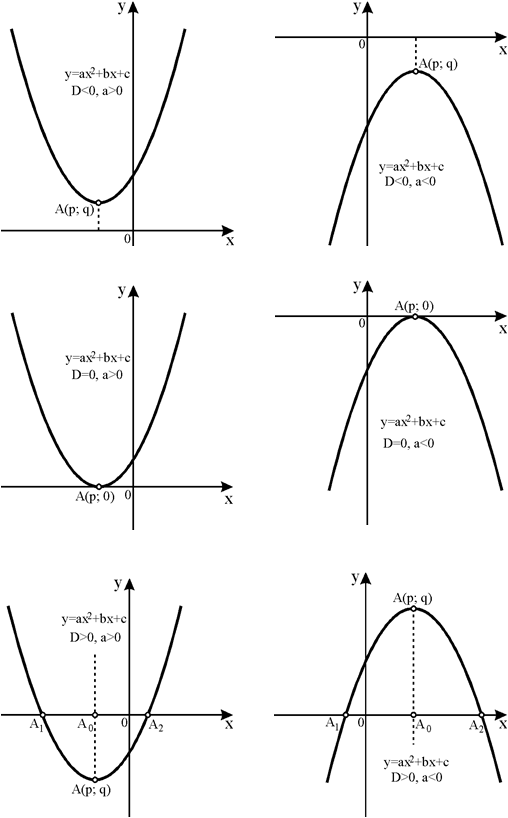 После нанесения этих пяти точек на координатную плоскость у вас должен получиться график, похожий на Рисунок 06 ниже.
После нанесения этих пяти точек на координатную плоскость у вас должен получиться график, похожий на Рисунок 06 ниже.
Рисунок 06: Как построить параболу: начертите все точки из таблицы функций.
После того, как ваши точки были нанесены, вы готовы построить свою параболу, нарисовав U-образную кривую, которая проходит через все пять точек, как показано на рисунке 9.2 -2(1) -6 → f(1) = 1- 2 -6 = -7 → y=-7
Итак, координаты вершины параболы равны (1,-7)
Шаг 2: Создайте таблицу функций и «постройте» две точки с каждой стороны вершины
Теперь, когда вы знаете координаты точки вершины (1,-7), вы можно начать построение точек по обе стороны от вершины, вводя значения x, которые меньше 1 (0 и -1 в этом примере) и больше 1 (2 и 3 в этом примере) в исходную функцию и выводят значения координаты y.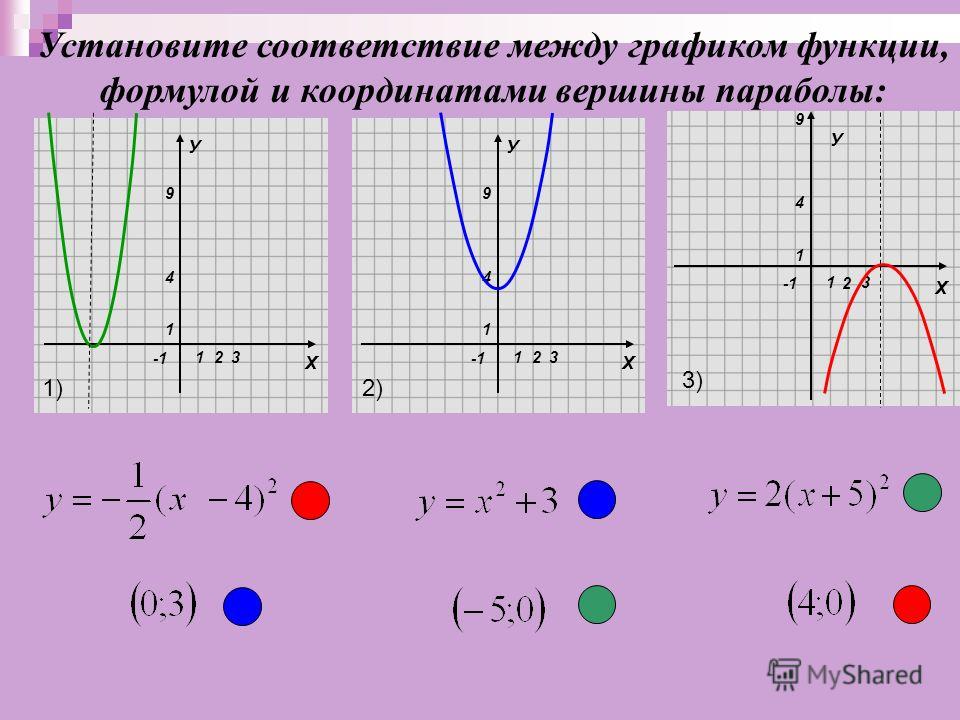 92-2(0)-6 = 0-0-6 = -6
92-2(0)-6 = 0-0-6 = -6
Итак, вы можете заключить, что, когда x равно 0, y равно -6 (и что (-6,0) является точкой на параболе На рисунке 08 ниже показано, как рассчитать f(0), а также все другие точки в таблице данных.
Рисунок 08: Заполненная таблица данных
Шаг 3: Нанесите точки и постройте кривую (параболу)
После того, как вы заполнили таблицу данных, вы готовы нанести все пять следующих точек на координатную плоскость: (-1,-3), (0,-6), (1,-7), (2,-6) и (3,-3). 92 +8(4) -12 → f(4) = -16 + 32 — 12 → y=4
Итак, координаты вершины параболы равны (4,4)
Шаг 2: Создайте таблицу функций и «постройте» две точки на каждой стороне вершины
Затем используйте точку вершины (4,4) для построения точек на каждой стороне вершины путем ввода значений x, которые оба меньше 4 (3 и 2 в этом примере) и больше 4 (5 и 6 в этом примере) в исходную функцию и выводят значения координаты y. 92+8(5)-12 = -25 + 40 — 12 = 3
92+8(5)-12 = -25 + 40 — 12 = 3
Итак, вы можете заключить, что когда x равно 5, y равно 3 (и что (5,3) является точкой на параболе. На рисунке 11 ниже показано, как вычислить f(5), а также все другие точки в таблице данных.
Рисунок 11: Завершенная функциональная схема
Шаг 3: Нанесите точки и постройте кривую (параболу)
Теперь вы готовы нанести точки (2,0), (3,3), (4,4), (5,3), и (6,0) на координатной плоскости, как показано на Рисунок 12 ниже:
Рисунок 12
Обратите внимание, что парабола в примере №3 раскрывается вниз (в то время как параболы в примерах 1 и 2 раскрываются вверх). Это совершенно нормально, так как параболы могут раскрываться вверх или вниз.
Последним шагом будет начертить кривую, проходящую через точки, чтобы завершить построение параболы, как показано на .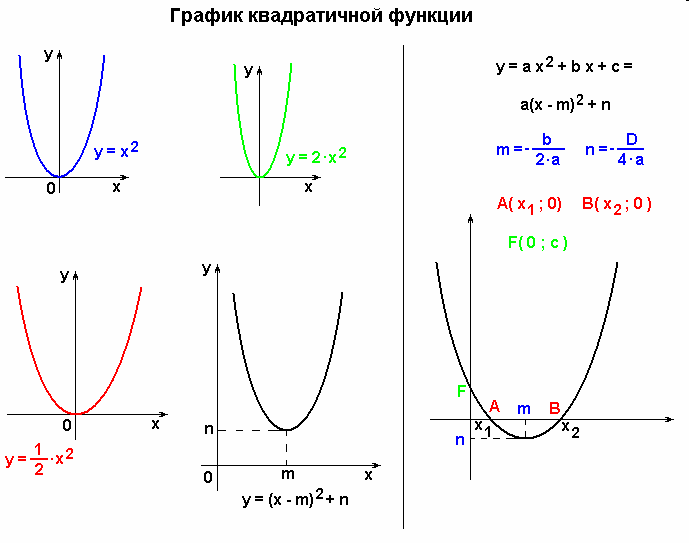


 33).
33).