Ромб. Формулы, признаки и свойства ромба
Ромб. Формулы, признаки и свойства ромбаНавигация по странице: Определение ромба Признаки ромба Основные свойства ромба Стороны ромба Диагонали ромба Периметр ромба Площадь ромба Окружность вписанная в ромб
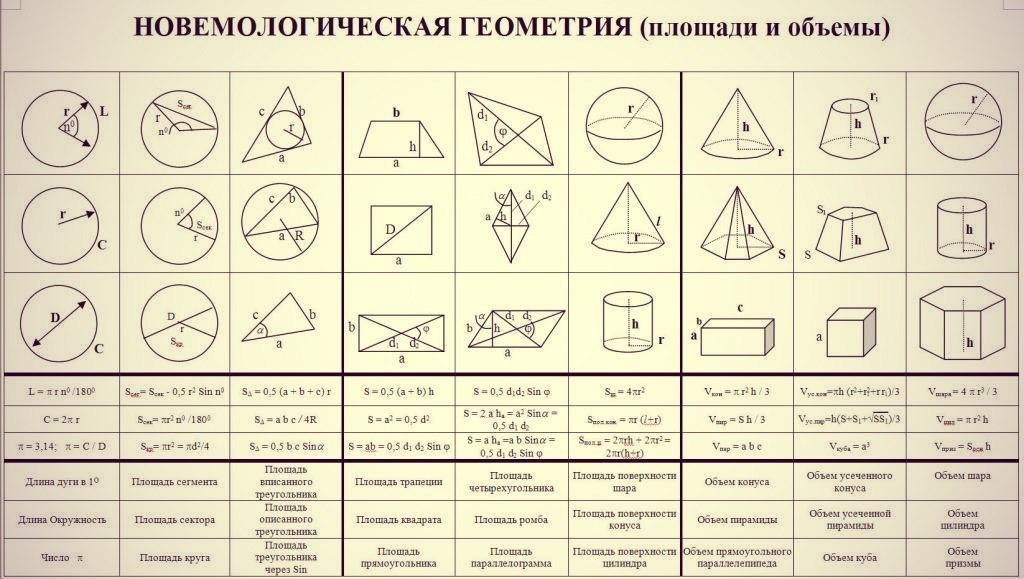
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
| Рис.1 | Рис.2 |
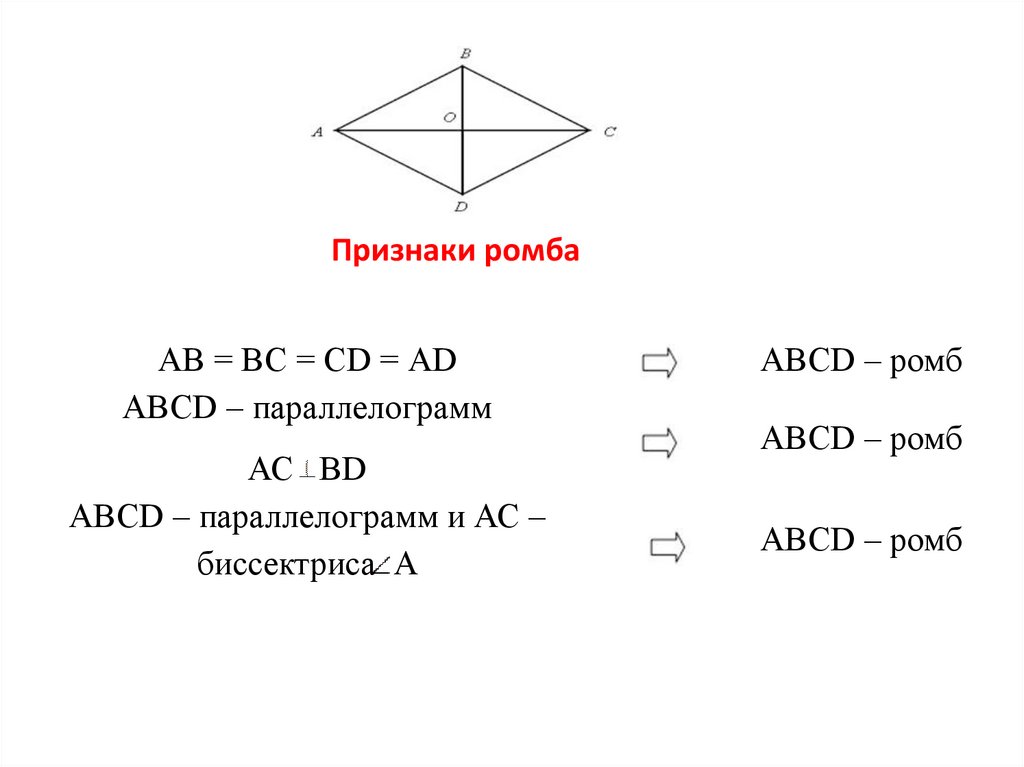
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2.
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
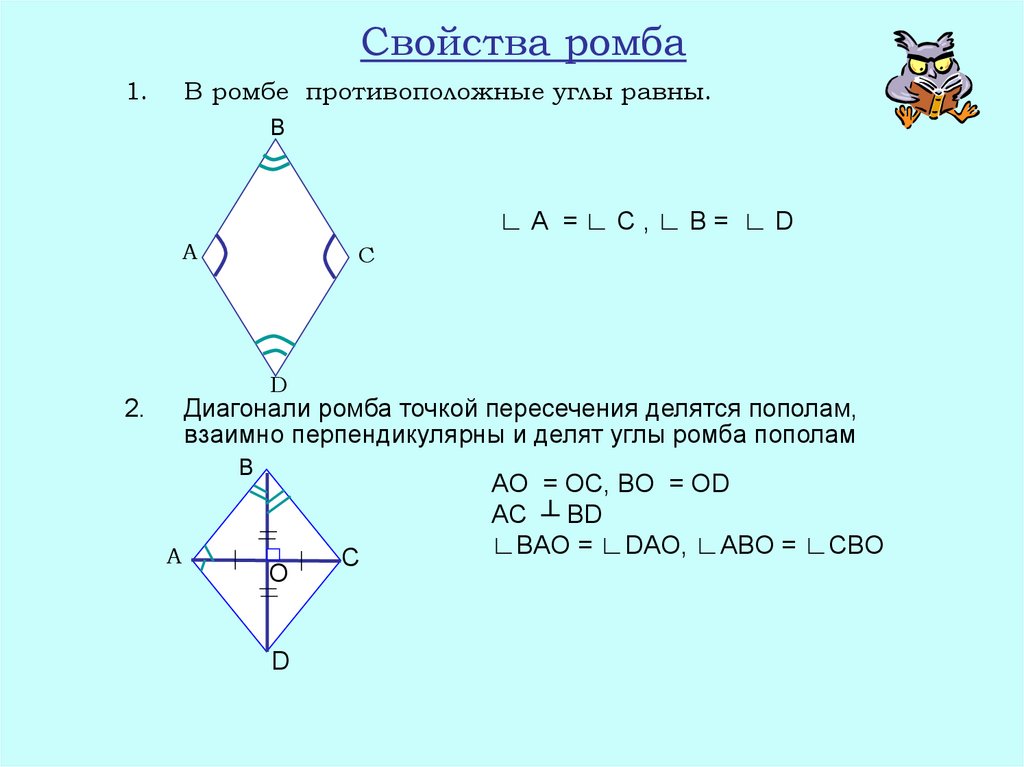
Основные свойства ромба
1. Имеет все свойства параллелограмма
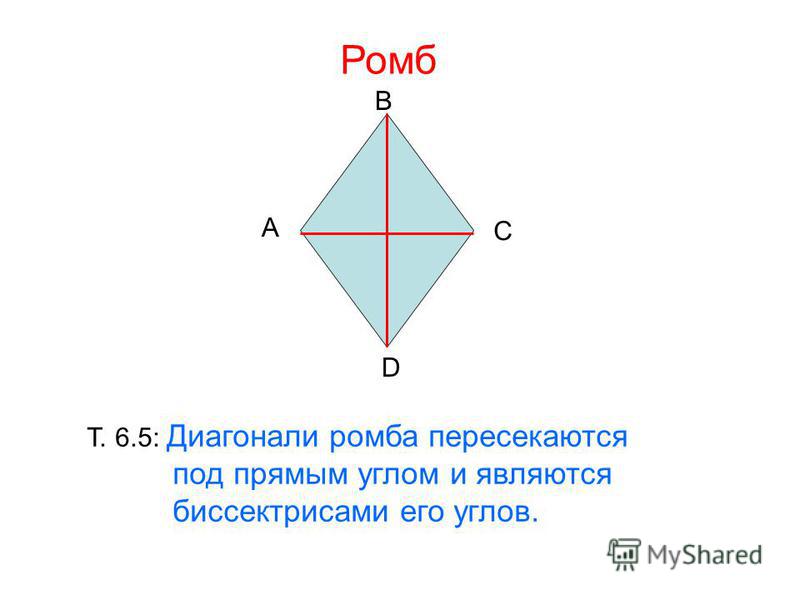
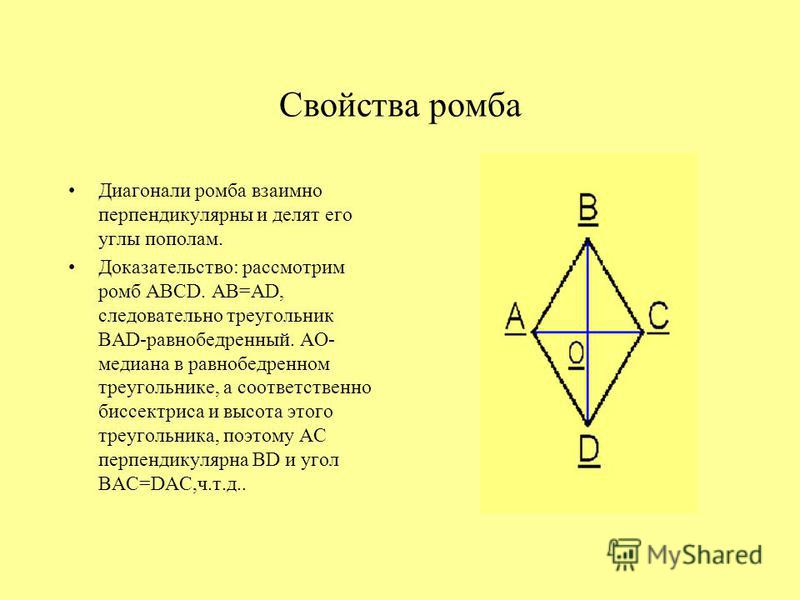
2. Диагонали перпендикулярны:
AC┴BD
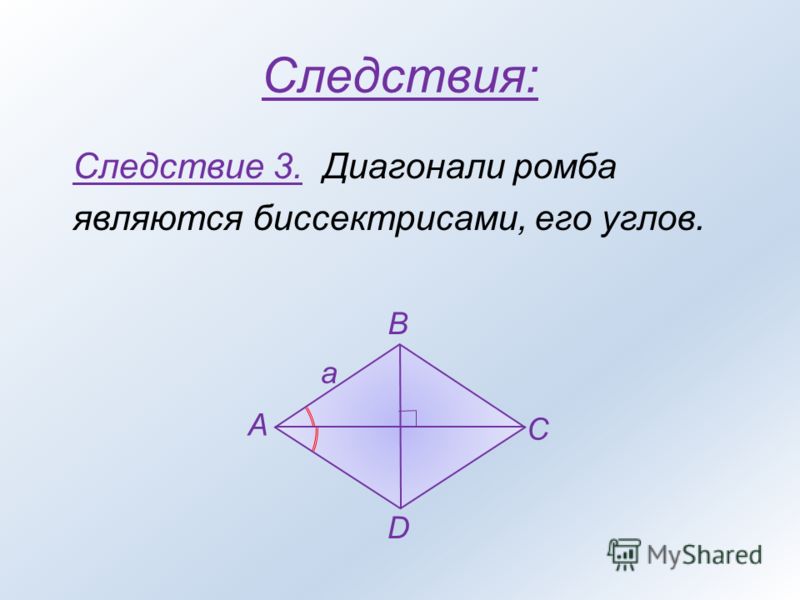
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √S |
| √sinα |
| a = | √S |
| √sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2r |
4. Формула стороны ромба через две диагонали:
| a = | √d |
| 2 |
5.
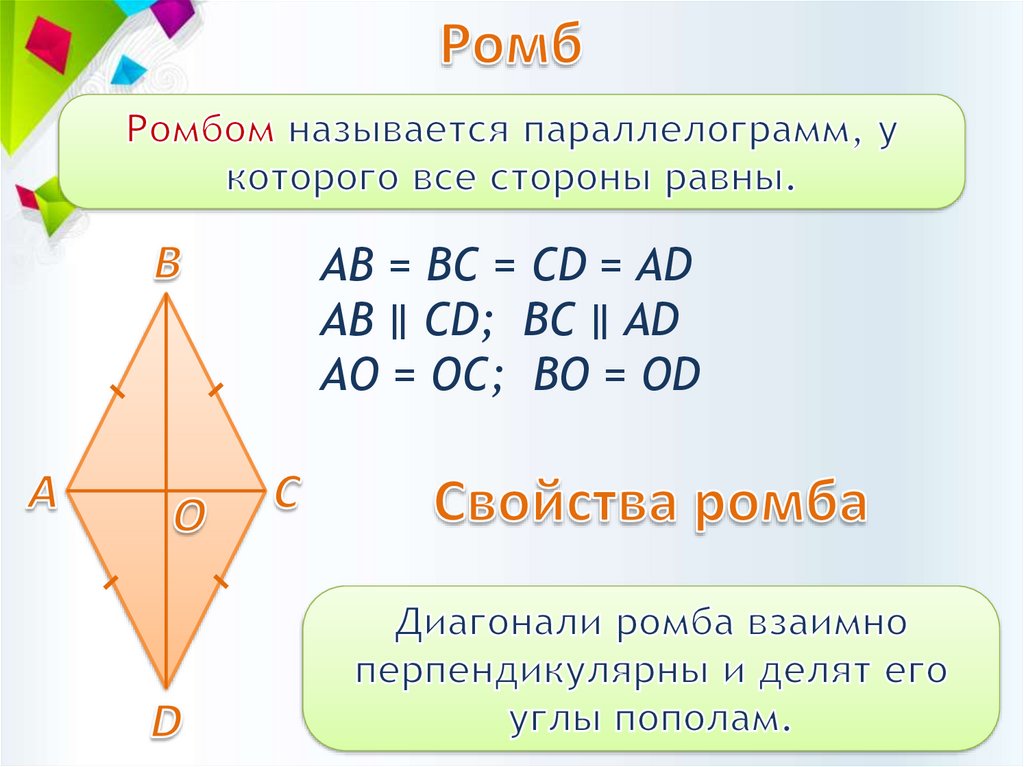Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
| a = | d1 |
| √2 + 2 cosα |
| a = | d2 |
| √2 — 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d1 |
| 2cos(α/2) |
| a = | d1 |
| 2sin(β/2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d2 |
| 2cos(β/2) |
| a = | d2 |
| 2sin(α/2) |
8. Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Диагонали ромба
Определение.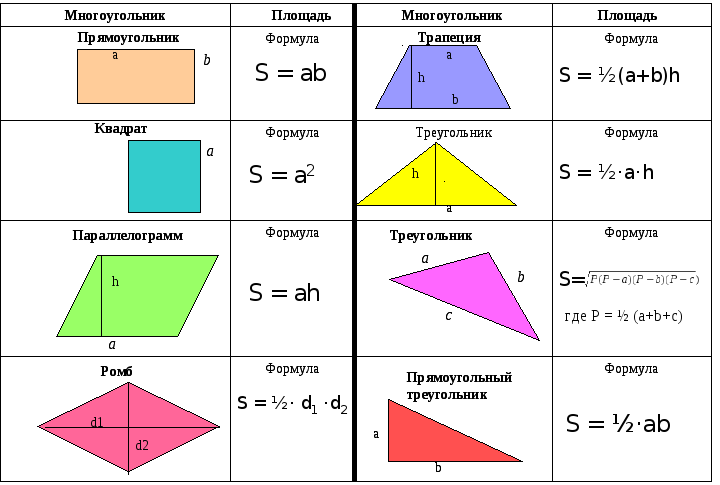
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали — длинную d1, и короткую — d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 — 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 — 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5.
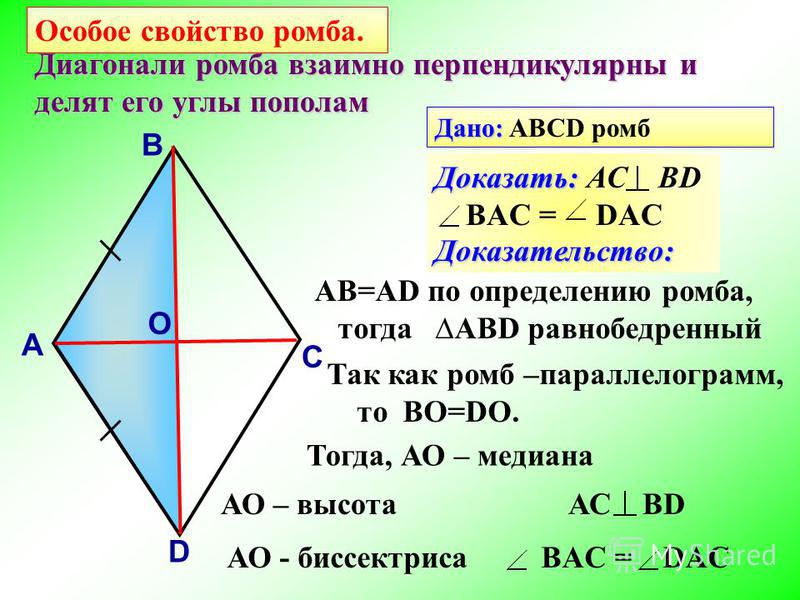Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 — d22
d2 = √4a2 — d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
| d1 = | 2S |
| d2 |
| d2 = | 2S |
| d1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d1 = | 2r |
| sin(α/2) |
| d2 = | 2r |
| sin(β/2) |
Периметр ромба
Определение.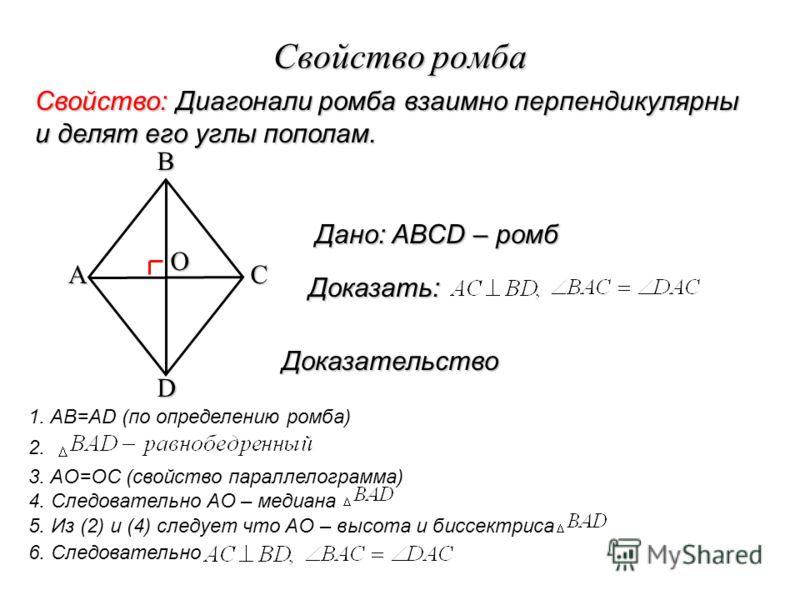
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
| S = | 1 | d |
| 2 |
5.
Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4r2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
| S = | 1 | d12 · tg(α/2) |
| 2 |
| S = | 1 | d22 · tg(β/2) |
| 2 |
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2.
Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d1 · sin(α/2) |
| 2 |
| r = | d2 · sin(β/2) |
| 2 |
6.
Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d1 · d2 |
| 2√d12 + d22 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d1 · d2 |
| 4a |
Все таблицы и формулы
Ромб. Формулы, признаки и свойства ромба
Навигация по странице: Определение ромба Признаки ромба Основные свойства ромба Стороны ромба Диагонали ромба Периметр ромба Площадь ромба Окружность вписанная в ромб
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Рис. 1 | Рис.2 |
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (бисектрисса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
1. Имеет все свойства параллелограмма
2. Диагонали перпендикулярны:
AC┴BD
3.
Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √S |
| √sinα |
| a = | √S |
| √sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2r |
4.
Формула стороны ромба через две диагонали:
| a = | √d12 + d22 |
| 2 |
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
| a = | d1 |
| √2 + 2 cosα |
| a = | d2 |
| √2 — 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d1 |
| 2cos(α/2) |
| a = | d1 |
| 2sin(β/2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d2 |
| 2cos(β/2) |
| a = | d2 |
| 2sin(α/2) |
8.
Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали — длинную d1, и короткую — d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 — 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 — 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4.
Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 — d22
d2 = √4a2 — d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
| d1 = | 2S |
| d2 |
| d2 = | 2S |
| d1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d1 = | 2r |
| sin(α/2) |
| d2 = | 2r |
| sin(β/2) |
Периметр ромба
Определение.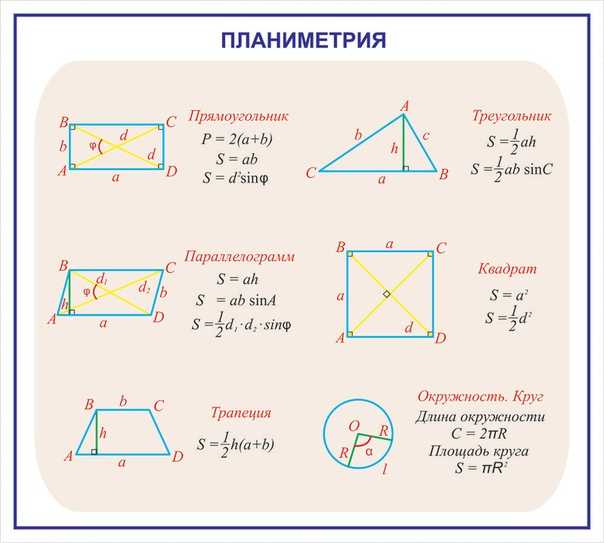
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можна найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
| S = | 1 | d1d2 |
| 2 |
5.
Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4r2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
| S = | 1 | d12 · tg(α/2) |
| 2 |
| S = | 1 | d22 · tg(β/2) |
| 2 |
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2.
Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d1 · sin(α/2) |
| 2 |
| r = | d2 · sin(β/2) |
| 2 |
6.
Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d1 · d2 |
| 2√d12 + d22 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d1 · d2 |
| 4a |
Формулы по геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур
Все таблицы и формулы
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Объем призмы — определение, формулы, примеры и диаграммы
Объем призмы — определение, формулы, примеры и диаграммыСодержание
Последнее изменение: 6 сентября 2022 г.
Оглавление
Объем призмы — это общее количество пространства, которое она занимает в трехмерной плоскости. Измеряется в кубических единицах, таких как см 3 , м 3 , дюймы 3 , футы 3 , ярды 3 .
Формулы
Общая формула для нахождения объема любой призмы: базы.
Однако существуют специальные формулы для расчета объема различных призм из-за их различной формы.
Они приведены ниже:
Объем призмыНекоторые формулы имеют дополнительную маркировку для конкретных призм.
В треугольных, прямоугольных и трапециевидных призмах « l » (или длина) обозначает расстояние между основаниями, а « h » обозначает высоту многоугольного основания.
‘ l ’ — длина квадратной призмы, а ‘ a ’ представляет четыре конгруэнтных базовых ребра. Для пятиугольных и шестиугольных призм « a » — это апофема, а « b » — ребро основания.
Давайте решим несколько примеров с использованием приведенных выше формул, чтобы лучше понять концепцию.
Решенные примеры
Найдите объем треугольной призмы, основание которой равно 40 см, высота 15 см, а длина 60 см.
Решение:
Как известно,
Объем ( V ) = ${\dfrac{1}{2}\times b\times h\times l}$, здесь b = 40 см, h = 15 см, л = 60 см
∴ V = ${\dfrac{1}{2}\times 40\times 15\times 60}$
= 18000 см 3
Найдите ширину прямоугольной призмы 7 см, высота 12 см, длина 16 см.
Решение:
Как мы знаем,
Объем (V) = l × w × h , здесь l = 16 cm, w = 7 cm, h = 12 cm
∴ V = 16 × 7 × 12
= 1344 cm 3
Find the volume of a пятиугольная призма, основание которой 6 см, апофема 4,13 см, высота 8 см.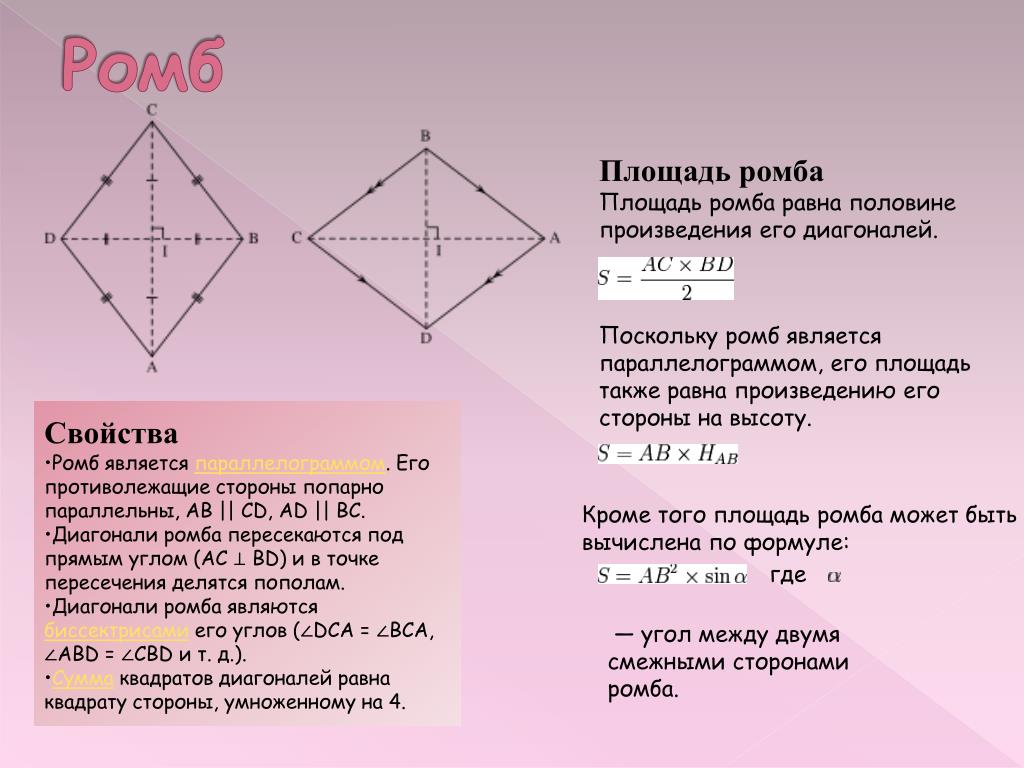
Решение:
Как известно,
Объем ( V ) = ${\dfrac{5}{2}abh}$, здесь a = 4,13 см, b = 6 см, ч = 8 см
∴ V = ${\dfrac{5}{2}\times 4,13\times 6\times 8}$
= 495,6 см³
Найдите объем шестиугольной призмы, основание которой равно 12 см, апофема равна 10,39 см и высота 20 см.
Решение:
, как мы знаем,
объем ( V ) = 3 ABH , здесь A = 10,39 см, B = 12 CM, H = 20 СМ
≈ 7480,8 см³
Найдите объем трапециевидной призмы, ребра основания которой равны 34 см и 22 см, высота по вертикали 12 см, а длина 52 см.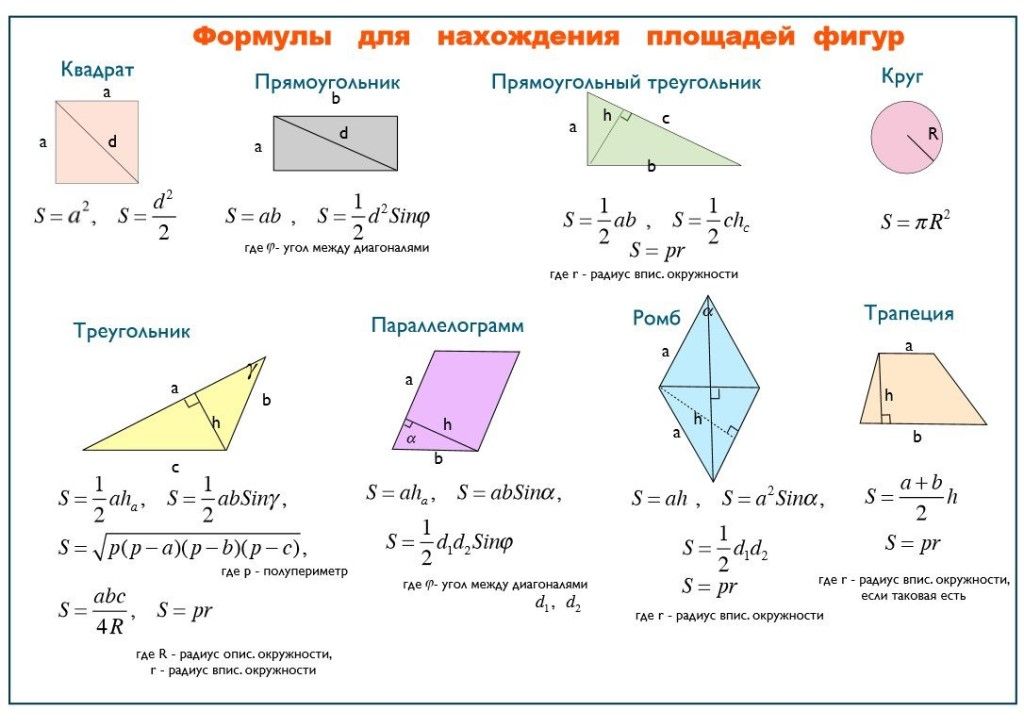
Решение:
Как мы знаем,
Объем ( V ) = ${\dfrac{1}{2}\left(a+b\right) \times h\times l}$, здесь a = 34 см, b = 22 см, h = 12 см, l = 52 см
∴ V = ${\dfrac{1}{2}\times \left( 34+22 \справа) \раз 12\раз 52}$
= 17472 см 3
Найдите объем квадратной призмы, длина ребра которой равна 7 дюймов, а длина равна 11 дюймам .
Решение:
Как мы знаем,
объем ( V ) = A 2 × L , здесь A = 7 в, L = 11 в
∴ v 9 V
v V = = v V = = 11. 7 2 × 11
= 539 в 3
- Дополнительные ресурсы:
- Объем призмы
- Surface Area of a Prism
- Right Prism
- Oblique Prism
- Rectangular Prism
- Volume of a Rectangular Prism
- Surface Area of a Rectangular Prism
- Triangular Prism
- Volume of a Triangular Prism
- Surface Area of a Треугольная призма
- Шестиугольная призма
- Объем шестиугольной призмы
- Площадь поверхности шестиугольной призмы
- Пятиугольная призма
- Объем пятиугольной призмы
- Surface Area of a Pentagonal Prism
- Trapezoidal Prism
- Volume of a Trapezoidal Prism
- Surface Area of a Trapezoidal Prism
- Square Prism
- Volume of a Square Prism
- Surface Area of a Square Prism
- Octagonal Prism
- Семиугольная призма
- Десятиугольная призма
Последнее изменение: 6 сентября 2022 г.
Его свойства, форма, диагонали, стороны и формула площади
Вероятно, самым известным ромбом является бейсбольный ромб. Расстояние между каждым основанием одинаковое, придаем форму ромба!
Больше интересных математических фактов!
Ромб — разновидность параллелограмма, и что отличает его форму, так это то, что все четыре его стороны конгруэнтный.
Есть несколько формул для ромба, которые связаны с ним:
- Стороны (нажмите, чтобы узнать подробнее)
Все 4 стороны равны.
- углов
Диагонали делят углы при вершине пополам.
- Диагонали
Диагонали перпендикулярны.
- Район
Является ли квадрат ромбом?
Отвечать:
Да, квадрат — это ромб
У квадрата должны быть 4 равные стороны. Каждый ромб имеет 4 равные стороны, поэтому каждый квадрат также является ромбом. Квадрат – это особый ромб, у которого тоже 4 прямых угла.
Имейте в виду, что на вопрос «Является ли квадрат ромбом?» означает Всегда ли каждый квадрат также является ромбом?
Является ли ромб квадратом?
Отвечать:
Нет, ромб не квадрат
У квадрата должно быть 4 прямых угла. С другой стороны, ромб не имеет никаких правил относительно его углов, поэтому существует множество примеров ромба, которые не являются также квадратами.
Имейте в виду, что на вопрос «Является ли ромб квадратом?» означает Всегда ли каждый ромб является квадратом?
Диаграмма 2
Как вы можете видеть на диаграмме 2, можно создать ромб, который не является квадратом.
Все стороны ромба равны.
$ \overline{AB} \cong \overline{BC} \\ \overline{BC} \cong \overline{CD} \\ \overline{CD} \cong \overline{DA} $
Уголки
Диагонали делят пополам углы при вершине ромба.
Доказательство этого свойства диагоналей.
Диагонали
Диагонали перпендикулярны.
$$ \ угол AOD = 9{\ круг} \\ $$
Площадь ромба
Площадь = ½ (диагональ 1 × диагональ 2 )Алекс, пожалуйста, поместите сюда калькулятор ромбов. вход 1) длина стороны 2) вывод — измерения углов и площади
Практические задачи
Собираем все вместе
- Исходная проблема
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
- Шаг 6
- Шаг 7
ЗВЕЗДА – это ромб. Мера диагоналей SA равно 24, а размер TR равен 10, каков периметр этого ромба?
Спросите себя: что верно в отношении углов, образованных диагоналями ромба?
Углы перпендикулярны!
Что верно в отношении диагоналей всех параллелограммов?
Диагонали параллелограмма делят друг друга пополам.
Следовательно, ZA = 12, ZT = 5
Что за треугольник ЗТА?
Прямоугольный треугольник!
Таким образом, вы можете использовать теорему Пифагора найти меру стороны TA
Теперь, когда вы знаете длину TA? Как можно использовать тот факт, что стороны ромба конгруэнтны, чтобы закончить эту задачу?
Так как все 4 стороны должны быть 13.
Периметр = 13 + 13 + 13 +13 = 52
Проблема 1
Если сторона WX = 22, что такое WZ?
ВЗ = 22
Проблема 2
Если сторона MN ромба LMNO равна X + 5, а сторона LM равна 2x − 9, каким должно быть значение х?
Проблема 3
Каким должен быть x, если сторона BA = 5x-11
и сторона
АД = 6х-18?
Так как эта фигура является ромбом, вы можете положить любую его сторону равной друг другу.
Проблема 4
Является ли четырехгранная фигура внизу, MNOP, ромбом? Если нет, классифицируйте форму.
Фигура ниже не является ромбом, потому что его диагонали не равны.