Периметр параллелограмма — онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Периметр параллелограмма рассчитывается как удвоенная сумма сторон фигуры. Несложные действия можно произвести самостоятельно. Если перед вычислениями необходимо выполнить конвертацию из одних единиц измерения в другие, потребуется больше времени. Неверный перевод приводит к ошибочному ответу.
Набор программ по основным математическим темам помогает получать верное решение и ответ без предварительных переводов. Вам понадобится ввести данные из задачи, после чего будет доступно подробное вычисление.
- Введите стороны параллелограмма.
- Установите единицы измерения для сторон фигуры и искомого периметра.
- Получите решение и ответ.
Ответ:
Решение
Ответ:
Похожие калькуляторы:
- Длина окружности круга (По радиусу)
- Длина окружности круга (По диаметру)
- Периметр квадрата
- Периметр треугольника
- Периметр трапеции
- Периметр прямоугольника
- Периметр ромба
- Периметр квадрата по диагонали
Программа позволяет вычислить периметр параллелограмма по формуле:
где a, b – стороны фигуры.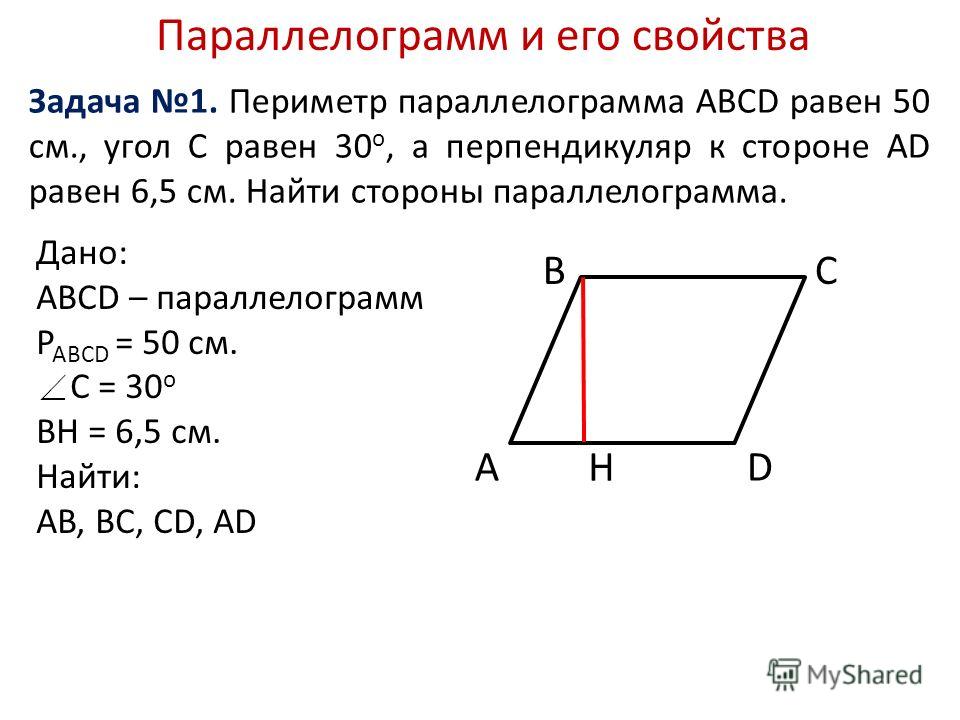
Сервис протестирован перед запуском. Вы получите бесплатное подробное решение. Автоматические подсчеты исключают ошибки. Для использования калькуляторов нет необходимости в регистрации. Расчеты не ограничиваются.
Нас выбирают:
- Школьники. Подготовку к экзаменам и поступлению можно осуществлять самостоятельно без затрат на репетитора. Темы по алгебре, геометрии сгруппированы по разделам. Так легче осваивать и повторять материал.
- Родители учеников. Теперь проверка домашних заданий, помощь в объяснении материала ребенку не будет вызывать трудностей и отнимать много времени. Изучать тему самому, искать подходящую формулу также не понадобится.
- Преподаватели. Большой объем заданий легче проверять автоматически. Также планирование уроков и подготовку задач для контрольных быстрее делать с помощью сервиса.
Студенты. Во время зачетов и экзаменов важна скорость получения решения. Моментальный расчет с помощью сервиса поможет сдать требуемые задания на хорошую оценку.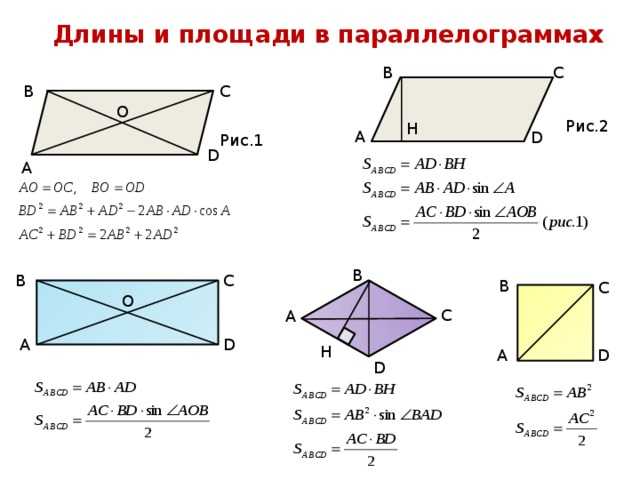
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Процент
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Все наши услуги
Узнай бесплатно стоимость работыНе получается написать работу самому?
Доверь это кандидату наук!
Периметр паралелограма.
Як знайти периметр паралелограмаПериметр паралелограма визначається як сума довжин усіх сторін паралелограма. Периметр паралелограма також можна знайтим за довжиною основи, довжиною висоти та внутрішнім кутом.
Зазначимо, що в даній публікації ми ознайомимося з двома формулами, за допомогою яких можна знайти периметр паралелограма. Крім того, будемо використовувати ці формули для рішення деяких задач.
Навігація по сторінці.
- Як знайти периметр паралелограма?
- Периметр паралелограма – приклади з відповідями.
- Блок-схема алгоритму знаходження периметра паралелограма.
Як знайти периметр паралелограма?
Периметр паралелограма, як і будь-якого багатокутника, дорівнює сумі довжин кожної з його сторін. До прикладу, периметр зображеного нижче паралелограма дорівнює сумі довжин сторін і .
Проте, скориставшись однійє з властивостей паралелограма, а саме властивістю яка свідчить про те, що протилежні його сторони рівні, приходимо до висновку, що для того, щоб знайти периметр паралелограма, достатньо суму довжин його суміжних сторін помножити на два, тобто , де – периметр паралелограма .
Периметр паралелограма за основою, висотою і кутом.
Знайдемо периметр паралелограма за основою, висотою і будь-яким кутом при вершині.
Для цього, знову-таки, розглянемо паралелограм , для якого проведемо висоту і припустимо, що – невідома сторона даного паралелограма.
Для початку знайдемо довжину невідомої сторони.
Отже, розглянемо прямокутний трикутник . Застосовуючи до даного трикутника теорему синусів отримаємо, що . Звідси, .
Далі, скориставшись означенням периметра паралелограма та властивістю про протилежні сторони матимемо: , де – периметр паралелограма .
Зауваження: оскільки , то у формулі периметра паралелограма через основу, висоту і кут не важливо який із кутів при вершині брати.
Зауваження: якщо позначити довжини суміжних сторін та висоту паралелограма буквами , і відповідно, то формули периметра перепишеться у більш звичній буквенній формі:
Периметр паралелограма – приклади з відповідями.
Для вирішення наступних прикладів застосовується формула периметра паралелограми. Спробуйте розв’язати приклади самостійно, перш ніж дивитись на рішення.
Приклад 1: знайти периметр паралелограма, якщо його сторони дорівнюють і .
Отже, за умовою маємо, що сторони паралелограма рівні і відповідно. Скориставшись формулою периметра із заданими значенням матимемо:
Таким чином, периметр паралелограма дорівнює .
Приклад 2: знайти периметр паралелограма, якщо його сторони дорівнюють і .
Зазначимо, що у цьому випадку сторони паралелограма рівні та . Тому, замінивши та у формулі периметра заданим значенням отримаємо:
Отже, периметр паралелограма дорівнює .
Приклад 3: периметр паралелограми дорівнює . Одна з його сторін має довжину . Яка довжина іншої сторони?
Зазначимо, що у цьому випадку, знаючи периметр та довжину сторони, ми повинні знайти іншу сторону паралелограма. Отже, використовуючи ту ж формулу, підставляємо задані значення та знаходимо невідому сторону :
Звідси, довжина іншої сторони паралелограма дорівнює .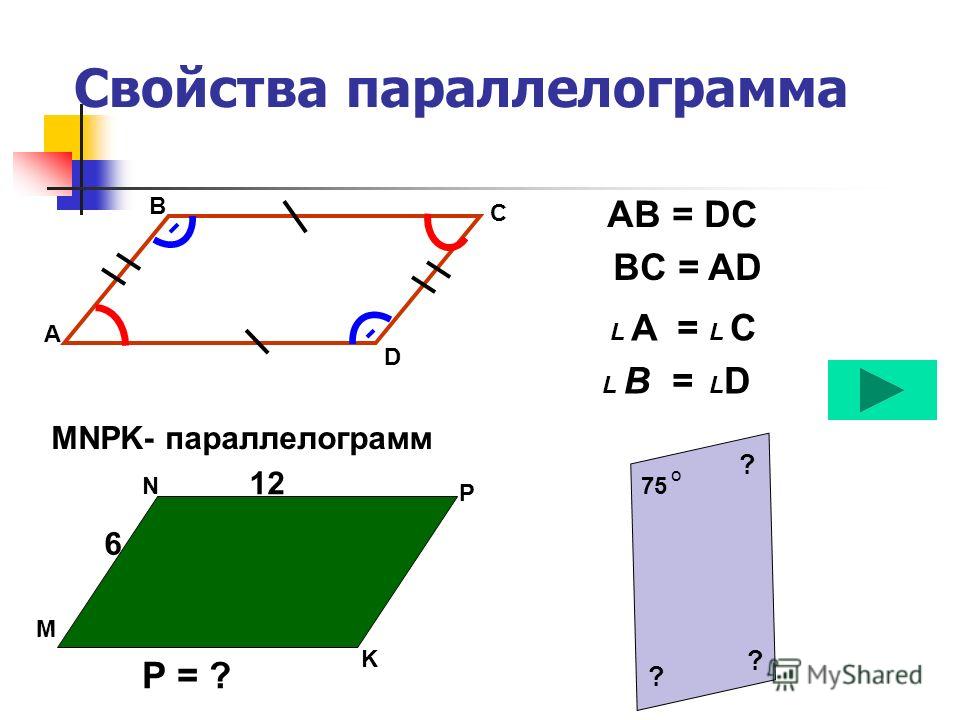
Приклад 4: паралелограм має висоту і основу довжиною . Чому дорівнює периметр паралелограма, якщо один з його кутів становить ?
Отже, скориставшись формулою обчислення периметра паралелограма через основу, висоту і кут матимемо:
Таким чином, периметр паралелограма дорівнює .
Приклад 5: бісектриса кута паралелограма перетинає сторону в точці . Знайти периметр паралелограма, якщо відомо, що і .
Виходячи з того, що кути і рівні як різносторонні при паралельних прямих і та січній ( – бісектриса кута ), приходимо до висновку, що .
Звідси, трикутник рівнобедрений, а отже .
Далі, скориставшись формулою обчислення периметра паралелограма, отримаємо:
Отже, периметр паралелограма дорівнює .
Дивіться також:
Хочете дізнатися більше про паралелограми? Перегляньте ці сторінки:
- Паралелограм і його властивості.
- Діагональ паралелограма – формули та приклади.
- Площа паралелограма – формули та приклади.
Блок-схема алгоритму знаходження периметра паралелограма
Ми в соціальних мережах
Площадь и периметр параллелограмма: формулы и примеры решения
Четырехугольник — замкнутая фигура, образованная пересечением четырех отрезков. Параллелограмм образуется, когда противоположные стороны четырехугольника параллельны и имеют одинаковую длину.
Длина непрерывной линии, образуемой границей параллелограмма, является его периметром. Площадью параллелограмма называют пространство, занимаемое параллелограммом в двумерной плоскости.
В этой статье мы узнаем все о площади и периметре параллелограмма с формулами, диаграммами и решенными примерами.
Площадь и периметр параллелограмма
Площадь двумерной фигуры – это пространство, ограниченное периметром данной фигуры. Чтобы вычислить площадь различных фигур, используйте разные формулы, основанные на количестве сторон и других характеристиках, таких как углы между сторонами.
Периметр двумерной фигуры — это общее расстояние вокруг соответствующей фигуры. Для фигур с прямыми сторонами, таких как треугольники, прямоугольники, квадраты или многоугольники; периметр это сумма длин всех сторон.
Параллелограмм представляет собой плоскую фигуру с четырьмя прямыми, соединенными сторонами, так что противоположные стороны конгруэнтны и параллельны. Это означает, что параллелограмм является плоской фигурой, замкнутой формой и четырехугольником.
Периметр
Периметр параллелограмма — это длина границы параллелограмма. Проще говоря, это сумма всех сторон параллелограмма.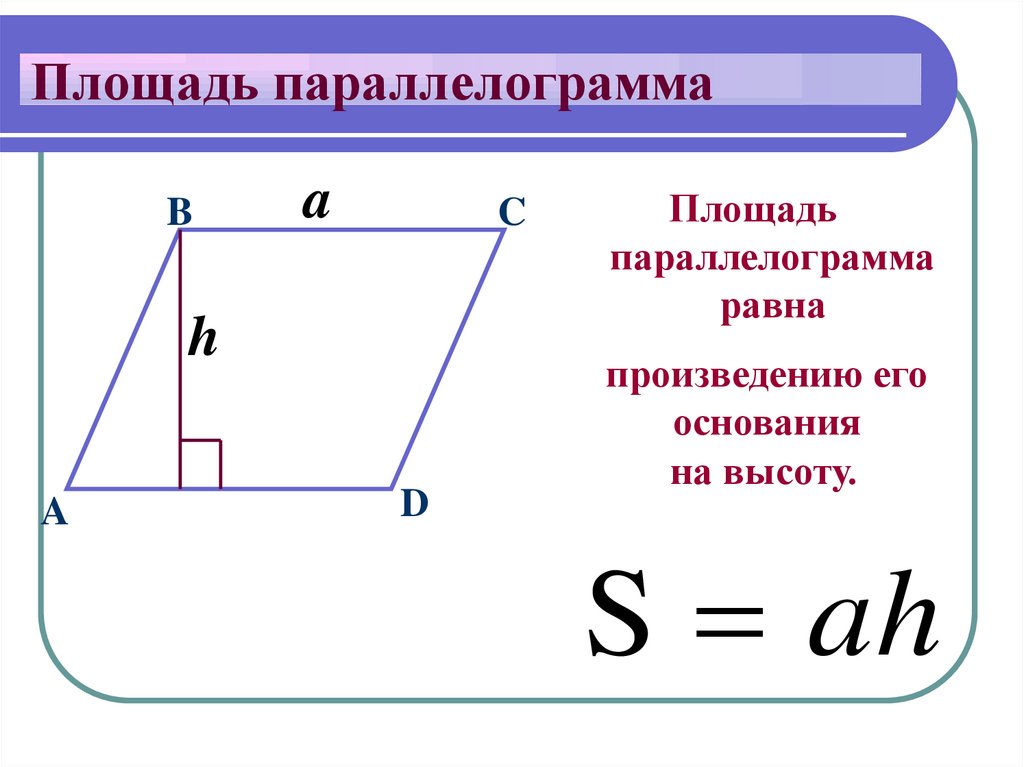
Более простой способ понять это — взять нить. Теперь расположите нить на плоской поверхности так, чтобы получился параллелограмм. Длина используемой нити равна периметру параллелограмма. Таким образом, мы можем сделать вывод, что периметр параллелограмма — это полное расстояние вокруг границы параллелограмма.
Параллелограмм — двумерная замкнутая фигура, ограниченная четырьмя сторонами. Итак, периметр параллелограмма будет равен сумме всех этих четырех сторон.
Площадь
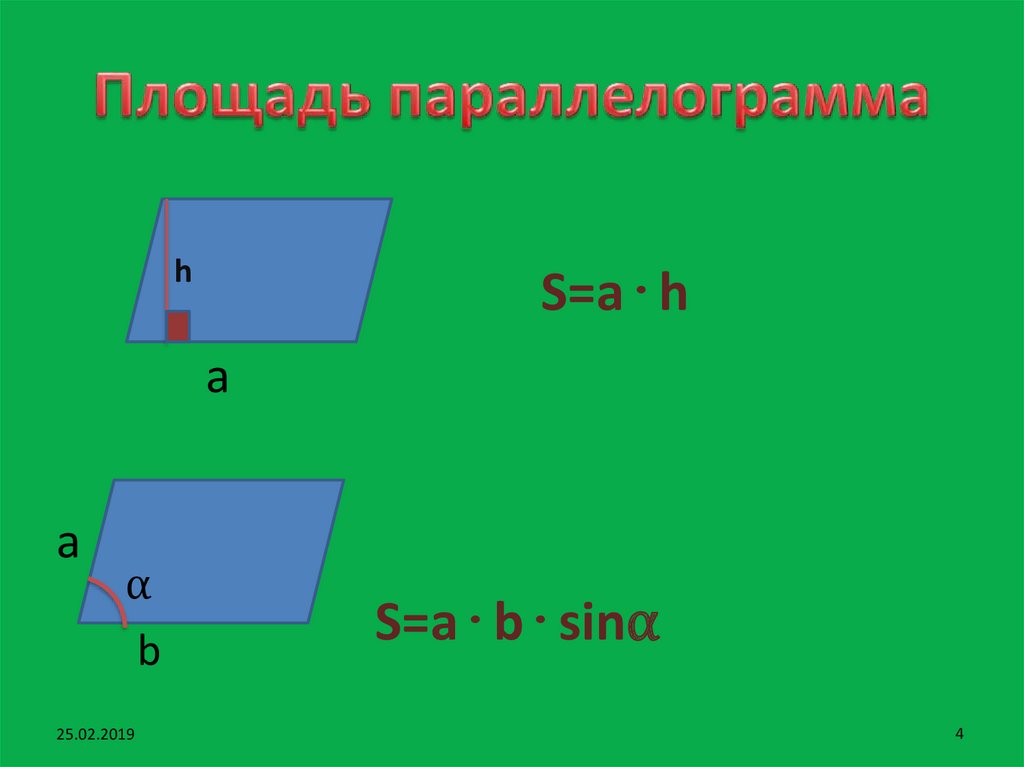
Площадь параллелограмма — это площадь, покрытая параллелограммом в плоской двумерной области. Параллелограмм – это особый тип четырехугольника. Чтобы найти площадь параллелограмма, умножьте основание на его высоту и наоборот. Другими словами, площадь параллелограмма равна основанию, умноженному на высоту.
Если вы хотите понять концепцию площади и периметра, возьмите физический пример, как описано ниже:
Рассмотрим участок земли в виде параллелограмма с противоположными сторонами 10 м и 12 м.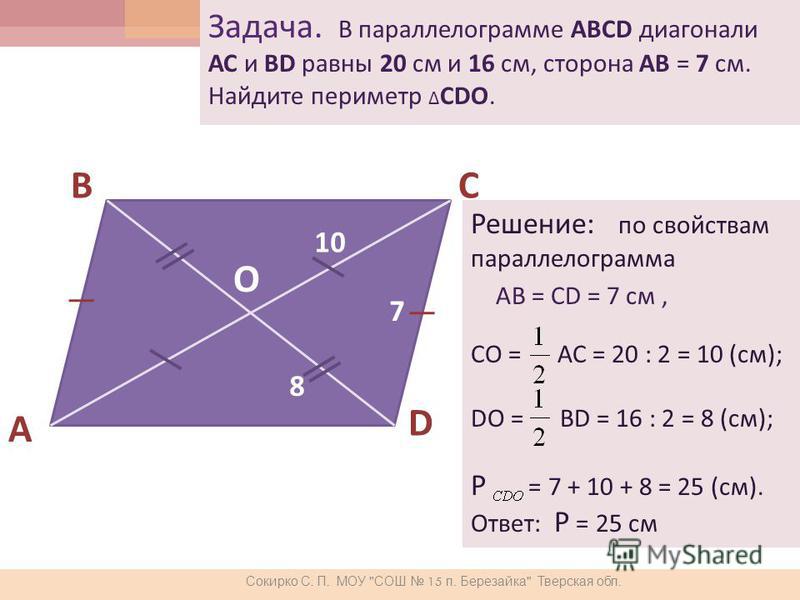
Владелец хочет покрыть землю зеленой травой и поставить забор вокруг земли. Для этого он нанимает ландшафтного дизайнера. Ландшафтному дизайнеру необходимо заказать материалы. Как он рассчитает необходимое количество травяных циновок и деревянных заборов?
Ответ прост: вычислив площадь и периметр параллелограмма. В этом случае количество необходимых травяных матов будет определяться площадью треугольника, поскольку это дает нам количество пространства, покрытого землей. С другой стороны, периметр расскажет нам о длине забора.
Формула площади и периметра параллелограмма
Чтобы найти площадь параллелограмма, умножьте основание на его высоту и наоборот. Другими словами, площадь параллелограмма равна основанию, умноженному на высоту.
Формула периметра
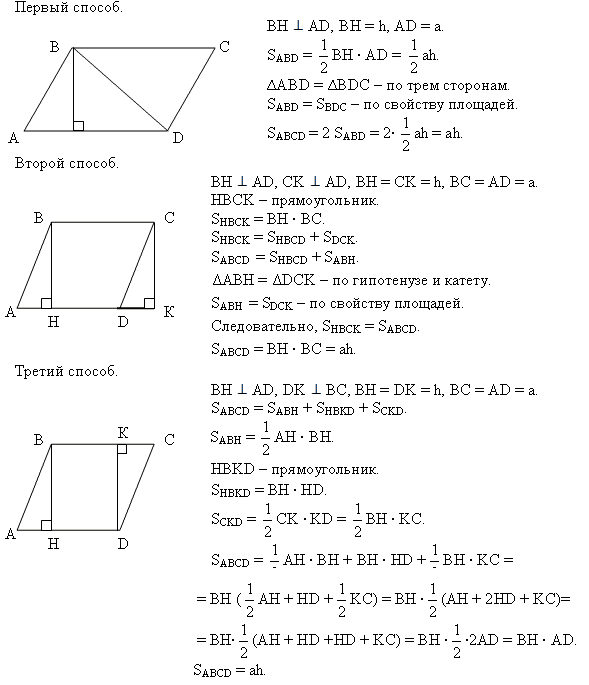
Длина непрерывной линии, образуемой границей параллелограмма, является его периметром. В случае параллелограмма его периметр будет получен путем сложения длин всех его четырех сторон.
Итак, если длины сторон параллелограмма, показанного на рисунке выше, равны a и b, то периметр (P) параллелограмма со сторонами равен P=2(a+b) единицам.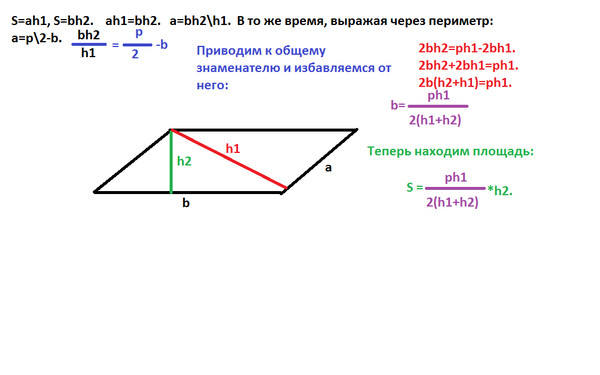
Таким образом, для параллелограмма ABCD, как показано ниже,
Периметр = l(AB) + l(BC) + l(CD) + l(DA).
Формула площади
Площадь параллелограмма равна произведению основания и высоты.
\(A=b\times{h}\)
Приведенная выше формула не используется для определения площади прямоугольника, не так ли? Они похожи друг на друга? Кажется неясным, не так ли? Давайте лучше поймем это, используя приведенную ниже диаграмму.
Мы преобразовали параллелограмм в прямоугольник с тем же основанием и высотой. Учитывая, что параллелограмм и прямоугольник имеют одинаковые основания и высоты:
Площадь параллелограмма = Площадь прямоугольника AEFD
=EF×AE=BC×AE
=основание×высота
Умножьте основание на высоту перпендикуляра, чтобы найти площадь параллелограмма. Основание и высота параллелограмма, как видно, перпендикулярны друг другу, а боковая сторона — нет.
Однако какое число в нашей задаче соответствует основанию, а какое — высоте? Пунктирная линия с символом прямого угла является ключом.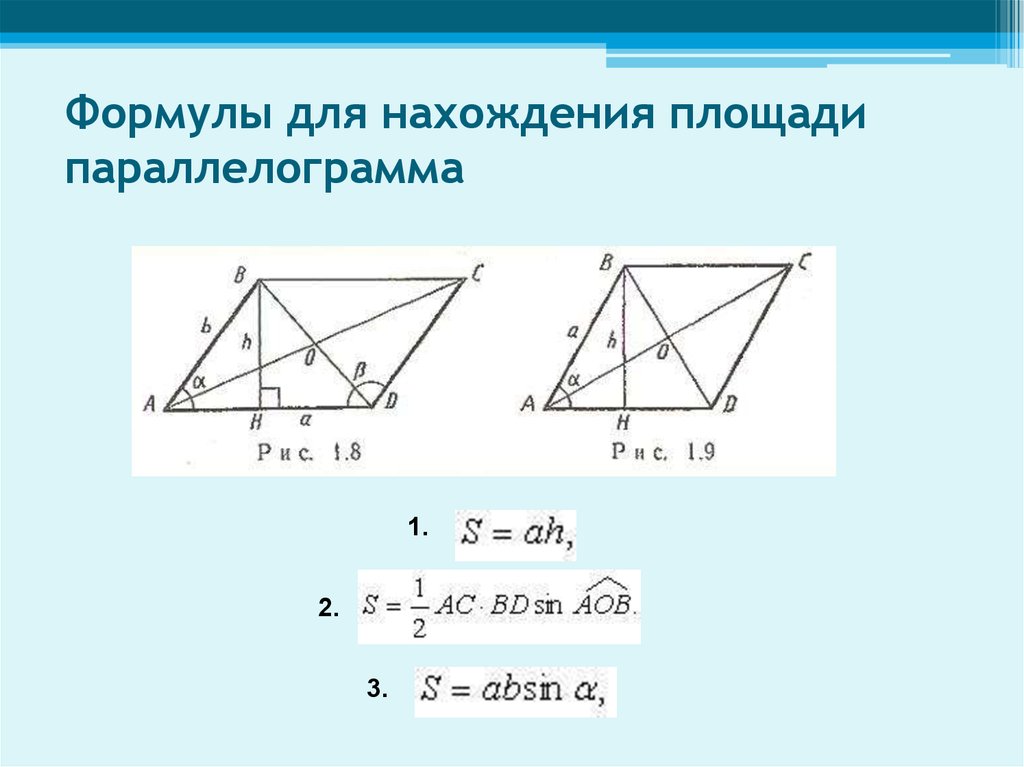
Это высота, также называемая высотой. В нашем образце это 6 см. Поскольку высота или высота перпендикулярна основанию, мы можем определить основание после определения высоты. В результате в данном случае высота параллельна верхней и нижней сторонам параллелограмма. Мы можем выбрать верх или низ в качестве основы, потому что они оба конгруэнтны.
Периметр параллелограмма
Давайте лучше разберемся с периметром параллелограмма на примере. Найдите периметр параллелограмма PQRS.
решение: \(Периметр = 2(12 + 7)\)
\(Периметр = 2\х19\)
\(Периметр = 38\) см.
Простейшая формула периметра треугольника — это сумма всех сторон. Однако что, если вы не знаете длины всех или некоторых сторон? В этом случае у нас есть дополнительные формулы для вычисления периметра параллелограмма. Эти формулы выводятся из свойств параллелограмма. Есть три варианта, они: 92})\)
Давайте рассмотрим их один за другим.
Периметр параллелограмма с двумя смежными сторонами
Рассмотрим параллелограмм ниже.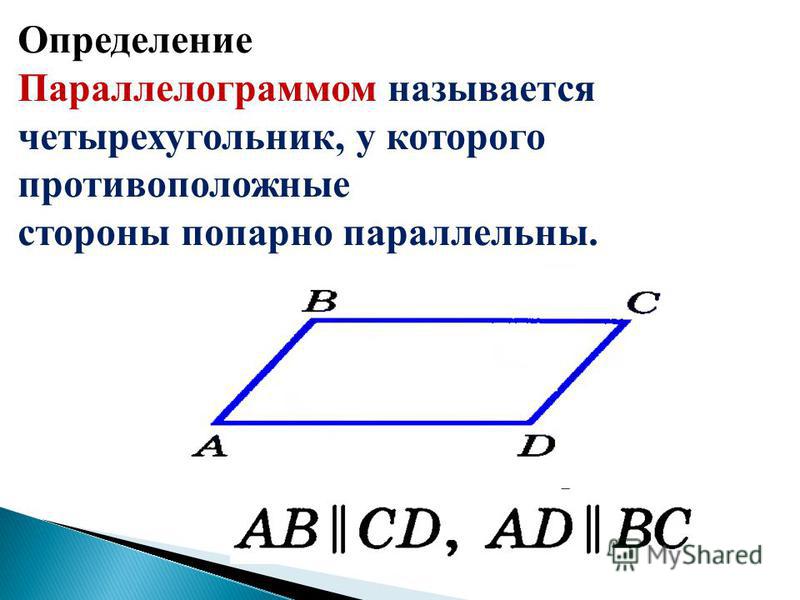
У него одна сторона длины \(a\), а другая \(b\)
Параллелограмм по определению имеет противоположные стороны, равные и параллельные. Следовательно,
\(l(AD) = l(BC) = b\)
\(l(AB) = l(CD) = a\)
Теперь мы видим, что \(Периметр = l( АВ) + 1(ВС) + 1(CD) + 1(DA)\).
Таким образом, \(Периметр = a + b + a + b\)
\(Периметр = 2a + 2b\)
\(Периметр = 2(a + b)\)
Таким образом, периметр параллелограмма равен удвоенной сумме двух его смежных сторон.
Пример: Найдите периметр следующего параллелограмма.
[
латекс]l(AB) = 7[/латекс] см
\(l(BC) = 5\) см
\(Периметр = 2(a + b)\)
\ (Периметр = 2(7 + 5)\)
\(Периметр = 2\х12\)
\(Периметр = 24\) см.
9о\) и \(l(DC)\) — гипотенуза. Кроме того, \(l(EC)=h\) Следовательно,\(\sin\theta=\frac{\text{противоположная сторона}}{\text{гипотенуза}}=\frac{l(EC)}{ l(DC)}=\frac{h}{l(DC)}\)
Таким образом, \(l(DC)=\frac{h}{sin\theta}\) ………….
(i)
Подстановка значения \(l(DC)\) в \(Периметр =2(l(DC)+b)\)
\(Периметр =2(\frac{h}{sin\theta }+б)\).
Это уравнение периметра параллелограмма через одну сторону, один угол и одно основание.
Пример: Найдите периметр параллелограмма ниже 9о\)
Таким образом, \(Периметр =2(\frac{12}{sin60}+17)\)
\(Периметр = 61,71\)см
Периметр формулы параллелограмма с диагоналями
Рассмотрим параллелограмм ниже . Его сторона имеет длину \(a\), а диагонали имеют длины \(x\) и \(y\)
По свойству параллелограмма
\(l(AB) = l(CD) = а\)
Рассмотрим треугольник ABC и треугольник DCB.
Если мы применим закон косинусов к треугольнику ABC, мы получим, 92})\)
\(Периметр = 30,94\) единиц
Площадь параллелограмма
Подобно методам определения периметра, существуют различные методы определения площади параллелограмма в зависимости от имеющихся данных.
Площадь параллелограмма из сторон без высоты с двух сторон
Если высота параллелограмма нам неизвестна, то мы можем использовать понятие тригонометрии здесь, чтобы найти его площадь.
Применяем тот же метод, что и для параллелограмма, чтобы получить формулу: 9\circ\)
\(Площадь = ab sin (x)\)
\(A = 8\times9\sin(60)\)
\(A = 72sin60\)
\(A = 62,35\) ) кв.см.
Площадь параллелограмма с использованием диагоналей
Площадь любого параллелограмма также можно рассчитать с помощью длин его диагоналей. Как известно, у параллелограмма есть две диагонали, которые пересекаются друг с другом. Предположим, диагонали пересекаются друг с другом под углом y, тогда площадь параллелограмма равна:
\(Площадь = \frac{1}{2}\times{d_1}\times{d_2}\sin(\ альфа)\)
Где,
\(d_1\) = диагональ параллелограмма
\(d_2\) = диагональ параллелограмма
\(\alpha\) = любой угол между точками пересечения диагоналей
Пример : Определить площадь параллелограмма, если угол между двумя пересекающимися диагоналями параллелограмма равен 70 градусов, а длины его смежных сторон равны 12 см и 16 см.
Решение:
Длина одной диагонали (d_1) = 12 см,
Длина другой диагонали (d_2) = 16 см,
Угол между двумя пересекающимися диагоналями (\alpha) = 70 градусов
Формула для вычисления площади параллелограмма:
\(Площадь = \frac{1}{2}\times{d_1}\times{ d_2}\sin(\alpha)\)
\(Площадь = \frac{1}{2}\times{12}\times{16}\sin(70)\)
= 60 кв.
см.
Площадь и периметр параллелограмма из вершин
Точка, в которой пересекаются любые две стороны параллелограмма, называется вершиной параллелограмма. Мы можем найти периметр и площадь параллелограмма, зная координаты его вершин. Рассмотрим параллелограмм ABCD, где \(A\equiv(x_1, y_1), B\equiv(x_2, y_2)\), \(C\equiv(x_3, y_3)\) и \(D\equiv(x_4, y_4) \) являются вершинами параллелограмма. Длины сторон равны длинам отрезков AB, BC, CD и DA. Их можно найти, используя конечные точки сегментов по формуле расстояния: 92}\)
Теперь, когда мы знаем длины сторон, мы можем легко найти периметр, сложив расстояния.
Таким образом, периметр = AB + BC + AC.
Шаги для нахождения площади и периметра параллелограмма
Теперь, когда мы изучили различные формулы для вычисления площади и периметра параллелограмма, давайте посмотрим, как мы можем вычислить периметр параллелограмма.
Шаг 1: Ознакомьтесь с приведенными данными и внимательно запишите имеющиеся у вас размеры.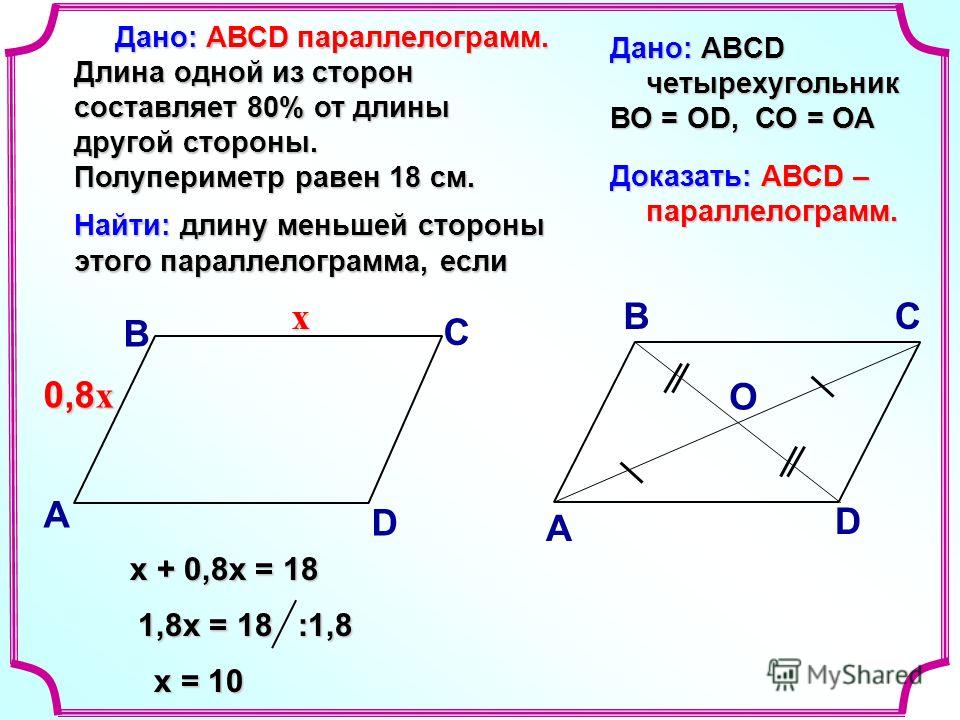
Это поможет нарисовать фактическую диаграмму и отметить значения.
Шаг 2: Выберите правильную формулу для расчета площади и периметра и примените ее.
Площадь и периметр параллелограмма
В следующей таблице перечислены важные различия между площадью и периметром.
| Площадь | Периметр |
| Площадь параллелограмма относится к пространству, занимаемому параллелограммом. | Периметр параллелограмма относится к мере длины контура или границы параллелограмма. |
| Площадь параллелограмма измеряется в квадратных единицах. Например, если размеры указаны в сантиметрах, то площадь выражается в квадратных сантиметрах. | Периметр параллелограмма измеряется в линейных единицах. Например, если размеры указаны в дюймах, то периметр выражается в дюймах. |
| Площадь параллелограмма определяется как \(A=b\times{h}\) | Периметр параллелограмма определяется как \(Периметр = 2(a + b)\) |
Задачи на площадь и периметр параллелограмма
Мы узнали все, что нужно знать о площади и периметре параллелограмма.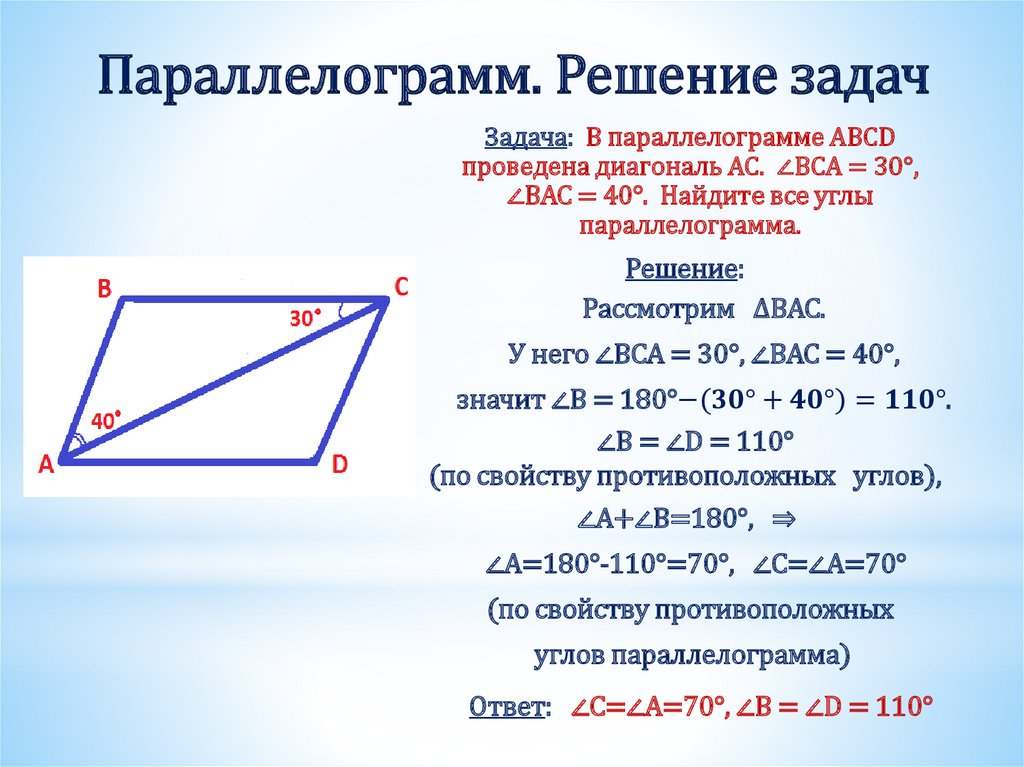
Теперь вы можете решить любую проблему, основанную на этой теме. Вспомните формулы. Вот суть.
Для решения задач на основе периметра треугольника есть три формулы, как показано ниже:
| Периметр | Формула | 92})\)
| Когда заданы основание и высота | \(Периметр =2(\frac{h}{sin\theta}+b)\) |
Аналогично, есть три формулы for the area of the parallelogram
| Area | Formula |
| When Base & Height are Given | \(A=b\times{h}\) |
| When Two Даны стороны | Площадь = абсин\((\тета)\) |
| Когда даны диагонали | \(Площадь = \frac{1}{2}\times{d_1}\times{d_2}\sin(\alpha)\) |
Решенные примеры на площади и периметр параллелограмма
Теперь давайте рассмотрим несколько решенных примеров на площади и периметре параллелограмма.
сторон составляет 30 градусов.
Решение: 9о\)
Таким образом, \(Периметр =2(\frac{4}{sin30}+5)\)
\(Периметр = 26\)см
\(A=b\times{h}\)
Подставим полученное значение
\(b=5\) см
\(h=4\) см
\(A=5\times{4}\)
Решено Пример 2: Определить площадь и периметр параллелограмма, если угол между двумя пересекающимися диагоналями параллелограмма равен 90 градусов, а длины его прилежащих сторон равны 4 см и 8 см. Угол между двумя сторонами равен 30 градусов, а высота равна 3 см. 9\circ\)
\(Площадь = \frac{1}{2}\times{4}\times{8}\sin(90)\)
= 16 кв. см.
Теперь на основе имеющихся данных мы можем найти периметр параллелограмма, используя формулу с высотой, основанием и углом между двумя сторонами. Но нам нужно найти базу для этого.
Мы знаем, что
\(A=b\times{h}\)
Таким образом, \(b=\frac{Area}{h}=\frac{16}{3}\)
Таким образом ,
\(Периметр =2(\frac{h}{sin\theta}+b)\).
Подставим значение, как указано 9о\)
Таким образом, \(Периметр =2(\frac{3}{sin30}+\frac{16}{3})\)
\(Периметр = \frac{68}{3}\)см
Надеюсь, что эта статья о площади и периметре параллелограмма была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о площади и периметре параллелограмма
В.1 Какова формула периметра параллелограмма?
Ответ 1 Когда даны две стороны, \(периметр = 2(a + b)\)
Q.2 Какова площадь параллелограмма?
Ответ 2 Площадь параллелограмма относится к пространству, занимаемому параллелограммом.
Q.3 Является ли параллелограмм квадратом?
Ответ 3 Если диагонали параллелограмма равны и перпендикулярны, параллелограмм является квадратом. Таким образом, все квадраты являются параллелограммами, но не все параллелограммы квадратные.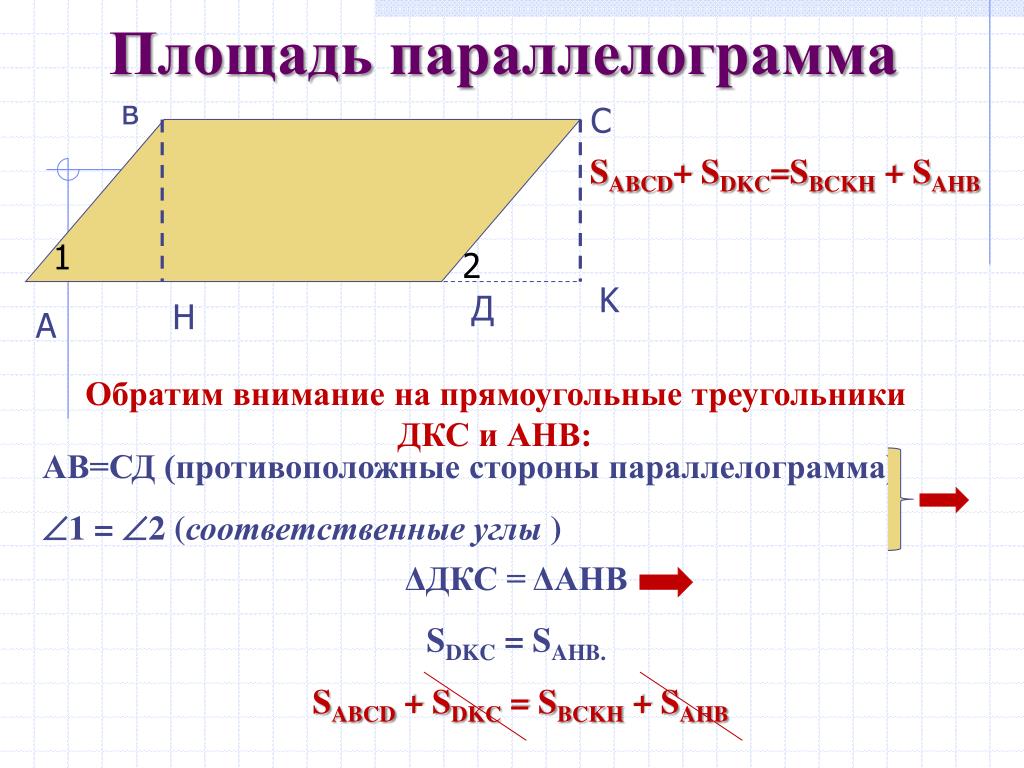
Q.4 Каковы типы параллелограммов?
Анс.4 Квадрат Прямоугольник, Ромб являются типами параллелограмма.
Q.5 Является ли алмаз параллелограммом?
Ответ 5 Да, ромб или ромб — это параллелограмм.
Скачать публикацию в формате PDF| График параболы: определение, типы, уравнения с решенными примерами0365 |
Обратная теорема Пифагора: пояснение с формулировкой, доказательством и примерами решенияКак найти площадь и периметр параллелограммаПериметр параллелограмма — это общая длина, покрываемая его границей. Параллелограмм имеет четыре стороны, так как это четырехугольник. Периметр параллелограмма равен сумме этих четырех сторон. Геометрия — это дисциплина математики, изучающая различные геометрические фигуры. Параллелограмм — четырехсторонняя двумерная геометрическая фигура. ПараллелограммПараллелограмм — это тип четырехугольника с двумя наборами параллельных сторон в евклидовой геометрии. Противоположные или обращенные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма равны. Постулат евклидовой параллельности следует непосредственно из конгруэнтности противоположных сторон и противоположных углов, и ни одно из условий не может быть доказано без использования постулата евклидовой параллельности или одной из его эквивалентных формулировок. ХарактеристикиЧетырехугольник является параллелограммом тогда и только тогда, когда верно любое из следующих утверждений:
Нахождение периметра параллелограммаПериметр вычисляется путем сложения длин всех четырех сторон. Периметр параллелограмма — это все расстояние за пределами геометрической формы. Противоположные стороны параллелограмма равны, следовательно, периметр равен сумме двух параллельных сторон. Периметр = 2(a+b)единиц Длина регулярного узора, образуемого границей параллелограмма, является его периметром.
В следующих ситуациях можно наблюдать периметр параллелограмма:
Нахождение площади параллелограммаПлощадь параллелограмма в двумерной плоскости рассчитывается как область или поверхность, которую он покрывает. Параллелограмм — это тип четырехугольника, который отличается от других. Параллелограмм определяется как четырехугольник с двумя параллельными противоположными сторонами. К параллелограммам относятся прямоугольники, квадраты и ромбы. Формы, как 2D, так и 3D, важны для геометрии. Каждая фигура имеет свой собственный набор атрибутов и формул площади. Общее количество единичных квадратов, которые могут поместиться внутри параллелограмма, называется его площадью и измеряется в квадратных единицах (например, см 2 ,м 2 ,в 2 ). Параллелограмм представляет собой четырехстороннюю двумерную фигуру со следующими свойствами: две равные и противоположные стороны, две пересекающиеся, но не равные диагонали и два равных и противоположных угла. Формула площади параллелограмма Площадь параллелограмма вычисляется путем сложения его основания и высоты. Площадь = b×h квадратных единиц Здесь b — основание А h — высота Решенные примерыВычислите площадь и периметр параллелограмма, основание и высота которого равны 2 и 3 см. Решение: Площадь параллелограмма определяется как: b×h = 2×3 = 6 см 2 Периметр параллелограмма определяется как: 2(a+b) = 2(2+3) = 2×5 = 10см. Заключение Вычисление пространства внутри четырех сторон параллелограмма называется его площадью. Параллелограмм — двумерный четырехугольник с равными и параллельными противоположными сторонами, состоящий из прямоугольника, ромба и квадрата. Площадь параллелограмма равна произведению его длины на высоту, а сумма всех его углов равна 360 градусам. Параллелограмм имеет площадь и периметр, потому что это двумерная фигура. |
Параллелограмм обладает следующими свойствами: Противоположные стороны параллелограмма параллельны и равны друг другу, С точки зрения размера противоположные углы равны, Диагонали параллелограмма делятся пополам.
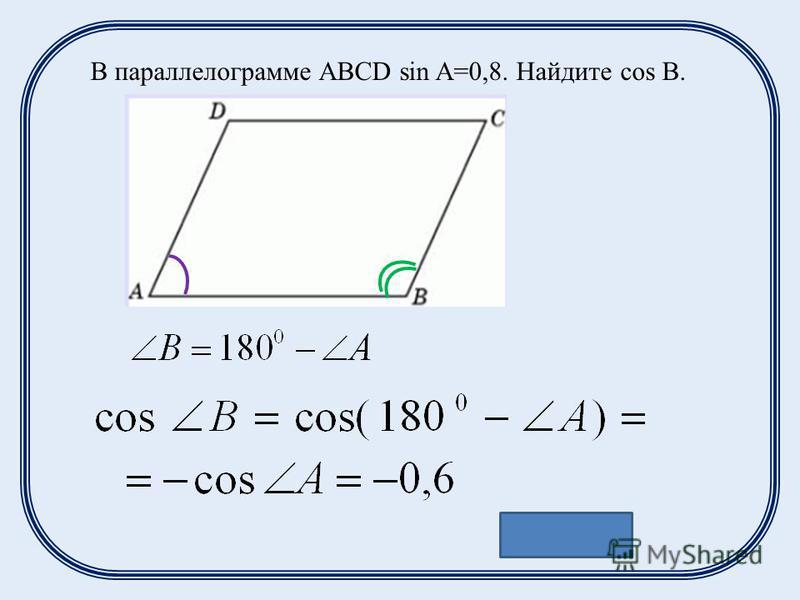Он разделяет ту же единицу, что и его стороны. Если противоположные стороны четырехугольника параллельны и имеют одинаковую длину, он называется параллелограммом. Параллелограмм обладает следующими качествами. Другими словами, периметр параллелограмма равен сумме его четырех сторон.
Основание и высота параллелограмма перпендикулярны друг другу. Таким образом, площадь параллелограмма можно рассчитать по формуле: