Произведение векторов по координатам скалярное по координатам: Как найти скалярное произведение векторов? Ответ на webmath.ru

Скалярное произведение в координатах / Соотношения между сторонами и углами треугольника. Скалярное произведение векторов / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
5. Скалярное произведение в координатах

Теорема

В прямоугольной системе координат скалярное произведение векторов    и  выражается формулой        (1)

Доказательство

Дано: ,

Доказать:

Доказательство:

Каждая координата вектора равна разности соответствующих координат его конца и начала, поэтому если хотя бы один из векторов нулевой, то справедливость равенства очевидна, так как координаты нулевого вектора равны нулю.

Рассмотрим ненулевые векторы и . Отложим от произвольной точки О векторы = и = :

1 случай: векторы и не коллинеарны:

Тогда по теореме косинусов получаем

.      (2)

2 случай: векторы и сонаправленные:

Тогда и получаем, что

3 случай: векторы и противоположно направленные:

Тогда и получаем, что

Итак, мы получили, что равенство (2) верно для любых двух ненулевых векторов и .

Так как = — , = , = , то равенство (2) можно записать следующим образом:

Следовательно,

Вектора имеют следующие координаты , и ( — ), при этом длина вектора равна квадратному корню из суммы квадратов координат данного вектора, поэтому

,

Учитывая это, получаем

Итак, , что и требовалось доказать. Теорема доказана.

Следствие 1

Ненулевые векторы   и  перпендикулярны тогда и только тогда, когда  .

Следствие 2

Косинус угла  между ненулевыми векторами и выражается формулой .

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Синус, косинус, тангенс, котангенс

Основное тригонометрическое тождество. Формулы приведения.

Формулы для вычисления координат точки

Теорема о площади треугольника

Теорема синусов

Теорема косинусов

Решение треугольников

Измерительные работы

Угол между векторами

Скалярное произведение векторов

Свойства скалярного произведения векторов

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов

Правило встречается в следующих упражнениях:

7 класс

Задание 1044, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 20, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1073, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

Как ⭐ найти скалярное произведение векторов по координатам: теорема и доказательство

Физический смысл скалярного произведения

Распространенное понятие такое, как скалярное произведение обладает физическим смыслом. Его можно объяснить так, что работа А является результатом умножения силы F, которая производится постоянно во время движения тела, вектора а и составляющий с направлением силы F угол ϕ:

A=∣F∣·∣a∣=∣F∣·∣a∣·cosϕ

В качестве презентации введенного понятия рассмотрим рисунок:

Источник: matematicus.ru

На рисунке изображены следующие величины, с которыми можно часто встретиться в классе на уроках алгебры, геометрии и физики при рассмотрении различных теорем и доказательств:

• A является скалярной величиной и обозначением работы;
• a представляет собой вектор перемещения (смещения) материальной точки;
• F определяется, как вектор силы, которая оказывает воздействие на данную точку;
• ϕ является углом силы F, действующим к смещению a.

Пример 1

В качестве примера разберем простую задачу. Предположим, что имеется два вектора а и b с длинами 3 м и 2 м соответственно. Угол между этими векторами составляет 120 градусов. Требуется определить, чему равно скалярное произведение этих векторов.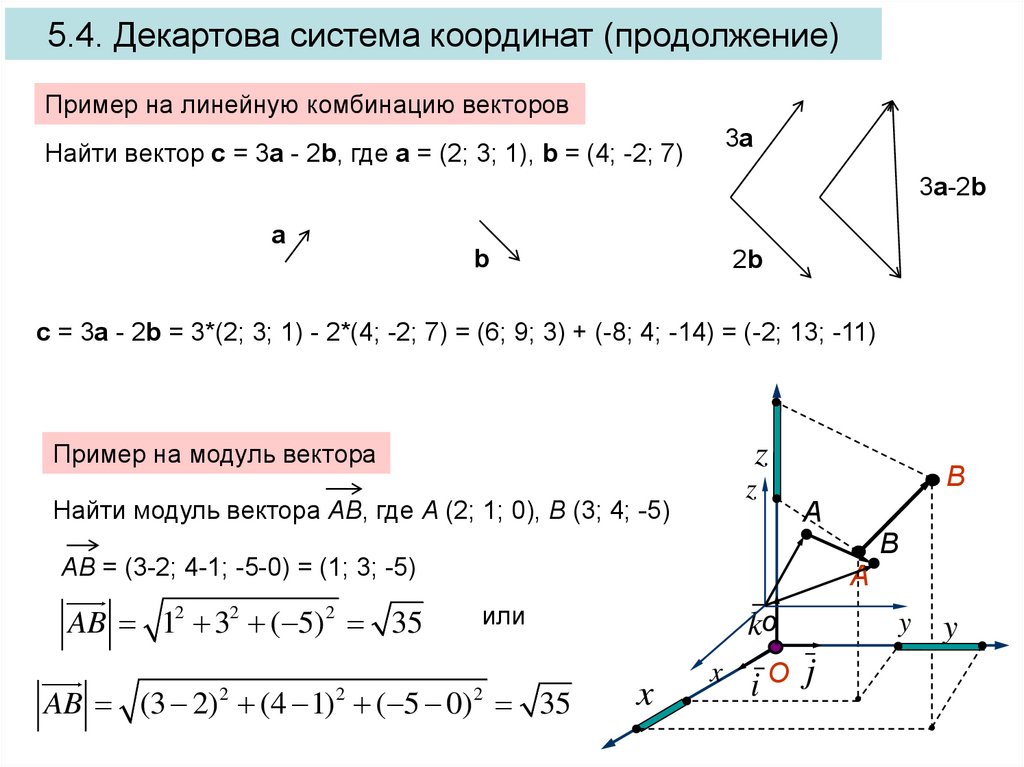

Решение будет выглядеть следующим образом:

a·b=∣a∣·∣b∣·cos(ϕ)=3·2·cos(120)=−3м2

Основные определения

Определение 1

Системой координат называют метод определения положения и перемещения точки или тела с использованием чисел и других символов.

Определение 2

Координаты представляют собой совокупность чисел, определяющих положение некого объекта относительно прямой, плоскости, поверхности, либо пространства.

Определение 3

Скаляр является величиной, полностью определяемой в какой-либо системе координат с помощью одного числа или функции.

Определение 4

Вектор является направленным отрезком прямой, для которого известны точки начала и конца.

Если вектор начинается в точке А, а заканчивается в точке В, то его обозначают, как AB→. Допускается обозначение вектора с помощью малых латинских букв, над которыми изображены стрелочки или черточки, к примеру, a→.

Определение 5

Скалярное произведение пары векторов a¯ и b¯, отличных от нуля, представляет собой число, равное произведению длин данных векторов на косинус угла между ними:

a¯b¯=a¯·b¯=(a¯,b¯)=|a¯||b¯|cos(a¯,b¯)

Пример 2

Рассмотрим типичный пример. Требуется продемонстрировать, как будет вычисляться скалярное произведение векторов a¯ и b¯. Данные векторы обладают длинами 2 и 3 соответственно, а разделяет их угол в 60°.

Запишем условие задания:

|a¯|=2

|b¯|=3

(a¯,b¯)

В результате:

a¯·b¯=(a¯,b¯)=2·3·cos60°=6·12=3

Примечание 1

Особым случаем является равенство какого-либо из векторов a¯ или b¯ нулевому вектору. Тогда (a¯,b¯)=0.

Скалярное произведение пары векторов характеризуется следующими свойствами:

1. Если вычислить скалярное произведение вектора a¯ самого на себя, то результат в любом случае будет положительным, либо имеет нулевое значение: a¯·a¯=a¯2=a¯, a¯≥0. Выражение a¯·a¯=a¯2=a¯, a¯ является скалярным квадратом вектора a¯.
2. Нулевое значение скалярного произведения вектора самого на себя возможно лишь в том случае, когда рассматривается нулевой вектор: a¯·a¯=0⇔=a¯=0¯.
3. Значение скалярного произведения вектора самого на себя представляет собой квадрат модуля заданного вектора: a¯·a¯=a¯2=a¯2.
4. Действие по поиску скалярного произведения является коммуникативным, то есть: a¯, b¯=b¯, a¯.
5. В том случае, когда скалярное произведение пары ненулевых векторов имеет нулевое значение, данные вектора являются ортогональными, то есть перпендикулярными: a¯, b¯=0, a¯, b¯≠0¯⇔a¯⊥b¯.
6. λa¯, b¯=λ·a¯, b¯
7. Действие по поиску результата скалярного произведения векторов является дистрибутивным, то есть: a¯+b¯, c¯=a¯, c¯+b¯, c¯.
8. Знак скалярного произведения зависит от значения угла между векторами. В том случае, когда угол, разделяющий вектора, является острым, скалярное произведение имеет знак плюс, то есть обладает положительным значением. Это объясняется положительным значением косинуса острого угла. Если вектора составляют тупой угол, то скалярное произведение данных векторов будет иметь знак минус, то есть являться отрицательным. Причиной этому служит отрицательное значение величины косинуса тупого угла. Справедливыми являются и обратные утверждения.
9. Угол между сонаправленными векторами составляет 0°. В таком случае скалярное произведение этих векторов обладает положительным значением. Вектора, имеющие противоположные направления, разделены углом в 180°. Тогда скалярное произведение данных векторов обладает отрицательным значением.

Формулы скалярного произведения векторов заданных координатами

Формула 1

В том случае, когда векторы a¯ и b¯ характеризуются координатами:

a¯=a1;a2;a3,

b¯=b1;b2;b3

Скалярное произведение данных векторов модно определить с помощью следующей формулы:

(a¯,b¯)=a1b1+a2b2+a3b3

Определение 6

Скалярным произведением векторов, которые заданы собственными координатами, называют сумму произведений соответствующих им координат.

Пример 3

Рассмотрим пример. Попробуем определить скалярное произведение двух векторов с координатами:

a¯=(3;-1)

b¯=(-2;7)

Воспользуемся уже знакомой формулой:

a¯b¯=3·(-2)+(-1)·7=-6-7=-13

Формула 2

Определить, какой длиной обладает вектор a¯=a1;a2;a3 с собственными координатами, можно с помощью формулы:

|a¯|=a12+a22+a32

Определение 7

Длина, или модуль вектора с заданными собственными координатами является корнем квадратным из суммы квадратов координат.

Пример 4

Рассмотрим типичный пример. Представим, что требуется найти длину вектора с заданными координатами:

a¯=(-4;3)

Воспользуемся записанной выше формулой и получим:

|a¯|=(-4)2+32=16+9=25=5

Формула 3

Формула для расчета угла, который разделяет два вектора a¯=a1;a2;a3,b¯=b1;b2;b3:

cos(a¯,b¯)=(a¯;b¯)|a¯|·|b¯|=a1b1+a2b2+a3b3a12+a22+a32·b12+b22+b32

Пример 5

Постараемся решить задачу. Требуется вычислить угол, расположенный между двух векторов a¯=(1;3)иb¯=(1;0).

Воспользуемся записанной формулой и выполним вычисления:

cos(a¯,b¯)=1·1+3·012+(3)2·12+02=12

(a¯,b¯)=arccos12=60°

Примеры задач на вычисление скалярного произведения векторов

Задача 1

Даны два вектора с определенными координатами, скалярное произведение которых требуется вычислить:

a¯=(-1;2) и b¯=(2;1)

Решение

Заметим, что для векторов указаны координаты. Применим соответствующую формулу. В процессе выполним умножение соответствующих координат и найдем их сумму:

(a¯,b¯)=-1·2+2·1=-2+2=0

В итоге произведение обладает нулевым значением.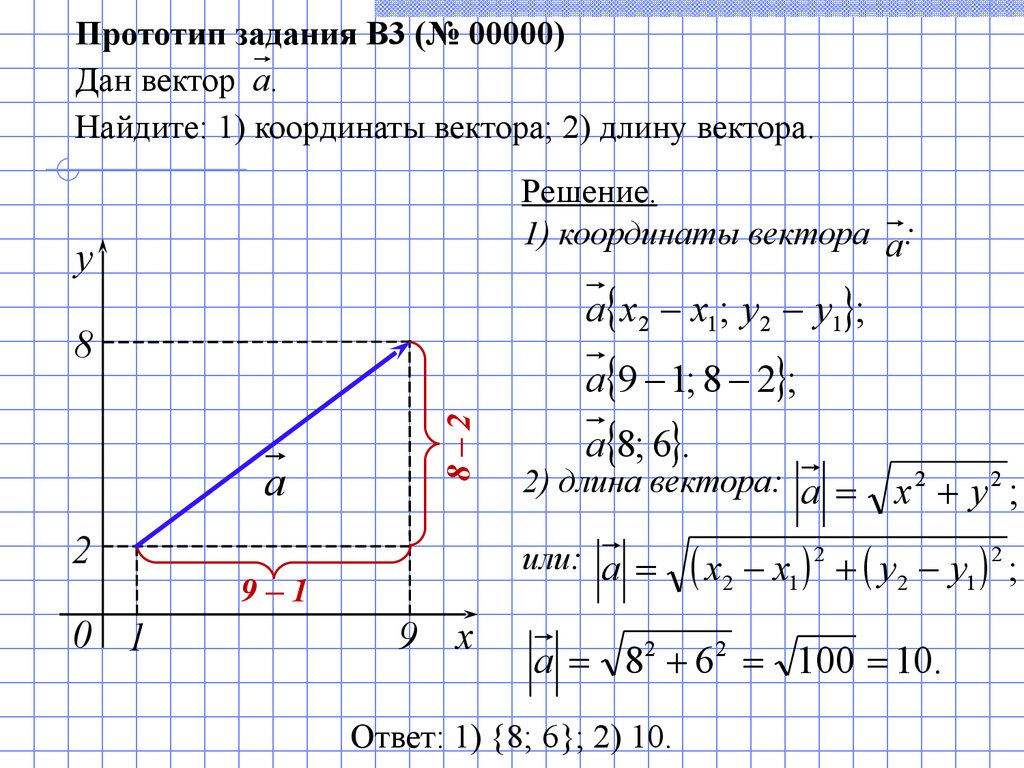 Данный результат означает, что векторы расположены перпендикулярно относительно друг друга, или являются ортогональными. Запишем ответ.

Ответ: (a¯,b¯)=0

Задача 2

В пространстве задана пара векторов, которые имеют определенное в нем начало и конец:

A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2)

Необходимо вычислить, чему равно скалярное произведение векторов AB¯ и AC¯.

Решение

В данном случае не получится найти скалярное произведение векторов, так как имеются лишь заданные в условии точки. По этой причине сначала следует определить непосредственно сами векторы AB¯ и AC¯. Для этого вычислим разность конца и начала каждого вектора, то есть найдем разность соответствующих координат данных точек:

AB¯=(-1-1;4-3;1-(-2))=(-2;1;3)

AC¯=(2-1;1-3;-2-(-2))=(1;-2;0)

Далее можно приступать к вычислению скалярного произведения найденных векторов:

(AB¯,AC¯)=-2·1+1·(-2)+3·0=-2-2+0=-4

Ответ: (AB¯,AC¯)=-4

Задача 3

Даны вектора, скалярное произведение которых требуется определить:

a¯=-1; 2; 3, b¯=2; 0; -1.

Решение

Воспользуемся уже знакомой формулой, согласно которой скалярное произведение пары векторов соответствует сумме произведений их координат, которые определены:

a¯, b¯=-1·2+2·0+3·-1=-2+0-3=-5

Ответ: a¯, b¯=-5.

Задача 4

Дана пара векторов:

a¯=x; -1 и b¯=3; 2

Необходимо вычислить такие значения х, при которых записанные векторы являются ортогональными, то есть векторы расположены перпендикулярно по отношению друг к другу.

Решение

Условие задачи, то есть ортогональность заданных векторов, выполняется лишь в том случае, когда скалярное произведение этих векторов обладает нулевым значением. Найдем его по уже известной формуле:

a¯·b¯=x·3+-1·2=3x-2=0⇒3x=2⇒x=23

Ответ: x=23

Задача 5

Дан некий треугольник с равными друг другу сторонами ∆ABC. Длины его сторон составляют 1. Требуется определить, чему равно:

AB→·BC→+BC→·CA→+CA→·AB→

Решение

Ответ: =-32

Задача 6

Имеется пара векторов, которые являются неколлинеарными:

a и b

Нужно определить вектор x, который будет компланарен заданным векторам a и b, а также соответствует следующей системе уравнений:

Решение

Заметим, что в том случае, когда вектора a и b являются неколлинеарными, данные вектора составляют базис относительно плоскости. Какой-либо компланарный вектор для данных векторов допустимо представить в следующем виде:

x=λa+μb

Используя записанное соотношение, изменим вид начальной системы из условий задачи:

Найдем решения записанной системы:

В результате получим нужный вектор:

x=(b·b)a+(a·b)b(a·a)(b·b)-(a·b)2

Ответ: x=(b·b)a+(a·b)b(a·a)(b·b)-(a·b)2

Задача 7

Имеется некий параллелограмм OACB. Для этой геометрической фигуры предусмотрены следующие параметры:

длина |OA|=a

длина |OB|=b

угол ∠AOB=α

Необходимо найти, чему равна длина d диагонали OC параллелограмма, а также определить значение косинусов углов, которые расположены между диагональю и сторонами параллелограмма.

Решение

Заметим, что:

OC→=OA→+OB→

В результате длина диагонали составит:

Углы, которые разделяют диагональ и стороны параллелограмма, можно вычислить таким образом:

Ответ: a2+b2+2abcosα,a+bcosαa2+b2+2abcosα,acosα+ba2+b2+2abcosα.

j$, если вы понимаете определение каждого символа, встречающегося в этой формуле.

---

Учитывая, что я написал ответ в первой ссылке, кажется уместным сказать несколько слов (которых, к сожалению, не так мало, как я надеялся). В общем случае, если у вас есть $n$-мерное (псевдо)риманово многообразие $(M,g)$, то для каждого $p\in M$ по определению $g_p$ является (псевдо) скалярным произведением на касательной пробел $T_pM$. Итак, если у вас есть два вектора $v,w\in T_pM$, величина $g_p(v,w)$ является элементом $\Bbb{R}$. Теперь, если у вас есть карта $(U,x)$ на многообразии (т.е. система координат), то для каждого $p\in U$ мы можем рассмотреть 9n$, когда вы впервые изучаете эти вещи) никогда не будет хорошей идеей, если вы уже не знаете, что делаете (в этом случае вы, конечно, можете делать все, что хотите) или если вы не используете диаграмму идентичности ( то есть декартовы координаты), потому что в этом случае все будет работать хорошо, хотя вы, возможно, не до конца понимаете, почему. Итак, если вы планируете использовать полярную/параболическую/гиперболическую/эллиптическую/сферическую или любые другие распространенные системы координат, вы должны быть особенно осторожны в отношении различий (поскольку $g_{ij}$ больше не являются постоянными функциями).

2\\ &= 4. \end{выравнивание}

Просто ради интереса посмотрим, что получится, если мы выразим $v,w$ через $\frac{\partial}{\partial x}(p)$ и $\frac{\partial}{\partial у}(р)$. Итак, имеем следующую «формулу смены базиса»: \начать{выравнивать} \begin{случаи} \frac{\partial}{\partial r}(p)&= \frac{\partial x}{\partial r}(p)\cdot \frac{\partial}{\partial x}(p) + \frac {\ парциальное у} {\ парциальное г} (р) \ cdot \ гидроразрыва {\ парциальное} {\ парциальное у} (р) \\ & = \ cos (\ тета (р)) \ гидроразрыва {\ парциальное} {\ парциальное х} (р) + \ грех (\ тета (р)) \ гидроразрыва {\ парциальное} {\ парциальное у} (р) \ \ &= \frac{1}{2}\frac{\partial}{\partial x}(p) + \frac{\sqrt{3}}{2}\frac{\partial}{\partial y}(p )\\\\ \frac{\partial}{\partial \theta}(p)&= \frac{\partial x}{\partial \theta}(p)\cdot \frac{\partial}{\partial x}(p) + \ гидроразрыва {\ парциальное у} {\ парциальное \ тета} (р) \ cdot \ гидроразрыва {\ парциальное} {\ парциальное у} (р) \\ &= -r(p)\sin(\theta(p))\frac{\partial}{\partial x}(p) + r(p)\cos(\theta(p))\frac{\partial} {\ парциальное у} (р) \\ &= -\sqrt{3}\frac{\partial}{\partial x}(p) + \frac{\partial}{\partial y}(p) \end{случаи} \end{выравнивание} Итак, если вы делаете замены, вы должны найти \начать{выравнивать} v&= \left(\frac{1}{2}-\sqrt{3}\right)\frac{\partial}{\partial x}(p) +\left(\frac{\sqrt{3}}{ 2}+1\справа)\frac{\partial}{\partial y}(p) \end{выравнивание} и \начать{выравнивать} w&= -\sqrt{3}\frac{\partial}{\partial x}(p) + \frac{\partial}{\partial y}(p) \end{выравнивание} Другими словами, мы имеем $v^x=\frac{1}{2}-\sqrt{3}, v^y=\frac{\sqrt{3}}{2}+1, w^x=- \sqrt{3}, w^y=1$.

y = 4, \end{выравнивание} это именно то, что мы нашли выше. 9( а также как сделать замену базиса в касательном пространстве).

многомерное исчисление — скалярное произведение между двумя векторами в цилиндрических координатах?

В таких вопросах, как этот, я предпочитаю различать (евклидово) скалярное произведение двух векторов $\mathbf a$ и $\mathbf b$, определяемое как $\langle\mathbf a,\mathbf b\ rangle = \lVert\mathbf a\rVert \lVert\mathbf b\rVert\cos\phi$, где $\phi$ — угол между векторами, а 9TM=I$ и формула сводится к скалярному произведению. Итак, в любом ортонормированном базисе евклидово скалярное произведение двух векторов равно скалярному произведению их координат.

Говоря об операторах $\operatorname{grad}$ и им подобных, мы имеем дело с векторными полями, и в этом контексте также важно различать точки и векторы. Основная идея заключается в том, что к каждой точке прикреплено векторное пространство, состоящее из всех возможных касательных векторов к кривым, проходящим через эту точку — 9n$, поэтому мы обычно можем идентифицировать точки с векторами и беспечно перемещать касательные векторы от точки к точке.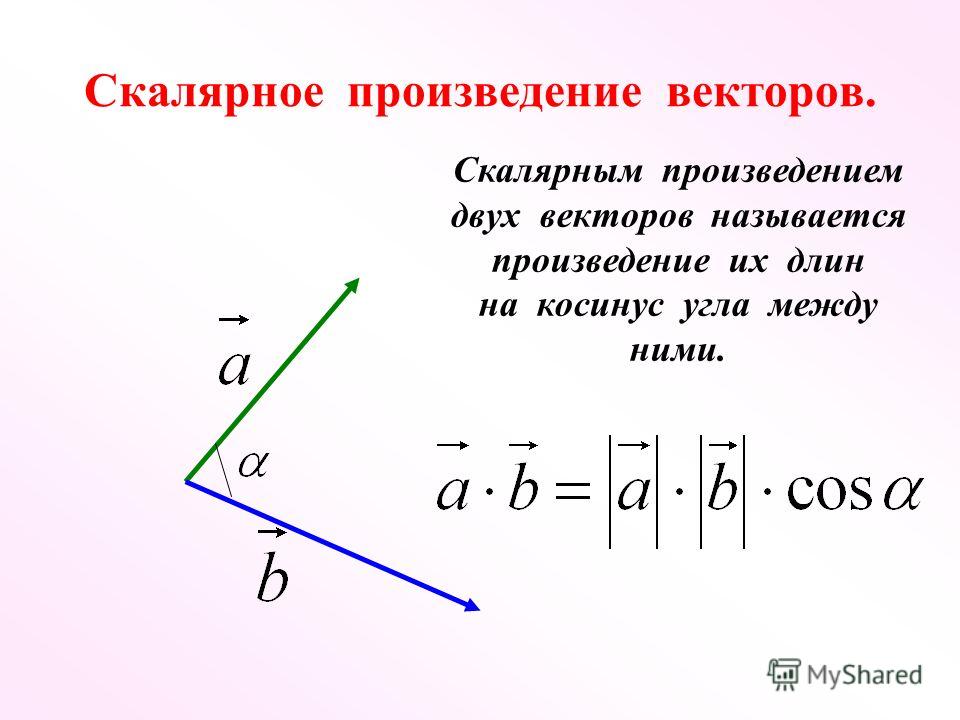

Базисные векторы $\hat{\mathbf r}$, $\hat{\mathbf\theta}$ и $\hat{\mathbf z}$ живут в этих касательных пространствах, как и стандартные базисные векторы $\hat {\mathbf i}$, $\hat{\mathbf j}$ и $\hat{\mathbf k}$, и преобразование между ними не является преобразованием цилиндрической точки в декартову координату, которое вы использовали. Эти цилиндрические базисные векторы для касательного пространства в точке являются единичными нормалями к поверхностям $r=\text{const}$, $\theta=\text{const}$ и $z=\text{const}$, которые проходят через точка. Ясно, что эти векторы меняются от одной точки к другой. Должно быть легко видеть, что эти единичные векторы попарно ортогональны, поэтому в цилиндрических координатах внутреннее произведение двух векторов является скалярным произведением координат, как и в стандартном базисе.

Вы можете убедиться в этом напрямую. Немного поработав, мы можем найти, что $$\begin{bmatrix}\hat{\mathbf r}\\\hat{\mathbf\theta}\\\hat{\mathbf z}\end{bmatrix} = \ begin{bmatrix}\cos\theta&\sin\theta&0\\-\sin\theta&\cos\theta&0\\0&0&1\end{bmatrix} \begin{bmatrix}\hat{\mathbf i}\\\hat{\mathbf j}\\\hat{\mathbf k}\end{bmatrix}$$ так, что $$\hat{\mathbf A} = A_r\hat{\mathbf r}+A_\theta\hat{\mathbf\theta} +A_z\hat{\mathbf z} = (A_r\cos\theta-A_\theta\sin\theta)\,\hat{\mathbf i} + (A_r\sin\theta+A_\theta\cos\theta) \,\hat{\mathbf j}+A_z\,\hat{\mathbf k}$$ и аналогично для $\hat{\mathbf B}$.