Задачи про площадь квадрата и многое другое
Такой удивительный и знакомый квадрат. Он симметричен относительно своего центра и осей, проведенных по диагоналям и через центры сторон. А искать площадь квадрата или его объем вообще не составляет большого труда. Особенно если известна длина его стороны.
Несколько слов о фигуре и ее свойствах
Первые два свойства связаны с определением. Все стороны фигуры равны друг другу. Ведь квадрат — это правильный четырехугольник. Причем у него обязательно все стороны равны и углы имеют одинаковое значение, а именно — 90 градусов. Это второе свойство.
Третье связано с длиной диагоналей. Они тоже оказываются равными друг другу. Причем пересекаются под прямыми углами и в точках середины.
Формула, в которой используется только длина стороны
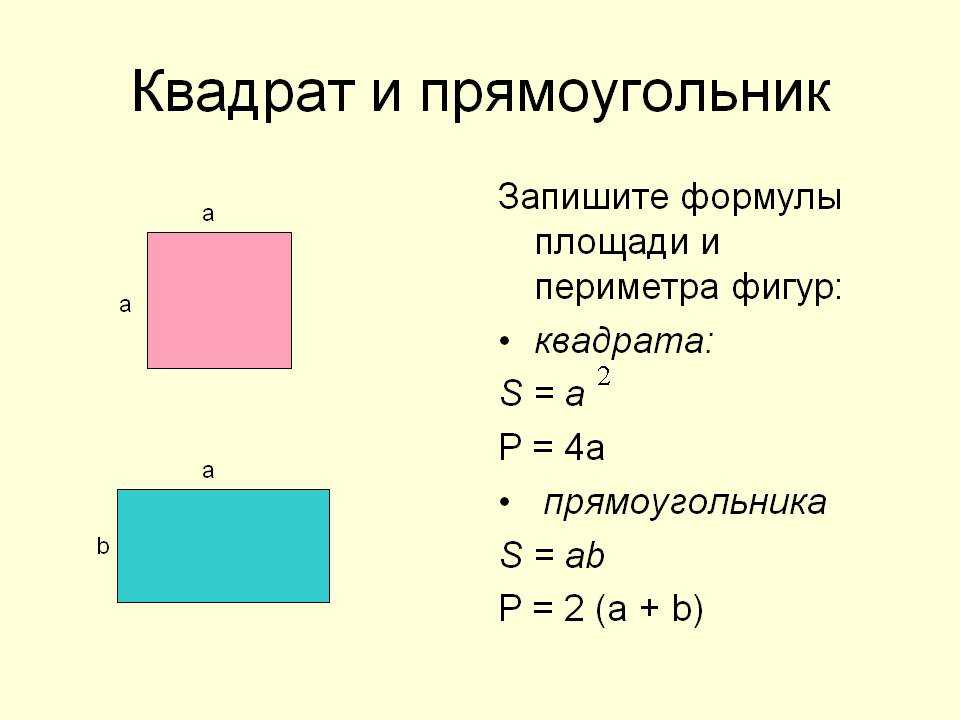
Сначала об обозначении. Для длины стороны принято выбирать букву «а». Тогда площадь квадрата вычисляется по формуле: S = а2.
Она легко получается из той, что известна для прямоугольника.
В ней длина и ширина перемножаются. У квадрата эти два элемента оказываются равными. Поэтому в формуле появляется квадрат этой одной величины.
Формула, в которой фигурирует длина диагонали
Она является гипотенузой в треугольнике, катетами которого являются стороны фигуры. Поэтому можно воспользоваться формулой теоремы Пифагора и вывести равенство, в котором сторона выражена через диагональ.
Проведя такие несложные преобразования, получаем, что площадь квадрата через диагональ вычисляется по такой формуле:
S = d2 / 2. Здесь буквой d обозначена диагональ квадрата.
Формула по периметру
В такой ситуации необходимо выразить сторону через периметр и подставить его в формулу площади. Поскольку одинаковых сторон у фигуры четыре, то периметр придется разделить на 4. Это будет значение стороны, которую потом можно подставить в начальную и сосчитать площадь квадрата.
Формула в общем виде выглядит так: S = (Р/4)2.
Задачи на расчеты
№ 1. Имеется квадрат. Сумма двух его сторон равна 12 см. Вычислите площадь квадрата и его периметр.
Решение. Поскольку дана сумма двух сторон, то нужно узнать длину одной. Так как они одинаковые, то известное число нужно просто разделить на два. То есть сторона данной фигуры равна 6 см.
Тогда его периметр и площадь легко вычисляются по приведенным формулам. Первый равен 24 см, а вторая — 36 см2.
Ответ. Периметр квадрата равняется 24 см, а его площадь — 36 см2.
№ 2. Узнайте площадь квадрата с периметром, равным 32 мм.
Решение. Достаточно просто подставить значение периметра в написанную выше формулу. Хотя можно сначала узнать сторону квадрата, а уже потом его площадь.
В обоих случаях в действиях сначала будет идти деление, а потом возведение в степень. Простые расчеты приводят к тому, что площадь представленного квадрата равна 64 мм2.
Ответ.
Искомая площадь равна 64 мм2.
№ 3. Сторона квадрата равна 4 дм. Размеры прямоугольника: 2 и 6 дм. У какой из этих двух фигур больше площадь? На сколько?
Решение. Пусть сторона квадрата будет обозначена буквой а1, тогда длина и ширина прямоугольника а2 и в2. Для определения площади квадрата значение а1 полагается возвести в квадрат, а прямоугольника — перемножить а2 и в2 . Это несложно.
Получается, что площадь квадрата равна 16 дм2, а прямоугольника — 12 дм2. Очевидно, что первая фигура больше второй. Это при том, что они равновелики, то есть имеют одинаковый периметр. Для проверки можно сосчитать периметры. У квадрата сторону нужно умножить на 4, получится 16 дм. У прямоугольника сложить стороны и умножить на 2. Будет то же число.
В задаче требуется еще ответить, на сколько площади различаются. Для этого из большего числа вычитают меньшее. Разница оказывается равной 4 дм2.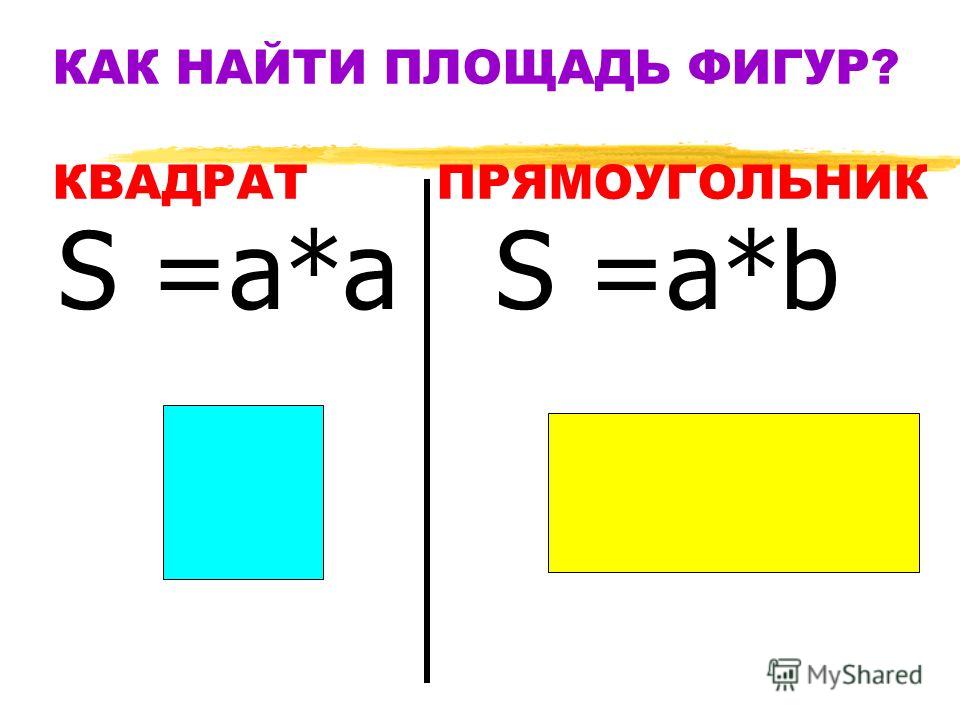
Ответ. Площади равны 16 дм2 и 12 дм2. У квадрата она больше на 4 дм2.
Задача на доказательство
Условие. На катете равнобедренного прямоугольного треугольника построен квадрат. К его гипотенузе построена высота, на которой построен еще один квадрат. Доказать, что площадь первого в два раза больше, чем второго.
Решение. Введем обозначения. Пусть катет равен а, а высота, проведенная к гипотенузе, х. Площадь первого квадрата — S1, второго — S2.
Площадь квадрата, построенного на катете, вычисляется просто. Она оказывается равной а2. Со вторым значением все не так просто.
Для начала нужно узнать длину гипотенузы. Для этого пригодится формула теоремы Пифагора. Простые преобразования приводят к такому выражению: а√2.
Поскольку высота в равнобедренном треугольнике, проведенная к основанию, является еще и медианой и высотой, то она делит большой треугольник на два равных равнобедренных прямоугольных треугольника.
Поэтому высота равна половине гипотенузы. То есть х = (а√2)/2. Отсюда легко узнать площадь S2. Она получается равной а2/2.
Очевидно, что записанные значения отличаются ровно в два раза. Причем вторая в это число раз меньше. Что и требовалось доказать.
Необычная головоломка — танграм
Она делается из квадрата. Его необходимо по определенным правилам разрезать на различные фигуры. Всего частей должно оказаться 7.
Правила предполагают, что в процессе игры будут использоваться все получившиеся детали. Из них нужно составлять другие геометрические фигуры. Например, прямоугольник, трапецию или параллелограмм.
Но еще интереснее, когда из кусочков получаются силуэты животных или предметов. Причем оказывается, что площадь всех производных фигур равна той, что была у начального квадрата.
Фракталы (Федер Е.)
Фракталы (Федер Е.)
ОглавлениеПредисловиеГлава 2. Фрактальная размерность 2.2. Парадокс Шварца с площадью боковой поверхности цилиндра 2.3. Фрактальная размерность 2.4. Триадная кривая Кох 2.5. Подобие и скейлинг 2.6. Кривые Мандельброта-Гивена и Серпинского 2.7. Еще о скейлинге 2.8. Функция Вейерштрасса-Мандельброта Глава 3. Фрактальная размерность кластеров 3.  1. Измерения фрактальных размерностей кластеровГлава 4. Образование вязких пальцев в пористых средах 4.1. Течение жидкости в ячейке Хеле-Шоу 4.2. Вязкие пальцы в ячейках Хеле-Шоу 4.3. Вязкие пальцы в двумерных пористых средах 4.4. Образование вязких пальцев и ОДА 4.5. Вязкие пальцы в трехмерных пористых средах Глава 5. Канторовские множества 5.1. Триадное канторовское множество 5.2. Скейлинг с неравными отношениями Глава 6. Мультифрактальные меры 6.1. Свертывание и чертова лестница 6.2. Биномиальный мультипликативный процесс 6.3. Фрактальные подмножества 6.4. Показатель Липшица-Гёльдера a 6.5. Кривая f(a) 6.6. Концентрация меры 6.7. Последовательность показателей массы t(q) 6.8. Соотношение между t(q) и f(a) 6.9. Свертывание с несколькими масштабами длины 6.10. Мультифрактальная конвекция Рэлея-Бенара 6.11. ОДА и гармонические меры 6.12. Мультифрактальный рост вязких пальцев Глава 7. Протекание 7.  1. Протекание от узла к узлу на квадратной решетке7.2. Бесконечный кластер при … 7.3. Самоподобие перколяционных кластеров 7.4. Конечные кластеры при протекании 7.5. Распределение величины кластеров при … 7.6. Корреляционная длина 7.7. Остов перколяционного кластера 7.9. Фрактальный диффузионный фронт Глава 8. Фрактальные временные ряды 8.1. Эмпирический закон Херста и метод нормированного размаха 8.2. Моделирование случайных рядов 8.3. Моделирование долговременных изменений Глава 9. Случайное блуждание и фракталы 9.2. Одномерное случайное блуждание 9.3. Свойства подобия одномерных случайных блужданий 9.4. Обобщенное броуновское движение 9.5. Определение обобщенного броуновского движения 9.6. Моделирование обобщенного броуновского движения 9.7. Метод R/S для обобщенного броуновского движения 9.8. Последовательные случайные сложения Глава 10. Самоподобие и самоаффинность 10.  1. Стратегия смелой игрыГлава 11. Статистика высоты волн 11.1. Метод R/S для наблюдений 11.2. R/S для данных, очищенных от сезонных вариаций Глава 12. Соотношение периметра и площади 12.1. Фрактальная размерность облаков 12.2. Фрактальная размерность рек Глава 13. Фрактальные поверхности 13.1. Фрактальная поверхность Кох 13.2. Поверхности случайного переноса 13.3. Построение фрактальных поверхностей 13.4. Поверхности случайного сложения 13.5. Комментарии к фрактальным пейзажам Глава 14. Исследования фрактальных поверхностей 14.2. Фрактальная размерность ландшафтов и параметров окружающей среды 14.3. Молекулярные фрактальные поверхности |
Фракталы: Пер. с англ.-М.: Мир, 1991. — 254 с.
Площадь и периметр
Площадь и периметр — два часто обсуждаемых измерения двумерных фигур (плоских фигур).
Площадь
Площадь фигуры — это измерение площади, которую занимает фигура. Другой способ думать о площади — это мера пространства, ограниченного фигурой.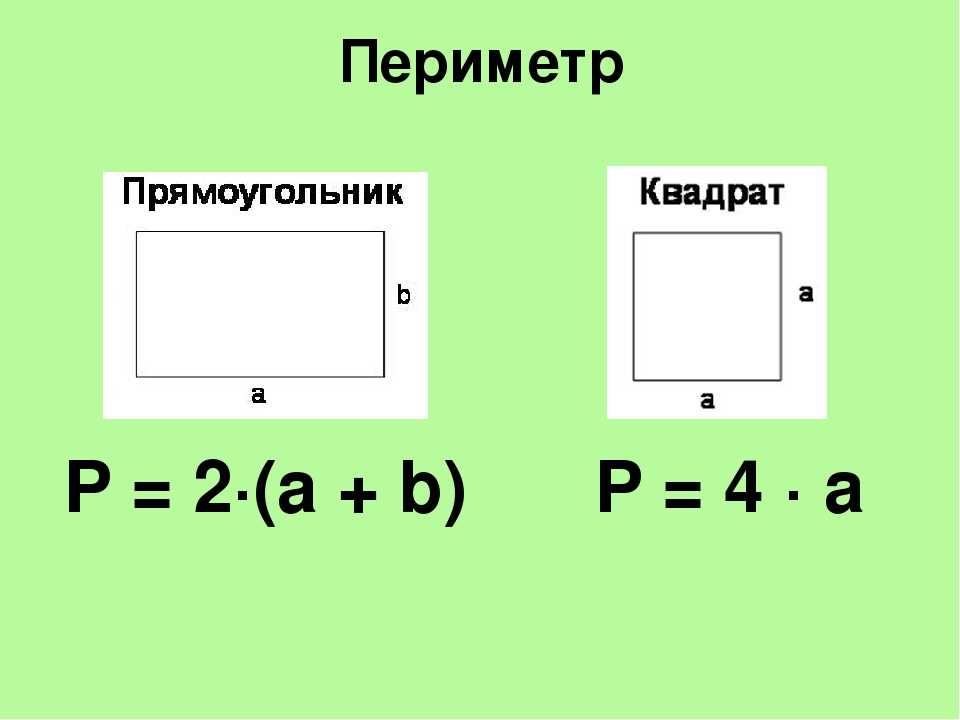
Например, площадь квадрата состоит из пространства между каждой стороной квадрата. На рисунке ниже площадь изображена как заштрихованная часть (все, что находится внутри сторон квадрата) квадрата:
Площадь квадрата рассчитывается как произведение его длины и ширины, которые одинаковы. Используя приведенный выше рисунок, площадь квадрата равна 5 × 5 = 25. Когда единица измерения неизвестна, обычно площадь описывается в терминах «квадратных единиц». Таким образом, квадрат выше имеет площадь 25 квадратных единиц. Обычно используемые меры площади включают квадратные футы (футы 2 ), квадратные метры (м 2 ), квадратные мили (ми 2 ) и так далее.
Расчетная область
Существует несколько различных способов вычисления площади геометрических фигур. Например, существуют четко определенные формулы площади для простых фигур, таких как квадраты, треугольники, круги и т. д. В зависимости от известной информации вычисление площади фигуры может быть таким же простым, как вставка информации в формулу.
Посетите страницу формулы площади, чтобы ознакомиться с формулами площади для ряда простых фигур.
Для сложных фигур, состоящих из простых фигур, общая площадь может быть определена как сумма площадей составляющих ее простых фигур. Например, рисунок ниже состоит из квадрата и прямоугольного треугольника.
Площадь квадрата, рассчитанная выше, составляет 25 квадратных единиц. Площадь треугольника можно определить как A = ½bh, где b — основание, а h — высота:
½(5)(8) = 20
Таким образом, общая площадь равна:
25 + 20 = 45 квадратных единиц
Площадь также может быть определена с использованием понятия единичных квадратов. Единичный квадрат — это квадрат со стороной, равной 1, такой, что площадь квадрата равна 1 квадратной единице. Общую площадь фигуры можно определить, подсчитав количество единичных квадратов, которые вписываются в фигуру; это может быть точным в зависимости от фигуры, а если нет, то для аппроксимации площади можно использовать единичные квадраты.
Площади приведенных выше фигур можно определить, подсчитав единичные квадраты или используя соответствующие формулы площади. В любом случае их площади будут одинаковыми; площадь прямоугольника 12 квадратных единиц; площадь квадрата 9 квадратных единиц, а площадь треугольника 12,5 квадратных единиц.
Периметр
В геометрии периметром фигуры называется расстояние вокруг нее. Посетите страницу периметра, чтобы ознакомиться с формулами для периметров некоторых основных 2D-фигур.
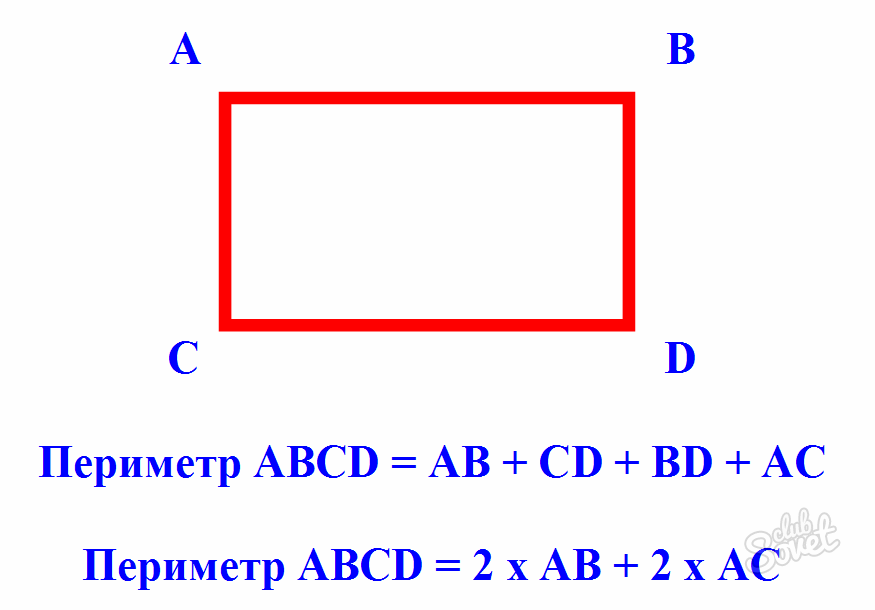
Вкратце, периметр многоугольника — это сумма сторон многоугольника. Например, для квадрата периметр равен сумме его 4-х сторон; для треугольника это сумма трех его сторон и так далее. Периметры следующих фигур определяются суммированием каждой стороны фигуры:
Изогнутые фигуры, такие как круги, также имеют периметры. В случае круга периметр вместо этого называется окружностью круга. Вычисление периметра изогнутых поверхностей, особенно неправильных, может быть намного сложнее, чем вычисление периметра фигур, состоящих из отрезков.
Периметр многих распространенных изогнутых форм (например, кругов) можно найти с помощью известных формул. Для менее правильных фигур необходима более сложная математика. Один из способов измерения периметра изогнутых фигур в реальных условиях — это использовать веревку или веревку, чтобы сформировать контур фигуры, а затем измерить длину веревки, необходимой для контура фигуры. Однако в зависимости от размера фигуры, а также других факторов это может оказаться невозможным.
Периметр квадрата равен 32 футам найдите площадь квадрата
Геометрия
Эддисон Б.
спросил 18.09.19Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Сара Б.
ответил 18.09.19
Репетитор
5 (3)
Опытный учитель/репетитор геометрии
Смотрите таких репетиторов
Смотрите таких репетиторов
Исходя из определения квадрата, мы знаем, что все стороны конгруэнтны!
Итак, мы можем разделить 32 на 4 (количество сторон), чтобы получить 8. Теперь мы знаем, что каждая сторона имеет длину 8 футов.
Теперь мы можем применить формулу площади: A=bh, где и основание, и высота равны 8.
Итак, 8×8=64=A
Площадь квадрата равна 64 футам!
Голосовать за 0 голос против
ПодробнееОтчет
Мигель С. ответил 18.09.19
Репетитор
4.
4
(12)
Магистр прикладной статистики с более чем 5-летним опытом преподавания/репетиторства
См. таких преподавателей
Смотрите таких репетиторов
Формула периметра прямоугольника: 2*длина стороны + 2*ширина стороны. В этом случае вы работаете с квадратом, поэтому все стороны имеют одинаковую длину. Другими словами, у вас есть: Периметр = 4*сторона квадрата.
И поскольку вы знаете, что сумма равна 32, у нас есть простое уравнение, в котором мы можем найти одну сторону квадрата.
32 = 4*сторона квадрата
Разделив обе стороны на 4, мы получим длину одной стороны. 32/4 ровно 8.
Итак, каждая сторона нашего квадрата равна 8.
Наконец, мы используем формулу площади квадрата, которая равна основанию * высоте. В этом случае основание равно высоте, потому что это квадрат. Таким образом, площадь = 8 * 8 = 64
Следовательно, если ПЕРИМЕТР квадрата равен 32, то его общая ПЛОЩАДЬ равна ровно 64.