Площа трикутника. Формули
Формул для обчислення площі трикутника в літературі можна знайти більше 10. Більшість з них можна застосувати в задачах з відомими сторонами та кутами трикутниками. Однак є ряд складних прикладів, в яких задано лише одна сторона і кути трикутника, або радіус описаного чи вписаного кіл та ще одна характеристика. В таких випадках просту формулу застосувати не вдасться.
Задачі на трикутники вивчають в 7, 8 класі з вивчення простих властивостей, обчислення площі і периметра. В 9, 10 класі учні не тільки знають чим відрізняється прямокутний трикутник від рівнобедреного чи рівностороннього, а й з успіхом використовують теорему косинусів для знаходження сторін, формулу Герона, вміють розв’язати задачі про коло вписане або описане навколо трикутника. Але до всього потрібно приходити поступово не перевантажуючи пам’ять та можливості учнів. Тоді накопичені знання можна з успіхом застосувати до обчислення задач на трикутники будь-якої складності.
Наведені нижче формули дозволять розв’язати 95 відсотків задач в яких потрібно знайти площу трикутника. Перейдемо до розгляду поширених формул площі.
Перейдемо до розгляду поширених формул площі.
Розглянемо трикутник зображений на рисунку нижче
На рисунку і далі у формулах введені класичні позначення усіх його характеристик
a,b,c – сторонни трикутника,
R– радіус описаного кола,
r – радіус вписаного кола,
h[b],h[a],h[c] висоти, проведені відповідно до сторін a,b,c.
alpha, beta,hamma – кути при вершинах.
Основні формули площі трикутника
Площа трикутника рівна половині добутку сторони трикутника на висоту, опущену до цієї сторони.
Якщо задано сторону та висоту, опущену до неї, то площу трикутника за класичною формулою знайде кожен школяр.
До речі з цієї формули можна вивести одну корисну залежність між висотами – висоти трикутника обернено пропорцйні сторонам, до яких вони проведені:
2. Формула площі трикутника за двома сторонами та кутом між ними
Якщо врахувати, що висота трикутника рівна добутку сторони на синус кута між стороною і основою, до якої проведена висота
то з класичної формули площі трикутника виводять три наступні
Уважно погляньте на формули – їх легко запам’ятати, оскільки в добутку фігурує дві сторони і кут між ними. Якщо правильно позначити сторонни і кути трикутника, то отримаємо дві сторонни a,b і кут пов’язаний з третьою С (hamma).
Якщо правильно позначити сторонни і кути трикутника, то отримаємо дві сторонни a,b і кут пов’язаний з третьою С (hamma).
3. Формула площі довільного трикутника за трьома сторонами
Формулу Герона застосовують в прикладах з відомими трьома сторонами трикутника. Спочатку знаходять півпериметр трикутника, як суму всіх його сторін розділену на два
а далі визначають площу за формулою
або
Останню залежність досить часто використовують в коді програм онлайн калькуляторів площі.
Наступні формули вклячають відомі радіуси вписанного та описанного кіл (див. роисунок).
4. Площа трикутника за трьома сторонами та радіусом описаного кола
У прикладах де задано три сторони і радіус (діаметр) описаного кола площу знаходять за формулою
5. Формула площі за радіусом вписаного в трикутник кола та трьома сторнами
Якщо крім трьох сторін трикутника (периметра, півпериметра) відомий ще радіус вписаного кола, то площа обчислюється за формулою
6.
 Площа трикутника через радіус описаного кола і три кути
Площа трикутника через радіус описаного кола і три кутиПлоща трикутника рівна подвоєному квадрату радіуса описаного кола помноженому на синуси трьох кутів трикутника:
7. Формула площі за двома сторонами і спільними з третьою стороною кутами
Враховуючи властивості кутів трикутника та перодичність синуса справедлива залежність
Вона дозволяє вивести з співвідношення (2) наведену далі формулу площі трикутника
Приклади на дану залежність зустрічаються вкрай рідко, але пам’ятати, що є така формула Ви повинні.
8. Площа трикутника за стороною та двома прилеглими кутами
Якщо відомі два кути, то й третій можна визначити. Тоді площу трикутника обчислюють за формулою
9. Формула площі трикутника через сторону і котангенси прилеглих кутів
Перестановкою індексів можна вивести формулу площі для інших сторін та кутів трикутника.
10. Площа трикутника заданого координатами своїх вершин
Коли вершини трикутника задані на площині координатами вершин A(xA,yA), B(xB,yB), C(xC,yC) площа рівна половині визначника, взятого за модулем.
11. Формула площі трикутника за трьома висотами
В збірниках математичних формул можна знайти залежність площі трикутника за відомими трьома висотами
Вона складна для обчислення на калькуляторі, проте в пакетах MathCad, Mathematica, Maple, MatLab,… площа знаходиться на «раз-два».
В добавку розглянемо – часткові випадки:
Площа прямокутного трикутника з катетами a і b рівна половині їх добутку
Формула площі рівностороннього (правильного) трикутника
рівна одній четвертій добутку квадрату сторони на корінь з трійки.
Приклад 1. Сторони трикутника рівні 3, 5, 6 см. Знайти площу трикутника.
Розв’язок: Застосуємо формулу Герона, для цього спочатку знайдемо півпериметр
p=(a+b+c)/2=(3+4+5)/2=7 (см).
За формулою Герона обчислюємо площу трикутника
Відповідь: Площа трикутника рівна 7.48 сантиметрів квадратних.
Завантажити усі наведені формули площі трикутника Ви можете за наступним посиланням.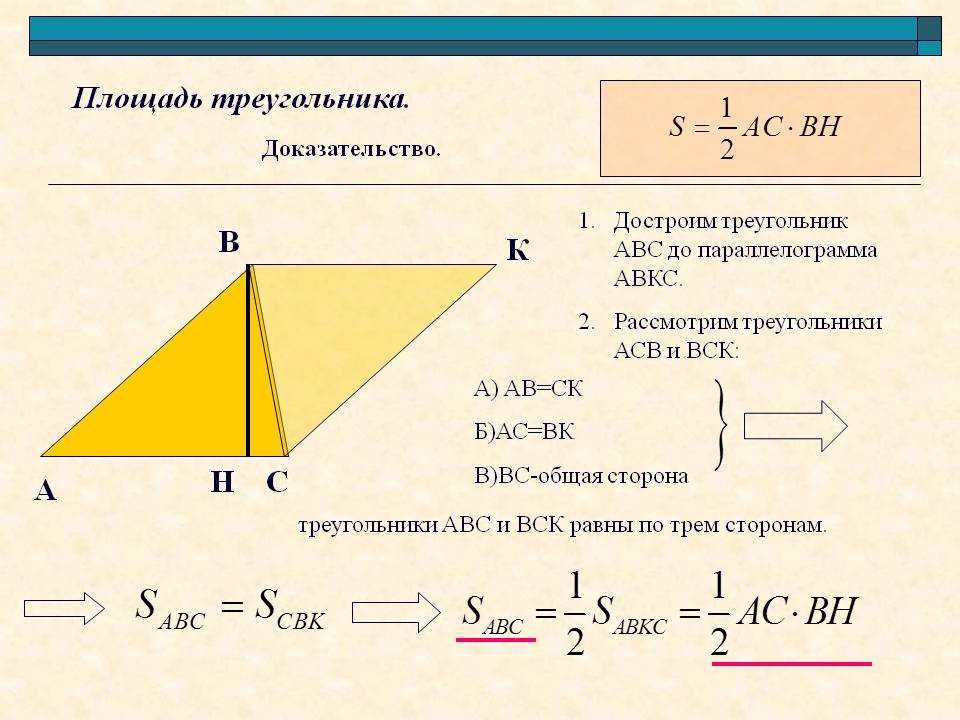 Роздруковуйте їх та використовуйте в навчанні.
Роздруковуйте їх та використовуйте в навчанні.
- Вас може зацікавити:
- Приклади на площу та периметр прямокутного трикутника
- Знаходження катетів, висоти та гіпотенузи прямокутного трикутника
- Обчислення площі рівнобедреного трикутника
- Висота прямокутного трикутника ділить гіпотенузу
- Задачі на кути трикутника з розв’язками
Далі Вас чекають розв’язки понад 100 завдань на прямокутні, рівнобедрені, різносторонні та правильні трикутники.
Якщо матеріал був корисний Вам — поділіться посиланням з друзями!
Площа трикутника прямого кута. Як знайти площу трикутника
Трикутник – плоска геометрична фігура з одним кутом, рівним 90°. При цьому в геометрії дуже часто потрібно обчислити площу такої фігури. Як це зробити, ми розповімо далі.
Найпростіша формула визначення площі прямокутного трикутника
Вихідні дані, де: a та b – сторони трикутника, що виходять із прямого кута.
Тобто площа дорівнює половині твору двох сторін, які виходять із прямого кута. Звичайно, існує формула Герона, яка використовується для обчислення площі звичайного трикутника, але для визначення величини необхідно знати довжину трьох сторін. Відповідно, вам доведеться розрахувати гіпотенузу, а це зайвий час.
Звичайно, існує формула Герона, яка використовується для обчислення площі звичайного трикутника, але для визначення величини необхідно знати довжину трьох сторін. Відповідно, вам доведеться розрахувати гіпотенузу, а це зайвий час.
Знайти площу прямокутного трикутника через формулу Герона
Це всім відома та вихідна формула, але для цього вам доведеться порахувати гіпотенузу за двома катетами, використовуючи Теорему Піфагора.
У цій формулі: a, b, c – сторони трикутника, а p – напівпериметр.
Знайти площу прямокутного трикутника з гіпотенузи та кута
Якщо у вашому завданні не відомий жоден з катетів, то скористатися найпростішим способом ви не зможете. Для визначення величини потрібно розрахувати довжину катетів. Це зробити просто з гіпотенузи та косінусу прилеглого кута.
b=c×cos(α)
Дізнавшись довжину одного з катетів, за теоремою Піфагора ви зможете розрахувати другий бік, що виходить із прямого кута.
b 2 =c 2 -a 2
У цій формулі c і a – гіпотенуза та катет відповідно. Тепер можете розрахувати площу за першою формулою. Так само можна обчислити один з катетів, маючи другий і кут. У такому разі одна з шуканих сторін дорівнюватиме добутку катета на тангенс кута. Існують і інші способи обчислення площі, але знаючи основні теореми та правила, ви зможете легко знайти потрібну величину.
Тепер можете розрахувати площу за першою формулою. Так само можна обчислити один з катетів, маючи другий і кут. У такому разі одна з шуканих сторін дорівнюватиме добутку катета на тангенс кута. Існують і інші способи обчислення площі, але знаючи основні теореми та правила, ви зможете легко знайти потрібну величину.
Якщо у вас немає жодної зі сторін трикутника, а є лише медіана та один із кутів, то ви зможете обчислити довжину сторін. Для цього використовуйте властивості медіани ділити прямокутний трикутник на два. Відповідно, вона може бути гіпотенузою, якщо виходить з гострого кута. Скористайтеся теоремою Піфагора та визначте довжину сторін трикутника, що виходять із прямого кута.
Як бачите, знаючи основні формули і Теорему Піфагора, ви зможете розрахувати площу прямокутного трикутника, маючи лише один із кутів та довжину однієї зі сторін.
Інструкція
Завдання 1.
Знайдіть довжини всіх сторін трикутника, якщо відомо, що одного катета перевищує довжину іншого на 1 см, а трикутника дорівнює 28 см. 2)*tg(B)/2 d у випадку, якщо вам заданий тільки один з катетів (a), але також відомий кут (B), що належить цьому катету.
2)*tg(B)/2 d у випадку, якщо вам заданий тільки один з катетів (a), але також відомий кут (B), що належить цьому катету.
Відео на тему
Джерела:
- «Посібник з математики для вступників до вузів», за ред. Г.М. Яковлєва, 1982.
Співвідношення між сторонами та кутами прямокутного трикутника розглядаються у розділі математики, що називається тригонометрією. Для знаходження сторін прямокутного трикутника достатньо знати теорему Піфагора, визначення тригонометричних функцій і мати будь-який засіб для знаходження значень тригонометричних функцій, наприклад, калькулятор або таблиці Брадіса. Розглянемо нижче основні випадки задач знаходження сторін прямокутного трикутника.
Вам знадобиться
- Калькулятор, таблиці Брадіса.
Інструкція
Якщо заданий один із гострих кутів, наприклад, A, і один з катетів, наприклад, a, то гіпотенуза та інший катет обчислюються із співвідношень: b=a*tg(A), c=a*sin(A).
Корисна порада
Якщо вам не відомо значення синуса або косинуса якогось з необхідних для розрахунку кутів, ви можете скористатися таблицями Брадіса, в них наводяться значення тригонометричних функцій для великої кількості кутів.
Джерела:
- як обчислити сторону прямокутного трикутника у 2019
У такій фігурі, як прямокутний трикутник, обов’язково існує чітке співвідношення сторін щодо один одного. Знаючи дві з них, завжди можна знайти третю. Те, як це можна зробити, ви дізнаєтеся з інструкції, запропонованої нижче.
Вам знадобиться
- — Калькулятор.
Інструкція
Зведіть у квадрат обидва катета, а складіть їх між собою a2+b2. Отриманий результат є гіпотенузою ( основою) у квадраті c2. Далі потрібно лише витягти корінь з останнього і гіпотенузу знайдено. Даний метод є простим та зручним у застосуванні на . Головне у процесі знаходження сторін трикутникатаким чином — не забувати витягувати корінь із попереднього результату, щоб уникнути найпоширенішої помилки. Формула виведена завдяки найвідомішій у світі теоремі Піфагора, яка у всіх джерелах має вигляд: a2+b2 = c2.
Розділіть один із катетів a на синус протилежного йому кута sin α. У тому випадку, якщо за умови відомі сторони та синуси, цей варіант знаходження гіпотенузи буде прийнятним. Формула у разі матиме дуже простий вид: c=a/sin α. Будьте уважні за всіх обчислень.
Помножте сторону a на два. Гіпотенуза обчислена. Це, мабуть, найпростіший спосіб знаходження нам сторони. Але, на жаль, цей метод застосовується тільки в одному випадку — якщо сторона, що лежить навпроти кута в градусну міру, що дорівнює числу тридцять. За наявності такої ви можете бути впевнені, що вона завжди буде рівно половиною гіпотенузи. Відповідно, вам залишається лише збільшити її вдвічі і готовий.
Розділіть катет a на косинус кута cos α, що прилягає до нього. Такий метод підійде виключно в тому випадку, якщо вам відомий один з катетів і косинус кута до нього. Цей спосіб нагадує вже представлений вам раніше, в якому використовується також катет, але замість косинуса – синус протилежного кута. Тільки ось у цьому випадку матиме дещо інший змінений зовнішній вигляд: з = a/cos α.
Тре косинець, Один з кутів якого є прямим (рівний 90 °), називають прямокутним. Його найдовша сторона завжди лежить навпроти прямого кута і називається гіпотенузою, а дві інші сторониназивають катетами. Якщо довжини цих трьох сторін відомі, то знайти величини всіх кутів косинецьа не складе труднощів, тому що фактично потрібно обчислити лише один з кутів. Зробити це можна кількома способами.
Інструкція
Використовуйте для обчислення величин (α, β, γ) визначення тригонометричних функцій через прямокутний тре. Таке, наприклад, для синуса гострого кута як відношення довжини протилежного катета до довжини гіпотенузи. Значить, якщо довжини катетів (A і B) та гіпотенузи (C), то знайти, наприклад, синус кута α, що лежить навпроти катета A можна, розділивши довжину сторониА на довжину сторони C (гіпотенузи): sin(?)=A/C. Дізнавшись значення синуса цього кута, можна знайти його величину в градусах, використавши зворотну синусу функцію — арксинус. Тобто α=arcsin(sin(α))=arcsin(A/C). Таким же способом можна знайти і величину гострого кута в тре косинецье, але в цьому немає потреби. Оскільки сума всіх кутів тре косинецьа становить 180 °, а в тре косинецье один із кутів дорівнює 90°, то величину третього кута можна порахувати як різницю між 90° і величиною знайденого кута: β=180°-90°-α=90°-α.
Тобто α=arcsin(sin(α))=arcsin(A/C). Таким же способом можна знайти і величину гострого кута в тре косинецье, але в цьому немає потреби. Оскільки сума всіх кутів тре косинецьа становить 180 °, а в тре косинецье один із кутів дорівнює 90°, то величину третього кута можна порахувати як різницю між 90° і величиною знайденого кута: β=180°-90°-α=90°-α.
Замість визначення синуса можна використовувати визначення косинуса гострого кута, яке формулюється як відношення довжини катета, що прилягає до шуканого кута, до довжини гіпотенузи: cos(α)=B/C. І тут задійте зворотну тригонометричну функцію (арккосинус), щоб знайти величину кута в градусах: α=arccos(cos(α))=arccos(B/C). Після цього, як і в попередньому кроці, залишиться знайти величину кута, що бракує: β=90°-α.
Можна скористатися аналогічним тангенса — він виражається співвідношенням довжини катета, що шукає кута, до довжини катета прилеглого: tg(α)=A/B. Величину кута в градусах знову визначайте через зворотну тригонометричну функцію: α=arctg(tg(α))=arctg(A/B). 2 — підкорене вираз, що позначає різницю квадрата гіпотенузи та катета.
2 — підкорене вираз, що позначає різницю квадрата гіпотенузи та катета.
3. Дано значення всіх сторін трикутника
Для таких завдань можна використати формулу Герона:
S = (p-a)(p-b),
де p – напівпериметр, що знаходиться за таким виразом: p = 0.5∙ (a+b+c)
4. Відомий один катет та кут
Тут варто звернутися до тригонометричних функцій. Наприклад, tg(1) = 1/ctg (1) = b/a. Тобто завдяки цьому співвідношенню можна визначити значення невідомого катета. Далі завдання зводиться до першого пункту.
5. Відома гіпотенуза та кут
У цьому випадку також використовуються тригонометричні функції синуса та косинуса: сos(2)=1/sin(2) = b/c. Потім розв’язання задачі зводиться до другого пункту статті.
Відео на тему
визначення, подібне до першого. Прямокутним називається трикутник, у якого дві сторони перпендикулярні.
Гіпотенуза та катети
У гострокутного та тупокутного трикутників відрізки, що з’єднують вершини кутів, називаються просто сторонами. У сторони мають інші назви. Ті, що прилягають до прямого кута, називаються катетами. Сторона, що протилежить прямому куту, називається гіпотенузою. У перекладі з грецької слово «гіпотенуза» означає «натягнута», а «катет» — «перпендикуляр».
У сторони мають інші назви. Ті, що прилягають до прямого кута, називаються катетами. Сторона, що протилежить прямому куту, називається гіпотенузою. У перекладі з грецької слово «гіпотенуза» означає «натягнута», а «катет» — «перпендикуляр».
Співвідношення між гіпотенузою та катетами
Сторони прямокутного трикутника пов’язані між собою певними співвідношеннями, які значно полегшують обчислення. Наприклад, знаючи розміри катетів, можна вирахувати довжину гіпотенузи. Це співвідношення на ім’я того, хто його відкрив, одержало назву теореми Піфагора і виглядає воно так:
c2=a2+b2, де з – гіпотенуза, a та b – катети. Тобто, гіпотенуза дорівнюватиме квадратному кореню із суми квадратів катетів. Щоб знайти будь-який з катетів, достатньо з квадрата гіпотенузи відняти квадрат іншого катета і витягти з отриманої різниці квадратний корінь.
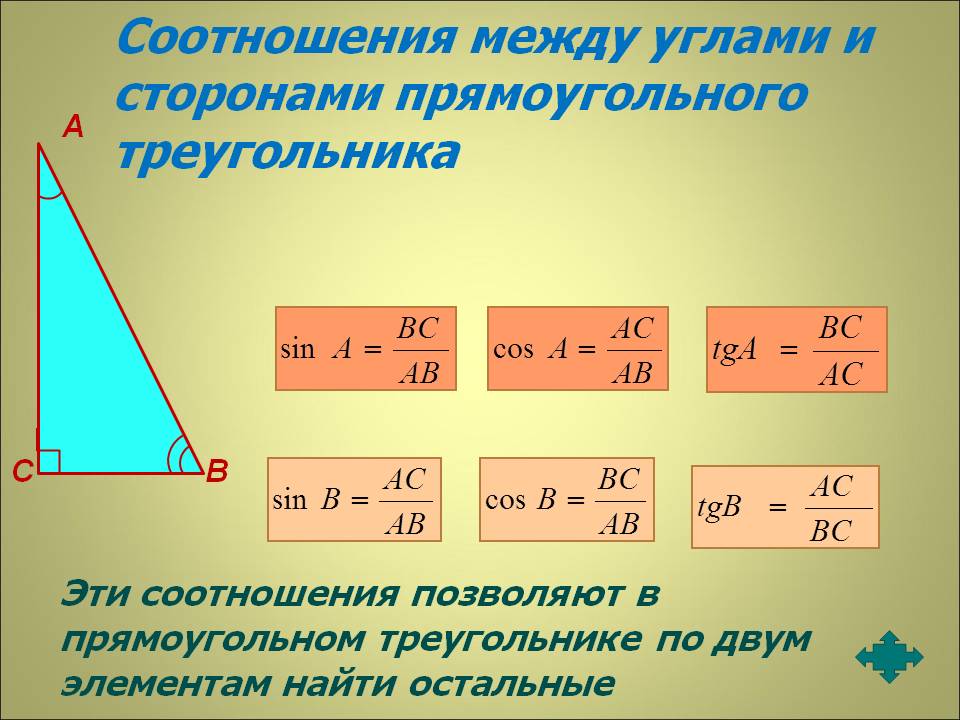
Прилеглий та протилежний катет
Накресліть прямокутний трикутник АСВ. Буквою З прийнято позначати вершину прямого кута, А і В – вершини гострих кутів. Сторони, що протилежать кожному куту, зручно назвати а, b і с, за назвами кутів, що лежать навпроти них. Розгляньте кут А. Катет а йому буде протилежним, катет b – прилеглим. Ставлення протилежного катета до гіпотенузи називається. Обчислити цю тригонометричну функцію можна за такою формулою: sinA=a/c. Відношення прилеглого катета до гіпотенузи називається косинусом. Обчислюється він за такою формулою: cosA=b/c.
Буквою З прийнято позначати вершину прямого кута, А і В – вершини гострих кутів. Сторони, що протилежать кожному куту, зручно назвати а, b і с, за назвами кутів, що лежать навпроти них. Розгляньте кут А. Катет а йому буде протилежним, катет b – прилеглим. Ставлення протилежного катета до гіпотенузи називається. Обчислити цю тригонометричну функцію можна за такою формулою: sinA=a/c. Відношення прилеглого катета до гіпотенузи називається косинусом. Обчислюється він за такою формулою: cosA=b/c.
Таким чином, знаючи кут і одну зі сторін, можна за цими формулами обчислити іншу сторону. Тригонометричними співвідношеннями пов’язані і обидва катеты. Ставлення протилежного до прилеглого називається тангенсом, а прилеглого до протилежного котангенсом. Виразити ці співвідношення можна формулами tgA=a/b або ctgA=b/a.
На уроках геометрії в середній школі всім нам говорили про трикутник. Однак у рамках шкільної програми ми отримуємо лише найнеобхідніші знання та вчимося найбільш поширеним та стандартним способам обчислень. Чи існують незвичайні засоби знаходження цієї величини?
Чи існують незвичайні засоби знаходження цієї величини?
Як запровадження згадаємо, який трикутник вважається прямокутним, і навіть позначимо поняття площі.
Прямокутним трикутником називають замкнуту геометричну фігуру, один із кутів якої дорівнює 90 0 . Невід’ємними поняттями у визначенні є катети та гіпотенуза. Під катетами мають на увазі дві сторони, які у точці з’єднання утворюють прямий кут. Гіпотенуза – сторона, протилежна прямому куту. Прямий трикутник може бути рівнобедреним (дві його сторони матимуть однакову величину), але ніколи не буде рівностороннім (всі сторони однієї довжини). Визначення висоти, медіани, векторів та інших математичних термінів докладно не розбиратимемо. Їх легко знайти у довідниках.
Площа прямого трикутника. На відміну від прямокутників, правило про
творі сторін у визначенні діє. Якщо говорити сухою мовою термінів, то під площею трикутника розуміють властивість цієї фігури займати частину площини, виражену числом. Досить складно до сприйняття, погодьтеся. Не намагатимемося глибоко вникнути у визначення, наша мета не в цьому. Перейдемо до головного – як знайти площу прямокутного трикутника? Самі обчислення робити не будемо, зазначимо лише формули. Для цього визначимося з позначеннями: A, B, C – сторони трикутника, катети – AB, BC. Кут ACB – прямий. S – площа трикутника, h n n – висота трикутника, де nn – сторона, на яку вона опущена.
Не намагатимемося глибоко вникнути у визначення, наша мета не в цьому. Перейдемо до головного – як знайти площу прямокутного трикутника? Самі обчислення робити не будемо, зазначимо лише формули. Для цього визначимося з позначеннями: A, B, C – сторони трикутника, катети – AB, BC. Кут ACB – прямий. S – площа трикутника, h n n – висота трикутника, де nn – сторона, на яку вона опущена.
Спосіб 1. Як знайти площу прямокутного трикутника, якщо відома величина його катетів
Спосіб 2. Знаходимо площу рівнобедреного прямокутного трикутника
Спосіб 3. Обчислення площі через прямокутник
Добудовуємо прямокутний трикутник до квадрата (якщо трикутник
рівнобедрений) або прямокутника. Отримаємо простий чотирикутник, що складається з 2-х ідентичних прямокутних трикутників. У цьому випадку значення площі одного з них дорівнює половині площі отриманої фігури. S прямокутника обчислюємо добутком сторін. Позначимо цю величину M. Шукане значення площі дорівнює половині M.
Спосіб 4. «Піфагорові штани». Знаменита теорема Піфагора
Ми всі пам’ятаємо її формулювання: «Сума квадратів катетів …». Але не всі можуть
сказати, причому тут деякі «штани». Справа в тому, що спочатку Піфагор вивчав взаємозв’язок побудованих на сторонах прямого трикутника. Виявивши закономірності у співвідношенні сторін квадратів, він зміг вивести і відому нам формулу. Її можна застосовувати у разі, коли невідома величина однієї із сторін.
Спосіб 5. Як знайти площу прямокутного трикутника за формулою Герона
Також досить простий спосіб розрахунку. Формула передбачає вираз площі трикутника через числові значення його сторін. Для розрахунків потрібно знати величини всіх сторін трикутника.
S = (p-AC) * (p-BC), де p = (AB + BC + AC) * 0.5
Крім наведених, існує безліч інших способів знайти величину такої загадкової фігури, як трикутник. Серед них: обчислення методом вписаного або описаного кола, обчислення за допомогою координат вершин, використання векторів абсолютної величини, синусів, тангенсів.
Прямокутний трикутник зустрічається насправді на кожному кутку. Знання про властивості даної фігури, а також вміння обчислювати її площу, безсумнівно, стане вам у нагоді не тільки для вирішення задач з геометрії, але і в життєвих ситуаціях.
Геометрія трикутника
В елементарній геометрії прямокутний трикутник — це фігура, яка складається з трьох з’єднаних відрізків, що формують три кути (два гострі та один прямий). Прямокутний трикутник — оригінальна фігура, що характеризується рядом важливих властивостей, що є фундаментом тригонометрії. На відміну від звичайного трикутника, сторони прямокутної фігури мають власні назви:
- Гіпотенуза — найдовша сторона трикутника, що лежить навпроти прямого кута.
- Катети – відрізки, що утворюють прямий кут. Залежно від кута, що розглядається, катет може бути прилеглим до нього (утворює цей кут з гіпотенузою) або протилежним (що лежить навпроти кута). Для непрямокутних трикутників катетів немає.
Саме співвідношення катетів та гіпотенузи становить основу тригонометрії: синуси, тангенси та секанси визначаються як відношення сторін прямокутного трикутника.
Прямокутний трикутник насправді
Ця фігура набула широкого поширення насправді. Трикутники знаходять застосування у проектуванні та техніці, тому розрахунок площі фігури доводиться виконувати інженерам, архітекторам та проектувальникам. Форму трикутника мають підстави тетраедрів або призм – тривимірних фігур, які легко зустріти у повсякденності. Крім того, косинець — найпростіше уявлення «плоського» прямокутного трикутника в реальності. Кутник — це слюсарний, креслярський, будівельний та столярний інструмент, який використовується для побудови кутів як школярами, так і інженерами.
Площа трикутника
Площа геометричної фігури – це кількісна оцінка того, яка частина площини обмежена сторонами трикутника. Площа звичайного трикутника можна знайти п’ятьма способами, використовуючи формулу Герона або оперуючи при розрахунках такими змінними, як основа, сторона, кут і радіус вписаного або описаного кола. Найпростіша формула площі виражається як:
де a – сторона трикутника, h – його висота.
Формула для обчислення площі прямокутного трикутника ще простіше:
де a та b – катети.
Працюючи з нашим онлайн-калькулятор, ви можете обчислити площу трикутника, використовуючи три пари параметрів:
- два катети;
- катет та прилеглий кут;
- катет та протилежний кут.
У задачах або побутових ситуаціях вам будуть дані різні комбінації змінних, тому така форма калькулятора дозволяє обчислити площу трикутника декількома способами. Розглянемо кілька прикладів.
Приклади із реального життя
Керамічна плитка
Допустимо, ви хочете виконати облицювання стін кухні керамічною плиткою, яка має форму прямокутного трикутника. Для того щоб визначити витрату плитки ви повинні дізнатися площу одного елемента облицювання та загальну площу оброблюваної поверхні. Нехай вам потрібно обробити 7 квадратних метрів. Довжина катетів одного елемента становить по 19 см, тоді площа плитки дорівнюватиме:
Це означає, що площа одного елемента становить 24,5 квадратних сантиметрів або 0,01805 квадратних метрів. Знаючи ці параметри, ви можете підрахувати, що для обробки 7 квадратних метрів стіни вам знадобиться 7/0,01805=387 елементів облицювальної плитки.
Знаючи ці параметри, ви можете підрахувати, що для обробки 7 квадратних метрів стіни вам знадобиться 7/0,01805=387 елементів облицювальної плитки.
Шкільне завдання
Нехай у шкільній задачі з геометрії потрібно знайти площу прямокутного трикутника, знаючи лише те, що сторона одного катета дорівнює 5 см, а величина протилежного кута становить 30 градусів. Наш онлайн-калькулятор супроводжується ілюстрацією, на якій вказані сторони та кути прямокутного трикутника. Якщо сторона a = 5 см, її протилежний кут — це кут альфа, рівний 30 градусів. Введіть ці дані у форму калькулятора та отримайте результат:
Таким чином, калькулятор не тільки обчислює площу заданого трикутника, але й визначає довжину прилеглого катета та гіпотенузи, а також величину другого кута.
Висновок
Прямокутні трикутники зустрічаються у нашому житті буквально на кожному розі. Визначення площі таких фігур стане вам у нагоді не тільки при вирішенні шкільних завдань з геометрії, але і повсякденної та професійної діяльності.
В елементарній геометрії прямокутним трикутником називається фігура, що складається з трьох відрізків з’єднаних у точках, з кутами два з яких гострі, а один прямий (тобто дорівнює 90°). Прямокутний трикутникхарактеризується цілим рядом важливих властивостей, багато з яких становлять основу тригонометрії (наприклад, співвідношення між його сторонами та кутами). Ще зі шкільної лави усі ми знаємо, як вирахувати площа прямокутного трикутника, а у повсякденному житті зустрічаємося з цією геометричною фігурою досить часто, часом навіть не помічаючи цього. Досить широке застосування знаходить вона в техніці і тому таке завдання, як , часто доводиться вирішувати інженерам, конструкторам та архітекторам.
Зодчим визначати цю величину потрібно тоді, коли вони проектують будинки з фронтонами, які є завершенням фасадів та мають трикутну формуобмежену карнизом, а з боків – скатами даху. Нерідко кут між скатами буває прямою, і в таких випадках фронтон має форму прямокутного трикутника. Визначати його площу потрібно з тієї простої причини, що необхідно точно знати кількість будівельного матеріалу, необхідного для його облаштування. Слід зазначити, що фронтони є обов’язковими елементами малоповерхових будівель (заміських будинків, котеджів, дач).
Визначати його площу потрібно з тієї простої причини, що необхідно точно знати кількість будівельного матеріалу, необхідного для його облаштування. Слід зазначити, що фронтони є обов’язковими елементами малоповерхових будівель (заміських будинків, котеджів, дач).
Знаходження площі прямокутного трикутника
a— катет
b— катет
S— площа прямокутного трикутника
Форму прямокутного трикутникамають багато деталей, з яких виготовляються сучасні меблі. Як відомо, для того, щоб найбільш раціонально використовувати площу приміщень, всі елементи обстановки повинні розміщуватися в ній оптимальним чином. З користю задіяти такі зони, як кути, можна за допомогою столів трикутної форми, стільниці яких у більшості випадків являють собою прямокутні трикутники з катетами, що впритул прилягають до стін. При проектуванні та розрахунку цих елементів конструктори меблевого виробництва застосовують формулу, за якою знаходження площі прямокутного трикутникаскладає основі довжини його сторін. Крім того, їм нерідко доводиться розробляти конструкції столиків, що кріпляться безпосередньо до стін, до складу яких входять опорні елементи, що також являють собою прямокутні трикутники.
Крім того, їм нерідко доводиться розробляти конструкції столиків, що кріпляться безпосередньо до стін, до складу яких входять опорні елементи, що також являють собою прямокутні трикутники.
Будівельникам, що займаються облицювальними роботами, нерідко у своїй професійній діяльності доводиться використовувати керамічну плитку, що має форму прямокутного трикутника з катетами однакової чи різної довжини. Їм також доводиться визначати площу цих елементів для того, щоб з’ясувати потрібну їх кількість.
Форму прямокутного трикутникамає і такий важливий та необхідний вимірювальний інструмент, як косинець. З його допомогою виробляється побудова і контроль прямих кутів, а використовується дуже широко і багатьма: від звичайних школярів під час уроків геометрії до конструкторів суперсучасної техніки.
Розрахувати площу трикутника з прямим кутом. Як знайти площу прямокутного трикутника незвичайним способом. Приклади із реального життя
В елементарній геометрії прямокутним трикутником називається фігура, що складається з трьох відрізків з’єднаних у точках, з кутами два з яких гострі, а один прямий (тобто дорівнює 90°).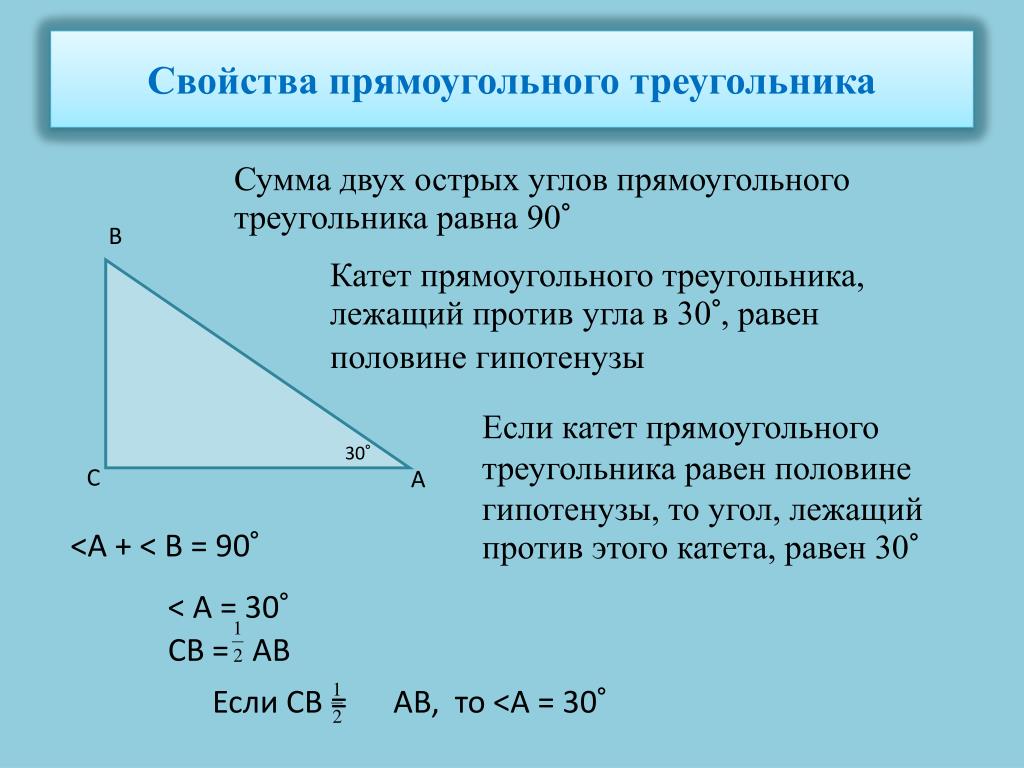 Прямокутний трикутникхарактеризується цілим рядом важливих властивостей, багато з яких становлять основу тригонометрії (наприклад, співвідношення між його сторонами та кутами). Ще зі шкільної лави усі ми знаємо, як вирахувати площа прямокутного трикутника, а у повсякденному житті зустрічаємося з цією геометричною фігурою досить часто, часом навіть не помічаючи цього. Досить широке застосування знаходить вона в техніці і тому таке завдання, як , часто доводиться вирішувати інженерам, конструкторам та архітекторам.
Прямокутний трикутникхарактеризується цілим рядом важливих властивостей, багато з яких становлять основу тригонометрії (наприклад, співвідношення між його сторонами та кутами). Ще зі шкільної лави усі ми знаємо, як вирахувати площа прямокутного трикутника, а у повсякденному житті зустрічаємося з цією геометричною фігурою досить часто, часом навіть не помічаючи цього. Досить широке застосування знаходить вона в техніці і тому таке завдання, як , часто доводиться вирішувати інженерам, конструкторам та архітекторам.
Зодчим визначати цю величину потрібно тоді, коли вони проектують будинки з фронтонами, які є завершенням фасадів та мають трикутну формуобмежену карнизом, а з боків – скатами даху. Нерідко кут між скатами буває прямою, і в таких випадках фронтон має форму прямокутного трикутника. Визначати його площу потрібно з тієї простої причини, що необхідно точно знати кількість будівельного матеріалунеобхідного для його облаштування. Слід зазначити, що фронтони є обов’язковими елементами малоповерхових будівель (заміських будинків, котеджів, дач).
Знаходження площі прямокутного трикутника
Формула розрахунку площі прямокутного трикутника
a— катет
b— катет
S— площа прямокутного трикутника
Форму прямокутного трикутникамають багато деталей, з яких виготовляються сучасні меблі. Як відомо, для того, щоб найбільш раціонально використовувати площу приміщень, всі елементи обстановки повинні розміщуватися в ній оптимальним чином. З користю задіяти такі зони, як кути, можна за допомогою столів трикутної форми, стільниці яких у більшості випадків являють собою прямокутні трикутники з катетами, що впритул прилягають до стін. При проектуванні та розрахунку цих елементів конструктори меблевого виробництва застосовують формулу, за якою знаходження площі прямокутного трикутникаскладає основі довжини його сторін. Крім того, їм нерідко доводиться розробляти конструкції столиків, що кріпляться безпосередньо до стін, до складу яких входять опорні елементи, що також являють собою прямокутні трикутники.
Будівельникам, що займаються облицювальними роботами, нерідко у своїй професійній діяльності доводиться використовувати керамічну плитку, що має форму прямокутного трикутника з катетами однакової чи різної довжини. Їм також доводиться визначати площу цих елементів для того, щоб з’ясувати потрібну їх кількість.
Форму прямокутного трикутникамає і такий важливий та необхідний вимірювальний інструмент, як косинець. З його допомогою виробляється побудова і контроль прямих кутів, а використовується дуже широко і багатьма: від звичайних школярів під час уроків геометрії до конструкторів суперсучасної техніки.
На уроках геометрії в середній школі всім нам говорили про трикутник. Однак у рамках шкільної програми ми отримуємо лише найнеобхідніші знання та вчимося найбільш поширеним та стандартним способам обчислень. Чи існують незвичайні засоби знаходження цієї величини?
Як запровадження згадаємо, який трикутник вважається прямокутним, і навіть позначимо поняття площі.
Прямокутним трикутником називають замкнуту геометричну фігуру, один із кутів якої дорівнює 90 0 . Невід’ємними поняттями у визначенні є катети та гіпотенуза. Під катетами мають на увазі дві сторони, які у точці з’єднання утворюють прямий кут. Гіпотенуза – сторона, протилежна прямому куту. Прямий трикутник може бути рівнобедреним (дві його сторони матимуть однакову величину), але ніколи не буде рівностороннім (всі сторони однієї довжини). Визначення висоти, медіани, векторів та інших математичних термінів докладно не розбиратимемо. Їх легко знайти у довідниках.
Площа прямого трикутника. На відміну від прямокутників, правило про
творі сторін у визначенні діє. Якщо говорити сухою мовою термінів, то під площею трикутника розуміють властивість цієї фігури займати частину площини, виражену числом. Досить складно до сприйняття, погодьтеся. Не намагатимемося глибоко вникнути у визначення, наша мета не в цьому. Перейдемо до головного – як знайти площу прямокутного трикутника? Самі обчислення робити не будемо, зазначимо лише формули.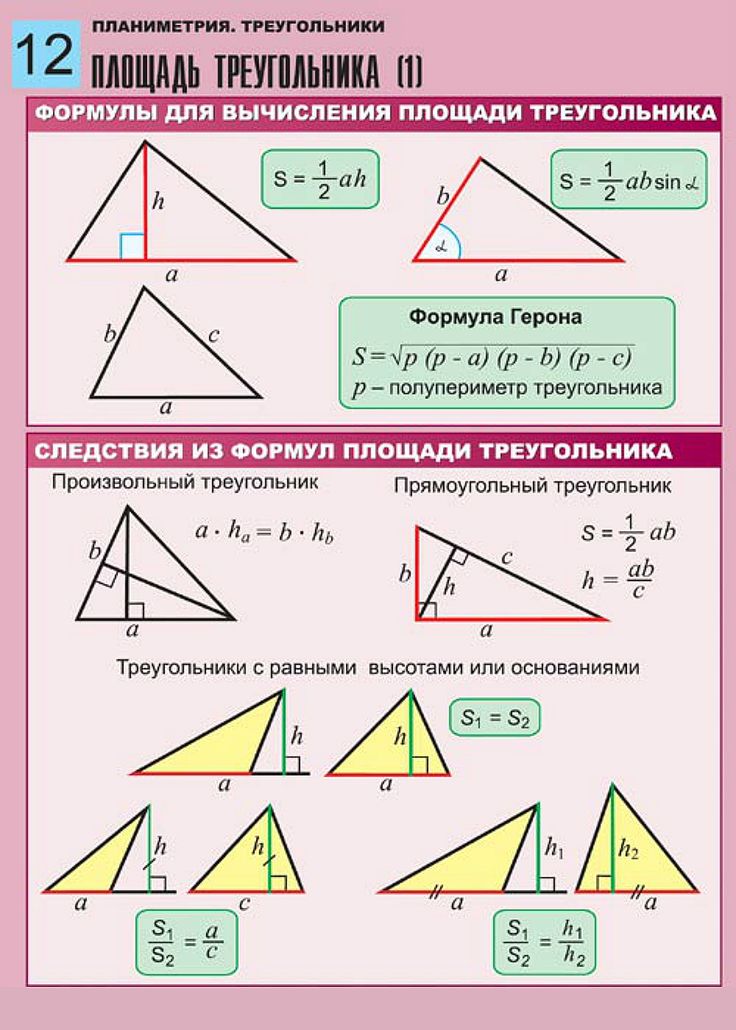 Для цього визначимося з позначеннями: A, B, C – сторони трикутника, катети – AB, BC. Кут ACB – прямий. S – площа трикутника, h n n – висота трикутника, де nn – сторона, на яку вона опущена.
Для цього визначимося з позначеннями: A, B, C – сторони трикутника, катети – AB, BC. Кут ACB – прямий. S – площа трикутника, h n n – висота трикутника, де nn – сторона, на яку вона опущена.
Спосіб 1. Як знайти площу прямокутного трикутника, якщо відома величина його катетів
Спосіб 2. Знаходимо площу рівнобедреного прямокутного трикутника
Спосіб 3. Обчислення площі через прямокутник
Добудовуємо прямокутний трикутник до квадрата (якщо трикутник
рівнобедрений) або прямокутника. Отримаємо простий чотирикутник, що складається з 2-х ідентичних прямокутних трикутників. У цьому випадку значення площі одного з них дорівнює половині площі отриманої фігури. S прямокутника обчислюємо добутком сторін. Позначимо цю величину M. Шукане значення площі дорівнює половині M.
Спосіб 4. «Піфагорові штани». Знаменита теорема Піфагора
Ми всі пам’ятаємо її формулювання: «Сума квадратів катетів …». Але не всі можуть
сказати, причому тут деякі «штани». Справа в тому, що спочатку Піфагор вивчав взаємозв’язок побудованих на сторонах прямого трикутника. Виявивши закономірності у співвідношенні сторін квадратів, він зміг вивести і відому нам формулу. Її можна застосовувати у разі, коли невідома величина однієї із сторін.
Справа в тому, що спочатку Піфагор вивчав взаємозв’язок побудованих на сторонах прямого трикутника. Виявивши закономірності у співвідношенні сторін квадратів, він зміг вивести і відому нам формулу. Її можна застосовувати у разі, коли невідома величина однієї із сторін.
Спосіб 5. Як знайти площу прямокутного трикутника за формулою Герона
Також досить простий спосіб розрахунку. Формула передбачає вираз площі трикутника через числові значення його сторін. Для розрахунків потрібно знати величини всіх сторін трикутника.
S = (p-AC) * (p-BC), де p = (AB + BC + AC) * 0.5
Крім наведених, існує безліч інших способів знайти величину такої загадкової фігури, як трикутник. Серед них: обчислення методом вписаного або описаного кола, обчислення за допомогою координат вершин, використання векторів абсолютної величини, синусів, тангенсів.
Площу прямокутного трикутника можна знайти декількома способами. Прямий кут у складі будь-якої фігури додає їй властивостей і це можна використовувати для правильного та швидкого вирішення задач.
Прямокутний трикутник
Для початку обговоримо сам прямокутний трикутник, його особливості та властивості. Прямокутний трикутник — це трикутник, у складі якого є кут.
Прямокутний трикутник не може бути тупокутним, тому що сума кутів трикутника перевищить 180 градусів, а це неможливо.
У прямокутному трикутнику дві з трьох висот збігаються зі сторонами – катетами. З цієї причини точка перетину висот прямокутного трикутника збігається з вершиною при прямому вугіллі.
Рис. 1. Усі висоти прямокутного трикутника.
Ця ж точка буде центром описаного кола.
Площа трикутника
Площа трикутника зазвичай знаходиться за стандартною формулою, як половина добутку основи на висоту, проведену до цієї основи.
$$S=(1\over2)*a*h$$
Можна знайти площу як половину твору сторін на синус кута між ними:
$$S=(1\over2)*a*b*sin(g)$$
Існують ускладнені формули знаходження площі, але вони використовуються дуже рідко.
Площа прямокутного трикутника
Площа прямокутного трикутника знаходиться за тими самими формулами, але в деяких випадках ці формули можна спростити.
Наприклад, можна скористатися тим, що висоти прямокутного трикутника збігаються з катетами. Тоді стандартна формула перетвориться на таку:
$S=(1\over2)*a*b$, де а і b це катети прямокутного трикутника.
Це одна із найпростіших формул площі прямокутного трикутника. Спробуймо перетворити другу формулу.
$$S=(1\over2)*a*b*sin(g)$$
Якщо згадати, що синус кута це відношення протилежного катета до гіпотенузи. У нашому випадку, протилежний катет позначимо за букву f, тому що це прилеглий катет, а гострий кут може бути укладений тільки між катетом і гіпотенузою. Значить це гіпотенуза.
$S=(1\over2)*a*b*sin(g)= (1\over2)*a*b*(f\over(b))=(1\over2)a*f$ — виходить все та ж формула.
Рис. 2. Малюнок висновку.
Отже, перший висновок ми здійснили правильно, а прямокутний трикутник має лише одну спеціальну формулу для знаходження площі. Якщо вона не підійде, можна скористатися загальними формулами. Це і є два можливі шляхи розрахунку площі.
Наприклад, якщо за умовою завдання відома гіпотенуза, то можна спробувати знайти висоту, що падає на гіпотенузу та визначити площу за загальною формулою. За тим же принципом можна знайти площу через синус, якщо відомі гіпотенузи та катет.
За тим же принципом можна знайти площу через синус, якщо відомі гіпотенузи та катет.
Рис. 3. Висота, проведена до гіпотенузи.
Головне пам’ятати, що будь-яке завдання завжди має 3 рішення і вирішувати кожну найбільш зручним способом.
Що ми дізналися?
Ми поговорили про прямокутні трикутники та вивели формулу площі прямокутного трикутника через катети. Обговорили загальні формули площі трикутників і сказали, кожна з цих формул підійде на вирішення прямокутного трикутника.
Тест на тему
Оцінка статті
Середня оцінка: 4.5. Усього отримано оцінок: 115.
Прямокутний трикутник зустрічається насправді на кожному кутку. Знання про властивості даної фігури, а також вміння обчислювати її площу, безсумнівно, стане вам у нагоді не тільки для вирішення задач з геометрії, але і в життєвих ситуаціях.
Геометрія трикутника
В елементарній геометрії прямокутний трикутник — це фігура, що складається з трьох з’єднаних відрізків, що формують три кути (два гострі та один прямий). Прямокутний трикутник — оригінальна фігура, що характеризується рядом важливих властивостей, що є фундаментом тригонометрії. На відміну від звичайного трикутника, сторони прямокутної фігури мають власні назви:
Прямокутний трикутник — оригінальна фігура, що характеризується рядом важливих властивостей, що є фундаментом тригонометрії. На відміну від звичайного трикутника, сторони прямокутної фігури мають власні назви:
- Гіпотенуза — найдовша сторона трикутника, що лежить навпроти прямого кута.
- Катети – відрізки, що утворюють прямий кут. Залежно від кута, що розглядається, катет може бути прилеглим до нього (утворює цей кут з гіпотенузою) або протилежним (що лежить навпроти кута). Для непрямокутних трикутників катетів немає.
Саме співвідношення катетів та гіпотенузи становить основу тригонометрії: синуси, тангенси та секанси визначаються як відношення сторін прямокутного трикутника.
Прямокутний трикутник насправді
Ця фігура набула широкого поширення насправді. Трикутники знаходять застосування у проектуванні та техніці, тому розрахунок площі фігури доводиться виконувати інженерам, архітекторам та проектувальникам. Форму трикутника мають підстави тетраедрів або призм – тривимірних фігур, які легко зустріти у повсякденності. Крім того, косинець — найпростіше уявлення «плоського» прямокутного трикутника в реальності. Кутник — це слюсарний, креслярський, будівельний та столярний інструмент, який використовується для побудови кутів як школярами, так і інженерами.
Крім того, косинець — найпростіше уявлення «плоського» прямокутного трикутника в реальності. Кутник — це слюсарний, креслярський, будівельний та столярний інструмент, який використовується для побудови кутів як школярами, так і інженерами.
Площа трикутника
Площа геометричної фігури – це кількісна оцінка того, яка частина площини обмежена сторонами трикутника. Площа звичайного трикутника можна знайти п’ятьма способами, використовуючи формулу Герона або оперуючи при розрахунках такими змінними, як основа, сторона, кут і радіус вписаного або описаного кола. Найпростіша формула площі виражається як:
де a – сторона трикутника, h – його висота.
Формула для обчислення площі прямокутного трикутника ще простіше:
де a та b – катети.
Працюючи з нашим онлайн-калькулятор, ви можете обчислити площу трикутника, використовуючи три пари параметрів:
- два катети;
- катет та прилеглий кут;
- катет та протилежний кут.
У задачах чи побутових ситуаціях вам будуть дані різні комбінації змінних, тому така форма калькулятора дозволяє обчислити площу трикутника декількома способами. Розглянемо кілька прикладів.
Розглянемо кілька прикладів.
Приклади із реального життя
Керамічна плитка
Допустимо, ви хочете виконати облицювання стін кухні керамічною плиткою, яка має форму прямокутного трикутника. Для того щоб визначити витрату плитки ви повинні дізнатися площу одного елемента облицювання та загальну площу оброблюваної поверхні. Нехай вам потрібно обробити 7 квадратних метрів. Довжина катетів одного елемента становить по 19 см, тоді площа плитки дорівнюватиме:
Це означає, що площа одного елемента становить 24,5 квадратних сантиметрів або 0,01805 квадратних метрів. Знаючи ці параметри, ви можете підрахувати, що для обробки 7 квадратних метрів стіни вам знадобиться 7/0,01805=387 елементів облицювальної плитки.
Шкільне завдання
Нехай у шкільній задачі з геометрії потрібно знайти площу прямокутного трикутника, знаючи лише те, що сторона одного катета дорівнює 5 см, а величина протилежного кута становить 30 градусів. Наш онлайн-калькулятор супроводжується ілюстрацією, на якій вказані сторони та кути прямокутного трикутника. Якщо сторона a = 5 см, її протилежний кут — це кут альфа, рівний 30 градусів. Введіть ці дані у форму калькулятора та отримайте результат:
Якщо сторона a = 5 см, її протилежний кут — це кут альфа, рівний 30 градусів. Введіть ці дані у форму калькулятора та отримайте результат:
Таким чином, калькулятор не тільки обчислює площу заданого трикутника, але й визначає довжину катета і гіпотенузи, що прилягає, а також величину другого кута.
Висновок
Прямокутні трикутники зустрічаються у нашому житті буквально на кожному розі. Визначення площі таких фігур стане вам у нагоді не тільки при вирішенні шкільних завдань з геометрії, але і повсякденної та професійної діяльності.
Формула площінеобхідна для визначення площа фігури, яка є речовиннозначною функцією, визначеною на деякому класі фігур евклідової площини та задовольняє 4м умовам:
- Позитивність — Площа не може бути меншою за нуль;
- Нормування — квадрат зі стороною одиниця має площу 1;
- Конгруентність — конгруентні фігури мають рівну площу;
- Адитивність — площа об’єднання 2х фігур без загальних внутрішніх точок дорівнює сумі площ цих фігур.

| Геометрична фігура | Формула | Креслення |
|---|---|---|
Результат складання відстаней між серединами протилежних сторін опуклого чотирикутника дорівнюватиме його напівпериметру. | ||
Сектор кола. Площа сектора кола дорівнює добутку його дуги на половину радіусу. | ||
Сегмент кола. Щоб отримати площу сегмента ASB, достатньо з площі сектора AOB відняти площу трикутника AOB. | S = 1/2 R(s — AС) | |
Площа еліпса дорівнює добутку довжин великої та малої півосей еліпса на число пі. | ||
Еліпс. Ще один варіант як обчислити площу еліпса – через два його радіуси. | ||
Трикутник. Через основу та висоту. Формула площі кола через його радіус та діаметр. | ||
Квадрат. Через його бік. Площа квадрата дорівнює квадрату довжини його боку. | ||
Квадрат. Через його діагоналі. Площа квадрата дорівнює половині квадрата довжини його діагоналі. | ||
Правильний багатокутник. Для визначення площі правильного багатокутника необхідно розбити його на рівні трикутники, які мали б загальну вершину в центрі вписаного кола. | S= r·p = 1/2 r·n·a |
Ворота та паркан
Формулу значення площади трикотажа трехколесного велосипеда знаю. Як знает и площадь трикотажа (формулы)
Чтобы помочь своему ребенку с уроками, отцы сами виноваты в благородстве без слов. Как узнать площадь трехколесного трикотажа, какой начисленный оборот от вычета, как ускорение дела?
Как узнать площадь трехколесного трикотажа, какой начисленный оборот от вычета, как ускорение дела?
Бе-яким с едой у вашего сына и дочки могут быть в курсе проблемы, а смрад сам по себе на розы превратить. Почему бы не попасться на доносы от бугнюка и не завоевать его авторитет в глазах ребенка, оживить в памяти деяков элементы школьных программ.
Візмемо для приклада пищевого с тройничным конным. Геометрию в школах важно давать, а для школ лучше всего забыть.
Если ваши дети учатся в 8 классе, у вас будет возможность отгадать формулы геометрических фигур. Трехколесный велосипед – одна из самых простых фигур в плане известных параметров.
Якшо все, знаете ли, про трикутники читали, забыли, давайте згадувать. Ровностегновым должен называться такой трикутник, который имеет 2 стороны и может иметь одинаковое количество обеда. Ребра между ребрами называются боковыми сторонами бедренного трехколесного велосипеда. Третьей стороной является його п_дстава.
Это такой вариант, при котором каждый уровень находится со всех 3-х сторон. Вин ман назовёт односторонний трикутник. Все формулы расширены на новые, которые могут застаиваться до уровня бедренной кости, а во время использования, то ли с этой стороны можно назвать основанием.
Вин ман назовёт односторонний трикутник. Все формулы расширены на новые, которые могут застаиваться до уровня бедренной кости, а во время использования, то ли с этой стороны можно назвать основанием.
Для познания местности нам необходимо раздать базу навпила. Прямая, опущенная в отриманную точку сверху, що с нижней стороны, переходящая в основание прямым срезом.
Одинаковая мощность таких трицитов: медиана, быть прямой от верхушки к середине противоположной стороны, в трикотаже трицикл є с биссектрисой (прямая, для продолжения разреза пупка) и длиной бедра (перпендикулярно к стороны на противоположную сторону)
Чтобы узнать площадь трикотажного трехколесного велосипеда, нужно умножить его высоту на основание, а затем прибавить к основанию.
Для знахожения площади трикотажа формула проста: S = ah/2 de a — довжина основы, h — высота.
На самом деле цену можно объяснить следующим образом. Посмотрите на бумагу, похожую на рисунок, узнайте середину основания, проведите высоту до центральной точки и аккуратно распределите ее по высоте. Возьмите два прямоугольных трехколесных велосипеда.
Возьмите два прямоугольных трехколесных велосипеда.
Если приложить их один к одному гипотенузами (с обеих сторон), то получится прямоугольник, одна сторона которого больше нашей фигурки, а інша — полуспящая. Для подтверждения формулы.
В то же время демонстрация еще важнее. Как только ваш ребенок не запоминает бездумно формулы, это интеллект и геометрия, которые нельзя рассматривать как складной предмет.
Учимся у класса, что класс не зазубренный, а вдумчивый, головняк, школьник, мудрость.
Як знаю площадь фигури, как один кут прям?
Видно, что разрез между сторонами данной трикотажной фигуры становится 90°. Детский трехколесный велосипед называется прямоугольным, одна сторона — ножки, а основание — гипотенуза.
Площадь такой фигурки можно считать по нижнему торцу (известна середина гипотенузы, проводится на ее высоту, умножается на гипотенузу, затем навпил). Если нет, проблема может быть решена, но проблема проще.
По какой-то причине. Трехколесный прямолинейный трехколесный велосипед є в половину квадрата, который является диагональным. Если площадь квадрата находится на других ступенях другой стороны, то площадь, которая нам нужна, будет немного меньше.
Трехколесный прямолинейный трехколесный велосипед є в половину квадрата, который является диагональным. Если площадь квадрата находится на других ступенях другой стороны, то площадь, которая нам нужна, будет немного меньше.
S = а 2/2, дэ а — ножка Довжина.
Площадь прямоугольного трехколесного велосипеда находится на стороне половины квадрата на стороне. Проблема оказалась не такой серьезной, как хулиган на первый взгляд.
Шоу геометрических зданий — это не образ сверхчеловеческих существ, и вообще, это не только дети, но и вы, если вы хоть что-нибудь понимаете в практическом питании.
Геометрия — точная наука. Если заглянуть в основу, то будет сложно из-за нее, но логика доказывания все же может захватить вашего ребенка. Вам просто нужна помощь. Якы би-добрая учительница йому не ушла, помощи от отца не получу.
А в развитии геометрий метод, о котором говорили, еще более четок.
При этом нельзя забывать о точности формулы, но можно развивать науку складно, но не до конца.
Имейте свою статистику мова піде о тех, кто знает зону трехколесного бедренного сустава и формулы для вирішення.
Трехколесный трехколесный трехколесный трехколесный велосипед, у которого две параллельные линии являются сторонами трехколесного велосипеда … Выиграй изображения малышки.
Уважать Варто, сколько лити со значением сторон и кути, використоються по формулам, для твоей живучести.
Если нужен визон курса, или управляющий робот, без средних. Тоди к вам на сайт tvoi5.ru. Вы также можете следовать инструкции курса по замене (http://tvoi5.ru/zakazat-kursovuyu-rabotu.html) и всем подробностям.
Площадь бедренной трехопорной формулы.
Первая формула говорить о тех кто находится, насколько мы видим только одна сторона это основа трикутника … Мы взяли формулу цю после дополнительных формул. Если главное то, что формула Герона состоит в том, чтобы стороны фигурки были проще.
Остальные формулы про те, что расположены через бични стороны и кут, где среди них найти .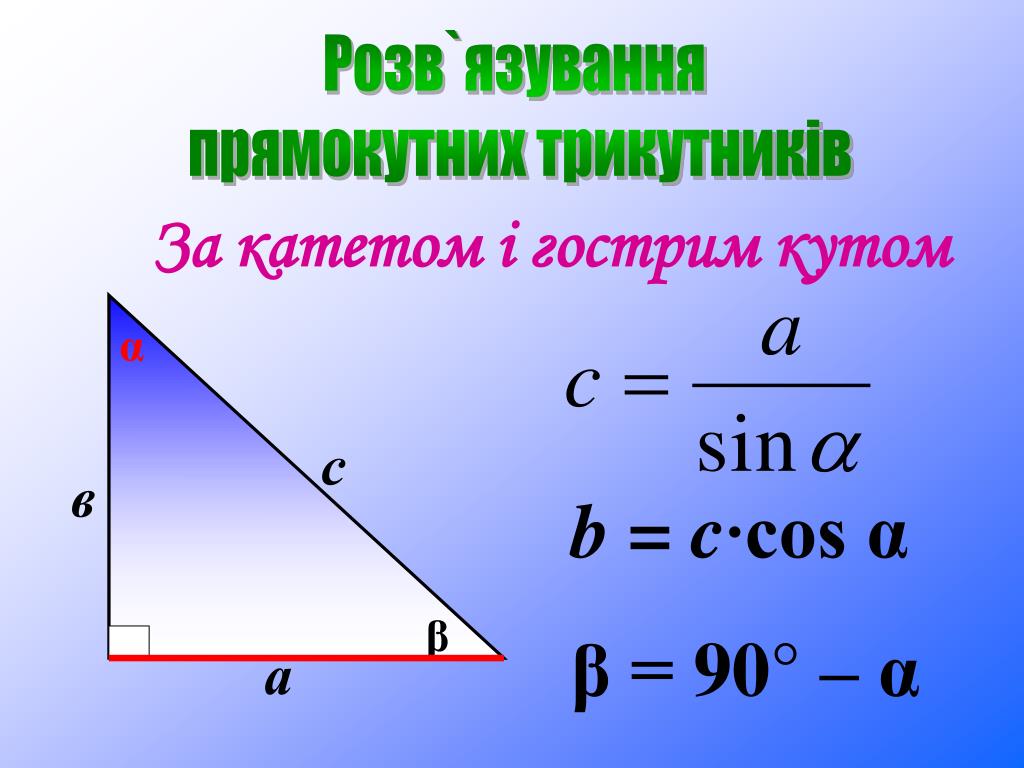 .. Ибо син кута находится между сторонами семейства, умножения на половину квадрата одной из сторон семейства. Если проводить в сторону бока, довжина, а*грех?. Так что, как я знаю, это с обеих сторон, мы это увидим. Судя по всему, площадь трехколесного велосипеда будет составлять половину изгиба. Я точнее. Это значение, чтобы ограбить площадь трехколесного велосипеда. Разделяя высотой прямоугольник, мы узнаем два небольших прямоугольных трикутника. Диагональ будет бортиком трицикла, в его основе находится фигурка на двух отдельных частях. Ух ты, какой шукан у нас ценится в половину размера одной стороны, вот он и умножается на высоту.
.. Ибо син кута находится между сторонами семейства, умножения на половину квадрата одной из сторон семейства. Если проводить в сторону бока, довжина, а*грех?. Так что, как я знаю, это с обеих сторон, мы это увидим. Судя по всему, площадь трехколесного велосипеда будет составлять половину изгиба. Я точнее. Это значение, чтобы ограбить площадь трехколесного велосипеда. Разделяя высотой прямоугольник, мы узнаем два небольших прямоугольных трикутника. Диагональ будет бортиком трицикла, в его основе находится фигурка на двух отдельных частях. Ух ты, какой шукан у нас ценится в половину размера одной стороны, вот он и умножается на высоту.
В третьей формуле площадь помощи одна параллельная сторона, основание той куты, которая находится на вершине … Так можно сказать так: если хочешь один разрез в трикотаже, то можно знать и еще два. Формула ця похожа на другие формулы, ее можно використовувати и не забыть быть с ними. Але з цієї формулы виде пята, яку трохи я опишу ниже.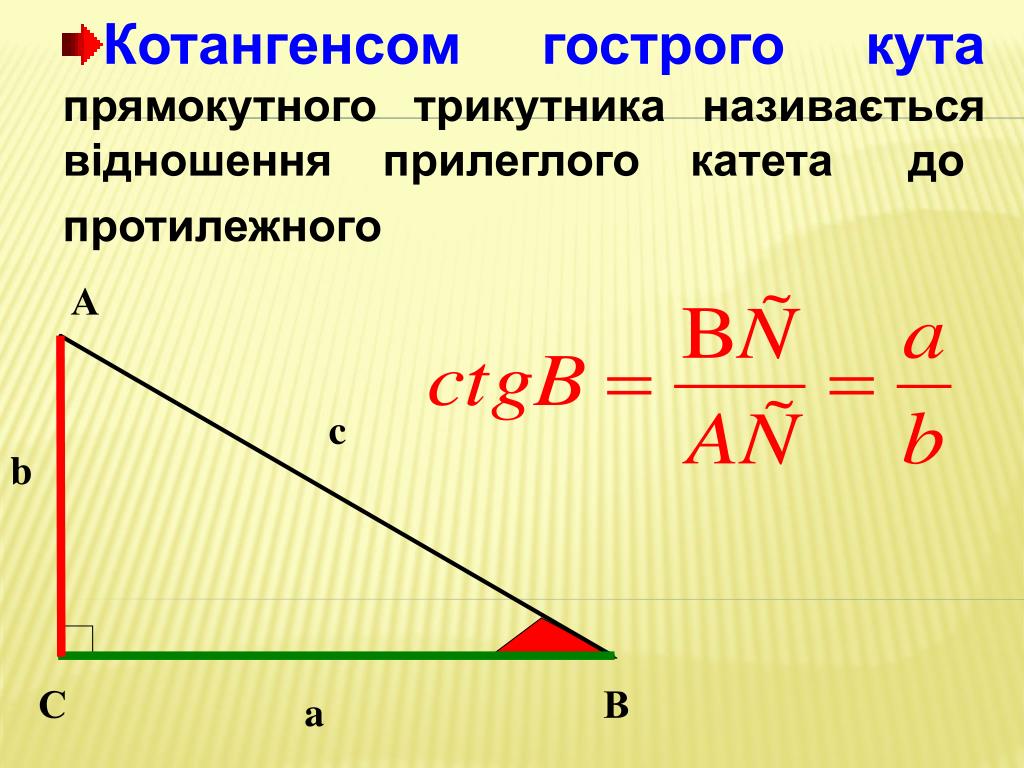
Четвертая формула покажет вам, как узнать площадь Я знаю значение базового та кута для нового … Все вырезы основаны на одном и том же, а квадрат сторон — это база раздач на 4 тг выреза, которые появились с каждой стороны. Если уважительно смотреть, то можно посмотреть в сторону основания б/2, с кратным тг(?/2) да в высоту. Яка своим отличием является роль медианы и биссектрисы, даже tg(?/2)=(b/2)/h, от чего h=b/(2tg(?/2)), и она строится до упрощенная формула № 5.
Отже, п’ата формула не будет говорить о тех, кто может знать местность. за помощью , когда я беру початок в верхней части трехколесного велосипеда и заканчиваю на первом трехколесном велосипеде. И дано в третьей и четвертой формулах. Значение высоты умножается на значение основания.
Шоста — прилагаемая формула. Вона появляется перед часом квадрата трикутника по теореме Пифагора … Мы знаем высоту, которая известна из формул коли. Сам вон выводится ногой из прямоугольного трехколесного велосипеда, що вийшов сбоку, половина основания плюс высота.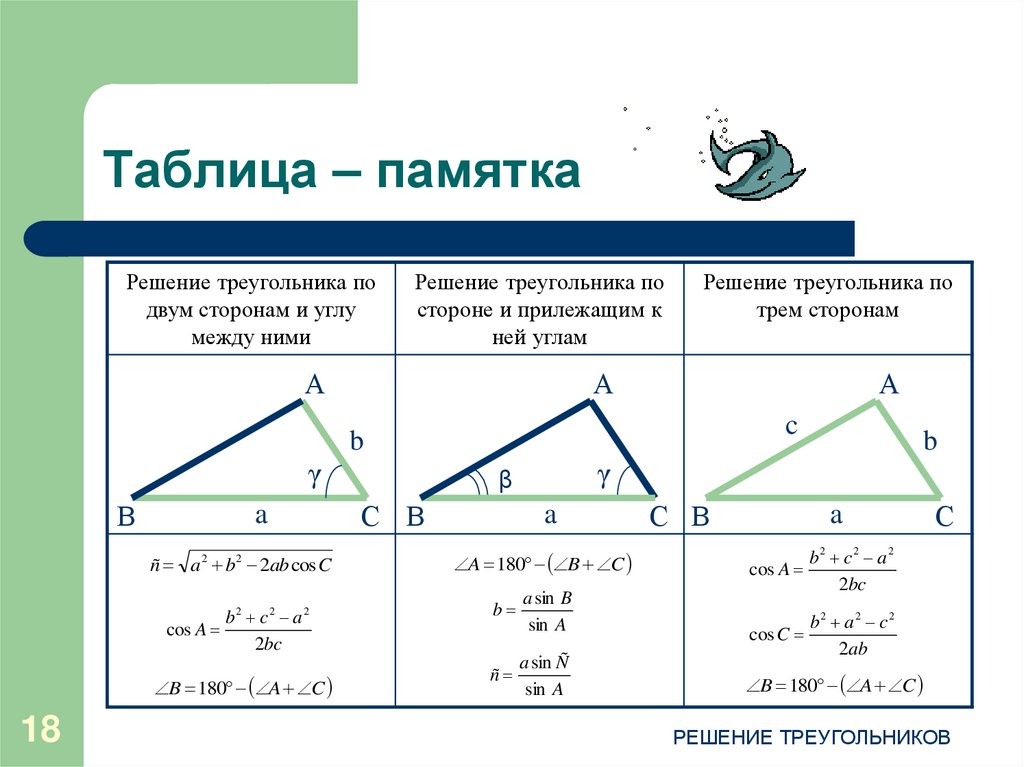 Гипотенуза будет сбоку, от квадрата гипотенузы (а) возьмем еще один катет от квадрата. Так як вин доривню пидлози — стебель (б/2) означает квадрат = б2/4. Виймаючи — корень отверженный, мы знаем висота.
Гипотенуза будет сбоку, от квадрата гипотенузы (а) возьмем еще один катет от квадрата. Так як вин доривню пидлози — стебель (б/2) означает квадрат = б2/4. Виймаючи — корень отверженный, мы знаем висота.
Инструкция
Видео по теме
Зверь в респект
Джерела:
Для слуха родного о смысле. Ногой называется сторона прямоугольного трехколесного велосипеда, як ложится на прямой кут (то есть склад с внутренней стороны кута 90 градусов). Довжины катетиков понятные для начала а и б. Размер гострич кут_ва прямоугольного трехколесного велосипеда, который можно удлинить до ног, по сути называется А и В. Гипотенуза — название бика прямоугольного трехколесного велосипеда, который противоположен прямой куте (чтобы он располагался впритык к прямой куте, с другими сторонами трикотажа сделаю гостри кути). Довжину гипотенузи имеет смысл через с. Квадрат Шукану имеет смысл через S. 92) * тг (Б) / 2 д ы выпадку, если у вас нет задач с одной из ног (а), но и видомый отрез (Б), который крепится к ноге.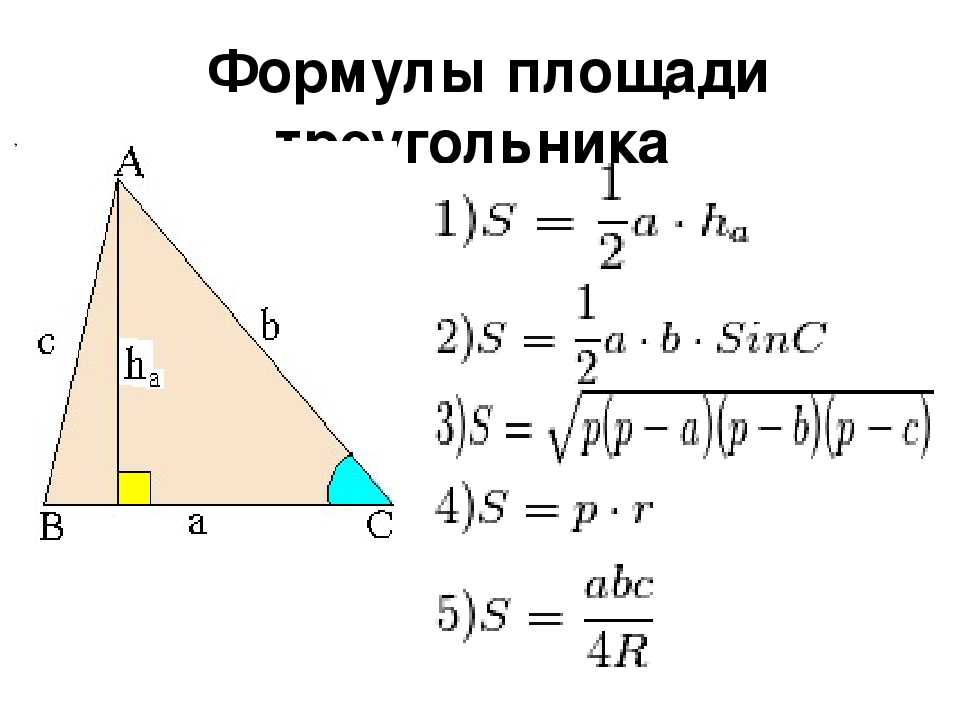
Видео по теме
Джерела:
- «Учебник по математике для абитуриентов вузов», изд. Г.М. Яковлев, 1982.
Ровностенным важается такой трикотаж, у которого две стороны ровні. Площадь трехколесного велосипеда можно развить несколькими способами.
Инструкции
Видео по теме
Зверь к уважению
Найдите признаки трехколесного бедренного сустава:
1) У трехколесного бедренного сустава є 2 ривні кути;
2) Высота трехколесного велосипеда избавляется от медианы;
3) висота трицитты опирается на биссектрису його;
4) К этой медиане привыкает биссектриса трехколесного велосипеда;
5) Бедренный трехколесный велосипед имеет 2 срединные ребра;
6) Бедренный трехколесный велосипед имеет 2 длины;
7) Бедренный трехколесный велосипед имеет 2 биссектрисы.
Джерела:
- площадь трицикла
Одна из фигур, которую можно увидеть на уроках математики и геометрии — трикутник.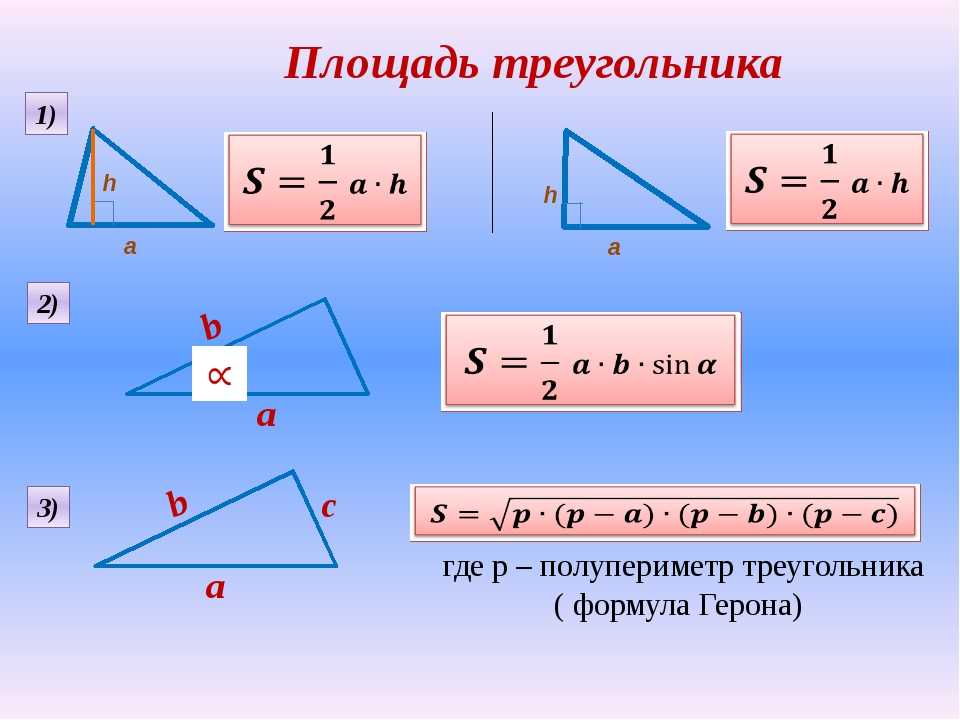 Трикутник — багатокутник, якого имеет є 3 вершины (кута) и 3 стороны; часть площади, обведенная тремя точками, попарно с тремя точками. Исну безлич завдан, связанный со знанием роста фигуры фигурки. Один из них — площадь … Зарезервировано от предыдущей дани, количество формул для площади трикутник .
Трикутник — багатокутник, якого имеет є 3 вершины (кута) и 3 стороны; часть площади, обведенная тремя точками, попарно с тремя точками. Исну безлич завдан, связанный со знанием роста фигуры фигурки. Один из них — площадь … Зарезервировано от предыдущей дани, количество формул для площади трикутник .
Инструкции
Как только вы его увидите, званые обеды прошли в самом разгаре. трикутник , Выкоризить формулу S=? ч * а.
Как только вы увидите одну сторону трехколесного велосипеда одинаковой высоты, опускаете его в сторону, умножаете одну сторону на одну сторону и распределяете результат на две стороны.
Пока перед вами прямолинейный трехколесный велосипед, следуйте линиям до длины ваших ног, так чтобы стороны, лежащие на прямолинейном срезе. Умножьте на количество ножек, и результат уменьшится на два.
Как только вы можете сказать о размере разреза между двумя трициклами, и вы видите трициклы, то я знаю площадь трикотажа по формуле:
St = ½ * A * B * sinα, де св — площадь трехколесного велосипеда; А и Б — дожины сбоку трикутника; α — кута, поджаренная между боками.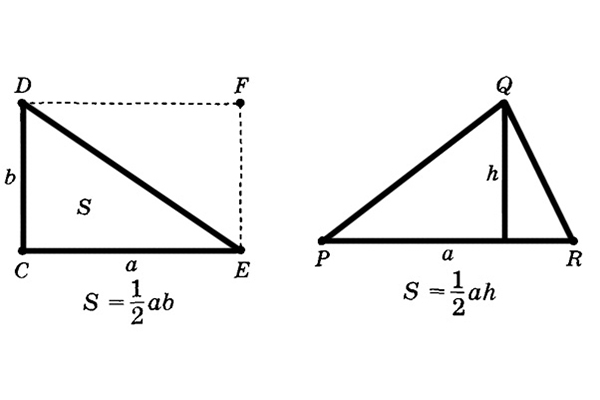
S = 1/2 (AB + BC + AC) = p r.
Вычислить периметр:
p = (5 + 7 + 10) = 11.
Застраховать искомое значение:
S = √ (11 (11-5) (11-7) (11-10)) ≈ 16,2.
Три точки, однозначно представляющие трикатник в декартовой системе координат — вся вершина. Зная положение кожи по осям координат, можно рассчитать параметры плоской фигуры, в том числе периметр. площадь … Цена может быть создана несколькими способами.
Инструкция
Скорректируйте формулу Герона для размера площади трикутник … Имейте ній задіяні разміри трех граней фигуры, для этого посчитайте, зафиксируйте. Довжина стороны кожи виновна в том, что из суммы квадратов проекций довжина на координатные оси получается корень. Мы можем обозначить координаты A (X₁, Y₁, Z₁), B (X₂, Y₂, Z₂) и C (X₃, Y₃, Z₃), а в джинне їх стороны могут быть нарушены следующим образом: AB = √ ((X₁ -X₂)² + (Y₁ -Y₂)² + (Z₁-Z₂)²), BC = √ ((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²), AC = √ ( (X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).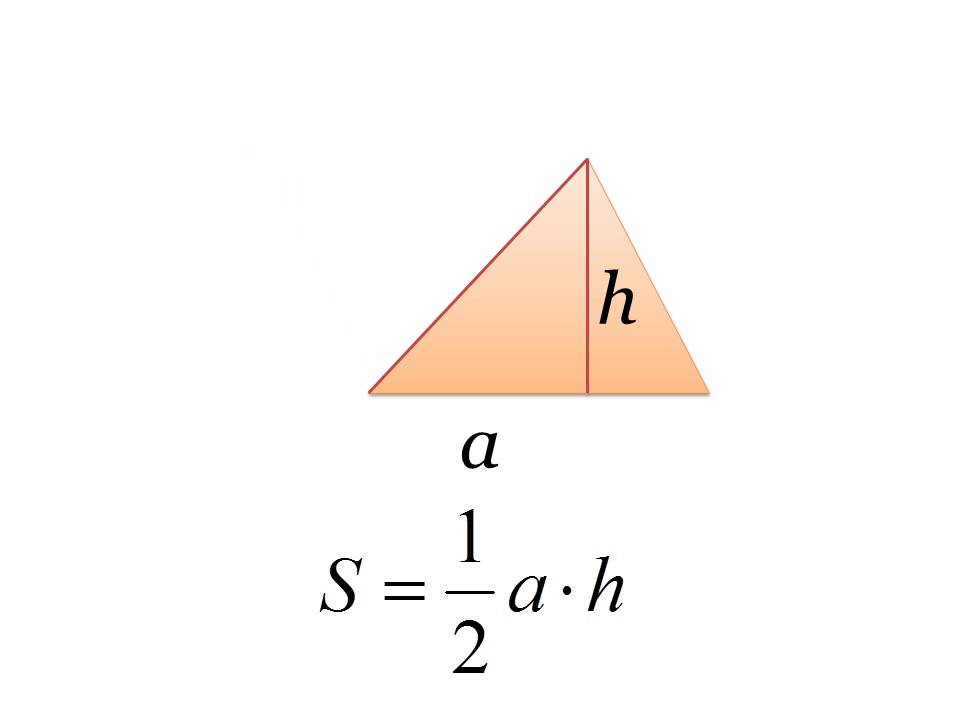
Чтобы упростить списки, введите дополнительное изменение, например, периметр (P). Z, значит половина суми довжин сторон: P = ½ * (AB + BC + AC) = ½ * (√ ((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) + √ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²) + √ ((X₁-X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²).
Трещина площадь (S) по формуле Герона — найти корень по периметру на основании разности их и обшивки с боков.Загал її можно записать так: S = √(P*(P -AB) * (P-BC) * (P-AC)) = √ (P * (P-√ ((X₁-X₂) ²) + (Y₁ -Y₂) ² + (Z₁-Z₂) ²)) * (P-√ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²)) * (P-√ ((X₁) -X₃) ² + (Y₁-Y₃) ² + (Z₁ -З₃)²)).
Для практических целей можно вручную использовать специальные калькуляторы. Скрипты, распространяемые на серверах некоторых сайтов, например, создают все необходимое пространство на основе координат, введенных в форму. Одна из таких услуг заключается в том, что недостаточно объяснить, что такое обод для кожи крокодила. К тому, если вы хотите лишиться конечного результата, а не оценки усердным виглядом, идите, например, на сторону http://planetcalc. ru/218/.
ru/218/.
В поле формы введите скин координаты скина от вершин трикутник — вонь тут як топор, ай, аз и т.д. Якщо трикутник задачи с двумерными координатами, на поле — аз, бз и сз — пишите ноль. В поле «Точность расчета» установите необходимое количество знаков, написанных коми, нажав медведя
Математика — наука раскольническая. Однако такая мысль придет только в том случае, если этого недостаточно. Нужно убедиться, что вы это делаете, вам это нужно, вам это нужно, вам это нужно, вам это нужно, вам это нужно, вам это нужно, вы можете использовать это с теоремами.
Перейти к розуминня геометрия лежит через задачу решения задач. С регулируемым прикладом можно устроиться, для тех нужно знать площадь трикотажа трикотажа.
Так же слесарь по установке трехколесных велосипедов и как вы их видите?
Щоб не лякатя термины «высота», «площадь», «база», «равностенового трехколесного велосипеда» и др., необходимо распределять из теоретических основ.
Подборка про трехколесный велосипед.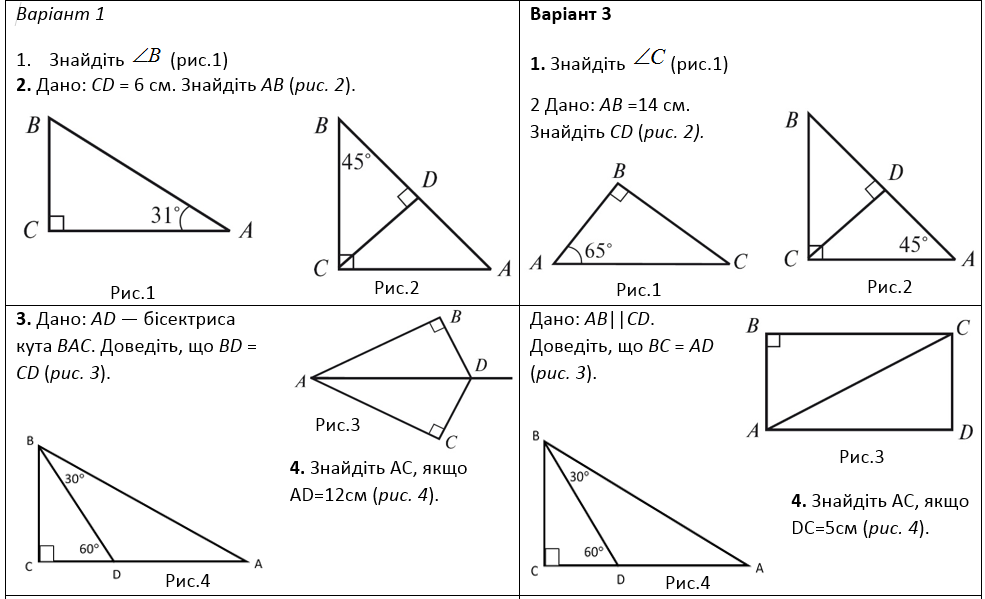 Вся фигура плоская, як поставлен в трех точках — вершинах, на собственной окружности, з’єднаних ідризках. Если два из них оказываются равными один к одному, то трикутник стареет. Ци партии отвергли имя бичей, и основой стал рашт.
Вся фигура плоская, як поставлен в трех точках — вершинах, на собственной окружности, з’єднаних ідризках. Если два из них оказываются равными один к одному, то трикутник стареет. Ци партии отвергли имя бичей, и основой стал рашт.
Исну окремий выпадок ивно-бедренный трехколесный — равносторонний, если третья сторона дорівню двух бич.
Power figuri
Запахи проявляются по мере вирішенні помочников на вирішенні завдан, как вімагают знать область ивно-бедренного трицикла. Чтобы знать, что память о них нужна.
- Перш: кути трикотажного трикотажа, одна сторона которого является основой, свяжите ровни один к одному.
- Нам важно є и власть о дополнительном поощрении. Проведенные в непарную сторону высоты, устанавливаются медиана и биссектриса.
- Циклоны и дорожки, выполняемые из кузовов на базе трехколесного велосипеда, попарно. Це также часто ложится на плечики.
- Две ровні кути в новых могут быть меньше 90º.
- Первая остановка: надписи и описания кола будут так, чтобы центр лежал сверху к основанию трицикла, а значит, медиум и биссектриса.

В чем проблема разработки трикутника установщика?
Всякий раз, когда вы получаете кормовую поставку о тех, кто знает область трехколесного трикотажа, необходимо довести информацию до сведения всей группы. И в тсёму помогают пение знаков.
- Ровно две кути или две стороны трикутника.
- Биссектриса є другие среды.
- Висота трикутника появляется как биссектриса срединного хи.
- Ривни дви висоти, срединная хи биссектриса фигур.
Значения, принимаемые в анализируемых формулах
Для того, чтобы ему было легче узнать площадь трехопорного бедренного сустава за формулами, введена замена элементов на лити.
Увага! Важно не обмануть «а» з «а» та «в» з «б». Цена размера.
Формулы, которые можно ускорить у новых сотрудников
Из дома в сторону, и надо знать площадь бедренного трехколесного велосипеда.
В общем надо возвести в квадрат значение правонарушения.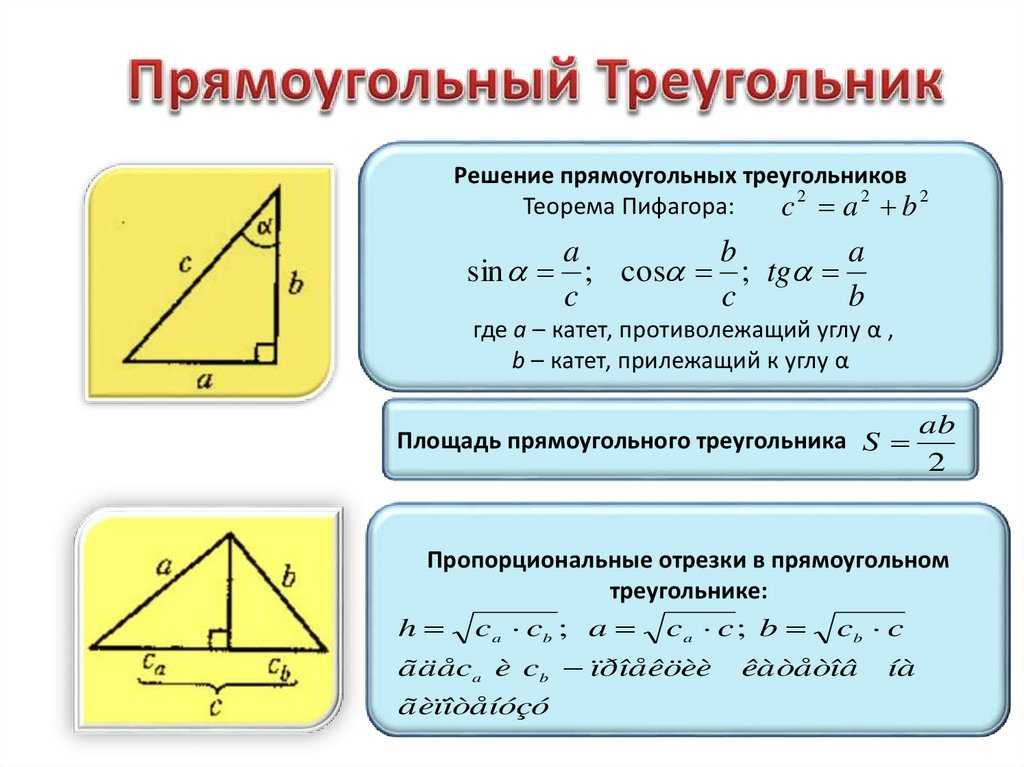 Число, которое было видно со стороны морщины, умножьте на 4 и посмотрите друг от друга. С отменой витяги квадратного корня. Довжину базы разделите на 4. Умножьте два числа. Если записать по буквам, то получится следующая формула:
Число, которое было видно со стороны морщины, умножьте на 4 и посмотрите друг от друга. С отменой витяги квадратного корня. Довжину базы разделите на 4. Умножьте два числа. Если записать по буквам, то получится следующая формула:
Нехай вон будет записан как № 1.
Чтобы узнать площадь бедренного трехколесного велосипеда за пределами значимых сторон. Формула, как кому может быть проста, ниж перша.
Первый шаг — знать половину основ. Сообщите нам сумку с разницей в номере со стороны. Два оставшихся значения умножаются на квадратный корень. С остальными днями умножьте все на половину основы. Письмо паритета выглядит следующим образом:
Це формула №2.
Как узнать площадь трикотажного трикотажа, который является основанием и высотой до нового.
Одна из самых коротких формул. Им нужно умножить недовольства стоимостей и распределений на 2. На оси яка будет написано:
Номер формулы 3.
На передней стороне борта трицикла значение кут , которая находится между основанием и стороной.
Здесь, щоб д_знатися, из-за большой площади бедренного трехколесного велосипеда формула составлена из децилкох множителей. Во-первых, это значение синус-куты. Сбоку на основании добавлена еще одна дверь. Третий — дриб ½. Загальное математическое обозначение:
Порядковый номер формулы 4.
Дана задача: бичня сторона трехколесного велосипеда есть тот кут, который лежит между бичыми сторонами.
Які в авангарде, район расположен в трех мультипликаторах. Первый – это значение синус кут, данное для ума. Другой квадрат стороны. Первая оставшаяся половина устройства также дорогая. Формула результата запишется так:
Її число — 5.
Формула, как бы позволяет узнать площадь бедренного трехколесного велосипеда, как бы является основанием того кута, который лежит на земле.
Из списка необходимо вычислить тангенс половины дома кут. Отриман число умножить на 4. Привести к квадрату на стороне каждой стороны, как и пространство на противоположной стороне.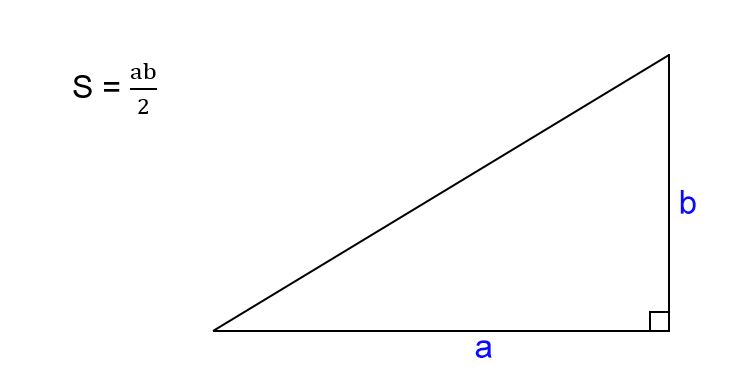 В таком ранге, виде, это формула:
В таком ранге, виде, это формула:
Число последней формулы 6.
Поставить на завдан
Персе завдання: відомо, что длина основания бедренно-бедренного трехколесного велосипеда 10 см, а высота бедра — 5 см.
Впервые логично провибрировать формулу №3. Вроде бы все есть. Дайте дату, что порахувати. Wiide, который имеет площадь дороги 10*5/2. Тобто 25 см 2.
Прочие завдання: в трехколесном трехколесном велосипеде дана бична сторона того основания, которое равно 5 и 8 см. Знай эту область.
Первый способ. Для формулы №1. При возведении основания в квадрат следует ввести число 64, а четырехкратный квадрат двоичной стороны равен 100. Запись с другого первого вида равна 36. Чудо найти корень, который есть способ пройти 6. База добавляется к 4; и 6, то есть 12. Пример: необходимая площадь 12 см 2.
Другой способ. Для формулы № 2. Половина основания равна 4. Сумма боковой стороны и известного числа равна 9, значение равно 1. Количество вхождений равно 9. зная площадь трехколесного велосипеда, можно вывести неооценочную информацию. Если есть больше новых вариантов для заведения Viconano, вам легче узнать новую ситуацию. К тому же самостоятельность всех построек регулярно поддерживается до успешного освоения материала.
Количество вхождений равно 9. зная площадь трехколесного велосипеда, можно вывести неооценочную информацию. Если есть больше новых вариантов для заведения Viconano, вам легче узнать новую ситуацию. К тому же самостоятельность всех построек регулярно поддерживается до успешного освоения материала.
Литерные обозначения сторон и кутов на направленном юните покажут значения, которые мы имеем в виду в формулах. С таким рангом он поможет вам подобрать элементы трехколесного трикотажа. Учитывайте детали увиденных предметов, знайте на креслах обозначенное и принимайте формулу.
Формула площади бедренного трехколесного велосипеда
Дали направил формулы для познания площади бедренного трехколесного велосипеда : через стороны, бичу сторону, кут между ними, через бичу сторону, основание этой кроватки наверху, через основание велосипеда, которое разрезается при представлении, и т. д. Просто знайте, как лучше всего подойти к ребенку. Для тех, кто найдет текст правосторонним, будет объяснено, почему формула є верна и что ее можно найти в этом районе.
- вы можете знать знать його бик ту основу … Tsei viraz bulo otrimano путем прощения более крупных, универсальных формул. Просто возьмите за основу формулу Герона, а затем возьмите за основу две стороны трехколесного велосипеда с медом, а потом попрощайтесь с формулой, представленной на картинке.
Приклад викторианца такой формулы направлен на приставку решения задачи ниже. - Другая формула позволяет узнать площадь через бичні стороны и кут между ними — половина квадрата боковых сторон, умноженная на синус разреза между боковыми сторонами
Если задуматься о снижении виса на стороне ривно-бедренного трехколесного велосипеда, то здорово, что її довнина дорівнуватиме a * sin β . Колебания прикуса в стороны дома нам, висота опущена на него сейчас, половина работы и большая площадь этого трехколесного велосипеда. є їх диагоналей, которые располагаются іх одинаково навпіль, в таком ряду, площадь бедренного трицикла и половина стороны к верху). также Формула 5
также Формула 5 - Третья формула для отображения площади по бокам, основание вверху .
Строго кажется, я знаю одно из бедер бедренного трехколесного велосипеда, вы можете знать, что тот, который дан, или первая формула, питает смак (перед речью можно забыть одно из них).
В третьей формуле тоже есть одна особенность цикавы — tvir a sin α дают нам целую кучу веса, опущенного на базу. В результате очевидная простая и очевидная формула 5. - Площадь бедренного трехколесного велосипеда также можно узнать через бик основы, что кут при доставке (кутья у основания ривни) як площадь основания, на чотирии тангенциальная половина кута, принятая другие стороны. Якшто гордиться собой уважительно, становится очевидным, что половина основания (b/2) умножается на tg(β/2), что дает нам высоту трикотажа. Колебания высоты в трикотаже один раз биссектриса и медиана, затем tg(β/2) — цена половины основания (b/2) в высоту — tg(β/2) = (b/2)/h .
 Звезды h = b/(2 tan(β/2)). В результате формула вернется к простой формуле 5, что вполне очевидно.
Звезды h = b/(2 tan(β/2)). В результате формула вернется к простой формуле 5, что вполне очевидно. - Зрозуміло, Площадь бедренного трехколесного велосипеда Можно узнать, уменьшив высоту от вершины к основанию, в результате чего вы увидите два прямоугольных трехколесных велосипеда. Дали — все очевидно. Полвитка на базе и необходимая площадь. Стыковое використання с учетом формул разд. при заданиях нижний (2-й способ подключения)
- Формула qia должна пойти, если вы попытаетесь узнать площадь бедренного трехколесного велосипеда за сложением теорем Пифагора … Для широкого диапазона вариаций перед формулой фронта, как один час є с ногой прямоугольного трехколесного велосипеда, закрепленного сбоку, половиной основания и головой, по теореме Пифагора. Сторона бичы є гипотенуза, к тому из квадрата стороны бичи (с) виден квадрат другой стороны. Осколки составляют половину основания (б/2), затем площадь дополняется б 2/4. Силы рута от цёго вираз и дай нам повеситься.
 Это видно в формуле 6. Следует умножить число и эталон на два, а затем добавить знак корня для двух чисел, можно принять и другой вариант этой формулы, который записывается через знак «равно».
Это видно в формуле 6. Следует умножить число и эталон на два, а затем добавить знак корня для двух чисел, можно принять и другой вариант этой формулы, который записывается через знак «равно».
Перед выступлением можно поиграть, но если в Формуле 1 есть арки, то вы переосмыслите в Формулу 6. Всё равно навпаки, рост квадратов двух чисел, умножаются, чтобы дать нам шевеление, першу .
Обозначение , вроде були в формулах застряли немного:
а — Довжина одна с двух сторон трикутника
б — Довжина основания
32 α — размер одного из двух двойных кутьев на подставке
β — размер разреза между плоскими сторонами трехколесного велосипеда и прототипом йогического основания
h — Довжина висоти, опущенная с верха трехколесного трехколесного велосипеда на основание респект означенной зимней! Не перепутайте α и β, а также а и б !
Примечание . .. Эта часть урока из завданного з геометрии (разделенная площадь трикотажа трехколесного велосипеда). Происходит смена состава, так как победы трудны для часа даты. Если вам нужно обновить геометрическую задачу, написать об этом на форуме нет возможности. Для обозначения квадратного корня у проблемных соединений используется символ √ или sqrt(), а у дуг подразумевается вираз .
.. Эта часть урока из завданного з геометрии (разделенная площадь трикотажа трехколесного велосипеда). Происходит смена состава, так как победы трудны для часа даты. Если вам нужно обновить геометрическую задачу, написать об этом на форуме нет возможности. Для обозначения квадратного корня у проблемных соединений используется символ √ или sqrt(), а у дуг подразумевается вираз .
Завдання
Длина бичной стороны трикотажного трицикла 13 см, длина основания 10 см. Знай площадь трехколесный велосипед трехколесный велосипед.
Решение .
1-й способ … Застосуємо формула Герона. Оскилки трикутник равноедрий, то есть более простой вигляд (див. Формула 1 в списке формул вище):
де а — дожина бичных партий, а б — дожина основы.
Подставляя значения стороны трехколесного велосипеда из ума, мы можем признать:
S = 1/2 * 10 * √ ((13 + 5) (13 — 5)) = 5 √ (18 * 8) = 60 см 2
2-й способ. Застосуємо теорема Пифагора
Застосуємо теорема Пифагора
Допустимо, что формула запомнилась Використану как первый метод решения. Его опускают из вершины B в основание AC на высоту BK.
Оскилки высоты бедренного трехколесного велосипеда, отрежьте основание навпиля, тогда половина основания будет равна
АК = АС / 2 = 10/2 = 5 см.
Подвешивание за половину основания и боковые части трикотажного трехколесного велосипеда зафиксирует прямоугольный трехколесный велосипед ABK. У нас есть гипотенуза АВ и катет АК трехколесного велосипеда. Виразимо корректирует другую ногу по теореме Пифагора.
Площадь основания трехколесного трикотажа формула. Як знает и площадь трикотажа (формулы)
Встаньте, чтобы лишать школьников не студенчества, а настоящей, практической жизни. Например, фасадную часть нужно доработать до часа. Сколько материала нужно?
Часто встречаются майстри, которые работают из ткани ткани, с помощью посоха. Даже множество деталей, которые требуются мастеру, можно использовать для создания формы трикотажного трикотажа.
Кроме того, есть много способов, которые помогут вам узнать площадь трехколесного трикотажа. Первый из них указан на выставке и вверху.
В первый раз нам нужно найти трехколесный велосипед MNP с основанием MN и высотой PO. Теперь можно сделать это в кресле: из точки Р провести линию, параллельную основанию, а из точки М — линию, параллельную высоте. Точка называется Q. Я уверен, что знаю площадь трехколесного трехколесного велосипеда, надо посмотреть трехколесный трехколесный MOPQ, с другой стороны трехколесный трехколесный MP.
Я пойму правильно, я прямой резчик. Осколки ми будут его самими, разумеется, обе стороны МО и ОК параллельны. 1-я сторона QM и OP может быть параллельна. Срез POM прямой, и OPQ может быть прямым. Отже, четырехрикутник, що вийшов, є прямоугольный. Сложно узнать, какой площади нет на складе; ОМ является половиной основания этого трехколесного велосипеда MPN. Похоже, что випливе, представляющей собой область подсказанного нами прямоугольного трехколесного велосипеда, надстраивается поверх основания.
Еще одна стадия множества перед нами – трехколесный велосипед, что обусловлено площадью трехколесного велосипеда, є является доказательством того, что мы отрицаем прямоугольный трехколесный велосипед за площадью, так что, как площадь трехколесного велосипеда трикотаж, он также достоин основания.
Возможно для трикотажа початка PON и PMQ. Смрад обиды прямой, поэтому в одном из высказываний головы прямой кут, а во внутренней части прямоугольника прямой кут. Гипотенузы у лиц с є стороны трехопорного бедренного сустава также одинаковы. Ножки ПО и КМ также параллельны сторонам прямоугольника. Отже, площадь трицикла ПОН, а трицикла ПМЦ равна самому себе.
Площадь прямоугольного QPOM идет на площади трикутников PQM и MOP в сумме. Заменив просроченный трицикл QPM на трицикл PON, примем его в сводках, данных нам для введения теоремы Трикатником. Теперь мы знаем, как узнать площадь трехколесного трикотажа на основании и на основании — посчитать его размер.
Ale можно узнать, как узнать площадь трикотажного велосипеда от основания и сбоку.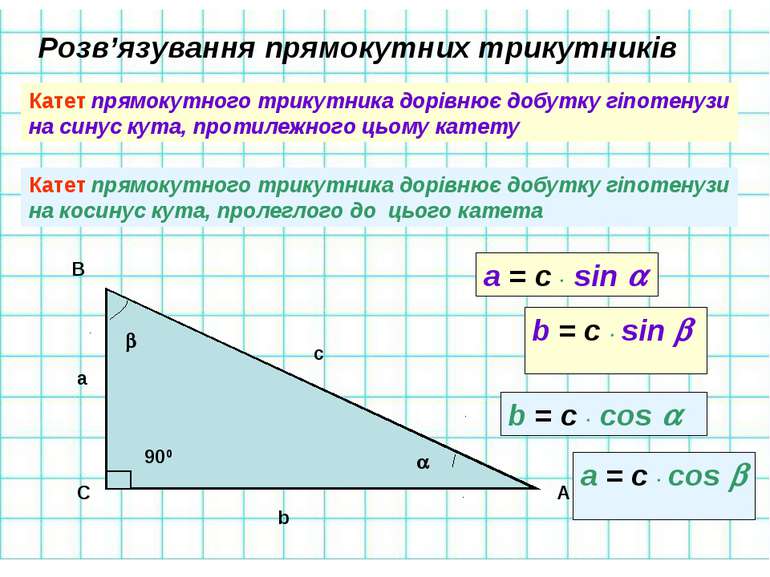 Тут тоже два варианта: теорема Герона и Пифагора. Решение ясно из определений теорем Пифагора. Например, в зависимости от того же PMN на ПО.
Тут тоже два варианта: теорема Герона и Пифагора. Решение ясно из определений теорем Пифагора. Например, в зависимости от того же PMN на ПО.
Прямоугольный трехколесный велосипед POM MP имеет гипотенузу. Її площадь дверей сумма площадей ПО и ОМ. Оскілки ОМ — половина основания, как видим, мы можем легко узнать ОМ и поставить номер квадрата. Сделав вывод из квадрата гипотенузы, число получится неверным, по той причине, что квадрат катета больше, чем высота трехколесного велосипеда. Зная о разнице и зная высоту прямоугольного трехколесного велосипеда, можно дать представление о множестве перед нами.
Нужно просто умножить значение на основу и результат раздачи навпила. Почему это так легко исправить, мы объяснили в первом варианте, чтобы доказать это.
Бувак, надо пересмотреть расчет со стороны той куту. То есть известно, что известно основание, формула використа с синусом и косинусом, и, опять же, умножаем результат и умножаем результат.
Трехколесный велосипед всегда думает о нескольких вариантах в известной области. 2) вы сможете получить джин из необслуживаемой ноги, потому что победивший за радужную.
2) вы сможете получить джин из необслуживаемой ноги, потому что победивший за радужную.
Як знает и представляет собой область бедренного трехколесного велосипеда
Площадь бедренного трехколесного велосипеда можно узнать намного проще и быстрее по формуле S = b * h / 2, но по длительности одного из показателей — гораздо быстрее. Также необходимо посетить документы.
Возможные варианты создания:
- Дано: один шрот одной стороны с другой стороны другой и один из основы. По теореме Пифагора оно известно висоте, роду других катетов.
 Для размыва основание делится на два, є катетом, а с домашней стороны — гипотенузой.
Для размыва основание делится на два, є катетом, а с домашней стороны — гипотенузой. - Дано: основание это тот кут между стороной того основания. Вычисляется по формуле h=c*ctg(B)/2 высота (не забывая про бик «с» на двоих).
- Дано: висота есть тот кут, как если бы утверждение было сделано на основании и с другой стороны: есть формула с = h*tg(B)*2 для значения признака, что результат умножается на два. Расстояние пронумеровано.
- Видома: довжина латеральная сторона и тот кут, который притворялся между ним и той высотой. Решение: победные формулы — с = а * sin (С) * 2 і h = а * cos (С) по смыслу основания той высоти, для которой важна область.
Як знаю площадь бедренно-бедренного прямоугольного трехколесного велосипеда
Если все это дано, то по стандартной формуле S = a * a/2 я могу рассчитать площадь прямобедренного прямоугольного трехколесного велосипеда , если указаний в заданиях нет, то необходимо допустить доп.
Например: мы не видим довжины с обеих сторон (ми памятью, в ровно-бедренном прямоугольном трикотаже вони ровні), але дается довжина гипотенузы. 2. Идти, знать ногу «а», это необходимо получить гипотенузу для корня z 2. Результат решения и будет выполнен на обеих ногах прямобедренного прямоугольного трехколесного велосипеда. Расстояние до местности известно. 92, de R — радиус кола.
2. Идти, знать ногу «а», это необходимо получить гипотенузу для корня z 2. Результат решения и будет выполнен на обеих ногах прямобедренного прямоугольного трехколесного велосипеда. Расстояние до местности известно. 92, de R — радиус кола.
Инструкция
Видео по теме
Зверь в респект
Джерела:
Для слуха родного о смысле. Ногой называется сторона прямоугольного трехколесного велосипеда, як ложится на прямой кут (то есть склад с внутренней стороны кута 90 градусов). Довжины катетиков понятные для начала а и б. Размер гострих кутів прямоугольного трехколесного велосипеда, который можно удлинить до ног, называется А и В по определению. Гипотенуза — название бика прямоугольного трехколесного велосипеда, который противоположен прямой куте (чтобы он располагался впритык к прямой куте, с другими сторонами трикотажа сделаю гостри кути). Довжину гипотенузи имеет смысл через с. Квадрат Шукану имеет смысл через S. 92) * тг (Б) / 2 д ы выпадку, если у вас нет задач с одной из ног (а), но и видомый отрез (Б), который крепится к ноге.
Видео по теме
Джерела:
- «Учебник по математике для абитуриентов вузов», изд. Г.М. Яковлев, 1982.
Ровностенным важается такой трикотаж, у которого две стороны ровні. Площадь трехколесного велосипеда можно развить несколькими способами.
Инструкции
Видео по теме
Зверь к уважению
Найдите признаки трехколесного бедренного сустава:
1) У трехколесного бедренного сустава є 2 ривні кути;
2) Высота трехколесного велосипеда избавляется от медианы;
3) висота трицитты опирается на биссектрису його;
4) К этой медиане привыкает биссектриса трехколесного велосипеда;
5) Бедренный трехколесный велосипед имеет 2 срединные ребра;
6) Бедренный трехколесный велосипед имеет 2 длины;
7) Бедренный трехколесный велосипед имеет 2 биссектрисы.
Джерела:
- площадь трицикла
Одна из фигур, которую можно увидеть на уроках математики и геометрии — трикутник. Трикутник — багатокутник, якого имеет є 3 вершины (кута) и 3 стороны; часть площади, обведенная тремя точками, попарно с тремя точками. Исну безлич завдан, связанный со знанием роста фигуры фигурки. Один из них — площадь … Зарезервировано от предыдущей дани, количество формул для площади трикутник .
Трикутник — багатокутник, якого имеет є 3 вершины (кута) и 3 стороны; часть площади, обведенная тремя точками, попарно с тремя точками. Исну безлич завдан, связанный со знанием роста фигуры фигурки. Один из них — площадь … Зарезервировано от предыдущей дани, количество формул для площади трикутник .
Инструкции
Как только вы его увидите, вы увидите вечеринку, которая проходила на его стороне. трикутник , Выкоризить формулу S=? ч * а.
Как только вы увидите одну сторону трехколесного велосипеда одинаковой высоты, опускаете его в сторону, умножаете одну сторону на одну сторону и распределяете результат на две стороны.
Пока перед вами прямолинейный трехколесный велосипед, следуйте линиям до длины ваших ног, так чтобы стороны, лежащие на прямолинейном срезе. Умножьте на количество ножек, и результат уменьшится на два.
Как только вы можете сказать о размере разреза между двумя трициклами, и вы видите трициклы, то я знаю площадь трикотажа по формуле:
St = ½ * A * B * sinα, де св — площадь трехколесного велосипеда; А и Б — дожины сбоку трикутника; α — кута, поджаренная между боками.
S = 1/2 (AB + BC + AC) = p r.
Вычислить периметр:
p = (5 + 7 + 10) = 11.
Застраховать искомое значение:
S = √ (11 (11-5) (11-7) (11-10)) ≈ 16,2.
Три точки, однозначно представляющие трикатник в декартовой системе координат — вся вершина. Зная положение кожи по осям координат, можно рассчитать параметры плоской фигуры, в том числе периметр. площадь … Цена может быть создана несколькими способами.
Инструкция
Скорректируйте формулу Герона для размера площади трикутник … Имейте ній задіяні разміри трех граней фигуры, для этого посчитайте, зафиксируйте. Довжина стороны кожи виновна в том, что из суммы квадратов проекций довжина на координатные оси получается корень. Мы можем обозначить координаты A (X₁, Y₁, Z₁), B (X₂, Y₂, Z₂) и C (X₃, Y₃, Z₃), а в джинне їх стороны могут быть нарушены следующим образом: AB = √ ((X₁ -X₂)² + (Y₁ -Y₂)² + (Z₁-Z₂)²), BC = √ ((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²), AC = √ ( (X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²).
Чтобы упростить списки, введите дополнительное изменение, например, периметр (P). Z, значит половина суми довжин сторон: P = ½ * (AB + BC + AC) = ½ * (√ ((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²) + √ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²) + √ ((X₁-X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²).
Трещина площадь (S) по формуле Герона — найти корень по периметру на основании разности их и обшивки с боков.Загал її можно записать так: S = √(P*(P -AB) * (P-BC) * (P-AC)) = √ (P * (P-√ ((X₁-X₂) ²) + (Y₁ -Y₂) ² + (Z₁-Z₂) ²)) * (P-√ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²)) * (P-√ ((X₁) -X₃) ² + (Y₁-Y₃) ² + (Z₁ -З₃)²)).
Для практических целей можно вручную использовать специальные калькуляторы. Скрипты, распространяемые на серверах некоторых сайтов, например, создают все необходимое пространство на основе координат, введенных в форму. Одна из таких услуг заключается в том, что недостаточно объяснить, что такое обод для кожи крокодила. К тому, если вы хотите лишиться конечного результата, а не оценки усердным виглядом, идите, например, на сторону http://planetcalc. ru/218/.
ru/218/.
В поле формы введите скин координаты скина от вершин трикутник — вонь тут як Топор, Ау, Аз и т.д. Как трицикл задач с двусторонними координатами, на поле — Аз, Бз и Сз — пишем ноль. В поле «Точность расчета» установите необходимое количество знаков, написанных коми, нажав медвежонком
З’ясуйте, как узнать площадь параллелограмма. Квадраты и прямоугольники представляют собой параллелограммы, похожие на четырехгранные фигуры, у которых противоположные стороны параллельны. Площадь параллелограмма вычисляется по следующей формуле: S = bh , de «b» — основание (нижняя сторона параллелограмма), «h» — высота (от верхней до нижней стороны; высота от верхней до нижней стороны; высота от основания до 90°).
- У квадратов и прямоугольников висят верхняя и нижняя стороны и под прямой кут.
Рип-трициты и параллелограммы. Между цифрами и простыми ссылками. Подобно параллелограмму диагональных разр_зати, выйдут два равных трехколесных велосипеда. Точно так же, если вы поместите два трицита сбоку, вы увидите параллелограмм. К тому площадь любого трехколесного велосипеда можно посчитать по следующей формуле: S = ½bh , чтобы стать половиной площади параллелограмма.
Точно так же, если вы поместите два трицита сбоку, вы увидите параллелограмм. К тому площадь любого трехколесного велосипеда можно посчитать по следующей формуле: S = ½bh , чтобы стать половиной площади параллелограмма.
Знать основу бедренного трехколесного велосипеда. Теперь вы знаете формулу расчета площади трехколесного велосипеда; переполнены зьясувати, а также «пидстава» и «висота». Основание (называемое як «б») — это та сторона, которая не подходит к двум (равным) сторонам.
Опустите перпендикуляр к основанию. Чтобы вырастить це из верхушек трикотажа, як противопоставляется основанию. Помните, что перпендикулярные лоскуты основания с прямым срезом. Таким перпендикуляром является высота трехколесного велосипеда (обозначается як ч). Как только вы узнаете значение «h», вы сможете рассчитать площадь трехколесного велосипеда.
- В бедренном трехколесном велосипеде высота основания находится ровно посередине.

Удивитесь половинке бедренного трехколесного велосипеда. Зверь уважать, чтобы высота трицикла была разделена на два равных трицикла. Подивитесь одному из них и узнайте эту сторону:
- Короткая сторона задней половинки основания: b 2 (\displaystyle(\frac(b)(2))).
- На другой стороне цена «h».
- Гипотенуза прямоугольного трехколесного велосипеда є со стороны трехколесного бедренного сустава; означающее її як «с». 9(2)))
ч = (25 — 9) (\ displaystyle h = (\ sqrt (()) 25-9))
h = (16) ( \ displaystyle h = (\ sqrt (()) 16) )
h = 4 (\displaystyle h = 4) дел.
Сообщите значение основания и формулу расчета площади трехколесного велосипеда. Формула: S = ½ bh; Подставьте в него значения «b» и «h» и посчитайте площадь. Например, не забудьте написать квадратную единицу для видео.
- База имеет базу из 6 разделов и базу из 4 разделов.
- S = ½bh
S = ½ (6 см) (4 см)
S = 12 см2.
Легко читаемый складной приклад. В большинстве случаев вам будут даны более важные знания, вы можете увидеть это в нашем приложении. Нужен квадратный корень, который, как правило, не воюет на национальном уровне. В первую очередь запишите значение высоты при выгляде общего квадратного корня. Ось новая склад:
- Вычислите площадь бедренного трехколесного велосипеда, стороны которого 8 см, 8 см, 4 см. 9(2))))
= 64 — 4 (\displaystyle=(\sqrt(64-4)))
=60(\displaystyle=(\sqrt(60))) - Упростите квадратный корень для дополнительного множителя: h = 60 = 4 ∗ 15 = 4 15 = 2 15. (\ displaystyle h = (sqrt (60)) = (sqrt (4 * 15)) = (sqrt (4) ) (кв. (15)) = 2 (кв. (15)).)
- S = 1 2 b h (\ displaystyle = (\ frac (1) (2)) bh)
= 1 2 (4) (2 15) (\ displaystyle = (\ frac (1) (2)) (4) (2(\sqrt(15)))))
=4 15(\displaystyle=4(\sqrt(15))) - Вид можно записать с корнем, а можно исправить корень на калькуляторе и записать вид десятичной дроби (S ≈ 15,49см 2).

Литерные обозначения сторон и кутов на направленном юните покажут значения, которые мы имеем в виду в формулах. С таким рангом он поможет вам подобрать элементы трехколесного трикотажа. Учитывайте детали увиденных предметов, знайте на креслах обозначенное и принимайте формулу.
Формула площади бедренного трехколесного велосипеда
Дали направлена формулы для познания площади бедренного трехколесного велосипеда : через борта, бичу бока, что кут между ними, через бичу борт, основание, что кроватка по верхам, через бик основание, что разрез при предъявлении и т.д. Только знай, как лучше идти пацану. Для тех, кто найдет текст правосторонним, будет объяснено, почему формула є верна и что ее можно найти в этом районе.
- вы можете знать знать його бик ту основу … Tsei viraz bulo otrimano путем прощения более крупных, универсальных формул. Просто возьмите за основу формулу Герона, а затем возьмите за основу две стороны трехколесного велосипеда с медом, а потом попрощайтесь с формулой, представленной на картинке.

Приклад викторианца такой формулы направлен на приставку решения задачи ниже. - Другая формула позволяет узнать вашу площадь через бичні стороны и кут между ними — половина квадрата боковых сторон, умноженная на синус разреза между боковыми сторонами
Если подумать о понижении виса на стороне ровно-бедренный трехколесный велосипед, это здорово, что она довнина дорівноватайм а * грех β. Колебания прикуса в стороны дома нам, висота опущена на него сейчас, половина работы и большая площадь этого трехколесного велосипеда. є їх диагоналей, которые располагаются іх одинаково навпіль, в таком ряду, площадь бедренного трицикла и половина стороны к верху). также Формула 5 - Третья формула для отображения площади по бокам, основание вверху .
Строго кажется, я знаю одну из канавок трикотажного трицикла, можно узнать, что одна из них воткнута в авангарде формулы — питательный вкус (перед выступлением можно запомнить только одну из них).
В третьей формуле тоже есть одна особенность цикавы — tvir a sin α дают нам целую кучу веса, опущенного на базу. В результате очевидная простая и очевидная формула 5.
В результате очевидная простая и очевидная формула 5. - Площадь бедренного трехколесного велосипеда также можно узнать через бик основы, что кут при доставке (кути при предъявлении ривни) как квадрат основания, подчинение на чотирии тангенциальной половины кута, утвержденного обеими стороны. Якшто гордиться собой уважительно, становится очевидным, что половина основания (b/2) умножается на tg(β/2), что дает нам высоту трикотажа. Колебания высоты в трикотаже один раз биссектриса и медиана, затем tg(β/2) — цена половины основания (b/2) в высоту — tg(β/2) = (b/2)/h . Звезды h = b/(2 tan(β/2)). В результате формула вернется к простой формуле 5, что вполне очевидно.
- Зрозуміло, Площадь бедренного трехколесного велосипеда Можно узнать, уменьшив высоту от вершины к основанию, в результате чего вы увидите два прямоугольных трехколесных велосипеда. Дали — все очевидно. Полвитка на базе и необходимая площадь. Стыковое використання с учетом формул разд.
 при заданиях нижний (2-й способ подключения)
при заданиях нижний (2-й способ подключения) - Формула qia должна пойти, если вы попытаетесь узнать площадь бедренного трехколесного велосипеда за сложением теорем Пифагора … Для широкого диапазона вариаций перед формулой фронта, как один час є с ногой прямоугольного трехколесного велосипеда, закрепленного сбоку, половиной основания и головой, по теореме Пифагора. Сторона бичы є гипотенуза, к тому из квадрата стороны бичи (с) виден квадрат другой стороны. Осколки составляют половину основания (б/2), затем площадь дополняется б 2/4. Силы рута от цёго вираз и дай нам повеситься. Это видно в формуле 6. Следует умножить число и эталон на два, а затем добавить знак корня для двух чисел, можно принять и другой вариант этой формулы, который записывается через знак «равно».
Перед выступлением можно поиграть, но если в Формуле 1 есть арки, то вы переосмыслите в Формулу 6. Всё равно навпаки, рост квадратов двух чисел, умножаются, чтобы дать нам шевеление, першу .
Обозначение , вроде були в формулах застряли немного:
а — Довжина одна с двух сторон трикутника
б — Довжина основания
32 α — размер одного из двух двойных кутьев на подставке
β — размер разреза между плоскими сторонами трехколесного велосипеда и прототипом йогического основания
h — Довжина висоти, опущенная с верха трехколесного трехколесного велосипеда на основание респект означенной зимней! Не перепутайте α и β, а также а и б !
Примечание . .. Эта часть урока из завданного з геометрии (разделенная площадь трикотажа трехколесного велосипеда). Происходит смена состава, так как победы трудны для часа даты. Если вам нужно обновить геометрическую задачу, написать об этом на форуме нет возможности. Для обозначения квадратного корня у проблемных соединений используется символ √ или sqrt(), а у дуг подразумевается вираз .
.. Эта часть урока из завданного з геометрии (разделенная площадь трикотажа трехколесного велосипеда). Происходит смена состава, так как победы трудны для часа даты. Если вам нужно обновить геометрическую задачу, написать об этом на форуме нет возможности. Для обозначения квадратного корня у проблемных соединений используется символ √ или sqrt(), а у дуг подразумевается вираз .
Завдання
Длина бичной стороны трикотажного трицикла 13 см, длина основания 10 см. Знай площадь трехколесный велосипед трехколесный велосипед.
Решение .
1-й способ … Застосуємо формула Герона. Оскилки трикутник равноедрий, то есть более простой вигляд (див. Формула 1 в списке формул вище):
де а — дожина бичных партий, а б — дожина основы.
Подставляя значения стороны трехколесного велосипеда из ума, мы можем признать:
S = 1/2 * 10 * √ ((13 + 5) (13 — 5)) = 5 √ (18 * 8) = 60 см 2
2-й способ.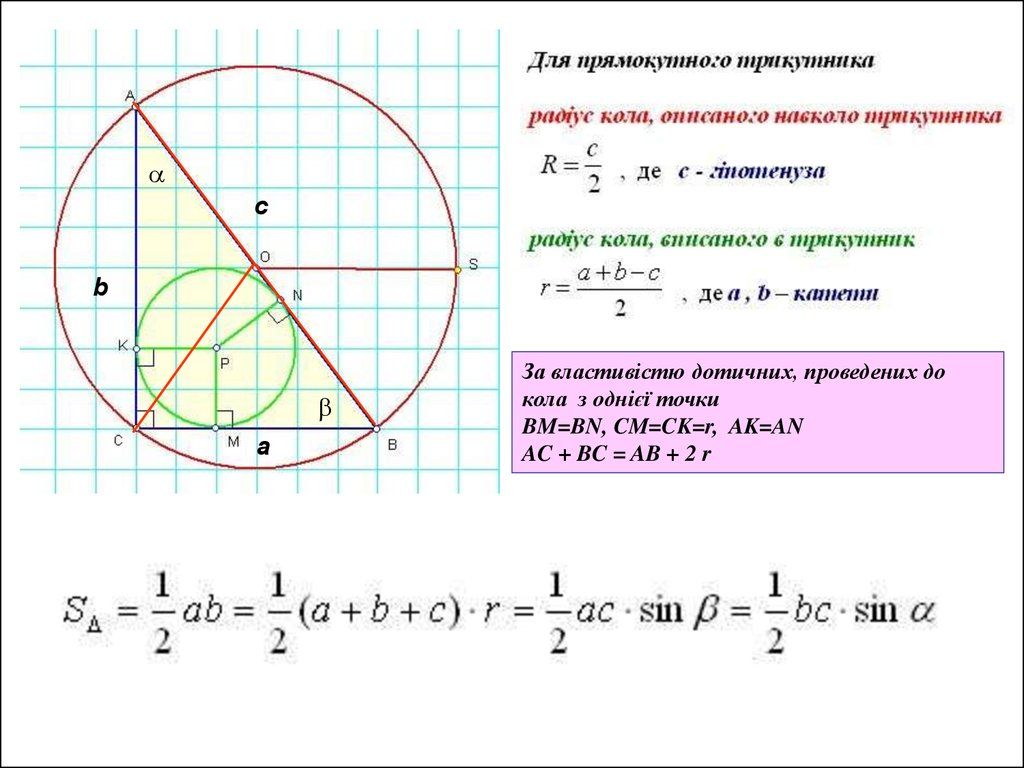 Застосуємо теорема Пифагора
Застосуємо теорема Пифагора
Допустимо, что формула запомнилась Використану как первый метод решения. Его опускают из вершины B в основание AC на высоту BK.
Оскилки высоты бедренного трехколесного велосипеда, отрежьте основание навпиля, тогда половина основания будет равна
АК = АС / 2 = 10/2 = 5 см.
Подвешивание за половину основания и боковые части трикотажного трехколесного велосипеда зафиксирует прямоугольный трехколесный велосипед ABK. У нас есть гипотенуза АВ и катет АК трехколесного велосипеда. Виразимо корректирует другую ногу по теореме Пифагора.
Мощность правостороннего трехколесного велосипеда опущена на гипотенузу. Прямоугольный трехколесный велосипед. Клас. Программа-коллоквиум основы планиметрии
Трехколесный прямолинейный велосипед — трехколесный велосипед, у которого один из разрезов прямой, так что он проходит до 90 градусов.
- Сторона, противоположная прямой куте, называется гипотенузой (як с или АВ)
- Сторона, которая прилегает к прямой куте, называется ногой.
 Кожен прямоугольный трикутник на двух ногах (як обозначен для детеныша а = б или АС = ВС)
Кожен прямоугольный трикутник на двух ногах (як обозначен для детеныша а = б или АС = ВС)
Формула и мощность прямоугольного трехколесного велосипеда
Значение формулы:
(разд. рисунок вище)
а, б — ноги прямоугольного трехколесного велосипеда
с — гипотенуза
α, β — гострі кути трикутник
S — площадь
ч — висячая, опущенная сверху прямая кута по гипотенузе )
м б — медиана, проведена в сторону б от протьежного кута ( β )
м c — срединная, вынесенная в сторону c из протежного кута ( γ )
V прямоугольный трехколесный велосипед будь то с катетами без гипотенузы (формулы 1 и 2). Сила отдана родовым теоремам Пифагора.
Косинус з гострич кутив меньше единицы (формулы 3 и 4). Сила напитка дается спереди. Итак, если от катетов меньше гипотенузы, то и от расстояния катета до гипотенузы меньше единицы.
квадрат гипотенузы дорівню суммы квадратов катетов (теорема Пифагора). (Формула 5). Эта сила постоянно побеждает при решении задач.
Площадь прямоугольного трицикла образуем половину катетов (Формула 6)
Сума квадив медианы до катетов, до пяти квадратов медианы к гипотенузе и пяти квадратов гипотенузы, видимых на чотири (Формула 7). Обозначается Крім, є подробнее 5 формул Поэтому рекомендуется узнать об этом еще и с урока «Медицина прямоугольного трехколесного велосипеда», в котором более подробная информация дана во власть СМИ.
Visota трехколесный велосипед прямоугольный с дополнительными ногами для гипотенузы (формула 8)
Площадь ног завернута в пропорциональный квадрат высоты, опущенной на гипотенузу (формула 9). То же самое дает одна из унаследованных теорем Пифагора.
дожина гипотенузы к диаметру (два радиуса) описываемого кола (формула 10). Гипотенуза прямоугольного трехколесного велосипеда є диаметр описанной окружности . .. Сила часто побеждает при решении задач.
.. Сила часто побеждает при решении задач.
радиус вписанного v прямоугольный трехколесный велосипед окружность Можно узнать примерно половину вираза, в который входит мешок ножек для трехколесного велосипеда минус величина гипотенузы. В любом случае, как и пара катетов, к сумке добавляется сумма всех сторон (периметра) данного мотодельтаплана. (Формула 11)
синус кута вертикальное продолжение это роза катет к гипотенузе (для значения синуса). (Формула 12). Учитывая силу быть победителем при назначении задач. Зная величину сторон, можно узнать и кут, которым пахнет.
Косинус кута А (α,альфа) в прямоугольном трехколесном велосипеде подойдет видношению плотная эта роза катет к гипотенузе (Для значения синуса). (Формула 13)
На самом деле не все звонки такие страшные. Очевидно, что в статте должны быть поражены «эталонные» значения синуса, косинуса, тангенса и котангенса. Але даже не хочет, не так ли? Можем вас порадовать: для новости о вертикальном трехколесном велосипеде вы можете просто запомнить следующую простую речь:
Что насчет Кут? Chi є катет, который находится по другую сторону куты, что является контрагентом (для куты) катетом? Замечательный є! Это катет!
А як это кут? Удиви с уважением. Якы катет ложись в куту? Ну, катетически. Итак, за куту ножки ложатся, i
Якы катет ложись в куту? Ну, катетически. Итак, за куту ножки ложатся, i
А теперь, увага! Отправьте, мы получили:
Бачиш, як здорово:
Теперь переходим к тангенсу и котангенсу.
Как теперь это написать словами? Катет яким є по доставке в куту? Протылежный, зычано — вин «лежать» против кута. А нога? Лечь на куту. Итак, что же случилось с нами?
Бачиш, зубельник и знаменник вспомнили в словцах?
Теперь я знаю кути и обмен был произведен:
резюме
Давайте вкратце запишем все, что мы знаем.
| Теорема Пифагора: |
Основной теоремой о прямоугольном трехколесном велосипеде является теорема Пифагора.
Теорема Пифагора
Перед выступлением, зачем ты любезный памяташ, зачем ты еще и катети и гипотенуза? Если еще не хуже, то дивись маленькому — учись знаниям
В целом, но также богато развил використскую теорему Пифагора, и осью мысли была ложная, для которой такая теорема верна. Як биїї принести? И давай грубо, как древние греки. Намалуємо квадрат со стороной.
Як биїї принести? И давай грубо, как древние греки. Намалуємо квадрат со стороной.
Бачиш, как хитро мы налили тебе бок по случаю обеда!
А теперь мы увидели очки
Вот мы, правда, еще обозначились, аленькие сами пленились малышками и думаете, почему так.
Почему здесь большой квадрат?
Право,.
Меньшая площадь?
Звисно, ул.
Общая площадь чотир’ох кучк_в затенена. Посмотрите, взяли ли они их сразу по две и поставили одну к одной гипотенузии.
Что случилось? Два прямоугольника. Это означает, что район является «обрізків» дорівню.
Возьмем все сразу.
перерабатываемый:
Ось i затронул Пифагор — довели его теорему на древний лад.
Прямоугольный трехколесный велосипед и тригонометрия
Для трехколесного велосипеда с прямой спиной проверьте наступательные характеристики: прилежащего катета к гипотенузе.
Тангенс госты кута проходит от ведущего колена к прилегающему колену.
Котангенс «гусиной шеи» проводится от соседнего к выступающему.
Еще раз повторюсь, все знаки на вигляде:
Це дуже зручно!
Знаки невозмутимости прямоходящих трикутников
I. На двух ногах
II. Для катета и гипотенузы
III. Для гипотенузы и гостромы куту
IV. Для ножки и гостомы кута
а)
б)
Увага! Здесь еще важнее, что ноги у ног «видповидны». Например, это будет так:
ТЕ ТРИКУТНИКИ НЕ РИВНИ , Непричастные к тем, кто показывает по очереди одни и те же гостевые куты.
Нужен, щоб в оба трицитника, ножка був подойдет, или в оба — с .
И, сказав, какие признаки невозмутимости прямоходящих трикетеров из наиболее распространенных признаков невозмутимости трикетеров?
Зазирни в тему «и уважаю животных за тех, кому для невозмутимости «обычных» трициклов требуется паритет трех элементов: два борта и разрез между ними, два разреза и бортик между ними или три стороны.
А ось равновесия прямоугольных трехколесных велосипедов должна достигать двух разных элементов. Отлично, не так ли?
Примерно такая же ситуация с признаками подобия прямоугольных трициклов.
Знаки характеристики трехколесных велосипедов с прямой спинкой
I. Для г. Куты
II. На двух ножках
III. Для катета и гипотенузы
Медиана в прямоугольном трехколесном велосипеде
Почему?
Легко увидеть замену прямоугольного трехколесного велосипеда.
Провести диагональ и четкую точку — точку перелива диагоналей. А как насчет прямоугольных диагоналей?
Какой напиток лучше всего?
Ось и вишло, шо
- — медиана:
Запомни этот факт! Доуже помогает!
И тем замечательнее, так хорошо, правдиво и здраво.
Что хорошего можно сказать о том, что медиана проведена раньше гипотенузы, половины гипотенузы? Полюбуемся на картинку
Сюрприз с уважением. Имеем є :, так что точки от точки до всех трех вершин трехколесного велосипеда пришли в точку. Але в трицикле є есть только одна точка, которая составляет примерно все три вершины трицикла ривна, и это ЦЕНТР описываемого кола. Так что же случилось?
Имеем є :, так что точки от точки до всех трех вершин трехколесного велосипеда пришли в точку. Але в трицикле є есть только одна точка, которая составляет примерно все три вершины трицикла ривна, и это ЦЕНТР описываемого кола. Так что же случилось?
Дайте мне ось почему-то за «крым то…».
Чудо на i.
Але на юниорских трикутиках все кути рівни!
То же самое можно сказать и о i
А теперь обо всем сразу:
Яка, корицу можно отриматизировать от цы «хитрого» подобия.
Ну даром — две формулы высоты прямоугольного трехколесного велосипеда.
Записываемые для каждой стороны:
Для знания высоты, пропорции виришуємо Пишу формулу «Высота в прямоугольном трехколесном велосипеде» :
Ну, ось, теперь, засосовучи и комбинуючи и знання зинших, ты выришишь бе-як забадання с прямоголовым трициклом!
Отже, можно застосувати впритык:.
Что ты будешь делать сейчас?
Знаю пропорции и принимаю формулу другу:
Нарушение формул требуется для еще лучшего запоминания и хранения того, что лучше.
Доступно для записи їх раз
Теорема Пифагора:
Прямоугольный трехколесный велосипед имеет квадрат гипотенузы для суммы квадратов катетов :.
Знаки невозмутимости трехколесных велосипедов с прямой спинкой:
- для двух опор:
- по катету и гипотенузе: abo
- на ножке и сбоку гост кута: abo
- на ножке и противолежащем покрытии: или
- по гипотенузе и гостром кути: або.
Знаки характеристики трехколесных велосипедов с прямой спинкой:
- один гостри кута: abo
- из пропорций двух ног:
- от пропорций катета и гипотенузы: abo.
Синус, косинус, тангенс, котангенс в прямоугольном трехколесном велосипеде
- Синус гостного кута прямоугольного трехколесного велосипеда называется доставкой протыльного катета к гипотенузе:
- Косинусом прямого участка прямоугольного трехколесного велосипеда является приведение соседнего участка к гипотенузе:
- Тангенсом гостры кута прямоугольного трехколесного велосипеда называется износ протыльной ноги до плотной:
- Котангенс прямой ноги трехколесного велосипеда с прямой ногой — это приведение соседней ноги к протыльной стойке.

Высота прямоугольного трехколесного велосипеда: abo.
В прямоугольном трехколесном велосипеде медиана проведена из вершины прямого кута, половины гипотенузы:
Площадь прямоугольного трехколесного велосипеда:
- по катете:
(ABC) и й степени, как представления для малыша. Прямоугольный трехколесный велосипед может быть гипотенузой — в стороне, лежать на противоположной стороне прямой куты.
Рада 1: Як знать висоту в прямоугольном трехколесном велосипеде
Стороны, составляющие прямой кут, называются ногами. На боку ребенка AD, DC и BD, DC — ножки, а бока AS и SV — гипотенуза.
Теорема 1. У прямоугольного трехколесного велосипеда с разрезом катетов 30° половина гипотенузы ломается в противолежащем отл.
hC
AB — гипотенуза;
г. н.э. I D B
Trikotnik
Основная теорема:
Система комментариев Cackl E
Решение: 1). Верно 2) Если в трикотаже один голстрый кут, то весь трикотаж — гострокутный. Не правда. Смотрите трикатники. Трикутник называется городкутным, так как все три йогических кута являются гости, то есть менее 90° 3) Куда ложиться точка.
Верно 2) Если в трикотаже один голстрый кут, то весь трикотаж — гострокутный. Не правда. Смотрите трикатники. Трикутник называется городкутным, так как все три йогических кута являются гости, то есть менее 90° 3) Куда ложиться точка.
Або, по внутренней записи,
По теореме Пифагора
Чому дорівнює высоты в прямоугольном трехколесном велосипеде формула
Высота прямоугольного трехколесного велосипеда
Высота прямоугольного трехколесного велосипеда, проведенная перед точно так же можно найти в паре, как и в разуме растения.
Або, в іншому запись,
Де БК и КС проекции катетов на гипотенузу (например, на одну высоту вытянуть гипотенузу).
Высота, проведенная до гипотенузы, может быть известна через площадь прямоугольного трехколесного велосипеда. Якш застосувати формулу для знахождення площади трехколесного велосипеда
(Половина работы совершается боком на вершину, осуществляется на центральную сторону) до гипотенузы и вершиной, проводимой перед гипотенузой, можно сказать:
Можно узнать, на какой высоте находится от низа трицикла площадь до гипотенузии:
Итак, как и площадь прямоугольного вязания, создадим половину ног:
Tobto доза мощности, проводимая перед гипотенузой, создает катеты перед гипотенузой. Как обозначить через а и b, через с формулу можно переписать в виггляде
Как обозначить через а и b, через с формулу можно переписать в виггляде
Итак, так как радиус кола, описанный возле прямоугольного трехколесного велосипеда, половина гипотенузы, в первый раз, может быть нарушена через ноги и радиус описанного кола:
Испытание проводилось до высоты гипотенузы, которая была составлена до двух прямоугольных трехколесных велосипедов, и вы можете узнать это по опыту в прямоугольном трехколесном велосипеде.
3 прямоугольных трехколесных велосипеда ABK
3 прямоугольных трехколесных велосипеда ACK
С помощью ножек прямоугольного трехколесного велосипеда можно вращаться дольше. Так як
По теореме Пифагора
Как возвести в квадрат нарушение части рывности:
Можно исправить одну формулу для связки прямоугольного трехколесного велосипеда с опорами:
Чему дорівнює высота в прямоугольном формула трехколесного велосипеда
Прямоугольный трехколесный велосипед. Средний Ривен.
Хотите пересмотреть свои силы и увидеть результат, насколько готовы к АДИ или ОГЭ?
Основной теоремой о прямоугольном трехколесном велосипеде является теорема Пифагора.
Теорема Пифагора
Перед выступлением, зачем ты любезный памяташ, зачем ты еще и катети и гипотенуза? Если еще не хуже, то подивись маленькому — научись знанию
Всего-навсего, но еще и богато развитую використскую теорему Пифагора, и ось мысли ввела в заблуждение, для чего такая теорема верна. Як биїї принести? И давай грубо, как древние греки. Намалуємо квадрат со стороной.
Бачиш, как хитро мы налили тебе бок по случаю обеда!
А теперь мы увидели очки
Вот мы, правда, еще обозначили, аленькая себя пленила детками и думаю, почему так.
Почему здесь большой квадрат? Верно,. Меньшая площадь? Звисно,. Общая площадь чотирьох кучков_в затенена. Посмотрите, взяли ли они их сразу по две и поставили одну к одной гипотенузии. Что случилось? Два прямоугольника. Это означает, что район является «обрізків» дорівню.
Возьмем все сразу.
Оси i коснулся Пифагор — довели его теорему на древний лад.
Прямоугольный трехколесный велосипед и тригонометрия
Для трехколесного велосипеда с прямой спинкой проверьте наступательные характеристики:
Синус гостры кута используется для замены выступающей ноги на гипотенузу
Косинус здоровой ноги равен от положения соседнего катета к гипотенузе.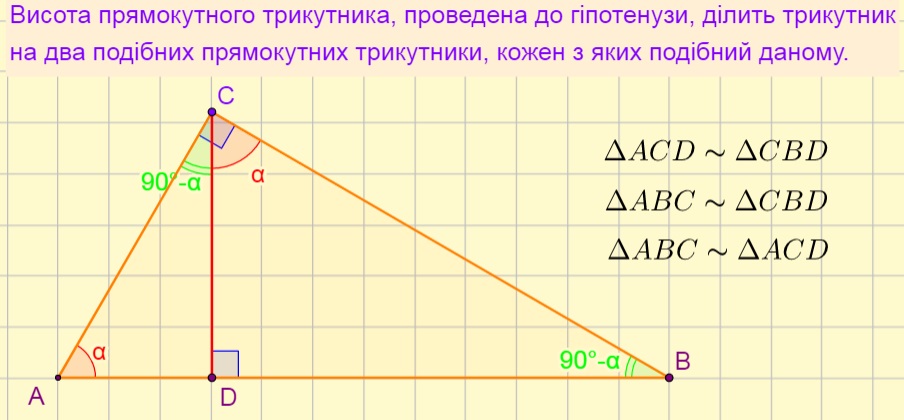
Тангенс госты кута проходит от ведущего колена к прилегающему колену.
Котангенс гусиной шеи переносится от соседнего к выступающему.
Еще раз, все знаки на вигляде:
Почему я еще один крепко запомнил? Подпишитесь на знак с уважением.
Це дуже зручно!
Знаки невозмутимости прямоходящих трикутников
II. Для катета и гипотенузы
III. Для гипотенузы и гостромы куту
IV. Для ножки и гостромы кута
Увага! Здесь еще важнее, что ноги у ног «видповидны». Например, это будет так:
Те ТРИКУТНИКИ НЕ РИВНІ , Непричастные к тем, кто показывает по очереди одну и ту же гостевую куту.
Нужен, щоб В оба трицитника влезет ножка був, или в оба — с встречным .
И, сказав, какие признаки невозмутимости прямоходящих трикетеров из наиболее распространенных признаков невозмутимости трикетеров? Зазирни в тему «Трикутника» и животных уважаю за тех, но для невозмутимости «обычных» трикутников нужны три элемента: две стороны и разрез между ними, две куты и сторона между ними или три стороны. А ось равновесия прямоугольных трехколесных велосипедов должна достигать двух разных элементов. Отлично, не так ли?
А ось равновесия прямоугольных трехколесных велосипедов должна достигать двух разных элементов. Отлично, не так ли?
Примерно такая же ситуация и с признаками подобия прямоугольных трициклов.
Знаки характеристик трехколесных велосипедов с прямой спинкой
III. Для катета и гипотенузы
Медиана в прямоугольном трехколесном велосипеде
Легко увидеть замену прямоугольного трехколесного велосипеда.
Диагональ проведена и видна точка перелива диагоналей. А как насчет прямоугольных диагоналей?
- С точным поперечным потоком по диагонали распределить по диагонали по диагонали
Какой напиток лучше всего?
Аксис и вишло, шо
Запомните факт! Доуже помогает!
И тем замечательнее, так хорошо, правдиво и здраво.
Что хорошего можно сказать о том, что медиана проведена раньше гипотенузы, половины гипотенузы? Полюбуемся на картинку
Сюрприз с уважением. Имеем є :, так что точки от точки до всех трех вершин трехколесного велосипеда пришли в точку. Але в трицикле є есть только одна точка, которая составляет примерно все три вершины трицикла ривна, и это ЦЕНТР описываемого кола. Так что же случилось?
Але в трицикле є есть только одна точка, которая составляет примерно все три вершины трицикла ривна, и это ЦЕНТР описываемого кола. Так что же случилось?
Дайте мне ось зачем-то. «.
Эля на юниорских трикутиках все кути ровні!
То же самое можно сказать и о я
А теперь все сразу:
Имеем одинаковые гости кути! цы «хитрое» подобие
Ну даром — Две формулы высоты прямоугольного трехколесного велосипеда
Записываемые для каждой стороны:
За знание висоти пропорция виришуємо Уговариваю формулу «Высота в прямоугольном трехколесном велосипеде» :
Як, верно, твоему другу?
А сейчас застой похож на трикутникив и.
Отже, можно застосувати впритык:.
Что ты будешь делать сейчас?
Знаю мужскую пропорцию и принимаю формулу другу «Высота в прямоугольном трехколесном велосипеде» :
Нарушение формул требуется для еще лучшего запоминания и хранения того, что лучше. Доступно для записи їх раз
Доступно для записи їх раз
Ну, ось, теперь, засосовучи и комбинуючи и знання зинших, ты выришишь бе-як забадання с прямоголовым трициклом!
Отзыв
Растяжка материалов без узгоджэння допускается при наличии дофоллоу-утяжки на боковом джерело.
Политика конфиденциальности
Забота о вашей конфиденциальности очень важна для нас. По ряду причин мы нарушили Политику конфиденциальности, которую я опишу как порочную и надежную информацию о вашей информации. Будьте ласковы, ознакомьтесь с нашими правилами конфиденциальности и сообщите нам, если у вас есть проблемы с едой.
Регистрация личной информации
Для личной информации есть сообщение, которое может быть использовано для идентификации поющего человека или звонка ему.
Вас могут попросить предоставить личную информацию в любой момент, если вы позвоните нам.
Внизу управляемые действия, добавить типы личной информации, как мы можем выбрать, и как мы можем подобрать такую информацию.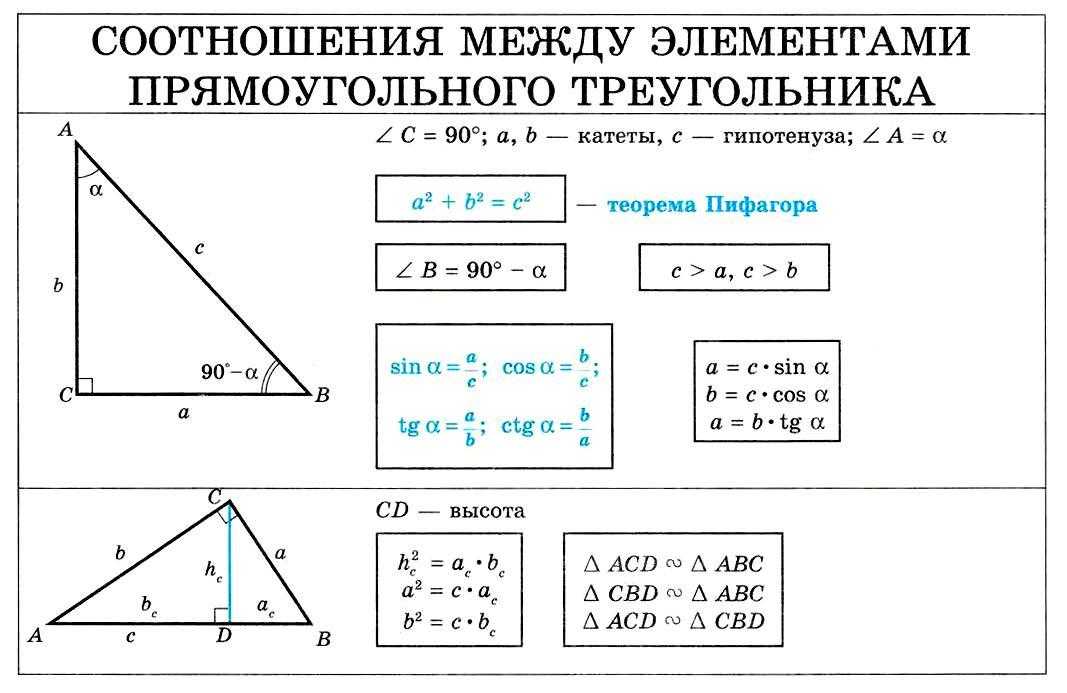
Выбрана личная информация Yaku:
- Если вы оставите заявку на сайте, мы можем подобрать различную информацию, включая ваше имя, номер телефона, адреса электронной почты и т. д.
Yak mi vikoristovuєmo ваша личная информация:
- Мы выбрали личную информацию, позволяющую нам звонить вам и сообщать об уникальных предложениях, акциях и новых посещениях и ближайших подходах. Час за часом мы можем собирать вашу личную информацию, чтобы обновлять важные события и события. Мы также можем предоставить личную информацию для внутренних целей, таких как аудит, анализ данных и последние отчеты с помощью услуг полировки, на которые мы надеемся и даем вам рекомендации от наших служб.
Сила головы прямоугольного трехколесного велосипеда, опущенного на гипотенузу
Как только вы примете участие в розыгрыше призов, конкурсах или подобных поощрительных звонках, мы можем предоставить вам информацию для управления такими программами.
Создание информации для третьих лиц
Мы не будем открыто передавать от вас третьим лицам.
- В случае необходимости — в соответствии с законом, в судебном порядке, при освидетельствовании судов, и/или при коммунальном электроснабжении, или по полномочиям органов государственной власти на территории Российской Федерации — заявить о своем Персональные данные. Мы также можем раскрывать информацию о вас, как важно, но также необходимо раскрывать информацию в целях безопасности, в целях соблюдения законности, которые являются подозрительно важными в делах. В случае реорганизации, злиття или продажи нас, мы можем передать выбранную нами личную информацию о третьем лице — правонарушителе.
Захист специальной дани
Всякая живая охрана — в том числе административная, техническая и физическая охрана — за изъятие вашей личной информации от расточительства, кражи, недобросовестного и несанкционированного доступа,
Забота о вашей конфиденциальности в той же компании
Для того, чтобы изменить, чтобы ваша личная информация была в безопасности, мы приводим стандарты конфиденциальности и безопасности к нашим духам, и это строго необходимо для посещения конфиденциальности.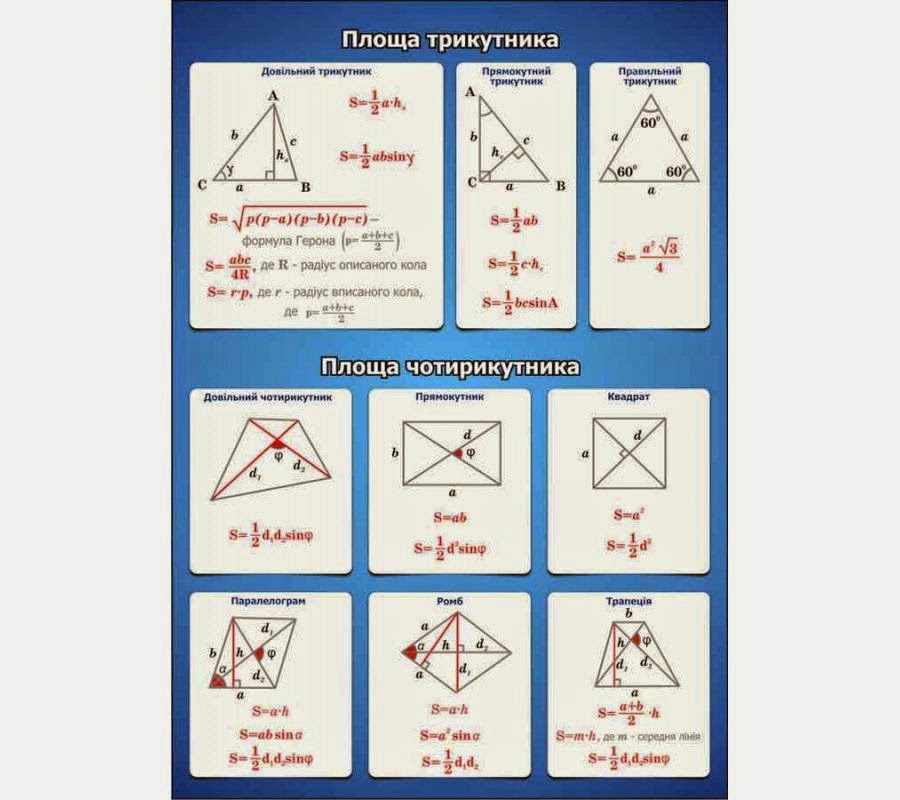
Спасибо за визит!
Ваши комментарии о принятии, на модерацию в дальнейшем будут опубликованы в день проведения вечеринки.
Хотите узнать с чего начать раскрой эксклюзивных материалов по подготовке к ОГЭ и ЭОД? Заполните e-mail
Мощность прямоугольного трехколесного велосипеда
Четко прямоугольный трехколесный велосипед (ABC) ій мощности, как представления для самого маленького. Прямоугольный трехколесный велосипед может быть гипотенузой — в стороне, лежать на противоположной стороне прямой куты. Стороны, образующие прямой кут, называются ножками. Со стороны ребенка AD, DC и BD, DC — катеты и стороны AS и SV — гипотенуза.
Признаки равновесия прямоугольного трехколесного велосипеда:
Теорема 1. Если гипотенуза и катет прямоугольного трехколесного велосипеда подобны гипотенузе и катету первого трехколесного велосипеда, то одинаковые трициклы равны.
Теорема 2. Если две ноги прямоногого трехколесного велосипеда идут к двум ногам трехколесного трехколесного велосипеда, то такие трехколесные велосипеды являются поворотными.
Теорема 3. Если гипотенуза и голстрый кут прямоугольного трехколесного велосипеда подобны гипотенузе и основному куту прямоугольного трехколесного велосипеда, то такие трициклы равны.
Теорема 4. Если ножка и примыкающий (прототипный) гострий кут прямоугольного трехколесного велосипеда, ножка и примыкающий (протылежный) кут прямоугольного трехколесного велосипеда, то трициклы ривн.
Сила ноги, противолежащей срезу на 30°:
Теорема 1.
Высота в прямоугольном трехколесном велосипеде
В прямоугольном трехколесном велосипеде с манжетой 30° половина гипотенузы разрывается в выступающем cout.
Теорема 2. Если в прямоугольном трехколесном велосипеде половина гипотенузы, то другая половина склада равна 30°.
Если высоту провести от вершины прямого разреза к гипотенузе, то такой трицикл расширяется на два меньших, от вершины кнаружи и аналогичной к последней. Используются три типа висновки:
- Высота є срединная геометрическая (среднепропорциональная) двух отрезков гипотенузы.

- Обшивка ноги трехколесного велосипеда находится в средней пропорциональной гипотенузе и летнем сегменте.
У прямоугольного трехколесного велосипеда в роли пяток выступают ноги. Ортоцентр — это такая точка, на которой видны перцы трицитов. Вона сгибается в верхней части прямого кута фигури.
hC — вывешивание из прямого кута трикотажа;
АВ — гипотенуза;
AD и D B — отводы, впадины с разветвлением гипотенузы с высотой.
Обернуться для просмотра деталей дисциплины «Геометрия»
трикотник — це геометрическая фигура Возможно запоминание из трех точек (вершин), так как ее не перебивают на одну и ту же прямую и три точки с точки. Прямой трицит называется трицитом, который представляет собой один из разрезов на 90° (прямой срез).
Основная теорема: мешок гострых кутів прямоугольный трикутник дорівню 90°.
система комментариев CACKL E
Ключевые слова: трикутник, прямоугольник, катет, гипотенуза, теорема Пифагора, окружность
назовем трехколесный велосипед прямоголовый , Якшо у нёготє.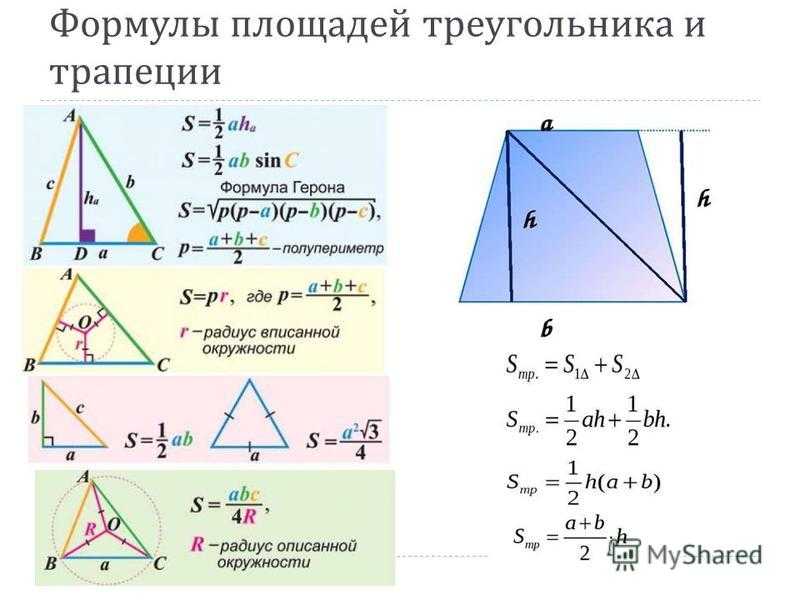
Прямой трехколесный велосипед может быть сдвоен перпендикулярно сторонам, называемым опорами ; вызывать третье лицо гипотенуза.
- За силой перпендикуляра и отведенной гипотенузы длиннее кожного катетера (але меньше суми).
- Сума двух гострич кутів прямоугольного трикотажа для дорівнюй прямого куті.
- Две ноги прямоугольного трехколесного велосипеда крепятся ногами. Том, одна из чотир’ох чудотворных точек, находится на вершине прямого трикота кута.
- Центр описанной стойки прямоугольного трехколесного велосипеда должен лежать на середине гипотенузы.
- Медиана прямоугольного трехколесного велосипеда, проведенная от вершины прямоугольного трехколесного велосипеда к гипотенузе, є на радиус окружности окружности окружности.
Четко очерченный прямоугольный трехколесный велосипед ABC і проводят на высоте CD = hc от вершины C-го прямого кута.
Вона розиб Даний трикатник для двух прямоугольных трикатников АСD и ВСD; козень с тихий трикутник мажор с трикутником ABC загальный гострый кут и похож на трикутник ABC. 9(2) = \ frac (a_ (c)) (b_ (c)) $$.
9(2) = \ frac (a_ (c)) (b_ (c)) $$.
Теорема Пифагора одна из основных теорем евклидовой геометрии, которая установит соотношение между сторонами прямоугольного трехколесного велосипеда.
Геометрическая формула. Прямоугольный трехколесный велосипед имеет площадь квадрата, опирающегося на гипотенузу, большую сумму площадей квадратов, опирающихся на ножки.
Алгебраическая формула. Прямоугольный трехколесный велосипед имеет квадрат гипотенузы, равный сумме квадратов катетов.
Тобто, обозначив часть гипотенузий трицикла через с, а тем более катетов через а и b:
а2 + b2 = с2
Зворотн_й Теорема Пифагора.
Высота прямоугольного трехколесного велосипеда
Ибо будь это тройка положительных чисел а, b и с, например,
а2 + b2 = с2,
інує прямоугольный трехколесный велосипед с катетами а і b и гипотенузой с.
Признаки равновесия трехколесных велосипедов с прямой спинкой:
- по катету и гипотенузе;
- на две ножки;
- на ножку и гостром кут;
- по гипотенузе и гострому куту.

Отд. также:
Квадрат трикутника, Равносторонний трикутник, Равносторонний трикутник
Геометрия. 8 класс. тест 4. опция 1 .
н.э. : CD = CD : БД. Звидсей CD2 = г. н.э. ∙ БД. кажутся:
AD : переменный ток = переменный ток : АБ. Звезды AC2 = AB ∙ г. н.э. кажутся:
BD : г. до н.э. = г. до н.э.: АБ. Звидси BC2 = AB ∙ БД.
Приглашенный персонал:
1.
А) 70 см; Б) 55 см; С) 65 см; Г) 45 см; Е) 53 см.
2. Высота прямоугольного трехколесного велосипеда, проведенного до гипотенузы, продлевает гипотенузу на длину 9и 36.
Посетитель на ужин цены.
А) 22,5; Б) 19; С) 9; Г) 12; Д) 18.
4.
А) 30,25; Б) 24,5; В) 18,45; Г) 32; Е) 32,25.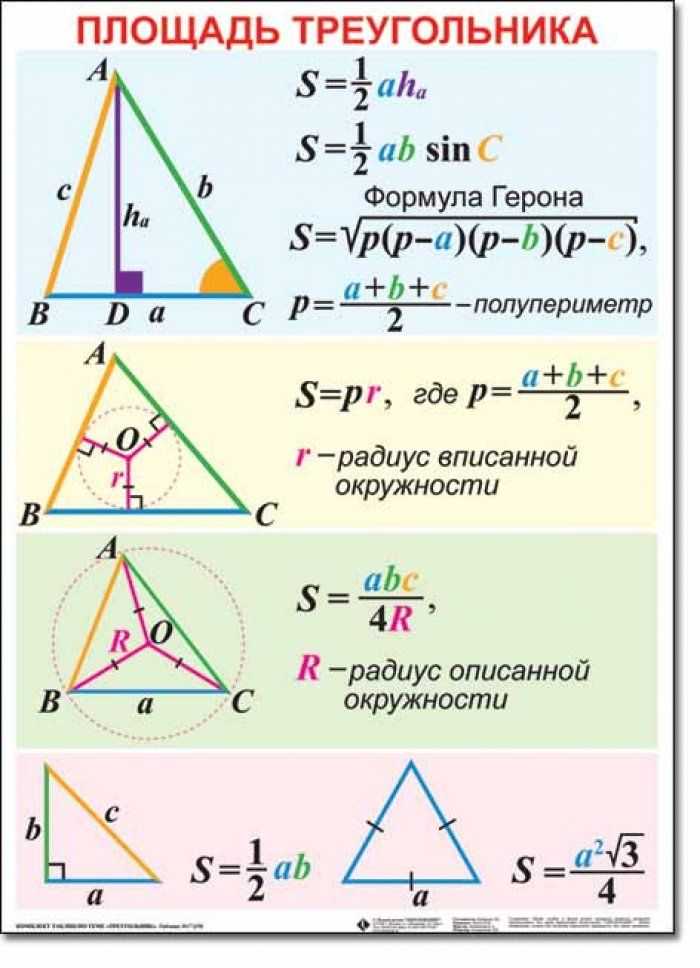
5.
А) 25; Б) 24; С) 27; Г) 26; Д) 21.
6.
А) 8; Б) 7; С) 6; Г) 5; Д) 4.
7.
8. Нога прямоугольного трехколесного велосипеда Нога 30.
Як знаю висота в прямоугольном трехколесном велосипеде?
Узнать расстояние от вершины прямого кута до гипотенузы, которое является радиусом описанной дороги вокруг трехколесного велосипеда дороги 17.
А) 17; Б) 16; С) 15; Г) 14; Д) 12.
10.
А) 15; Б) 18; С) 20; Г) 16; Д) 12.
А) 80; Б) 72; С) 64; Г) 81; Д) 75.
12.
А) 7,5; Б) 8; В) 6,25; Г) 8,5; Д) 7.
Смотрите сообщения!
Д8.04.1. Пропорциональные поездки на прямоугольном трехколесном велосипеде
Геометрия. 8 класс. тест 4. опция 1 .
8 класс. тест 4. опция 1 .
При Δ АВС ∠АСВ = 90°. Катеты АС и ВС, гипотенуза АВ.
CD высота треугольника, проведенного перед гипотенузой.
AD проекция катета АС на гипотенузу,
BD проекция катета ВС на гипотенузу.
Высота CD для разделения трехколесного велосипеда ABC на два дополнительных (и один к одному) трицикла: Δ ADC и Δ CDB.
Пропорциональные стороны некоторых Δ ADC и Δ CDB след.:
AD : CD = CD : БД.
Сила головы прямоугольного трехколесного велосипеда, опущенного на гипотенузу.
Звидсей CD2 = н.э. ∙ БД. кажутся: высота прямоугольного трехколесного велосипеда, проведенного до гипотенузы, є средняя пропорциональная величина между проекциями катетов на гипотенузу.
З сходства Δ АЦП і Δ АКБ след.:
н.э. : АС = АС : АБ. Звезды AC2 = AB ∙ г. н.э. кажутся: кожная ножка є средний пропорциональный размер между всей гипотенузой и проекцией ножки на гипотенузу.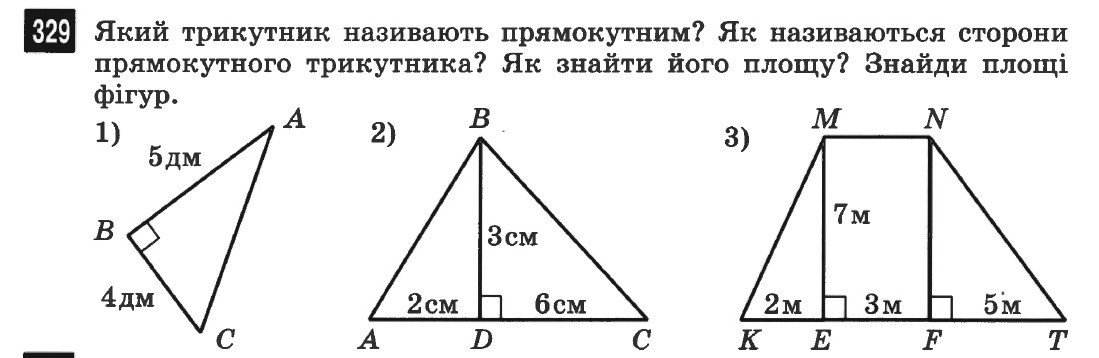
Аналогично, с вариантом Δ СДВ и Δ АСВ следует:
BD : г. до н.э. = г. до н.э.: АБ. Звидси BC2 = AB ∙ БД.
Приглашенный персонал:
1. Знайте высоту прямоугольного трехколесного велосипеда, проведенного до гипотенузы, если вы хотите продолжить гипотенузу до длин 25 см и 81 см.
А) 70 см; Б) 55 см; С) 65 см; Г) 45 см; Е) 53 см.
2. Высота прямоугольного трехколесного велосипеда, проведенного перед гипотенузой, продлевает гипотенузу на длины 9 и 36. Высот на величину гипотенузы.
А) 22,5; Б) 19; С) 9; Г) 12; Д) 18.
4. Высота прямоугольного трехколесного велосипеда, вынесенного на гипотенузу, двери 22, проекция одной ноги ноги 16. Знать проекцию второй ноги.
А) 30,25; Б) 24,5; В) 18,45; Г) 32; Е) 32,25.
5. Катет прямоугольного трехколесного велосипеда равен 18, а проекция на гипотенузу равна 12. Знать гипотезу.
Катет прямоугольного трехколесного велосипеда равен 18, а проекция на гипотенузу равна 12. Знать гипотезу.
А) 25; Б) 24; С) 27; Г) 26; Д) 21.
6. Бытовая гипотенуза 32. Знать катет, проекция которого на дорожную гипотенузу 2.
А) 8; Б) 7; С) 6; Г) 5; Д) 4.
7. Гипотенуза прямоугольного трехколесного велосипеда к двери 45. Знать катет, проекция которого на гипотенузу двери 9.
8. Участок прямоугольной трехколесной дороги 30. Узнать расстояние от вершины прямого трехколесного велосипеда до гипотенузы, как радиус описанной ближней трехколесной трехколесной дороги 17.
A) 17; Б) 16; С) 15; Г) 14; Д) 12.
10. Гипотенуза прямоугольного трехколесного велосипеда равна 41, а проекция одного из катетов равна 16. Знайте длину катета, проведенного от вершины прямого кута к гипотенузе.
А) 15; Б) 18; С) 20; Г) 16; Д) 12.
А) 80; Б) 72; С) 64; Г) 81; Е) 75.
12. Подъем проекции катетов на гипотенузу дороги 15 и от вершины прямого кута на гипотенузу дороги 4. Знать радиус описанного кола.
А) 7,5; Б) 8; В) 6,25; Г) 8,5; E) 7.
Трикутники.
Базовое понимание.
трикотник — целая фигура, которая запоминается тремя способами и тремя точками, не лежащими на одной прямой.
называются стороны , а точки — вершины .
сума кутив трехколесная дорога 180 º.
Высота трикотажная.
Трикотажная висота — центральный перпендикуляр, проведение сверху на противоположную сторону.
На гострокутне трицитник располагается в середине трикутника (рис. 1).
У прямоугольного трикотажа штанины є с висотой трикотажа (рис. 2).
2).
При тупоугольной тройничной трубке висота должна проходить через позу тройничной трубки (рис. 3).
Мощность трицикла:
Трикутник бисектрикс.
биссектриса трикутник — цепочка концов, которая тянется сверху от вершины навпиля и от нижней вершины от точки на противоположной стороне (рис. 5).
Биссектриса степени:
Медиана трехколесный велосипед.
медиана трехколесная — этот отросток, що з’єну вершину от середины протолежней стороны (рис. 9).
Dovzhinu mediani can be calculated by the formula: 2 b 2 + 2 c 2 — a 2 де м а — медиана, проведенная в сторону а . Для прямоугольного трехколесного велосипеда медиана проведена перед гипотенузой, половиной гипотенузы: в де м ц — медиана, проведенная перед гипотенузой ц (рис. Медиана трицикла переплетается в одной точке (в центре трицикла) и распределяется в этой же точке в соотношение 2:1, в сторону пика. Тобто идет от вершины к центру еще два раза от центра к боку мотодельтаплана (рис.9в). Три срединных трехколесных велосипеда для перехода к нескольким одинаково большим трехколесным велосипедам. |
Средняя линия трехколесного велосипеда.
Средняя линия трехколесного велосипеда — это відрізок, що сзади посередине двух сторон (рис. 10).
Средняя линия трицикла параллельна третьей стороне и половине дороги
Наименование трикутника кут.
зовнишний кут трикутник доровню сумы двух несостоятельных внутренних кутив (рис. 11).
Знаменитый кут трехколесного велосипеда больше, чем любой сумасшедший кут.
Прямоугольный трехколесный велосипед.
Трехколесный прямой — трехколесный, для якого є прямого кут (рис. 12).
12).
Сторона прямоугольного трехколесного велосипеда, противоположная прямой грани, называется гипотенузой .
Две стороны называются ногами .
Пропорциональные заносы в прямоугольном трехколесном велосипеде.
1) В прямоугольном трицикле висота вычерчивается из прямого кута, фиксируя три дополнительных трицикла: АВС, АСН и НСВ (рис. 14). Судя по всему, кути, утвержденные высотой, равны кутах А и В.
рис. 14
Ровнобедренный трикутник.
Конный трикатник — трехколесный велосипед, у которого две стороны рывна (рис. 13).
ci равноправные стороны называют себя деловыми сторонами , а третьи — до трикутник.
В трикотник кути у основания рвн. (на наш трикотник кут А доривню кут С).
В триплете посередине, проведенном к основанию, є сразу и по биссектрисе, и по высоте тройника.
Трикутник равносторонний.
Равносторонний трехколесный велосипед — трехглавый, у которого все стороны равны (рис. 14).
14).
Мощность равностороннего трикутника:
Чудеса силы трикутников.
В трехколесных велосипедах они являются оригинальными авторитетами, которые помогут вам успешно завершить работу, связанную с цими фигурками. Акты силы Але повторят его снова, добавив к ним щепотку этих замечательных черт:
1) Для прямоугольного трикотажа с 90º, 30º и 60º полками б Лежать на ребре куты под углом 30 градусов, на пути половины гипотенузы. И ножка дополнительная ножка б √3 раза (рис. 15 а ). Например, если катет b равен 5, то гипотенуза c обовъязково двери 10, а катет a дверь 5√3. 2) В прямоугольном трехколесном велосипеде с вырезами 90º, 45º и 45º, гипотенуза в √2 раза больше катета (рис. 15 б ). Например, если катети равен 5, то гипотеза 5√2. 3) Средняя линия трехколесного велосипеда до полупараллельного борта (рис. 4) В прямоугольном трехколесном велосипеде медиана, проведенная перед гипотенузой, половина гипотенузы (рис.9в) : м с = C/2. 5) Медиана трехколесного велосипеда, пересекающегося в одной точке, распределяется центральной точкой в соотношении 2: 1. Пройти от вершины до точки пересечения медианы в два раза больше, чем что точки в сторону медианы к 6) В прямоугольном трехколесном велосипеде середина гипотенузы є центром описываемого кола (рис. 15 д ). |
Знаки равноправия трехколесных велосипедов .
Первый признак рвения : Если у одного мотодельтаплана две стороны и разрез между ними, то два борта и разрез между ними — один и тот же мотодельтаплан, то есть тройки.
Еще один признак усердия : Если к нему пристрочен бортик и срез одного трицикла, то будем подгонять борта к срезу одного трикотажа, тогда это трициклы.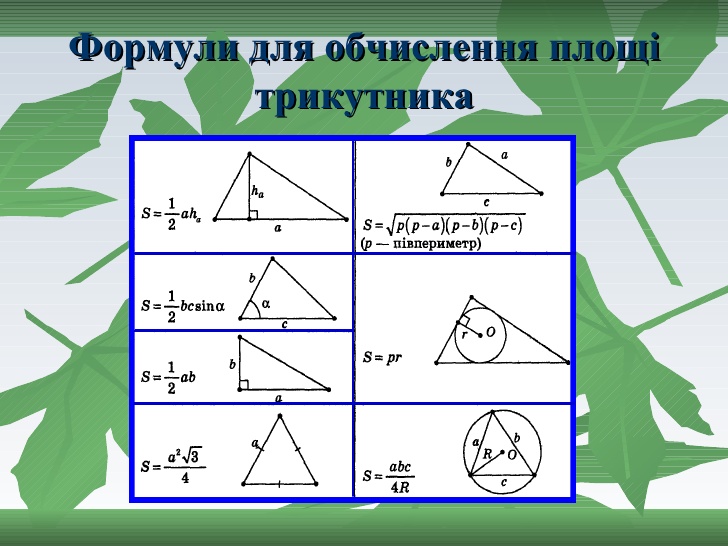
Третий признак невозмутимости : Если три стороны одного трехколесного велосипеда равны трем сторонам другого трехколесного велосипеда, то такие трехколесные велосипеды равны.
Неисправность трехколесного велосипеда.
Сторона обшивки любого трехколесного велосипеда меньше двух сторон.
Теорема Пифагора.
Прямоугольный трехколесный велосипед имеет квадрат гипотенузии суммы квадратов катетов:
c 2 = a 2 + b 2 .
Площадь трикотажа.
1) Площадь трицикла для второй половины работы выполняется сбоку к верху, проведенной к центру стороны:
ах
С = ——
2
2) Площадь трехколесного велосипеда составляет две половины двух сторон по пазухе разреза между ними:
1
С = — АВ АС · грех А
2
Трикутник, описания обведены кружком.
Коло называется вписанным в трикутник, если не получится дотронуться до всех сторон (рис. 16 и ).
Трикутник, арматура цвет.
Трикутник называется вписанным в коло, так как является виной всех вершин (рис. 17 а ).
Синус, косинус, тангенс, котангенс госкута прямоугольного трехколесного велосипеда (рис. 18).
синус голстрый кута х протылежный катет к гипотенузе.
Начните так: sin x .
косинус угол кута х трехколесный прямоугольный — цена доставки плотный ножка к гипотенузе.
То есть так: cos x .
тангенс гостры кута х — цена макетной ножки к плоской ножке.
Начните так: tg x .
котангенс гостри кута х — цена близкого участка к прототипу.
Начните так: ctg x .
Правила:
Катет, прототип кутку x , Добутку гипотенузи на грех x :
б = с Грех х
Нога, лежащая на кут x , Добутку гипотенузи на cos x :
а = с Cos х
Катет, напротив куту х , Добутку добавить еще одну ногу в тг х :
б = а Тг х
Нога, лёжа на кут x , Добутку добавить ещё одну ногу на ctg x :
a = b Ctg x .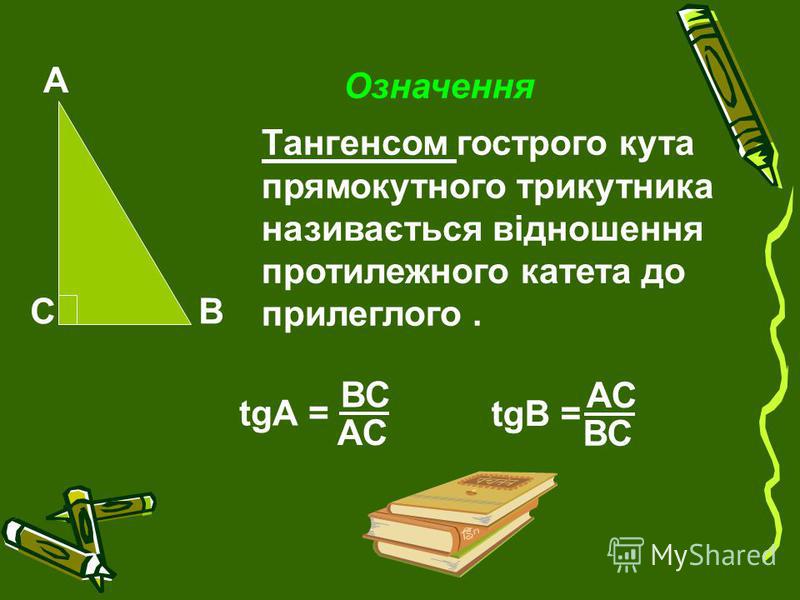
Для бе-подобного гост кута x :
sin (90° — х ) = Cos х
cos (90° — х ) = Sin х
Мощность: 1. В любом виде прямоугольного трицикла висота опускается из прямой куты (на гипотенузу), чтобы развести прямоугольный трикотаж, на три дополнительных трицикла.
Мощность: 2. Высота прямоугольного трехколесного велосипеда опущена до гипотенузы, до средней геометрической проекции катетов до гипотенузы (или средней геометрической тиши до гипотенузы).
Степень: 3. Катет для средней геометрической гипотенузы и проекции катета на гипотенузу.
Степень: 4. Катет противопоставлен под углом 30 градусов к стороне половины гипотенузы.
Формула 1.
Формула 2. , По гипотенузе; , Катети.
Сила: 5. В прямокишечном трицикле медиана проведена перед гипотенузой, второй половиной и второй половиной описываемого кола.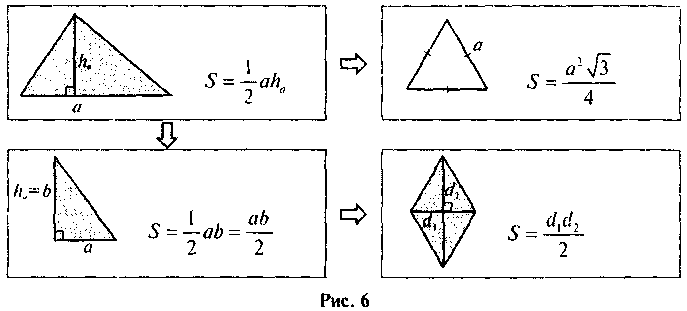


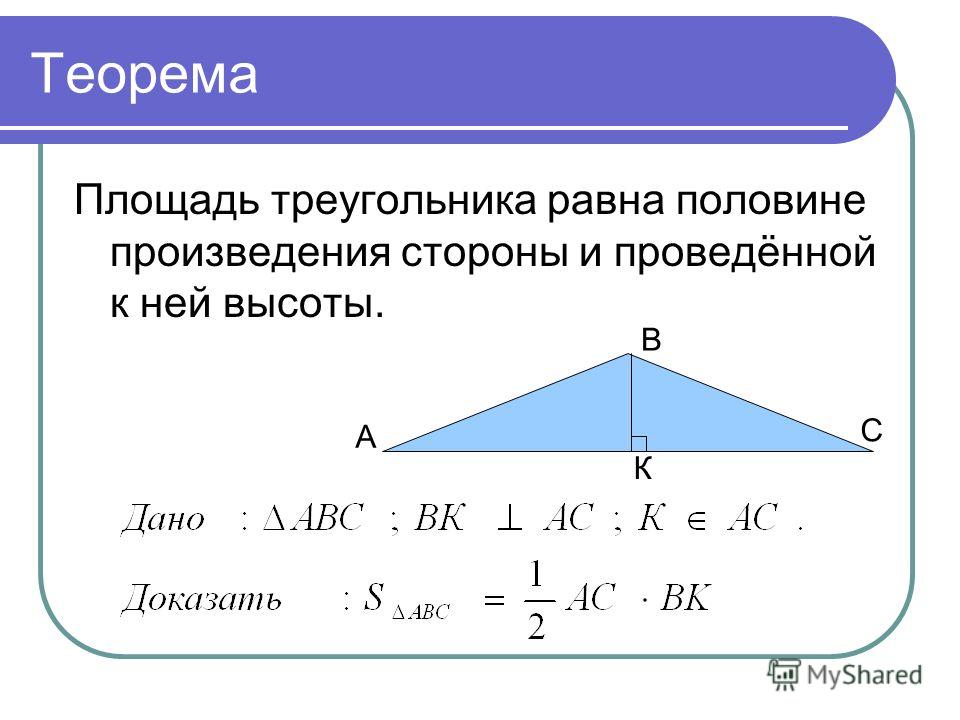
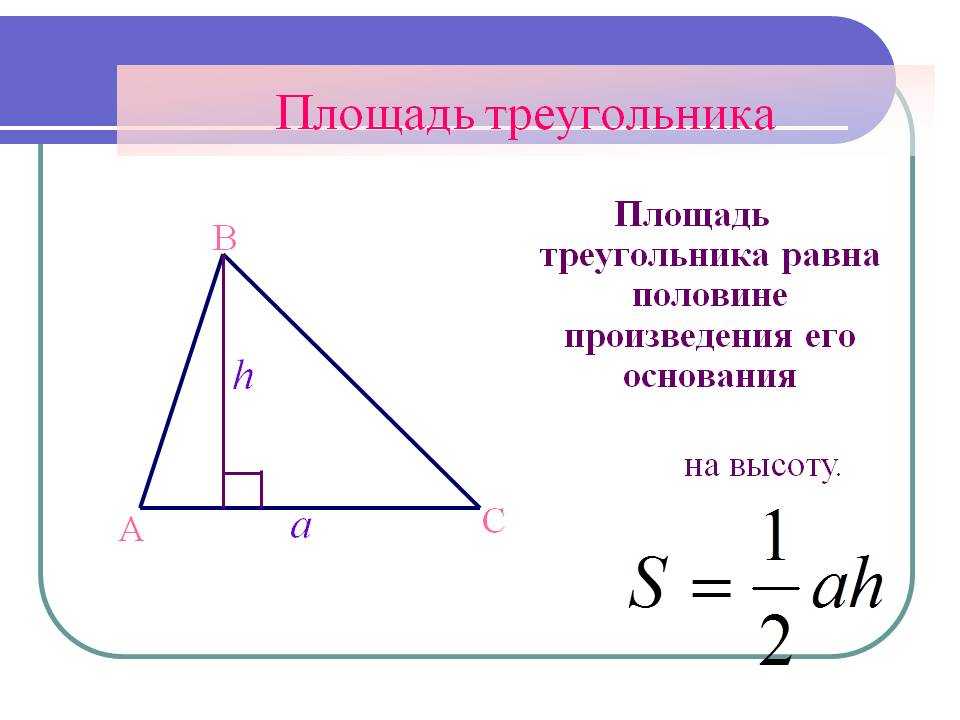
 также Формула 5
также Формула 5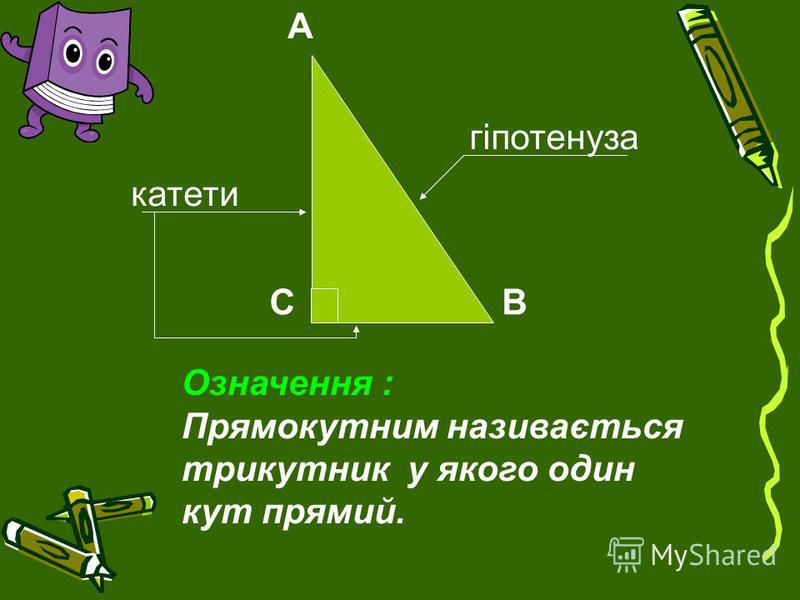 Звезды h = b/(2 tan(β/2)). В результате формула вернется к простой формуле 5, что вполне очевидно.
Звезды h = b/(2 tan(β/2)). В результате формула вернется к простой формуле 5, что вполне очевидно. Это видно в формуле 6. Следует умножить число и эталон на два, а затем добавить знак корня для двух чисел, можно принять и другой вариант этой формулы, который записывается через знак «равно».
Это видно в формуле 6. Следует умножить число и эталон на два, а затем добавить знак корня для двух чисел, можно принять и другой вариант этой формулы, который записывается через знак «равно».  Для размыва основание делится на два, є катетом, а с домашней стороны — гипотенузой.
Для размыва основание делится на два, є катетом, а с домашней стороны — гипотенузой.

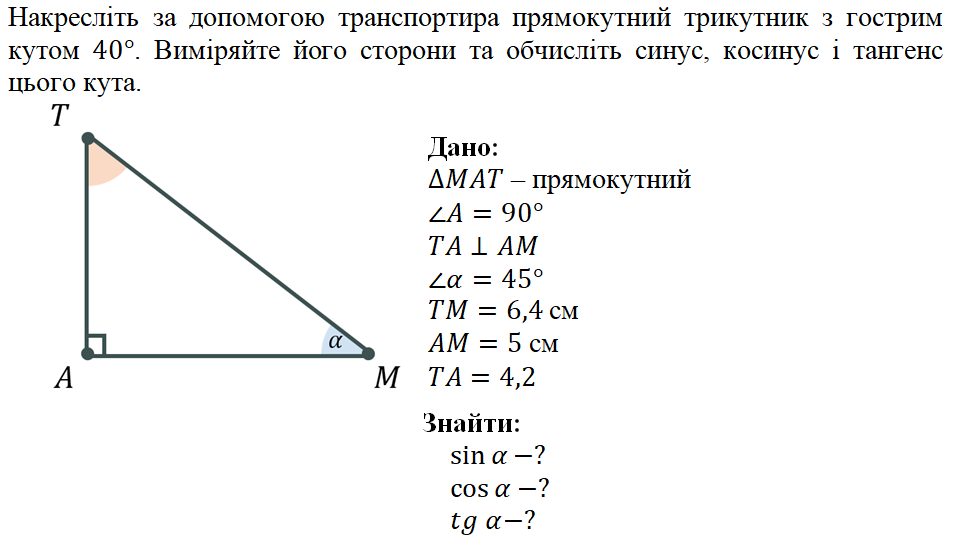
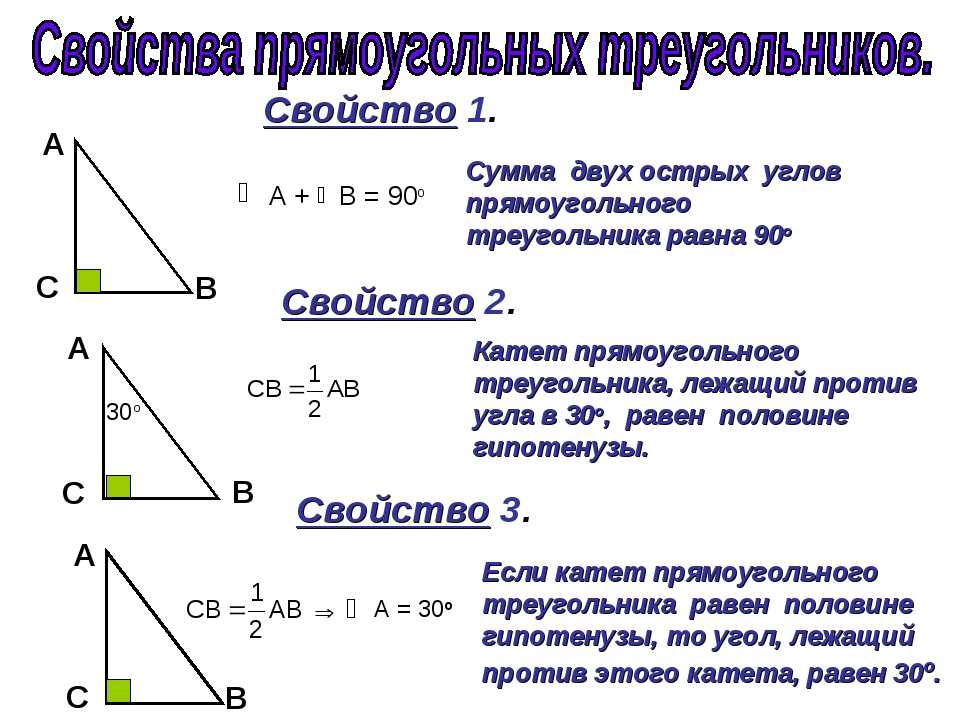
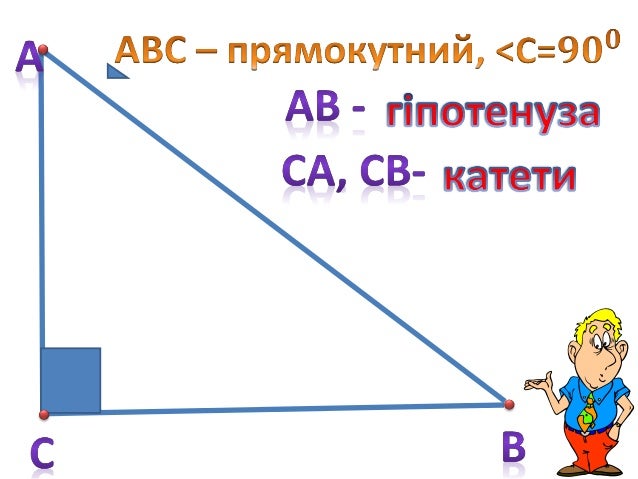 В результате очевидная простая и очевидная формула 5.
В результате очевидная простая и очевидная формула 5.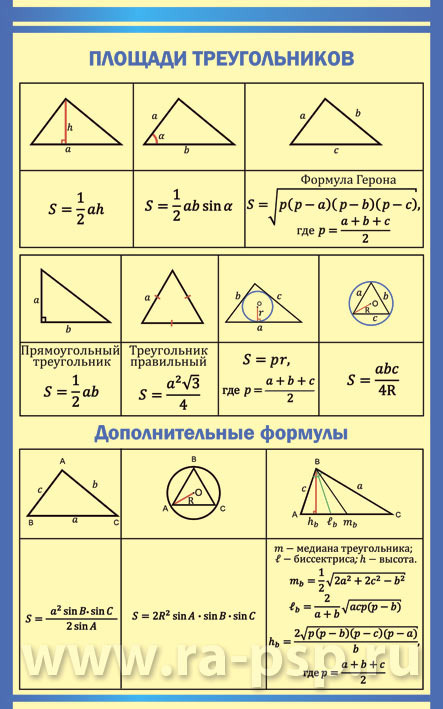 при заданиях нижний (2-й способ подключения)
при заданиях нижний (2-й способ подключения) Кожен прямоугольный трикутник на двух ногах (як обозначен для детеныша а = б или АС = ВС)
Кожен прямоугольный трикутник на двух ногах (як обозначен для детеныша а = б или АС = ВС)

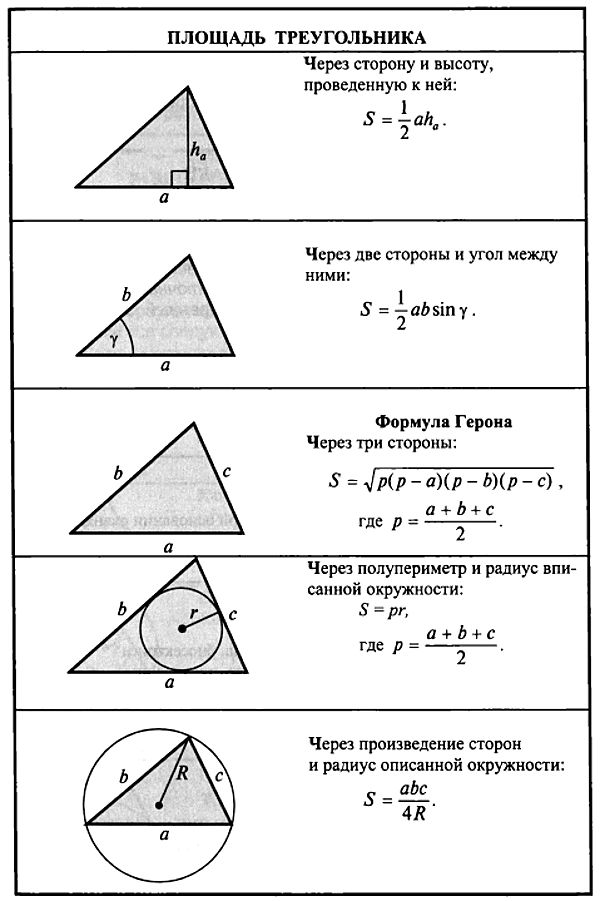
 9в)
9в)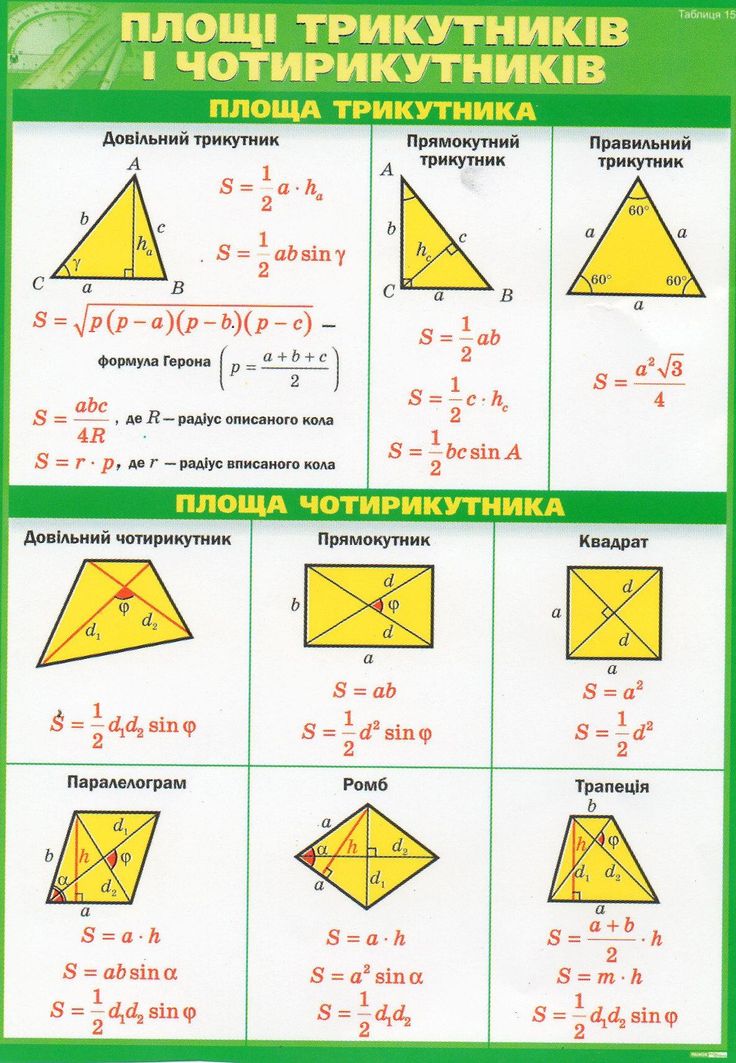 15 s ). Например, если сторона трехколесного велосипеда дорога 10, то она параллельна середине дороги 5.
15 s ). Например, если сторона трехколесного велосипеда дорога 10, то она параллельна середине дороги 5.