Прямокутний трикутник
Прямокутний трикутник — це трикутник, у якого один з кутів прямий, тобто дорівнює 90 градусам.
- Сторона, протилежна прямому куту називається гіпотенузою (на малюнку позначено як c або AB)
- Сторона, прилегла до прямого кута, називається катетом. Кожен прямокутний трикутник має два катета (на малюнку позначені як a і b або AC і BC)
Формули та властивості прямокутного трикутника
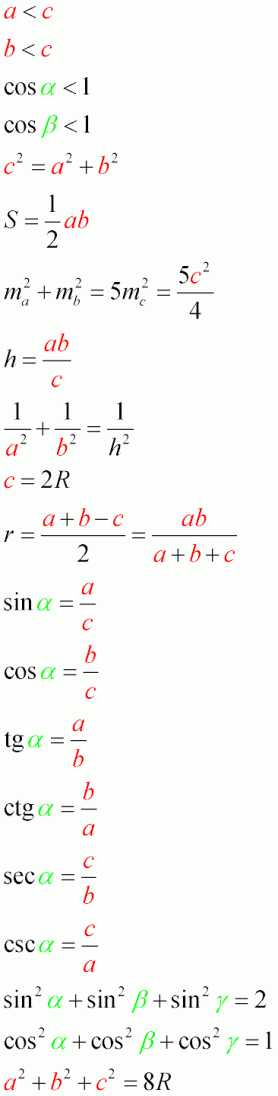Позначення формул: (див. малюнок вище)
a, b — катети прямокутного трикутника
c — гіпотенуза
α, β — гострі кути трикутникаS — площа
h — висота, опущена з вершини прямого кута на гіпотенузу
ma — медіана, проведена до сторони a з противолежащего кута (α)mc — медіана, проведена до сторони c з противолежащего кута (γ)
У прямокутному трикутнику будь-який з катетів менше гіпотенузи (Формули 1 і 2). Дана властивість є наслідком теореми Піфагора.
Косинус будь-якого з гострих кутів менше одиниці (Формули 3 і 4). Дана властивість випливає з попереднього. Так як будь-який з катетів менше гіпотенузи, то з співвідношення катета до гіпотенузі завжди менше одиниці.
Квадрат гіпотенузи дорівнює сумі квадратів катетів (теорема Піфагора). (Формула 5). Це властивість постійно використовується при вирішенні завдань.
Площа прямокутного трикутника дорівнює половині добутку катетів (Формула 6)
Сума квадратів медіан до катетiв, дорівнює п’яти квадратам медіани до гіпотенузі і п’яти квадратах гіпотенузи, ділених на чотири ( Формула 7). Крім зазначених, є ще 5 формул, тому рекомендується ознайомитися також і з уроком «Медіана прямокутного трикутника», в якому більш детально викладені властивості медіани.
Висота прямокутного трикутника дорівнює добутку катетів, поділеному на гіпотенузу (Формула 8)
Квадрати катетів обернено пропорційні квадрату висоти, опущеної на гіпотенузу (Формула 9). Дана тотожність також є одним з наслідків теореми Піфагора.Довжина гіпотенузи дорівнює діаметру (двом радіусам) описаного кола (Формула 10). Гіпотенуза прямокутного трикутника є діаметром описаної окружності. Це властивість часто використовується при вирішенні завдань.
Радіус вписаного в прямокутний трикутник кола можна знайти як половину від виразу, що включає в себе суму катетів трикутника мінус довжину гіпотенузи. Або як добуток катетів, поділений на суму всіх сторін (периметр) даного трикутника. (
Косинус кута А (α, альфа) у прямокутному трикутнику дорівнює відношенню прилеглого до даного кута катета до гіпотенузи (за визначенням синуса). (Формула 13)
См. також: Співвідношення між кутами і сторонами прямокутного трикутника вивчає Тригонометрія.
Площа рівнобедреного трикутника | Описание курса | Чотирикутник
profmeter.com.ua
Площа трикутника. Формули
Формул для обчислення площі трикутника в літературі можна знайти більше 10. Більшість з них можна застосувати в задачах з відомими сторонами та кутами трикутниками. Однак є ряд складних прикладів, в яких задано лише одна сторона і кути трикутника, або радіус описаного чи вписаного кола та ще одна характеристика. В таких випадках просту формулу застосувати не вдасться.
Задачі на трикутники вивчають в 7, 8 класі з вивчення простих властивостей, обчислення площі і периметра. В 9, 10 класі учні не тільки знають чим відрізняється прямокутний трикутник від рівнобедреного чи рівностороннього, а й з успіхом використовують теорему косинусів для знаходження сторін, формулу Герона, вміють розв’язати задачі про коло вписане або описане навколо трикутника. Але до всього потрібно приходити поступово не перевантажуючи пам’ять та можливості учнів. Тоді накопичені знання можна з успіхом застосувати до обчислення задач на трикутники будь-якої складності.
Наведені нижче формули дозволять розв’язати 95 відсотків задач в яких потрібно знайти площу трикутника. Перейдемо до розгляду поширених формул площі.
Розглянемо трикутник зображений на рисунку нижче
На рисунку і далі у формулах введені класичні позначення усіх його характеристик
a,b,c – сторонни трикутника,
R– радіус описаного кола,
r – радіус вписаного кола,
h[b],h[a],h[c] висоти, проведені відповідно до сторін a,b,c.
alpha, beta,hamma – кути при вершинах.
Основні формули площі трикутника
1. Площа трикутника рівна половині добутку сторони трикутника на висоту, опущену до цієї сторони. На мові формул це визначення можна записати так
Таким чином, якщо відомо сторону та висоту, опущену до неї, то площу знайде кожен школяр.
До речі з цієї формули можна вивести одну корисну залежність між висотами
2. Якщо врахувати, що висота трикутника через сусідню сторону виражається залежністю
то з першої формули площі випливають однотипні другі
Уважно погляньте на формули – їх легко запам’ятати, оскільки в добутку фігурує дві сторони і кут між ними. Якщо правильно позначити сторонни і кути трикутника, то отримаємо дві сторонни a,b і кут пов’язаний з третьою С (hamma).
3. Для кутів трикутника справедливе співвідношення
Залежність дозволяє застосовувати в обчисленнях наступну формулу площі трикутника
Приклади на дану залежність зустрічаються вкрай рідко, але пам’ятати, що є така формула Ви повинні.
4. Якщо відома сторона і два прилеглі кути, то площа знаходиться за формулою
5. Формула площі трикутника через сторону і котангенси прилеглих кутів
Перестановкою індексів можете отримати для інших сторін.
6. Наведена нижче формула площі використовується в задачах коли вершини трикутника задані на площині координатами . В цьому випадку площа трикутника рівна половині визначника, взятого за модулем.
7. Формулу Герона застосовують в прикладах з відомими сторонами трикутника. Спочатку знаходять півпериметр трикутника
а далі визначають площу за формулою
або
Її досить часто використовують в коді програм калькуляторів.
8. Якщо відомі всі висоти трикутника то площу визначають за формулою
Вона складна для обчислення на калькуляторі, проте в пакетах MathCad, Mathematica, Maple площа знаходиться на «раз два».
9. Наступні формули вклячають відомі радіуси вписанного та описанного кіл (див. роисунок).
Зокрема, якщо відомо радіус і сторонни трикутника, чи його периметр то площа обчислюється згідно формули
10. У прикладах де задано сторони і радіус (діаметр) описаного кола площу знаходять за формулою
11. Наступна формула визначає площу трикутника через сторону і кути трикутника.
Ну і наостанок – часткові випадки:
Площа прямокутного трикутника з катетами a і b рівна половині їх добутку
Формула площі рівностороннього (правильного) трикутника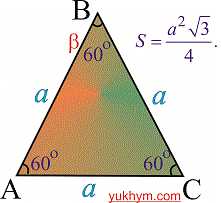 
рівна одній четвертій добутку квадрату сторони на корінь з трійки.
Приклад. Сторони трикутника рівні 3, 5, 6 см. Знайти площу трикутника.
Розв’язок: Застосуємо формулу Герона, для цього спочатку знайдемо півпериметр
Підставляємо в формулу площі
Відповідь: Площа трикутника рівна 7.48 сантиметрів квадратних.
Завантажити усі наведені формули площі трикутника Ви можете за наступним посиланням. Роздруковуйте їх та використовуйте в навчанні.
Схожі матеріали:
Якщо матеріал був корисний Вам — поділіться посиланням з друзями.
yukhym.com
Прямоугольный треугольник
Прямоугольный треугольник — это треугольник, у которого один из углов — прямой, то есть равен 90 градусам.
- Сторона, противолежащая прямому углу называется гипотенузой (на рисунке обозначена как c или AB)
- Сторона, прилежащая к прямому углу, называется катетом. Каждый прямоугольный треугольник имеет два катета (на рисунке обозначены как a и b или AC и BC)
Формулы и свойства прямоугольного треугольника
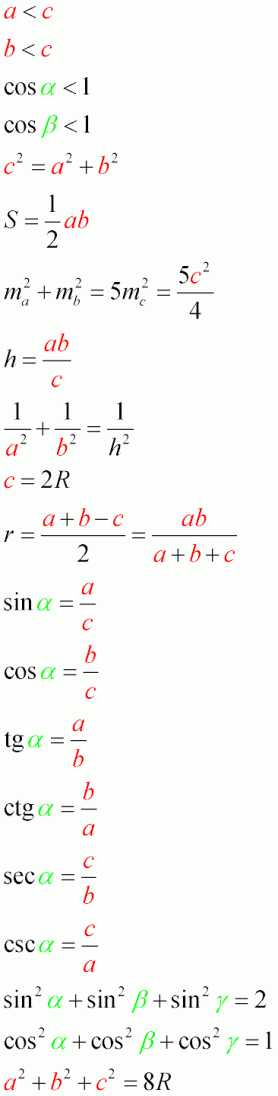Обозначения формул:(см. рисунок выше)
a, b — катеты прямоугольного треугольника
c — гипотенуза
α, β — острые углы треугольника
S — площадь
h — высота, опущенная из вершины прямого угла на гипотенузу
ma— медиана, проведенная к стороне a из противолежащего угла (α)
mb — медиана, проведенная к стороне b из противолежащего угла (β)
mc — медиана, проведенная к стороне c из противолежащего угла (γ)
В прямоугольном треугольнике любой из катетов меньше гипотенузы (Формулы 1 и 2). Данное свойство является следствием теоремы Пифагора.
Косинус любого из острых углов меньше единицы (Формулы 3 и 4). Данное свойство следует из предыдущего. Так как любой из катетов меньше гипотенузы, то из соотношение катета к гипотенузе всегда меньше единицы.
Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора). (Формула 5). Это свойство постоянно используется при решении задач.
Площадь прямоугольного треугольника
равна половине произведения катетов (Формула 6)Сумма квадратов медиан к катетам, равна пяти квадратам медианы к гипотенузе и пяти квадратам гипотенузы, деленных на четыре (Формула 7). Кроме указанной, есть еще 5 формул, поэтому рекомендуется ознакомиться также и с уроком «Медиана прямоугольного треугольника», в котором более подробно изложены свойства медианы.
Высота прямоугольного треугольника равна произведению катетов, деленному на гипотенузу (Формула 8)
Квадраты катетов обратно пропорциональны квадрату высоты, опущенной на гипотенузу (Формула 9). Данное тождество также является одним из следствий теоремы Пифагора.
Длина гипотенузы равна диаметру (двум радиусам) описанной окружности (Формула 10). Гипотенуза прямоугольного треугольника является диаметром описанной окружности. Это свойство часто используется при решении задач.
Радиус вписанной в прямоугольный треугольник окружности можно найти как половину от выражения, включающего в себя сумму катетов этого треугольника минус длину гипотенузы. Или как произведение катетов, деленное на сумму всех сторон (периметр) данного треугольника. (Формула 11)
Синус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению противолежащего данному углу катета к гипотенузе (по определению синуса). (Формула 12). Данное свойство используется при решении задач. Зная величины сторон, можно найти угол, который они образуют.
Косинус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению прилежащего данному углу катета к гипотенузе (по определению синуса). (Формула 13)
См. также Соотношения между углами и сторонами прямоугольного треугольника изучает Тригонометрия.
Содержание главы:
Подобие треугольников. Использование в задачах | Описание курса | Прямоугольный треугольник
profmeter.com.ua
Как найти площадь прямого треугольника 🚩 Математика
Автор КакПросто!
Треугольник – это простейший многоугольник, имеющий три вершины и три стороны. Треугольник, один из углов которого является прямым, называется прямоугольным. Для прямоугольных треугольников применимы все формулы для треугольников общего вида. Однако их можно видоизменить, учитывая свойства прямого угла.
Статьи по теме:
Инструкция
Основная формула для нахождения площади треугольника через основание и высоту выглядит следующим образом: S = 1/2 * b * h, где b – это сторона треугольника, а h – высота треугольника. Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. Для прямоугольного треугольника высота к катету b совпадает с катетом а. Таким образом, вы получите формулу для вычисления площади треугольника с прямым углом: S = 1/2 * a * b. Рассмотрите пример. Пусть в прямоугольном треугольнике а = 3, b = 4. Тогда S = 1/2 * 3 * 4 = 6. Посчитайте площадь того же треугольника, но теперь пусть известен только один катет b = 4. А также известен угол α, tg α = 3/4. Тогда из выражения для тригонометрической функции тангенс угла α выразите катет a: tg α = a/b => a = b * tg α. Подставьте это значение в формулу для вычисления площади прямоугольного треугольника и получаем: S = 1/2 * a * b = 1/2 *b^2 * tg α = 1/2 * 16 * 3/4 = 6.Рассмотрите как частный случай вычисление площади равнобедренного прямоугольного треугольника. Равнобедренный треугольник – это треугольник, в котором две стороны равны между собой. В случае прямоугольного треугольника получается a = b. Запишите теорему Пифагора для этого случая: c^2 = a^2 + b^2 = 2 * a^2. Далее подставьте это значение в формулу вычисления площади следующим образом: S = 1/2 * a * b = 1/2 * a^2 = 1/2 * (c^2 / 2) = c^2 / 4.
Посчитайте площадь равнобедренного прямоугольного треугольника. Пусть гипотенуза равна 4 * √2. Тогда площадь треугольника вычисляется как S = c^2 / 4 = 16 * 2 / 4 = 8.
Если известны радиусы вписанной r и описанной R окружностей, то площадь прямоугольного треугольника вычисляется по формуле S = r^2 + 2 * r * R. Пусть радиус вписанной в треугольник окружности r = 1, радиус описанной вокруг треугольника окружности R = 5/2. Тогда S = 1 + 2 * 1 * 5 / 2 = 6.
Видео по теме
Полезный совет
Радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы: R = c / 2. Радиус окружности, вписанной в прямоугольный треугольник, находится по формуле r = (a + b – c) / 2.
Совет полезен?
Распечатать
Как найти площадь прямого треугольника
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Как найти площадь прямоугольного треугольника
Автор КакПросто!
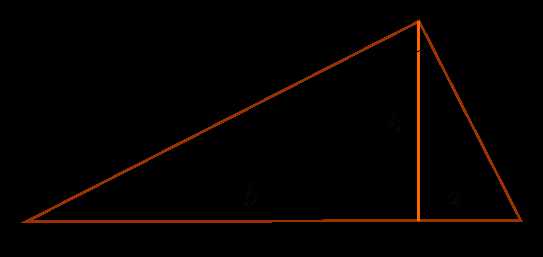
Для начала договоримся об обозначениях. Катетом называют сторону прямоугольного треугольника, которая прилежит к прямому углу (т.е. составляет с другой стороной угол 90 градусов). Длины катетов условимся обозначать a и b. Величины острых углов прямоугольного треугольника, противолежащих катетам, назовём A и B соответственно. Гипотенузой называют сторону прямоугольного треугольника, которая противолежит прямому углу (т.е. находится напротив прямого угла, с другими сторонами треугольника образует острые углы). Длину гипотенузы обозначим через с. Искомую площадь обозначим через S.
Статьи по теме:
Инструкция
Определите, какие величины рассматриваемого прямоугольного треугольника вам известны. Исходя из этого, выберите подходящее выражение. Вычислите площадь прямоугольного треугольника, как половину произведения катетов, т.е. S=0.5*a*b в том случае, если вам известны их длины. Расчитайте площадь по формуле S = b*c*sin(A)/2, если вам задан один из катетов (b), гипотенуза (с), а так же угол между ними (A). Эта формула справедлива не только для прямоугольного треугольника, но для любого треугольника вообще.Примените формулу S = (a^2)/(2*tg(A)) в том случае, если вам задан только один из катетов (a), но также известен и противолежащий этому катету угол (A). Знаком «^2» обозначена операция возведения в квадрат.
Используйте формулу S=(a^2)*tg(B)/2 d случае, если вам задан только один из катетов (a), но также известен и прилежащий этому катету угол (B).
Вычислите площать по формуле S = a*sqrt(c^2 – a^2)/2, если вам известны величины катета (a) и гипотенузы (c). Операцию sqrt обозначает квадратный корень.
Воспользуйтесь выражением S = (c^2)*sin(A)*cos(A)/2, eсли задана гипотенуза (c) и один из острых углов (A).
Видео по теме
Источники:
- «Пособие по математике для поступающих в вузы», под ред. Г.Н. Яковлева, 1982.
Совет полезен?
Распечатать
Как найти площадь прямоугольного треугольника
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Найти площадь треугольника
Треугольник это плоская фигура, которая имеет три стороны и три угла. Сумма всех трех углов, равна 180 градусов.
Высота треугольника это — опущенный перпендикуляр из вершины угла на противоположенную сторону или ее продолжение, которую в этом случае, называют основанием.
Что бы найти площадь треугольника,
для этого надо основание умножить на высоту и разделить на два
1. Площадь разностороннего треугольника
h — высота треугольника
a — основание
Формула площади треугольника (S):
2. Площадь треугольника с тупым углом
h — высота треугольника
a — основание
Формула площади треугольника с тупым углом (S):
Формулы для треугольника:
- Подробности
- Автор: Сергей Кондратов
www-formula.ru