Формула площадь фигуры 3 класс: Площадь фигур. Площадь прямоугольника — урок. Математика, 3 класс.

Площадь. Нахождение площади. 3-й класс

Тип урока: урок закрепления изученных знаний, урок знакомства с новой темой и мультимедиа-ресурсом.

Вид урока: проблемный урок с элементами исследования, с элементами игровой деятельности.

Методы обучения: проектно-исследовательский метод, методы наблюдения, конструирования, беседы, тестирования, контроля и самоконтроля. Метод стимулирования и авансирования, эмоционального воздействия, наглядности.

Материалы и оборудование: Учебник для общеобразовательных учреждений (в двух частях) под редакцией М.И. Моро, М.А. Бантовой, Г.В. Бельтюковой, С.И. Волковой, С.В. Степановой «Математика», 3 класс, серия «Школа России». Издательство «Просвещение», 2010, С. 55. Рабочие тетради; детские ноутбуки; медиапроектор, компьютер, экран; тесты, карточки с формулами нахождения периметра и площади прямоугольника, индивидуальные геометрические фигуры и картинка с «Карандашом», палетки.

Продолжительность: урок 45 минут.

Авторский медиапродукт: презентация к уроку (25 минут).

Цель урока: Создание условий для становления и развития психических функций, способностей, мотивационных установок, творческого исследовательского мышления через вовлечение учащихся в активную учебно-исследовательскую деятельность на уроке математики.

Межпредметные связи: урок окружающего мира, урок русского языка и технологии.

	Слайд 1 Орг. момент Учитель читает стихи про карандаш.
	Слайды 2-6 Устный счёт «Собери букет», «Испеки пирог». (таблица умножения на 8, 9)
	Слайд 7 – Ребята, какая я невнимательная, забыла написать тему сегодняшнего урока. Как быть? Слайд 8
	– Прочитайте задание на слайде. – Открываем тетрадь. Прочитайте внимательно задания теста. – Выполните все задания теста. Время – 5минут! – Так какая тема сегодняшнего урока?
	Слайд 9 – Совершенно верно, тема сегодняшнего урока: «Площадь прямоугольника». – Перед нами стоят такие задачи: 1) Выяснить значения слова площадь; 2) Повторить способы сравнения площади фигур и познакомиться с новым способом; 3) Сформулировать правило нахождения площади прямоугольника и вывести формулу; 4) Уметь решать задачи на нахождение площади прямоугольника.
	Слайд 10 – Какие ассоциации у вас возникают при слове «площадь»? Что сразу приходит на ум? – Пожалуйста, поделитесь своими мыслями. Учитель заслушивает все варианты ответа. (площадь в центре города, строительная площадка, площадка во дворе для игр, спортивная площадка, лестничная площадка, площадь обоев, площадь стола, площадь футбольного поля, площадь поля, засеянного какими-либо культурами и др.)
	Слайд 11 – Посмотрите, что изображено на слайде? – Да, это Красная площадь – центральная площадь Москвы. Возникновение Красной площади относится к концу 15 века, когда по приказу царя Ивана III были снесены деревянные постройки вокруг Кремля, угрожавшие постоянными пожарами. На их месте была организована площадь для мелкой торговли. Первоначально она так и называлась – Торговая. Красной площадь стали называть только в 17 веке. – А это что за площадь? Это одна из центральных площадей города Санкт-Петербурга. Она называется Сенатская площадь. Сенатская площадь была названа так после размещения на ней правительственного учреждения Сената. Сенатская площадь является одной из самых старых площадей Санкт-Петербурга. – Все узнали центральную площадь нашего города. Кто знает, как она называется? Совершенно верно, это площадь Ленинского комсомола. – Почему её так назвали? В каком году была построена площадь? Какие важные здания находятся на этой площади? – Обратитесь за помощью к родителям, бабушкам и дедушкам, справочной литературе, сети Интернет, чтобы найти ответы на эти вопросы. А на ближайшем уроке окружающего мира мы вернёмся к этой теме.
	Слайд 12 – Давайте прочитаем значения слова «площадь». Два ученика по слайду зачитывают по просьбе учителя.
	Слайд 13 – Заглянем в толковый словарь русского языка В.И. Даля. – Внимательно прочитайте значение слова «площадь». Вдумайтесь в смысл!
	Слайд 14 – Какие способы измерения площади фигур вам известны? Учитель заслушивает все варианты ответа.
	Слайд 15 – Действительно, существует несколько способов: визуально, т.е. на глаз, способ наложения фигур и с использованием мерок.
	Слайд 16 – Сравните на глаз площади треугольников. Что вы можете о них сказать? – Какова площадь круга: больше или меньше?
	Слайд 17 – Что можете сказать о площади квадратов? – Почему площадь зелёного квадрата меньше? (полностью помещается в розовом квадрате) – Можно ли утверждать, что площадь треугольника больше площади самого маленького квадрата? – Почему?
	Слайд 18 – Ещё один способ: подсчёт количества мерок, уложившихся в той или иной фигуре. – Сколько мерок уложилось в жёлтом прямоугольнике? – Сколько мерок уложилось в розовом прямоугольнике? – Сколько мерок уложилось в зелёном прямоугольнике? – Площадь какого прямоугольника больше? – Почему? (уложилось большее количество мерок) – Что получится, если я буду использовать разные мерки для сравнения площадей этих прямоугольников: квадраты, круги, треугольники, овалы и т.д.?
	Слайд 19 – Прочитаем вывод хором! Учитель говорит о том, что пришло время отдохнуть, напоминает о взаимной вежливости.
	Слайд 20 Физ.минутка
	Слайд 21 Учитель зачитывает по слайду. Гиперссылка = нажать на слово «единицы». – Если данная мерка – это один квадратный сантиметр, то чему тогда равна площадь каждого прямоугольника? (ответы детей) Гиперссылка = нажать на слово «мерка».
	Слайд 22 – Есть ли такие единицы измерения площади, как квадратный дециметр, квадратный метр?Учитель заслушивает все варианты ответов. – Об этом мы узнаем на ближайших уроках математики.
	Слайд 23 лежат конверты. Откройте их, достаньте геометрические фигуры. – Прочитайте задание на слайде. – Работа в парах: нужно сравнить площади этих фигур. – Как это сделать? Время для работы – одна минута!
	– Ребята, вы молодцы! – Есть такое приспособление в математике!Слайд 24 Учитель зачитывает по слайду, раздаёт всем палетки. – Измерьте при помощи палетки площади данных фигур. – Что вы заметили?
	Слайд 25 Дети сравнивают свои ответы с данным. – Молодцы!
	Слайд 26 – Прочитайте вывод.

План-конспект урока по математике (3 класс) по теме: Математика 3 класс Нахождение площади фигуры

Урок математики 3 класс.

Тема: ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА.

Тип урока: урок изучения нового и первичного закрепления новых знаний

Цели урока:

1. Обеспечить усвоение детьми способа нахождения  площади прямоугольника.
2. Способствовать формированию ключевых компетентностей: познавательной, информационной, коммуникативной, развивающей.

Задачи урока:

Образовательные:

1. Вывести правило вычисления площади прямоугольника.
2. Актуализировать знания о признаках и свойствах геометрических фигур.
3. Закреплять умение решать задачи на приведение к единице, записывая условие в таблицу.
4. Способствовать совершенствованию вычислительных навыков.

Развивающие:

1. Способствовать развитию основных операций мышления (сравнение, обобщение, умение делать выводы на основе полученной информации).
2. Развитие умения анализировать и находить пути решения поднимаемой проблемы.
3. Формирование основных компонентов УУД (умение ставить учебную задачу, обобщать, делать выводы)

Воспитательные:

4. Содействовать повышению  интереса к чтению книг.
5. Формировать навыки самоанализа.

Технологии: игровая, информационно-компьютерная, развивающая, образовательная (выбор оптимальной модели обучения для данных конкретных условий).

Методы: словесные, наглядные, деятельностные, практические, (выполнение учащимися практических действий)

Оборудование:

1. Презентация  Рower Point.
2. Вееры с цифрами 25 штук,
3. Конверты (по 1 шт. на парту) 15 штук.
4. Палетки 15 штук.
5. Прямоугольник 2см х6см  15штук.
6. Карточки – помогайки:  1 см2, Sпр.=а х в,

единицы длины, таблица умножения, порядок действий.

7. Текст задачи 15 штук.
8. Мартышка 1 штука.
9. Корзина 1 штука.
10. Бананы (жёлтые и зелёные) по 2 штуки 25 штук.

Ход урока.

1. Организационный момент.
2. Самоопределение.

1. Поднимите руки те, кто из вас любит сказки?

Сегодня к нам на урок придут герои одной очень известной сказки. А чтобы узнать  автора этой сказки  —  надо разгадать кроссворд.

3. Устный счёт.

А) Отгадайте кроссворд.

Возьмите в руки вееры, показывайте только  одни ответы:

1. Сколько раз по 4 содержится в 12 (три)
2. На сколько надо разделить 49,  чтобы получить 7 ( на семь) 
3. 36 уменьши в 6 раз (шесть)
4. 53 уменьши на 48 (пять)
5. 4 увеличь в 2 раза (восемь)

2. Кто автор этой сказки? (Григорий Остер)
3. Кто догадался, как называется сказка?

 («38 попугаев»)

Б) Геометрический материал.

1.  Какого героя вы видите на экране? (Удава)

Он принёс вам следующее задание. Рассмотрите фигуры.

2. Какая из данных фигур лишняя? (треугольник)
3. Почему? (все остальные – четырехугольники)
4. Теперь какая фигура лишняя? (№1 – не прямые углы),
5. У какой из этих фигур все стороны равны? (квадрат)
6. Как называется данная фигура? (прямоугольник)
7. Какие свойства прямоугольника вы знаете? (4 угла, 4 стороны, углы прямые, противоположные стороны равны

В) Единицы измерения величин.

Какие единицы измерения длины  вы знаете? (см, мм, дм, м)

Герои мультфильма решили поиграть.  Чтобы узнать кому какой мяч достался, расставим величины в порядке возрастания. (мм, см, дм, м)

Г) Вырази. Герои сказки принесли для вас ещё  интересное задание:

1. Толщина кожи слона составляет 2 см 5 мм. Сколько это будет мм? (25мм)
2. У некоторых обезьян хвост может быть длиннее их тела. Длина хвоста обезьяны 65 см. Сколько это дм и см? (6 дм 5 см)
3. Длина обычного удава в природе 3 м. Сколько это дм? (30 дм)
4. Длина тела самых мелких попугайчиков не более 1 дм. Сколько это см? (10 см)

4. Подводящий диалог.

Д) Найди пару. Обезьяна, Попугай и Слонёнок не могут справиться с заданием. Давайте им поможем.

Рассмотрите фигуры.

4. Что общего у этих фигур? (Фигуры разбиты на равные квадраты, эти фигуры прямоугольники)
5. Какая из данных записей подходит к первому прямоугольнику?(3х4)

---

Фигура №1.

---

---

6.  Сколько квадратов в первом столбце?(3)

---

---

7.  Сколько квадратов в строке?(4)

---

---

8. Сколько раз по 3 взяли? (4)

---

9. Докажите.  (3 квадрата в одном  столбце и 4 квадрата в строке)
10. Чему равно произведение? Покажите ответ на веерах.
11. Что такое 12 в этом прямоугольнике? (количество одинаковых квадратов в прямоугольнике)

12. Какая запись подходит ко второй фигуре? (2 х 3). Чему равно произведение? (6)

13. Какая запись подходит к третьей  фигуре? (2 х 5). Чему равно произведение? (10)

14. Если мы будем знать площадь каждого из этих квадратиков, что мы сможем узнать? (площадь прямоугольника)
15. Кто догадался, какая тема сегодняшнего урока? («Нахождение площади прямоугольника»)

5. Определение темы.

Сегодня мы должны научиться находить площадь прямоугольника удобным и быстрым способом.

16. Зачем нам надо уметь находить площадь прямоугольника? (поклеить обои, покрасить пол, поклеить потолок).
17. Какие единицы площади вы знаете?   (см2)
18. Что значит квадратный сантиметр? (площадь квадрата, сторона которого 1 см)

6. Открытие новых знаний.

1. Практическая работа в парах.

Откройте конверты, достаньте прямоугольник и палетку. ( Прямоугольник 2см на 6 см)

19. Наложите палетку и  посчитайте сколько квадратных см укладывается в прямоугольнике? (12 см2 )
20. Сколько полос с квадратами в прямоугольнике? (2 полосы)
21. Сколько квадратов в каждой полосе? (6)
22. Как узнать сколько всего квадратов? (по 2 взяли 6 раз, т.е 2х6)
23. Что такое 6 см в прямоугольнике? (длина)
24. Что такое 2 см? (ширина)
25. Как нашли площадь? (длину умножили на ширину)

Записываем в тетрадь. 1 ученик на доске.

№1.

6 х 2 = 12 (см2)

Ответ: 12 см2.

26. А Слонёнок нашёл площадь этого прямоугольника  вот так: по 2 взял 6 раз.

27. Как вы думаете  можно ли таким способом найти площадь прямоугольника?
28. Какой вывод можно сделать? Как найти площадь? (длину умножить на ширину или ширину умножить на длину)

2. Нахождение площади (формула)

Если длина прямоугольника  а, ширина  в.

29. Как узнать площадь прямоугольника?

В математике принято площадь обозначать буквой S. И сегодня вы сами вывели формулу нахождения площади прямоугольника.

Давайте проверим. Откройте учебник с.54, прочитайте правило.

---

Для нахождения площади прямоугольника достаточно измерить его длину и ширину в см и полученные числа перемножить. Площадь прямоугольника будет выражена в квадратных см.

---

Формулу записываем в тетрадь.

7. Физ. минутка

Под музыку из мультфильма.

8. Первичное закрепление материала.

№ 3 (1) Прочитайте задание. Начертите прямоугольник, длина которого 9 см, а ширина 2 см.

30. Найдите площадь прямоугольника , пользуясь формулой.
31.  Запишите решение в тетрадь (один ученик  диктует).

9 х 2 = 18 (см2)

Ответ: 18 см2.

А обезьяна нашла площадь по-другому.  Прочитайте 2 х 9=18 (см2 )

32. Как вы думаете, правильно  ли она нашла площадь ?

9. Решение задачи.

33. Что больше всего любят есть обезьяны? (бананы). Обезьянка приготовила для вас задачу.

20 кг бананов разложили в 4 одинаковых ящика. Сколько потребуется таких ящиков, чтобы разложить 30кг бананов.

34. Что известно в задаче?  ( 20 кг бананов разложили в 4 одинаковых ящика)
35. Что такое 20кг? (общая масса)
36. Сколько было ящиков? (4)
37. Что известно про ящики? (одинаковые)
38. Нам известна масса 1 ящика? (нет)
39. Что надо узнать в задаче? (сколько потребуется ящиков, чтобы разложить 30 кг бананов)
40. Что такое 30 кг? (общая масса)
41. Количество ящиков? (не знаем, но все ящики одинаковые)
42. Каким действием найти массу одного  ящика? (делением)
43. Каким действием можно узнать количество  ящиков, чтобы разложить 30 кг бананов? (делением)

Запишите решение самостоятельно.

Проверка с доской.

10.  Самостоятельная работа с. 73 №5

1в. – 1 строчка

2в. – 2 строчка

2 ученика за доской – потом проверяют.

44. Поднимите руки, кто решил примеры без ошибок?
45. Кто допустил ошибки?

11.  Итог урока.

46. Что нового узнали на уроке? (как вычислить площадь прямоугольника)
47. Как найти площадь прямоугольника? (надо длину умножить на ширину)
48. Кто написал сказку «38 попугаев»? (Григорий Остер)

Он написал ещё много увлекательных книг: «Середина сосиски», «Книга о вкусной и здоровой пище людоеда», «Вредные советы и другие истории», которые я рекомендую вам прочитать.

12. Домашнее задание

с. 55  № 4, 7. Правило с. 73  наизусть.

13.  Рефлексия.

Герои сказки прощаются с нами.

Кому было сегодня на уроке легко и интересно положите в корзину Обезьяны жёлтый банан, а кому было трудно – зелёный.

Урок окончен!

Учебно-методический материал по математике (3 класс) на тему: Задачи на нахождение площади и периметра геометрических фигур

Задачи на нахождение площади и периметра

геометрических фигур

                                                                                 Составила: 

учитель начальных классов

МКОУ СОШ №1  имени А.М.Горького

городского округа город Фролово

Кислова Людмила Борисовна

                                                                                   

                                                               

                                                               г. Фролово– 2014 год

I уровень.

1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.

2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.

3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.

4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.

5.Длина прямоугольника 8 дм, ширина 5 дм. Найди его площадь.

6.Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.

7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.

8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.

9.Длина стороны квадрата 6 см. Узнай площадь.

10.Вычисли периметр квадрата со стороной  4 см.

11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.

12.Длина  прямоугольника равна 5 дм, ширина — на 4 см меньше.  Найдите Р и S этого прямоугольника. 

13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.

14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.

 15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше. Вычисли его периметр.

16.Сторона квадрата равна 3 см. Чему равен периметр?

17.Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?

18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?

19.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.

20.Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.

21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?

II уровень

1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.

2.Длина  прямоугольника равна 5 дм, ширина — на 4 см меньше.  Найдите Р и S этого прямоугольника. 

3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше.  Найди Р и S.

4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.

5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.

6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.

7.Периметр квадрата равен 32 см. Чему равна его сторона?

8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.

9.Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.

10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника. 

11.Периметр прямоугольника равен 54 м.  Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.

12.Найдите площадь квадрата, периметр которого равен 360 мм.

13.Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?

14.Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами  2 см и 6 см.

15.Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?

16.Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?

17.У какой фигуры площадь больше и на сколько: у квадрата со стороной  4см  или у прямоугольника со сторонами 2 см и 6 см?

18.Периметр прямоугольника равен 54 м. Найди площадь этого прямоугольника, если одна его сторона равна 18 м.

19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.

20.Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.

Использованы ресурсы сети Интернет

Урок 22. площадь прямоугольника — Математика — 3 класс

Математика, 3 класс

Урок №22. Площадь прямоугольника

Перечень вопросов, рассматриваемых в теме:

1. Как вычислить площадь прямоугольника?
2. В каких единицах измеряется площадь?
3. Какими способами можно сравнить геометрические фигуры?

Глоссарий по теме:

Площадь – внутренняя часть любой плоской геометрической фигуры.

Квадрат – это прямоугольник, у которого все стороны равны.

Прямоугольник – это четырёхугольник, у которого все углы прямые.

Квадратный сантиметр – квадрат со стороной 1 сантиметр.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.

2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.

3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.

Теоретический материал для самостоятельного изучения

Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат.  Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.

Найдём площадь геометрической фигуры.

Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.

Найдём площадь прямоугольника со сторонами 6 см и 3 см.

Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см²

Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.

S = a ∙ b

S – площадь

a – длина

b – ширина

Задания тренировочного модуля:

1. Заполните пропуски в таблице.

Правильный ответ:

2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.

12 см; 32 см; 24 см²; 32 см²; 24; 12 см².

Правильный ответ: 32см².

Конспект урока по математике на тему «Площадь. Сравнение площадей фигур» (3 класс)

МОУ «Ферзиковская средняя общеобразовательная школа»

Конспект урока по математике

в 3 классе

Тема: «Площадь. Сравнение площадей фигур»

подготовила

учитель начальных классов

Фроликова Анна Викторовна

п. Ферзиково

Тема «Площадь. Сравнение площади»

Тип урока: урок  открытия нового  знания.

Технология  деятельностного   подхода.  

Цель: научиться сравнивать площади.

Задачи: надо узнать, что такое площадь, понять, как сравнивать площади, научиться сравнению площадей.

Универсальные учебные действия учащихся:

познавательные УУД – найти и использовать разные способы сравнения и вычисления площади фигуры;

регулятивные УУД – уметь организовывать свое рабочее место, использовать линейку как простейший чертежный прибор;

личностные УУД – формировать интерес к предмету, развивать психические процессы (воображение, внимание, память, мышление, речь), уважать мнение одноклассников;

коммуникативные УУД – участвовать в диалоге на уроке, отвечать на вопросы учителя, слушать и понимать речь других.

Оборудование: задания для устного счета, индивидуальные компьютеры для детей, мультимедийная доска, цветные картонные геометрические фигуры, записи на классной доске.

Ход урока

1. Мотивация к учебной деятельности

Прозвенел звонок для нас.

Встали все у парт красиво,

Поздоровались учтиво.

Тихо сели, спинки прямо.

Вижу, класс наш хоть куда.

Мы начнём урок, друзья.

Будем отвечать активно,

Хорошо себя вести,

Чтобы гости дорогие.

Захотели вновь прийти!

2. Включение в предметную деятельность

Cлайд 2

— Прочитайте высказывание на доске.

«Все познается в сравнении»

— О чем здесь говорится? (Выслушиваются мнения детей).

— Чем будем заниматься сегодня на уроке? (Сравнивать.)

Слайд 2

— А что будем сравнивать, узнаете, заполнив таблицу. (Данную таблицу заполняют, работая в паре.)

6 _* 7 = П 7_* 9 = Ь 49 : 7 = О 42 : 6 = Д

7 _* 5 = Щ 56 : 7 = Л 4 _* 7 = А

— Какое слово у вас получилось? (Площадь.)

Слайд 3

3. Анализ проблемной ситуации и постановка учебной задачи

— Что будем сравнивать? (Будем сравнивать площади.)

Слайд 4

— Какую цель перед собой поставите (Научиться сравнивать площади.)

— Какие задачи будем решать? (Надо узнать, что такое площадь, понять, как сравнивать площади, научиться сравнению площадей.)

4. Открытия нового знания

4.1 Определение значение понятия

— Вы только что сказали, что надо понять, что такое площадь, тогда попробуйте сами объяснить значение слова площадь. (Выслушиваются высказывания учащихся.)

— Давайте теперь обратимся к толковым словарям (с.343) (работа в группах). Найдите значение слова ПЛОЩАДЬ в словаре.

Слайд 5

(По мере изысканий на интерактивной доске открываются значения слова:

1. Часть плоскости, ограниченная замкнутой ломаной или кривой линией.

2. Незастроенное большое и ровное место (в городе, селе), от которого обычно расходятся в разные стороны улицы.

3. Пространство, помещение, предназначенное для какой-нибудь цели.

— Какое определение слова больше всего подходит к нашему уроку?

— Выделите в этом значении слова главное. («Площадь – это плоскость фигуры».)

Слайд 6

Определите, какую фигуру образует крышка парты? (Прямоугольник.)

— Покажите всю поверхность крышки парты. Что вы, только что показали? (Площадь.)

— Верно. А площадь чего еще можете показать? (Учащиеся называют и показывают площадь классной доски, площадь тетради, площадь дневника, площадь учебника, площадь пенала, площадь окна, площадь пола, площадь стены и т.д.)

4.2 Обучение сравнению площади

1) — Можно ли сравнить площадь классной доски и потолка?

— Чья площадь будет больше, и чья будет меньше? (Учащиеся безошибочно отвечают на данный вопрос.)

Слайд 7

— Как вы это определили? (На глаз.)

2) — Перед вами лежат две фигуры, назовите их. (Квадрат и круг.)

— Как можно сравнить площади этих фигур? (Учащиеся сначала предлагают сравнить их «на глаз». Они пробуют — не получается. Тогда учащиеся предлагают сравнить площади фигур с помощью наложения. Пробуют – получается.)

Слайд 8

— Какой вывод можем сделать о площадях этих фигур? (Площадь квадрата больше площади круг.)

— Итак, сделайте вывод о том, какими способами можно сравнивать площади фигур? (Площади фигур можно сравнивать «на глаз» и с помощью наложения фигур.)

3) — А теперь попробуйте сравнить площади фигур, которые вы видите на доске.

Слайд 9

(Учащиеся предлагают свои варианты сравнения: сравнить «на глаз», наложением.)

— Получается ли сравнить площади этих фигур такими способами?

— Давайте придумаем новые способы. (Учащиеся предлагают разные способы и один из них – надо взять какую-нибудь мерку.)

Слайд 10

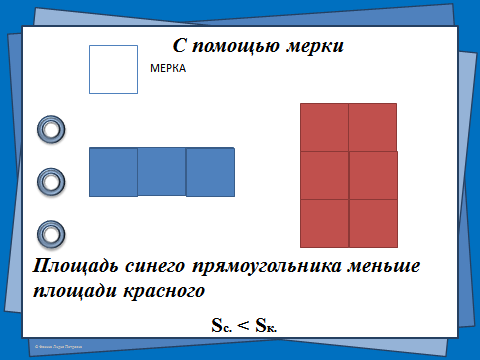
— Какую мерку здесь удобнее взять? (Учащиеся предлагают квадратик.)

— Пробуем. Получилось!

— Как измерить площадь?

Нет задачи проще!

Поглядите-ка сюда –

Встали мерки в три ряда.

Будто бы солдатики –

Ровные квадратики!

Чтобы площадь нам узнать,

Надо их пересчитать!

— Сделайте вывод о том, как еще можно сравнивать площади фигур. (Можно сравнивать площади с помощью мерки, например квадратика.)

4) Решение задачи

Слайд 11

(На доске открывается рисунок двух полей, расчерченных на квадратики. Большое поле состоит из больших квадратиков, маленькое – из маленьких квадратиков.)

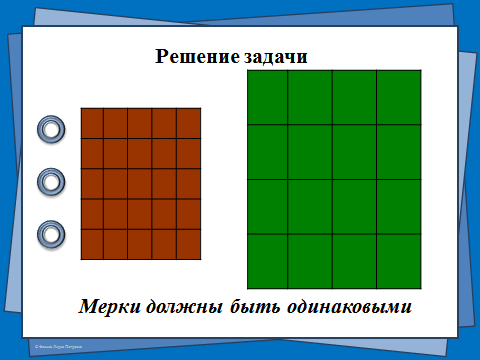
— Сравните площади этих полей сначала на глаз. На глаз видно, что зеленое поле больше. Затем предлагается сравнить по меркам. Выясняется, что маленькое поле по меркам больше зеленого.

— Почему так у нас получилось? (Так получилось, потому что мерки разные.)

— Какие мерки должны быть, чтобы сравнение было правильным? Сделайте вывод о том, какие должны быть мерки? (Мерки должны быть одинаковые.)

5) Подведение итога.

— Какие три способа измерения площадей фигур мы с вами открыли?

Слайд 12

5. Закрепления изученного материала

5.1 Работа по учебнику

1) №1 с.57

Слайды 13 — 14

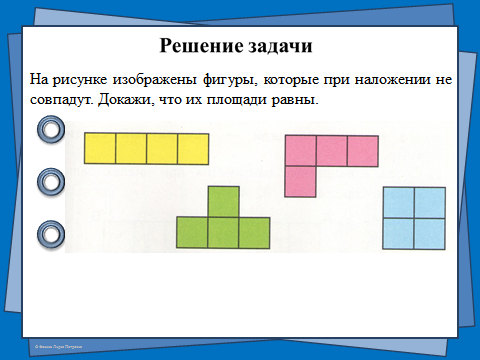
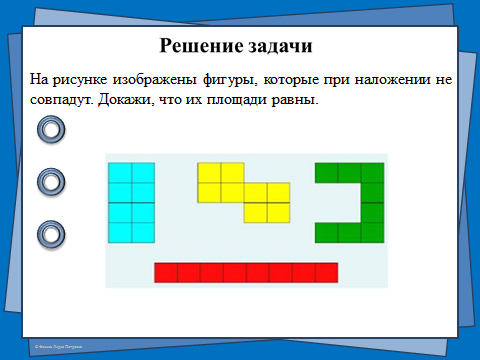
Слайды 15 — 16

2) № под чертой – (в парах)

5.2 Работа по презентации

1) задача на слайде

Слайд 17

5.3 Работа по электронному приложению (в парах)

Слайд 18

Математика, 1 часть

Тема «Площадь. Способы сравнения фигур по площади»

Задания 1, 2

1. П – 28 клеток, О – 32 клетки, Н – 28 клеток

2. Верблюд – 11 клеток, жираф – 16, слон – 22.

5.4 Работа по учебнику

1) №4 с.57 (коллективный разбор)

Было – 8м

Отпилили — 2 м

Осталось — ?

во ? раз

1. 8 – 2 = 6 (м) – осталось.

2. 6 : 2 = 3 (раза) больше оставшаяся часть доски, чем отпиленная.

3. Ответ: в 3 раза.

2) №3 с.57 (самостоятельно). Самооценка

1) 7, 14, 21, 28, 35, 42, 49, 56, 63.

2) 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.

5. Рефлексии деятельности

— Давайте вспомним, какую цель мы перед собой ставили (Научиться сравнивать площади.) и подумаем, достигли ли вы её?

— Что такое площадь? (Площадь – это плоскость фигуры.)

— Перечислите способы определения площади фигур. («На глаз», с помощью наложения фигур, с помощью мерки.)

— Какое нужно соблюдать условие для третьего способа? (Мерки должны быть одинаковыми.)

Слайд 19

Оцените свои результаты (Учащиеся выходят к доске и прикрепляют квадраты магнитом к доске, определяют «Какая площадь больше (1, 2, 3)?»):

1. У меня все получилось!

2. Были затруднения, но я справился.

3. Мне было плохо, неинтересно.

7. Домашнее задание

1) № 2 с.57;

2) карточка

В классе 10 мальчиков и 14 девочек. Всех детей разделили на группы по 4 человека и каждой группе поручили посадить 2 дерева. Сколько деревьев посадят дети?

3) карточка

Сравните площади фигур (S1, S2, S3).

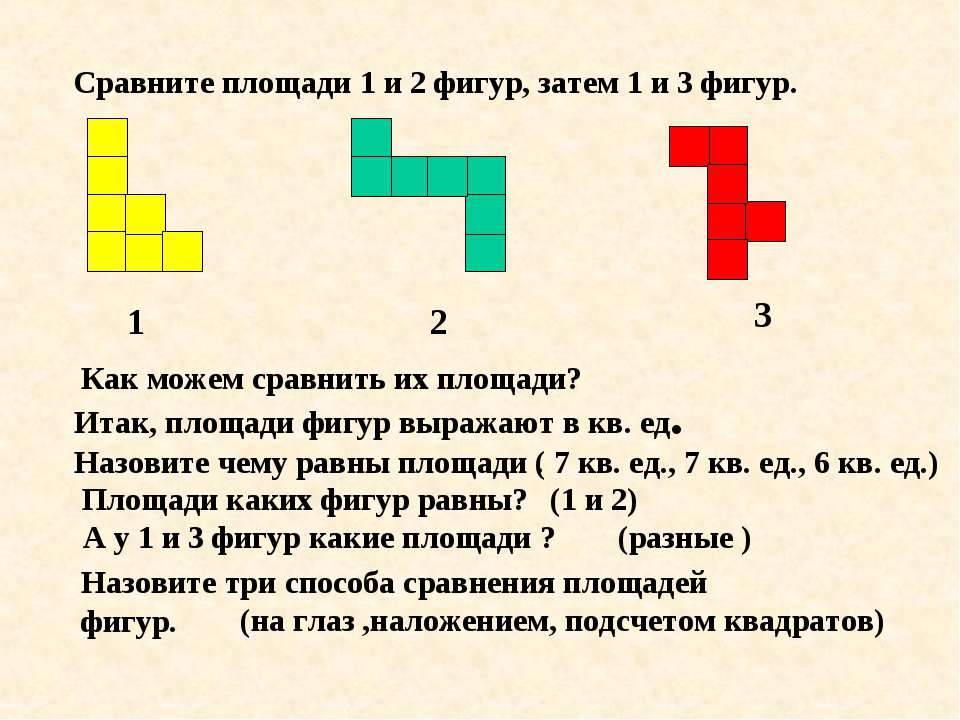
Приложение

Карточка 1

6 х 7 = П 7 х 9 = Ь 49 : 7 = О 42 : 6 = Д

7 х 5 = Щ 56 : 7 = Л 4 х 7 = А

42

₈

₇

₃₅

₂₈

₇

₆₃

Карточка 2

Площадь – плоскость фигуры

№ п/п

Способы сравнения площадей

Карточка 3

Карточка 4

№3 с.57

1) 7, 14, 21, 28, 35, 42, 49, 56, 63.

2) 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.

Карточка 5

Домашнее задание (по выбору):

1) № 2 с.57;

2) карточка

Решите задачу. В классе 10 мальчиков и 14 девочек. Всех детей разделили на группы по 4 человека и каждой группе поручили посадить 2 дерева. Сколько деревьев посадят дети?

3) карточка

Сравните площади фигур (S1, S2, S3).

Как найти площадь любого треугольника — Лайфхакер

Вспоминаем геометрию: формулы для произвольных, прямоугольных, равнобедренных и равносторонних фигур.

Как найти площадь любого треугольника

Посчитать площадь треугольника можно разными способами. Выбирайте формулу в зависимости от известных вам величин.

Зная сторону и высоту

1. Умножьте сторону треугольника на высоту, проведённую к этой стороне.
2. Поделите результат на два.

• S — искомая площадь треугольника.
• a — сторона треугольника.
• h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.

Зная две стороны и угол между ними

1. Посчитайте произведение двух известных сторон треугольника.
2. Найдите синус угла между выбранными сторонами.
3. Перемножьте полученные числа.
4. Поделите результат на два.

• S — искомая площадь треугольника.
• a и b — стороны треугольника.
• α — угол между сторонами a и b.

Сейчас читают 🔥

Зная три стороны (формула Герона)

1. Посчитайте разности полупериметра треугольника и каждой из его сторон.
2. Найдите произведение полученных чисел.
3. Умножьте результат на полупериметр.
4. Найдите корень из полученного числа.

• S — искомая площадь треугольника.
• a, b, c — стороны треугольника.
• p — полупериметр (равен половине от суммы всех сторон треугольника).

Зная три стороны и радиус описанной окружности

1. Найдите произведение всех сторон треугольника.
2. Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.

• S — искомая площадь треугольника.
• R — радиус описанной окружности.
• a, b, c — стороны треугольника.

Зная радиус вписанной окружности и полупериметр

Умножьте радиус окружности, вписанной в треугольник, на полупериметр.

• S — искомая площадь треугольника.
• r — радиус вписанной окружности.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

Как найти площадь прямоугольного треугольника

1. Посчитайте произведение катетов треугольника.
2. Поделите результат на два.

• S — искомая площадь треугольника.
• a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.

Как найти площадь равнобедренного треугольника

1. Умножьте основание на высоту треугольника.
2. Поделите результат на два.

• S — искомая площадь треугольника.
• a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
• h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.

Как найти площадь равностороннего треугольника

1. Умножьте квадрат стороны треугольника на корень из трёх.
2. Поделите результат на четыре.

• S — искомая площадь треугольника.
• a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

Читайте также 🧠👨🏻‍🎓✍🏻

Площадь фигуры. Площадь прямоугольника. Математика, 3 класс: уроки, тесты, задания.

1.	Площадь квадрата Сложность: лёгкое	1
2.	Площадь прямоугольника Сложность: лёгкое	1
3.	Найди сторону прямоугольника, зная его площадь Сложность: лёгкое	1
4.	Найди площадь квадрата, зная его периметр Сложность: среднее	2
5.	Найди периметр прямоугольника, зная его площадь Сложность: среднее	2
6.	У какой клумбы больше площадь? Сложность: среднее	2
7.	Площадь незакрашенной части прямоугольника Сложность: среднее	2
8.	Изменится ли периметр и площадь клумбы Сложность: сложное	3
9.	Площадь дорожки в саду Сложность: сложное	3
10.	Сравни площади квадратов Сложность: сложное	3

Формулы площади поверхности для геометрических фигур

Площадь поверхности прямоугольной призмы

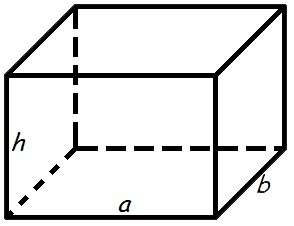
Площадь поверхности прямоугольной призмы — это площадь шести прямоугольников, покрывающих ее.

Формула площади поверхности прямоугольной призмы:

A = 2 (a · b + a · h + b · h)

где A — площадь поверхности прямоугольной призмы,
а — длина,
b — ширина,
h — высота.

Площадь цилиндра

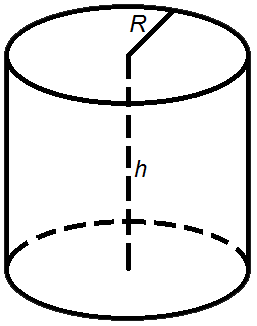
Площадь стороны цилиндра — периметр верха, умноженный на высоту.

Формула площади стороны цилиндра:

А = 2 π R ч

Площадь поверхности цилиндра — это сумма площадей стороны цилиндра и двух площадей сверху.

Формула площади поверхности цилиндра:

A = 2 π R h + 2 π R ² = 2 π R (R + h)

где А — площадь,
R — радиус верха,
h — высота цилиндра,
π = 3,141592.

Площадь правого кругового конуса

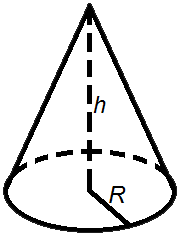
Площадь боковой поверхности конуса равна наклону, умноженному на радиус, умноженному на π.

Формула площади боковой поверхности конуса:

А = π R l

Площадь поверхности конуса — это сумма площади основания (круглого дна) и площади боковой поверхности.

Формула площади конуса:

A = π R ² + π R l = π R (R + l)

где А — площадь,
R — радиус основания,
л — наклонная высота,
π = 3.141592.

Площадь поверхности сферы

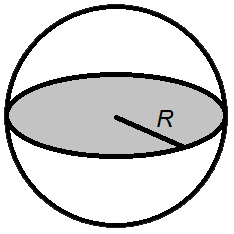
Формулы площади поверхности сферы:

• Формула площади поверхности сферы равна 4 квадрату радиуса, умноженному на π.

  A = 4 π R ²

• Формула площади поверхности сферы — это квадрат диаметра, умноженный на π.

  А = π D ²

где A — площадь поверхности шара,
R — радиус,
D — диаметр,
π = 3.141592.

,

Площадь треугольника (координатная геометрия)

Площадь треугольника (координатная геометрия) — Math Open Reference

Зная координаты трех вершин треугольника ABC, площадь можно вычислить по формуле ниже.

Попробуй это Перетащите любую точку A, B, C. Площадь треугольника ABC непрерывно пересчитывается по приведенной выше формуле. Вы также можете перетащить исходную точку на (0,0).

Учитывая координаты трех вершин любого треугольника, площадь треугольника определяется как: где A _x и A _y — координаты x и y точки A и т. д.,

Эта формула позволяет вычислить площадь треугольника, зная координаты всех трех Вершины. Неважно, какие точки обозначены A, B или C, и он будет работать с любым треугольником, включая те, у которых некоторые или все координаты отрицательны.

Глядя на формулу выше, вы увидите, что она заключена в две вертикальные полосы, например: Две вертикальные полосы означают «абсолютное значение». Это означает, что он всегда положительный, даже если формула дала отрицательный результат.У полигонов никогда не может быть отрицательной области.

«Ручная работа» точки B

Если вы выполните это вычисление, но пропустите последний шаг, на котором вы берете абсолютное значение, результат может быть отрицательным. Если он отрицательный, это означает, что 2-я точка (B) находится слева от отрезка AC. Здесь мы имеем в виду «левый» в том смысле, что если бы вы стояли в точке A и смотрели на C, то B был бы слева от вас.

Если область нулевая

Если площадь равна нулю, это означает, что три точки коллинеарны.Они лежат прямой линией и не образуют треугольника. Вы можете перетащить точки выше, чтобы создать это условие.

Вы также можете использовать Формулу Герона

Формула Герона позволяет вычислить площадь треугольника, если вам известны длины всех трех сторон. (См. Формулу Герона). В координатной геометрии мы можем найти расстояние между любыми двумя точками если мы знаем их координаты, и поэтому мы можем найти длины трех сторон треугольника, а затем подставить их в формулу Герона найти область.

Если одна сторона вертикальная или горизонтальная

В треугольнике выше сторона AC равна вертикальный (параллельно оси y). В этом случае легко использовать традиционный метод «половина основания, умноженная на высоту». См. Площадь треугольника — традиционный метод.

Здесь AC выбран в качестве базы и имеет длину 8, найденная путем вычитания y-координат A и C. Аналогичным образом высота равна 11, найденная вычитанием x-координат B и A. Таким образом, площадь равна половине 8 умножить на 11 или 44.

Ящик метод

Вы также можете использовать метод коробки, который действительно работает для любого многоугольника. Подробнее об этом см. Площадь треугольника — прямоугольный метод (Координатная геометрия)

Что попробовать

1. На схеме вверху страницы перетащите точки A, B или C и обратите внимание, как при вычислении площади используются координаты. Попробуйте точки с отрицательными значениями x и y. Вы можете перетащить исходную точку, чтобы переместить оси.
2. Нажмите «скрыть детали».Перетащите треугольник к какой-нибудь новой случайной форме. Вычислите его площадь и нажмите «показать подробности», чтобы узнать, правильно ли вы поняли.
3. После вышеизложенного оцените площадь, посчитав квадраты сетки внутри треугольника. (Каждый квадрат 5 на 5, поэтому имеет площадь 25).

После того, как вы сделаете вышеуказанное, вы можете нажать на «печать», и он распечатает диаграмму точно так, как вы ее установили.

Ограничения

Для большей ясности в апплете выше координаты округлены до целых чисел, а длины округлены до одного десятичного знака.Это может привести к небольшому отклонению расчетов.

Подробнее см. Учебные заметки

Другие темы о координатной геометрии

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

,

Площадь трапеции. Определение, формула и калькулятор

Площадь трапеции. Определение, формула и калькулятор — Открытый справочник по математике Количество квадратных единиц, необходимое для полного заполнения трапеции.
Формула: Средняя ширина × высота

Попробуйте это Перетащите оранжевые точки, чтобы переместить и изменить размер трапеции. Как размер трапеции изменяется, пересчитывается площадь.

Формула площади

Площадь трапеции — это средняя ширина, умноженная на высоту, или формула: где
b1, b2 — длины каждого основания
h — высота (высота)

Напомним, что основания — это две параллельные стороны трапеции.Высота (или высота) трапеции — это перпендикулярное расстояние между двумя базами.

В приведенном выше апплете нажмите «заморозить размеры». Когда вы перетаскиваете любую вершину, вы увидите, что трапеция перерисовывается, сохраняя неизменными высоту и основания. Обратите внимание, как область в отображаемой формуле не меняется. Площадь зависит только от высоты и длины основания, поэтому, как видите, существует множество трапеций с заданным набором размеров, которые имеют одинаковую площадь.

Вывод формулы

См. Как получить формулу площади трапеции.

Калькулятор

Используйте калькулятор выше, чтобы рассчитать высоту, базовую длину и площадь трапеции.

Введите любые три значения, и будет вычислено недостающее. Например: введите высоту и две базовые длины и нажмите «Рассчитать». Площадь будет рассчитана.

Точно так же, если вы введете площадь и две длины основания, будет рассчитана высота, необходимая для получения этой площади.

Определение высоты по площади

Как найти высоту (высоту) трапеции, задайте две базы и площадь.Приведенная выше основная формула площади имеет четыре переменных (площадь, два основания и высота). Если мы знаем какие-то три, мы всегда можем найти четвертый. Так, например, если мы знаем площадь и две базы, мы можем найти высоту, просто изменив основную формулу: Где a — это площадь, а b1, b2 — две базы.

Поиск базы в районе

Как найти основание трапеции, укажите одно из оснований, высоту и площадь. Приведенная выше основная формула площади имеет четыре переменных (площадь, два основания и высота).Если мы знаем какие-то три, мы всегда можем найти четвертый. Так, например, если мы знаем площадь, одно основание и высоту, мы можем найти недостающее основание, просто изменив основную формулу: Где a — площадь, b — известная база, а h — высота (высота).

Если известно медианное значение

Напомним, что медиана (м) трапеции — отрезок, соединяющий середины непараллельных сторон. Напомним также, что длина медианы — это среднее значение двух параллельных сторон.См. Медиана трапеции

Где м — это медиана, а ч — высота (высота).

Площадь как сложная форма

Другой способ найти площадь трапеции — рассматривать ее как несколько более простых форм, а затем добавлять или вычитать их площади, чтобы найти результат. Для Например, трапецию можно рассматривать как меньший прямоугольник плюс два прямоугольных треугольника: Дополнительные сведения об этой общей технике см. В разделе «Область неправильных многоугольников».

Координатная геометрия

В координатной геометрии, если вы знаете координаты четырех вершин, вы можете рассчитать различные его свойства, в том числе площадь и периметр.Подробнее об этом см. Площадь и периметр трапеции (координатная геометрия).

Что попробовать

1. На рисунке выше нажмите «скрыть детали»
2. Перетащите оранжевые точки на вершинах, чтобы создать трапецию произвольного размера.
3. Рассчитайте площадь по формуле
4. Теперь попробуйте оценить площадь трапеции, просто глядя на
   квадратов внутри нее.
5. Когда вы закончите, нажмите «Показать подробности», чтобы увидеть, насколько близко вы подошли.

Другие полигоны

Общие

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

,