Т-критерий Стьюдента за 12 минут
Кирилл Сергеевич Мильчаков
Сегодня мы говорим о t-критерии. Т-критерий наиболее популярный статистический тест в биомедицинских исследованиях. Также его называют парный Т-критерий Стьюдента, t-test, two-sample unpaired t-test. Однако, при использовании этого статистического инструмента допускается достаточно много ошибок. Сегодня в этой статье мы постараемся разобраться, как избежать ошибок применения t-критерия Стьюдента, как интерпретировать его результаты и как рассчитывать t-критерий самостоятельно. Об этом обо всем читайте далее.
При описании любого статистического критерия, будь то t-критерий Стьюдента, либо какой-либо еще, нужно вспомнить о том, как же вообще используются статистические критерии. Для того, чтобы понять, как используется любой критерий, нужно перейти к нескольким достаточно логичным для понимания этапам:
Этапы статистического вывода (statistic inference)
- Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
- Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
- Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
- Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
- Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.
Предлагаю долго не ходить вокруг да около и посмотреть применение t-критерия Стьюдента на реальном примере.
Видео-версия статьи
Пример использования т-критерия Стьюдента
А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.
Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.
Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.
Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅1914 и в 2014 году x̅2014. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅1914≠x̅2014). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅1914=x̅2014), то есть о том, что все эти находки случайны, и я, по сути, не прав.
Теперь нужно дать какой-то аргументированный ответ. Даем его с помощью статистического критерия. Соответственно теперь наступает самое важное: как выбрать статистический критерий? Я думаю, это будет темой отдельной статьи. Для корректности использования t-критерия Стьюдента лишь скажу, что нужно, чтобы:
Условия применения статистического критерия т-теста (критерия Стьюдента)
— данные распределялись по закону нормального распределения;
— данные были количественными;
— и это две независимые между собой выборки (независимые это значит, что в этих группах разные люди, а никак, например, до и после применения препарата у одной группы, люди должны быть разными, тогда группы являются несвязанными, либо независимыми), этот аспект стоит учитывать для выбора вида т-критерия Стьюдента, так как для парных выборок существует свой парный т-критерий (paired t-test).
В итоге Мы определились с тем, что это будет t-критерий Стьюдента.
Формула t-критерия Стьюдента достаточно простая. Она гласит о том, что в числителе у нас разница средних, в знаменателе у нас корень квадратный суммы ошибок репрезентативности по этим группам:
Ошибки репрезентативности были подробно объяснены мною в статье по доверительным интервалам. Поэтому я рекомендую вам ознакомиться с ней, чтобы лучше разобраться, что такое ошибки репрезентативности, что такое выборка, как она соотносится с генеральной совокупностью.
Для того, чтобы не тратить время, я в принципе все уже рассчитал по каждой из групп: средняя (x̅) ,стандартное отклонение (SD) и ошибка репрезентативности (mr).
Давайте остановимся на том, что же значат эти значения:
— средняя (x̅) это среднеарифметическое по 5 наблюдениям в каждой группе;
— если совсем упрощать значение стандартного отклонения (SD), то можно сказать, что оно представляет собой обобщенную среднюю отклонения каждого значения от среднего (стандартное отклонение показывает, насколько широко значения рассеяны (разбросаны) относительно средней). И дальше мы находим нечто среднее отклонений каждого варианта в группе от среднего;
— и ошибка репрезентативности она тоже находится достаточно просто: это как раз наше отклонение от средней некоторое стандартизованное, поэтому стандартное отклонение на размер выборки ( mr=).
Итак, продолжаем. В ходе подстановки каждого значения в нашу формулу, мы находим, что t-критерий Стьюдента равен 3,78. Однако, я думаю, пока тем, кто не знаком со статистическими критериями, это мало о чем говорит.
Итак, теперь настает четвертый этап вопрос интерпретации. Ранее мы получили значение t-критерия в 3,78. Однако, что же это значит? Стоит отметить, что результаты статистических критериев и вообще их интерпретация не говорит о точном «да», либо «нет» в выводе, то есть рост отличается, либо рост не отличается. Всегда это вопрос определенной доли вероятности – доли вероятности ошибиться при констатации положительного результата (речь об ошибке первого рода (I type error, Alpha)). То есть, например, если мы скажем, что средний рост в начале ХХ и в начале XXI века отличаются с долей ошибкой меньше 5 %. Как раз эта величина в 5 % и фиксируется как достаточная для большинства биомедицинских исследований, помните, р больше, либо меньше 0,05.
Итак, как нам перейти от нашей t к р вероятности? Это сделать достаточно просто, стоит лишь воспользоваться табличными значениями t для определенных степеней свободы. Теперь вопрос: как найти эти степени свободы? Но это сделать достаточно просто. Для того, чтобы обнаружить степени свободы для наших групп, нужно лишь сложить количество наблюдений 5 и 5 в нашем случае и вычесть 2. В нашем случае степень свободы равна 8.
Итак, t=3,78, степень свободы равна 8. Переходим в табличное значение и получаем р вероятность – вероятность равна 0,005. То есть вероятность того, что мы ошибаемся при констатации факта различия роста ранее и сейчас, крайне мала – это 0,005 %, не 5 %, а 0,005 %. То есть мы можем говорить с высокой долей достоверности того, что наш рост сейчас в XXI веке и 100 лет назад отличаются.
Вот то, что касается расчета t-критерия Стьюдента и его интерпретации.
На этом наш разговор о t-критерии Стьюдента закончен. Спасибо, что ознакомились с этой статьей. Я очень надеюсь на вашу обратную связь. Пожалуйста, подписывайтесь на наш сайте, ставьте лайки, предлагайте свои темы для следующих выпусков. Спасибо большое за поддержку. С вами был Кирилл Мильчаков. Пока, до новых встреч!
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
lit-review.ru
Таблица критических точек t-критерия Стьюдента
t-критерий Стьюдента – общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента.
Таблица значений критерия Стьюдента в теории вероятностей и математической статистике используется довольно часто. На сайте можно посмотреть примеры ее использования в следующих задачах:
Ниже размещена таблица критический точек t-критерия Стьюдента для односторонней и двусторонней критической области.
| Число степеней свободы k | Уровень значимости α (двусторонняя критическая область) | |||||
| 0,1 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 | |
| 1 | 6,31 | 12,70 | 31,82 | 63,70 | 318,30 | 637,00 |
| 2 | 2,92 | 4,30 | 6,97 | 9,92 | 22,33 | 31,60 |
| 2,35 | 3,18 | 4,54 | 5,84 | 10,22 | 12,90 | |
| 4 | 2,13 | 2,78 | 3,75 | 4,60 | 7,17 | 8,61 |
| 5 | 2,01 | 2,57 | 3,37 | 4,03 | 5,89 | 6,86 |
| 6 | 1,94 | 2,45 | 3,14 | 3,71 | 5,21 | 5,96 |
| 7 | 1,89 | 2,36 | 3,00 | 3,50 | 4,79 | 5,40 |
| 8 | 1,86 | 2,31 | 2,90 | 3,36 | 4,50 | 5,04 |
| 9 | 1,83 | 2,26 | 2,82 | 3,25 | 4,30 | 4,78 |
| 10 | 1,81 | 2,23 | 2,76 | 3,17 | 4,14 | 4,59 |
| 11 | 1,80 | 2,20 | 2,72 | 3,11 | 4,03 | 4,44 |
| 12 | 1,78 | 2,18 | 2,68 | 3,05 | 3,93 | 4,32 |
| 13 | 1,77 | 2,16 | 2,65 | 3,01 | 3,85 | 4,22 |
| 14 | 1,76 | 2,14 | 2,62 | 2,98 | 3,79 | 4,14 |
| 15 | 1,75 | 2,13 | 2,60 | 2,95 | 3,73 | 4,07 |
| 16 | 1,75 | 2,12 | 2,58 | 2,92 | 3,69 | 4,01 |
| 17 | 1,74 | 2,11 | 2,57 | 2,90 | 3,65 | 3,95 |
| 18 | 1,73 | 2,10 | 2,55 | 2,88 | 3,61 | 3,92 |
| 19 | 1,73 | 2,09 | 2,54 | 2,86 | 3,58 | 3,88 |
| 20 | 1,73 | 2,09 | 2,53 | 2,85 | 3,55 | 3,85 |
| 21 | 1,72 | 2,08 | 2,52 | 2,83 | 3,53 | 3,82 |
| 22 | 1,72 | 2,07 | 2,51 | 2,82 | 3,51 | 3,79 |
| 23 | 1,71 | 2,07 | 2,50 | 2,81 | 3,59 | 3,77 |
| 24 | 1,71 | 2,06 | 2,49 | 2,80 | 3,47 | 3,74 |
| 25 | 1,71 | 2,06 | 2,49 | 2,79 | 3,45 | 3,72 |
| 26 | 1,71 | 2,06 | 2,48 | 2,78 | 3,44 | 3,71 |
| 27 | 1,71 | 2,05 | 2,47 | 2,77 | 3,42 | 3,69 |
| 28 | 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 |
| 29 | 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 |
| 30 | 1,70 | 2,04 | 2,46 | 2,75 | 3,39 | 3,65 |
| 40 | 1,68 | 2,02 | 2,42 | 2,70 | 3,31 | 3,55 |
| 60 | 1,67 | 2,00 | 2,39 | 2,66 | 3,23 | 3,46 |
| 120 | 1,66 | 1,98 | 2,36 | 2,62 | 3,17 | 3,37 |
| ∞ | 1,64 | 1,96 | 2,33 | 2,58 | 3,09 | 3,29 |
| Число степеней свободы k | 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 |
| Уровень значимости α (односторонняя критическая область) | ||||||
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение или онлайн-помощь на зачете/экзамене 〉〉
100task.ru
Критерий Стьюдента, t-тест и нормальное распределение
автор: Samoedd Сентябрь 8, 2016
Наступила осень, а значит, настало время для запуска нового тематического проекта «Статистический анализ с R». В нем мы рассмотрим статистические методы с точки зрения их применения на практике: узнаем какие методы существуют, в каких случаях и каким образом их проводить в среде R. На мой взгляд, Критерий Стьюдента или t-тест (от англ. t-test) идеально подходит в качестве введения в мир статистического анализа. Тест Стьюдента достаточно прост и показателен, а также требует минимум базовых знаний в статистике, с которыми читатель может ознакомиться в ходе прочтения этой статьи.
Примечание_1: здесь и в других статьях Вы не увидите формул и математических объяснений, т.к. информация рассчитана на студентов естественных и гуманитарных специальностей, которые делают лишь первые шаги в стат. анализе.
Примечание_2: перед прочтением, я рекомендую ознакомиться с этой статьей, чтобы вспомнить базовые понятия описательной статистики, такие как медиана, стандартное отклонение, квантили и прочее.
Что такое t-тест и в каких случаях его стоит применять
В начале следует сказать, что в статистике зачастую действует принцип бритвы Оккамы, который гласит, что нет смысла проводить сложный статистический анализ, если можно применить более простой (не стоит резать хлеб бензопилой, если есть нож). Именно поэтому, несмотря на свою простоту, t-тест является серьезным инструментом, если знать что он из себя представляет и в каких случаях его стоит применять.

Любопытно, что создал этот метод Уильямом Госсет — химик, приглашенный работать на фабрику Guinness. Разработанный им тест служил изначально для оценки качества пива. Однако, химикам фабрики запрещалось независимо публиковать научные работы под своим именем. Поэтому в 1908 году Уильям опубликовал свою статью в журнале «Biometrika» под псевдонимом «Стьюдент». Позже, выдающийся математик и статистик Рональд Фишер доработал метод, который затем получил массовое распространение под названием Student’s t-test.
Критерий Стьюдента (t-тест) — это статистический метод, который позволяет сравнивать средние значения двух выборок и на основе результатов теста делать заключение о том, различаются ли они друг от друга статистически или нет. Если Вы хотите узнать, отличается ли средний уровень продолжительности жизни в Вашем регионе от среднего уровня по стране; сравнить урожайность картофеля в разных районах; или изменяется ли кровяное давление до и после употребления нового лекарства, то t-тест может быть Вам полезен. Почему может быть? Потому что для его проведения, необходимо, чтобы данные выборок имели распределение близкое к нормальному. Для этого существуют методы оценки, которые позволяют сказать, допустимо ли в данном случае полагать, что данные распределены нормально или нет. Поговорим об этом подробнее.
Нормальное распределение данных и методы его оценки qqplot и shapiro.test
Нормальное распределение данных характерно для количественных данных, на распределение которых влияет множество факторов, либо оно случайно. Нормальное распределение характеризуется несколькими особенностями:
- Оно всегда симметрично и имеет форму колокола.
- Значения среднего и медианы совпадают.
- В пределах одного стандартного отклонения в обе стороны лежат 68.2% всех данных, в пределах двух — 95,5%, в пределах трех — 99,7%
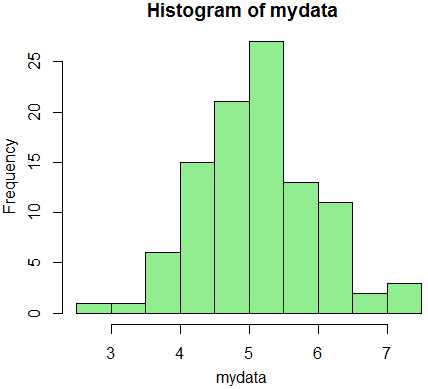
Давайте создадим случайную выборку с нормальным распределением на языке программирования R, где общее количество измерений = 100, среднее арифметическое = 5, а стандартное отклонение = 1. Затем отобразим его на графике в виде гистограммы:
mydata <- rnorm(100, mean = 5, sd = 1) hist(mydata, col = "light green")
Ваш график может слегка отличаться от моего, так как числа сгенерированы случайным образом. Как Вы видите, данные не идеально симметричны, но кажется сохраняют форму нормального распределения. Однако, мы воспользуемся более объективными методами определения нормальности данных.
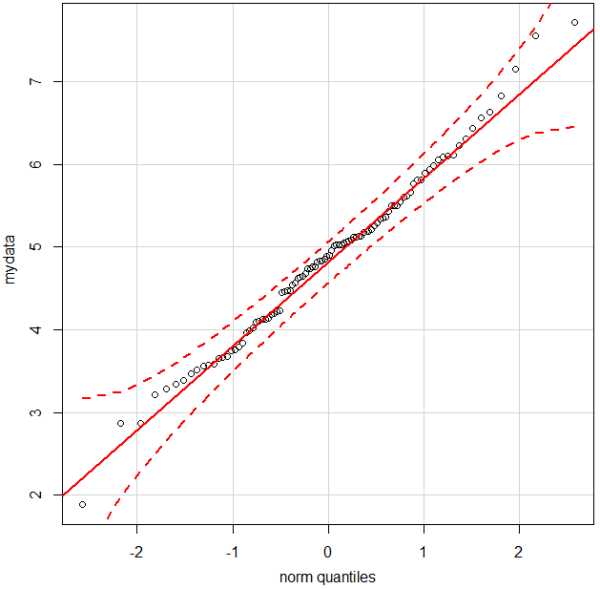
Одним из наиболее простых тестов нормальности является график квантилей (qqplot). Суть теста проста: если данные имеют нормальное распределение, то они не должны сильно отклоняться от линии теоретических квантилей и выходить за пределы доверительных интервалов. Давайте проделаем этот тест в R.
install.packages("car") #установка пакета "car"
library(car) #загрузка пакета "car" в среду R
qqPlot(mydata) #запустим тестКак видно из графика, наши данные не имеют серьезных отклонений от теоретического нормального распределения. Но порой при помощи qqplot невозможно дать однозначный ответ. В этом случае следует использовать тест Шапиро-Уилка, который основан на нулевой гипотезе, что наши данные распределены нормально. Если же P-значение менее 0.05 (p-value < 0.05), то мы вынуждены отклонить нулевую гипотезу. P-значение в этом случае будет говорить о том, что вероятность ошибки при отклонении нулевой гипотезы будет равна менее 5%.
Провести тест Шапиро-Уилка в R не составит труда. Для этого нужно всего лишь вызвать функцию shapiro.test, и в скобках вставить имя ваших данных. В нашем случае p-value должен быть значительно больше 0.05, что не позволяет отвергнуть нулевую гипотезу о том, что наши данные распределены нормально.
Запускаем t-тест Стьюдента в среде R
Итак, если данные из выборок имеют нормальное распределение, можно смело приступать к сравнению средних этих выборок. Существует три основных типа t-теста, которые применяются в различных ситуациях. Рассмотрим каждый из них с использованием наглядных примеров.
Одновыборочный критерий Стьюдента (one-sample t-test)
Одновыборочный t-тест следует выбирать, если Вы сравниваете выборку с общеизвестным средним. Например, отличается ли средний возраст жителей Северо-Кавказского Федерального округа от общего по России. Существует мнение, что климат Кавказа и культурные особенности населяющих его народов способствуют продлению жизни. Для того, чтобы проверить эту гипотезу, мы возьмем данные РосСтата (таблицы среднего ожидаемого продолжительности жизни по регионам России) и применим одновыборочный критерий Стьюдента. Так как критерий Стьюдента основан на проверке статистических гипотез, то за нулевую гипотезу будем принимать то, что различий между средним ожидаемым уровнем продолжительности по России и республикам Северного Кавказа нет. Если различия существуют, то для того, чтобы считать их статистически значимыми p-value должно быть менее 0.05 (логика та же, что и в вышеописанном тесте Шапиро-Уилка).
samoedd.com
Алгоритм расчета t-критерия Стьюдента для независимых выборок измерений
Определить расчетное значение t-критерия по формуле
- Определить критическое значение t-критерия с использованием таблицы 1 приложения, при заданном уровне значимости и степени свободы.
Сравнить расчетное и критическое значение t — критерия. Если расчетное значение больше или равно критическому, то гипотеза равенства средних значений в двух выборках изменений отвергается (Но). Во всех других случаях она принимается на заданном уровне значимости.
Пример. Две группы студентов обучались по двум различным методикам. В конце обучения с ними был проведен тест по всему курсу. Необходимо оценить, насколько существенны различия в полученных знаниях. Результаты тестирования представлены в таблице 4.
Таблица 4
25 | 18 | 9 | 13 | 8 | 20 | 25 | 18 | 6 | 12 |
19 | 13 | 12 | 12 | 18 | 9 | 7 | 10 | 18 | 20 |
Рассчитаем выборочное среднее, дисперсию и стандартное отклонение:
Определим значение tp по формуле tp = 0,45
По таблице 1 (см. приложение) находим критическое значение tk для уровня значимости р = 0,01
tk = 2,88
Вывод: так как расчетное значение критерия меньше критического 0,45<2,88 гипотеза Но подтверждается и существенных различий в методиках обучения нет на уровне значимости 0,01.
Алгоритм расчета t-критерия Стьюдента для зависимых выборок измерений
1. Определить расчетное значение t-критерия по формуле
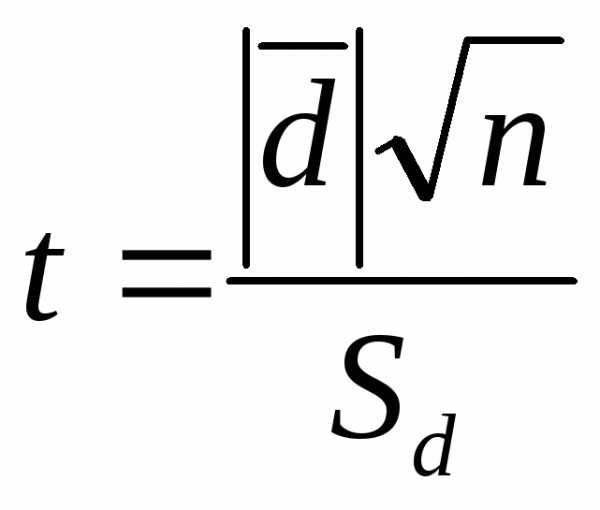 ,
где
,
где 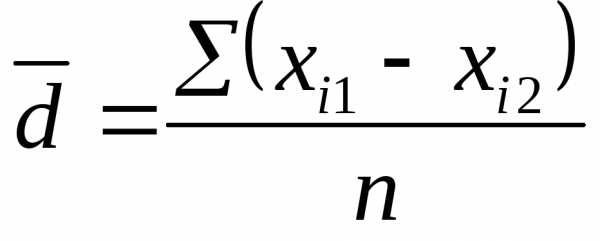
3. Определить критическое значение t-критерия по таблице 1 приложения.
4. Сравнить расчетное и критическое значение t-критерия. Если расчетное значение больше или равно критическому, то гипотеза равенства средних значений в двух выборках изменений отвергается (Но). Во всех других случаях она принимается на заданном уровне значимости.
U—критерий Манна—Уитни
Назначение критерия
Критерий предназначен для оценки различий между двумя непараметрическими выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n < 30.
Описание критерия
Этот метод определяет, достаточно ли мала зона пересекающихся значений между двумя рядами. Чем меньше эта область, тем более вероятно, что различия достоверны. Эмпирическое значение критерия U отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше U, тем более вероятно, что различия достоверны.
Гипотезы
НО: Уровень признака в группе 2 не ниже уровня признака в группе 1.
HI: Уровень признака в группе 2 ниже уровня признака в группе 1.
Алгоритм расчета критерия Манна-Уитни (u)
Перенести все данные испытуемых на индивидуальные карточки.
Пометить карточки испытуемых выборки 1 одним цветом, скажем красным, а все карточки из выборки 2 – другим, например, синим.
Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой.
Проранжировать значения на карточках, приписывая меньшему значению меньший ранг.
Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие – в другой.
Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли общая сумма рангов с расчетной.
Определить большую из двух ранговых сумм.
Определить значение U по формуле:
где n1 – количество испытуемых в выборке 1;
n2 – количество испытуемых в выборке 2,
Тх – большая из двух рантовых сумм;
nх – количество испытуемых в группе с большей суммой рангов.
9. Определить критические значения U по таблице 2 (см. приложение).
Если Uэмп.> Uкр0,05, то гипотеза Но принимается. Если Uэмп.≤ Uкр, то отвергается. Чем меньше значения U, тем достоверность различий выше.
Пример. Сравнить эффективность двух методов обучения в двух группах. Результаты испытаний представлены в таблице 5.
Таблица 5
18 | 10 | 7 | 15 | 14 | 11 | 13 | ||||
15 | 20 | 10 | 8 | 16 | 10 | 19 | 7 | 15 | 14 | 29 |
Перенесем все данные в другую таблицу, выделив данные второй группы подчеркиванием и сделаем ранжирование общей выборки (см. алгоритм ранжирования в методических указаниях к заданию 3).
Значения | 7 | 7 | 8 | 10 | 10 | 10 | 11 | 13 | 14 | 14 | 15 | 15 | 15 | 16 | 18 | 19 | 20 | 29 |
Ранги | 1,5 | 1,5 | 3 | 5 | 5 | 5 | 7 | 8 | 9,5 | 9,5 | 12 | 12 | 12 | 14 | 15 | 16 | 17 | 18 |
Номер | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
Найдем сумму рангов двух выборок и выберем большую из них: Тх = 113
Рассчитаем эмпирическое значение критерия по формуле 2: Up = 30.
Определим по таблице 2 приложения критическое значение критерия при уровне значимости р = 0.05 : Uk = 19.
Вывод: так как расчетное значение критерия U больше критического при уровне значимости р = 0.05 и 30 > 19, то гипотеза о равенстве средних принимается и различия в методиках обучения несущественны.
studfiles.net
Пример расчета t-критерия Стьюдента для зависимых выборок
Предположим, что необходимо сравнить между собой результаты выполнения логических задач до и после курса обучения. Чтобы узнать различаются ли результаты до курса обучения и после необходимо вычислить t-критерий Стьюдента для зависимых выборок.
Шаг 1. Занесем данные в общую таблицу:
| № | Результаты выполнения логических задач до курса (сек.) | Результаты выполнения логических задач после курса (сек.) |
| 1 | 25 | 22 |
| 2 | 23 | 25 |
| 3 | 28 | 23 |
| 4 | 29 | 22 |
| 5 | 35 | 30 |
| 6 | 31 | 27 |
| 7 | 24 | 20 |
| 8 | 24 | 19 |
| 9 | 38 | 32 |
| 10 | 26 | 25 |
| 11 | 20 | 20 |
Шаг 2.Рассчитаем разность для каждой пары значений
| № | Разность значений в каждой паре (до-после) |
| 1 | 3 |
| 2 | -2 |
| 3 | 5 |
| 4 | 7 |
| 5 | 5 |
| 6 | 4 |
| 7 | 4 |
| 8 | 5 |
| 9 | 6 |
| 10 | 1 |
| 11 | 0 |
Шаг 3. Вычисляем среднюю разность значений, стандартное отклонение и степени свободы
Для того, чтобы рассчитать стандартное отклонение нам необходимо знать среднее арифметическое в разности значений, а затем подставить имеющиеся значения в формулу стандартного отклонения.
3.1. Рассчитаем среднюю разность значений (среднее арифметическое по разности)
3.2. Подставим значение среднего арифметического в формулу стандартного отклонения:
Шаг 4. Подставляем полученные значения в формулу t-критерия Стьюдента для зависимых выборок.
Шаг 5. Определим по таблице критических значений t-Стьюдента уровень значимости:
Шаг 5.1. Найдем в таблице строку с количеством степеней свободы 10. df = 10
Шаг 5.2. В строке с df=10 найдем значения . Оно располагается между p<0,01 и p<0,001
Шаг 6. Следовательно уровень значимости меньше 0,01.
Результаты выполнения логических задач до и после курса различаются между собой.
statpsy.ru
Расчет критерия Стьюдента в Excel

Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Определение термина
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Расчет показателя в Excel
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
- Строим таблицу с двумя рядами переменных.
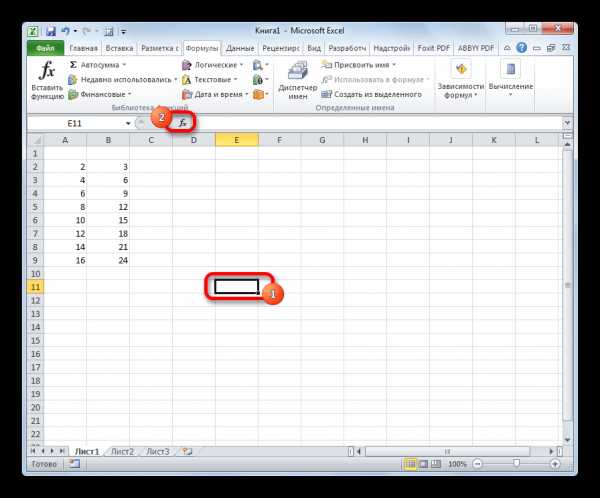
- Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.
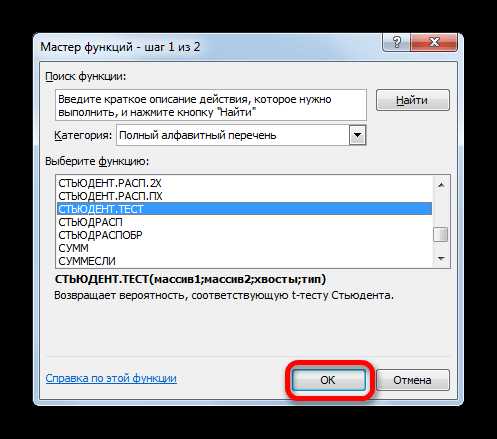
- После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».
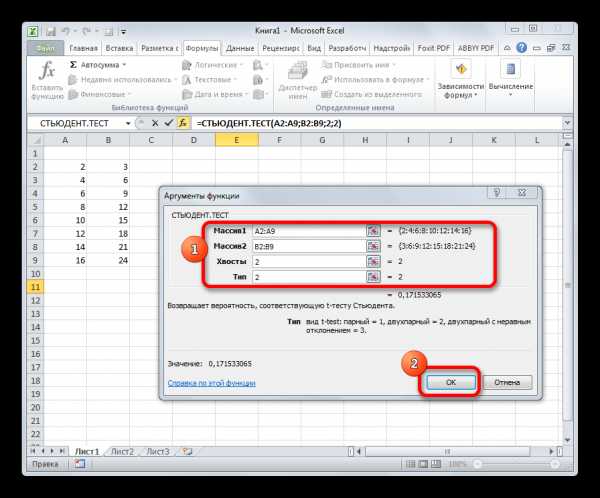
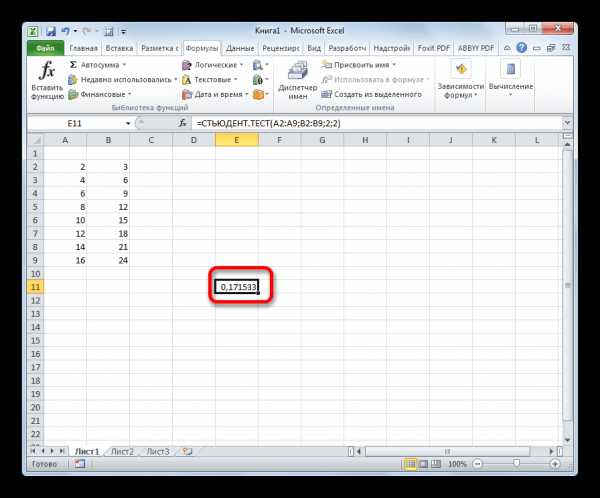
- Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
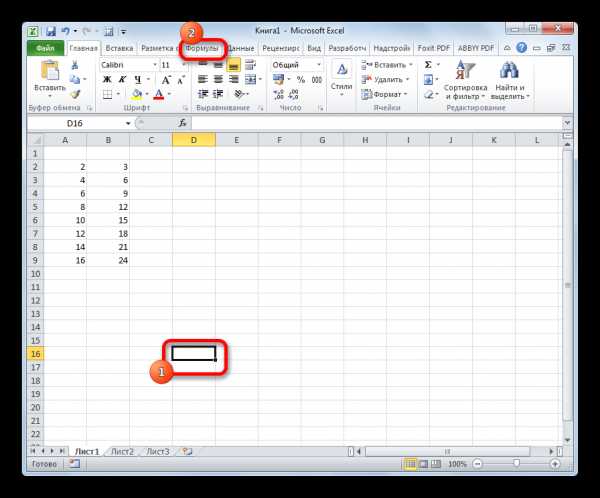
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».
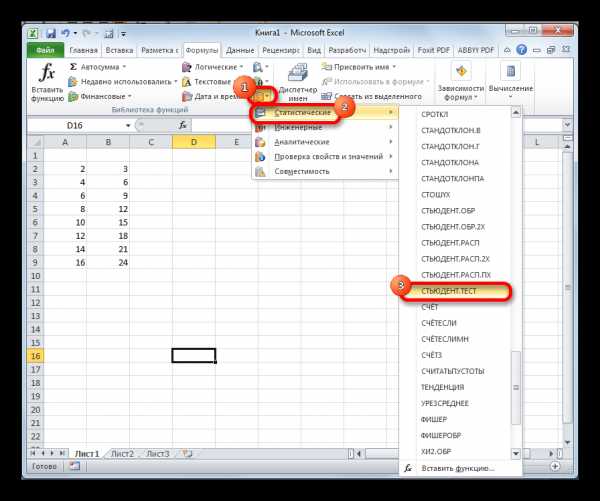
- Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».
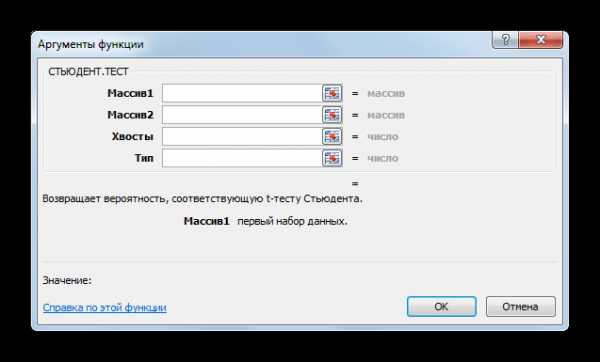
- Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
Способ 3: ручной ввод
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.
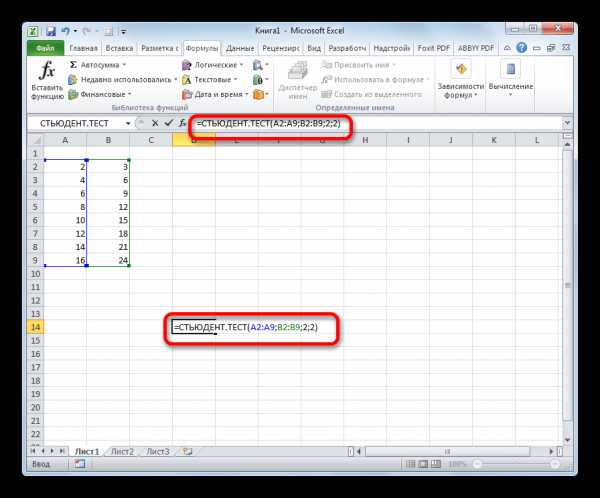
После того, как данные введены, жмем кнопку Enter для вывода результата на экран.
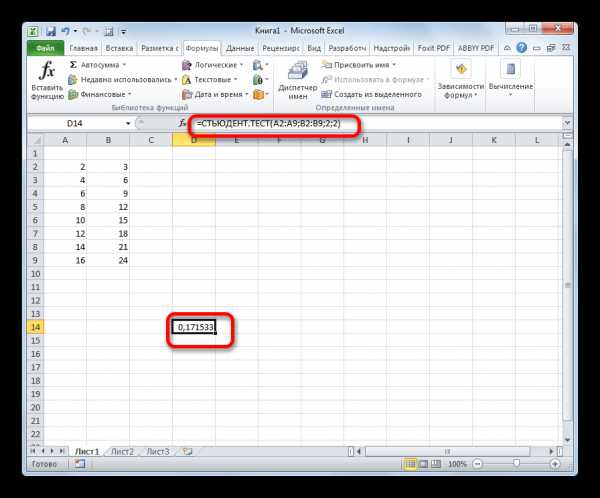
Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТlumpics.ru
t-критерий Стьюдента для независимых выборок
t-критерий Стьюдента для независимых выборок применяется для сравнения средних значений двух независимых между собой выборок.
Условия применения:
- Сравниваемые значения не составляют пару коррелирующих значений
- Распределение признаков в каждой выборке соответствует нормальному распределению
- Дисперсии признака в выборках примерно равны (проверяется с помощью критерия F-Фишера)
Альтернатива:
Формула t-критерий Стьюдента для независимых выборок:
,
где — среднее арифметическое первой выборки; — среднее арифметическое второй выборки; — стандартное отклонение первой выборки; — стандартное отклонение второй выборки; — объем первой выборки; — объем второй выборки.
statpsy.ru
