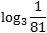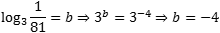Что такое в математике log: Что такое логарифм

Содержание

Что такое логарифм

11 июля 2011

Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.

Мы же определим логарифм просто и наглядно. Для этого составим таблицу:

Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.

А теперь — собственно, определение логарифма:

Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.

Обозначение: log_a x = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.

Например, 2³ = 8 ⇒ log₂ 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2³ = 8). С тем же успехом log₂ 64 = 6, поскольку 2⁶ = 64.

Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:

2¹	2²	2³	2⁴	2⁵	2⁶
2	4	8	16	32	64
log₂ 2 = 1	log₂ 4 = 2	log₂ 8 = 3	log₂ 16 = 4	log₂ 32 = 5	log₂ 64 = 6

К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log₂ 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке [2; 3]. Потому что 2

2 < 5 < 2³, а чем больше степень двойки, тем больше получится число.

Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами:
log₂ 5 = 2,32192809…
log₃ 8 = 1,89278926…
log₅ 100 = 2,86135311…

Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log₂ 5, log₃ 8, log₅ 100.

Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:

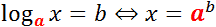
Перед нами — не что иное как определение логарифма. Вспомните:

логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.

Как считать логарифмы

С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:

Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!

Такие ограничения называются

областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log_a x = b ⇒ x > 0, a > 0, a ≠ 1.

Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log₂ 0,5 = −1, т.к. 0,5 = 2⁻¹.

Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.

Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:

Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
Решить относительно переменной b уравнение: x = a^b;
Полученное число b будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.

Посмотрим, как работает эта схема на конкретных примерах:

Задача. Вычислите логарифм: log₅ 25

Представим основание и аргумент как степень пятерки: 5 = 5¹; 25 = 5²;
Составим и решим уравнение:
log₅ 25 = b ⇒ (5¹)^b = 5² ⇒ 5^b = 5² ⇒ b = 2;
Получили ответ: 2.

Задача. Вычислите логарифм:

Представим основание и аргумент как степень тройки: 3 = 3¹; 1/81 = 81⁻¹ = (3⁴)⁻¹ = 3⁻⁴;
Составим и решим уравнение:
Получили ответ: −4.

Задача. Вычислите логарифм: log₄ 64

Представим основание и аргумент как степень двойки: 4 = 2²; 64 = 2⁶;
Составим и решим уравнение:
log₄ 64 = b ⇒ (2²)^b = 2⁶ ⇒ 2^2b = 2⁶ ⇒ 2b = 6 ⇒ b = 3;
Получили ответ: 3.

Задача. Вычислите логарифм: log₁₆ 1

Представим основание и аргумент как степень двойки: 16 = 2⁴; 1 = 2⁰;
Составим и решим уравнение:
log₁₆ 1 = b ⇒ (2⁴)^b = 2⁰ ⇒ 2^4b = 2⁰ ⇒ 4b = 0 ⇒ b = 0;
Получили ответ: 0.

Задача. Вычислите логарифм: log₇ 14

Представим основание и аргумент как степень семерки: 7 = 7¹; 14 в виде степени семерки не представляется, поскольку 7¹ < 14 < 7²;
Из предыдущего пункта следует, что логарифм не считается;
Ответ — без изменений: log₇ 14.

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.

Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2³ — точная степень, т.к. множитель всего один;

48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2⁴ — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3⁴ — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;

Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм

Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.

Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x. Обозначение: lg x.

Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.

Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log₁₀ x

Все, что верно для обычных логарифмов, верно и для десятичных.

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Натуральный логарифм от аргумента x — это логарифм по основанию e, т.е. степень, в которую надо возвести число e, чтобы получить число x. Обозначение: ln x.

Многие спросят: что еще за число e? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e = 2,718281828459…

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log_e x

Таким образом, ln e = 1; ln e² = 2; ln e¹⁶ = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

Смотрите также:

Тест к параграфу «Что такое логарифм» (легкий)
Тест к уроку «Что такое логарифм» (средний)
Десятичные дроби
Задачи B12, сводящиеся к линейным уравнениям
Метод коэффициентов, часть 2
Тригонометрия в задаче B15: решаем без производных

что это? Все формулы. Простейшие уравнения и неравенства

Что такое логарифм

Свойства логарифма

Логарифмические уравнения

Логарифмические неравенства

Сейчас речь пойдет о трех страшных буквах: l o g.
Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).

Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.

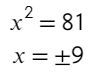
Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.

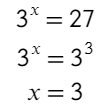
А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.

Тогда, если дело касается логарифма:

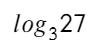
можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?

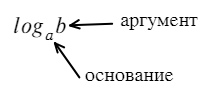
На самом деле в этом и заключается основная формула (определение логарифма):

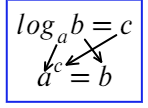
Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c». Логарифм — это действие, обратное возведению в степень.

У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).

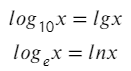
Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?

Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182…, мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).

А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).

Как мы не можем существовать без еды, воды, интернета… Так и логарифм не представляет свое существование без ОДЗ.

Всегда, когда существует логарифм, должно быть:

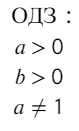
«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.

А теперь разберем теорию на практике:

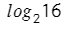
В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).

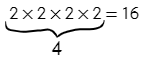
Два нужно четыре раза умножить само на себя, чтобы получить 16.

Ответ: 4.

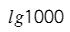
lg — это логарифм по основанию 10. 10 нужно 3 раза умножить само на себя, чтобы получить 1000.

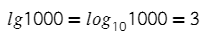
А теперь посложнее, перейдем по определнию к показательному уравнению :

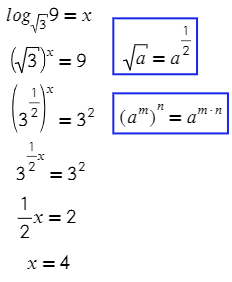
Следующий пример поможет нам узнать первую формулу логарифмов:

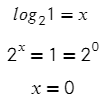
Преобразуем выражение по определению логарифма и получим показательное уравнение. Единица — это же любое значение в нулевой степени?

Тогда можно сделать вывод, что при любом основании и аргументе логарифма, равном 1, все эти логарифмы будут равны нулю.

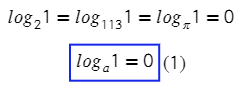
Нетрудно тогда понять, что есть еще одно следствие:

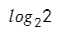
В какую степень нужно возвести 2, чтобы получить 2? Напряжем все свои извилины и получим — один!

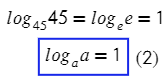
Дальше будут формулы, которые я позволю себе не выводить, чтобы не испугать неискушенных в математике читателей.

Хотя мой вам совет: отследить, откуда эта формула появилась. У логарифмов самое главное помнить, что логарифм — это действие, обратное возведению в степень.

Основное логарифмическое тождество:

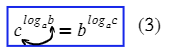
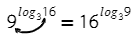
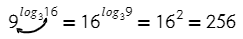
В какую степень нужно возвести 3, чтобы получить 9? Значит, логарифм в показателе степени равен двум.

Это единственная формула, где логарифм в показатели степени. Видишь логарифм в степени? Тебе поможет только эта формула.

Еще примерчик, двойка перед логарифмом никак не влияет, формула все так же работает:

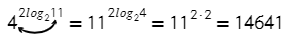
А вот квадрат в логарифме тоже быть может, только лучше сначала разложить:

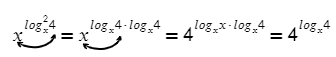
Дальше с этим ничего сделать не сможем.

Дальнейшие формулы тоже уникальны, это тебе не косинус двойного угла.

Видим сложение логарифмов, выпускаем эту формулы:

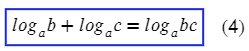
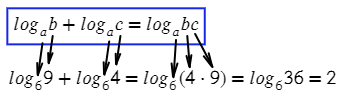
А вот примерчик, чтобы порадовать тебя этой формулой, только наоборот:

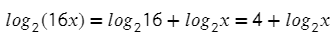
Видим разность логарифмов, выпускаем эту формулы:

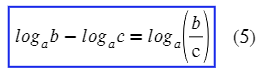
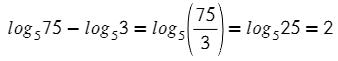
А теперь сразу сумма и разность. По отдельности логарифмы не найти, но вместе они и мы сила:

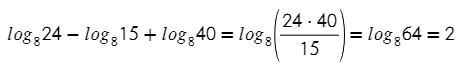
Теперь посмотрим на степени у аргмента логарифма:

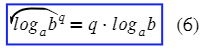
Пример:

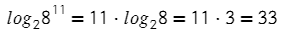
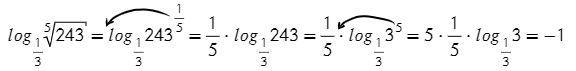
А в основании тоже можно? Нужно!

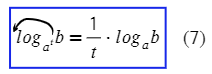
Минус два — это степень у основания:

А все вместе можно? Конечно, логарифмы — это такая свобода:

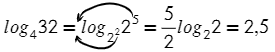
А здесь нужно будет соединить две формулы: 1) вынесение степени из основания и 2) разность логарифмов

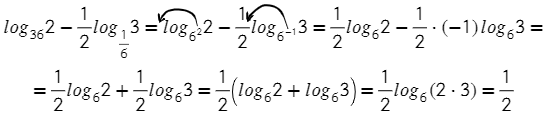
С основными формулами разобрались, теперь для решения более сложных уравнений/выражений.

Формула перехода к новому основанию:

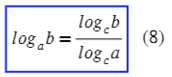
Обрати внимание, чем она отличается от разности логарифмов (4). Тут мы делим один логарифм на другой, а там деление происходит под логарифмом.

Тут все просто, разве что стоит вспомнить, что квадратный корень — это степень одна вторая.

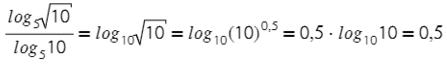
Тут первым действием воспользуемся изучаемой формулой, а дальше каждый логарифм в виде числа, потихонечку−полегонечку.

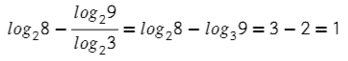
Последняя формула, меняем местами аргумент и основание логарифма:

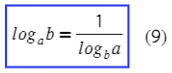
Используется тоже нечасто, но если ее не знаешь, то никак не выкрутишься через другие формулы.

Простенький примерчик:

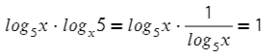
Закрепим обе формулы. Используем формулу (9), после (8), а так же не забудь порадовать десятичные дроби — переведи их в обыкновенные, а они порадуют тебя. Теперь посмотрим еще на пару примеров:

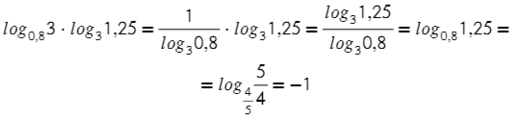
Логарифм в логарифме, что может быть прекраснее? Только решенный логарифм в логарифме.

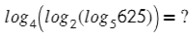
Начинаем с внутреннего:

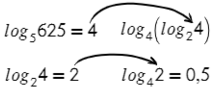
И постепенно раскрываем каждый последующий:

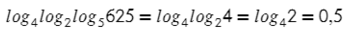
После того, как с формулами разобрались, (а их всего 9! Согласись, несложно выучить?), перейдем к уравнениям.

Все логарифмические уравнения решаем по одному из двух алгоритмов.

Первый появляется из определения логарифма:

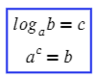
Только не забываем про ОДЗ:

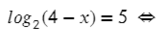
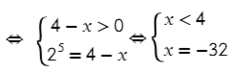
Второй вариант, когда логарифм с одним основанием равен логарифму с точно таким же основнанием:

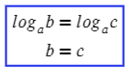
Не забываем про ОДЗ, тогда получится:

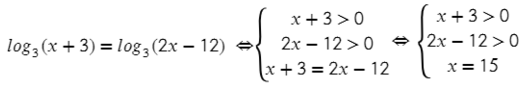
Подставив в ОДЗ x = 15, видим, что все выполняется!

Обязательно только логарифм (без всяких множителей и т.п.) с одним основанием должен быть равен другому логарифму с таким же основанием:

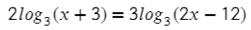
Здесь перед логарифмами стоят разные множители, поэтому прежде всего нужно их внести в логарифм (6 формула), а после убрать логарифмы:

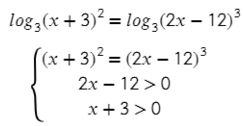
Если стоят одинаковые множители, их можно сократить сразу или сократить на общий множитель:

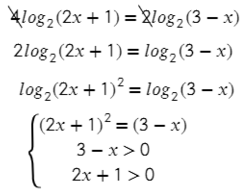
Бывает, что с одной стороны уравнения есть сумма логарифмов (4) или обычное число, сокращать их сразу нельзя! Только после того, как приведем и левую, и правую часть к одному логарифму:

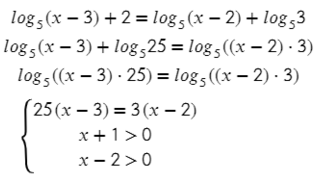
Что же касается неравенств, убирать логарифмы можно так же, как и в уравнениях, только здесь нужно внимательно смотреть на значение оснований. Если основание логарифма лежит в диапазоне 0 < a < 1 (также как в показательных неравенствах), то после зачеркивания логарифмов знак меняется на противоположный:

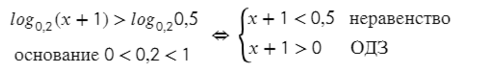
Если же основание а > 1, то убираем логарифмы без смены знака и дорешиваем обычное неравенство:

Вывод:

Л О Г — это не три страшные буквы, а обратное действие возведению в степень.
Хоть формул и целых девять, но они никак не пересекаются. Решая пример и ориентируясь в формулах, ты будешь однозначно выбирать необходимую формулу.
Видишь логарифм — ищи ОДЗ и решай его в первую очередь!
Решение уравнений происходит по одному из двух вариантов и больше никак.
В неравенствах главное — помнить об основании логарифма, когда зачеркиваем логарифмы.

Будь в курсе новых статеек, видео и легкого математического юмора.

Подготовка школьников к ЕГЭ (Справочник по математике — Алгебра

Определение логарифма, основное логарифмическое тождество

Рассмотрим два произвольных действительных числа a и b, удовлетворяющих условиям

Логарифмы свойства логарифмов основное логарифмическое тождество натуральные и десятичные логарифмы

(1)

Определение. Логарифмом числа b по основанию a называют такую степень, в которую надо возвести число a, чтобы получить число b.

Другими словами, логарифм числа b по основанию a – это такое число x, которое является решением уравнения

Доказательство того, что решение уравнения (2) существует и единственно, выходит за рамки школьной программы.

Для логарифма числа b по основанию a используется обозначение:

log_a b .

Таким образом, для всех действительных чисел a и b, удовлетворяющих условиям (1), справедливо равенство

которое часто называют основным логарифмическим тождеством.

Замечание. Обратим особое внимание на то, что при решении уравнения (2) мы ищем показатель степени, а при решении уравнения

x^a= b.

мы ищем основание степени, которое вычисляется по формуле

и в случае, когда a – натуральное число, является корнем натуральной степени из числа b.

Пример 1. Решить уравнение

x³= 81 .

Решение. Воспользовавшись понятием кубического корня и свойствами степеней, получаем

Ответ: .

Пример 2. Решить уравнение

3^x= 81 .

Решение. Воспользовавшись тем, что число 81 является четвертой степенью числа 3 , получаем:

Ответ: 4 .

Задача. Доказать, что число

log₂ 3

иррационально.

Решение. Предположим противное, т.е. предположим, что указанное число рационально. Тогда существует несократимая дробь

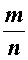числитель и знаменатель которой являются натуральными числами и такая, что справедливо равенство:

Из определения логарифма отсюда вытекает равенство:

следствием которого является равенство:

2^m= 3ⁿ .

Но последнее равенство невозможно, поскольку его левая часть четное число, а правая – нечетное. Полученное противоречие доказывает требуемое в задаче утверждение.

Свойства логарифмов

Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:

Использование свойств логарифмов при решении логарифмических уравнений и неравенств

Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.

Например, если при решении уравнения или неравенства требуется преобразовать выражение

log_a ( f (x)² ) ,

то вместо формулы

следует применять формулу

поскольку в противном случае можно потерять корни.

По той же причине при преобразовании выражений

log_a ( f (x) g (x)) и

следует использовать формулы:

Замечание. Желающим усовершенствовать свои знания и умения при решении уравнений и неравенств с логарифмами мы рекомендуем ознакомиться с нашими учебными пособиями «Решение логарифмических уравнений» и «Решение логарифмических неравенств».

Десятичные логарифмы и натуральные логарифмы

В математике, физике и во многих других областях естествознания и технологий важное место занимают десятичные логарифмы и натуральные логарифмы.

Десятичные логарифмы – это логарифмы с основанием 10, а основанием натуральных логарифмов является иррациональное и трансцендентное число e, которое определяется по формуле

доказательство которой выходит за рамки школьной программы.

Для десятичных и натуральных логарифмов используются соответственно обозначения:

lg b и ln b,

причем

lg e = 0,43429…,

ln 10 = 2,30259…

Графики логарифмических функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.

Подготовка к ЕГЭ и ОГЭ в учебном центре Резольвента

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

основание, свойства, формулы, функция, график

Свойств	Формула	Пример
Логарифм умножения	ln(x ∙ y) = ln(x) + ln(y)	ln(3 ∙ 7) = ln(3) + ln(7)
Логарифм деления	ln(x / y) = ln(x) — ln(y)	ln(3 / 7) = ln(3) — ln(7)
Логарифм степени	ln(x ^y) = y ∙ ln(x)	ln(2⁸) = 8∙ ln(2)
Логарифм корня
Производная логарифма	f (x) = ln(x)⇒ f ‘* (x) = 1 / x*
Интеграл логарифма	∫ ln(x)dx = x ∙ (ln(x) — 1) + C
Логарифм отрицательного числа	ln(x) не определен, если x ≤ 0
Логарифм числа 0	ln(0) не определен
Логарифм числа 1	ln(1) = 0
Логарифм комплексного числа	log z = ln(r) + i(θ+2nπ) = ln(√(x²+y²)) + i·arctan(y/x)), для комплексного числа z = re^iθ = x + iy
Логарифм бесконечности	lim ln(x) = ∞, если x→∞
Тождество Эйлера	ln(-1) = iπ

Логарифмы. Свойства логарифмов. Формулы с логарифмами. Десятичные, натуральные логарифмы, основное логарифмическое тождество

Определение логарифма

Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что a^c = b: log a b=c⇔ a c =b (a>0,a≠1,b>0) &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp

Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.

Основное логарифмическое тождество

a log a b =b (a>0,a≠1) (2)

Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.

Два очевидных следствия определения логарифма

log a a=1 (a>0,a≠1) (3)
log a 1=0 (a>0,a≠1) (4)

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.

Логарифм произведения и логарифм частного

log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0) (5)

log a b c = log a b− log a c (a>0,a≠1,b>0,c>0) (6)

Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.

Действительно, выражение log a (f(x)g(x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.

Преобразуя данное выражение в сумму log a f(x)+ log a g(x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).

Степень можно выносить за знак логарифма

log a b p =p log a b (a>0,a≠1,b>0) (7)

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

log a (f (x) 2 =2 log a f(x)

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Формула перехода к новому основанию

log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) (8)

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

log a b= 1 log b a (a>0,a≠1,b>0,b≠1) (9)

Десятичные и натуральные логарифмы

Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log₁₀x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy (x>0,y>0) .

Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам: log a b= lgb lga = lnb lna (a>0,a≠1,b>0)

Несколько простых примеров с логарифмами

Пример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.

Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log₅125 = 3. Мы использовали формулу перехода к новому основанию (8).

Таблица формул, связанных с логарифмами

a log a b =b (a>0,a≠1)

log a a=1 (a>0,a≠1)

log a 1=0 (a>0,a≠1)

log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0)

log a b c = log a b− log a c (a>0,a≠1,b>0,c>0)

log a b p =p log a b (a>0,a≠1,b>0)

log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1)

log a b= 1 log b a (a>0,a≠1,b>0,b≠1)

Возможно, вас заинтересуют также:

Натуральный логарифм, функция ln x

Основные формулы с натуральным логарифмом

Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.

Определение

Натуральный логарифм: – это функция y = ln x, обратная к экспоненте, x = e^y, и являющаяся логарифмом по основанию числа е: ln x = log_e x.

Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/x.

Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045…;
.

График натурального логарифма ln x

График функции y = ln x.

График натурального логарифма (функции y = ln x) получается из графика экспоненты зеркальным отражением относительно прямой y = x.

Натуральный логарифм определен при положительных значениях переменной x. Он монотонно возрастает на своей области определения.

При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).

При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x^a с положительным показателем степени a растет быстрее логарифма.

Свойства натурального логарифма

Область определения, множество значений, экстремумы, возрастание, убывание

Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.


Область определения	0 < x + ∞
Область значений	– ∞ < y < + ∞
Монотонность	монотонно возрастает
Нули, y = 0	x = 1
Точки пересечения с осью ординат, x = 0	нет
	+ ∞
	– ∞

Значения ln x

ln 1 = 0

Основные формулы натуральных логарифмов

Формулы, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:

Доказательства этих формул представлены в разделе «Логарифм».

Обратная функция

Обратной для натурального логарифма является экспонента.

Если , то

Если , то .

Производная ln x

Производная натурального логарифма:
.
Производная натурального логарифма от модуля x:
.
Производная n-го порядка:
.
Вывод формул > > >

Интеграл

Интеграл вычисляется интегрированием по частям:
.
Итак,

Выражения через комплексные числа

Рассмотрим функцию комплексной переменной z:
.
Выразим комплексную переменную z через модуль r и аргумент φ:
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n – целое,
то будет одним и тем же числом при различных n.

Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов. Опубликовано: 05-04-2014 Изменено: 20-03-2017

Натуральный логарифм — это… Что такое Натуральный логарифм?

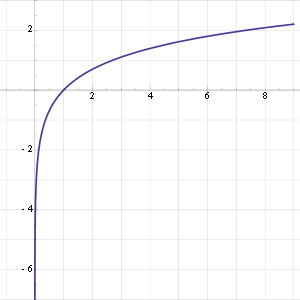График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x).

Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), log_e(x) или иногда просто log(x), если основание e подразумевается.^[1]

Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x. Например, ln(7,389…) равен 2, потому что e²=7,389…. Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e¹ = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e⁰ = 1.

Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.

Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:

Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:

Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.

История

Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia, опубликованной в 1668 году^[2], хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов.^[3] Ранее его называли гиперболическим логарифмом,^[4] поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.

Конвенции об обозначениях

Русская (и советская в целом) система

Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».

Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.

Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln² ln³ 4x⁵ = [ln([ln(4x⁵)]³)]².

Англо-американская система

Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x)», либо «ln(x)» , а для обозначения логарифма по основанию 10 — «log₁₀(x)».

Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «log_e(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log₁₀(x).

В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log₂(x)» (хотя часто вместо этого пишется просто lg(x)).

Техника

В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.

В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.

Происхождение термина натуральный логарифм

Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей.^[5] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60.^[6]^[7]^[8]

log_e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:^[9]

Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.

Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.^[10]

Определение

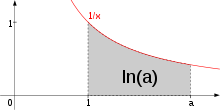$\frac{d}{dx}\log_b(x) = \frac{d}{dx} \left( \frac{1}{\ln(b)} \ln{x} \right) = \frac{1}{\ln(b)} \frac{d}{dx} \ln{x} = \frac{1}{x\ln(b)}$

ln(a) определяется как площадь под кривой f(x) = 1/x от 1 до a.

Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:

Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:

Это можно продемонстрировать, допуская следующим образом:

Число e может быть определено как единственное действительное число a такое, что ln(a) = 1.

Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что . Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.

Свойства

(комплексный логарифм)

Производная, ряд Тейлора

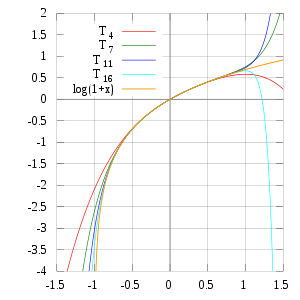$\lim_{x \to 0} \frac{\ln(1+x)}{x} = 1.\,$ Полиномы Тейлор дают точную аппроксимацию для только в диапазоне -1 x ≤ 1. Заметим, что для x > 1 полиномы Тейлора более высокой степени дают аппроксимацию хуже.

Производная натурального логарифма равна

На основании этого можно выполнить разложение в ряд Тейлора около 0, называемого иногда рядом Меркатора:

Справа дано изображение и некоторых её полиномов Тейлора около 0. Эти аппроксимации сходятся к функции только в области -1 < x ≤ 1, а за её пределами полиномы Тейлора высших степеней дают аппроксимацию менее точную.

Подставляя x-1 для x, получим альтернативную форму для ln(x), а именно:

^[11]

С помощью преобразования Эйлера ряда Меркатор можно получить следующее выражение, которое справедливо для любого х больше 1 по абсолютной величине:

Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.

Также заметим, что — это её собственная инверная функция, поэтому для получения натурального логарифма определенного числа y нужно просто для x присвоить значение .

Натуральный логарифм в интегрировании

Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:

В другом виде:

Ниже дан пример для g(x) = tan(x):

Пусть f(x) = cos(x) и f’(x)= — sin(x):

где C — произвольная константа.

Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:

Численное значение

Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:

Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:

при условии, что y = (x−1)/(x+1) и x > 0.

Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:

Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.

Высокая точность

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула:^[12]^[13]

где M обозначает арифметико-геометрическое среднее 1 и 4/s, и

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)

Вычислительная сложность

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Непрерывные дроби

Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:

Комплексные логарифмы

Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e^x для любого произвольного комплексного числа x, при этом используется бесконечный ряд с комплексным x. Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x, для которого e^x = 0, и оказывается, что e^2πi = 1 = e⁰. Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e^z = e^z+2nπi для всех комплексных z и целых n.

Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i⁴ = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.

Функции натурального логарифма на комплексной плоскости (главная ветвь)
$\log \left( 1+\frac{2x}{y} \right) = \cfrac{2x} {y+\cfrac{x} {1+\cfrac{x} {3y+\cfrac{2x} {1+\cfrac{2x} {5y+\cfrac{3x} {1+\ddots}}}}}} = \cfrac{2x} {y+x-\cfrac{(1x)^2} {3(y+x)-\cfrac{(2x)^2} {5(y+x)-\cfrac{(3x)^2} {7(y+x)-\ddots}}}}$
$\log \left( 1+\frac{2x}{y} \right) = \cfrac{2x} {y+\cfrac{x} {1+\cfrac{x} {3y+\cfrac{2x} {1+\cfrac{2x} {5y+\cfrac{3x} {1+\ddots}}}}}} = \cfrac{2x} {y+x-\cfrac{(1x)^2} {3(y+x)-\cfrac{(2x)^2} {5(y+x)-\cfrac{(3x)^2} {7(y+x)-\ddots}}}}$
$\log \left( 1+\frac{2x}{y} \right) = \cfrac{2x} {y+\cfrac{x} {1+\cfrac{x} {3y+\cfrac{2x} {1+\cfrac{2x} {5y+\cfrac{3x} {1+\ddots}}}}}} = \cfrac{2x} {y+x-\cfrac{(1x)^2} {3(y+x)-\cfrac{(2x)^2} {5(y+x)-\cfrac{(3x)^2} {7(y+x)-\ddots}}}}$
$\log \left( 1+\frac{2x}{y} \right) = \cfrac{2x} {y+\cfrac{x} {1+\cfrac{x} {3y+\cfrac{2x} {1+\cfrac{2x} {5y+\cfrac{3x} {1+\ddots}}}}}} = \cfrac{2x} {y+x-\cfrac{(1x)^2} {3(y+x)-\cfrac{(2x)^2} {5(y+x)-\cfrac{(3x)^2} {7(y+x)-\ddots}}}}$
Суперпозиция трёх предыдущих графиков

См. также

Примечания

↑ Mathematics for physical chemistry. — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5, Extract of page 9
↑ J J O’Connor and E F Robertson The number e. The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано из первоисточника 12 февраля 2012.
↑ Cajori Florian A History of Mathematics, 5th ed. — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
↑ Flashman, Martin Estimating Integrals using Polynomials. Архивировано из первоисточника 12 февраля 2012.
↑ Boyers Carl A History of Mathematics. — John Wiley & Sons, 1968.
↑ Harris, John (1987). «Australian Aboriginal and Islander mathematics» (PDF). Australian Aboriginal Studies 2: 29–37.
↑ Large, J.J. (1902). «The vigesimal system of enumeration». Journal of the Polynesian Society 11 (4): 260–261.
↑ Cajori first=Florian (1922). «Sexagesimal fractions among the Babylonians». American Mathematical Monthly 29 (1): 8–10. DOI:10.2307/2972914.
↑ Larson Ron Calculus: An Applied Approach. — 8th. — Cengage Learning, 2007. — P. 331. — ISBN 0-618-95825-8
↑ Ballew, Pat Math Words, and Some Other Words, of Interest. Архивировано из первоисточника 12 февраля 2012.
↑ «Logarithmic Expansions» at Math3.org
↑ (1982) «Practically fast multiple-precision evaluation of log(x)». Journal of Information Processing 5 (4): 247–250. Проверено 30 March 2011.
↑ (1999) «Fast computations of the exponential function» 1564: 302–312. DOI:10.1007/3-540-49116-3_28.

Ссылки

Расшифровка функции потерь журнала. Вы когда-нибудь работали над… | by Harshith

Вы когда-нибудь работали над проблемой классификации в машинном обучении? Если да, то вы могли столкнуться с функцией кросс-энтропии или потери журнала в логистической регрессии.

Для чего используется эта функция? Каково значение функции в задачах классификации?

Давайте выясним подробности, посмотрев на математику, лежащую в основе функции.

Прежде чем мы начнем углубляться в математику, лежащую в основе функции, и посмотрим, как она была получена, мы должны знать, что такое функция потерь.

Проще говоря, функция потерь: функция, используемая для оценки производительности алгоритма, используемого для решения задачи. Подробное определение

В алгоритме двоичной классификации, таком как логистическая регрессия, цель состоит в том, чтобы минимизировать функцию кросс-энтропии.

Кросс-энтропия — это мера разницы между двумя распределениями вероятностей для данной случайной переменной или набора событий — Джейсон Браунли

Давайте предположим, что у нас есть данные о пациентах, и задача состоит в том, чтобы найти, у кого из них есть рак.В нашем примере, поскольку у нас нет данных по всей совокупности, мы пытаемся предсказать вероятность заболевания раком человека на основе выборки данных. Нам нужно только предсказать для злокачественного класса , т.е. P (y = 1 | x) = p̂ , потому что вероятность отрицательного класса может быть получена из него , то есть P ( y = 0 | x) = 1-P (y = 1 | x) = 1-p̂ .

Хороший алгоритм бинарной классификации должен выдавать высокое значение p̂ (вероятность прогнозирования злокачественного класса для образца S), что является ближайшей оценкой к P (вероятность прогнозирования злокачественного класса. от общей численности населения).

В теории вероятностей функция плотности вероятности или плотность непрерывной случайной величины — это функция, значение которой в любой заданной выборке в пространстве выборки можно интерпретировать как обеспечивающую относительную вероятность того, что значение случайной переменной будет равно этот образец — Википедия

Идея состоит в том, чтобы найти максимум функции правдоподобия для определенного значения θ

Найти максимальное значение функции означает дифференцировать функцию (dL / dθ = 0)

Поскольку функция правдоподобия L является продуктом функции распределения вероятностей каждого Xi, мы должны использовать правило произведения при дифференцировании, чтобы дифференцировать такую функцию, что станет сложной задачей.

Здесь на помощь приходят логарифмы.
Log (xy) = Logx + Logy
Дифференциация: d (Logx) / dx = 1 / x

Применение журнала к функции правдоподобия упрощает выражение до суммы журнала вероятностей и не меняет график с относительно θ. Более того, дифференцирование логарифма функции правдоподобия даст ту же оценку θ из-за монотонного свойства логарифмической функции.

Это преобразование функции правдоподобия помогает найти значение θ, которое максимизирует функцию правдоподобия.

Выражение также называется распределением Бернулли.

В нашем примере вероятность того, что рак является злокачественным, равна P. Вероятность того, что рак является доброкачественным, будет равна 1-P.

В случае N наблюдений функция плотности вероятности f задается как произведение отдельных функций плотности вероятности. Совместная вероятность определяется следующим образом:

Для оценки максимального правдоподобия мы должны вычислить, для какого значения P будет dL / dP = 0, так что для этого, как обсуждалось ранее; функция правдоподобия преобразуется в логарифмическую функцию правдоподобия.

Как видите, мы вывели уравнение, которое почти аналогично функции логарифмических потерь / кросс-энтропии, только без знака минус. В логистической регрессии градиентный спуск используется для нахождения оптимального значения вместо градиентного подъема, потому что он рассматривается как задача минимизации потерь , поэтому здесь мы добавляем отрицательный знак к уравнению, что приводит к двоичную функцию потери кросс-энтропии.

Также обратите внимание, что максимизация функции логарифмического правдоподобия аналогична минимизации отрицательной логарифмической функции правдоподобия.

Функция потерь вычисляет ошибку для одного обучающего примера; функция стоимости — это среднее значение функций потерь всего обучающего набора — Andrew Ng

python — ошибка математического домена в math.log

Переполнение стека

Около
Товары
Для команд

Переполнение стека Общественные вопросы и ответы
Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
реклама Обратитесь к разработчикам и технологам со всего мира
О компании

math.log в Python — qaru.

Переполнение стека

Около
Товары
Для команд

Переполнение стека Общественные вопросы и ответы
Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
реклама Обратитесь к разработчикам и технологам со всего мира
О компании

журнал, logf, logl — cppreference.com

логарифм с плавающей запятой (аргумент с плавающей запятой);	(1)	(начиная с C99)
двойной лог (двойной аргумент);	(2)
long double logl (длинный двойной аргумент);	(3)	(начиная с C99)
#define log (arg)	(4)	(начиная с C99)

1-3) Вычисляет натуральный (с основанием e ) логарифм arg .

4) Типовой макрос: если arg имеет тип long double, вызывается logl . В противном случае, если arg имеет целочисленный тип или тип double, вызывается log . В противном случае вызывается logf . Если arg сложный или мнимый, то макрос вызывает соответствующую сложную функцию (clogf, clog, clogl).

[править] Параметры

аргументов

—

значение с плавающей запятой

[править] Возвращаемое значение

Если ошибок не возникает, возвращается натуральный (по основанию e ) логарифм arg (ln (arg) или log
e (arg)).

Если возникает ошибка домена, возвращается значение, определяемое реализацией (NaN, если поддерживается).

Если возникает ошибка полюса, возвращается -HUGE_VAL , -HUGE_VALF или -HUGE_VALL .

[править] Обработка ошибок

Об ошибках сообщается, как указано в math_errhandling.

Ошибка домена возникает, если arg меньше нуля.

Ошибка полюса может возникнуть, если arg равен нулю.

Если реализация поддерживает арифметику с плавающей запятой IEEE (IEC 60559),

Если аргумент равен ± 0, возвращается -∞ и возникает FE_DIVBYZERO.
Если аргумент равен 1, возвращается +0
Если аргумент отрицательный, возвращается NaN и возникает FE_INVALID.
Если аргумент равен + ∞, возвращается + ∞
Если аргумент NaN, возвращается NaN

[править] Пример

 #include 
#include 
#include 
#include 
#include 
#pragma STDC FENV_ACCESS ON
int main (пусто)
{
    printf ("журнал (1) =% f \ n", журнал (1));
    printf ("логарифм по основанию 5 от 125 =% f \ n", log (125) / log (5));
    // специальные значения
    printf ("журнал (1) =% f \ n", журнал (1));
    printf ("журнал (+ Inf) =% f \ n", журнал (БЕСКОНЕЧНОСТЬ));
    //обработка ошибок
    errno = 0; feclearexcept (FE_ALL_EXCEPT);
    printf ("журнал (0) =% f \ n", журнал (0));
    если (errno == ERANGE) perror ("errno == ERANGE");
    if (fetestexcept (FE_DIVBYZERO)) put ("FE_DIVBYZERO поднято");
}

Выход:

 журнал (1) = 0.000000
логарифм 125 по основанию 5 = 3.000000
журнал (1) = 0,000000
журнал (+ Inf) = inf
журнал (0) = -inf
    errno == ERANGE: числовой результат вне допустимого диапазона
    FE_DIVBYZERO собрал

[править] Ссылки

C11 (ISO / IEC 9899: 2011):

7.12.6.7 Функции журнала (стр: 244-245)

7.25 Типовой math (стр: 373-375)

F.10.3.7 Функции журнала (стр: 522)

C99 (ISO / IEC 9899: 1999):

7.12.6.7 Функции журнала (стр: 225)

7.22 Типовой math (p: 335-337)

F.9.3.7 Функции журнала (стр: 459)

Стандарт C89 / C90 (ISO / IEC 9899: 1990):

Что такое логарифм

Как считать логарифмы

Десятичный логарифм

Натуральный логарифм

что это? Все формулы. Простейшие уравнения и неравенства

Будь в курсе новых статеек, видео и легкого математического юмора.

Подготовка школьников к ЕГЭ (Справочник по математике — Алгебра

Определение логарифма, основное логарифмическое тождество

Свойства логарифмов

Использование свойств логарифмов при решении логарифмических уравнений и неравенств

Десятичные логарифмы и натуральные логарифмы

основание, свойства, формулы, функция, график

Логарифмы. Свойства логарифмов. Формулы с логарифмами. Десятичные, натуральные логарифмы, основное логарифмическое тождество

Определение логарифма

Основное логарифмическое тождество

Два очевидных следствия определения логарифма

Логарифм произведения и логарифм частного

Степень можно выносить за знак логарифма

Формула перехода к новому основанию

Десятичные и натуральные логарифмы

Несколько простых примеров с логарифмами

Таблица формул, связанных с логарифмами

Натуральный логарифм, функция ln x

Определение

График натурального логарифма ln x

Свойства натурального логарифма

Область определения, множество значений, экстремумы, возрастание, убывание

Значения ln x

Основные формулы натуральных логарифмов

Основное свойство логарифмов и его следствия

Формула замены основания

Обратная функция

Производная ln x

Интеграл

Выражения через комплексные числа

Разложение в степенной ряд

Натуральный логарифм — это… Что такое Натуральный логарифм?

История

Конвенции об обозначениях

Русская (и советская в целом) система

Англо-американская система

Техника

Происхождение термина натуральный логарифм

Определение

Свойства

Производная, ряд Тейлора

Натуральный логарифм в интегрировании

Численное значение

Высокая точность

Вычислительная сложность

Непрерывные дроби

Комплексные логарифмы

См. также

Примечания

Ссылки

Расшифровка функции потерь журнала. Вы когда-нибудь работали над… | by Harshith

python — ошибка математического домена в math.log

math.log в Python — qaru.

журнал, logf, logl — cppreference.com

[править] Параметры

[править] Возвращаемое значение

[править] Обработка ошибок

[править] Пример

[править] Ссылки

[править] См. Также

Добавить комментарий Отменить ответ