Формула площадь тора: Ваш браузер не поддерживается

Площадь поверхности Тора Калькулятор | Вычислить Площадь поверхности Тора

✖Большой радиус — это измерение наибольшего радиуса любой формы или объекта.ⓘ Большой радиус [rMajor]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%
✖Малый радиус — это измерение наименьшего радиуса любой формы или объекта. ⓘ Малый радиус [rMinor]		створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%

✖Площадь поверхности Многогранник — это площадь внешней части или самого верхнего слоя многогранника. ⓘ Площадь поверхности Тора [SAPolyhedron]

акрАкко (служба США)НаходятсяАрпентамбарКарроКруговая дюймаКруговая MilCuerdaарамДунамРаздел электрон КрестаГаусадьбаMuпингплощадьPyongклочок землиСабинРазделКвадратный АнгстремПлощадь СантиметрПлощадь цепи Площадь декаметровойквадратный дециметрКвадратный футКвадратный фут (служба США)Площадь гектометровыеКвадратный дюймквадратный километрКвадратный метрПлощадь микрометраПлощадь MilКвадратная миляКвадратная миля (римская)Квадратная миля (Статут)Квадратная миля (служба США)Площадь МиллиметрПлощадь NanometreМера площадиПлощадь полюсаПлощадь РодКвадратный Rod (служба США)Квадратный дворрастяжениегородокВарас Castellanas CuadВарас Conuqueras Cuad

⎘ копия

👎

Формула

сбросить

👍

Площадь поверхности Тора Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1.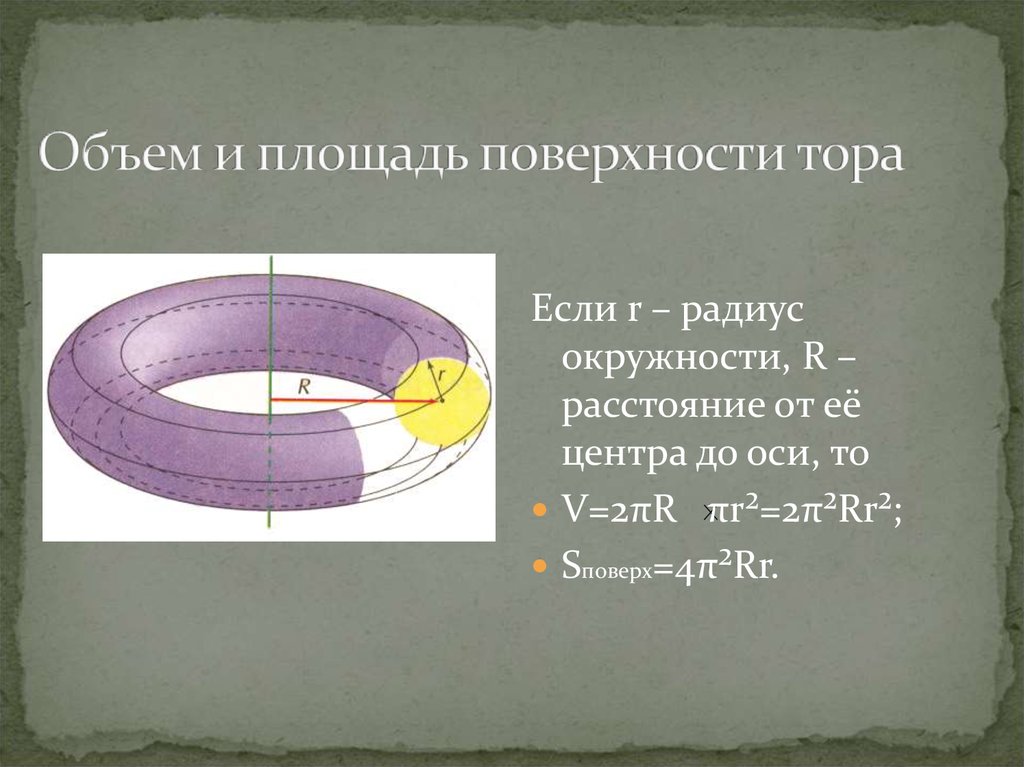 2)*r_Major*r_Minor

Что такое тор?

Тор — это поверхность или твердое тело, образованное вращением замкнутой кривой, особенно круга, вокруг линии, лежащей в той же плоскости, но не пересекающей ее. Обычно это похоже на кольцо.

Share

Copied!

Найти площадь поверхности тора онлайн

Пример решили: 1249 раз Сегодня решили: 0 раз

Введите радиусы R и r

Внешний радиус R Внутренний радиус r

Вычисление площади поверхности тора

Скачать решение в PDF

Порекомендуйте наш сервис друзьям

Вконтакте

Facebook

Twitter

Одноклассники

Google+

Тор (тороид) — поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности.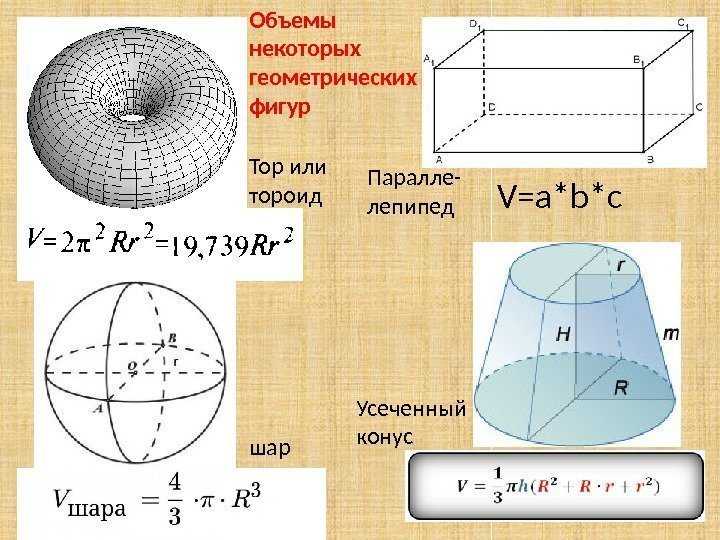 2 $$

Попробуйте другие сервисы

• Найти площадь треугольника

• Найти площадь поверхности параллелепипеда

• Найти площадь поверхности куба

• Найти площадь ромба

• Найти площадь кругового сектора

интегрирование — Площадь поверхности тора

спросил

7 лет, 5 месяцев назад

Изменено 1 год, 8 месяцев назад

Просмотрено 21к раз

$\begingroup$

Можно создать тор следующим образом: $\vec{g}=((b+a\cos u)\cos v, (b+a\cos u)\sin v, a \sin u)$. Чтобы найти его площадь, мы можем использовать поверхностный интеграл вида $S=\iint_{D_{uv}} {\lVert \frac{∂g}{∂u} \times \frac{∂g}{∂v} \rVert \, du \, dv}$. Однако в случае тора вычисление интеграла кажется излишне утомительным. Существуют ли более удобные подходы к оценке площади поверхности с использованием поверхностного интеграла ?

• интеграция
• норм.-пространства
• площадь

$\endgroup$

$\begingroup$

Другим способом было бы выписать поверхностный интеграл, используя дифференциальные формы. Для этого нам нужно настроить карту и систему координат на Торе. К счастью, нам нужна только одна карта, а систему координат можно сделать глобальной (используя координаты, уже введенные в вопросе $u,v$), поверхностный интеграл будет равен 92 аб $$

$\endgroup$

$\begingroup$

$$\frac{\partial\vec{g}}{\partial u}=(-a\sin u\cos v, -a\sin u\sin v, a \cos u),$$

$$\frac{\partial\vec{g}}{\partial v}=(-(b+a\cos u)\sin v, (b+a\cos u)\cos v, 0). 2 аб $$

$\endgroup$

3

$\begingroup$

При выборе тороидальной системы координат вычисление площади, как мне кажется, наиболее просто. Тем не менее, можно использовать как гибрид между сферической и цилиндрической системами координат.

Пусть радиус в венце равен $b$, радиус трубы $R$, $r$ переменный радиус цилиндрической системы координат и $\phi$ широта сферической системы. Площадь тора = 9{ \pi} ( b- R \cos \phi) d \phi = 2 \pi R \cdot 2 \pi b. $$

По сути, это генерация площади поверхности путем вращения с использованием теоремы Паппу.

$\endgroup$

$\begingroup$

На самом деле эта задача требует только простого интеграла, вам просто нужно проинтегрировать (b+cos(s)) 2 pi a ds от 0 до 2pi. Речь идет о добавлении бесконечного числа кругов бесконечно малой ширины а

ds. Радиус этих окружностей в среднем равен b, но может быть как b+a (внешний ребро тора), так и меньше b-a (внутренний ребро тора). Для любого s радиус окружности будет равен b+cos s, если мы выберем s так, чтобы s=0 соответствовало положению, в котором радиус максимален. Сначала я был очень обеспокоен, когда понял, что член косинуса становится равным нулю, когда мы интегрируем, так что формула сводится к абсурдно простому 2pi a умножить на 2 pi*b, умножить большой периметр на маленький периметр. Мы поймем, почему это так просто, если рассмотрим любой горизонтальный срез тора. Он будет состоять из двух окружностей радиусом b+cos(s) и b-cos(s), где s — угол, соответствующий одной из двух окружностей (подойдет любой, просто оставьте одинаковые s для обеих окружностей) . Косинусные члены всегда отменяются! Магия!

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

интегрирование — Расчет площади поверхности тора

спросил 7 лет, 1 месяц назад

Изменено 7 лет, 1 месяц назад

Просмотрено 7к раз

$\begingroup$

Я пытался вычислить площадь поверхности тора, радиус трубки которого равен r, а расстояние от «сингулярности» до центра трубки тора равно R.

Вот что я пытался сделать (Причина, по которой я думаю, что я ошибаюсь из-за страницы альфа-тора wolfram).

Должен отметить, что тем же методом удалось получить нужный объем.

92 рр$.

$\endgroup$

$\begingroup$

Геометрический подход : Существует более простой и легкий подход к нахождению площади поверхности тора, имеющего радиус трубы $r$ и расстояние $R$ от сингулярности до центра тора.

No related posts.