Теорема фалеса рисунок – формула и примеры решения задач

Теорема Фалеса | Треугольники

Теорема Фалеса может быть сформулирована не только для угла, но и для прямых. Кроме того, существует еще и обобщенная теорема Фалеса.

Теорема Фалеса.

Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне.

 

∠COD

   

Замечание.

Теорема Фалеса может быть сформулирована не только для угла, но и для прямых.

Теорема.

Если параллельные прямые пересекают две данные прямые и отсекают на одной прямой равные отрезки, то они отсекают равные отрезки и на другой прямой.

 

a и b — прямые

   

Теорема о пропорциональных отрезках (обобщенная теорема Фалеса).

Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

 

   

 

Теорема Фалеса и ее модификации применяется в том числе, и в задачах на построение (в частности, для деления отрезка на n равных частей и при построении четвертого пропорционального отрезка).

Четырехугольники

www.treugolniki.ru

Фалес Милетский, или о том, как важно знать подобие треугольников и теорему Фалеса.

Эта гробница мала, но слава над ней необъятна.
В ней перед тобою сокрыт многоразумный Фалес.

Надпись на гробнице Фалеса Милетского
 

Представьте себе такую картину. 600 г. до н.э. Египет. Перед вами огромнейшая египетская пирамида. Чтобы удивить фараона и остаться у него в фаворитах вам нужно измерить высоту этой пирамиды. В  распоряжении у вас… ничего. Можно пасть в отчаяние, а можно поступить, как Фалес Милетский: использовать теорему подобия треугольников. Да, оказывается, все достаточно просто. Фалес Милетский подождал пока длина его тени и его рост совпадут, а затем с помощью теоремы о подобии треугольников нашел длину тени пирамиды, которая соответственно, была равна тени, отбрасываемой пирамидой.  

Кто же такой этот Фалес Милетский? Человек, который обрел славу одного из «семи мудрецов» древности? Фалес Милетский – древнегреческий философ, который отличился успехами в области астрономии, а также математики и физики. Годы его жизни были установлены только приблизительно: 625-645 гг до н.э.

Среди доказательств знания Фалесом астрономии можно привести следующий пример. 28 мая 585 г до н.э. предсказание Милетским солнечного затмения помогло прекратить длившуюся уже 6 лет войну между Лидией и Мидией. Это явление настолько испугало мидян, что они согласились на невыгодные для себя условия заключения мира с лидийцами.

Довольно широко известна легенда, которая характеризует Фалеса как находчивого человека. Фалесу часто приходилось слышать нелестные отзывы о его бедности. Однажды он решил доказать то, что и философы могут при желании жить в достатке. Еще зимой Фалес по наблюдению за звездами определил, что летом будет хороший урожай маслин. Тогда же он нанял маслодавильни в Милете и на Хиосе. Это обошлось ему довольно дешево, так как зимой спрос на них практически отсутствует. Когда же маслины дали богатый урожай, свои маслодавильни Фалес начал сдавать внаем. Собранное большое количество денег таким методом расценивалось как доказательство того, что философы могут зарабатывать своим умом, но их призвание выше таких земных проблем. Эта легенда, кстати, повторялась самим Аристотелем.

Что же касается геометрии, то многое из его «открытий» было позаимствовано у египтян. И все же этот перенос знаний в Грецию считается одной из основных заслуг Фалеса Милетского.

Достижениями Фалеса считаются формулировка и доказательство следующих теорем:

• вертикальные углы равны;
• равными треугольниками признаются те, у которых сторона и два прилегающих угла соответственно равны;
• углы при основании равнобедренного треугольника равны;
• диаметр делит круг пополам;
• вписанный угол, опирающийся на диаметр, является прямым.

Именем Фалеса названа еще одна теорема, которая полезна при решении геометрических задач. Существует ее обобщенный и частный вид, обратная теорема, формулировки также могут немного отличаться в зависимости от источника, но смысл их всех остается одним. Рассмотрим эту теорему.

Если параллельные прямые пересекают стороны угла и отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Допустим, точки А₁, А₂, А₃ – точки пересечения параллельных прямых с одной из сторон угла, а В₁, В₂, В₃ – точки пересечения параллельных прямых с другой стороной угла. Необходимо доказать, что если А₁А₂ = А

2А₃, то и В₁В₂ = В₂В₃.

Через точку В₂ проведем прямую, параллельную прямой А₁А₂. Обозначим новую прямую С₁С₂. Рассмотрим параллелограммы A₁C₁B₂A₂ и A₂B₂C₂A₃.

Свойства параллелограмма позволяют нам утверждать, что A1A2 = C₁B₂ и A₂A₃ = B₂C₂.  А так как по нашему условию А₁А₂ = А₂А₃, то и C₁B₂ = В₂С₂.

И, наконец, рассмотрим треугольники Δ C₁B₂B₁ и Δ C₂B₂B₃.

C₁B₂ = B₂C₂ (доказано выше).

<C₁B₂B₁ и <C₂B₂B₃ вертикальные, т.е. равны.

<B₁C₁B₂ и <B₃C₂B₂ внутренние накрестлежащие.

А это значит, что Δ C₁B₂B₁ и Δ C₂B₂B₃ будут равны по второму признаку равенства треугольников (по стороне и прилегающим углам).

Таким образом, теорема Фалеса доказана.

Использование данной теоремы значительно облегчит и ускорит решение геометрических задач. Успехов в освоении этой занимательной науки математики!

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Интегрированный урок (математика + информатика) по теме: «Теорема Фалеса»

Разделы: Математика

---

Цели урока:

Образовательная: доказать теорему Фалеса, научить применять её при решении задач по математике и информатике.

Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике.

Воспитательная: воспитывать внимание, аккуратность, расширять кругозор учеников.

Оборудование и материалы:

Компьютер, экран, проектор.
Проектная работа “Теорема Фалеса”.
Программа “Живая геометрия”.
Плакат с рисунками 1,2,3.

Задачи учителей:

Показать практическое применение теоретических знаний учащихся при решении задач по геометрии и информатике.

Выявить глубокие связи между математикой и информатикой.

Ход урока:

Урок начинает учитель математики. Приветствие и вступительное слово о целях урока.

Фронтальный опрос учащихся:

1. Какие отрезки называются равными?

2. Какие прямые называются параллельными? На рис. 1 покажите параллельные прямые.

3. Какие углы называются вертикальными, внутренними накрест лежащими? Покажите их на рис.2

4. Сформулируйте теорему о свойстве параллельных прямых, пересечённых третьей прямой.

5. Сформулируйте признаки равенства треугольников. По каким признакам равны треугольники на рис 3?

Объяснение нового материала

Учитель математики объясняет новую тему с помощью просмотра проектной работы “Теорема Фалеса”.

(Приложение 1)

Сегодня мы докажем теорему, носящую имя древнегреческого учёного Фалеса, который жил в 624-547г.г. до н.э.

 

• Великий учёный Фалес Милетский основал одну из прекраснейших наук — геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Короче: он был то же для Греции, что Ломоносов для России
.

Карьеру он начинал как купец и ещё в молодости попал в Египет. В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Считается, что геометрию и астрономию в Грецию привёз он.

Фалес — математик. Он измерил по тени высоту пирамиды; установил, что окружность диаметром делится пополам, что углы при основании равнобедренного треугольника равны. Ему же принадлежит теорема, что вписанный угол, опирающийся на диаметр окружности- прямой.

Фалес доказал теорему: “Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне”.

При активном участии учащихся разбирается доказательство теоремы с последовательным показом на экране каждого этапа построения чертежа и доказательства теоремы.

Из условия теоремы Фалеса делается вывод, что вместо сторон угла можно взять любые две прямые.

Затем ученики выполняют в тетрадях практическую задачу на деление отрезка длиной в 7см. на 6 равных частей.

Греческие ученые открыли множество геометрических свойств и создали стройную систему геометрических знаний. В ее основу они положили простейшие геометрические свойства, подсказанные опытом. Остальные свойства выводились из простейших с помощью рассуждений.

Все этапы решения задачи учащиеся видят на экране. Это способствует зрительному запоминанию алгоритма решения данной задачи.

Показ проектной работы сопровождается музыкой- игрой на гитаре, что создаёт спокойную рабочую обстановку.

Вторую часть урока ведёт учитель информатики. С помощью программы “Живая геометрия” ученики вместе с учителем на компьютерах делят отрезок на три равные части.

Выполнение практического задания

Разделить данный отрезок на 3-равные части на компьютере с помощью программы “Живая геометрия”.

Используемые ИНСТРУМЕНТЫ “Живой геометрии”:

• стрелка;

• линейка (отрезок, луч).

Используемые КОМАНДЫ “Живой геометрии”:

• построения;

• правка;

Порядок работы:

1 .Построим данный отрезок АВ.

2.Проведем из т. А полупрямую а, не лежащую на прямой АВ.

3.Отложим на полупрямой а 3 равных отрезка.

Для этого используем команду ПОСТРОЕНИЯ— “окружность по центру и радиусу”; зададим произвольный радиус СО и построим на полупрямой а 3 окружности.

Они отсекают на полупрямой а равные отрезки АЕ=ЕР=РО.

4.Соединим точки В и О.

5. Проведем через точки Е и Р прямые, параллельные прямой ВО.

6. Они пересекают отрезок АВ в точках Н и I , которые делят отрезок АВ на 3 равные части; т

xn--i1abbnckbmcl9fb.xn--p1ai

Математика. Основы геометрии: Обобщенная теоремы Фалеса. Пропорции. Масштаб

Главная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >

<< Назад  |   Оглавление  |   Далее >>

Пропорции

Равенство вида

x1	=	y1
x2		y2

называется пропорцией. При этом говорят, что:

x₁ относится к x₂ как y₁ относится к y₂,

или

отношение чисел x₁ и x₂ равно отношению чисел y₁ и y₂,

или же

числа x₁ и x₂ соотносятся так же, как числа y₁ и y₂,

или, наконец,

числа x₁ и y₁ (!) пропорциональны числам x₂ и y₂ (то есть числители пропорциональны знаменателям).

Входящие сюда числа x₁, x₂, y₁ и y₂ называются членами пропорции. Обычно все они положительны, но это необязательно. Предполагается, однако, что ни одно из них не равно нулю. Особого названия это равенство удостоилось по той причине, что оно часто встречается при решении разных математических задач.

 

Пропорции можно преобразовывать, перенося члены «с верху» одной части равенства «в низ» другой части равенства и наоборот. Эту процедуру легко обосновать следующим образом. Допустим мы хотим перенести x₁ из левой части в правую. Для этого умножим обе части пропорции на 1/x₁:

1		x1	=	1		y1	.
x1		x2		x1		y2

В результате получаем

1	=	y1	,
x2		x1y2

то есть переменная x₁ у нас переместилась «по диагонали сверху вниз». Перенесем теперь «влево наверх» переменную y₂. Это достигается умножением на нее обеих частей данного равенства. В результате имеем

y2	=	y1	.
x2		x1

Мы получили новую пропорцию, которая отличается от исходной перестановкой членов, расположенных «по диагонали». Таким образом, в первоначальном равенстве

x1	=	y1
x2		y2

числители x₁ и y₁ соотносятся между собой точно так же, как и соответствующие им знаменатели x₂ и y₂.

Обобщенная теорема Фалеса

Теорема Фалеса, рассмотренная в прошлый раз, допускает следующее обобщение.

Пусть две произвольные прямые x и y пересекаются тремя параллельными прямыми n₁, n₂ и n₃ в точках X₁, X₂, X₃ и Y₁, Y₂, Y₃, как показано на рисунке:

 

Тогда длины отсекаемых отрезков образуют следующую пропорцию

|Y1Y2|	=	|X1X2|	.
|Y1Y3|		|X1X3|

Докажем эту теорему в случае, когда отношение длин

представляет собой рациональное число, то есть может быть выражено в виде несократимой дроби

|X1X2|	=	a	,
|X1X3|		b

где a и b — некоторые натуральные числа, a < b. Разобьем отрезок X₁X₃ на b одинаковых частей. (При этом точка X₂ окажется одной из точек деления.) Проведем через каждую точку деления прямые, параллельные n₁, n₂ и n₃. (Одна из этих прямых совпадет с прямой n₂.)

 

По теореме Фалеса (в ее первоначальном варианте), отрезок Y₁Y₃ также делится этими прямыми на b равных частей, из которых a частей составляют отрезок Y₁Y₂. Следовательно,

|Y1Y2|	=	a	=	|X1X2|	,
|Y1Y3|		b		|X1X3|

что и требовалось доказать. Из нашего построения следует также, что

|Y2Y3|	=	b − a	=	|X2X3|
|Y1Y3|		b		|X1X3|

и

|Y2Y3|	=	b − a	=	|X2X3|	.
|Y1Y2|		a		|X1X2|

Пользуясь свойствами пропорций, эти равенства можно переписать в виде одной цепочки:

|Y1Y2|	=	|Y2Y3|	=	|Y1Y3|	.
|X1X2|		|X2X3|		|X1X3|

Таким образом, отрезки отсекаемые на прямой y пропорциональны соответствующим отрезкам на прямой x.

 

Теоретически возможна также ситуация, когда отношение длин

не является рациональным числом, поскольку длины отрезков |X₁X₂| и |X₁X₃| могут, в принципе, выражаться иррациональными числами. Однако на практике такой случай никогда не встречается. Для определения длин отрезков мы всегда пользуемся каким-либо измерительным прибором (например, школьной линейкой), который выдает лишь округленные результаты в виде конечной десятичной дроби.

Важное следствие

Пусть даны несовпадающие прямые x и y, которые пересекаются в точке O, и еще — две параллельные прямые n₁ и n₂, которые пересекают прямую x в точках X₁ и X₂ и прямую y в точках Y₁ и Y₂, как показано на рисунке.

 

Введем обозначения:

x₁ = |OX₁|, x₂ = |OX₂|;

y₁ = |OY₁|, y₂ = |OY₂|;

z₁ = |X₁Y₁|, z₂ = |X₂Y₂|.

Тогда

x1	=	y1	=	z1	.
x2		y2		z2

Действительно, оба равенства в этой цепочке непосредственно следует из обобщенной теоремы Фалеса. Для первого равенства это ясно сразу, а для второго это становится очевидным после того, как мы через точку Y₁ проведем прямую m, параллельную прямой x.

 

Верно и обратное утверждение. Пусть дана та же геометрическая конструкция и известно, что

x1	=	y1	.
x2		y2

Тогда прямые n₁ и n₂ параллельны. В самом деле, проведем через точку X₁ вспомогательную прямую, параллельную прямой n₂. По обобщенной теореме Фалеса, эта вспомогательная прямая проходит через точку Y₁. Следовательно, она совпадает с прямой n₁. Таким образом, прямая n₁ параллельна прямой n₂.

Масштаб

Выйдем на улицу, прихватив с собой лист бумаги и карандаш. Расположим наш лист горизонтально и поставим на нем приблизительно посередине точку O. Из этой точки проведем мысленно лучи в направлении различных примечательных точек на местности, расположенных в радиусе примерно ста метров, — деревьев, столбов, углов зданий и того подобного.

Допустим, у нас есть возможность измерить расстояния до этих примечательных точек. Пусть, например, расстояние до ближайшего дерева равно 10 м. Мысленно отложим от точки O в направлении этого дерева отрезок, длина которого в 1000 раз меньше данного расстояния, и отметим карандашом на бумаге положение второго его конца. Нетрудно рассчитать, что расстояние от точки O до отметки составит 10 м/1000 = 1 см.

Подобным же образом, пусть расстояние до какого-то другого примечательного объекта равно x₁. Умножим это расстояние на число k, равное 1/1000. Мысленно отложим от точки O отрезок длиной x₂ = kx₁ вдоль луча, направленного на данный объект. В том месте на бумаге, где находится второй конец отрезка, сделаем отметку карандашом. Проделаем такую процедуру со всеми примечательными точками на местности, используя всё время одно и то же значение параметра k. Если какие-либо из этих точек соединены между собой забором или стеной или же чем-то подобным, то между соответствующими метками на бумаге также проведем линии.

В результате на нашем листе бумаги получится карта местности. В силу теоремы Фалеса и свойств пропорций, все соотношения между расстояниями на бумаге будут в точности такими же, как и в действительности. Более того, все линии на бумаге окажутся параллельны соответствующим линиям на местности. Эта параллельность, конечно, нарушится, когда мы унесем наш лист куда-нибудь в другое место, однако углы между линиями сохранятся.

Параметр k, который мы использовали в нашем построении, называется масштабным коэффициентом или просто масштабом. Разумеется, он необязательно должен быть равен 1/1000. Он может, в принципе, принимать любое значение, важно лишь, чтобы это значение оставалось всё время неизменным в процессе построения карты.

На настоящих географических картах масштаб обязательно указывается в легенде, при этом вместо дробной черты обычно используется двоеточие. Например, масштаб 1:100 000 означает, что один сантиметр на карте соответствует 100000 сантиметрам (то есть одному километру) на местности.

Технические чертежи также всегда выполняются, как говорят,  в определенном масштабе. Масштаб 1:1 означает, что деталь начерчена в натуральную величину. А масштаб 10:1 говорит о том, что чертеж выполнен с десятикратным увеличением.

Замечание о параллельных прямых

Мы назвали параллельными такие несовпадающие прямые, угол между которыми равен нулю. Мы отметили, что такие прямые нигде не пересекаются. Докажем теперь, что если прямые лежат в одной плоскости и не параллельны (то есть угол между ними отличен от нуля), то тогда они обязательно где-нибудь пересекутся.

Пусть на плоскости даны две прямые — x и n. Отметим на них произвольные точки — O и Y — и проведем через эти точки третью прямую — y. Если исходить из того, что угол между прямыми x и n не равен нулю, то смежные углы должны оказаться не равны друг другу. Пусть для определенности α₁ > α₂, как показано на рисунке.

 

Проведем через точку O прямую n₁, параллельную прямой n. Отметим на ней со стороны угла α₁ произвольную точку N₁ и проведем через эту точку прямую y₁, параллельную прямой y. При этом образуется параллелограмм, обозначенный на рисунке серым фоном.

 

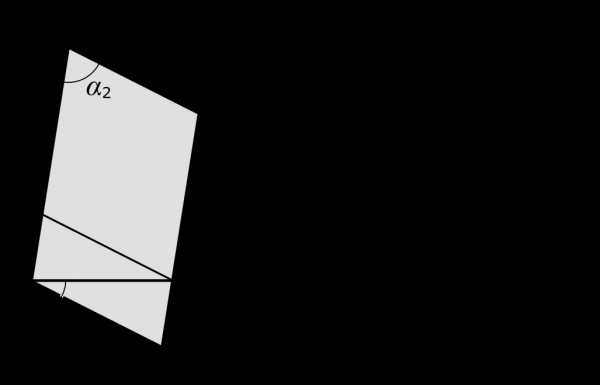
Это значит, что прямая y₁ пересекает прямую n в некоторой точке, которую мы обозначим через N. Прямая x, заходя на «территорию» параллелограмма в точке O, обязательно должна где-то оттуда выйти. Она может это сделать либо через отрезок YN, либо через отрезок N₁N. В первом случае сразу становится очевидно, что прямая x пересекает прямую n. Рассмотрим второй случай. Обозначим точку пересечения прямой x и отрезка N₁N через X₁. Проведем через нее прямую n₂, параллельную прямой n. Эта прямая разбивает параллелограмм ON₁NY на два новых параллелограмма и пересекает прямую y в некоторой точке Y₁. Отметим на прямой x такую точку X, для которой выполняется соотношение

|OY1|	=	|OX1|	.
|OY|		|OX|

Проведем через точки X и Y прямую. Согласно рассмотренному выше следствию из теоремы Фалеса, эта прямая параллельна прямой n₂, а значит, образует нулевой угол с прямой n. Следовательно, новая прямая совпадает с прямой n, которая, таким образом, пересекает прямую x в точке X.

Мы теперь можем утверждать, что следующие три утверждения о несовпадающих прямых a и b, лежащих в одной плоскости, означают в точности одно и то же:

(1) Угол между прямыми a и b равен нулю.

(2) Прямые a и b нигде не пересекаются.

(3) Прямые a и b параллельны.

В традиционных курсах геометрии определением параллельности прямых служит утверждение 2. Мы выбрали для этих целей утверждение 1. Ведь гораздо проще определить угол между двумя прямыми, чем удостовериться, что они нигде не пересекаются на всём своем бесконечном протяжении.

Конспект

1. Равенство вида x₁/x₂ = y₁/y₂ называется пропорцией. Числители пропорциональны знаменателям. Числитель и знаменатель одной дроби соотносятся так же, как числитель и знаменатель другой дроби. Эквивалентное равенство: x₁/y₁ = x₂/y₂.

2. Обобщенная теорема Фалеса. Пусть две произвольные прямые a и b пересекаются тремя параллельными прямыми. Тогда отрезки, отсекаемые на прямой a, пропорциональны соответствующим отрезкам, отсекаемым на прямой b.

3. Следствие 1. Пусть стороны угла с вершиной в точке O пересекаются двумя параллельными прямыми n₁ и n₂. Тогда отрезки, отсекаемые на прямых n₁ и n₂, соотносятся так же, как отрезки, отложенные на любой из сторон угла от точки O до соответствующих точек пересечения с прямыми n₁ и n₂.

4. Следствие 2. Пусть на сторонах угла отложены от вершины отрезки таким образом, что отрезки на одной стороне пропорциональны отрезкам на другой. Тогда прямые, проходящие через соответствующие концы этих отрезков, параллельны друг другу.

5. На карте сохраняются все соотношения между расстояниями и все углы. Отношение расстояния между некоторыми двумя точками на карте к расстоянию между соответствующими точками на местности не зависит от выбора точек и называется масштабом.

6. Если угол между двумя прямыми, лежащими в одной плоскости, не равен нулю, то такие прямые обязательно пересекаются.

 

 

www.nekin.info

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия

      Теорема Фалеса. Через произвольные точки

A₁,  A₂,  …   A_n–1,  A_n,

лежащие на стороне AO угла AOB (рис.1), проведены параллельные прямые, пересекающие сторону угла OB в точках

B₁,  B₂,  …  B_n–1,  B_n,

соответственно. Тогда справедливы равенства

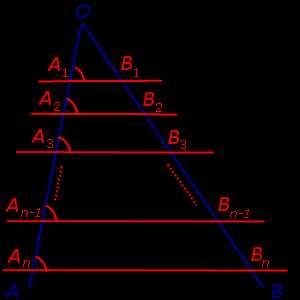
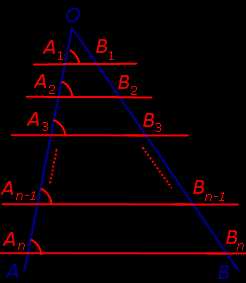
Рис.1

      Доказательство. Докажем сначала следующую лемму.

      Лемма. Через произвольную точку C, лежащую на стороне OA треугольника OAB, проведена прямая, параллельная прямой AB и пересекающая сторону OB в точке D (рис.2).

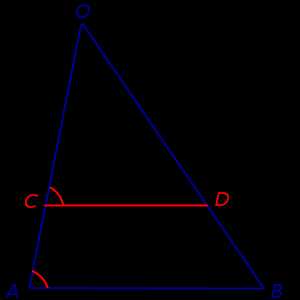
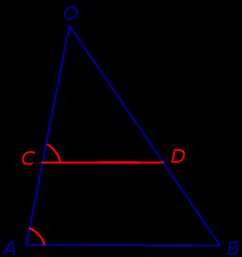
Рис.2

      Тогда справедливо равенство

(1)

      Доказательство леммы. Опустим из точек A и B перпендикуляры AK и BL на прямую CD (рис.3). Заметим, что эти перпендикуляры равны, поскольку AKLB – прямоугольникпрямоугольник.

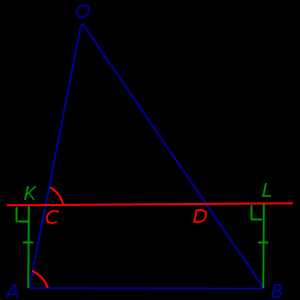
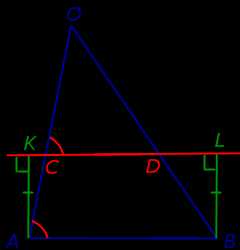
Рис.3

      Из точки D опустим перпендикуляр DF на прямую OA (рис.4).

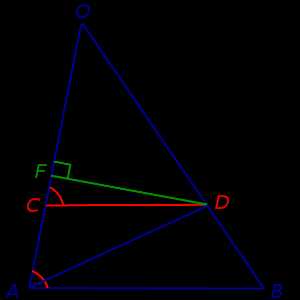
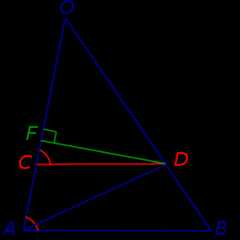
Рис.4

      Из точки C  опустим перпендикуляр CG на прямую OB (рис.5).

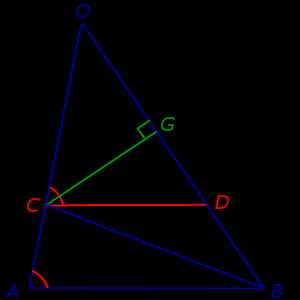
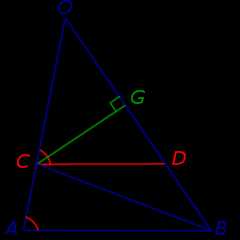
Рис.5

      В соответствии с рисунком 4 площади треугольников OCD и ACD можно вычислить по формулам

      Следовательно,

      В соответствии с рисунком 5 площади треугольников OCD и BCD можно вычислить по формулам

      Следовательно,

      Кроме того, заметим, что площади треугольников ACD и BCD равны. Действительно, в соответствии с рисунком 3 справедливы формулы

      Следовательно,

S_{Δ ACD} = S_{Δ BCD} ,

откуда получаем цепочку равенств

что и завершает доказательство леммы.

      Воспользовавшись леммой, заметим (рис.1), что из равенства (1) вытекают равенства

откуда на основе свойств производных пропорций, заключаем, что справедливы равенства

что и завершает доказательство теоремы Фалеса.

      Следствие. Если через точки

A₁,  A₂,  …   A_n–1,  A_n,

лежащие на стороне AO угла AOB (рис.6) и удовлетворяющие условию

A₁A₂ = A₂A₃ = … =
= A_n–2 A_n–1 = A_n–1A_n ,

проведены параллельные прямые, пересекающие сторону угла OB в точках

B₁, B₂,  …   B_{n –1},  B_n ,

соответственно, то справедливы равенства

B₁B₂ = B₂B₃ = … =
= B_n–2B_n–1 = B_n–1B_n ,

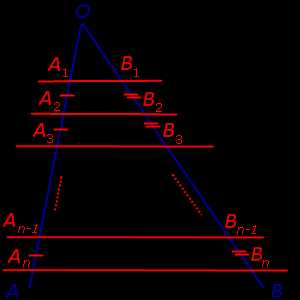
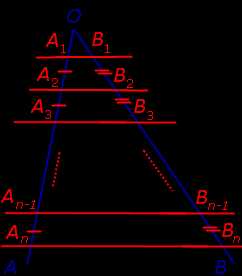
Рис.6

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Теорема Фалеса — это… Что такое Теорема Фалеса?

Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему.

Теорема Фалеса — одна из теорем планиметрии.

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также неважно, где находятся отрезки на секущих.

Доказательство в случае секущих  

Доказательство в случае параллельных прямых  

Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■

Также существует обобщённая теорема Фалеса:

Параллельные прямые отсекают на секущих пропорциональные отрезки:

Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Обратная теорема

Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:

Если прямые, пересекающие стороны угла, отсекают на одной и на другой стороне угла равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.

В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины

Таким образом (см. рис.) из того, что следует, что прямые .

Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).

Вариации и обобщения

Следующее утверждение, двойственно к лемме Соллертинского:

В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.

Это утверждение, в свою очередь, является предельным случаем следующего утверждения:

Пусть  — проективное преобразование коники. Тогда огибающей множества прямых будет коника (возможно, вырожденная).

Теорема Фалеса в культуре

Аргентинская музыкальная группа Les Luthiers (исп.) представила песню, посвящённую теореме. В видеоклипе для этой песни^[1] приводится доказательство для прямой теоремы для пропорциональных отрезков.

Интересные факты

• Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
• Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Литература

• Атанасян С.Л. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.

Примечания

dic.academic.ru

Обобщенная теорема Фалеса; Формулировка

скачать

Содержание:

1. 
   Введение;
   
2. 
   Обобщенная теорема Фалеса;
   

1. 
   Формулировка;
   
2. 
   Доказательство;
   

3. 
   Теорема о пропорциональных отрезках;
   
4. 
   Теорема Чевы;
   

1. 
   Формулировка;
   
2. 
   Доказательство;
   

5. 
   Теорема Менелая;
   

1. 
   Формулировка;
   
2. 
   Доказательство;
   

6. 
   Задачи и их решения;
   
7. 
   Заключение;
   
8. 
   Список использованных источников и литературы.
   

Введение.

Все незначительное нужно,

Чтобы значительному быть…

И. Северянин
Данный реферат посвящен применению метода параллельных прямых к доказательству теорем и решению задач. Почему мы обращаемся к этому методу? В этом учебном году на школьной олимпиаде по математике была предложена геометрическая задача, которая нам показалась очень сложной. Именно данная задача и дала импульс к началу работы по изучению и освоению метода параллельных прямых при решении задач на нахождение отношения длин отрезков.

Идея самого метода построена на использовании обобщенной теоремы Фалеса. Теорема Фалеса изучается в восьмом классе, ее обобщение и тема «Подобие фигур» в девятом и только в десятом классе, в ознакомительном плане, изучаются две важные теоремы Чевы и Менелая, с помощью которых относительно легко решается ряд задач на нахождение отношения длин отрезков. Поэтому на ступени основного образования мы можем решать довольно узкий круг задач по данному учебному материалу. Хотя на итоговой аттестации за курс основной школы и на ЕГЭ по математике задачи по данной теме (Теорема Фалеса. Подобие треугольников, коэффициент подобия. Признаки подобия треугольников) предлагаются во второй части экзаменационной работы и относятся к высокому уровню сложности.

В процессе работы над рефератом стало возможным углубление наших знаний по данной теме. Доказательство теоремы о пропорциональных отрезках в треугольнике (теорема не входит в школьную программу) построено на методе параллельных прямых. В свою очередь, данная теорема позволила предложить еще один способ доказательства теорем Чевы и Менелая. И в итоге мы смогли научиться решать более широкий круг задач на сравнение длин отрезков. В этом и заключается актуальность нашей работы.

Обобщенная теорема Фалеса.

Формулировка:

Параллельные прямые, пересекающие две данные прямые, отсекают на этих прямых пропорциональные отрезки.
Дано:

Прямая а рассечена параллельными прямыми (А₁В₁, А₂В₂, А₃В₃,…, А_nB_n) на отрезки А₁А₂, А₂А₃, …, A_n-1A_n, а прямая b— на отрезки В₁В₂, В₂В₃, …, В_n-1В_n.

Доказать:

Доказательство:

Докажем, например, что

Рассмотрим два случая:

1 случай (рис. б)

Прямые a и b параллельны. Тогда четырехугольники

А₁А₂В₂В₁ и А₂А₃В₃В₂ – параллелограммы. Поэтому

А₁А₂= В₁В₂ и А₂А₃=В₂В₃, откуда следует, что

2 случай (рис. в)

Прямые a и b не параллельны. Через точку А₁ проведем прямую с, параллельную прямой b. Она пересечет прямые А₂В₂ и А₃В₃ в некоторых точках С₂ и С₃. Треугольники А₁А₂С₂ и А₁А₃С₃подобны по двум углам (угол А₁ – общий, углы А₁А₂С₂ и А₁А₃С₃ равны как соответственные при параллельных прямых А₂В₂ и А₃В₃ секущей А₂А₃), поэтому

1+

Или по свойству пропорций

С другой стороны, по доказанному в первом случае имеем А₁С₂= В₁В₂, С₂С₃= В₂В₃. Заменяя в пропорции (1) А₁С₂на В₁В₂ и С₂С₃на В₂В₃, приходим к равенству

что и требовалось доказать.
Теорема о пропорциональных отрезках в треугольнике.

На сторонах АС и ВС треугольника АВС отмечены точки К и М так, что АК:КС=m:n, BM:MC=p:q. Отрезки АМ и ВК пересекаются в точке О(рис. 124б).

Доказать:

Доказательство:
Через точку М проведем прямую MD(рис. 124а), параллельную ВК. Она пересекает сторону АС в точке D, и согласно обобщению теоремы Фалеса

Пусть АК=mx. Тогда в соответствии с условием задачи КС=nx, а так как KD:DC=p:q, то Снова воспользуемся обобщением теоремы Фалеса:

Аналогично доказывается, что .

Теорема Чевы.
Теорема названа в честь итальянского математика Джованни Чевы, который доказал её в 1678 году.

Формулировка:

Если на сторонах АВ, ВС и СА треугольника АВС взяты соответственно точки С₁, А₁ и В₁, то отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке тогда и только тогда, когда

Дано:

Треугольник АВС и на его сторонах АВ, ВС и АС отмечены точки С₁, А₁ и В₁.

Доказать:

2.отрезки А А₁, ВВ₁ и СС₁ пересекаются в одной точке.

Доказательство:
1. Пусть отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке О. Докажем, что выполнено равенство (3). По теореме о пропорциональных отрезках в треугольнике¹ имеем:

Левые части этих равенств одинаковы, значит, равны и правые части. Приравнивая их, получаем

Разделив обе части на правую часть, приходим к равенству (3).

2. Докажем обратное утверждение. Пусть точки С₁, А₁ и В₁взяты на сторонах АВ, ВС и СА так, что выполнено равенство (3). Докажем, что отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке. Обозначим буквой О точку пересечения отрезков А А₁и ВВ₁ и проведем прямую СО. Она пересекает сторону АВ в некоторой точке, которую обозначим С₂. Так как отрезки АА₁, ВВ₁ и СС₁ пересекаются в одной точке, то по доказанному в первом пункте

Итак, имеют место равенства (3) и (4).

Сопоставляя их, приходим к равенству = , которое показывает, что точки C₁ и C₂ делят сторону AB в одном и том же отношении. Следовательно, точки C₁ и C₂ совпадают, и, значит, отрезки АА₁, ВВ₁ и СС₁ пересекаются в точке O.

Что и требовалось доказать.
Теорема Менелая.

Формулировка:

Если на сторонах АВ и ВС и продолжении стороны АС (либо на продолжениях сторон АВ, ВС и АС) взяты соответственно точки С₁, А₁, В₁, то эти точки лежат на одной прямой тогда и только тогда, когда

Дано:

Треугольник АВС и на его сторонах АВ, ВС и АС отмечены точки С₁, А₁ и В₁.

Доказать:

2. точки А₁,С₁ и В₁ лежат на одной прямой
Доказательство:
1. Пусть точки А₁,С₁ и В₁ лежат на одной прямой. Докажем, что выполнено равенство (5). Проведем AD,BE и CF параллельно прямой В₁А₁ (точка D лежит на прямой ВС). Согласно обобщенной теоремы Фалеса имеем:

Перемножая левые и правые части этих равенств, получаем

т.е. выполнено равенство (5).
2. Докажем обратное утверждение. Пусть точка В₁ взята на продолжении стороны АС, а точки С₁ и А₁ – на сторонах АВ и ВС, причем так, что выполнено равенство (5). Докажем, что точки А₁,С₁ и В₁ лежат на одной прямой. Пусть прямая А₁С₁пересекает продолжение стороны АС в точке В_2, тогда по доказанному в первом пункте

Сопоставляя (5) и (6), приходим к равенству = , которое показывает, что точки В₁ и В₂ делят сторону АС в одном и том же отношении. Следовательно, точки В₁ и В₂ совпадают, и, значит, точки А₁,С₁ и В₁ лежат на одной прямой. Аналогично доказывается обратное утверждение в случае, когда все три точки А₁,С₁ и В₁ лежат на продолжениях соответствующих сторон.

Что и требовалось доказать.

Решение задач.

Предлагается рассмотреть ряд задач на пропорциональное деление отрезков в треугольнике. Как было отмечено выше, для определения места расположения нужных в задаче точек существует несколько методов. В своей работе мы остановились на методе параллельных прямых. Теоретической основой данного метода является обобщенная теорема Фалеса, которая позволяет с помощью параллельных прямых переносить известные отношения пропорции с одной стороны угла на вторую его сторону, таким образом, нужно только удобным для решения задачи способом провести эти параллельные прямые.
Рассмотрим конкретные задачи:
Задача №1 В треугольнике АВС на стороне ВС взята точка М так, что ВМ:МС=3:2. Точка Р делит отрезок АМ в отношении 2:1. Прямая ВР пересекает сторону АС в точке В₁. В каком отношении точка В₁ делит сторону АС?

Решение: Нужно найти отношение АВ₁:В₁С, АС искомый отрезок на котором лежит точка В₁.

Метод параллельных заключается в следующем:

1. 
   рассечь искомый отрезок параллельными прямыми. Одна ВВ₁ уже есть, а вторую МN проведем через точку М, параллельно ВВ₁.
   
2. 
   Перенести известное отношение с одной стороны угла на другую его сторону, т.е. рассмотреть углы стороны, которых и рассекаются этими прямыми.
   

Стороны угла С рассекаются прямыми ВВ₁ и МN и по обобщенной теореме Фалеса заключаем В₁N=3р, NC=2р. Стороны угла МАС пересекают прямые РВ₁ и МN и делят его стороны в отношении 2:1, следовательно АВ₁:В₁N=2:1 и значит АВ₁=2n, В₁N=n. Так как В₁N=3р, и В₁N=n, то 3р= n.

Перейдем к интересующему нас отношению АВ₁:В₁С= АВ₁🙁 В₁N+ NС)= 2n:(3р+2р)=(2*3р):(5р)=6:5.

Ответ: АВ₁:В₁С = 6:5.

Замечание: Данную задачу можно было решить, используя теорему Менелая. Применив ее к треугольнику АМС. Тогда прямая ВВ₁ пересекает две стороны треугольника в точках В₁ и Р, а продолжение третьей в точке В. Значит применимо равенство: , следовательно
Задача №2 В треугольнике АВС АN – медиана. На стороне АС взята точка М так, что АМ : МС = 1 : 3. Отрезки AN и ВМ пересекаются в точке О, а луч СО пересекает АВ в точке К. В каком отношении точка К делит отрезок АВ.

Решение: Нужно найти отношение АК к КВ.

1) Проведем прямую NN₁ параллельную прямой СК и прямую NN₂ параллельную прямой ВМ.

2) Стороны угла АВС пересекаются прямыми СК и NN₁ и по обобщенной теореме Фалеса заключаем ВN₁:N₁K=1:1 или ВN₁= N₁K=y.

3) Стороны угла ВСM пересекаются прямыми BM и NN₂ и по обобщенной теореме Фалеса заключаем CN₂:N₂M=1:1 или CN₂= N₂M=3:2=1,5.

4) Стороны угла NАС пересекаются прямыми BM и NN₂ и по обобщенной теореме Фалеса заключаем АО: ОN=1:1,5 или АО=m ON=1,5m.

5) Стороны угла ВАN пересекаются прямыми СК и NN₁ и по обобщенной теореме Фалеса заключаем АK: KN₁=1:1,5 или АK=n KN₁=1,5n.

6) KN₁=y=1,5n.

Ответ: АК:КВ=1:3.

Замечание: Данную задачу можно было решить, используя теорему Чевы, применив ее к треугольнику АВС. По условию точки N, М, К лежат на сторонах треугольника АВС и отрезки АN, СК и ВМ пересекаются в одной точке, значит справедливо равенство: , подставим известные отношения, имеем , АК:КВ=1:3.

Задача№3 На стороне ВС треугольника АВС взята точка D такая, что ВD : DC = 2:5, а на стороне АС точка Е такая, что . В каком отношении делятся отрезки ВЕ и АD точкой К их пересечения?
Решение: Нужно найти 1) АК:КD=? 2) ВК:КЕ=?

1) Проведем прямую DD₁ параллельную прямой BE.

2) Стороны угла ВСЕ пересекаются прямыми ВЕ и DD₁ и по обобщенной теореме Фалеса заключаем CD₁😀₁E=5:2 или CD₁= 5z , D₁E=2z.

3) По условию АЕ:ЕС=1:2, т.е. АЕ=х, ЕС=2х, но ЕС= CD₁+ D₁E, значит 2у=5z+2z=7z, z=

4) Стороны угла DСA пересекаются прямыми ВЕ и DD₁ и по обобщенной теореме Фалеса заключаем

5) Для определения отношения ВК:КЕ проведем прямую ЕЕ₁ и рассуждая аналогичным образом получим

Ответ: АК:КD=7:4; ВК:КЕ=6:5.
Замечание: Данную задачу можно было решить, используя теорему Менелая. Применив ее к треугольнику ВЕС. Тогда прямая DA пересекает две стороны треугольника в точках D и K, а продолжение третьей в точке A. Значит применимо равенство: , следовательно ВК:КЕ=6:5. Рассуждая аналогично относительно треугольника ADC, получим , АК:КD=7:4.
Задача №4 В ∆ ABC биссектриса AD делит сторону BC в отношении 2 : 1. В каком отношении медиана CE делит эту биссектрису?

Решение: Пусть О точка пересечения биссектрисы AD и медианы СЕ. Нужно найти отношение АО:ОD.

1) Проведем прямую DD₁ параллельную прямой СE.

2) Стороны угла АВС пересекаются прямыми СЕ и DD₁ и по обобщенной теореме Фалеса заключаем ВD₁😀₁E=2:1 или ВD₁= 2p , D₁E=p.

3) По условию АЕ:ЕB=1:1, т.е. АЕ=y, ЕB=y, но EB= BD₁+ D₁E, значит у=2p+p=3p, p =
4) Стороны угла BAD пересекаются прямыми OЕ и DD₁ и по обобщенной теореме Фалеса заключаем _.

Ответ: АО:ОD=3:1.

Задача №5 На сторонах AB и АC ∆ABC даны соответственно точки M и N такие, что выполняются следующие равенства АМ:МВ=СN:NA=1:2. В каком соотношении точка S пересечения отрезков BN и CM делит каждый из этих отрезков.

Задача №6 На медиане АМ треугольника АВС взята точка К, причем АК:КМ=1:3. Найдите отношение, в котором прямая, проходящая через точку К параллельно стороне АС, делит сторону ВС.

Решение: Пусть М₁ точка пересечения прямой, проходящая через точку К параллельно стороне АС и стороны ВС. Нужно найти отношение ВМ₁:М₁С.

1) Стороны угла АМС пересекаются прямыми КМ₁ и АС_{и по обобщенной теореме Фалеса заключаем ММ1:М1С=3:1 или ММ1= 3z, М1С=z}

2) По условию ВМ:МС=1:1, т.е.ВМ=y, МС=y, но МС= ММ₁+ М₁С, значит у=3z+z=4z,

3) _.

Ответ: ВМ₁:М₁С =7:1.

Задача №7 Дан треугольник АВС. На продолжении стороны АС за точку С взята точка N, причем СN=АС; точка К- середина стороны АВ. В каком отношении прямая КN делит сторону ВС.

Замечание: Данную задачу можно было решить, используя теорему Менелая. Применив ее к треугольнику АВС. Тогда прямая КN пересекает две стороны треугольника в точках К и K₁, а продолжение третьей в точке N. Значит применимо равенство: , следовательно ВК₁:К₁С=2:1.

Задача №8
Сайты:

http://festival.1september.ru

http://www.problems.ru

http://interneturok.ru/

ЕГЭ 2011 Математика Задача С4 Р.К.Гордин М.: МЦНМО, 2011, — 148 с

Заключение:

Решение задач и теорем на нахождение отношения длин отрезков базируется на обобщенной теореме Фалеса. Мы сформулировали метод, который позволяет, не применяя теорему Фалеса, пользоваться параллельными прямыми, переносить известные пропорции с одной стороны угла на другую сторону и, таким образом, находить место расположения нужных нам точек и сравнивать длины. Работа над рефератом помогла нам научиться решать геометрические задачи высокого уровня сложности. Мы осознали правдивость слов известного русского поэта Игоря Северянина: «Все незначительное нужно, Чтобы значительному быть…» и уверены, что на ЕГЭ мы сможем найти решение предложенным задачам, используя метод параллельных прямых.

скачать

nenuda.ru