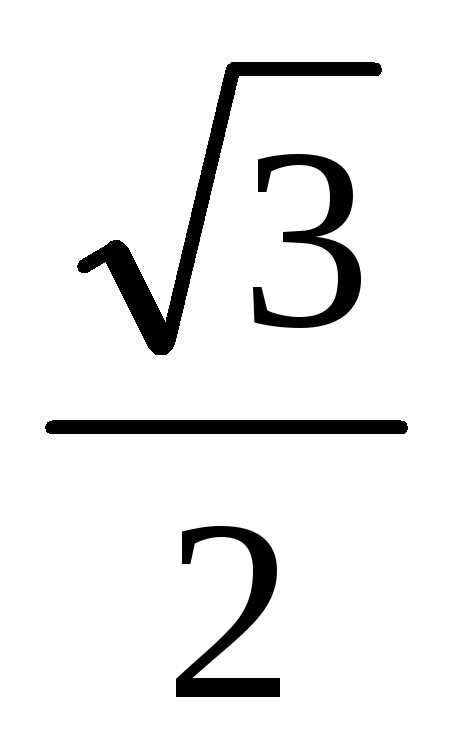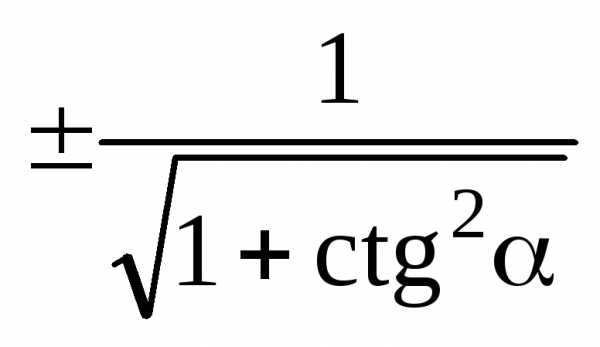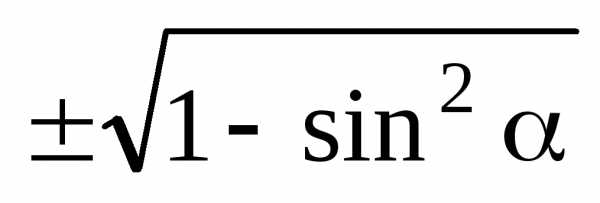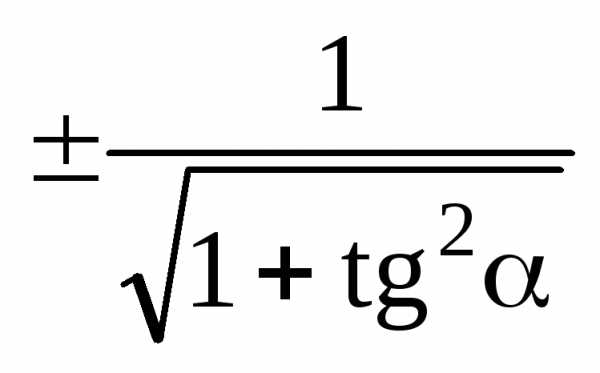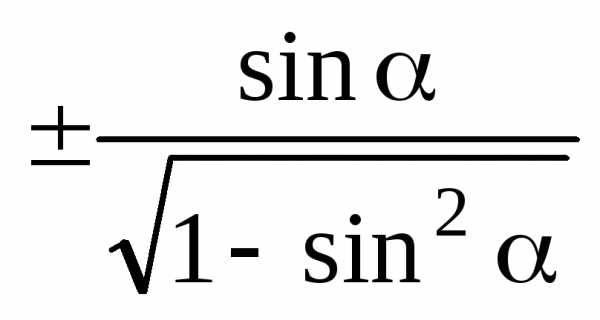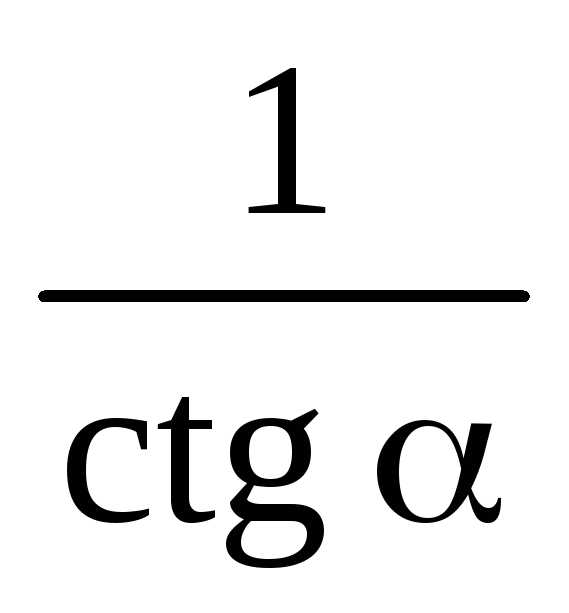Основное тригонометрическое тождество
Это последний и самый главный урок, необходимый для решения задач B11. Мы уже знаем, как переводить углы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а также умеем определять знак тригонометрической функции, ориентируясь по координатным четвертям (см. урок «Знаки тригонометрических функций»).
Дело осталось за малым: вычислить значение самой функции — то самое число, которое записывается в ответ. Здесь на помощь приходит основное тригонометрическое тождество.
Основное тригонометрическое тождество. Для любого угла α верно утверждение:
sin2α + cos2α = 1.
Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Обратите внимание на знак «±» перед корнями. Дело в том, что из основного тригонометрического тождества непонятно, каким был исходный синус и косинус: положительным или отрицательным. Ведь возведение в квадрат — четная функция, которая «сжигает» все минусы (если они были).
Именно поэтому во всех задачах B11, которые встречаются в ЕГЭ по математике, обязательно есть дополнительные условия, которые помогают избавиться от неопределенности со знаками. Обычно это указание на координатную четверть, по которой можно определить знак.
Внимательный читатель наверняка спросит: «А как быть с тангенсом и котангенсом?» Напрямую вычислить эти функции из приведенных выше формул нельзя. Однако существуют важные следствия из основного тригонометрического тождества, которые уже содержат тангенсы и котангенсы. А именно:
Важное следствие: для любого угла α можно переписать основное тригонометрическое тождество следующим образом:
Эти уравнения легко выводятся из основного тождества — достаточно разделить обе стороны на cos 2α (для получения тангенса) или на sin2α (для котангенса).
Рассмотрим все это на конкретных примерах. Ниже приведены настоящие задачи B11, которые взяты из пробных вариантов ЕГЭ по математике 2012.
Задача. Найдите sin α, если известно следующее:
Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:
sin2α + cos2α = 1 ⇒ sin2α + 99/100 = 1 ⇒sin2α = 1/100 ⇒sin α = ±1/10 = ±0,1.
Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π/2; π), то в градусной мере это записывается так: α ∈ (90°; 180°).
Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1.
Задача. Найдите cos α, если известно следующее:
Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:
sin2α + cos2α = 1 ⇒ 3/4 + cos2α = 1 ⇒cos2α = 1/4 ⇒cos α = ±1/2 = ±0,5.
Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α принадлежит промежутку (π 3π/2). Переведем углы из радианной меры в градусную — получим: α ∈ (180°; 270°).
Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.
Задача. Найдите tg α, если известно следующее:
Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:
Получаем: tg α = ±3. Знак тангенса определяем по углу α. Известно, что α ∈ (3π/2; 2π). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.
Задача. Найдите cos α, если известно следующее:
Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:
sin2α + cos2α = 1 ⇒ 0,64 + cos2α = 1 ⇒cos2α = 0,36 ⇒cos α = ±0,6.
Знак определяем по углу. Имеем: α ∈ (3π/2; 2π). Переведем углы из градусной меры в радианную: α ∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α = 0,6.
Задача. Найдите sin α, если известно следующее:
Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:
Отсюда получаем, что sin2α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π/2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.
Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2.
Смотрите также:
- Как формулы приведения работают в задаче B11
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Пробный ЕГЭ-2011 по математике, вариант №7
- Пробный ЕГЭ 2012. Вариант 2 (без логарифмов)
- Метод узлов в задаче B5
- Задача B5: площадь кольца
www.berdov.com
1.2.4 Основные тригонометрические тождества
Видеоурок: Тригонометрические тождества
Лекция: Основные тригонометрические тождества
Итак, напомним, что при рассмотрении тригонометрических функций, мы используем единичную окружность, с радиусом, равным единице.
Рассмотрим произвольный прямоугольный треугольник, полученный в результате движения радиус-вектора на некоторый угол.К прямоугольному треугольнику применима теорема Пифагора, в соответствии с которой квадрат гипотенузы будет равен сумме квадратов остальных сторон треугольника. Так как мы знаем, что синусу соответствует значение ординаты на плоскости, то есть величина противолежащего катета, а косинусу значение абсциссы (прилежащего катета). Так же нам известно, что гипотенуза треугольника является радиусом окружности, длина которого равна единицы, то теорему Пифагора можем получить в следующем виде:
Остальные тригонометрические тождества мы можем получить, зная определение тангенса и котангенса.
Давайте перемножим первое и второе уравнение и посмотрим, что получилось. В результате данного математического действия получим, что произведение тангенса на котангенс равно единице:
А теперь давайте возьмем первое основное тождество и почленно разделим все на cos2α или на sin2α. В результате этого получим:
Первое тождество справедливо для всех углов. Остальные же используются исключительно при углах, синус и косинус которых не равен 0.
cknow.ru
I. Основное тригонометрическое тождество и следствия из него:
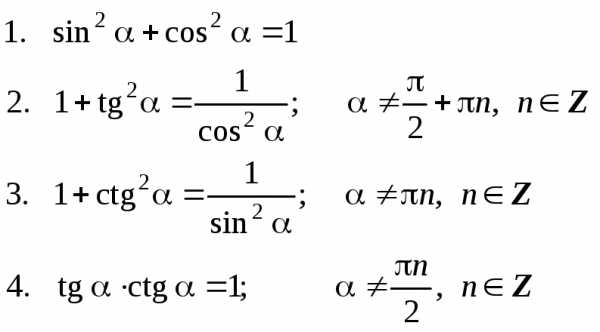
II. Формулы (теоремы) сложения аргументов:
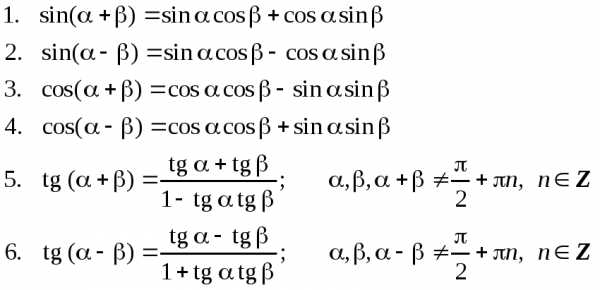
III. Формулы приведения:
1) функция меняется на кофункцию при переходе через вертикальную ось и не меняется при переходе через горизонтальную;
2) перед приведенной функцией ставится знак приводимой функции, считая углом первой четверти.
IV. Формулы двойного аргумента:
V. Формулы понижения степени:
Значения тригонометрических функций некоторых углов
таблица 1
0 | | ||||||
sin | 0 | | 1 | 0 | –1 | ||
cos | 1 |  | | 0 | –1 | 0 | |
tg | 0 | | 1 | | — | 0 | — |
ctg | — | | 1 | | 0 | — | 0 |
Связь между тригонометрическими функциями одного аргумента
таблица 2
Искомая функция | Выражение искомой функции через | |||
sin | cos | tg | сtg | |
sin = | sin | | | |
cos = | | cos | | |
tg = | | | tg | |
сtg = | | | | сtg |
6. Графики тригонометрических функций
Тригонометрический набор координат:
у = sin x синусоида
у = cos x косинусоида
у = tg x у = ctg x
тангенсоида котангенсоида
7. Свойства синуса и косинуса
Линия синусов | Область значений | Знаки по четвертям | Четность – нечетность |
|sin t| 1 | sin(–t) = –sin t |
Линия косинусов | Область значений | Знаки по четвертям | Четность – нечетность |
|cos t| 1 | cos(–t) = cos t |
Область определения | |
D(sin) = R | D(cos) = R |
Область значений | |
E(sin) = [–1; 1] | E(cos) = [–1; 1] |
Четность – нечетность | |
нечетная функция | четная функция |
Периодичность | |
sin(x 2) = sin x | cos(x 2) = cos x |
8. Свойства тангенса и котангенса
Линия тангенсов | Область значений | Знаки по четвертям | Четность – нечетность |
tg t (–; +) | tg(–t) = –tg t |
Линия котангенсов | Область значений | Знаки по четвертям | Четность – нечетность |
ctg t (–; +) | ctg(–t) = –ctg t |
Область определения | |
Область значений | |
E(tg) = (–; +) | E(ctg) = (–; +) |
Четность – нечетность | |
нечетная функция | нечетная функция |
Периодичность | |
tg(x ) = tg x | ctg(x ) = ctg x |
18 3
studfiles.net
Тригонометрические тождества.
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
.
Это соотношение называется основным тригонометрическим тождеством.
Если это уравнение поделить на квадрат косинуса и синуса соответственно имеем далее: и
Из определений тангенса и котангенса имеем, что .
Формулами приведения называются формулы следующего вида:
Здесь – любая тригонометрическая функция, – соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n – целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:
.
Правила преобразования:
1) Если аргумент содержит где – нечетное натуральное число , то функция меняется на «конфункцию», т.е. синус на косинус, тангенс на котангенс и наоборот. Если – четное натуральное число , то название функции не изменяется.
2) Определяем знак («+» или «–») значения первоначальной функции. Преобразованное выражение сохраняет знак своего родителя.
Формулы сложения
Значения тригонометрических функций суммы и разности двух углов:
Формулы для кратных углов
Формулы двойного угла:
Формулы половинного угла:
Произведения
Формулы для произведений функций двух углов:
Суммы
Обратные тригонометрические функции и их свойства. Арксинус, арккосинус, арктангенс, арккотангенс.
Функция
1.
2.
3.
4. функция нечетная, то есть
5. при ;
6. при ;
7. при ;
8. при ;
9. при .
Функция
1. ;
2.
3.
4. функция ни четная, ни нечетная, причем
5. при ;
6. при ;
7. при ;
8. при .
Функция
1.
2.
3.
4. функция нечетная, то есть
5. при ;
6. при ;
7. при ;
8. график функции имеет 2 асимптоты:
Функция
1.
2.
3.
4. функция ни четная, ни нечетная, причем
5. ни при каких ;
6. при ;
7. график функции имеет 2 асимптоты:
Тема 2.2 Обратные тригонометрические функции. Тригонометрические уравнения и неравенства
Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Простейшие тригонометрические неравенства. Арксинус, арккосинус, арктангенс, арккотангенс числа.
Тригонометрические уравнения
Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим.
Простейшие тригонометрические уравнения.
любое целое число;
любое целое число;
любое целое число;
здесь нет решений;
— любое целое число.
любое целое число;
любое целое число;
любое целое число;
здесь нет решений
— любое целое число.
– любое целое число;
— любое целое число.
— любое целое число;
— любое целое число.
Методы решения тригонометрических уравнений
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений.
1. Алгебраический метод. Этот метод нам хорошо известен из алгебры ( метод замены переменной и подстановки ).
Пример.Решить уравнение:
Решение. Используя формулы приведения, имеем: Делаем замену: тогда Находим корни: откуда следует два случая:
1)
2)
2. Разложение на множители. Этот метод рассмотрим на примерах.
Пример. Решить уравнение: .
Решение. Перенесём все члены уравнения влево: ,
преобразуем и разложим на множители выражение в левой части уравнения:
1)
2)
Пример. Решить уравнение: .
Решение. ,
2)
Пример. Решить уравнение:
Решение.
,
,
,
3.Приведение к однородному уравнению. Уравнение называется однородным относительно и , если все его члены одной и той же степени относительно и одного и того же угла. Чтобы решить однородное уравнение, надо:
а) перенести все его члены в левую часть;
б) вынести все общие множители за скобки;
в) приравнять все множители и скобки нулю;
г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на ( или ) в старшей степени;
д) решить полученное алгебраическое уравнение относительно .
Пример. Решить уравнение: .
Решение.
, отсюда ,
корни этого уравнения: отсюда
1)
2) .
4. Переход к половинному углу. Рассмотрим этот метод на примере:
Пример. Решить уравнение: .
Решение.
. . . . . . . . . .
5. Введение вспомогательного угла. Рассмотрим уравнение вида:
Где – коэффициенты; – неизвестное. Разделим обе части этого уравнения на :
.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как и (здесь — так называемый вспомогательный угол ), и наше уравнение принимает вид:
или и его решение: , где . Заметим, что введенные обозначения и взаимно заменяемы.
Пример. Решить уравнение: .
Решение. Здесь , поэтому делим обе части на
,
отсюда
6. Преобразование произведения в сумму. Здесь используются соответствующие формулы.
Пример. Решить уравнение: .
Решение. Преобразуем левую часть в сумму:
8. Универсальная подстановка. Рассмотрим этот метод на примере.
Пример.Решить уравнение:
Решение. Здесь возможны два случая:
1) , тогда
, . Делаем замену: , тогда , корни этого уравнения: :
а)
б)
2) , тогда .
Таким образом, решение даёт только первый случай
infopedia.su
[Билет 19] Основное тригонометрическое тождество. Формулы сложения. Формулы приведения. Тригонометрические формулы двойного угла, понижения степени и половинного аргумента. Универсальная тригонометрическая подстановка.
Основное тригонометрическое тождество.Для любого угла α справедливо равенство sin^2 α + cos^2 α = 1, называемое основным тригонометрическим тождеством.
Доказательство.
Формулы сложения.
Для любых углов α и β справедливы равенства:
| cos(α + β) = cos α cos β – sin α sin β Чтобы получить эту формулу рассмотрим единичный тригонометрическую окружность с двумя радиус векторами OA и OB, соответствующими углам α и β. По определению тригонометрических функций координаты векторов: ОА (cos α, sin α) и ОВ (cos β, sin β). Вычислим скалярное произведение этих векторов: ОА × ОВ = |ОА| × |ОВ| × cos (α+β) = cos (α+β) Вычислим скалярное прозведение векторов через координаты: ОА × ОВ = cos α cos β – sin α sin β. Так получается искомая формула: cos(α + β) = cos α cos β – sin α sin β |
| cos(α – β) = cos α cos β + sin α sin β Чтобы получить эту формулу нужно в предыдущей формуле заменить β на –β. |
| sin(α + β) = sin α cos β + cos α sin β Эта формула получается через использование формул приведения в предыдущей формуле. |
| sin(α – β) = sin α cos β – cos α sin β Эта формула получается через замену β на –β в предыдущей формуле. |
Для любых углов α и β таких, что α ≠ π/2 + πk, β ≠ π/2 + πn, α + β ≠ π/2 + πm (k, n, m принадлежат множеству Z), справедливо:
| tg(α + β) = (tg α + tg β)/(1 – tg α tg β) Эта формула получается через вычисления частного sin(α + β) и cos(α + β) |
Для любых углов α и β таких, что α ≠ π/2 + πk, β ≠ π/2 + πn, α – β ≠ π/2 + πm (k, n, m принадлежат множеству Z), справедливо:
| tg(α – β) = (tg α – tg β)/(1 + tg α tg β) Эта формула получается через вычисления частного sin(α – β) и cos(α – β) |
Для любых углов α и β таких, что α ≠ πk, β ≠ πn, α + β ≠ πm (k, n, m принадлежат множеству Z), справедливо:
| ctg(α + β) = (ctg α ctg β – 1)/(ctg β + ctg α) Эта формула получается через вычисления частного cos(α + β) и sin(α + β) |
Для любых углов α и β таких, что α ≠ πk, β ≠ πn, α – β ≠ πm (k, n, m принадлежат множеству Z), справедливо:
| ctg(α – β) = (ctg α ctg β + 1)/(ctg β – ctg α) Эта формула получается через вычисления частного cos(α – β) и sin(α – β) |
Формулы приведения.
Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет свое название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет свое название.
Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
1 четверть: sin:+ cos:+ tg, ctg:+
2 четверть: sin:+ cos:- tg, ctg:-
3 четверть: sin:- cos:- tg, ctg:+
4 четверть: sin:- cos:+ tg, ctg:-
Тригонометрические формулы двойного угла, понижения степени и половинного аргумента.
Формулы двойного угла
- cos 2α = cos² α — sin² α
- cos 2α = 2cos² α — 1
- cos 2α = 1 — 2sin² α
- sin 2α = 2sin α · cos α
- tg 2α = (2tg α) ÷ (1 — tg² α)
- ctg 2α = (ctg² α — 1) ÷ (2ctg α)
Понижение степени
cos2t=21+cos2t; sin2t=21−cos2t
Формулы половинного аргумента
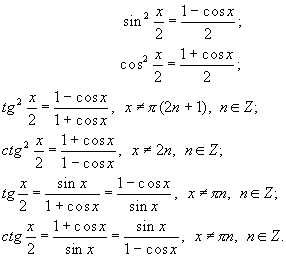
Универсальная тригонометрическая подстановка.
Определение. Универсальной тригонометрической подстановкой называются выражение тригонометрических функций через тангенс половинного аргумента.
Эти формулы позволяют выразить любую тригонометрическую функцию через тангенс половинного угла. Это дает возможность свести любое тригонометрическое уравнение к алгебраическому относительно этого тангенса. Пусть t = , тогда При использовании этих формул следует иметь в виду, что они имеют смысл только тогда, когда определен тангенс половинного угла, т.е. при ; в формуле для tg α требуется, кроме того, чтобы t не равнялось 1, а в формуле для ctg α – чтобы t не равнялось 0.
fizmatinf.blogspot.com
Тригонометрические тождества
Тригонометрические функции являются неотъемлемой частью тригонометрии, поэтому знание этих функций очень важно. Но на чем основываются эти функции? Конечно же, на тригонометрических тождествах.
Давайте разберемся, что же такое тождество вообще? Самое простое определение, это, конечно же, сходство. Если «копнуть» глубже, то мы можем говорить о том, что тождество – отношение между некоторыми предметами (реальными или абстрактными), что позволяет говорить об их неотличимости в каких-то характеристиках. На самом деле такое определение к тригонометрии подходит, ведь в каких-то характеристиках наши функции действительно схожи и неотъемлемы друг от друга.
Давайте подробнее рассмотрим каждое тригонометрическое тождество.
Соотношение синуса и косинуса одного и того же угла – именно это тригонометрическое тождество и является основным в тригонометрии. Выглядит это тождество следующим образом:
Sin2a +cos2a = 1
Попробуем объяснить, почему это тождество выглядит именно так. Изначально у нас есть прямоугольный треугольник с определенным углом а. Гипотенуза нашего треугольника равна 1. Один катет треугольника – это косинус, а другой – синус. Теперь применяем к нашему треугольнику теорему Пифагора и получаем наше тригонометрическое тождество.
Теперь рассмотрим зависимость между тангенсом и котангенсом. Тут все просто. Произведение тангенса и котангенса равно 1.
Зависимость между тангенсом и косинусом угла выводится очень просто. Для начала берем наше основное тригонометрическое тождество и делим его на квадрат косинуса, потом упрощаем левую часть уравнения и получаем наше третье тождество (при это важно помнить, что деление возможно только в том случае. если косинус не равняется нулю).
Тригонометрические тождества | ||||||||||||
| ||||||||||||
| ||||||||||||
| tgα * ctgα = 1 | ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
Выражения одних тригонометрических функций через другие | ||||||||||||
mateshka.ru
Основное тригонометрическое тождество: формулы приведения
На следующем рисунке представлена система координат Оху с изображенной в ней частью единичной полуокружности ACB с центром в точке О. Эта часть является дугой единичной окружности. Единичная окружность описывается уравнением x^2+y^2 = 1.
рисунок
Основное тригонометрическое тождество
Ординату у и абсциссу х можно представить в виде синуса и косинуса угла по следующим формулам:
sin(a) = у,
cos(a) = х.
Подставив эти значения в уравнения единичной окружности, имеем следующее равенство:
(sin(a))^2 + (cos(a))^2 = 1, которое будет выполняться для любого значения а из промежутка от 0 градусов до 180 градусов. Данное равенство называется основным тригонометрическим тождеством.
Формулы приведения
Формулы приведения используются для того, чтобы значения тригонометрических функций от аргументов вида (90˚ ±a), (180˚ ±a), выразить через значения sin(a), cos(a), tg(a) и ctg(a).
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (90˚ ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (180˚ ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, где схематично изображено, когда следует менять знак, а когда нет.
рисунок
2. Правило «каким ты был, таким ты и остался».
Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
рисунок
Нужна помощь в учебе?
Предыдущая тема: Признаки параллелограмма: доказательства и рисунки
Следующая тема:   Формулы для вычисления координат точки: алгоритмы и задачи
Все неприличные комментарии будут удаляться.
www.nado5.ru