Формула площадей трапеции: Площадь трапеции

Площадь трапеции

Дарим в подарок бесплатный вводный урок!

Немного истории

Для начала вспомним, что такое трапеция.

 

Трапеция – это фигура, у которой две стороны параллельны, а две другие не параллельны.     

    

Трапеция – одна из самых «загадочных» фигур школьной планиметрии. Она обладает некоторыми признаками параллелограмма, но сильно отличается от него разнообразием форм. Различают трапеции прямоугольные, равнобедренные, общего вида. Одно это разнообразие форм уже подозрительно. 

 

На практике форма трапеции встречается более часто, чем прямоугольники, квадраты или параллелограммы. Поэтому нахождение площади для трапеции – более актуальная задача, чем для других фигур.       

 

Покажем вам несколько формул, как найти площадь трапеции. Каждая формула площади трапеции подходит для решения соответствующего круга задач.

 

Основные формулы

1. Площадь трапеции через её основания и высоту:

2. Площадь трапеции через ее высоту и среднюю линию:

3. Площадь трапеции через ее диагонали и угол между ними:

 

Давайте разберем задачу, иллюстрирующую применение одной из этих формул:

 

Задача

Основания трапеции общего вида равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

 

Решение

 

Изобразим трапецию общего вида и введём обозначения, как показано на рисунке ниже.

 

 

 

По условию задачи, один из углов трапеции равен 150°. Этим углом может быть угол ADC. По свойству трапеции, также как и параллелограмма, сумма углов, прилежащих к боковой стороне, равна  180°. Отсюда несложно вычислить, что второй угол, DAН, прилежащий к этой боковой стороне, будет равен 30°.

 

Отрезком DH на рисунке является высота трапеции. Найдем эту высоту из прямоугольного треугольника AHD, где DH является противолежащим катетом, AD является гипотенузой:

 

 

Воспользуемся формулой (1) площади трапеции через ее основания и высоту. По этой формуле площадь трапеции равна произведению полусуммы оснований на ее высоту:

 

 

 

Ответ: 42

 

Итак, зная длины двух оснований трапеции и ее высоту, вычислить ее площадь достаточно просто. Сложности могут быть, если нам не известны один из требуемых элементов, например, высота трапеции. Но здесь на помощь приходят знания свойств трапеций и соотношений в прямоугольном треугольнике.

 

Часто задаваемые вопросы

✅ Что такое трапеция?

↪ Трапеция — это четырехугольник, у которого две противоположные стороны параллельны, а две другие стороны непараллельны.

✅ Как найти площадь трапеции?

↪ Площадь трапеции можно найти по формуле: S = (a + b) * h / 2, где a и b — длины оснований трапеции, а h — высота трапеции, опущенная на основание.

✅ Что происходит с площадью трапеции, если увеличить одно из оснований?

↪ Если увеличить одно из оснований трапеции, то ее площадь увеличится, при этом высота трапеции останется неизменной.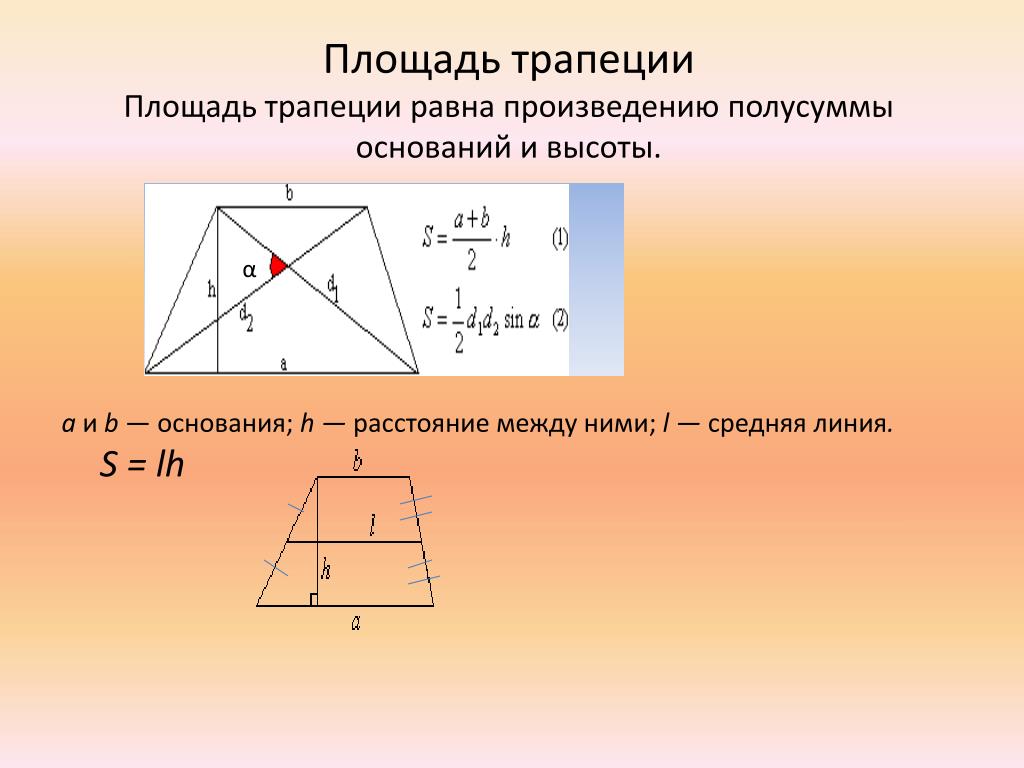 Если увеличить оба основания на одинаковую величину, то площадь трапеции увеличится в два раза.

Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

определение, формула вычисления, примеры решения задач

Что такое трапеция

Трапеция — это плоская фигура, ее изучают в курсе геометрии 8 класса.

Определение 1

Трапеция — четырехугольник, две стороны которого параллельны, и две другие стороны не параллельны.

Определение 2

Основаниями называются параллельные стороны трапеции. Непараллельные — боковые стороны.

Частный случай трапеции — равнобедренная трапеция, боковые стороны которой равны. Трапеция с углами по 90 градусов, прилежащими к одной боковой стороне, называется прямоугольной.

Определение 3

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон и параллельный основаниям.

ABCD — трапеция, EF — ее средняя линия, BC||EF||AD, BE=CF, AE=DF.

Формулы площади трапеции

Чтобы найти площадь трапеции можно использовать несколько формул. Выбор зависит от данных условия.

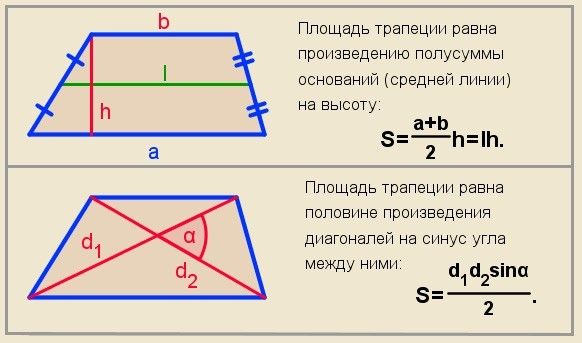
Площадь трапеции равна произведению половины суммы ее оснований на высоту.

Формула 1

Рассмотрим трапецию ABCD, AD||BC, BF — высота.  формула для нахождения площади трапеции будет выглядеть как .

Площадь трапеции равна произведению ее средней линии на высоту.

 Формула 2

Для данной трапеции  , а формула выглядит так: S=h·m, где h — высота, m — средняя линия.

Площадь трапеции равна половине произведения ее диагоналей на синус угла между ними.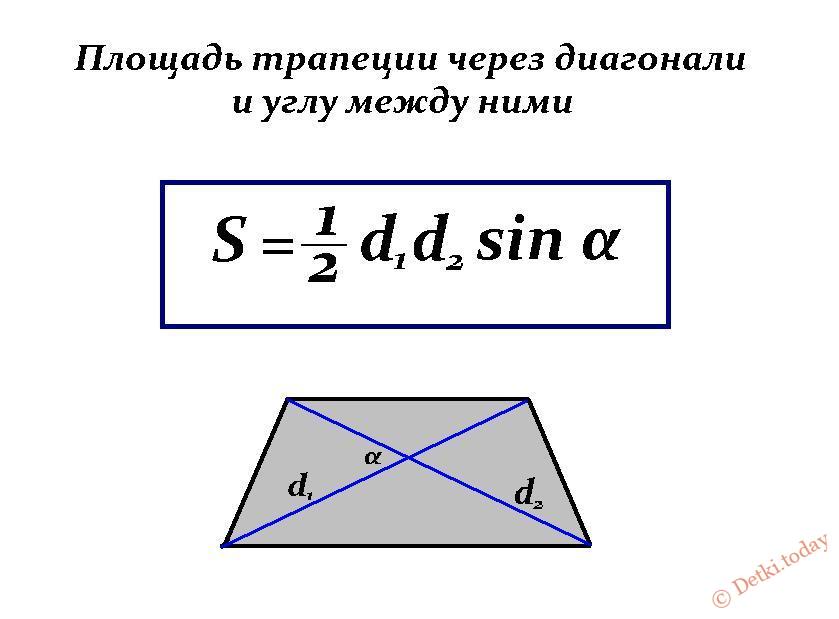

Формула 3

Формула 4

У трапеции, диагонали которой перпендикулярны, , так как sin 90º=1.

Площадь трапеции равна произведению половины ее периметра на радиус вписанной окружности. Если суммы противолежащих сторон трапеции равны, то в трапецию можно вписать окружность. Полупериметр трапеции равен половине суммы ее четырех сторон или сумме ее оснований. Зная основания трапеции и радиус вписанной окружности, можно посчитать ее площадь: , где a и b — основания, r — радиус вписанной окружности. Радиус вписанной в трапецию окружности равен половине высоты трапеции h, поэтому из формулы  можно получить .

Формула площади равнобедренной трапеции

Площадь равнобедренной трапеции можно рассчитать по тем же формулам. Некоторые из них имеют упрощенный вид.

1. Если известны основания a и b и высота трапеции h, то площадь рассчитывают как и в общем случае: .
2. S=h·m, где h — высота, m — средняя линия.
3. Площадь равнобедренной трапеции равна половине произведения её диагоналей  на синус угла между ними. У равнобедренной трапеции  (половине произведения квадрата ее диагонали на синус угла между диагоналями).

Площадь равнобедренной трапеции с перпендикулярными диагоналями

• Так как sin 90º=1, то .
• Площадь равнобедренной трапеции, диагонали которой перпендикулярны, равна квадрату ее высоты: 
• Если в трапецию можно вписать окружность, то применяется общая формула 

Формула площади криволинейной трапеции

Определение 2

Криволинейная трапеция — это плоская фигура, ограниченная графиком непрерывной и неотрицательной на отрезке [а;b] функции y=f(х), прямыми х=а, x=b и осью абсцисс.

Отрезок [a;b] называют основанием криволинейной трапеции. Отрезки, ограничивающие криволинейную трапецию слева и справа, могут вырождаться в точку.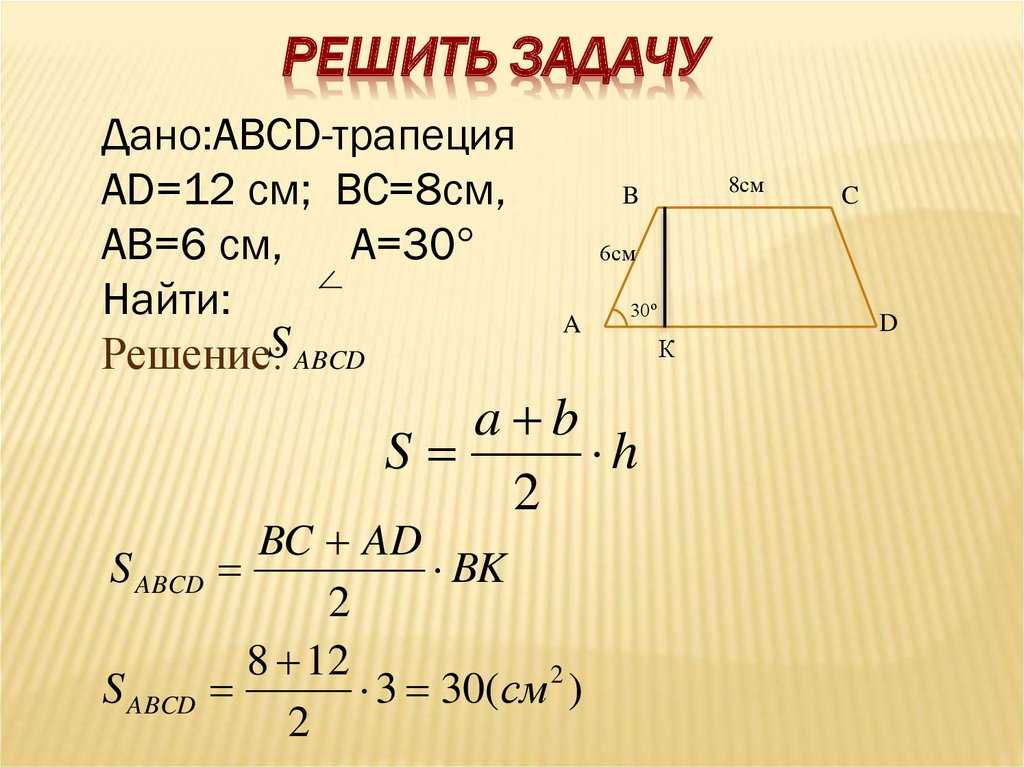 Верхняя граница криволинейной трапеции может быть задана разными формулами на разных частях отрезка.

 

Формула Ньютона-Лейбница

Нахождение площади криволинейной трапеции рассматривают в 11 классе как пример применения интеграла.

Площадь криволинейной трапеции, образованной графиком функции y=f(x) на интервале [a;b] записывают в виде определенного интеграла: 

По формуле Ньютона-Лейбница определенный интеграл равен:.

Пояснение на примерах

Задача 1

Найдите площадь трапеции, если ее основания равны 4 и 7 см, а высота — 4 см.

Решение:

Чтобы узнать площадь трапеции, используем формулу .

Ответ: 

Задача 2

Найдите площадь фигуры под кривой на заданном интервале: f(x)=x3+3, x∈[−1;1].

Решение:

S=∫−11(x3+3)dx=(x44+3x)|−11=14+3−(14−3)=6

Ответ: 6.

Площадь трапеции: Формула и примеры

Давайте узнаем, как найти площадь трапеции .

Что такое трапеция?

Трапеция представляет собой четырехстороннюю плоскую фигуру с одной парой параллельных сторон, называемых ее основаниями . Высота (также называемая высотой ) трапеции перпендикулярна ее основаниям. Две другие непараллельные стороны называются ножками . Примерами предметов в форме трапеции являются цветочные горшки, сумки, ведра и другие архитектурные вещи.

См. иллюстрацию трапеции ниже.

Как найти площадь трапеции

Площадь двумерной фигуры относится к общему объему пространства, заключенного внутри этой фигуры. Он измеряется в кубических единицах, таких как м ² , см ² , км ² , а в ² . Перед вычислением убедитесь, что все единицы одинаковы.

Связанные материалы: Площадь круга – формула и примеры

Чтобы найти площадь трапеции , умножьте среднее значение двух оснований (параллельных сторон) трапеции на ее высоту, как указано в этой формуле:

A = ( a + b ) / 2 • h
Где:
A = площадь трапеции
a = длина основания трапеции 1
b = длина основание трапеции 2
h = высота трапеция

Пример #1: Нахождение площади трапеции при заданных измерениях в одних и тех же единицах измерения

Найдите площадь трапеции при следующих измерениях:
a = 10 см, b = 8 см, h = 6 см

Решение примера №1:

Шаг 1. Запишите данные числа: a = 10 см, b = 8 см, h = 6 см.
Шаг 2. Подставьте цифры в формулу. Аналог 10см для a , 8 см для b и 6 см для ч .
A = ( a + b ) / 2 • h
= (10 см + 8 см) / 2 • (6 см)
Шаг 3. Упрощение.
A = 18 см / 2 • (6 см)
= 9 см • 6 см
A = 54 см ²

Следовательно, площадь трапеции это 54см ² .

Пример #2: Нахождение площади трапеции при заданных измерениях в разных единицах измерения

Найдите площадь трапеции, приведенной ниже.

Решение примера №2:

Шаг 1. Запишите данные измерения: a = 5 ярдов, b = 126 дюймов, ч = 4 ярда.
Шаг 2 . Поскольку все единицы измерения должны быть одинаковыми, преобразуйте 126 дюймов в ярды.
Напомним: 1 ярд = 36 дюймов. Запишите преобразование в виде дроби, равной 1: (1 ярд / 36 дюймов) = 1,
126 дюймов • (1 ярд / 36 дюймов) = 126 дюймов • (1 ярд / 36 дюймов ) = 126 ярдов / 36 = 3,5 ярда
Таким образом, преобразованное значение 9000 3 б это 3,5 ярда .
Шаг 3. Подставьте измерения в формулу. Замените 5 ярдов на a , 3,5 ярда на b и 4 ярда на 9004. 0 ч .
А = ( а + б ) / 2 • h
= (5 ярдов + 3,5 ярда) / 2 • (4 ярда)
Шаг 4. Упростить.
A = 8,5 ярда / 2 • (4 ярда)
= 4,25 ярда • 4 ярда
A = 17 ярдов ² 9000 5

Следовательно, площадь трапеции равна 17 ярдов ² .

Пример №3. Нахождение основания трапеции

Найдите другое основание трапеции площадью 71,5 см ² , высота 6,5 см, основание 9 см.

Решение примера №3: ​​

Шаг 1. Напишите формулу площади трапеции: A = ( a + b ) / 2 • 9 0040 ч ИЛИ А = ( a + b )h / 2.
Используйте последнее, чтобы найти недостающее основание.
Шаг 2. Пусть a будет недостающим основанием. Подставьте данные измерения в формулу.
Временно удалите юниты, чтобы избежать путаницы.
A = ( a + b )h / 2
71,5 = ( a + 9) (6,5) / 2
Шаг 3. Упростить.
Сначала умножьте 6,5 см на выражение ( a + 9).
71,5 = (6,5 a + 58,5) / 2
Умножьте обе части уравнения на 2. 0178 ]
143 = 6,5 a + 58,5
Вычтите 58,5 с обеих сторон.
143 – 58,5 = 6,5 a + 58,5 – 58,5
85 = 6,5 a
Разделите обе части на 6,5.
85 / 6,5 = 6,5 a / 6,5
13 = a

Следовательно, длина другого основания равна 9000 3 13см .

Проверка решения примера №3: ​​

Подставьте измерения в формулу площади трапеции.
A = ( a + b ) ч / 2
71,5 см ² = [(13 см + 9 см) (6,5 см)] /2
71,5 см ² = [(22 см) (6,5 см)] / 2
Упростить.
71,5 см ² = 143 см ² / 2
71,5 см ² = 71,5 см ²

Спасибо для чтения. Мы надеемся, что это эффективно! Всегда не стесняйтесь возвращаться на эту страницу, если у вас возникнут вопросы о площади трапеции .

Ознакомьтесь с некоторыми другими сообщениями в нашем блоге или инвестируйте в свое будущее с помощью одного из наших курсов самообучения!

Нажмите здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP по программе Calculus AB 2021 !

Как найти площадь трапеции (формула и видео) Пол Маццола

Что такое трапеция?

Трапеция  является четырехугольником с одной парой параллельных сторон.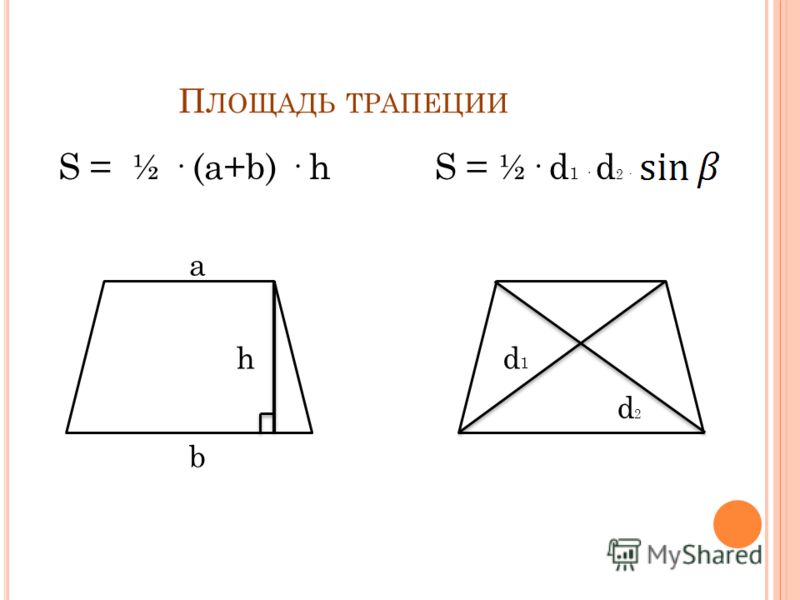 Итак, этот четырехугольник представляет собой плоскую фигуру и замкнутую форму. Он имеет четыре отрезка и четыре внутренних угла. Параллельные стороны — это две  9 трапеции.0398 оснований ; две другие стороны — его ноги.

Обычно трапецию изображают с более длинной параллельной стороной — основанием — горизонтальной.

Перпендикулярная линия от основания к другой параллельной стороне даст вам высоту трапеции или высоту .

Что такое трапеция?

Что такое средний балл по математике?

В математике  среднее  – это сумма группы чисел, деленная на количество элементов в группе.

Итак, если у вас есть три человека, держащие книги, вы можете найти среднее количество книг, которые они держат, следующим образом:

Мартин держит 5 книг, Мак держит 3 книги, а Мария держит 4 книги. Вместе 12 книг держат 3 человека .

Итак, 12 книг ÷ 3 человека = в среднем по 4 книги у каждого .

Чтобы найти площадь трапеции, нужно найти среднюю длину двух оснований.

Как найти площадь трапеции

Чтобы найти площадь любой трапеции, начните с обозначения ее оснований и высоты. В нашей трапеции обозначьте более длинное основание aa, а более короткое основание b . Отметьте линию, перпендикулярную двум основаниям h  для высоты или высоты трапеции.

Площадь трапеции

Обратите внимание, что мы не обозначили ноги. Нам не нужно ничего знать о длине катетов или углах вершин, чтобы найти площадь.

Площадь трапеции формула

Формула площади трапеции представляет собой произведение среднего основания на высоту. В формуле длинное и короткое основания равны a и b , а высота равна h :

Умножение на 12\frac {1}{2}21​ то же самое как деление на 222. Мы берем половину суммы длин двух оснований (их среднее значение), а затем умножаем ее на высоту или высоту, чтобы найти площадь в квадратных единицах.

Используя уравнение площади трапеции

Трапеция  LMNO  имеет параллельные основания  LM  и  NO . Отрезок LM имеет длину 7 см , а отрезок NO имеет длину 13 см . Мы обозначим более длинную сторону NO как a , а более короткую сторону LM как b . Высота ч , 5 см .

Используйте площадь уравнения трапеции

Во-первых, давайте подставим эти числа в нашу формулу:

Затем мы сложим 13 плюс 7 и получим:

Затем мы разделим на два, тогда и получим:

Наконец, мы умножим и получим наш ответ:

Площадь этой трапеции 50 квадратных сантиметров .

Площадь трапеции примеры

А теперь попробуй! Другая трапеция имеет длинное основание a , 11 метров и более короткое основание б , 7 метров . Его высота ч  составляет 9 метров . Какая площадь в квадратных метрах?

Вы получили 81 квадратный метр ? Ваш ответ для площади всегда в квадратных единицах линейного измерения.

Таким образом, трапеция, измеренная в футах, дает площадь в квадратных футах, сантиметры дают квадратные сантиметры и так далее.

Помните, что умножение на ½ равносильно делению на 9.0398 2 , поэтому вы можете сложить длины оснований, а затем разделить их сумму на два, если вам так проще.

Из-за коммутативного свойства умножения вы можете переставить эти три числа: 12\frac{1}{2}21​, высоту h и длину основания   a 9 0398  + b в любом порядке для облегчения расчета.

Таким образом, с трапецией  LMNO вы также могли бы написать формулу следующим образом:

Пример #2

Вот вам еще один пример. Новая трапеция перевернута, не так, как вы ее обычно видите, но пусть это вас не останавливает! Короткая база b имеет длину 21 дюйм . Длинное основание a (на этот раз вверху рисунка) имеет длину 31 дюйм . Высота h  (независимо от того, как вы смотрите на трапецию) составляет 5 дюймов .

No related posts.