Как найти площадь поверхности цилиндра: боковую, основания, полную
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение площади поверхности цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
- Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
S = π (d/2)2
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R2 или S = 2 π R (h + R)
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см2.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см.
Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Площадь поверхности цилиндра: расчет боковой, полной поверхности цилиндра, формула нахождения
Как вычислить площадь поверхности цилиндра — тема данной статьи.
В любой математической задаче начать нужно с ввода данных, определить, что известно и чем оперировать в дальнейшем, и лишь затем приступить непосредственно к расчету.
Данное объёмное тело представляет собой геометрическую фигуру цилиндрической формы, ограниченную сверху и снизу двумя параллельными плоскостями. Если приложить немного воображения, то можно заметить, что геометрическое тело образуется вращением прямоугольника вокруг оси, причем осью является одна из его сторон.
Отсюда вытекает, что описываемая кривая сверху и снизу цилиндра будет окружностью, основным показателем которой является радиус или диаметр.
Содержание
Площадь поверхности цилиндра онлайн калькулятор
Данная функция окончательно облегчает процесс расчета, и все сводится лишь автоматическому подставлению заданных значений высоты и радиуса (диаметра) основания фигуры. Единственное, что требуется — точно определить данные и не ошибиться при вводе цифр.
Площадь боковой поверхности цилиндра
Сначала нужно представить, как выглядит развертка в двухмерном пространстве.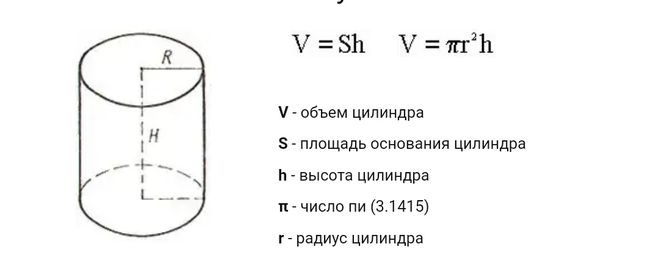
Это не что иное, как прямоугольник, одна сторона которого равна длине окружности. Формула ее известна с незапамятных времен —2π * r, где r — радиус окружности. Другая сторона прямоугольника равна высоте h. Найти искомое не составит труда.
Sбок = 2π * r * h,
где число π = 3.14.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.
Конечная формула выглядит следующим образом:
Sпол = 2π * r2 + 2π * r * h.
Площадь цилиндра формула через диаметр
Для облегчения расчетов иногда требуется произвести вычисления через диаметр.
Например, имеется кусок полой трубы известного диаметра.
Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.
Sпол = 2π * r2 + 2π * r * h = 2π * d2/4 + 2π * h * d/2 = π * d2/2 + π * d * h,
Вместо r в полную формулу нужно вставить значение r = d/2.
Примеры расчета площади цилиндра
Вооружившись знаниями, приступаем к практике.
Пример 1. Нужно вычислить площадь усеченного куска трубы, то есть цилиндра.
Имеем r = 24 mm, h = 100 mm. Использовать необходимо формулу через радиус:
Sпол = 2 * 3.14 * 242 + 2 * 3.14 * 24 * 100 = 3617,28 + 15072 = 18689,28 (мм2).
Переводим в привычные м2 и получаем 0,01868928, приблизительно 0.02 м2. Каталог индивидуалок проститутки Анапа Сайт для интим досуга
Пример 2. Требуется узнать площадь внутренней поверхности печной асбестовой трубы, стенки которой облицованы огнеупорным кирпичом.
Данные следующие: диаметр 0,2 м, высота 2 м. Используем формулу через диаметр:
Sпол = 3.14 * 0.22/2 + 3,14 * 0.2 * 2 = 0,0628 + 1.256 = 1.3188 м2.
Пример 3. Как узнать, сколько материла нужно для пошива мешка, r = 1 м и высотой 1 м.
Один момент, есть формула:
Sбок = 2 * 3.14 * 1 * 1 = 6.28 м2.
Заключение
В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.
Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом.
Точность – вежливость королей.
Площадь поверхности цилиндра
Цилиндр можно определить как твердую фигуру, ограниченную криволинейной поверхностью и двумя плоскими поверхностями. Площадь поверхности цилиндра можно найти, разбив ее на 2 части:
1. Две окружности, образующие крышки цилиндра.
2. Сторона цилиндра, которая в развернутом виде представляет собой прямоугольник.
Площадь каждой торцевой крышки можно найти по радиусу r окружности, который определяется как:
A = πr 2
Таким образом, общая площадь крышек равна 2πr 2 .
Площадь прямоугольника определяется как:
A = высота × ширина
Ширина – это высота h цилиндра, а длина – это расстояние вокруг концевых окружностей, или, другими словами, периметр / длина окружности основания/верхнего круга и определяется как:
P = 2πr
Таким образом, площадь прямоугольника переписывается как:
A = 2πr × h
Объединив эти части вместе, мы получим общую площадь поверхности цилиндра, и окончательная формула будет следующей:
A = 2πr 2 + 2πrh
где:
π – число Пи, примерно 3,142
.
r — радиус цилиндра
h высота цилиндра
Умножая 2πr из каждого члена, мы можем упростить формулу до:
A = 2πr(r + h)
Площадь боковой поверхности цилиндра просто определяется как: LSA = 2πr × h .
Пример 1 : Найдите площадь поверхности цилиндра с радиусом 4 см и высотой 3 см.
Решение:
SA = 2 × π × r 2 + 2 × π × r × h
SA = 2 × 3,14 × 4 2 + 2 × 3,14 × 4 × 3
90 16 + 6,28 × 12
SA = 100,48 + 75,36
SA = 175,84
Площадь поверхности = 175,84 см 2
3
1 : Найдите площадь поверхности цилиндра радиусом 5,5 см и высотой 10 см.Решение:
Радиус цилиндра = 5,5 см.
Высота цилиндра = 10 см.
Общая площадь поверхности цилиндра, следовательно, составляет:
TSA = 2πr (R+H)
TSA = 11π (5,5+10)
TSA = 170,5 π
TSA = 535,6 см 2
TSA = 535,6 см 2 2
TSA = 535,6 см 2
TSA = 535,6 см 2
Пример 3 : Найдите общую площадь поверхности цилиндрической банки радиусом 17 см и высотой 3 см.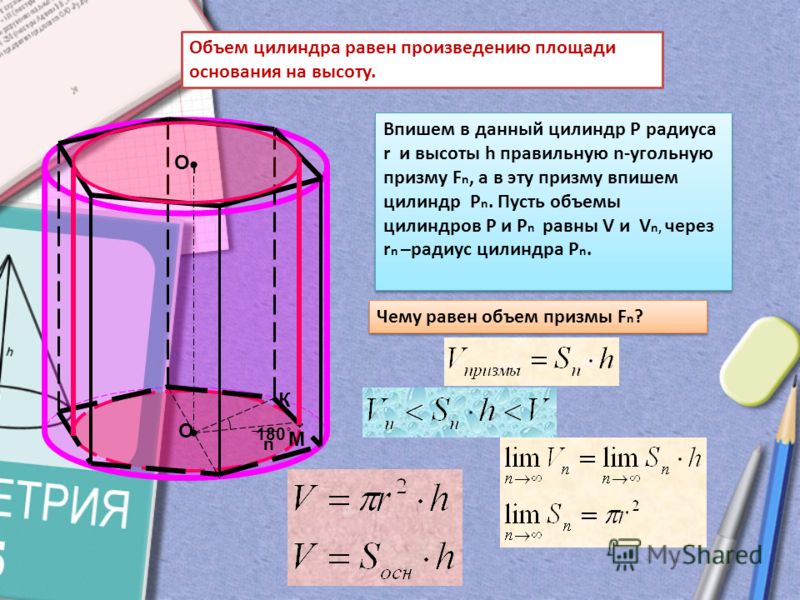
Решение:
Опять как в предыдущем примере:
TSA = 2πr(r+h)
TSA = 2π× 17(17+3)
TSA = 2π×17×20
TSA = 2136,510 см 2
Пример 4 : Найдите площадь поверхности цилиндра радиусом 6 см и высотой 9 см.
Решение:
Высота цилиндра: h = 9 см
Таким образом, общая площадь поверхности цилиндра:
TSA = 2πr (R + H)
TSA = 12π (6 + 9)
TSA = 180 π
TSA = 565,56 CM 2
Пример 5 : Найти RADIIS OF RADIIS OF RADIIS 5 : FIND RADIIS OF OF RADIIS OF FIDIOD OF RADIIS FIRIIS 5 : ERDIIS 5 9006: radiy orius. цилиндр с площадью боковой поверхности 150 см 2 и высотой 9 см.
Решение:
Площадь боковой поверхности цилиндра определяется как:
LSA = 2πrh
Учитывая, что:
LSA = 150 см 2
h = 9 см
π — константа, и ее значение = 3,14
Подставьте значения в формулу и найдите значение r, выделив его из уравнения:
LSA = 2πrh
150 = 2 × π × r × 9
r = 150 / (2×9× π)
r = 2,65 см
Значит, радиус цилиндра равен 2,65 см.
Калькулятор площади поверхности онлайн
Объяснение урока: Площади поверхностей цилиндров
В этом объяснении мы научимся вычислять площади поверхности цилиндров и использовать их для решения задач в реальных ситуациях.
Чтобы найти площадь поверхности цилиндра, нам сначала нужно рассмотреть его развертку. Давайте посмотрим на показанный цилиндр, который имеет радиус 𝑟 и высоту ℎ.
Если подумать о том, чтобы «распутать» изогнутую поверхность цилиндра, получится прямоугольник шириной ℎ и длина, равная длине окружности: 2𝜋𝑟. Верх и дно цилиндра — обе окружности с радиусом 𝑟. Таким образом, сеть цилиндра может быть вытянута как следует.
Чтобы найти площадь поверхности цилиндра, нам нужно вычислить площадь его сетки.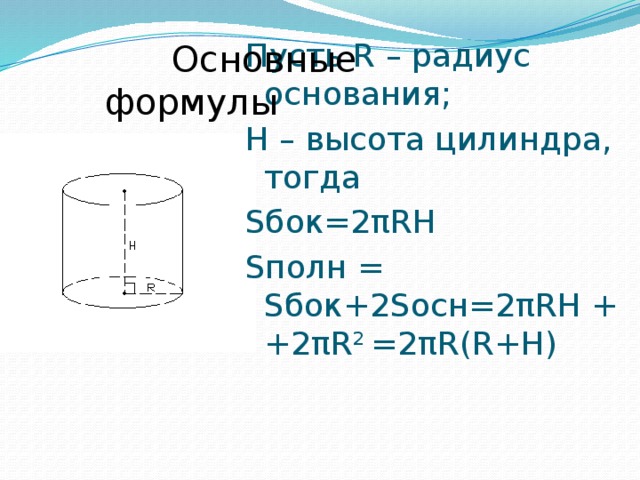
Площадь каждого из кругов равна
𝜋𝑟, а площадь прямоугольника вычисляется путем умножения его длины и ширины, чтобы получить
ℎ×2𝜋𝑟=2𝜋𝑟ℎ. Следовательно, общая площадь поверхности равна 2×𝜋𝑟+2𝜋𝑟ℎ,
что упрощается до 2𝜋𝑟+2𝜋𝑟ℎ.
Пока вы осваиваете этот метод, рекомендуется вытянуть сетку цилиндра, чтобы помочь вам запомнить метод и как вывести формулу.
Обратите внимание, что в некоторых вопросах по этой теме используется термин правый круговой цилиндр . Это просто еще один способ описать «обычный» цилиндр, верхняя круглая поверхность которого параллельна нижней круглой поверхности и находится непосредственно над ней.
Давайте рассмотрим пример с сеткой цилиндра.
Пример 1. Расчет площади поверхности цилиндра, образованного путем складывания прямоугольника
На приведенной ниже диаграмме показана развертка цилиндра, где 𝐴𝐵𝐶𝐷 представляет собой прямоугольник с 𝐴𝐵=20 см и 𝐴𝐷=44 см. Сеть формируется в цилиндр путем соединения
𝐴𝐵 с 𝐷𝐶, затем складываем два круга
радиусом 7 см, чтобы сделать вершину и основание.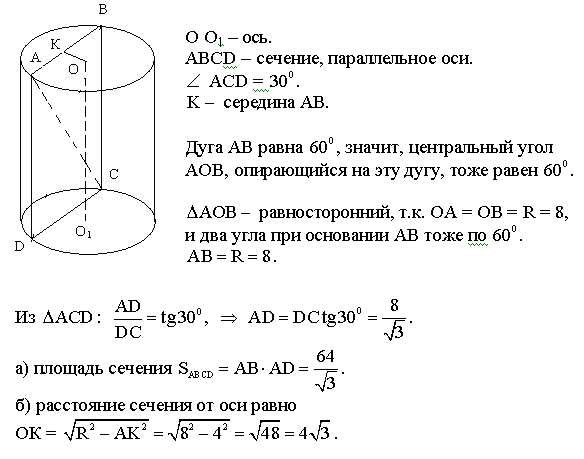
Какова общая площадь поверхности цилиндра? Используйте 𝜋 как 227.
Ответ
Напомним, что общая площадь поверхности цилиндра эквивалентна площади его сетки, а для цилиндра радиуса 𝑟 и высота ℎ, имеем формулу общая площадьплощадькруговплощадьпрямоугольникплощадьодногокругаширинавысота=+=(2×)+(×)=2×𝜋𝑟+(2𝜋𝑟×ℎ).
Используя информацию из вопроса, мы можем подставить в эту формулу, чтобы найти общую площадь поверхности цилиндра .
Во-первых, круги, образующие вершину и основание, имеют радиусы 7 см, значит 𝑟=7.
Тогда из диаграммы прямоугольник 𝐴𝐵𝐶𝐷 имеет высоту 20 см и шириной 44 см. Высота прямоугольника будет равна высоте цилиндр, поэтому ℎ=20. Точно так же ширина прямоугольника такая же, как длина окружности круглого лица. (длина которого равна 2𝜋𝑟), поэтому 2𝜋𝑟=44.
Следовательно, общая площадь поверхности этого цилиндра равна сумме площадей двух окружностей радиуса 𝑟=7 и
прямоугольник шириной 2𝜋𝑟=44 и высотой ℎ=20; так,
общая площадь поверхности=2×𝜋𝑟+(2𝜋𝑟×ℎ)=2×𝜋×7+(44×20)=(2×𝜋×49)+880=(98×𝜋)+880.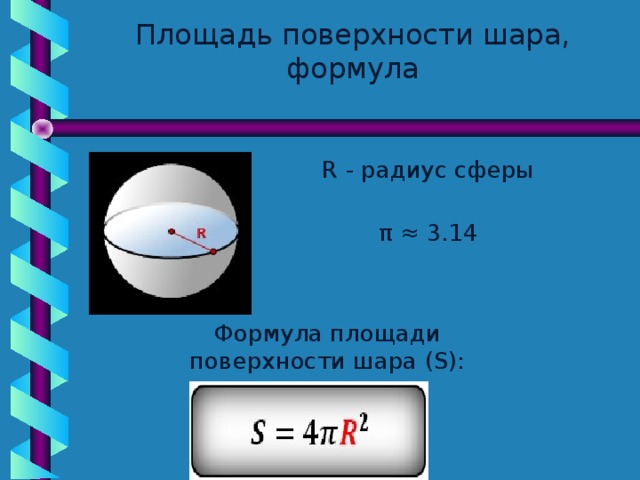
Используя данное приближение 227 для 𝜋, это становится общая площадь=98×227+880=987×22+880=(14×22)+880=308+880=1188.
Все длины даны в сантиметрах, поэтому общая площадь поверхности должна быть в квадратных сантиметров. Общая площадь поверхности цилиндр 1 188 см 2 .
Поскольку общая площадь поверхности цилиндра эквивалентна площади его сетки, то для цилиндра радиуса 𝑟 и высота ℎ, имеем следующую общую формулу.
Формула: Общая площадь поверхности цилиндра
Общая площадь поверхности цилиндра радиуса 𝑟 и высоты ℎ определяется по формуле totalsurfacearea=2𝜋𝑟+2𝜋𝑟ℎ.
Поскольку 𝜋=3,14159… это просто число, это означает, что пока мы знаем радиус и высоту
цилиндра, мы всегда можем применить эту формулу, чтобы найти его общую площадь поверхности. Таким образом, в первом примере мы могли бы заменить
значения ℎ и 𝑟 непосредственно в эту формулу, которая дала бы тот же ответ.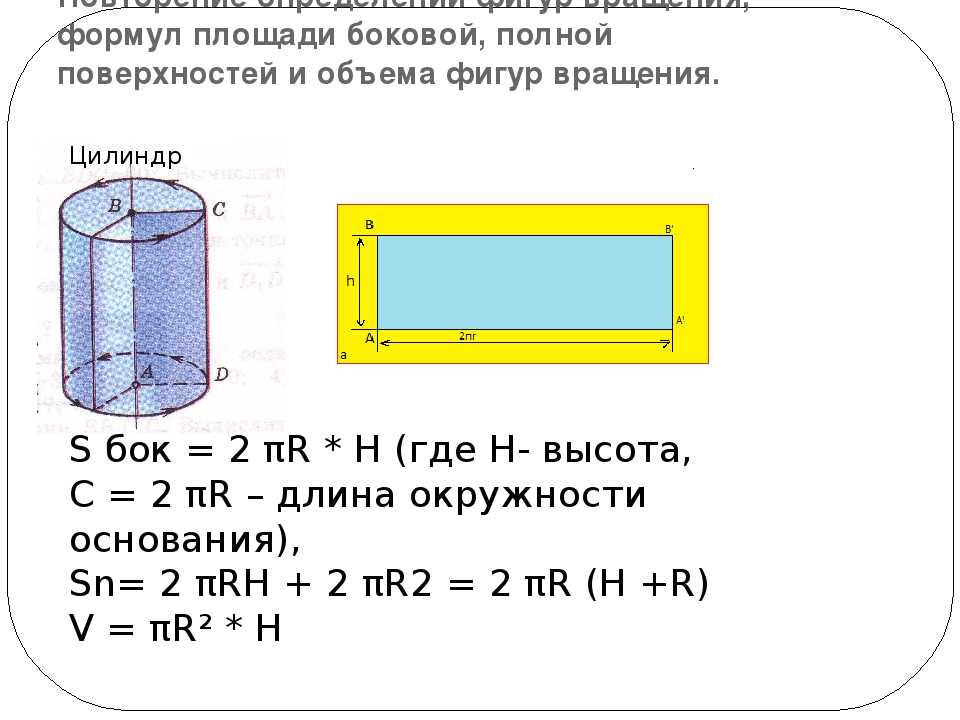
В некоторых вопросах вас могут попросить найти площадь боковой поверхности цилиндра. Если это так, вам нужно только проработать поверхность площадь криволинейной поверхности цилиндра и не включает окружности сверху и снизу. Поэтому имеем более простую формулу для этого случая.
Формула: площадь боковой поверхности цилиндра
Площадь боковой поверхности цилиндра радиуса 𝑟 и высоты ℎ определяется по формуле площадь боковой поверхности=2𝜋𝑟ℎ.
Опять же, если мы знаем радиус и высоту цилиндра, мы всегда можем применить эту формулу, чтобы найти его боковую поверхность область. Рассмотрим пример этого типа.
Пример 2. Определение площади боковой поверхности цилиндра
Определите с точностью до десятых площадь боковой поверхности показанного цилиндра.
Ответ
Здесь нас попросили найти площадь боковой поверхности цилиндра, а это значит, что нам нужно найти площадь всего лишь
криволинейная поверхность цилиндра.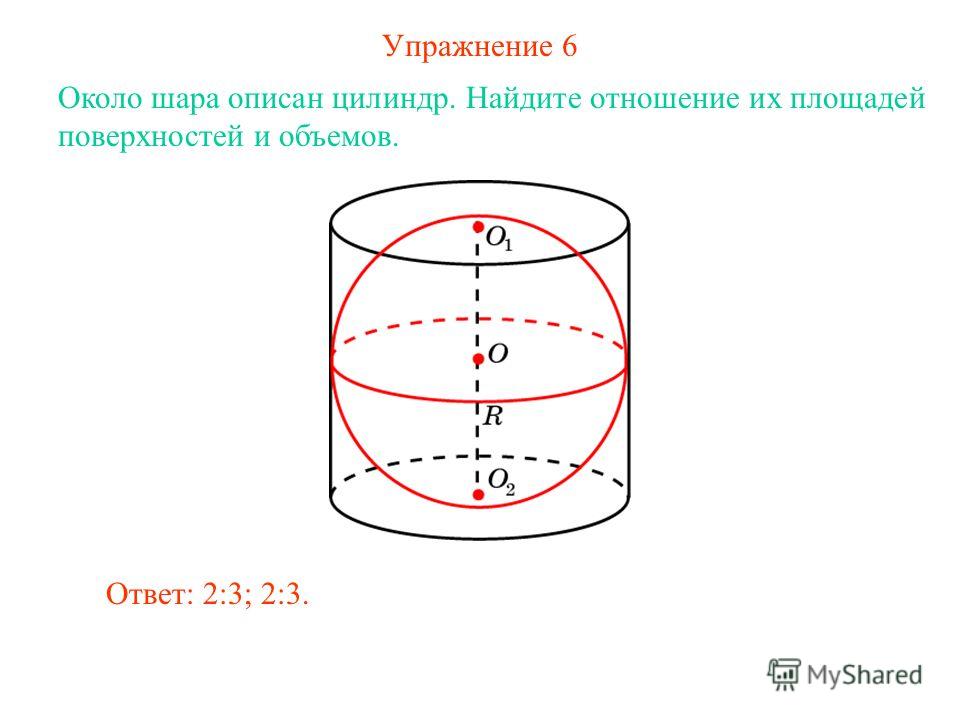
Напомним, что формула площади боковой поверхности цилиндра радиуса
𝑟 и высота ℎ определяется выражением
площадь боковой поверхности=2𝜋𝑟ℎ.
Цилиндр в этом вопросе имеет радиус 𝑟=13 и высоту ℎ=23, поэтому мы можем заменить эти значения в формулу, чтобы получить площадь боковой поверхности=2×𝜋×𝑟×ℎ=2×𝜋×13×23=𝜋×598=1878,672….
Нас попросили округлить ответ до десятых. Помните, что десятая цифра является первой цифра после запятой, в данном случае 6. Следующая за ней цифра (сотые цифра) равна 7, поэтому ответ округляется до 1 878,7 с точностью до десятых.
Поскольку радиус и высота цилиндра указаны в футах, площадь боковой поверхности должна быть в квадратный фут. боковой площадь поверхности цилиндра, округленная до десятых, составляет 1 878,7 футов 2 .
Вы могли заметить, что в приведенных выше примерах мы показывали всю нашу работу с точки зрения 𝜋 и оценивали только
ответы в конце работы.
Это отличная привычка, поскольку она поможет избежать ошибок округления и
улучшить свои алгебраические навыки. Кроме того, на некоторые вопросы вам будет предложено оставить свой ответ с точки зрения 𝜋, поэтому вам нужно
быть уверенным, делая это в любом случае.
Далее мы рассмотрим пример, в котором нам дан диаметр цилиндра, а не радиус. Наш подход очень аналогично, но с одним дополнительным шагом. Всегда проверяйте, указан ли вам в вопросе радиус или диаметр.
Пример 3: Определение площади поверхности цилиндра
Найдите с точностью до десятых общую площадь поверхности этого цилиндра.
Ответ
Напомним, что общая площадь поверхности цилиндра радиуса 𝑟 и высоты ℎ определяется выражением формула общая площадь поверхности = 2𝜋𝑟+2𝜋𝑟ℎ.
Обратите внимание, что на приведенной выше схеме показан цилиндр высотой 12 мм.
и диаметром 16 мм. Для подстановки в формулу нужно знать
радиус 𝑟, который составляет половину диаметра.
Поэтому наш первый шаг — вычислить радиус, разделив
диаметр на 2, что дает 𝑟=16÷2=8. Затем мы можем подставить это значение в формулу вместе
с ℎ=12, чтобы получить
общая площадь поверхности=2×𝜋×𝑟+(2×𝜋×𝑟×ℎ)=2×𝜋×8+(2×𝜋×8×12)=(2×𝜋×64)+(2×𝜋 ×96)=128𝜋+192𝜋=320𝜋=1005,309….
Ответ на вопрос нужно округлить до десятых. Десятая цифра — это первая цифра после запятой, который здесь равен 3. Цифра, следующая за этой (цифра сотых), равна 0, поэтому наш ответ должен быть округлен до 1 005,3 до ближайшего десятый.
Диаметр и высота цилиндра указаны в миллиметрах, поэтому объем в квадратных миллиметрах. Делаем вывод, что общая поверхность площадь цилиндра 1 005,3 мм 2 , округляется до десятых долей квадратный миллиметр.
Обратите внимание, что формулы для боковой и полной площадей поверхности выражаются через переменные 𝑟 и
ℎ. Формула площади боковой поверхности является более простой из двух, и мы всегда можем работать с ней в обратном порядке, чтобы вычислить
радиус или высота цилиндра, если дана площадь боковой поверхности и одно из двух других измерений.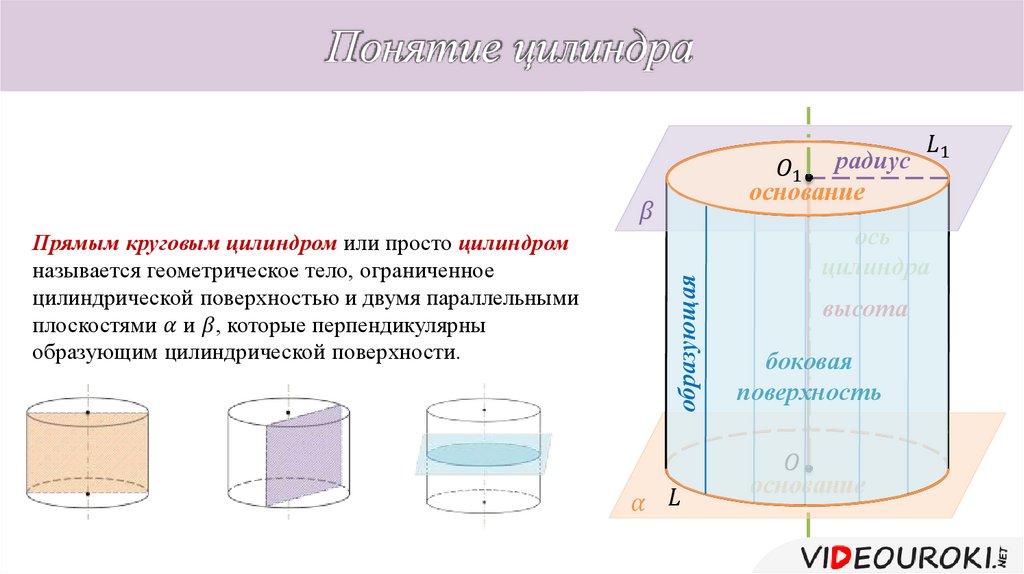
Общая площадь поверхности
формула более сложная, но мы всегда можем работать в обратном направлении, чтобы вычислить высоту цилиндра, если известна общая поверхность
площадь и радиус.
В следующем примере показано, как изменить формулу площади боковой поверхности для решения такого рода задач. В общем, если вопрос относится к «площади поверхности», мы можем предположить, что это означает общую площадь поверхности. В противном случае, если вопрос касается площадь боковой поверхности, нам всегда будут говорить об этом явно, как в данном случае.
Пример 4. Нахождение диаметра цилиндра по площади его боковой поверхности и высоте
Найдите диаметр основания цилиндра, если площадь боковой поверхности равна 434𝜋 квадратных сантиметра и высота 31 сантиметр.
Ответ
Вспомним формулу площади боковой поверхности цилиндра радиуса 𝑟 и высоты ℎ: площадь боковой поверхности=2𝜋𝑟ℎ.
В этом вопросе нам даны площадь боковой поверхности и высота цилиндра, и нас просят найти диаметр.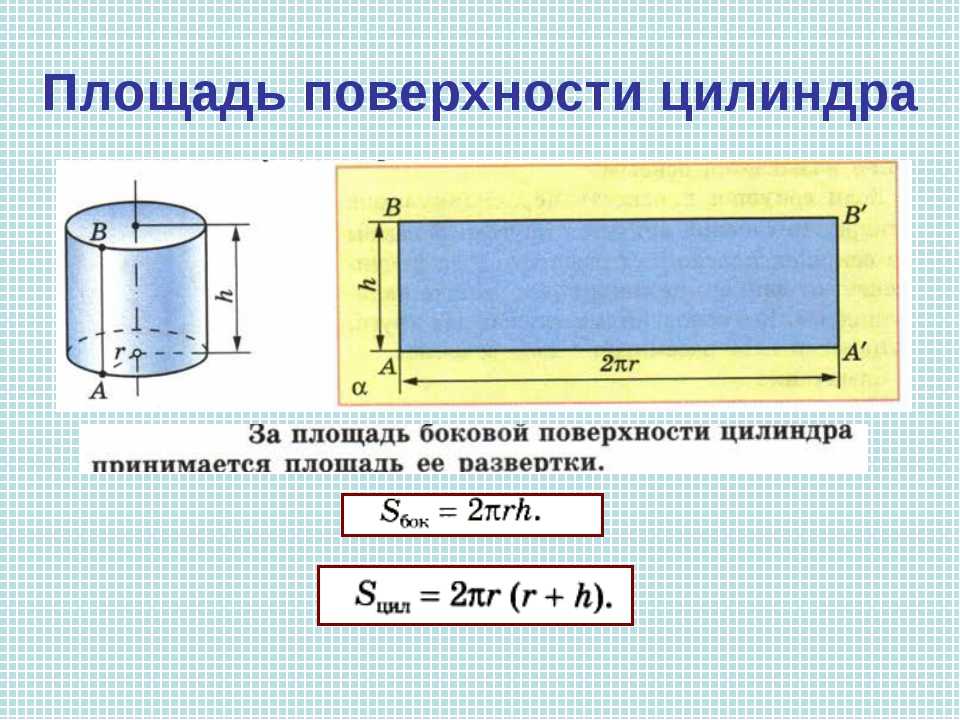
Поэтому наш метод будет заключаться в подстановке в формулу и решении полученного уравнения для радиуса 𝑟. Сделав это, мы можем удвоить ответ, чтобы получить диаметр.
Взяв формулу площади боковой поверхности и подставив значения 434𝜋 для площади боковой поверхности и 31 за ℎ получаем 434𝜋=2×𝜋×𝑟×31=62𝜋𝑟.
Деление обеих частей на 62 и затем 𝜋 дает 7=𝑟.
Итак, мы вычислили радиус цилиндра, но так как нас попросили найти диаметр, мы должны удвоить это значение чтобы получить 2×7=14.
Так как высота указана в сантиметрах, то диаметр будет иметь одну и ту же единицу измерения; диаметр цилиндра 14 см.
В нашем последнем примере нам дана общая площадь поверхности цилиндра вместе с соотношением между высотой и радиус. На этот раз нам нужно будет работать в обратном направлении от формулы общей площади поверхности, чтобы найти высоту цилиндра.
Пример 5: Определение высоты цилиндра по его радиусу и площади поверхности
Цилиндр имеет площадь поверхности 72 см 2 и его высота равна
к его базовому радиусу.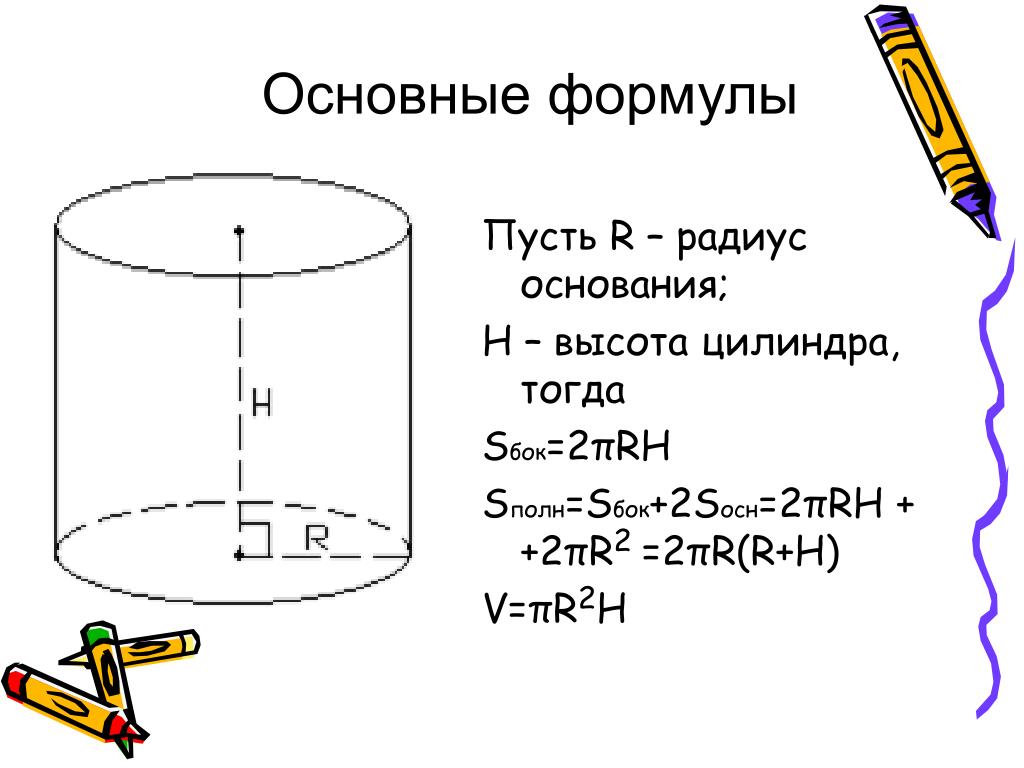
Найдите высоту цилиндра, давая ответ с точностью до двух знаков после запятой.
Ответ
Напомним, что общую площадь поверхности цилиндра радиуса 𝑟 и высоты ℎ можно рассчитать используя формулу totalsurfacearea=2𝜋𝑟+2𝜋𝑟ℎ.
Здесь нам дана площадь поверхности цилиндра и соотношение между высотой и радиусом. Наша стратегия будет состоять в том, чтобы подставьте эту информацию в формулу и переставьте, чтобы найти высоту.
Так как площадь поверхности равна 72𝜋, то в формуле имеем 72𝜋=2𝜋𝑟+2𝜋𝑟ℎ.
Кроме того, высота равна радиусу основания, поэтому ℎ=𝑟. Так как нас просят найти высоту, то ℎ должен появиться в нашем уравнении, поэтому мы заменяем 𝑟 на ℎ везде, чтобы получить 72𝜋=2𝜋ℎ+2𝜋ℎ=4𝜋ℎ.
Деление обеих частей на 4 и затем 𝜋 дает 18=ℎ.
Наконец, мы извлекаем квадратный корень из обеих частей, поэтому √18=√ℎ, что упрощает до 4,242…=ℎ.
То же, что и ℎ=4,242…, и это значение округляется до 4,24 с точностью до двух знаков после запятой.
Так как площадь поверхности дана в квадратных сантиметрах, то высота должно быть в сантиметрах. Мы обнаружили, что высота цилиндр, округленный до двух знаков после запятой, равен 4,24 см.
Давайте закончим повторением некоторых ключевых понятий из этого объяснения.
Ключевые точки
- Общая площадь поверхности цилиндра радиуса 𝑟 и высоты ℎ определяется по формуле общая площадь поверхности = 2𝜋𝑟+2𝜋𝑟ℎ.
- Площадь боковой поверхности цилиндра радиуса 𝑟 и высоты ℎ находится по формуле площадь боковой поверхности=2𝜋𝑟ℎ.
- Всегда проверяйте, указан ли в вопросе радиус или диаметр цилиндра.
- Из соображений точности часто имеет смысл завершить всю вашу работу с точки зрения 𝜋 и оценивайте ответ только в конце, если вас об этом попросят.
- Мы всегда можем работать в обратном направлении от формулы площади боковой поверхности, чтобы вычислить радиус или высоту цилиндра, если они заданы
площадь боковой поверхности и одно из двух других измерений.
