Как находится площадь прямоугольника формула
Статьи › Школа
Когда известно значение длины и ширины фигуры
Для вычисления необходимо умножить их друг на друга. S = a × b, где S — площадь; a, b — длина и ширина.
- Как найти площадь прямоугольника в 4 классе
- Как найти площадь прямоугольника 3 класс примеры
- Как найти площадь и периметр прямоугольника
- Как найти площадь прямоугольника если длина
- Чему равна площадь прямоугольника 3 класс
- Чему равна площадь прямоугольника 5 класс
- Как можно вычислить площадь прямоугольника двумя способами
- Как вычислить площадь прямоугольника 2 класс
- Как найти стороны прямоугольника 4 класс
- Какая формула у прямоугольника
- Как найти площадь прямоугольника со сторонами 8 см и 3 см
- Чему равна площадь и периметр
- Как найти площадь и ширину прямоугольника
- Как найти площадь прямоугольника если его длина 9 см а ширина на 5 см меньше
- Как найти площади
- Как найти площадь прямоугольника 4 см
- Как найти площадь прямоугольника со сторонами 2 см и 4 см
- Как найти площадь прямоугольника длина 4 см ширина 2 см
- Как найти площадь прямоугольника и квадрата 4 класс
- Как найти периметр и площадь 4 класс
Как найти площадь прямоугольника в 4 классе
Известно, что площадь прямоугольника равна произведению длин его сторон: S пр = a ⋅ b.
Как найти площадь прямоугольника 3 класс примеры
Чтобы найти площадь прямоугольника, надо найти произведение длин его сторон. 2 см ⋅ 4 см = 8 см 2. Длина и ширина прямоугольника должны быть выражены (записаны) в одинаковых единицах длины.
Как найти площадь и периметр прямоугольника
Ответы1. Периметр прямоугольника — это сумма всех его сторон. Формула нахождения площади прямоугольника: S = a × b, где а — ширина, b — длина прямоугольника.
Как найти площадь прямоугольника если длина
Чтобы найти площадь прямоугольника необходимо умножить длину прямоугольника на ширину. Найдем площадь прямоугольника длина которого 9 см, а ширина 2 см. S = 9 см * 2 см = 18 см².
Чему равна площадь прямоугольника 3 класс
Площадь — внутренняя часть любой плоской геометрической фигуры. Квадрат — это прямоугольник, у которого все стороны равны. Прямоугольник — это четырёхугольник, у которого все углы прямые. Квадратный сантиметр — квадрат со стороной 1 сантиметр.
Чему равна площадь прямоугольника 5 класс
Площадь прямоугольника находится как произведение ширины на его длину. S = a * b.
Как можно вычислить площадь прямоугольника двумя способами
S = b * a. Оба полученных выражения равны (по тому же переместительному свойству умножения), т. e: S = a * b = b * a.
Как вычислить площадь прямоугольника 2 класс
Прямоугольник Прямоугольник — это параллелограмм, у которого все углы прямые. Узнать площадь прямоугольника помогут следующие формулы: S = a × b, где a, b — длина и ширина прямоугольника.
Как найти стороны прямоугольника 4 класс
А = S: b, где S — площадь прямоугольника, b — сторона прямоугольника.
Какая формула у прямоугольника
Формула нахождения периметра прямоугольника
P = a + b + c + d, где a, b, c, d — стороны. P = 2 × (a + b), где a и b — соседние стороны.
Как найти площадь прямоугольника со сторонами 8 см и 3 см
Площадь прямоугольника равна произведению сторон прямоугольника, следовательно: S = 8 * 3 = 24 см².
Чему равна площадь и периметр
Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины.
Как найти площадь и ширину прямоугольника
Ширину можно вычислить по длине, если известна еще площадь или периметр прямоугольника. Например, зная площадь и длину, можно найти ширину по формуле а = S/b. А зная периметр и длину, можно вычислить ширину по формуле a = (P — 2b) / 2.
Как найти площадь прямоугольника если его длина 9 см а ширина на 5 см меньше
S = 9 * 4 = 36 см².
Как найти площади
S = a ⋅ b, где a и b — длина и ширина.
Как найти площадь прямоугольника 4 см
Для того, чтоб найти площадь прямоугольника необходимо длину прямоугольника умножить на его ширину: S = a * b, где S -площадь прямоугольника, a — длина прямоугольника, b — ширина прямоугольника. По условию задачи ширина прямоугольника 4 см, а длина в 2 раза больше, тогда длина прямоугольника будет равна 4 * 2 = 8 см.
Как найти площадь прямоугольника со сторонами 2 см и 4 см
Вычислим площадь прямоугольника со сторонами 2 см и 4 см. S = 2 * 4 = 8 кв. см.
Как найти площадь прямоугольника длина 4 см ширина 2 см
S = a × b = 4 × 2 = 8 (см2).
Как найти площадь прямоугольника и квадрата 4 класс
Площадь прямоугольника равна произведению его длины и ширины: ・. Площадь квадрата равна произведению двух его соседних сторон: ・.
Как найти периметр и площадь 4 класс
Ответы2. Периметром (P) называют сумму всех сторон. Чтобы найти периметр, нужно сложить все стороны. Площадь (S) показывает размер фигуры.
- Как найти площадь и ширину прямоугольника
- Как найти площадь прямоугольника 3 класс примеры
- Как найти площадь прямоугольника 4 см
- Как найти площадь прямоугольника длина 4 см ширина 2 см
- Как найти площадь прямоугольника если длина
- Как найти площадь прямоугольника если его длина 9 см а ширина на 5 см меньше
- Как найти площадь прямоугольника и квадрата 4 класс
- Как найти площадь прямоугольника со сторонами 2 см и 4 см
- Как найти площадь прямоугольника со сторонами 8 см и 3 см
Правило как находить площадь периметр.
Как найти площадь и периметр прямоугольника? Периметр и площадь прямоугольникаПериметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ.
- 2 способ. Сложить ширину и длину, и умножить на 2.
P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Среди неиссякаемого многообразия геометрических фигур есть те, которые наиболее применимы в нашей жизни, например, параллелограмм, круг, овал и др. Геометрические фигуры повсюду, в связи с этим зачастую возникает необходимость определения их числовых характеристик: площадь, периметр, объем.
- это плоская геометрическая фигура;
- это четырехугольник;
- это фигура, у которой противоположные стороны равны и параллельны, все углы прямые, т. е. по 90°.
е. по 90°.- имеется прямоугольник ABCD;
- стороны AB и CD равны 5 см;
- стороны BC и AD равны 7 см.
Для того, чтобы находить периметр и площадь прямоугольника, нужно знать формулы и главное — уметь применять их для решения задач — ведь они бывают разной сложности.
Очень часто при решении задач легкого уровня достаточно знать основные формулы и решить их просто подставляя нужные значения.
Если задачи посложнее и в их условии нет данных нужных для формулы, нужно их находить с помощью других алгебраических действий.
В этом случае можно навести следующий пример
нужно найти площадь прямоугольника, если его периметр равен 120 см, а стороны относятся как 2 к 3
сначала составляем уравнение , чтобы найти стороны используя при этом формулу периметра (P=2(а+b ):
2*(2х+3Х)=120 решаем его, х=12 значит стороны равны 24 см и 36 см и теперь уже подставляем значения в формулу площади S=ab и находим ее S=24*36=864 см.кв.
Площадь прямоугольника равна произведению длины и ширины и вычисляется по формуле a*b, где а и b -стороны прямоугольника. Периметр прямоугольника равен сумме всех его сторон и вычисляется по формуле a+b+a+b.
Нахождение площади прямоугольника — умножим длину прямоугольника на его ширину.
Нахождение периметра прямоугольника (сумма длин всех сторон) — простым сложением длин всех сторон, либо к длине продольной стороны прямоугольника, прибавляем длину поперечной и полученную сумму умножаем на два.
Если представить, что ваш огород прямоугольной формы и вам необходимо участок обложить забором, то наверное перед вами возникнет вопрос, а какой длины будет забор, чтобы правильно рассчитать расход стройматериалов. Вы сложите длины сторон забора и найдете ПЕРИМЕТР. Если зададитесь вопросом, какое количество земли нужно перекопать на этом участке, то придется искать ПЛОЩАДЬ, а для этого нужно будет перемножить длину на ширину участка, ведь как известно у прямоугольника противоположные стороны попарно равны. Не стоит забывать, что квадрат тоже прямоугольник, чтобы найти периметр квадрата, нужно длину умножить на 4, а площадь — длину стороны умножить на себя.
Вспомним школьный курс математики. Так периметр прямоугольника находится по формуле суммы двух его сторон умноженных на 2. То есть Р=2*(а+b), где а и b это стороны прямоугольника. Площадь, соответственно находится с помощью формулы S=a*b, где a и b также являются его сторонами.
Если не вдаваться в глубокие подробности, то найти площадь и периметр геометрической фигуры прямоугольник очень просто.
Площадь прямоугольника:
Периметр прямоугольника:
S = a + b + c + d
Периметр прямоугольника — это длины всех его сторон. Исходя из того, что у этой фигуры четыре стороны, или две пары, при этом противолежащие стороны равны друг другу, можно прийти к выводу, что уместно сложить значения двух разновеликих сторон и умножить полученное значение на два.
Площадь находится также просто: мы просто перемножаем разновеликие стороны.
Площадь вычисляется при умножении длинной стороны прямоугольника с короткой. А периметр-это (длин. сторона+ кор. сторона)*2
Можно пойти самым простым путем нахождения площади прямоугольника. А именно, умножить длину прямоугольника (как правило, это a) на ширину прямоугольника (как правило, это B). А вот периметр ищем при помощи сложения всех сторон, или, проще говоря: 2a+2b
Прямоугольник это геометрическая фигура, а именно четырехугольник, у которого все углы прямые.
Получается, что противоположные стороны равны друг другу.
Периметр прямоугольника это сумма длин всех сторон прямоугольника, либо сумма длины и ширины, умноженная на 2.
Периметр это длина всех сторон прямоугольника, то он измеряется в единицах длины: см, мм, м, дм, км.
P=AB+CD+AD+BC или P=2*(AB+AD).
Площадь измеряется квадратными единицами длины: м2, см2, дм2 и обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника рассчитывается путем умножения его длины на ширину полученное произведение и будет площадь.
Периметр прямоугольника находится путем суммирования длины и ширины, полученную сумму нужно еще умножить на два, это и будет искомый периметр.
Если у прямоугольника заданы две противолежащие стороны, то все просто перемножаем их и получаем площадь, складываем и удваиваем и получаем периметр. Однако чаще в учебниках задают самый разнобой — сторону и периметр, сторону и площадь, сторону и диагональ.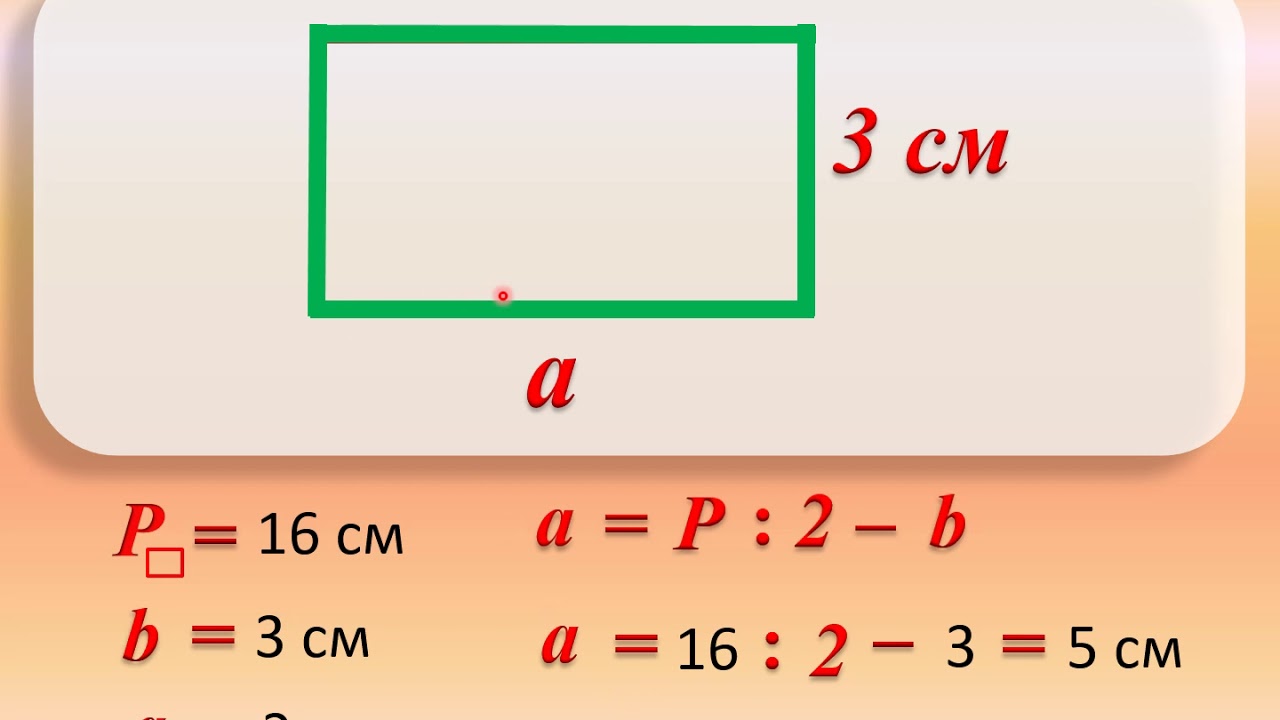
Как поступать в этих случаях.
Вот это идеальная задача.
Могут быть заданы сторона и диагональ. В этом случае находим вторую сторону по теореме Пифагора — как второй катет в треугольнике где гипотенуза диагональ прямоугольника.
В итоге мы имеем вот какие формулы для нахождения периметра прямоугольника:
А если по простому преобразовать эти же формулы, то получаются формулы для нахождения площади во всех вариантах задач:
Одним из базовых понятий математики является периметр прямоугольника. На эту тему существует множество задач, при решении которых не обойтись без формулы периметра и навыков его вычисления.
Основные понятия
Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника, например, поверхность стола, тетрадь и прочее.
Рассмотрим пример: по границам земельного участка необходимо поставить забор.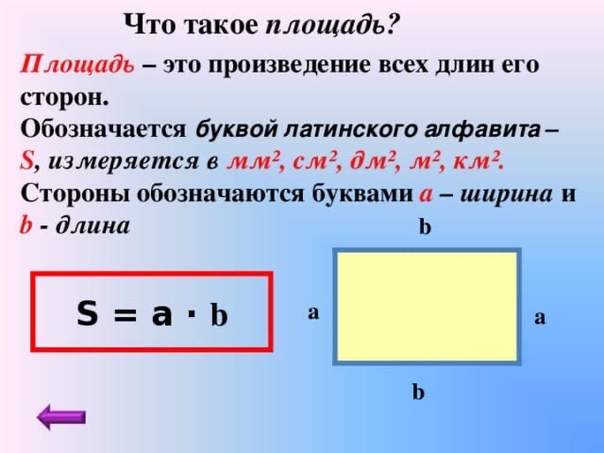
Для того чтобы узнать длину каждой из сторон необходимо их измерить.
Рис. 1. Земельный участок формой прямоугольника.
Земельный участок имеет стороны длиной 2 м., 4 м., 2 м., 4 м. потому чтобы общую узнать длину забора необходимо сложить длины всех сторон:
2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.
Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют букву P.
Для вычисления периметра прямоугольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.
Периметр прямоугольника измеряется в мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одинаковую систему измерения.
Периметр прямоугольника измеряется в различных единицах: мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одну систему измерения.
Формула периметра фигуры
Если принять к вниманию тот факт, что противоположные стороны прямоугольника равны, то можно вывести формула периметра прямоугольника:
$P = (a+b) * 2$, где а, b – стороны фигуры.
Рис. 2. Прямоугольник, с обозначенными противоположными сторонами.
Существует и другой способ найти периметр. Если в задание дано лишь одну сторону и площадь фигуры, можно использовать выразить другую сторону через площадь. Тогда формула будет выглядеть следующим образом:
$P = {{2S + 2a2}\over{a}}$, где S – площадь прямоугольника.
Рис. 3. Прямоугольник с сторонами a, b .
Задание : Вычислить периметр прямоугольника, если его стороны равны 4 см. и 6 см.
Решение:
Используем формулу $P = (a+b)*2$
$P = (4+6)*2=20 см$
Таким образом, периметр фигуры $P = 20 см$.
Так как периметр – это сумма все сторон фигуры, то полупериметр это сумма только одной длины и ширины. Чтобы получить периметр необходимо полупериметр умножить на 2.
Площадь и периметр – это два основных понятия измерения любой фигуры. Их нельзя путать, хоть они и связаны между собой. Если увеличить, либо уменьшить площадь, то, соответственно, увеличится либо уменьшится его периметр.
Прежде, чем решать задачи на нахождение периметра и площади геометрических фигур, напомню, что….
I уровень
1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.
2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.
5.Длина прямоугольника 8 дм, ширина 5 дм. Найди его площадь.
6.Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.
7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.
8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.
9.Длина стороны квадрата 6 см.
Узнай площадь.
10.Вычисли периметр квадрата со стороной 4 см.
11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.
12.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.
14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.
15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше. Вычисли его периметр.
16.Сторона квадрата равна 3 см. Чему равен периметр?
17.Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?
18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?
19.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
20.
Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.
21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?
II уровень
1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.
2.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше. Найди Р и S.
4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.
5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.
6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.
7.Периметр квадрата равен 32 см. Чему равна его сторона?
8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.
9.Периметр прямоугольника 20 см. Длина его стороны 6 см.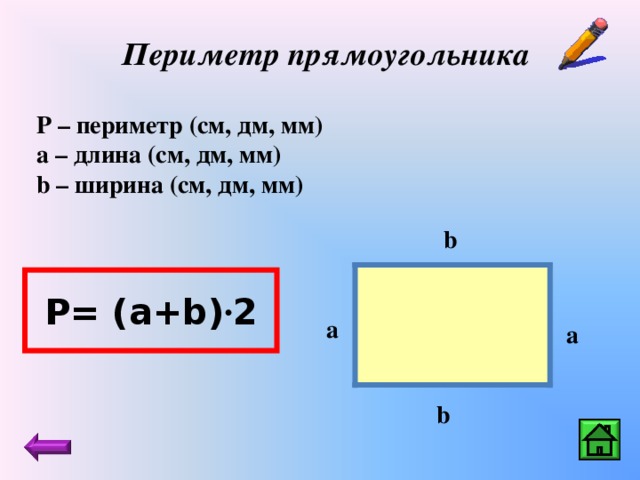
Узнайте ширину прямоугольника и начертите его.
10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника.
11.Периметр прямоугольника равен 54 м . Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.
12. Найдите площадь квадрата, периметр которого равен 360 мм.
13. Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?
14. Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами 2 см и 6 см.
15. Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?
16. Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?
17. У какой фигуры площадь больше и на сколько: у квадрата со стороной 4см или у прямоугольника со сторонами 2 см и 6 см?
18. Периметр прямоугольника равен 54 м. Найди площадь этого прямоугольника, если одна его сторона равна 18 м.
19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.
20. Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.
Составила К ислова Людмила Борисовна
| |||||||
| |||||||
| |||||||
У нас есть два ответа для вас Привет, Бруклин, Предположим, у вас есть 4 фута материала для фоторамки, и вы хотите сделать рамку для одной из своих фотографий. или вы можете сделать рамку для фотографии вашего любимого жирафа или за фотографию, которую вы сделали во время поездки в горы. Каждый из этих прямоугольников имеет одинаковый периметр, 4 фута, но площади совершенно разные. Между периметром прямоугольника и его площадью нет прямой зависимости. Пенни
Привет, Бруклин, Вам нужно знать комбинацию любых двух из следующих: длина, ширина, периметр, площадь. Очевидно, если вы знаете длину и ширину, вы установили! Вы можете рассчитать периметр, используя P = 2L + 2W, и вы можете рассчитать площадь, используя A = LW . Если известна площадь и длина или ширина, можно использовать формулу площади для определения другого измерения: Если известен периметр, а также длина или ширина, можно использовать формулу периметра для определения другого измерения: Если вы знаете и площадь, и периметр, вы также можете определить размеры, но это требует немного больше усилий и требует либо угадывания и проверки (что может оказаться трудным или невозможным, если какое-либо измерение иррационально), либо решения квадратного уравнения. Дано A = 15, P = 16 15 = L(8 — L) Мы бы выбрали L = 5 (только потому, что по соглашению мы думаем, что длина — это более длинная сторона), и подставив в одно из наших исходных уравнений, мы находим, что ширина равна 3,9.0055 Надеюсь, это поможет,
| |||||||
Вы можете сделать рамку для своей фотографии новорожденного ребенка тети Марты и дяди Фреда.
Прямоугольник: Примеры, Свойства, Формулы и Площадь
Когда смотришь на объект, на ум приходят некоторые вопросы, и тут же даешь быстрые ответы на многие из них. Одним из таких вопросов, на который дается ответ, является форма объекта.
В этой статье мы рассмотрим определение прямоугольника, его свойства, формулы периметра и площади прямоугольника и примеры их применения.
Определение прямоугольника
Прямоугольник представляет собой четырехугольник с четырьмя сторонами и четырьмя углами, все внутренние углы которого прямые (90 градусов).
Прямоугольник является частным случаем параллелограмма. Другими словами, параллелограмм становится прямоугольником, если его стороны перпендикулярны друг другу. Это можно проиллюстрировать на изображении ниже.
Прямоугольник — StudySmarter Original
Мы можем заметить, что противоположные стороны AB и CD равны по размеру и параллельны, то же самое для BC и AD. Кроме того, четыре стороны перпендикулярны друг другу, таким образом, четырехугольник является прямоугольником.
Свойства прямоугольников
Прямоугольник, являющийся параллелограммом, обладает всеми свойствами параллелограмма, но, будучи его частным случаем, имеет свои уникальные свойства, которые делают его геометрической формой.
Чтобы лучше понять свойства прямоугольника, давайте рассмотрим следующий прямоугольник ABCD на изображении ниже.
Прямоугольник ABCD — оригинал StudySmarter
Свойство | Пример |
1. Противоположные стороны прямоугольника равны и параллельны. | AB = CD, а AB параллельна CD. Аналогично, AD = BC, а AD параллелен BC. |
2. Все четыре угла прямоугольника прямые. | ∠A=∠B=∠C=∠D=90° |
3. Сумма всех внутренних углов прямоугольника равна 360º. | ∠A+∠B+∠C+∠D=360° |
4. Диагонали прямоугольника равны по длине и делят друг друга пополам – они пересекаются посередине. | AC и BD — диагонали прямоугольника ABCD. AC = BD AC делит пополам BD и BD делит AC пополам. |
Построение прямоугольника
Для построения прямоугольника выполните следующие действия.
Шаг 1 : Нарисуйте прямую линию (R), затем поместите на ней 2 точки A и B.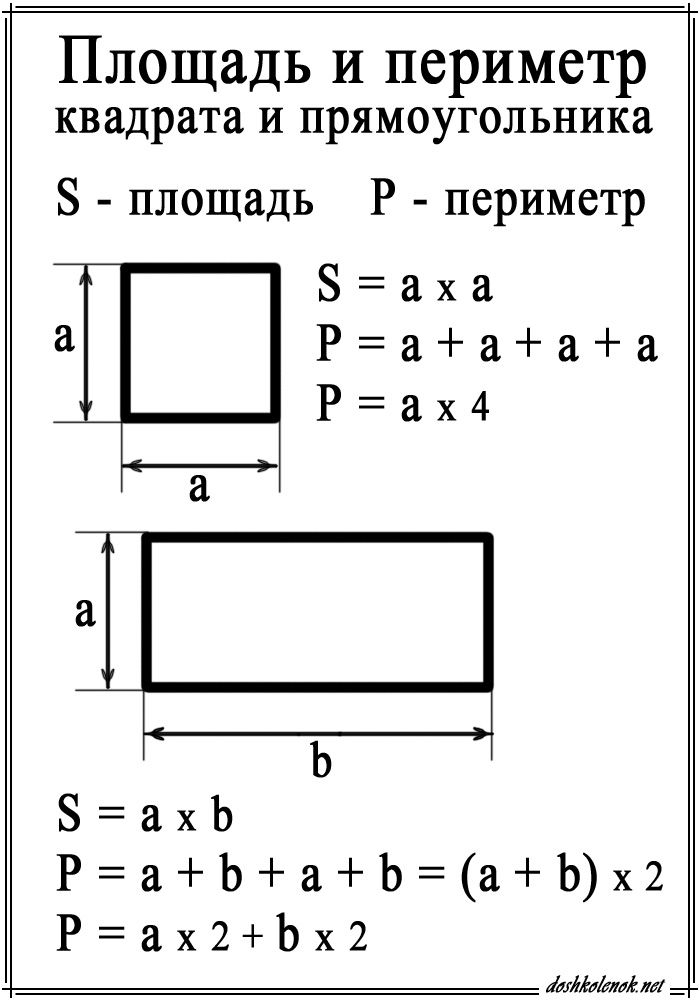
Шаг 2: Нарисуйте 2 перпендикулярные линии (S) и (T), проходящие через две точки A и B.
Шаг 3: Найдите две точки C и D соответственно на двух линиях (S) и (Т). Однако C и D должны быть на одном уровне.
Три вышеупомянутых шага можно проиллюстрировать на рисунке ниже:
Изображение, полученное в результате шагов 1, 2 и 3 — StudySmarter Original
Шаг 4: Проведите прямую линию, соединяющую две точки C и D, как показано на рисунке. на картинке ниже:
Изображение, полученное в результате шага 4 — оригинал StudySmarter
Достигнув шага 4, вы заметите, что 4 точки A, B, C и D образуют прямоугольную форму.
Формула площади прямоугольника
Площадь плоской формы или поверхности объекта может быть определена в геометрии как занимаемое им пространство.
Площадь фигуры обычно измеряется с учетом количества единичных квадратов, покрывающих поверхность фигуры.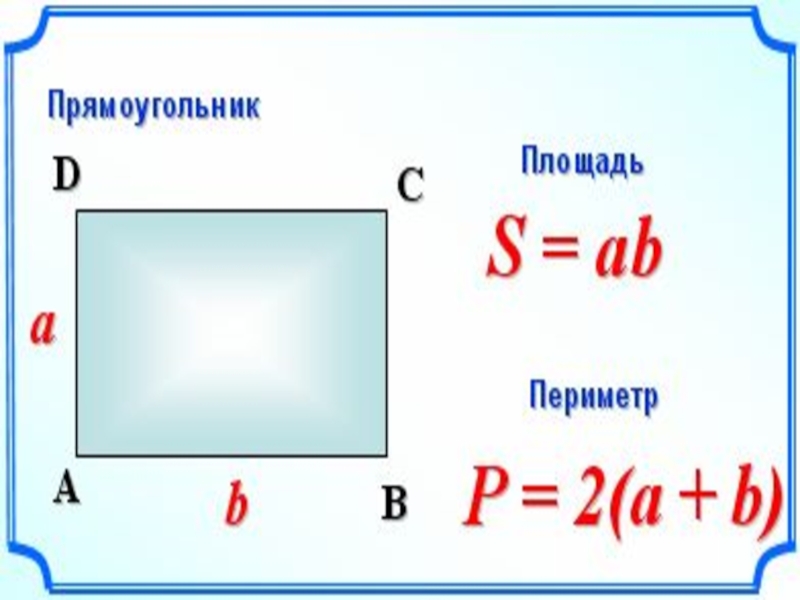
Квадратные сантиметры, квадратные футы, квадратные дюймы и другие подобные единицы используются для измерения площади.
Дан прямоугольник высотой h и основанием b, его площадь будет равна:
A=b×h.
Найдите площадь прямоугольной формы на изображении ниже. Рассмотрим квадрат, состоящий из 25 меньших квадратов, квадрат со стороной 1 единица.
Мы можем заметить, что высота прямоугольника равна 2 единицам квадратов, поэтому его длина равна 2 единицам. Аналогично, основание прямоугольника равно 5 единицам. Таким образом, площадь этого прямоугольника можно вычислить, умножив высоту на основание:
A= 2 ед. × 5 ед. = 10 ед.
Следовательно, периметр фигуры вычисляется путем суммирования длин всех ее сторон. Та же концепция применима и к прямоугольной форме. Таким образом, общая длина всех сторон прямоугольника называется периметром.
Противоположные стороны прямоугольника равны друг другу (одно из его свойств).
Таким образом, периметр прямоугольника со сторонами длины a, b, a, b равен P = a + b + a + b, или P = 2a + 2b, или даже P = 2 (a + b).
Итак, нам нужно вычислить длины двух сторон, чтобы найти периметр прямоугольника, так как противоположные стороны прямоугольника всегда равны.
Найдите периметр и площадь фигуры, показанной на рисунке ниже:
Шаг 1 : Попробуйте определить фигуры прямоугольника. Мы можем заметить, что в фигуре выше присутствуют 2 прямоугольника. Идентифицированные прямоугольники показаны на изображении ниже:
Следующие свойства проверяются, чтобы убедиться, что идентифицированные фигуры являются прямоугольниками:
- Противоположные стороны равны и параллельны. Например, у первого идентифицированного прямоугольника противоположные стороны параллельны и равны 8, а две другие противоположные стороны также параллельны и равны 3.
- Все углы прямые, или, другими словами, все стороны перпендикулярны друг другу. другие.
другие.Периметр первого прямоугольника P A можно рассчитать следующим образом:
PA=(4+4+3+3)cm=14cm
Периметр второго прямоугольника P B можно рассчитать следующим образом:
PB=(10+10+5+5)см=30см
Периметр общей формы P AB :
PAB=PA+PB=(14+30 )см=44см
Площадь первого прямоугольника A A можно рассчитать следующим образом:
AA=высота×основание=4см×3см=12см2
Площадь второго прямоугольника A B можно рассчитать следующим образом:
AB=высота×основание=5см×10см=50см2
Площадь общей формы:
AAB=AA+AB=12см2+50см2=62см2
Квадрат и прямоугольник
На рисунке ниже видно, что квадрат и прямоугольник являются четырехугольниками с четырьмя сторонами.
Прямоугольник и квадрат — StudySmarter Original
Квадрат и прямоугольник имеют сходные свойства, как показано в таблице ниже:
X
✔
✔ 9 0055
✔
✔
✔
✔
✔
✔
✔
✔
✔
✔
Что характеризует квадрат как уникальный прямоугольник?
Как показано в таблице выше, квадрат является особым типом прямоугольника по следующим причинам:
Квадрат обладает всеми свойствами прямоугольника.
