Формула площади прямоугольного треугольника через синус: Площадь треугольника

Что площадь прямоугольного треугольника. Как найти площадь треугольника

Что площадь прямоугольного треугольника. Как найти площадь треугольника

На уроках геометрии в средней школе всем нам говорили о том, треугольника. Однако в рамках школьной программы мы получаем только самые необходимые знания и учимся наиболее распространенным и стандартным способам вычислений. Существуют ли необычные способы нахождения этой величины?

В качестве введения вспомним, какой треугольник считается прямоугольным, а также обозначим понятие площади.

Прямоугольным треугольником называют замкнутую геометрическую фигуру, один из углов которой равен 90 0 . Неотъемлемыми понятиями в определении являются катеты и гипотенуза. Под катетами подразумевают две стороны, которые в точке соединения образуют прямой угол. Гипотенуза — сторона, противоположная прямому углу. Прямой треугольник может быть равнобедренным (две его стороны будут иметь одинаковую величину), но никогда не будет равносторонним (все стороны одной длины). Определения высоты, медианы, векторов и прочих математических терминов подробно разбирать не будем. Их легко найти в справочниках.

Площадь прямого треугольника. В отличие от прямоугольников, правило о

произведении сторон в определении не действует. Если говорить сухим языком терминов, то под площадью треугольника понимают свойство этой фигуры занимать часть плоскости, выраженное числом. Довольно сложно к восприятию, согласитесь. Не будем пытаться глубоко вникнуть в определение, наша цель не в этом. Перейдем к главному — как найти площадь прямоугольного треугольника? Сами вычисления производить не будем, укажем только формулы. Для этого определимся с обозначениями: A,B,C — стороны треугольника, катеты — AB, BC. Угол ACB — прямой. S — площадь треугольника, h n n — высота треугольника, где nn — сторона, на которую она опущена.

Способ 1. Как найти площадь прямоугольного треугольника, если известна величина его катетов

Способ 2. Находим площадь равнобедренного прямоугольного треугольника

Способ 3.

Вычисление площади через прямоугольник

Достраиваем прямоугольный треугольник до квадрата (если треугольник

равнобедренный) или прямоугольника. Получим простой четырехугольник, составленный из 2-х идентичных прямоугольных треугольников. В этом случае значение площади одного из них будет равно половине площади полученной фигуры. S прямоугольника вычисляем произведением сторон. Обозначим эту величину M. Искомое значение площади будет равно половине M.

Способ 4. «Пифагоровы штаны». Знаменитая теорема Пифагора

Мы все помним ее формулировку: «сумма квадратов катетов…». Но не все могут

сказать, причем тут некие «штаны». Дело в том, что изначально Пифагор изучал взаимосвязь построенных на сторонах прямого треугольника. Выявив закономерности в соотношении сторон квадратов, он смог вывести и известную всем нам формулу. Ее можно применять в случае, когда неизвестна величина одной из сторон.

Способ 5. Как найти площадь прямоугольного треугольника по формуле Герона

Тоже достаточно простой способ расчета. Формула предполагает выражение площади треугольника через числовые значения его сторон. Для расчетов необходимо знать величины всех сторон треугольника.

S = (p-AC)*(p-BC), где p = (AB+BC+AC)*0.5

Кроме приведенных, существует множество других способов найти величину такой загадочной фигуры, как треугольник. Среди них: вычисление методом вписанной или описанной окружности, вычисление при помощи координат вершин, использование векторов, абсолютной величины, синусов, тангенсов.

Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.

Геометрия треугольника

В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии.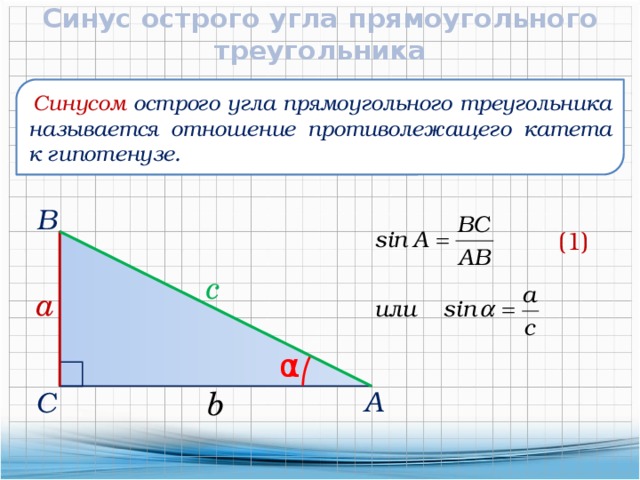 В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:

• Гипотенуза — самая длинная сторона треугольника, лежащая напротив прямого угла.
• Катеты — отрезки, образующие прямой угол. В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.

Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.

Прямоугольный треугольник в реальности

Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности. Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.

Площадь треугольника

Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника. Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:

где a – сторона треугольника, h – его высота.

Формула для вычисления площади прямоугольного треугольника еще проще:

где a и b – катеты.

Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:

• два катета;
• катет и прилежащий угол;
• катет и противолежащий угол.

В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.

Примеры из реальной жизни

Керамическая плитка

Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника. Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:

Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.

Школьная задача

Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:

Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.

Заключение

Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.

Инструкция

Задача 1.
Найдите длины всех сторон треугольника, если известно, что одного катета превышает длину другого на 1 см, а треугольника равна 28 см.

Решение.
Запишите основную формулу площади S = (a*b)/2 = 28. Известно, что b = a + 1, подставьте это значение в формулу: 28 = (a*(a+1))/2. 2)*tg(B)/2 d случае, если вам задан только один из катетов (a), но также известен и прилежащий этому катету угол (B).

Видео по теме

Источники:

• «Пособие по математике для поступающих в вузы», под ред. Г.Н. Яковлева, 1982.

Соотношения между сторонами и углами прямоугольного треугольника рассматриваются в разделе математики, который называется тригонометрией. Для нахождения сторон прямоугольного треугольника достаточно знать теорему Пифагора, определения тригонометрических функций, и иметь какое-либо средство для нахождения значений тригонометрических функций, например, калькулятор или таблицы Брадиса. Рассмотрим ниже основные случаи задач нахождения сторон прямоугольного треугольника.

Вам понадобится

• Калькулятор, таблицы Брадиса.

Инструкция

Если задан один из острых углов, например, A, и один из катетов, например, a, то гипотенуза и другой катет вычисляются из соотношений: b=a*tg(A), c=a*sin(A).

Полезный совет

В том случае, если вам не известно значение синуса или косинуса какого-то из необходимых для расчёта углов, вы можете воспользоваться таблицами Брадиса, в них приводятся значения тригонометрических функций для большого числа углов.

Кроме того, большинство современных калькуляторов способны рассчитывать синусы и косинусы углов.

Источники:

• как вычислить сторону прямоугольного треугольника в 2019

В такой фигуре как прямоугольный треугольник обязательно существует четкое соотношение сторон относительно друг друга. Зная две из них, всегда можно найти третью. То, каким образом это возможно сделать, вы узнаете из инструкции, предложенной ниже.

Вам понадобится

• — калькулятор.

Инструкция

Возведите в квадрат оба катета, а сложите их между собой a2+b2. Полученный результат является гипотенузой (основанием ) в квадрате c2. Далее нужно лишь извлечь корень из последнего , и гипотенуза найдена. Данный метод является простым и удобным в применении на . Главное в процессе нахождения сторон треугольника

таким образом — не забывать извлекать корень из предварительного результата, чтобы избежать самой распространенной ошибки. Формула выведена, благодаря самой известной в мире теореме Пифагора, которая во всех источниках имеет вид: a2+b2 = c2.

Разделите один из катетов a на синус противолежащего ему угла sin α. В том случае, если в условии известны стороны и синусы, этот вариант нахождения гипотенузы будет приемлемым. Формула в данном случае будет иметь совсем простой вид: c=a/sin α. Будьте внимательны при всех вычислениях.

Умножьте сторону a на два. Гипотенуза вычислена. Это, пожалуй, самый элементарный способ нахождения нам стороны. Но, к сожалению, этот метод применяется только в одном случае — если сторона, которая лежит напротив угла в градусную меру, равную числу тридцать. При наличии таковой вы можете быть уверены, что она всегда будет являть собой ровно половину гипотенузы. Соответственно, вам остается лишь увеличить ее в два раза и готов.

Разделите катет a на косинус прилежащего к нему угла cos α. Такой метод подойдет исключительно в том случае, если вам известен один из катетов и косинус угла к нему прилежащего. Этот способ напоминает уже представленный вам ранее, в котором используется также катет, но вместо косинуса — синус противолежащего угла. Только вот в этом случае будет иметь несколько другой измененный внешний вид: с=a/ cos α. Вот и все.

Треугольник , один из углов которого является прямым (равен 90°), называют прямоугольным. Его самая длинная сторона всегда лежит напротив прямого угла и называется гипотенузой, а две другие стороны называют катетами. Если длины этих трех сторон известны, то найти величины всех углов треугольник а не составит труда, так как фактически потребуется вычислить всего один из углов. Сделать это можно несколькими способами.

Инструкция

Используйте для вычисления величин (α, β, γ) определения тригонометрических функций через прямоугольный тре. Такое , например, для синуса острого угла как отношение длины противолежащего катета к длине гипотенузы. Значит, если длины катетов (A и B) и гипотенузы (C), то найти, например, синус угла α, лежащего напротив катета A можно, разделив длину стороны А на длину стороны C (гипотенузы): sin(α)=A/C. Узнав значение синуса этого угла можно найти его величину в градусах, использовав обратную синусу функцию — арксинус. То есть α=arcsin(sin(α))=arcsin(A/C). Таким же способом можно найти и величину острого угла в треугольник е, но в этом нет необходимости. Так как сумма всех углов треугольник а составляет 180°, а в треугольник е один из углов равен 90°, то величину третьего угла можно посчитать как разность между 90° и величиной найденного угла: β=180°-90°-α=90°-α.

Вместо определения синуса можно использовать определение косинуса острого угла, которое формулируется как отношение длины прилежащего к искомому углу катета к длине гипотенузы: cos(α)=B/C. И здесь задействуйте обратную тригонометрическую функцию (арккосинус), чтобы найти величину угла в градусах: α=arccos(cos(α))=arccos(B/C). После этого, как и в предыдущем шаге, останется найти величину недостающего угла: β=90°-α.

Можно воспользоваться аналогичным тангенса — он выражается соотношением длины противолежащего искомому углу катета к длине катета прилежащего: tg(α)=A/B. Величину угла в градусах снова определяйте через обратную тригонометрическую функцию — : α=arctg(tg(α))=arctg(A/B). 2 – подкоренное выражение, обозначающее разность квадрата гипотенузы и катета.

3. Даны значения всех сторон треугольника

Для таких задач можно использовать формулу Герона:
S = (p-a)(p-b),
где p – полупериметр, который находится по следующему выражению: p = 0.5∙ (a+b+c)

4. Известен один катет и угол

Тут стоит обратиться к тригонометрическим функциям. Например, tg(1) = 1/сtg (1) = b/a. То есть, благодаря этому соотношению можно определить значение неизвестного катета. Далее задача сводится к первому пункту.

5. Известна гипотенуза и угол

В данном случае также используются тригонометрические функции синуса и косинуса: сos(2)=1/sin(2) = b/c. Затем решение задачи сводится ко второму пункту статьи.

Видео по теме

определение , схожее с первым. Прямоугольным называется треугольник, у которого две стороны перпендикулярны.

Гипотенуза и катеты

У остроугольного и тупоугольного треугольников отрезки, соединяющие вершины углов, называются просто сторонами. У стороны имеют и другие названия. Те, которые прилегают к прямому углу, называются катетами. Сторона, противолежащая прямому углу, называется гипотенузой. В переводе с греческого слово «гипотенуза» означает «натянутая», а «катет» — «перпендикуляр».

Соотношения между гипотенузой и катетами

Стороны прямоугольного треугольника связаны между собой определенными соотношениями, которые значительно облегчают вычисления. Например, зная размеры катетов, можно вычислить длину гипотенузы. Это соотношение по имени открывшего его получило название теоремы Пифагора и выглядит оно так:

c2=a2+b2, где с – гипотенуза, a и b – катеты. То есть, гипотенуза будет равна квадратному корню из суммы квадратов катетов. Чтобы найти любой из катетов, достаточно из квадрата гипотенузы вычесть квадрат другого катета и извлечь из полученной разности квадратный корень.

Прилежащий и противолежащий катет

Начертите прямоугольный треугольник АСВ. Буквой С принято обозначать вершину прямого угла, А и В – вершины острых углов. Стороны, противолежащие каждому углу, удобно назвать а, b и с, по названиям лежащих напротив них углов. Рассмотрите угол А. Катет а для него будет противолежащим, катет b – прилежащим. Отношение противолежащего катета к гипотенузе называется . Вычислить эту тригонометрическую функцию можно по формуле: sinA=a/c. Отношение прилежащего катета к гипотенузе называется косинусом. Вычисляется он по формуле: cosA=b/c.

Таким образом, зная угол и одну из сторон, можно по этим формулам вычислить другую сторону. Тригонометрическими соотношениями связаны и оба катета. Отношение противолежащего к прилежащему называется тангенсом, а прилежащего к противолежащему – котангенсом. Выразить эти соотношения можно формулами tgA=a/b или ctgA=b/a.

Как вы можете помнить из школьной программы по геометрии, треугольник – это фигура, образованная из трех отрезков, соединяющихся тремя точками, не лежащими на одной прямой. Треугольник образует три угла, отсюда и название фигуры. Определение может быть и иным. Треугольник можно так же назвать многоугольником с тремя углами, ответ будет так же верным. Треугольники делятся по числу равных сторон и по величине углов в фигурах. Так выделяют такие треугольники, как равнобедренный, равносторонний и разносторонний, а так же прямоугольный, остроугольный и тупоугольный, соответственно.

Формул вычисления площади треугольника очень много. Выбирать, как найти площадь треугольника, т.е. какой формулой воспользоваться, только вам. Но стоит отметить лишь некоторые обозначения, которые используются во многих формулах вычисления площади треугольника. Итак, запоминайте:

S – это площадь треугольника,

a, b, c – это стороны треугольника,

h – это высота треугольника,

R – это радиус описанной окружности,

p – это полупериметр.

Вот основные обозначения, которые могут вам пригодиться, если вы совершенно забыли курс геометрии. Ниже будут приведены наиболее понятные и не сложные варианты вычисления неизвестной и загадочной площади треугольника. Это не сложно и пригодится как вам в домашних нуждах, так и для помощи своим детям . Давайте вспомним, как вычислить площадь треугольника проще простого:

В нашем случае площадь треугольника равна: S = ½ * 2,2 см. * 2,5 см. = 2,75 кв.см. Помните, что площадь измеряется в квадратных сантиметрах (кв.см.).

Прямоугольный треугольник и его площадь.

Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к. сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.

1. Самый простой способ определения площади прямоугольного треугольника высчитывается по следующей формуле:

В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.

В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.

2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:

Мы решили воспользоваться первой формулой и с небольшими помарками (чертили в блокноте и использовали старую линейку и транспортир), но у нас вышел верный расчет:

S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.

Равнобедренный треугольник и его площадь.

Если перед вами стоит задача вычислить формулу равнобедренного треугольника, то проще всего воспользоваться главной и как считается классической формулой площади треугольника.

Но для начала, перед тем, как найти площадь равнобедренного треугольника, узнаем, что это за фигура такая. Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Эти две стороны называются боковыми, третья сторона называется основанием. Не путайте равнобедренный треугольник с равносторонним, т.е. правильным треугольником, у которого все три стороны равны. В таком треугольнике нет особых тенденций к углам, точнее к их величине. Однако углы у основания в равнобедренном треугольнике равны, но отличаются от угла между равными сторонами. Итак, первую и главную формулу вы уже знаете, осталось узнать, какие еще формулы определения площади равнобедренного треугольника известны:

Как найти площадь треугольника – все способы с формулами в одной статье

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Если известны длины трех сторон

Делайте так:

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА

Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети

ПОДПИСАТЬСЯ

Ваш браузер устарел рекомендуем обновить его до последней версии
или использовать другой более современный.

Как вычислить площадь треугольника по одной стороне

Обновлено 14 декабря 2020 г.

Автор Скотт Дэймон

Геометрия — это изучение форм и фигур, занимающих заданное пространство. Геометрические задачи пытаются определить размер и объем этих форм путем решения математических уравнений. Задачи геометрии имеют два типа информации: «данные» и «неизвестные». Данные представляют собой информацию в задаче, которая вам дана. Неизвестные — это части уравнения, которые вы должны решить. Можно найти площадь треугольника, зная длину только одной стороны. Однако для решения задачи вам также необходимо знать два внутренних угла.

TL;DR (слишком длинно, не читал)

Чтобы вычислить площадь треугольника по одной стороне и двум углам, найдите другую сторону по закону синусов, затем найдите площадь по формуле: площадь = 1/2 × b × c × sin(A).

Найти третий угол

Определить третий угол треугольника.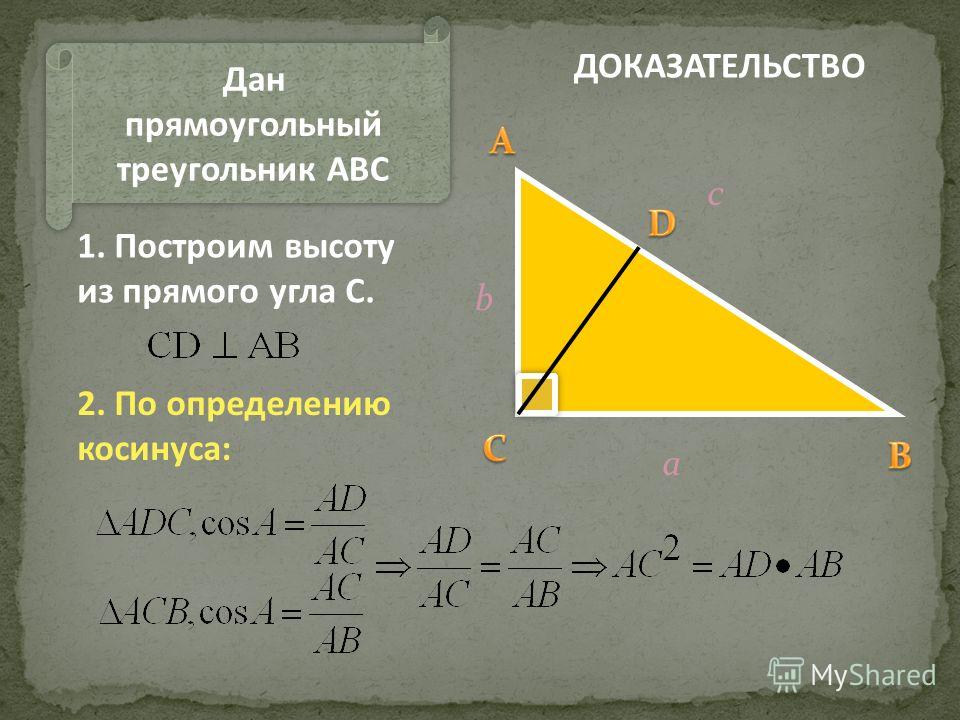 Например, в примере задачи есть треугольник, сторона которого B равна 10 единицам. Оба уголка A и уголок B ​ 50 градусов. Найдите угол C . Математический закон гласит, что сумма углов треугольника равна 180 градусам, поэтому

\text{Угол} A + \text{Угол} B + \text{Угол} C = 180.

Подставьте данные углы в уравнение .

50 + 50 + C = 180

Найдите ​ C ​, сложив первые два угла и вычтя из 180.

Настройка правила синусов

Воспользуйтесь правилом синусов, чтобы переписать уравнение. Правило синусов — это математическое правило, которое помогает найти неизвестные углы и длины. Он гласит:

\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}

В уравнении малое a ,​ b ​ и ​ c ​ представляют длины, а заглавные ​ A ​, ​ B ​ и ​ C ​ представляют собой внутренние углы треугольника. Поскольку все части уравнения равны друг другу, вы можете использовать любые две части. Используйте часть для той стороны, которую вам дали. В примере задачи это сторона B ​, 10 шт.

Следуя законам математики, перепишите уравнение следующим образом:

c = \frac{b \sin C}{\sin B}

Маленький ​ c ​ представляет сторону, которую вы решаете. Заглавная буква C перемещается в числитель на противоположной стороне уравнения, потому что по законам математики вы должны изолировать c , чтобы найти ее. При перемещении знаменателя он переходит в числитель, чтобы впоследствии его можно было умножить.

Решите правило синусов

Вставьте данные в ваше новое уравнение.

c = \frac{10 × \sin (100)}{\sin (50)}

Введите это в калькулятор геометрии, чтобы получить результат: Найдите площадь треугольника. Чтобы найти площадь треугольника, вам нужны две длины сторон, которые вы получили. Одно уравнение для площади треугольника:

\text{площадь} = \frac{1}{2} × b × c × \sin(A) 92 \end{aligned}

Формула нахождения площади прямоугольного треугольника через синус.

Площадь треугольника равна половине произведения его сторон на синус угла между ними.

Доказательство:

Рассмотрим произвольный треугольник ABC. Пусть в нем сторона ВС = а, сторона СА = b и S — площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .

Для начала введем прямоугольную систему координат и поместим начало координат в точку C. Поместим нашу систему координат так, чтобы точка B лежала на положительном направлении оси Cx, а точка A имела бы положительную ординату.

Если все сделано правильно, то должна получиться следующая цифра.

Площадь данного треугольника можно рассчитать по следующей формуле: S = (1/2)*a*h , где h — высота треугольника. В нашем случае высота треугольника h равна ординате точки А, то есть h = b * sin(C).

Учитывая полученные результаты, формулу площади треугольника можно переписать следующим образом: S = (1/2)*a*b*sin(C). КЭД

92. Найдите сторону АВ, если АС = 15 см, угол А = 30˚.

Пусть S — площадь треугольника ABC. По теореме площади треугольника имеем:

S = (1/2)*AB*AC*sin(A).

Подставляем в него значения, которые у нас есть:

60 = (1/2)*AB*15*sin30˚ = (1/2)*15*(1/2)*AB=(15/4) *АБ.

Отсюда выразим длину стороны AB: AB = (60*4)/15 = 16.

Если в задаче заданы длины двух сторон треугольника и угол между ними, то можно применить формула площади треугольника через синус.

Пример вычисления площади треугольника с помощью синуса. Даны стороны a = 3, b = 4 и угол γ = 30°. Синус угла 30° равен 0,5

Площадь треугольника будет 3 кв.см.

Могут быть и другие условия. Если дана длина одной стороны и углы, то сначала нужно вычислить недостающий угол. Поскольку сумма всех углов треугольника равна 180°, тогда:

Площадь будет равна половине квадрата стороны, умноженной на дробь.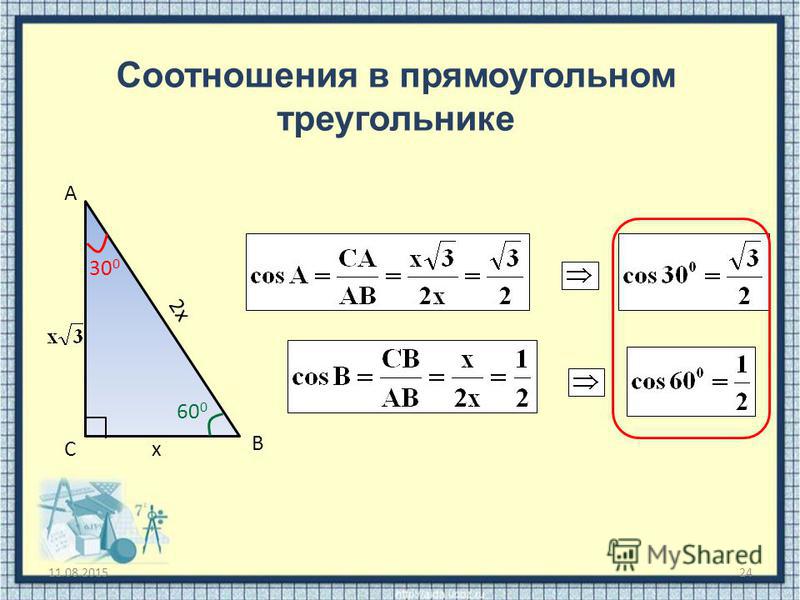 В его числителе произведение синусов смежных углов, а в знаменателе синус противоположного угла. Теперь посчитаем площадь по следующим формулам:

Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Подставляя данные в формулу
Получаем, что площадь треугольника 3,87 квадратных метра. см.

II. Площадь треугольника через косинус

Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти неизвестные стороны, и только потом использовать .
По закону косинусов квадрат неизвестной стороны треугольника равен сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Из теоремы выводим формулы для нахождения длины неизвестной стороны:

Зная, как найти недостающую сторону, имея две стороны и угол между ними, можно легко вычислить площадь. Формула площади треугольника через косинус помогает быстро и легко найти решение различных задач.

Пример вычисления формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4 и углом γ = 45°. Сначала найдем недостающую часть. с . По косинусу 45°=0,7. Для этого подставим данные в уравнение, полученное из теоремы косинусов.
Теперь по формуле находим

В жизни нам часто приходится сталкиваться с задачками по математике: в школе, в университете, а потом помогать ребенку с домашним заданием. Люди определенных профессий будут ежедневно сталкиваться с математикой. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем один из них: нахождение катета прямоугольного треугольника.

Что такое прямоугольный треугольник

Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, соединяющих точки, не лежащие на одной прямой, причем один из углов этой фигуры равен 90 градусов. Стороны, образующие прямой угол, называются катетами, а сторона, лежащая против прямого угла, называется гипотенузой.

Нахождение катета прямоугольного треугольника

Есть несколько способов узнать длину катета. Я хотел бы рассмотреть их более подробно.

Теорема Пифагора для нахождения катета прямоугольного треугольника

Если мы знаем гипотенузу и катет, то мы можем найти длину неизвестного катета, используя теорему Пифагора. Звучит это так: «Квадрат гипотенузы равен сумме квадратов катетов». Формула: c²=a²+b², где c — гипотенуза, a и b — катеты. Преобразуем формулу и получим: a²=c²-b².

Пример. Гипотенуза 5 см, катет 3 см. Преобразуем формулу: c²=a²+b² → a²=c²-b². Далее определяем: a²=5²-3²; а²=25-9; а²=16; а=√16; а=4 (см).

Тригонометрические соотношения для нахождения стороны прямоугольного треугольника

Также можно найти неизвестную сторону, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Существует четыре варианта нахождения катета с помощью тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет приведенная ниже таблица. Рассмотрим эти варианты.

Найдите катет прямоугольного треугольника с помощью синуса

Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin = a/c, где a – катет, противолежащий данному углу, а c – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.

Пример. Гипотенуза равна 10 см, а угол А равен 30 градусам. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠A*c; а=1/2*10; а=5 (см).

Найдите катет прямоугольного треугольника с помощью косинуса

Косинус угла (cos) представляет собой отношение прилежащего катета к гипотенузе. Формула: cos = b/c, где b – катет, примыкающий к данному углу, а c – гипотенуза. Преобразуем формулу и получим: b=cos*c.

Пример. Угол А равен 60 градусов, гипотенуза 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).

Найдите катет прямоугольного треугольника с помощью касательной

Тангенс угла (tg) представляет собой отношение противолежащего катета к прилежащему. Формула: tg = a/b, где а — катет, противоположный углу, а b — смежный. Преобразуем формулу и получим: a=tg*b.

Пример. Угол А равен 45 градусов, гипотенуза 10 см. По таблице вычисляем тангенс угла А, он равен Решите: a=tg∠A*b; а=1*10; а=10 (см).

Найдите катет прямоугольного треугольника с помощью котангенса

Котангенс угла (ctg) представляет собой отношение прилежащего катета к противолежащему. Формула: ctg = b/a, где b – катет, примыкающий к углу, а противоположный. Другими словами, котангенс — это «перевернутый тангенс». Получаем: b=ctg*a.

Пример. Угол А равен 30 градусов, длина противолежащего катета 5 см. Согласно таблице тангенс угла А равен √3. Вычислить: b=ctg∠A*a; б=√3*5; b=5√3 (см).

Итак, теперь вы знаете, как найти катет прямоугольного треугольника.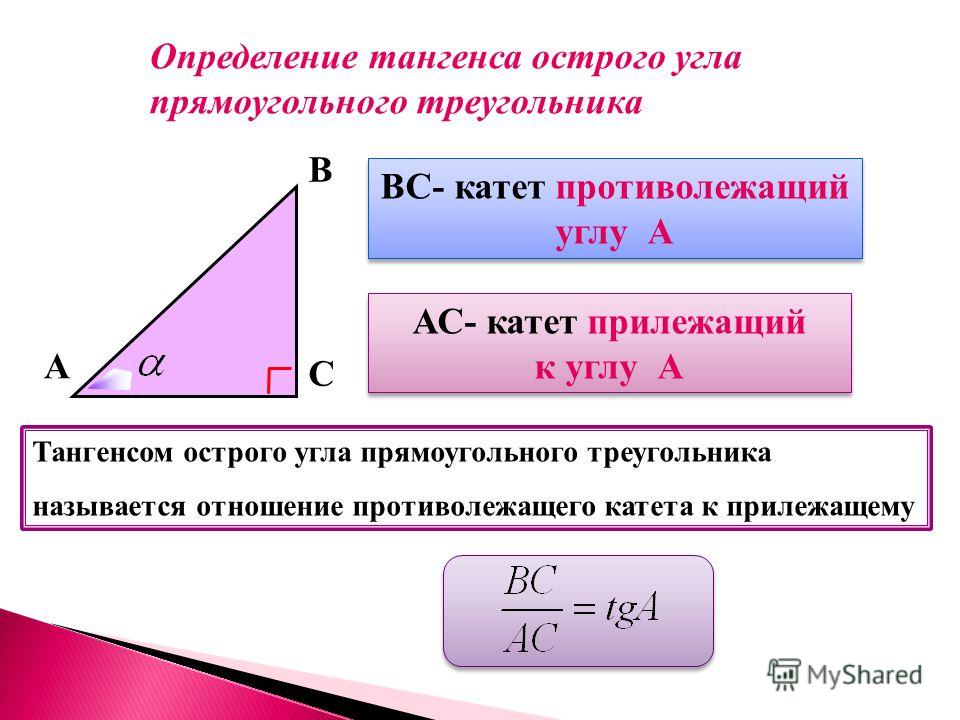 Как видите, это не так уж и сложно, главное запомнить формулы.

Синус — одна из основных тригонометрических функций, применение которой не ограничивается только геометрией. Таблицы для вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда есть под рукой, а вычисление синуса иногда необходимо для решения различных задач. В целом вычисление синуса поможет закрепить навыки рисования и знания тригонометрических тождеств.

Игры с линейкой и карандашом

Простая задача: как найти синус угла, начерченного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейший способ вычисления синуса угла — деление дальнего катета треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно достроить острый угол до фигуры прямоугольного треугольника, проведя линию, перпендикулярную одному из лучей на произвольном расстоянии от вершины угла. Нужно будет соблюсти угол ровно 90°, для чего нам нужен канцелярский треугольник.

С помощью компаса немного точнее, но это займет больше времени. На одном из лучей нужно отметить 2 точки на определенном расстоянии, задать на компасе радиус, примерно равный расстоянию между точками, и провести полуокружности с центрами в этих точках до пересечения этих линий. Соединив точки пересечения наших окружностей друг с другом, мы получим строгий перпендикуляр к лучу нашего угла, осталось только продолжить линию до пересечения с другим лучом.

В получившемся треугольнике нужно измерить линейкой сторону, противоположную углу, и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомым значением синуса острого угла.

Найдите синус угла больше 90°

Для тупого угла задача ненамного сложнее. Необходимо провести из вершины луч в обратном направлении с помощью линейки, чтобы образовать прямую линию с одним из лучей интересующего нас угла. С получившимся острым углом следует действовать, как описано выше, синусы смежных углов, образующих вместе развернутый угол 180°, равны.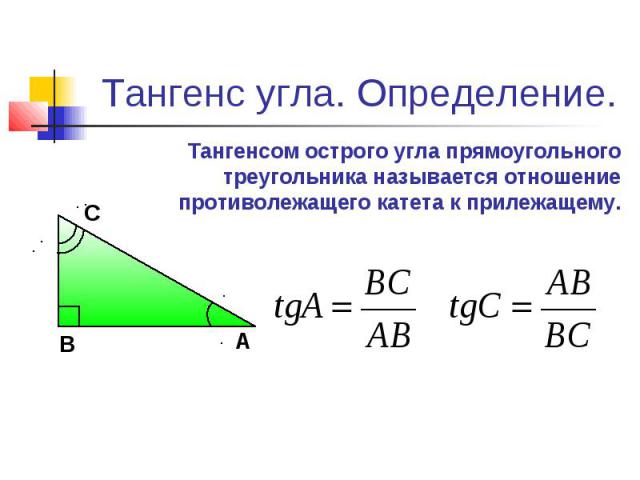

Вычисление синуса из других тригонометрических функций

Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Давайте рассмотрим распространенные примеры.

Как найти синус по известному косинусу угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.

Как найти синус по известному тангенсу угла? Тангенс получается делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синус будет произведением косинуса и тангенса, а квадрат синуса будет квадратом этого произведения. Заменяем квадрат косинуса на разность между единицей и квадратом синуса по первому тригонометрическому тождеству и путем нехитрых манипуляций приводим уравнение для вычисления квадратного синуса через тангенс, соответственно для вычисления синуса придется извлечь корень из полученного результата.

Как найти синус по известному котангенсу угла? Значение котангенса можно вычислить путем деления длины ближнего катета от угла катета на длину дальнего, а также делением косинуса на синус, то есть котангенс есть обратная функция тангенса по отношению к числу 1. Для вычисления синуса можно вычислить тангенс по формуле tg α = 1/ctg α и использовать формулу во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть так.

Как найти синус трех сторон треугольника

Существует формула для нахождения длины неизвестной стороны любого треугольника, а не только прямоугольного, по двум известным сторонам с помощью тригонометрической функции косинус противоположного угла. Она выглядит так.

Ну а синус можно еще вычислить из косинуса по формулам выше.

сторона треугольники могут быть обнаружены не только по периметру и площади, но и по заданной стороне и углам. Для этого используются тригонометрические функции — синус и ко синус . Задачи с их применением встречаются в школьном курсе геометрии, а также в университетском курсе аналитической геометрии и линейной алгебры.

Инструкция

1. Если одна из сторон треугольника и угол между ней и другой его стороной известны, используйте тригонометрические функции — синус ом и со синус ом. Представьте себе прямоугольный треугольник HBC, у которого есть угол? равен 60 градусам. На рисунке изображен треугольник HBC. Из-за синус , как известно, является отношением противолежащего катета к гипотенузе, а к синус — отношением прилежащего катета к гипотенузе, для решения задачи используйте дальнейшее соотношение между этими параметрами: sin? =HB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу следующим образом:

2. Если, наоборот, в условии задачи задан катет треугольника, найти его гипотенузу, руководствуясь дальнейшим соотношением между данными величинами: ВС = НВ / sin? По аналогии найдите стороны треугольника и с помощью sinus a, изменив предыдущее выражение следующим образом: cos ?=HC/BC

3.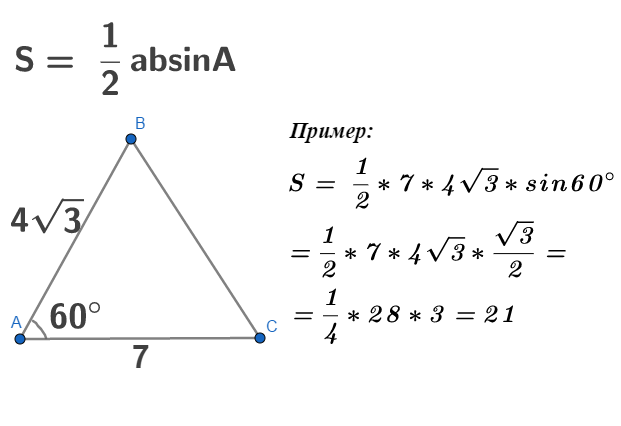 В элементарной математике есть представление теоремы синус ов. Руководствуясь фактами, которые описывает эта теорема, также можно найти стороны треугольника. Кроме того, он позволяет найти стороны треугольника, вписанного в окружность, если известен радиус последней. Для этого используйте следующее соотношение: a/sin ?=b/sin b=c/sin y=2R . 92-2ab*cos ?

Геометрическая фигура, состоящая из трех точек, не принадлежащих одной прямой, называемых вершинами, и трех попарно соединяющих их отрезков, называемых сторонами, называется треугольником. Существует множество задач на нахождение сторон и углов треугольника по ограниченному количеству исходных данных, одна из таких задач — нахождение стороны треугольника по одной из его сторон и двум углам .

Инструкция

1. Построить треугольник? АВС и знаменитые — стороны ВС и углы?? и ??. Известно, что сумма углов любого треугольника равна 180? будут равны? = 180? – (?? + ??). Можно найти стороны AC и AB, применяя теорему синусов, которая читается как AB/sin?? = БК/грех?? = AC/грех?? = 2*R, где R — радиус окружности, описанной около треугольника? ABC, то получаем R=BC/sin??, AB=2*R*sin??, AC=2*R*sin??. Теорему синусов можно использовать для любых заданных двух углов и стороны.

2. Стороны данного треугольника можно найти, вычислив его площадь по формуле S = 2 * R? *грех?? *грех?? * sin??, где R вычисляется по формуле R = BC/sin??, R — радиус описанного треугольника? АВС отсюда Тогда сторона АВ можно найти, вычислив опущенную на нее высоту h = ВС * sin??, из формулы S = 1/2 * h * АВ имеем АВ = 2 * S/h сторона АС .

3. Если внешние углы треугольника даны как углы? а??, тогда можно обнаружить внутренние углы при поддержке соответствующих соотношений? = 180? — ???, ?? = 180? — ???, ?? = 180? – (?? + ??). Дальше действуем как первые два пункта.

Постижением треугольников занимаются математики уже несколько тысячелетий. Наука о треугольниках — тригонометрия — использует специальные величины: синус и косинус.

Прямоугольный треугольник

Изначально синус и косинус появились из-за необходимости вычисления величин в прямоугольных треугольниках.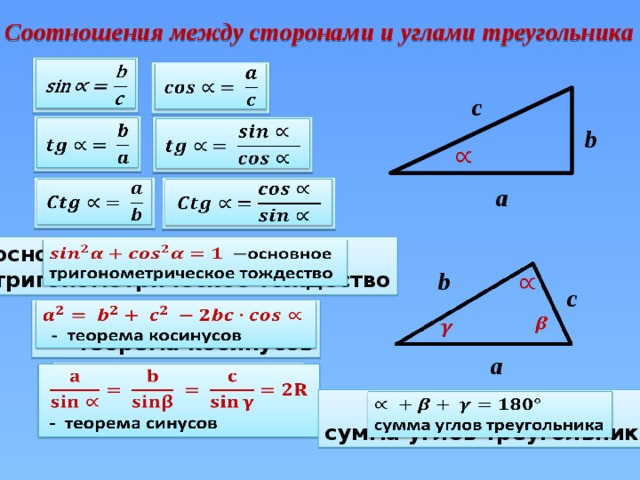 Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не меняется, то соотношение сторон, как бы ни изменялись длины этих сторон, остается неизменно одинаковым. Так были введены представления синуса и косинуса. Синус острого угла прямоугольного треугольника — это отношение противолежащего катета к гипотенузе, а косинус — отношение прилежащего катета к гипотенузе.

Теоремы косинусов и синусов

Но косинусы и синусы можно использовать не только в прямоугольных треугольниках. Для того, чтобы узнать значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов. Теорема косинусов довольно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом двойного произведения этих сторон на косинус угла между ними». Есть две интерпретации теоремы синусов: малая и расширенная. По малому: «В треугольнике углы пропорциональны противолежащим сторонам». Эту теорему часто расширяют за счет свойства окружности, описанной около треугольника: «В треугольнике углы пропорциональны противоположным сторонам, а их отношение равно диаметру описанной окружности».

Производные

Производная — это математический инструмент, который показывает, насколько быстро функция изменяется в зависимости от метаморфозы ее аргумента. Производные используются в алгебре, геометрии, экономике и физике, а также в ряде технических дисциплин. При решении задач необходимо знать табличные значения производных тригонометрических функций: синуса и косинуса. Производная синуса — это косинус, а производная косинуса — это синус, но со знаком минус.

Применение в математике

Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и связанных с ними задач. Удобство синусов и косинусов нашло свое отражение в технике. Было примитивно оценивать углы и стороны по теоремам косинусов и синусов, разбивая сложные фигуры и объекты на «примитивные» треугольники. Инженеры и архитекторы, которые часто имеют дело с соотношениями сторон и градусами, потратили много времени и усилий на вычисление косинусов и синусов нетабличных углов.