Формули для обчислення площі круга та кругового сектора
Нагадаємо, що кругом називається частина площини, обмежена колом. Тобто круг радіуса з центром містить точку і всі точки площини, що знаходяться від даної точки на відстані, що не більша за .
Виведемо формулу, яка дозволить знайти площу круга радіус якого дорівнює . Для цього розглянемо правильний -кутник , вписаний в коло, що обмежує круг. Очевидно, площа даного кола більша площі багатокутника , так як він цілком міститься в даному колі. З іншого боку, площа кола, вписаного в багатокутник, менша , так як це коло цілком міститься в даному багатокутнику. Отже:
Будемо тепер необмежено збільшувати число сторін -кутника. Зазначимо, що в такому випадку збільшуватиметься і радіус вписаного в багатокутник кола і при , величина буде як завгодно мало відрізнятися від , а отже, наближатиметься до одиниці, тому . Іншими словами, при необмеженому збільшенні числа сторін багатокутника, вписане в нього коло збігатиметься до описаного кола, тому при .
Звідси і з нерівності (1) випливає, що при .
Далі, скориставшись формулою обчислення площі правильного -кутника, а саме (де – його периметр і – радіус вписаного кола) і врахувавши, що при , будемо мати: . Отже, для обчислення площі круга радіус якого дорівнює , отримаємо наступну формулу:
Зауваження: оскільки радіус тісно пов’язаний з діаметром і довжиною кола, то шляхом нехитрих замін можна також обчислити площу круга через діаметр або довжину кола. Діаметр – це подвоєний радіус, отже, підставляючи його в формулу замість останнього, потрібно розділити його на два. Так як в формулі (2) радіус зводиться до другого степеня, отримана половина діаметра також повинна бути в квадраті. Таким чином, формула площу круга через його діаметр буде виглядати наступним чином:
Довжина кола являє собою подвоєний добуток радіуса і числа : . Зворотним методом отримуємо, що радіус дорівнює довжині кола, розділеної на його множник: .
Підставляючи це в формулу (2) (не забуваємо звести вираз в другу степінь), отримаємо формулу обчислення площі круга через довжину кола:
Сектором круга або просто сектором називається частина круга, обмежена дугою і двома радіусами, що з’єднують кінці дуги з центром кола. Дуга, яка обмежує сектор, називається дугою сектора. На малюнку що міститься нижче, зображено два сектора з дугами і . Перший з цих секторів зафарбований.
Сектор круга з градусною мірою α
Виведемо формулу для обчислення площі сектора круга радіуса , обмеженого дугою з градусною мірою . Отже, виходячи з того, що площа всього круга дорівнює , то площа кругового сектора, обмеженого дугою в , дорівнює . Тому площа виражається формулою:
Площа круга – приклад:
Довжина кола дорівнює . Знайти площу круга, обмеженого цим колом.
Оскільки довжина кола визначається формулою , то за умовою .
Звідси — радіус заданого кола. Далі, прийнявши в якості наближеного значення число та скориставшись формулою (2), отримаємо шукану площу круга: .
Площа сектора круга – приклад:
Сторона квадрата, зображеного на малюнку, що міститься нижче, дорівнює . Обчислити площу зафарбованої фігури .
Фігура
EFGHЯк відомо, площа квадрата дорівнює квадрату його сторони, значить . В квадраті виділено чотири кругових сектори. Радіус кожного з цих секторів дорівнює половині сторони квадрата, тобто . Так як нам дано квадрат, то градусна міра кожного з розглядуваних секторів дорівнює . Отже, згідно з сказаним вище приходимо до висновку, що площа кожного з секторів дорівнює:
Далі, віднявши від площі квадрата площі кругових секторів, визначимо площу зафарбованої фігури : .
Блок-схема алгоритму знаходження площі круга через радіус
Блок-схема алгоритму знаходження площі сектора круга з градусною мірою
Ми в соціальних мережах
2.
Вывести формулу площади круга, кругового сектора и сегмента.Билет № 1.
1. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная.
1. Если два катета одного треугольника соответственно равны двум катетам другого треугольника, то такие прямоугольные треугольники равны (частный случай первого признака равенства треугольников).
2 . Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны
3.
Если гипотенуза и острый угол одного
треугольника соответственно равны
гипотенузе и острому углу другого
треугольника, то такие прямоугольные
треугольники равны.
─ следствие из 2 признака равенства треугольников.
4. Если катет и противолежащий острый угол одного треугольника соответственно равны катету и противолежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).
Доказывается аналогично предыдущей теореме ─ следствие из II признака равенства треугольников.
5. Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.
Доказательство:
1.
Т. к. С
= С1,
то АВС
можно наложить на А1В1С1 так, что вершина С совместится с
вершиной С1,
а стороны СА и СВ наложатся
соответственно на лучи СА1 и СВ1.
2. Т. к. СА = С1А1, то вершина А совместится с вершиной А1. Остается доказать, что совместятся точки В и В1.
3. Предположим, что точки В и В1 не совместятся. Рассмотрим Δ А1В1В2 – равнобедренный, так как АВ = A1B1 А1В2 = A1B1. Тогда A1B1В2 = A1В2B1. Заметим, что A1B1
С1 — острый угол прямоугольного треугольника А1В1С1, а A1B1В2, смежный с ним, — тупой.
Поскольку в
треугольнике не может быть двух тупых
углов, то это невозможно. Значит,
точки В и В1 совместятся. Пусть р – любая прямая и точка А не лежит на ней. Из точки А опустим перпендикуляр АС на прямую р.
О пределение 1. Точка С называется проекцией точки А на прямую р. Если точка А лежит на прямой, то ее проекцией на эту прямую является сама точка А. Точка С также называется основанием перпендикуляра АС.
Возьмем на прямой р точку В, отличную от точки С, и соединим точки А и В отрезком.
Определение 2. Отрезок АВ называется наклонной, проведенной из точки А на прямую р, а отрезок СВ называется проекцией наклонной АВ на прямую р.
Наклонная,
проекция наклонной и перпендикуляр
являются гипотенузой и катетами
прямоугольного треугольника АВС.
По
т-ме Пифагора Поэтому Аналогично
С войство наклонной. Если из одной и той же точки проведены к некоторой прямой перпендикуляр и наклонная, то перпендикуляр и проекция наклонной всегда короче наклонной.
Теорема 1 (прямая). Если из одной точки проведены две наклонные к прямой, то большая наклонная имеет большую проекцию, меньшая наклонная – меньшую проекцию, равные наклонные имеют равные проекции.
Доказательство:
1) Рассмотрим АВТ и АСТ. АТВ = АТС = 90°; АТ – общая; AB > AC. Тогда по теореме Пифагора
2)
Рассмотрим АВТ
и АЕТ. АТВ
= АТЕ
= 90°; АТ – общая; AB = AЕ.
Тогда по теореме Пифагора
Теорема 2 (обратная). Если из одной точки проведены две наклонные к прямой, то больше та наклонная, проекция которой больше.
Доказательство:
Тогда по теореме Пифагора
Определение 3. Расстоянием от точки А до фигуры F называется кратчайший отрезок, соединяющий любую граничную точку фигуры F с точкой А. Расстояние от точки А до фигуры F обозначается
Кратчайшим расстоянием от точки А до прямой р является перпендикуляр АС, опущенный из точки А на прямую р.
Определение
4.
Расстоянием от точки до прямой
называется перпендикуляр, опущенный
из точки на данную прямую.
Теорема 1 (о площади круга). Площадь S круга радиусом R выражается формулой S = R2.
Пусть F – круг радиуса R, а Q – описанный около него правильный n-угольник. Тогда
Если число сторон многоугольника неограниченно возрастает, то его периметр сколь угодно мало отличается от длины окружности C = 2R
Следствие 1. Площади кругов относятся как квадраты радиусов или диаметров.
Пусть S1 и S2 – площади кругов радиуса R1 и R2 соответственно. Тогда
Примечание 1. Квадратурой круга названа задача о построении циркулем и линейкой квадрата, равновеликого данному кругу, т. е. имеющего ту же площадь. Невозможность ее решения была доказана в конце XIX
века.Определение 2. Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Теорема
2 (о площади сектор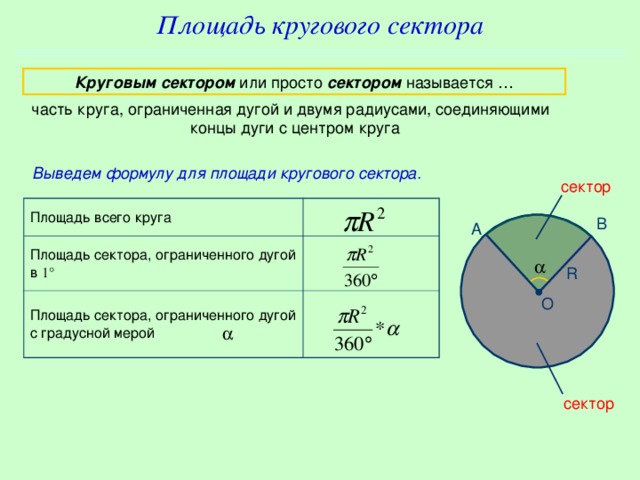а).
Площадь сектора равна произведению
длины его дуги на половину радиуса:
Из чертежа очевидно, что площадь сектора зависит от градусной меры центрального угла, образованного радиусами, ограничивающими данный сектор. Она может быть определена как соответствующая часть площади руга.
Площадь сектора с центральным углом в 1° составляет часть площади круга, а площадь сектора с центральным углом в ° составляет часть площади круга и определяется по формуле: Преобразуем полученную формулу:
С ледует заметить, что площадь вектора однозначно определяется величиной центрального угла. Чем больше центральный угол сектора, тем больше длина дуги и, соответственно, площадь сектора.
О
пределение
3. Сегментом называется часть круга,
ограниченная дугой и хордой, соединяющими
концы этой дуги.
Вывод формулы площади сегмента.
Из чертежа очевидно, что площадь сегмента может быть определена:
а) как разность площадей сектора 1 и треугольника AOB, если АОВ < 180°;
б) как сумма площадей сектора 2 и треугольника AOB, если АОВ > 180°.
Если
градусная мера дуги АВ (соответствующего
ей центрального угла) невелика, то
площадь сегмента может быть определена
по приближенной формуле: где b – есть основание сегмента или длина
хорды АВ, а h – высота сегмента (стрелка сегмента).
Стрелкой сегмента называется часть
диаметра круга, перпендикулярного
его хорде, лежащая в сегменте. h = CD.
Если градусная мера дуги не превышает
50°, то погрешность в вычислении
площади не превышает 1 %.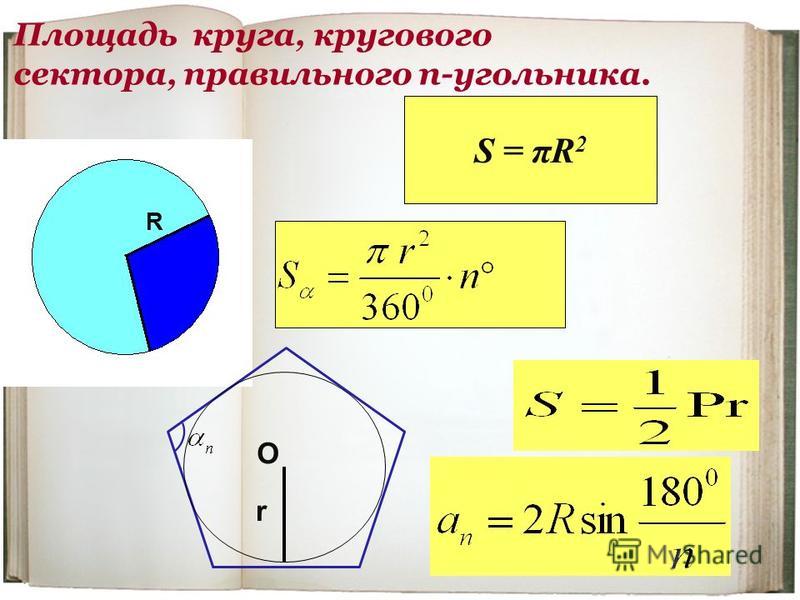
Билет № 2.
Площадь круга | Формула радиуса, диаметра и окружности
Автор:
Malcolm McKinsey