Как найти площадь поверхности прямоугольного параллелепипеда: формула
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение площади прямоугольного параллелепипеда: формула и пример
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)
Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a
- четыре боковые грани: со стороной a/b и высотой c.

- два основания: со сторонами a
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Площадь прямоугольного треугольника – как найти по формуле
Площадь прямоугольного треугольника – это далеко не самая сложная тема по математике, но все же она нередко вызывает вопросы у школьников. В этой статье мы расскажем об основных способах нахождения этой величины и подберем формулы, подходящие для решения заданий из школьной программы.
В этой статье мы расскажем об основных способах нахождения этой величины и подберем формулы, подходящие для решения заданий из школьной программы.
Математические определения
Прямоугольный треугольник – это тот, один из углов которого является прямым, то есть равен 90 градусам. Чтобы научиться находить площадь этой фигуры, сначала нужно запомнить следующие определения:
- гипотенуза – это сторона, которая противоположна прямому углу.
- катеты – это две стороны, которые прилегают к прямому углу.
- высота – это линия, которая проведена от угла к противоположной ему стороне под прямым углом. В прямоугольном треугольнике две высоты совпадают с его катетами.
Формулы определения площади прямоугольного треугольника
Для нахождения площади этого треугольника можно использовать разные формулы в зависимости от того, какие данные даются в задаче.
Если известны:
- оба катета, то следует найти их произведение и разделить на два (рис.
 1): S= (a*b)/2. Прямоугольный треугольник — это половина прямоугольника. А площадь прямоугольника как раз и находится произведением S= (a*b)
1): S= (a*b)/2. Прямоугольный треугольник — это половина прямоугольника. А площадь прямоугольника как раз и находится произведением S= (a*b) - гипотенуза и проведенная к ней из прямого угла высота, то найти площадь можно, умножив их друг на друга и разделив на два (рис. 2): S= (c*h)/2.
Задачи для тренировки
Теперь нужно закрепить знания и научиться находить площадь прямоугольного треугольника по формулам, которые мы рассмотрели ранее. Для этого рассмотрим две типовые задачи:
Задача №1 (рисунок 1). Известно, что у треугольника ABC c ∠ABC = 90° сторона AB = 3 см, а BC = 6 см. Нужно найти площадь этой фигуры.
Нам нужно воспользоваться первой из ранее рассмотренных формул и найти половину от произведения катетов: (3*6)/2 = 9 см².
Задача №2 (рисунок 2). Из прямого угла в треугольнике BCD проведена высота BO = 4 дм, а сторона BD = 8 дм. Чему будет равна S?
В этом случае воспользуемся второй по счету формулой, и с ее помощью найдем половину от произведения гипотенузы и высоты: (4*8)/2 = 16 дм².
Курсы по математике
Тема, рассмотренная в данной статье, является лишь одной из многих, которые детям предстоит освоить. Математика включает в себя широкий комплекс знаний, и чтобы хорошо знать этот предмет, школьникам нужно не только последовательно проходить материал, но и дополнительно развивать свои математические способности.
Помочь справиться с этой задачей может курс по математике для учеников 1-4 классов Амаматика от академии развития интеллекта AMAkids. На занятиях ребята не только расширят свои математические знания, но и познакомятся со смежными областями математики. Благодаря использованию развивающих игр и различных интерактивных материалов дети с интересом будут развивать свои способности – логику, мышление, креативность.
Запишитесь на курс Амаматика и начните развивать навыки ребенка уже сейчас!
Что такое Формула площади прямоугольника? Определение, примеры, факты
Площадь прямоугольника Формула
Прямоугольник — это двумерная фигура/многоугольник с четырьмя сторонами, четырьмя вершинами и четырьмя прямыми углами. Две противоположные стороны прямоугольника равны и параллельны друг другу. Какова площадь прямоугольника? Это пространство, охватываемое фигурой, или пространство внутри периметра прямоугольника. Альтернативно, пространство внутри периметра прямоугольника является площадью прямоугольника.
Две противоположные стороны прямоугольника равны и параллельны друг другу. Какова площадь прямоугольника? Это пространство, охватываемое фигурой, или пространство внутри периметра прямоугольника. Альтернативно, пространство внутри периметра прямоугольника является площадью прямоугольника.
В геометрии понятие площади в двумерной или трехмерной фигуре помогает нам найти объем занимаемого ими пространства. Например, для заданного прямоугольника количество цвета, необходимое для заполнения прямоугольника, можно найти, определив его площадь.
Некоторыми примерами прямоугольных фигур являются сельскохозяйственные поля, парки, плитка, предметы повседневной жизни, такие как кастрюли, стакан, стол, поднос и т. д.
В следующем разделе обсуждаются методы, позволяющие понять, почему площадь прямоугольника является произведением двух его сторон, а также единицы измерения.
Родственные игры
Как вычислить площадь прямоугольника?
Чтобы получить площадь прямоугольника, мы используем единичные квадраты. Как найти площадь прямоугольника, используя единичные квадраты?
Как найти площадь прямоугольника, используя единичные квадраты?
Мы можем найти площадь любой двумерной фигуры, разделив ее на более мелкие квадраты. Поскольку каждый единичный квадрат занимает одну квадратную единицу пространства, общее количество единичных квадратов в фигуре дает его площадь. Площадь фигуры измеряется в квадратных единицах. Итак, единицей площади прямоугольника являются «квадратные единицы». Давайте разберемся, как найти площадь прямоугольника, используя единичные квадраты.
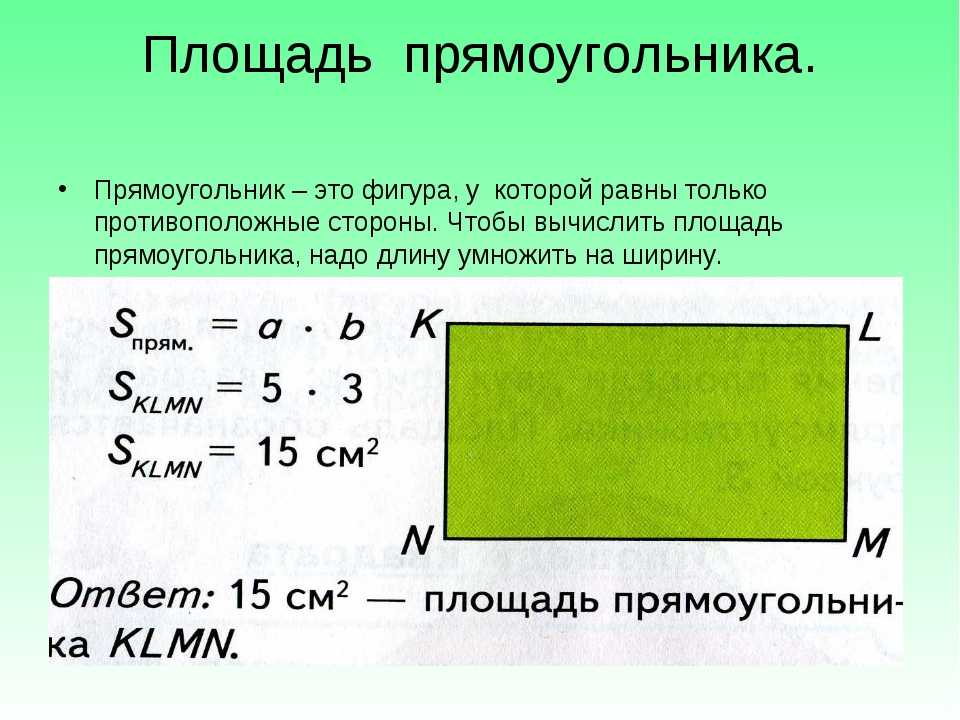
Пример 1: Разделите прямоугольник ABCD на единичные квадраты, как показано на рисунке. Площадь прямоугольника ABCD равна количеству содержащихся в нем единичных квадратов.
Таким образом, общая площадь прямоугольника ABCD равна 48 кв. дюймам.
Кроме того, используя этот подход, мы находим, что площадь прямоугольника всегда равна произведению двух его сторон. Здесь длина АВ равна 8 дюймам, а длина ВС — 6 дюймам. Площадь ABCD равна произведению 6 и 8, что равно 48.
Пример 2: Рассмотрим прямоугольник длиной 6 дюймов и шириной 3 дюйма. Он может быть заполнен 3 строками и 6 столбцами единичных квадратов.
Каждый из этих квадратов имеет площадь 1 квадратный дюйм, а в прямоугольнике 18 таких квадратов. Значит, площадь прямоугольника 18 квадратных дюймов.
Единицей площади прямоугольника является «квадратные единицы» (квадратные дюймы, квадратные футы и т. д.), поскольку длины перемножаются вместе, то же самое происходит и с единицами измерения.
Связанные рабочие листы
Формула для нахождения площади прямоугольника
Площадь прямоугольника $= \text{length} \text{(l)} \times \text{width} \text{(w)}$
Для пример , если длина прямоугольника 35 м, а ширина 25 м, то площадь равна 35 $ \ умножить на 25 = 875 $ квадратных метров.
В качестве альтернативы, формула для вычисления площади прямоугольника получается путем деления фигуры на два прямоугольных треугольника одинакового размера. Например, в данном прямоугольнике ABCD проведена диагональ из вершины A в C.
Например, в данном прямоугольнике ABCD проведена диагональ из вершины A в C.
Диагональ AC делит прямоугольник на два равных прямоугольных треугольника.
Таким образом, площадь ABCD будет:
$⇒ \text{Площадь} (▭\text{ABCD}) = \text{Площадь} (\Delta \text{ABC}) + \text{Площадь} ( \Delta \text{ADC})$
$⇒ \text{Площадь} (▭\text{ABCD}) = 2 \times \text{Площадь} (\Delta \text{ABC})$
Здесь, Площадь $(\Delta \text{ABC}) = \frac{1}{2} \times \text{основание} \times \text{высота}$
$⇒ \text{Площадь} (▭\text{ABCD} ) = 2 \times (\frac{1}{2} \times \text{b} \times \text{h})$
$⇒ \text{Площадь} (▭\text{ABCD}) = \text{b} \times \text{h}$
Приложения
Ранние записи вавилонской культуры означают использование геометрических фигур с длинами , углы и площади для строительства и астрономии. Знание основных форм резки камня, таких как треугольники, квадраты и прямоугольники, а также принципов, касающихся площади и периметра, помогло египтянам строить гигантские сооружения, такие как пирамиды. В современной математике эти понятия используются при составлении карт, топографической съемке, моделировании объектов и т. д.
В современной математике эти понятия используются при составлении карт, топографической съемке, моделировании объектов и т. д.
Интересные факты
1. Обе диагонали прямоугольника имеют одинаковую длину.
2. Окружность может содержать прямоугольник, все вершины которого касаются окружности; он называется циклическим прямоугольником.
3. Квадрат – это особый тип прямоугольника, длина и ширина которого одинаковы. Следовательно, площадь квадрата получается путем умножения длины каждой стороны на себя.
Решенные примеры
1. Вычислите площадь прямоугольника шириной 5 см и длиной 20 см. 92$
Длина окна $= \text{l} = 25$ футов
Площадь $= \text{l} \times \text{w}$
$100 = 25 \times \text{w}$
Таким образом, ширина окна $= \frac{100}{25} = 4$ футов
4. Прямоугольная комната имеет длину 12 футов и ширину 14 футов. Сколько ковра требуется, чтобы покрыть всю комнату?
Площадь ковра равна площади комнаты.
Площадь комнаты можно найти, умножив ее длину на ширину.
Площадь ковра $= \text{длина} \times \text{ширина}$
Площадь ковра $= 12 \times 14 = 168$ квадратных футов.
Следовательно, чтобы покрыть комнату, требуется 168 квадратных футов ковра.
Практические задачи
1
Длина прямоугольника на 2 см больше его ширины. Какова длина прямоугольника, если его ширина 5 см?
15 кв. см
63 кв. см
12 кв. см
35 кв. см
Правильный ответ: 63 кв. см
Площадь прямоугольника $= \text{длина} \times \text{ширина}$.
Ширина $= 5$ см
Длина $= 5 + 2 = 7$ см.
Площадь $= 7 х 5 = 35$ кв.см
2
Длина прямоугольника вдвое больше его ширины. Чему равна площадь прямоугольника, если ширина прямоугольника равна 4 единицам?
8 квадратных единиц
16 квадратных единиц
24 квадратных единицы
32 квадратных единицы
Правильный ответ: 32 квадратных единицы
Длина $= 2 \times \text{width} = 2 \times 4 \text{units } = 8 \text{единиц}$.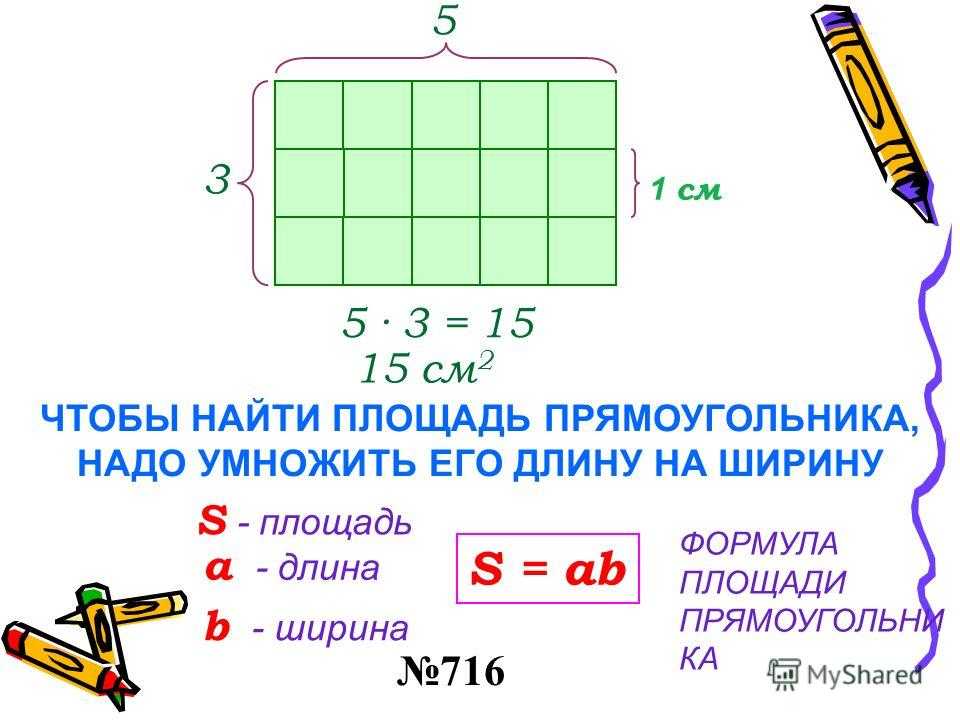
Площадь прямоугольника $= \text{длина} \times \text{ширина}$,
$= 8 \text{единиц} \times 4 \text{единиц}$
$= 24$ квадратных единиц.
3
Площадь прямоугольника 24 квадратных единицы. Чему равна длина прямоугольника, если ширина прямоугольника равна 4 единицам?
6 единиц
8 единиц
20 единиц
28 единиц
Правильный ответ: 6 единиц
Площадь прямоугольника $= \text{length} \times \text{width}$.
24 доллара = \text{длина} \times 4$
Итак, длина $= 6$ единиц.
4
Какова площадь прямоугольника длиной 8 футов и шириной 5 футов?
13 кв.см
26 кв.см
40 кв.см
80 кв.см
Правильный ответ: 40 кв.см
Площадь прямоугольника $= \text{length} \times \text{width} = 8 \text{футы} \times 5 \text{футы} = 40$ квадратных футов.
5
Стена длиной и шириной 10 м и 30 м соответственно должна быть покрыта мраморными блоками.
 Размер блоков $2 \text{m} \times 1 \text{m}$. Найдите общее количество блоков, необходимых для полного покрытия стены. 92$
Размер блоков $2 \text{m} \times 1 \text{m}$. Найдите общее количество блоков, необходимых для полного покрытия стены. 92$$\$360$
$\$300$
$\$350$
$\$400$
Правильный ответ: $\$360$
Стоимость покраски стены $=$ Стоимость окраски $\ times$ Площадь стены = $\$1,2 \times (15 \times 20) =$ $\$360$
7
Найдите площадь прямоугольного листа, длина которого 20 см, а ширина 4 см.
85 кв. см
80 кв. см
90 кв. см
95 кв. см
Правильный ответ: 80 кв. см 92$
Часто задаваемые вопросы
По какой формуле найти площадь прямоугольника?
Площадь прямоугольника $=$ Длина $\times$ Ширина
Если длину прямоугольника удвоить, как изменится его площадь?
Если длину прямоугольника удвоить, то его площадь также удвоится.
Как найти недостающую длину прямоугольника, если известны его ширина и площадь?
Недостающую длину можно найти, разделив площадь на ширину прямоугольника. Длина прямоугольника $= \frac{Area}{Width}$
Длина прямоугольника $= \frac{Area}{Width}$
В каких единицах измеряется площадь прямоугольника?
Единицей площади прямоугольника являются квадратные единицы. Например, если длина и ширина прямоугольника равны 2 см и 5 см соответственно, то его площадь равна 10 кв. см.
По какой формуле вычисляется площадь квадрата?
Квадрат — это особый тип прямоугольника, длина и ширина которого одинаковы. Следовательно, площадь квадрата получается путем умножения длины каждой стороны на себя.
Площадь квадрата $= \text{сторона} \times \text{сторона}$.
Площадь прямоугольника — формула
Площадь прямоугольника — это область, занимаемая границами прямоугольника. Другими словами, количество поверхности, заключенной в прямоугольник, называется площадью прямоугольника. Это можно рассчитать, используя формулу площади прямоугольника и используя различные методы в зависимости от заданных размеров. На этом уроке мы научимся находить площадь прямоугольника.
| 1. | Что такое площадь прямоугольника? |
| 2. | Формула площади прямоугольника |
| 3. | Как найти площадь прямоугольника? |
| 4. | Площадь прямоугольника по диагонали |
| 5. | Часто задаваемые вопросы о площади прямоугольника |
Что такое площадь прямоугольника?
Площадь прямоугольника — это количество единичных квадратов, которые могут поместиться в прямоугольник. Площадь определяется как количество пространства, занимаемого плоской поверхностью определенной формы. Площадь любой формы — это количество единичных квадратов, которые могут в нее поместиться, и она измеряется с точки зрения «количества» квадратных единиц (квадратных сантиметров, квадратных дюймов, квадратных футов и т. д.). Некоторыми примерами прямоугольных форм являются плоские поверхности мониторов ноутбуков, школьных досок, холста для рисования и т.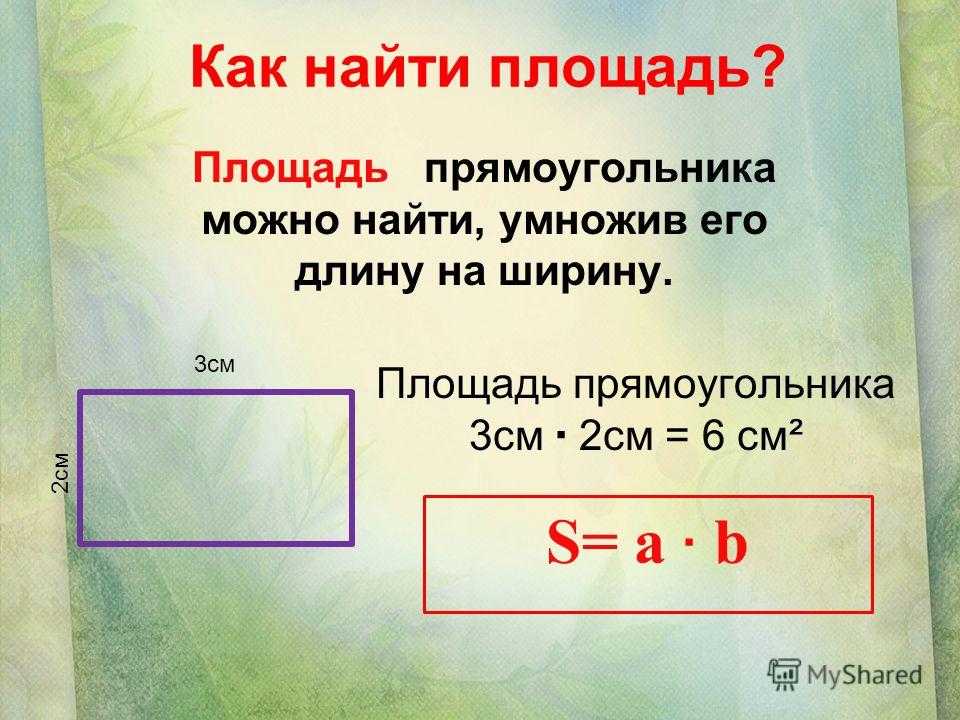
Площадь прямоугольника Определение
Область, занимаемая прямоугольником внутри его границ, определяется как площадь прямоугольника.
Формула площади прямоугольника
Формула площади прямоугольника используется для нахождения площади, занимаемой прямоугольником внутри его границы. Площадь прямоугольника получается путем умножения его длины на ширину (ширину). Таким образом, формула площади прямоугольника, длина и ширина которого равны «l» и «w» соответственно, выражается следующим образом. Площадь прямоугольника = l × w. Другими словами,
Как найти площадь прямоугольника?
Площадь прямоугольника равна произведению его длины на ширину (ширину). Площадь прямоугольника можно рассчитать, используя следующие шаги:
- Шаг 1: Обратите внимание на размеры длины и ширины (ширины) по заданным данным.

- Шаг 2: Найдите произведение значений длины и ширины.
- Шаг 3: Дайте ответ в квадратных единицах.
Давайте рассмотрим пример, чтобы понять вычисление площади прямоугольника.
Пример: Найдите площадь прямоугольника, длина которого 15 единиц, а ширина 4 единицы.
Решение:
Дано, длина = 15 единиц, а ширина = 4 единицы.Формула для нахождения площади прямоугольника: A = l × w. Подставьте 15 вместо «l» и 4 вместо «w» в этой формуле. Следовательно, площадь прямоугольника = 15 × 4 = 60
Следовательно, площадь прямоугольника = 60 квадратных единиц.
Единица площади прямоугольника
единица площади прямоугольника выражается в квадратных единицах. Мы знаем, что длина всегда измеряется и выражается в таких единицах, как сантиметры, дюймы и т. д. Теперь давайте разберемся, почему площадь прямоугольника выражается в квадратных единицах, используя следующий пример.
Пример: Длина прямоугольника 4 дюйма, а ширина 3 дюйма. Обратите внимание на рисунок, приведенный ниже, на котором мы можем разделить фигуру на 12 маленьких квадратов, каждый из которых является квадратом, то есть по 1 дюйму с каждой стороны, то есть по 1 квадратному дюйму. Поскольку в этом прямоугольнике может поместиться 12 квадратов одинакового размера, они также показывают пространство, занимаемое всем прямоугольником. Итак, прямоугольник со сторонами 4 дюйма и 3 дюйма имеет площадь 12 квадратных дюймов или 12 дюймов 9.0412 2
В этом случае, поскольку длина и ширина этого прямоугольника даны в дюймах, площадь измеряется и записывается в квадратных дюймах (в 2 ). Точно так же, если длина и ширина любого прямоугольника даны в см, то площадь будет выражена в квадратных сантиметрах (см 2 ).
Площадь прямоугольника по диагонали
Площадь прямоугольника можно вычислить, если известны диагональ и одна сторона. Диагональ прямоугольника — это прямая линия внутри прямоугольника, соединяющая его противоположные вершины. В прямоугольнике две диагонали и обе имеют одинаковую длину. Есть два способа, которыми мы можем найти площадь прямоугольника, используя диагональ.
Метод 1:
Мы можем найти значение недостающей стороны, используя теорему Пифагора, а затем найти площадь. Давайте разберемся в этом на примере.
Пример: Найдите площадь прямоугольника, длина которого 4 см, а диагональ 5 см.
Решение:
Ширина прямоугольника отсутствует, и ее можно рассчитать по теореме Пифагора, поскольку диагонали прямоугольника образуют 2 прямоугольных треугольника.
В этом случае ширину можно рассчитать по формуле ширина = ⎷[(Диагональ) 2 — (длина) 2 ]
После подстановки данных значений получаем, ширина = ⎷[(Диагональ ) 2 — (длина) 2 ]
ширина = ⎷[(5) 2 — (4) 2 ]
ширина = ⎷(25 — 16)
ширина = ⎷(25 — 16) 39005
ширина = ⎷9
Теперь мы знаем, что длина = 4 см, ширина = 3 см.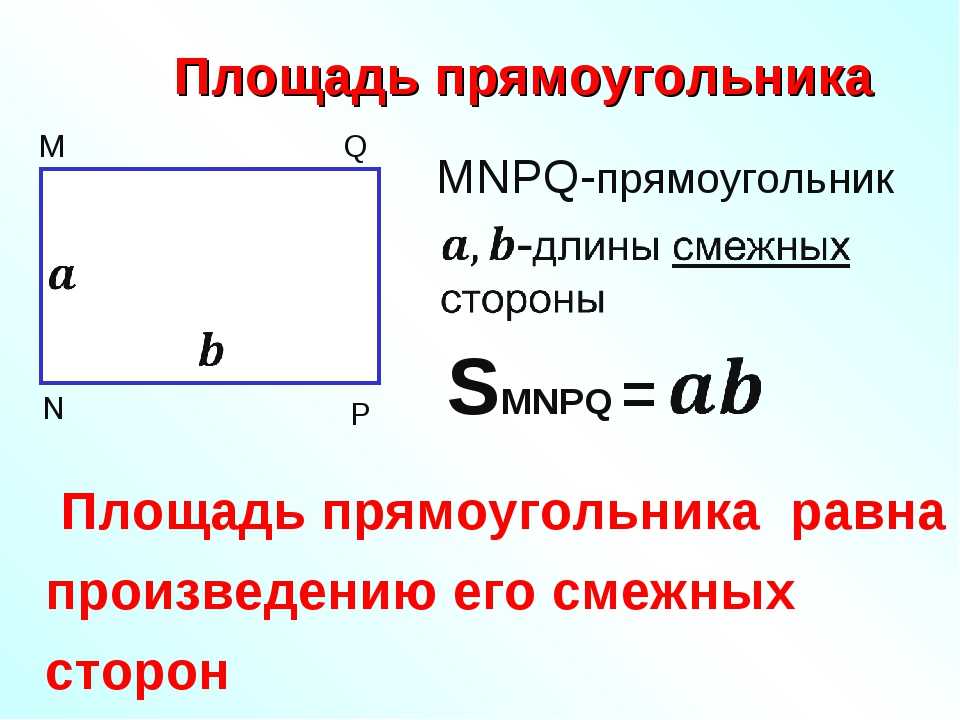 Итак, площадь прямоугольника = l × w. В этом случае
Итак, площадь прямоугольника = l × w. В этом случае
A = l × w
Площадь = 4 × 3 = 12 см 2
Метод 2:
Этот метод также использует ту же логику, но мы используем прямую формулу для нахождения площади прямоугольника.
- Например, если длина прямоугольника отсутствует, а нам известны диагональ и ширина, то мы можем выразить длину через ширину и диагональ и затем использовать это в формуле площади прямоугольника .
- Мы знаем, что (Диагональ) 2 = (Длина) 2 + (Ширина) 2 . Таким образом, это также можно записать как (Длина) 2 = (Диагональ) 2 — (Ширина) 2 . Кроме того, это можно выразить как Длина = ⎷[(Диагональ) 2 — (Ширина) 2 ]. Здесь длина выражается через диагональ и ширину. Эту формулу можно использовать вместо длины.
- Мы знаем, что формула для вычисления площади прямоугольника: Площадь прямоугольника = Длина × Ширина.
 Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина
Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина - Итак, площадь прямоугольника = ширина ⎷[(диагональ) 2 — (ширина) 2 ]
- Мы можем использовать ту же формулу, если мы знаем длину и если ширина отсутствует.
Давайте рассмотрим это на примере.
Пример: Найдите площадь прямоугольника, у которого ширина 6 единиц, а диагональ 10 единиц.
Решение: Нам известны диагональ и ширина прямоугольника. Итак, применим прямую формулу Площадь прямоугольника = Ширина ⎷[(Диагональ) 2 — (Ширина) 2 ]
После подстановки значений диагонали = 10 единиц и ширины = 6 единиц, мы получаем Площадь прямоугольника = Ширина ⎷ [(Диагональ) 2 — (Ширина) 2 ]
Площадь = 6 ⎷[(10) 2 — (6) 2 ]
Площадь = 6 ⎷(100 — 36)
Площадь = 6 ×
прямоугольника = 48 квадратных единицПлощадь прямоугольника с использованием периметра
Площадь прямоугольника можно вычислить, если известны периметр и одна из его сторон. С помощью периметра мы можем найти неизвестную сторону, а затем вычислить площадь по той же формуле: площадь прямоугольника = длина × ширина. Давайте разберемся в этом с помощью примера.
С помощью периметра мы можем найти неизвестную сторону, а затем вычислить площадь по той же формуле: площадь прямоугольника = длина × ширина. Давайте разберемся в этом с помощью примера.
Пример: Найдите площадь прямоугольника, если периметр равен 24 единицам, а длина 7 единицам.
Решение: Периметр прямоугольника = 24 единицы, длина = 7 единиц. Мы можем найти ширину, используя формулу:
Периметр прямоугольника = 2 (l + w)
24 = 2 (7 + w)
12 = 7 + w
w = 5 единиц
Теперь, когда мы знаем ширина = 5 единиц и длина = 7 единиц, мы можем найти площадь.
Площадь прямоугольника = l × w
Площадь = 7 × 5 = 35 квадратных единиц
Вывод формулы площади прямоугольника
Формула обратной стороны прямоугольника может быть получена с использованием следующего объяснения. Прямоугольник ABCD имеет диагональ. Мы видим, что диагональ AC делит прямоугольник ABCD на два равных треугольника.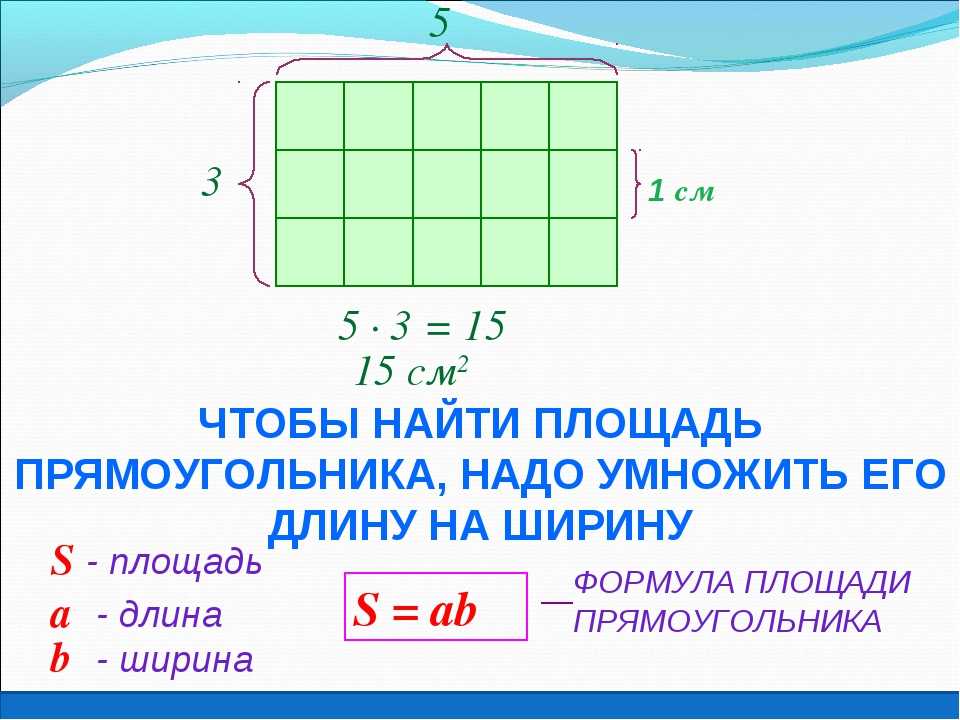 Площадь прямоугольника равна сумме площадей этих двух треугольников.
Площадь прямоугольника равна сумме площадей этих двух треугольников.
Площадь прямоугольника ABCD = площадь треугольника ABC + площадь треугольника ADC
Поскольку оба треугольника (ABC и ADC) равны, мы можем выразить это следующим образом.
Площадь прямоугольника ABCD = 2 × площадь треугольника ABC
Площадь прямоугольника ABCD = 2 × (1/2 × основание × высота)
Площадь прямоугольника ABCD = 2 × 1/2 × AB × BC
Площадь прямоугольника ABCD = AB × BC
Следовательно, площадь прямоугольника = длина × ширина
Cuemath — одна из ведущих в мире платформ для обучения математике, которая предлагает онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Пример 1: Длина и ширина прямоугольной фермы равны 80 ярдам и 60 ярдам. Найдите площадь фермы. Решение: Длина фермы l = 80 ярдов и ширина фермы w = 60 ярдов Мы знаем, что формула площади прямоугольника равна Площадь прямоугольника = длина × ширина Итак, площадь фермы равна: A = l × w = 80 × 60 = 4800 квадратных метров Следовательно, площадь фермы составляет 4800 квадратных метров. Пример 2: Найдите площадь прямоугольника, длина и ширина которого равны 25 см и 16 см соответственно. Solution Длина прямоугольника = 25 см Ширина (ширина) прямоугольника = 16 см Площадь прямоугольника = l × w Площадь прямоугольника = 25 × 16 Площадь прямоугольника = 400 см 2 Пример 3: Найдите площадь прямоугольника, длина которого = 4,5 см, а ширина = 2 см. Решение Длина прямоугольника = 4,5 см Ширина (ширина) прямоугольника = 2 см Площадь прямоугольника = 4,5 × 2 Площадь прямоугольника = 9 см 05 2 перейти к слайдуперейти к слайдуперейти к слайду У вас есть вопросы по основным математическим понятиям? Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Закажите бесплатный пробный урок перейти к слайдуперейти к слайду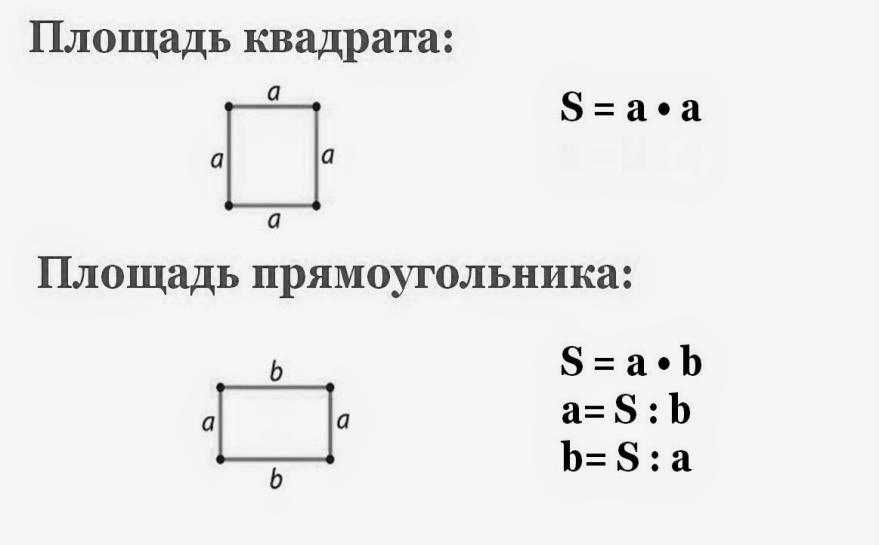 Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении. Площадь прямоугольника Примеры
Практические вопросы по площади прямоугольника
Часто задаваемые вопросы о площади прямоугольника
Какова площадь прямоугольника в геометрии?
Площадь прямоугольника — это пространство, занимаемое внутри прямоугольника. Он рассчитывается путем нахождения произведения длины и ширины (ширины) прямоугольника и выражается в квадратных единицах.
Что такое периметр и площадь прямоугольника?
Периметр прямоугольника равен сумме его четырех сторон. Он рассчитывается по формуле Периметр прямоугольника = 2 (длина + ширина). Площадь прямоугольника — это область, охватываемая его границами, и ее можно рассчитать по формуле площадь прямоугольника = длина × ширина.
Какая формула площади прямоугольника?
Формула площади прямоугольника представляет собой произведение его длины на ширину (ширину). Это выражается как Площадь прямоугольника = длина × ширина
Какова единица площади прямоугольника?
Площадь прямоугольника выражается в квадратных единицах. Например, если размеры прямоугольника даны в дюймах, то площадь выражается в квадратных дюймах (в 2 ). Точно так же, если размеры даны в см, то площадь выражается в квадратных см (см 2 ). Например, если длина прямоугольника 4 см, а ширина 3 см, то его площадь = 4 × 3 = 12 см 2
Как найти площадь прямоугольника по диагонали?
Площадь прямоугольника можно вычислить, если известны диагональ и одна из его сторон. Мы можем найти значение недостающей стороны, используя теорему Пифагора, а затем найти площадь. Например, давайте найдем площадь прямоугольника, диагональ которого равна 10 единицам, а длина — 8 единицам, используя следующие шаги.
Мы можем найти значение недостающей стороны, используя теорему Пифагора, а затем найти площадь. Например, давайте найдем площадь прямоугольника, диагональ которого равна 10 единицам, а длина — 8 единицам, используя следующие шаги.
- Шаг 1: В этом случае мы можем найти ширину по формуле Ширина = ⎷[(Диагональ) 2 — (Длина) 2 ]
- Шаг 2: После подстановки заданных значений получаем ширину = ⎷[(10) 2 — (8) 2 ] = ⎷36 = 6 единиц
- Шаг 3: Теперь мы знаем, что длина = 8 единиц, ширина = 6 см. Итак, площадь прямоугольника = l × w. В этом случае Площадь = 8 × 6 = 48 единиц 2
Что такое прямоугольник?
Прямоугольник – это замкнутая двумерная фигура с четырьмя сторонами, где противоположные стороны равны и параллельны друг другу. У прямоугольника все углы равны 90°.
Как найти площадь прямоугольника с дробями?
Площадь прямоугольника с дробями можно вычислить так же, как и с другими целыми числами. Нам просто нужно упростить дроби, используя их правила упрощения. Если у нас есть правильные дроби, мы можем просто использовать формулу площади прямоугольника и умножить длину и ширину. Однако, если у нас есть размеры, данные в смешанных дробях, нам нужно преобразовать их в неправильные дроби, а затем упростить, используя та же формула. Например, давайте найдем площадь прямоугольника, в котором длина задана как \(2\dfrac{1}{3}\) единиц, а ширина задана как \(1\dfrac{1}{3}\) единиц, теперь мы преобразуем смешанные дроби в неправильные дроби, и мы получим длину как 7/3, а ширину как 4/3. Теперь мы можем найти площадь, Площадь прямоугольника = 7/3 × 4/3 = 28/9= \(3\dfrac{1}{9}\) квадратных единиц.
Нам просто нужно упростить дроби, используя их правила упрощения. Если у нас есть правильные дроби, мы можем просто использовать формулу площади прямоугольника и умножить длину и ширину. Однако, если у нас есть размеры, данные в смешанных дробях, нам нужно преобразовать их в неправильные дроби, а затем упростить, используя та же формула. Например, давайте найдем площадь прямоугольника, в котором длина задана как \(2\dfrac{1}{3}\) единиц, а ширина задана как \(1\dfrac{1}{3}\) единиц, теперь мы преобразуем смешанные дроби в неправильные дроби, и мы получим длину как 7/3, а ширину как 4/3. Теперь мы можем найти площадь, Площадь прямоугольника = 7/3 × 4/3 = 28/9= \(3\dfrac{1}{9}\) квадратных единиц.
Как найти площадь прямоугольника, зная периметр?
Площадь прямоугольника можно вычислить, если известны периметр и одна из его сторон. С помощью периметра мы можем найти недостающую сторону, а затем вычислить площадь прямоугольника по той же формуле: площадь прямоугольника = длина × ширина.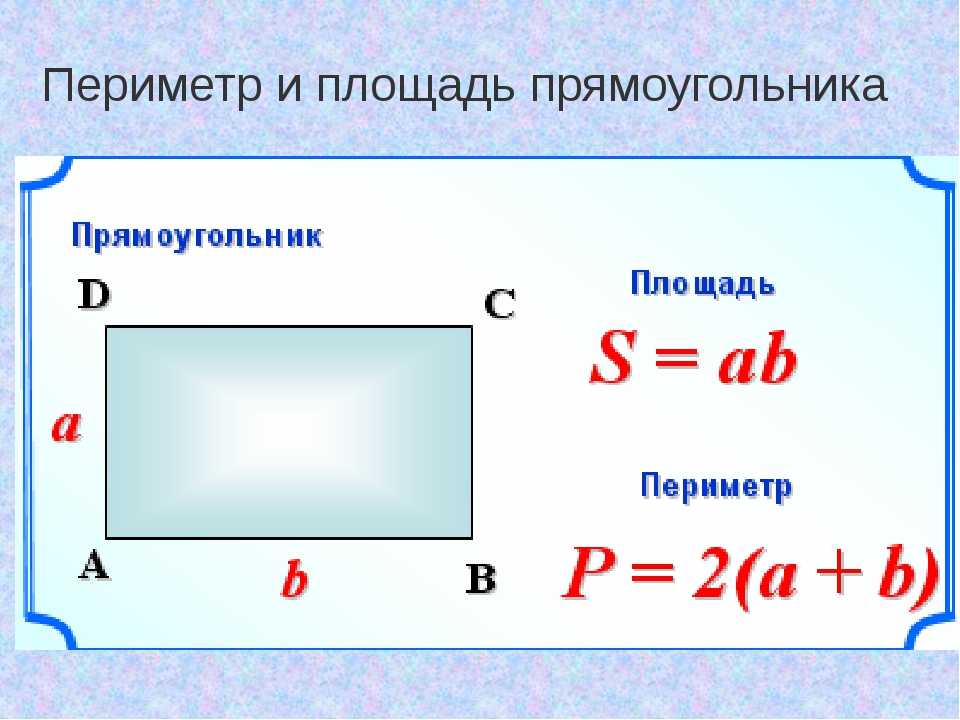


 1): S= (a*b)/2. Прямоугольный треугольник — это половина прямоугольника. А площадь прямоугольника как раз и находится произведением S= (a*b)
1): S= (a*b)/2. Прямоугольный треугольник — это половина прямоугольника. А площадь прямоугольника как раз и находится произведением S= (a*b)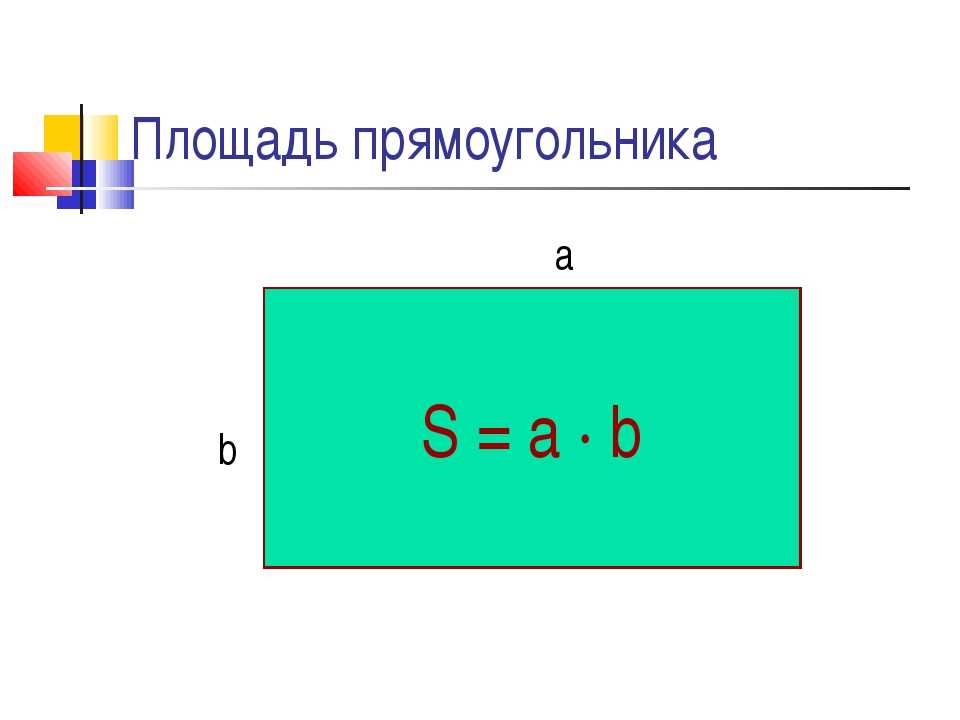
 Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина
Теперь, если мы заменим приведенную выше формулу длины формулой площади прямоугольника, то формула площади прямоугольника может быть выражена следующим образом: Площадь прямоугольника = ⎷[(Диагональ) 2 — (Ширина) 2 ] × Ширина