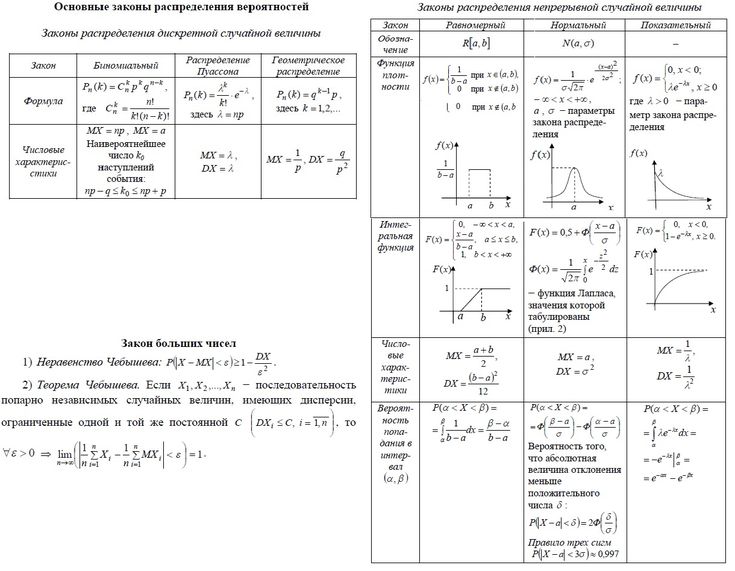
Теория вероятностей
Теория вероятностей
ОглавлениеГлава 1. ВведениеПРЕДИСЛОВИЕ 1.  Теория вероятностей: 1.2. Краткие исторические сведения Глава 2. Основные понятия теории вероятностей 2.1. Событие. Вероятность события 2.2. Непосредственный подсчет вероятностей 2.3. Частота, или статистическая вероятность, события 2.4. Случайная величина 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности Глава 3. Основные теоремы теории вероятностей 3.1. Назначение основных теорем. Сумма и произведение событий 3.2. Теорема сложения вероятностей 3.3. Теорема умножения вероятностей 3.4. Формула полной вероятности 3.5. Теорема гипотез (формула Бейеса) Глава 4. Повторение опытов 4.1. Частная теорема о повторении опытов 4.2. Общая теорема о повторении опытов Глава 5. Случайные величины и их законы распределения 5.1. Ряд распределения. Многоугольник распределения 5.2. Функция распределения 5.3. Вероятность попадания случайной величины на заданный участок 5.  4. Плотность распределения5.5. Числовые характеристики случайных величин. Их роль и назначение 5.6. Характеристики положения (математическое ожидание, мода, медиана) 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение 5.8. Закон равномерной плотности 5.9. Закон Пуассона Глава 6. Нормальный закон распределения 6.1. Нормальный закон распределения и его параметры 6.2. Моменты нормального распределения 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения 6.4. Вероятное (срединное) отклонение Глава 7. Определение законов распределения случайных величин на основе опытных данных 7.1. Основные задачи математической статистики 7.2. Простая статистическая совокупность. Статистическая функция распределения 7.3. Статистический ряд. Гистограмма 7.5. Выравнивание статистических рядов 7.6. Критерии согласия Глава 8.  Системы случайных величин8.1. Понятие о системе случайных величин 8.2. Функция распределения системы двух случайных величин 8.3. Плотность распределения системы двух случайных величин 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения 8.5 Зависимые и независимые случайные величины 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции 8.7. Система произвольного числа случайных величин 8.8. Числовые характеристики системы нескольких случайных величин Глава 9. Нормальный закон распределении дли системы случайных величин 9.1. Нормальный закон на плоскости 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания 9.4. Вероятность попадания в эллипс рассеивания 9.5. Вероятность попадания в область произвольной формы 9.6. Нормальный закон в пространстве трех измерений.  Общая запись нормального закона для системы произвольного числа случайных величинГлава 10. Числовые характеристики функций случайных величин 10.1. Математическое ожидание функции. Дисперсия функции 10.2. Теоремы о числовых характеристиках 10.3. Применения теорем о числовых характеристиках Глава 11. Линеаризация функций 11.1. Метод линеаризации функций случайных аргументов 11.2. Линеаризация функции одного случайного аргумента 11.3. Линеаризация функции нескольких случайных аргументов 11.4. Уточнение результатов, полученных методом линеаризации 12.1. Закон распределения монотонной функции одного случайного аргумента 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону 12.3. Закон распределения немонотонной функции одного случайного аргумента 12.4. Закон распределения функции двух случайных величин 12.5. Закон распределения суммы двух случайных величин.  Композиция законов распределения12.6. Композиция нормальных законов 12.7. Линейные функции от нормально распределенных аргументов 12.8. Композиция нормальных законов на плоскости Глава 13. Предельные теоремы теории вероятностей 13.1. Закон больших чисел и центральная предельная теорема 13.2. Неравенство Чебышева 13.3. Закон больших чисел (теорема Чебышева) 13.4. Обобщенная теорема Чебышева. Теорема Маркова 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона 13.6. Массовые случайные явления и центральная предельная теорема 13.7. Характеристические функции 13.8. Центральная предельная теорема для одинаково распределенных слагаемых 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении Глава 14. Обработка опытов 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения 14.2. Оценки для математического ожидания и дисперсии 14.  3. Доверительный интервал. Доверительная вероятность14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону 14.5. Оценка вероятности по частоте 14.6. Оценки для числовых характеристик системы случайных величин 14.7. Обработка стрельб 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов 15.1. Понятие о случайной функции 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции 15.3. Характеристики случайных функций 15.4. Определение характеристик случайной функции из опыта 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций 15.6. Линейные и нелинейные операторы. Оператор динамической системы 15.7. Линейные преобразования случайных функций 15.7.1. Интеграл от случайной функции 15.  7.2. Производная от случайной функции15.8. Сложение случайных функций 15.9. Комплексные случайные функции Глава 16. Канонические разложения случайных функций 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций 16.2. Каноническое разложение случайной функции 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями Глава 17. Стационарные случайные функции 17.1. Понятие о стационарном случайном процессе 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции 17.4. Спектральное разложение случайной функции в комплексной форме 17.5. Преобразование стационарной случайной функции стационарной линейной системой 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем 17. 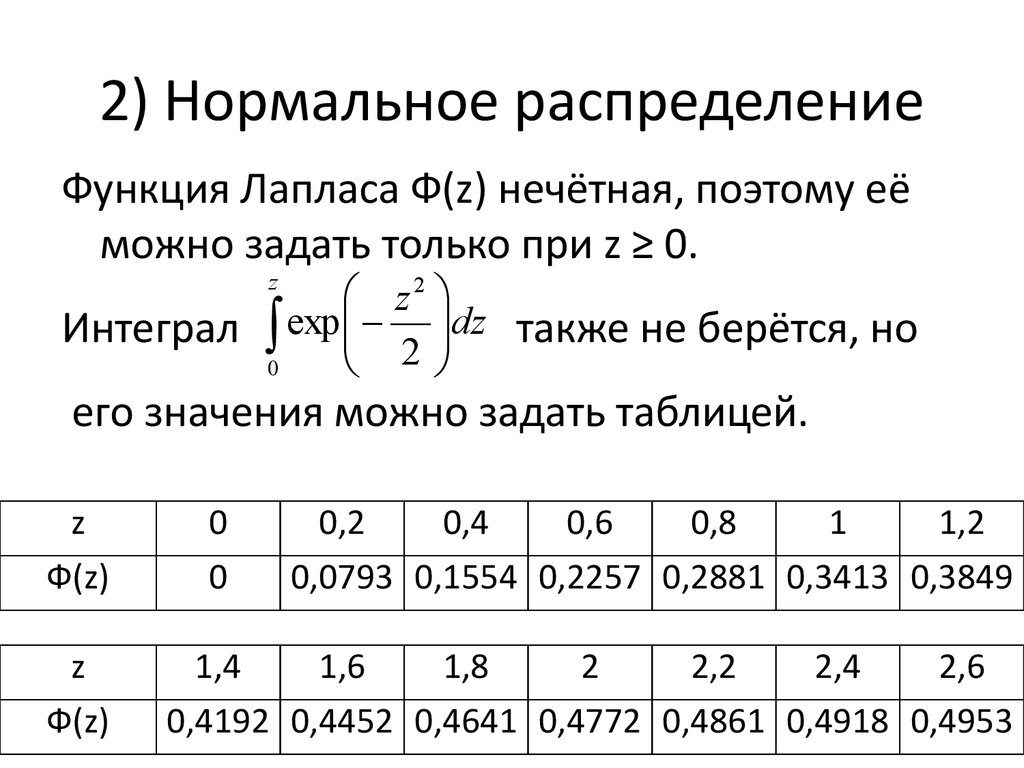 7. Эргодическое свойство стационарных случайных функцийГлава 18. Основные понятия теории информации 18.1. Предмет и задачи теории информации 18.2. Энтропия как мера степени неопределенности состояния физической системы 18.3. Энтропия сложной системы. Теорема сложения энтропий 18.4. Условная энтропия. Объединение зависимых систем 18.5. Энтропия и информация 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии 18.7. Энтропия и информация для систем с непрерывным множеством состояний 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно 18.9. Передача информации с искажениями. Пропускная способность канала с помехами Глава 19. Элементы теории массового обслуживания 19.1. Предмет теории массового обслуживания 19.2. Случайный процесс со счетным множеством состояний 19.  3. Поток событий. Простейший поток и его свойства19.4 Нестационарный пуассоновский поток 19.5. Поток с ограниченным последействием (поток Пальма) 19.6. Время обслуживания 19.7. Марковский случайный процесс 19.8. Система массового обслуживания с отказами. Уравнения Эрланга 19.9. Установившийся режим обслуживания. Формулы Эрланга 19.10. Система массового обслуживания с ожиданием 19.11. Система смешанного типа с ограничением по длине очереди Приложения Таблица 1 Значения нормальной функции распределения Таблица 2. Значения экспоненциальной функции Таблица 3. Значения нормальной функции Таблица 4. Значения “хи-квадрат” в зависимости от r и p Таблица 5. Значения удовлетворяющие равенству Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100 Таблица 7. Таблица значений функции Таблица 8. Значения распределение Пуассона |
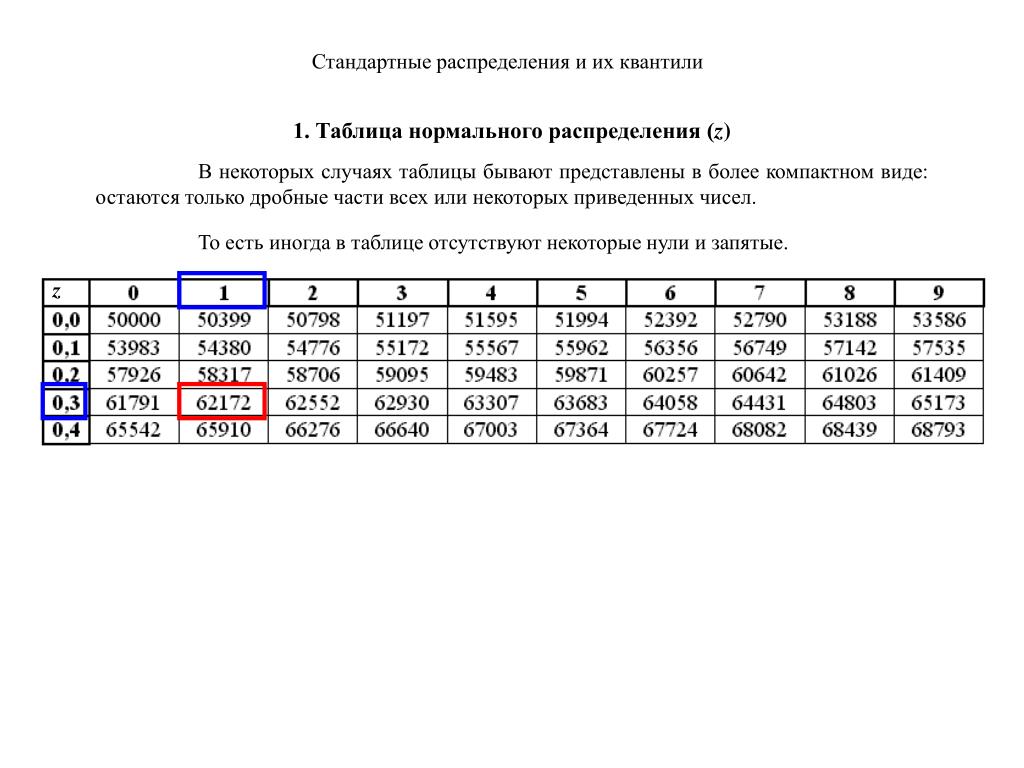
Как использовать таблицу Z (с примерами)
Z-таблица — это таблица, в которой указано, какой процент значений падает ниже определенного z-показателя в стандартном нормальном распределении.
Z-оценка просто сообщает вам, на сколько стандартных отклонений отдельное значение данных отпадает от среднего значения. Он рассчитывается как:
z-оценка = (x – μ) / σ
куда:
- x: индивидуальное значение данных
- μ: среднее значение населения
- σ: стандартное отклонение населения
В этом руководстве показано несколько примеров использования таблицы z.
Пример 1Баллы на определенном вступительном экзамене в колледж обычно распределяются со средним значением μ = 82 и стандартным отклонением σ = 8. Какой примерно процент студентов набирает на экзамене менее 84 баллов?
Шаг 1: Найдите z-оценку.
Во-первых, мы найдем z-показатель, связанный с экзаменационным баллом 84:
z-показатель = (x — μ) / σ = (84 — 82) / 8 = 2 / 8 = 0,25
Шаг 2: Используйте z-таблицу, чтобы найти процент, соответствующий z-оценке.
Далее мы найдем значение 0,25 в z-таблице :
Приблизительно 59,87% студентов набрали на этом экзамене менее 84 баллов.
Пример 2Высота растений в определенном саду нормально распределяется со средним значением μ = 26,5 дюймов и стандартным отклонением σ = 2,5 дюйма. Примерно какой процент растений имеет высоту более 26 дюймов?
Шаг 1: Найдите z-оценку.
Во-первых, мы найдем z-значение, связанное с высотой 26 дюймов.
z-показатель = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2
Шаг 2: Используйте z-таблицу, чтобы найти процент, соответствующий z-оценке.
Далее мы найдем значение -0,2 .в z-таблице :
Мы видим, что 42,07% значений падают ниже z-показателя, равного -0,2. Однако в этом примере мы хотим знать, какой процент значений больше -0,2, что мы можем найти, используя формулу 100% — 42,07% = 57,93%.
Таким образом, примерно 59,87% растений в этом саду имеют высоту более 26 дюймов.
Пример 3Вес определенного вида дельфинов нормально распределяется со средним значением μ = 400 фунтов и стандартным отклонением σ = 25 фунтов. Приблизительно какой процент дельфинов весит от 410 до 425 фунтов?
Шаг 1: Найдите z-показатели.
Во-первых, мы найдем z-показатели, связанные с 410 фунтами и 425 фунтами.
Z-показатель 410 = (x — μ) / σ = (410 — 400) / 25 = 10 / 25 = 0,4
Z-показатель 425 = (x — μ) / σ = (425 — 400) / 25 = 25 / 25 = 1
Шаг 2: Используйте z-таблицу, чтобы найти проценты, соответствующие каждому z-показателю.
Сначала мы найдем значение 0,4 .в z-таблице :
Затем мы будем искать значение 1в z-таблице :
Наконец, мы вычтем меньшее значение из большего значения: 0,8413 – 0,6554 = 0,1859 .
Таким образом, примерно 18,59% дельфинов весят от 410 до 425 фунтов.
Дополнительные ресурсыВведение в нормальное распределение
Калькулятор площади нормального распределения
Калькулятор Z-счета
Таблица распределения частот – значение и примеры
В таблице распределения частот упорядоченно отображается частота каждого набора данных. Это помогает нам находить закономерности в данных, а также позволяет нам анализировать данные, используя показатели центральной тенденции и дисперсии. Первый шаг, который математик делает с собранными данными, — это организация их в виде таблицы частотного распределения. Все расчеты и статистические проверки и анализы будут позже.
| 1. | Что такое таблица распределения частот? |
| 2. | Как составить таблицу распределения частот? |
| 3. | Что такое таблица частотного распределения в статистике? |
4. | Таблица распределения частот для сгруппированных данных |
| 5. | Таблица 9 кумулятивного распределения частоты0008 |
| 6. | Часто задаваемые вопросы по таблице частотного распределения |
Что такое таблица распределения частот?
Таблица частотного распределения — это способ организации данных, который делает их более значимыми. Таблица частотного распределения представляет собой диаграмму, которая суммирует все данные в двух столбцах — переменные/категории и их частота. Он состоит из двух или трех столбцов. Обычно в первом столбце перечислены все результаты в виде отдельных значений или в виде интервалов классов, в зависимости от размера набора данных. Второй столбец включает итоговые оценки каждого результата. В третьем столбце указана частота каждого результата. Кроме того, второй столбец является необязательным.
Вы знаете значение слова «частота»? Частота показывает, как часто что-то происходит.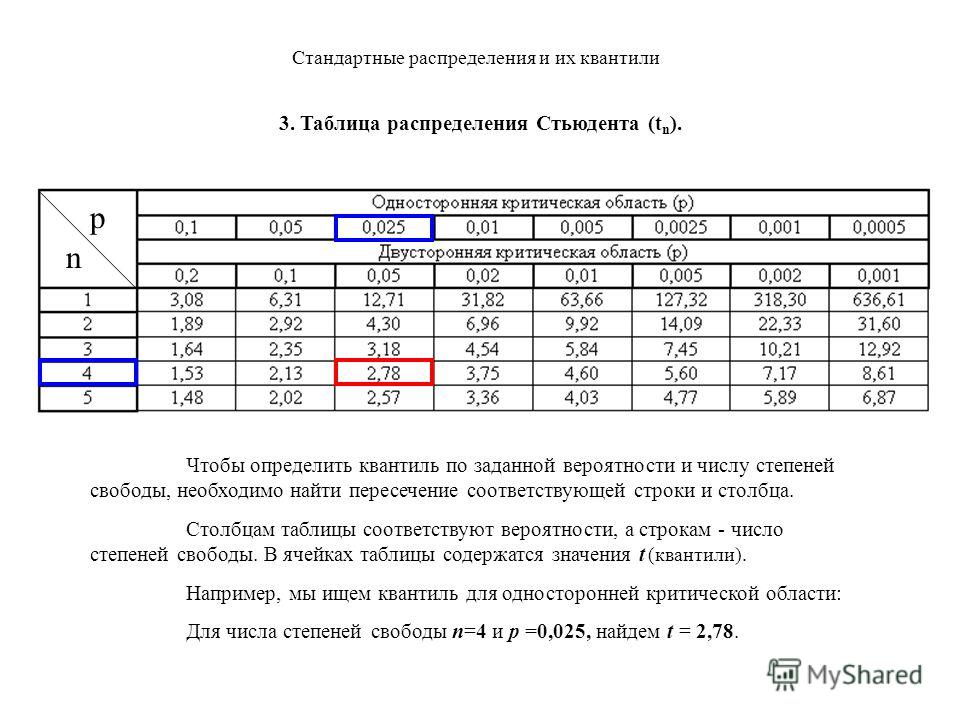
Например, ваше сердцебиение составляет 72 удара в минуту в нормальных условиях. Частота соответствует числу появлений значения.
В нашей повседневной жизни мы сталкиваемся с большим количеством информации в виде числовых цифр, таблиц, графиков и т. д. Это могут быть оценки, выставленные учениками, температуры разных городов, очки, набранные в матчах, и т. д. Информация, которая собирается, называется данные . После того, как данные собраны, мы должны представить их осмысленным образом, чтобы их можно было легко понять. Таблица распределения частот является одним из способов организации данных.
Вот пример таблицы распределения частот, чтобы вы могли лучше понять эту концепцию. Джейн любит играть в кости. Она бросает кости и каждый раз отмечает наблюдения. Вот ее наблюдения: 4, 6, 1, 2, 2, 5, 6, 6, 5, 4, 2, 3. Чтобы узнать точное количество раз, которое она получила каждую цифру (1, 2, 3, 4, 5 , 6) в результате она классифицирует их по категориям. Самый простой способ — нарисовать таблицу частотного распределения с метками.
| Результаты | Учетные отметки | Частота |
|---|---|---|
| 1 | я | 1 |
| 2 | я я я | 3 |
| 3 | я | 1 |
| 4 | я я | 2 |
| 5 | я я | 2 |
| 6 | я я я | 3 |
Приведенная выше таблица является примером таблицы распределения частот. Вы можете заметить, что все собранные данные были организованы по трем столбцам. Таким образом, таблица частотного распределения представляет собой диаграмму, суммирующую значения и их частоты. Другими словами, это инструмент для организации данных. Это облегчает нам понимание данного набора информации.
Таким образом, таблица частотного распределения в статистике помогает нам сжать данные в более простой форме, чтобы нам было легко наблюдать их особенности с первого взгляда.
Как составить таблицу распределения частот?
Таблицу частотного распределения легко составить, выполнив следующие шаги:
- Шаг 1: Создайте таблицу с двумя столбцами — один с заголовком данных, которые вы систематизируете, а другой столбец будет для частота. [Нарисуйте три столбца, если вы хотите также добавить метки для подсчета]
- Шаг 2: Посмотрите на элементы, записанные в данных, и решите, хотите ли вы нарисовать таблицу распределения частот без групп или таблицу распределения частот с группами. Если имеется слишком много разных значений, то обычно лучше использовать сгруппированную таблицу распределения частот.
- Шаг 3: Запишите значения набора данных в первый столбец.
- Шаг 4: Подсчитайте, сколько раз каждый элемент повторяется в собранных данных. Другими словами, найдите частоту каждого элемента путем подсчета.
- Шаг 5: Запишите частоту во втором столбце, соответствующем каждому элементу.
- Шаг 6: Наконец, вы также можете записать общую частоту в последней строке таблицы.
Давайте рассмотрим пример. Мисс Дженнифер работает учителем. Она хочет посмотреть на оценки, полученные учениками ее класса на последнем экзамене. У нее нет времени просматривать каждую тестовую работу по отдельности, чтобы увидеть оценки. Поэтому она просит мистера Томаса организовать данные в виде таблицы, чтобы ей было легче смотреть на оценки всех вместе. Г-жа Дженнифер предлагает использовать таблицу частотного распределения для организации данных, чтобы получить более полное представление о данных, а не использовать простой список.
Использование здесь таблицы частотного распределения является хорошим способом представления данных, так как г-жа Дженнифер покажет все оценки учащихся в одной таблице. Но как составить таблицу частотного распределения? Мистер Томас упорно трудится, чтобы собрать воедино все данные. В следующей таблице показаны результаты тестов 20 учащихся, т.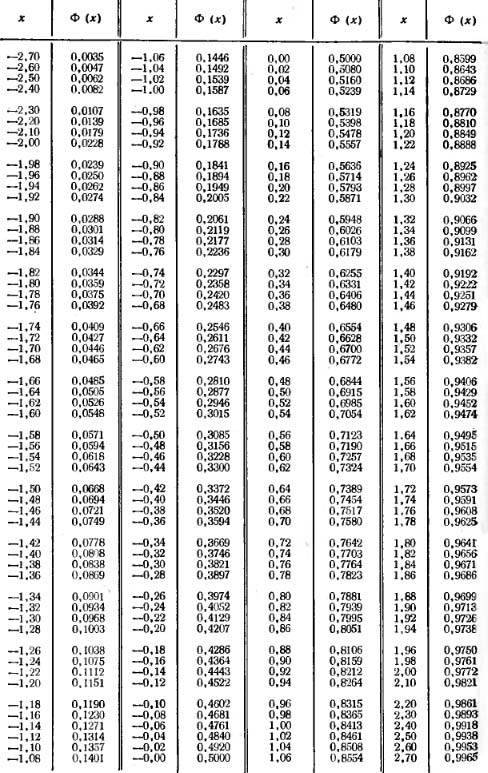
е. для одного класса.
| Баллы, полученные за тест | Количество студентов (частота) |
|---|---|
| 9 | 1 |
| 11 | 4 |
| 13 | 1 |
| 18 | 1 |
| 20 | 1 |
| 21 | 2 |
| 22 | 1 |
| 23 | 3 |
| 25 | 1 |
| 26 | 3 |
| 29 | 1 |
| 30 | 1 |
| Итого | 20 |
Нарисованная выше таблица частотного распределения называется негруппированной таблицей частотного распределения . Это представление несгруппированных данных, которое обычно используется при наличии небольшого набора данных. Представьте, как сложно было бы создать подобную таблицу, если у вас есть большое количество наблюдений, например, оценки учеников трех классов.
Таблица, которую мы получим, будет довольно длинной, а данные будут запутанными.
Следовательно, в таких случаях мы формируем интервалы классов для подсчета частоты данных, принадлежащих этому конкретному интервалу классов. Чтобы составить такую таблицу частотного распределения, сначала запишите интервалы классов в один столбец. Затем подсчитайте числа в каждой категории в зависимости от того, сколько раз она появляется. Наконец, напишите частоту в последней колонке.
| Баллы, полученные за тест | Количество студентов (частота) |
|---|---|
| 0 — 5 | 3 |
| 5 — 10 | 11 |
| 10 — 15 | 12 |
| 15 — 20 | 19 |
| 20 — 25 | 7 |
| 25 — 30 | 8 |
| Итого | 60 |
Нарисованная выше таблица частотного распределения называется сгруппированной таблицей частотного распределения .
Что такое таблица частотного распределения в статистике?
Частотное распределение в статистике — это представление данных, отображающих количество наблюдений в заданном интервале. Представление частотного распределения может быть графическим или табличным. Теперь давайте рассмотрим другой способ представления данных, т. е. графическое представление данных. Это делается с помощью графика таблицы частотного распределения. Такие графики облегчают понимание собранных данных.
- Гистограммы представляют данные с помощью столбцов одинаковой ширины с одинаковым расстоянием между ними.
- На круговой диаграмме показан целый круг, разделенный на сектора, где каждый сектор пропорционален информации, которую он представляет.
- Многоугольник частот строится путем соединения средних точек столбцов гистограммы.
Таблица распределения частот для сгруппированных данных
Таблица частотного распределения для сгруппированных данных называется сгруппированной таблицей частотного распределения.
Он основан на частотах интервалов классов. Как уже обсуждалось выше, в этой таблице все категории данных разбиты на разные классовые интервалы одинаковой ширины, например, 0-10, 10-20, 20-30 и т.д. интервал класса отмечен против каждого интервала. Посмотрите на пример таблицы распределения частот для сгруппированных данных, приведенный на изображении ниже.
Таблица кумулятивного распределения частот
Суммарная частота означает сумму частот класса и всех классов ниже него. Он рассчитывается путем добавления частоты каждого класса ниже соответствующего интервала класса или категории. Пример сводной таблицы частотного распределения приведен ниже:
Калькуляторы совокупной таблицы частотного распределения экономят много времени при табулировании данных. Это упрощает расчеты и приводит к организации данных за считанные секунды.
Таблица распределения частот Статьи по теме
Проверьте эти статьи, связанные с концепцией таблицы распределения частот в математике.
- Распределение частот
- Формула частотного распределения
- Суммарная частота
- Как найти относительную частоту
Часто задаваемые вопросы по таблице частотного распределения
Что такое Таблица распределения частот?
Таблица распределения частот представляет собой табличное представление частот указанных категорий. Он представляет данные организованным образом, который полезен для графического представления данных или для вычисления среднего значения, медианы, моды, дисперсии и т. д. Обычно он имеет два столбца, один из которых относится к категориям набора данных, а другой соответствует частоте каждой категории. Иногда перед частотой также добавляется столбец подсчета, который помогает подсчитать частоту.
Для чего нужна таблица распределения частот?
Таблица частотного распределения полезна для выполнения расчетов по заданным данным. Он включает в себя расчеты, включающие меры центральной тенденции, дисперсии, статистические тесты и анализ.
Кроме того, таблица частотного распределения полезна для представления данных в аккуратном и легком для понимания виде.
Как составить негруппированную таблицу распределения частот?
Чтобы составить таблицу частотного распределения без групп, выполните следующие действия:
- Определите все категории, указанные в данных.
- Нарисуйте таблицу с двумя столбцами: один с категориями, а другой с соответствующими частотами. Нарисуйте три столбца, если вы хотите также добавить метки.
- Запишите каждую категорию в отдельной строке в столбце 1.
- Подсчитайте, сколько раз они встречаются или повторяются в собранных данных.
- Запишите эти частоты для каждой категории в столбце 2.
Что такое сгруппированная таблица распределения частот?
Сгруппированная таблица частотного распределения представляет собой таблицу, которая представляет категории в виде интервалов классов. Он в основном используется с большими наборами данных.
Что такое cf в таблице распределения частот?
В таблице распределения частот cf означает кумулятивную частоту. Cf представляет общую или общую частоту категории и всех категорий ниже или выше этой.
Как интерпретировать таблицу распределения частот?
При интерпретации таблицы распределения частот необходимо учитывать следующие моменты:
- Первый столбец обычно относится к категориям набора данных, а второй или третий столбцы обычно относятся к частоте каждой категории.
- Число, написанное справа от каждой категории, является ее частотой. Он лежит в том же ряду.
- Других категорий лжи, кроме тех, что указаны в первой колонке таблицы, нет.
Как нарисовать таблицу распределения частот?
Обычно в таблице распределения частот есть два или три столбца: столбец 1 для категорий, столбец 2 для итоговых меток и столбец 3 для частоты. Итак, чтобы нарисовать таблицу частотного распределения, мы должны записывать данные только в этом порядке.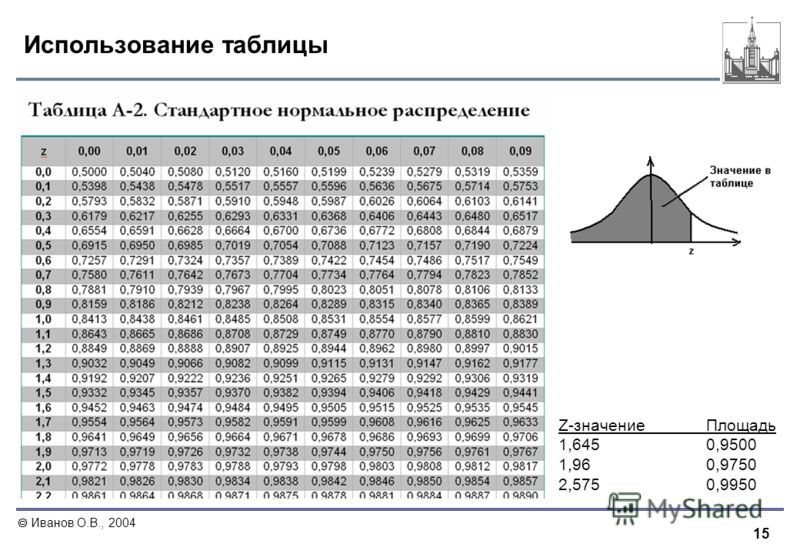
Сначала выявляем все категории или интервалы классов, затем записываем их отдельными строками в столбец 1. После этого фокусируемся на каждой категории по очереди и подсчитываем их частоты. Мы пишем их соответствующую частоту в третьем столбце. Вот как мы можем нарисовать таблицу частотного распределения.
Как получить границу класса в таблице распределения частот?
Граница класса — это число, которое разделяет интервалы классов, не оставляя пробелов. Например, если два последующих интервала занятий указаны как 20-29 и 30-39. Граница класса рассчитывается как (верхний предел интервала первого класса + нижний предел интервала второго класса)/2. Итак, здесь граница класса = (29+30)/2, что равно 29,5.
Какие существуют типы таблиц распределения частот?
В основном существует три типа таблиц распределения частот, которые приведены ниже:
- Таблица распределения частот без групп
- Сгруппированная таблица частотного распределения
- Совокупная таблица частотного распределения
4.
3 Распределение частотСодержание
Текст начинается
Тематическая навигация
- 4 Исследование данных
- 4.1 Инструменты исследования данных
- 4.2 Типы переменных
- 4.3 Распределение частот
- 4.4 Меры центральной тенденции
- 4.5 Меры рассеивания
- 4.6 Упражнения
- 4.7 Ответы
частота ( f ) определенного значения – это количество раз, когда это значение встречается в данных. Распределение переменной представляет собой шаблон частот, означающий набор всех возможных значений и частот, связанных с этими значениями. Распределения частот изображаются в виде частотных таблиц или диаграмм.
Распределения частот могут отображать либо фактическое количество наблюдений, попадающих в каждый диапазон, либо процент наблюдений.
В последнем случае распределение называется относительное частотное распределение .
Таблицы частотного распределения можно использовать как для категориальных, так и для числовых переменных. Непрерывные переменные следует использовать только с интервалами классов, что будет объяснено в ближайшее время.
Давайте рассмотрим несколько примеров частотного распределения и относительного частотного распределения для дискретных переменных.
Пример 1. Составление таблицы частотного распределенияНа Мейпл-авеню было проведено обследование. В каждом из 20 домов людей спрашивали, сколько автомобилей зарегистрировано на их домохозяйства. Результаты были записаны следующим образом:
1, 2, 1, 0, 3, 4, 0, 1, 1, 1, 2, 2, 3, 2, 3, 2, 1, 4, 0, 0
Используйте следующие шаги для представления этого данные в таблице частотного распределения.
- Разделите результаты ( x ) на интервалы, а затем подсчитайте количество результатов в каждом интервале. В этом случае интервалами будут количество домохозяйств без машины (0), одна машина (1), две машины (2) и так далее.
- Составьте таблицу с отдельными столбцами для номеров интервалов (количество автомобилей на домохозяйство), подсчитанных результатов и частоты результатов в каждом интервале. Обозначьте эти столбцы Количество автомобилей , Сумма и Частота .
- Прочитайте список данных слева направо и поставьте отметку в соответствующей строке. Например, первый результат — 1, поэтому поставьте отметку в строке рядом с тем местом, где 1 появляется в столбце интервала ( Количество автомобилей ). Следующим результатом будет 2, поэтому поставьте отметку в ряду рядом с 2 и так далее. Когда вы дойдете до пятой контрольной отметки, проведите контрольную линию через предыдущие четыре отметки, чтобы облегчить чтение окончательных расчетов частоты.
- Сложите количество контрольных точек в каждой строке и запишите их в последний столбец, озаглавленный Частота .
В этом случае интервалами будут количество домохозяйств без машины (0), одна машина (1), две машины (2) и так далее.
Таблица распределения частот для этого упражнения должна выглядеть следующим образом:
| Количество вагонов (х) | Частота (f) |
|---|---|
| 0 | 4 |
| 1 | 6 |
| 2 | 5 |
| 3 | 3 |
| 4 | 2 |
Быстро взглянув на эту таблицу частотного распределения, мы увидим, что из 20 обследованных домохозяйств в 4 домохозяйствах не было автомобилей, в 6 домохозяйствах была 1 машина и т.
д.
кумулятивного распределения частот Таблица кумулятивного распределения частот является более подробной таблицей. Она выглядит почти так же, как таблица распределения частот, но в нее добавлены столбцы, которые также показывают совокупную частоту и совокупный процент результатов.
На недавнем шахматном турнире все 10 участников должны были заполнить форму, в которой были указаны их имена, адреса и возраст. Возраст участников был записан следующим образом:
36, 48, 54, 92, 57, 63, 66, 76, 66, 80
Используйте следующие шаги, чтобы представить эти данные в таблице распределения совокупной частоты.
- Разделите результаты на интервалы, а затем подсчитайте количество результатов в каждом интервале. В этом случае подходят интервалы 10. Поскольку 36 лет — самый низкий возраст, а 92 — самый высокий, начните интервалы с 35 до 44 и закончите интервалы с 85 до 94.
- Создайте таблицу, аналогичную таблице частотного распределения, но с тремя дополнительными столбцами.
Совокупная таблица распределения частот должна выглядеть так:
Таблица 4.3.2
Возраст участников шахматного турнира
Сводка таблицы
В этой таблице отображаются результаты Возрастов участников шахматного турнира. Информация сгруппирована по нижнему значению (отображается в виде заголовков строк), верхнему значению, частоте (f), совокупной частоте, проценту и совокупному проценту (отображается в виде заголовков столбцов).Нижнее значение Верхнее значение Частота (f) Суммарная частота Процент Суммарный процент 35 44 1 1 10,0 10,0 45 54 2 3 20,0 30,0 55 64 2 5 20,0 50,0 65 74 2 7 20,0 70,0 75 84 2 9 20,0 90,0 85 94 1 10 10,0 100,0
Интервалы классов
Если переменная принимает большое количество значений, то данные проще представлять и обрабатывать, группируя значения в интервалы классов.
Непрерывные переменные с большей вероятностью будут представлены в интервалах классов, в то время как дискретные переменные могут быть сгруппированы в интервалы классов или нет.
Для иллюстрации предположим, что мы установили возрастные диапазоны для исследования молодых людей, допуская при этом возможность того, что некоторые пожилые люди также могут попасть в сферу нашего исследования.
Частота интервала класса — это количество наблюдений, происходящих в конкретном предопределенном интервале. Так, например, если в данных нашего исследования фигурируют 20 человек в возрасте от 5 до 9 лет, частота интервала 5–9 будет равна 20.
. Итак, интервалы в нашем исследовании составляют от 0 до 4 лет, от 5 до 9 лет.лет, от 10 до 14 лет, от 15 до 19 лет, от 20 до 24 лет и от 25 лет и старше. Конечные точки первого интервала равны 0 и 4, если переменная дискретна, и 0 и 4,999, если переменная непрерывна. Таким же образом будут определены конечные точки других интервалов класса.
Ширина интервала класса — это разница между нижней конечной точкой интервала и нижней конечной точкой следующего интервала. Таким образом, если непрерывные интервалы нашего исследования равны от 0 до 4, от 5 до 9 и т. д., ширина первых пяти интервалов равна 5, а последний интервал открыт, поскольку ему не назначена более высокая конечная точка. Интервалы также могут быть записаны как от 0 до менее 5, от 5 до менее 10, от 10 до менее 15, от 15 до менее 20, от 20 до менее 25, от 25 и более.
Правила для наборов данных, содержащих большое количество наблюдений
Таким образом, следуйте этим основным правилам при построении таблицы распределения частот для набора данных, содержащего большое количество наблюдений:
- найдите наименьшее и наибольшее значения переменные
- принять решение о ширине интервалов классов
- включают все возможные значения переменной.
При выборе ширины интервалов классов вам придется найти компромисс между интервалами, достаточно короткими, чтобы не все наблюдения попадали в один и тот же интервал, и достаточно длинными, чтобы не остаться только с одним наблюдения за интервал.
Также важно убедиться, что интервалы классов являются взаимоисключающими и в совокупности исчерпывающими.
Пример 3. Составление таблицы частотного распределения для большого количества наблюденийТридцать батареек типа АА были протестированы, чтобы определить, как долго они будут работать. Результаты с точностью до минуты были записаны следующим образом:
423, 369, 387, 411, 393, 394, 371, 377, 389, 409, 392, 408, 431, 401, 363, 391, 405, 382 , 400, 381, 399, 415, 428, 422, 396, 372, 410, 419, 386, 390
Используйте шаги из примера 1 и приведенные выше правила, чтобы составить таблицу частотного распределения.
Ответ
Наименьшее значение – 363, а наибольшее – 431.
Используя данные и интервал классов, равный 10, интервал для первого класса составляет от 360 до 369 и включает 363 (наименьшее значение). Помните, всегда должно быть достаточно интервалов занятий, чтобы было включено самое высокое значение.
Заполненная таблица частотного распределения должна выглядеть следующим образом:
| Срок службы батареи, мин ( x ) | Частота (f) |
|---|---|
| 360–369 | 2 |
| 370–379 | 3 |
| 380–389 | 5 |
| 390–399 | 7 |
| 400–409 | 5 |
| 410–419 | 4 |
| 420–429 | 3 |
| 430–439 | 1 |
| Итого | 30 |
Составление таблиц относительной частоты и частоты в процентахАналитик, изучающий данные из примера 3, может захотеть узнать не только о том, как долго работают батареи, но и о том, какая доля батарей попадает в каждый класс интервалов срока службы батарей.
Эта относительная частота конкретного интервала наблюдения или класса находится путем деления частоты ( f ) по количеству наблюдений ( n ): то есть ( f ÷ n ). Таким образом:
Относительная частота = частота ÷ количество наблюдений
Частота в процентах находится путем умножения каждого значения относительной частоты на 100. Таким образом:
Частота в процентах = относительная частота X 100 = f ÷ n X 100
Используйте данные из Примера 3, чтобы составить таблицу, содержащую относительную частоту и процентную частоту каждого интервала срока службы батареи.
Вот как выглядит эта таблица:
| Срок службы батареи, мин ( х ) | Частота (f) | Относительная частота | Процентная частота |
|---|---|---|---|
| 360–369 | 2 | 0,07 | 7 |
| 370–379 | 3 | 0,1 | 10 |
| 380–389 | 5 | 0,17 | 17 |
| 390–399 | 7 | 0,23 | 23 |
| 400–409 | 5 | 0,17 | 17 |
| 410–419 | 4 | 0,13 | 13 |
| 420–429 | 3 | 0,1 | 10 |
| 430–439 | 1 | 0,03 | 3 |
| Итого | 30 | 1 | 100 |
Аналитик этих данных теперь может сказать, что:
- 7% батарей типа АА имеют срок службы от 360 минут до, но менее 370 минут, и что
- вероятность того, что любая случайно выбранная батарея типа АА будет иметь срок службы в этом диапазоне, составляет приблизительно 0,07.
Как показано ранее в примере 2, кумулятивная частота используется для определения количества наблюдений, которые лежат ниже определенного значения в наборе данных. Совокупная частота рассчитывается путем добавления каждой частоты из таблицы распределения частот к сумме ее предшественников. Последнее значение всегда будет равно сумме по всем наблюдениям, так как все частоты уже будут добавлены к предыдущей сумме. Давайте рассмотрим еще один пример расчета кумулятивной частоты.
Ежедневное количество скалолазов в Лейк-Луизе, Альберта, регистрировалось в течение 30-дневного периода. Результаты следующие:
31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56 , 4, 54, 39, 52, 35, 51, 63, 42.
Количество скалолазов колеблется от 4 до 65. Для составления таблицы частот данные лучше сгруппировать по классам с интервалом 10. Каждый интервал может быть одной строкой в таблице частот. В столбце Частота указано количество наблюдений, найденных в пределах интервала класса. Например, в интервале от 10 до 20 всего два значения, тогда его частота равна 2 в таблице соответственно.
Используйте столбец Частота для расчета совокупной частоты.
- Сначала добавьте число из столбца Частота к его предшественнику. Например, в первой строке у нас есть только одно наблюдение и нет предшественников. Суммарная частота равна единице.
1 + 0 = 1 - Однако во второй строке есть два наблюдения. Добавьте эти два к предыдущей кумулятивной частоте (один), и в результате получится три.
1 + 2 = 3 - Запишите результаты в столбце Суммарная частота .
Аналогично рассчитываются и другие записи в таблице. Результаты представлены в таблице 4. 3.5.
| Количество скалолазов | Частота (f) | Суммарная частота |
|---|---|---|
| <10 | 1 | 1 |
| от 10 до <20 | 2 | 1 + 2 = 3 |
| от 20 до <30 | 3 | 3 + 3 = 6 |
| от 30 до <40 | 5 | 6 + 5 = 11 |
| от 40 до <50 | 6 | 11 + 6 = 17 |
| от 50 до <60 | 9 | 17 + 9 = 26 |
| >= 60 | 4 | 26 + 4 = 30 |
Суммарная относительная частота — еще один способ выражения частотного распределения. Он получается путем вычисления процента кумулятивной частоты в пределах каждого интервала.
Совокупный процент рассчитывается путем деления кумулятивной частоты на общее количество наблюдений ( n ), затем умножая на 100 (последнее значение всегда будет равно 100%). Таким образом,
кумулятивная относительная частота = (кумулятивная частота ÷ n) x 100
В четвертом столбце таблицы 4.3.6 показан расчет кумулятивной относительной частоты ежедневного числа скалолазов, зарегистрированных в Лейк-Луизе.
| Количество скалолазов | Частота (f) | Суммарная частота | Суммарная относительная частота (%) |
|---|---|---|---|
| <10 | 1 | 1 | 1 ÷ 30 х 100 = 3 |
| от 10 до <20 | 2 | 1 + 2 = 3 | 3 ÷ 30 х 100 = 10 |
| 20 до <30 | 3 | 3 + 3 = 6 | 6 ÷ 30 х 100 = 20 |
| от 30 до <40 | 5 | 6 + 5 = 11 | 11 ÷ 30 х 100 = 37 |
| от 40 до <50 | 6 | 11 + 6 = 17 | 17 ÷ 30 х 100 = 57 |
| от 50 до <60 | 9 | 17 + 9 = 26 | 26 ÷ 30 х 100 = 87 |
| >= 60 | 4 | 26 + 4 = 30 | 30 ÷ 30 х 100 = 100 |
Кумулятивное распределение относительной частоты можно визуализировать с помощью гистограммы или линейной диаграммы, как на диаграмме 4. 3.1 ниже. Значение на горизонтальной оси является верхней границей интервала класса.
| Верхняя граница интервала классов суточной численности скалолазов | Суммарная относительная частота (%) |
|---|---|
| 9 | 3 |
| 19 | 10 |
| 29 | 20 |
| 39 | 37 |
| 49 | 57 |
| 59 | 87 |
| 69 | 100 |
Из диаграммы 4.