13.4. Системы неравенств (Задачи ОГЭ)
Задачи ОГЭ
№3125
Сложность:
31 %
!
Укажите решение системы неравенств
\(\begin{cases} -9+3x< 0,\\ 2-3x< -10.\end{cases}\)
1) \((-\infty; 3)\)
2) нет решений
3) \((4;+\infty)\)
4) \((3;4)\)
Подпишись на ютуб канал
Подписаться
№2133
Сложность:
31 %
!
На каком рисунке изображено множество решений системы неравеств?
\(\begin{cases} x<3\\ 4-x< 0 \end{cases}\)
Подпишись на ютуб канал
Подписаться
№1925
Сложность:
32 %
!
Решите систему неравенств
\(\begin{cases} x+2{,}6\leqslant 0\\x+5\geqslant 1\end{cases}\)
Подпишись на ютуб канал
Подписаться
№1693
Сложность:
33 %
!
Выберите верное множество решений системы неравенств:
\(\begin{cases} -12x+12\geqslant 4x+4\\-4x+11\leqslant 3x+9\end{cases}\)
1) \(\left(-\infty;\dfrac27\right]\cup\left[\dfrac12;+\infty\right)\)
2) \(\left[ \dfrac27; \dfrac12\right]\)
3)\(\left[ \dfrac12; \dfrac72\right]\)
4)\(\left[ -\dfrac12; \dfrac27\right]\)
Подпишись на ютуб канал
Подписаться
№2322
Сложность:
34 %
!
Укажите множество решений системы неравенств
\(\begin{cases} -12 + 3x > 0\\ 9 — 4x> -3\end{cases}\)
1) Система не имеет решений
2)
3)
4)
Подпишись на ютуб канал
Подписаться
№2546
Сложность:
34 %
!
Решите систему неравенств \(\begin{cases} 5(x+3) > 7(x+1),\\ -5-1{,}25x<0.
\end{cases}\)
В каком из приведённых случаев изображено множество её решений?
Подпишись на ютуб канал
Подписаться
№305
Сложность:
37 %
!
Укажите номер рисунка, на котором изображено множество решений системы неравенств
\(\begin{cases} 5x+9>-2x-9\\ 13x-5\geqslant 4x+6\end{cases}\)
1)
2)
3)
Подпишись на ютуб канал
Подписаться
№2558
Сложность:
37 %
!
На какой из координатных прямых изображено множество решений системы неравенств
\(\begin{cases} 2x-3> 0,\\ 16-5x<1. \end{cases}\)
Подпишись на ютуб канал
Подписаться
№2403
Сложность:
38 %
!
Укажите решение системы неравенств
\(\begin{cases} x+2{,}8 \leqslant 0\\ x+0{,}3\leqslant -1{,}4\end{cases}\)
1) \((-\infty; -2{,}8]\)
2) \((-\infty; -2{,}8] \cup [-1{,}7;+\infty)\)
3) \([-2{,}8;-1{,}7]\)
4) \([-1{,}7;+\infty)\)
Подпишись на ютуб канал
Подписаться
№3146
Сложность:
42 %
!
Укажите решение системы неравенств
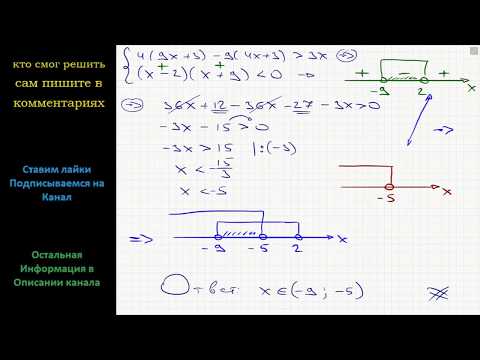
\(\begin{cases} -35+5x< 0,\\ 6-3x>-18.
2-1)≥0\\x<3\end{cases}\)
Чтобы
решить систему неравенств нужно найти значения иксов, которые подойдут всем неравенствам в системе – это и значит, что они выполняются одновременно.
Пример. Решим систему \(\begin{cases}x>4\\x\leq7\end{cases}\)
Решение: Первое неравенство становится верным, если икс больше \(4\). То есть, решения первого неравенства – все значения иксов из интервала \((4;\infty)\), или на числовой оси:
Второму неравенству подойдут значения иксов меньшие чем 7, включая саму семерку, то есть любой икс из интервала \((-\infty;7]\) или на числовой оси:
А какие значения подойдут обоим неравенствам? Те, которые принадлежат обоим промежуткам, то есть где промежутки пересекаются.
Ответ: \((4;7]\)
Как вы могли заметить для пересечения решений неравенств в системе удобно использовать числовые оси.
Пример: (Задание из ОГЭ) Решить систему \(\begin{cases} 7(3x+2)-3(7x+2)>2x\\(x-5)(x+8)<0\end{cases}\)
Решение:
|
\(\begin{cases} 7(3x+2)-3(7x+2)>2x\\(x-5)(x+8)<0\end{cases}\) |
Давайте каждое неравенство решим отдельно от другого. |
|
|
1) \(7(3x+2)-3(7x+2)>2x\) |
Раскроем скобки . |
|
|
\(21x+14-21x-6>2x\) |
Приведем подобные слагаемые. |
|
|
\(8>2x\) |
Перевернем получившееся неравенство. |
|
|
\(2x<8\) |
Поделим все неравенство на \(2\). |
|
|
\(x<4\) |
Отметим решение на числовой прямой. |
|
|
Запишем ответ для первого неравенства. |
||
|
\(x∈(-∞;4)\) |
Теперь решим второе неравенство. |
|
|
2) \((x-5)(x+8)<0\) |
Неравенство уже в идеальном виде для применения метода интервалов.
|
|
|
Запишем ответ для второго неравенства. |
||
|
\(10-2x≥0\) |
Перед нами обычное линейное неравенство – выразим \(x\). Для этого перенесем \(10\) в правую часть. |
|
|
\(-2x≥-10\) |
Поделим неравенство на \(-2\). Так как число отрицательное меняем знак неравенства. |
|
|
\(x≤5\) |
Отметим решение на числовой прямой. |
|
|
Запишем ответ к первому неравенству. |
||
|
\(x∈(-∞;5]\) |
На данном этапе главное не забыть, что есть второе неравенство. |
|
|
2) \(2-7x≤14-3x\) |
Опять линейное неравенство – опять выражаем \(x\). |
В первом перенесем все слагаемые в левую часть. И приведем подобные слагаемые. |
|
\(\begin{cases}-27x+54<0\\(x-5)(x-50)≥0\\x>14\end{cases}\) |
Теперь в нем же перенесем \(54\) в левую сторону и поделим обе части на \((-27)\), не забыв при этом перевернуть знак сравнения. |
|
|
\(\begin{cases}x>2\\(x-5)(x-50)≥0\\x>14\end{cases}\) |
Отметим решения неравенств на числовых прямых. |
|
|
Решения подходящие всем неравенствам системы находятся от \(50\) и дальше. Запишем ответ. |
2\)
2-28x+196\\(x-5)(x-50)≥0\\x>14\end{cases}\)Ответ: \([50;+∞)\)
Смотрите также:
Системы линейных неравенств
Совокупности неравенств
Задавать вопрос
спросил
Изменено 7 лет, 1 месяц назад
Просмотрено 385 раз
$\begingroup$
92+1$$Итак, для существования решения Здесь $-\frac{2}{3}\leq \alpha \leq 1$.
Теперь, как я могу найти уникальное решение?
- алгебра-предварительное исчисление
$\endgroup$
$\begingroup$
Поскольку оба квадратных неравенства меньше нуля, мы можем сказать, что их дискриминант
Итак, получим $$4-4\alpha \ge 0$$ $$16 + 24\alpha \ge 0$$Решая эти уравнения, получим $$\frac{-2}3 \le \alpha \le 1$$ Теперь мы можем определить корни этих квадратных уравнений как $$-1 \pm \sqrt{1-\alpha}$$ $$2 \pm \sqrt{4 + 6\alpha}$$ Теперь , мы видим, что оба корня первого уравнения равны отрицательное и один из корней другого уравнения положительный .
Следовательно, для единственного решения второй корень второго уравнения должен быть отрицательным . Таким образом, $$2 — \sqrt{4 + 6\alpha} \lt 0$$ Решая это, мы получаем $$\alpha \gt 0$$ и знаем, что $$\frac{-2}3 \le \alpha \le 1$$ Таким образом, требуемый набор значений $\alpha$ равен $$0 \lt \alpha \le 1$$
$\endgroup$
1
$\begingroup$
Это две параболы, направленные вверх.
Оба являются $\leq 0$ в некотором интервале $[x_1, x_2]$, где это действительные корни соответствующей параболы (если, конечно, существуют действительные корни, мы хотим, чтобы они существовали, даже если они совпадают, отсюда и ограничения, которые вы найдено для $\alpha$ гарантирует это, ОК).
Теперь нарисуйте грубый рисунок. Чтобы эта система имела единственное решение, больший корень одной из парабол должен быть равен меньшему корню другой параболы (если это не так, то пересечение этих двух отрезков будет либо пустым, либо нет решений системе/ или невырожденный интервал /бесконечное число решений/). 92-4x-6\alpha = (x-b)(x-d)$
А также: $d \leq b \leq c$ или $c \leq b \leq d$.
$\endgroup$
$\begingroup$
Способ, который, возможно, может помочь вам полностью понять то, что вы хотите знать, это войти в калькулятор Desmos и отметить «ползунок» для числа $\alpha$ ($a$ на рисунке для значения $a= 0$).