Функция область значения и область определения: область определения и область значений функций + ПРИМЕРЫ

тригонометрической, множество функций, порядок нахождения

Содержание:

• Что такое функция в алгебре
• Виды функций
  • Линейная
  • Обратная пропорциональность
  • Квадратичная (квадратная)
  • Степенная
  • Показательная
  • Логарифмическая
  • Тригонометрические
• Типы функций
  • Важные свойства
• Методы нахождения
  • Перебор значений
  • Графический метод
  • Учет непрерывности и монотонности
  • Производная, min и max
• Пример решения

Содержание

• Что такое функция в алгебре
• Виды функций
  • Линейная
  • Обратная пропорциональность
  • Квадратичная (квадратная)
  • Степенная
  • Показательная
  • Логарифмическая
  • Тригонометрические
• Типы функций
  • Важные свойства
• Методы нахождения
  • Перебор значений
  • Графический метод
  • Учет непрерывности и монотонности
  • Производная, min и max
• Пример решения

Что такое функция в алгебре

Определение

Функция в алгебре — некое математическое выражение y=f(x), где каждому значению переменной x соответствует одно значение переменной y.

Из этого следует, что решений у функции может быть много. Для обозначения совокупностей таких решений вводятся особые термины.

Определние

Множество значений функции y=f(x) — совокупность значений переменной y, которые она принимает при переборе всех значений переменной x на заданном отрезке X.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Определение

Областью значений функции y=f(x) называется такое множество значений, которые функция y принимает при переборе всех значений аргумента x из области определения. Область значений обозначается как E(f).

Определение

Область допустимых значений (область определения) функции — такое множество всех значений переменных, при которых функция имеет смысл, то есть решается. {\mathrm x}\)

Для показательной функции существует одно определяющее условие: \(\mathrm a>0\). В связи с этим область ее значений включает в себя все положительные числа:

\(\mathrm E(\mathrm f)=(0;\;+\infty) \)

Логарифмическая

\(\mathrm y=\log_{\mathrm a}\left(\mathrm x\right)\)

По своим свойствам логарифмическая функция обратна показательной. Для данных функций область определения и область значений меняются местами соответственно. ОЗ логарифмической функции включает в себя все действительные числа:

\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)

Тригонометрические

Рассмотрим четыре базовые тригонометрические функции:

• синус;
• косинус;
• тангенс;
• котангенс.

Первые две периодически повторяются в промежутке между -1 и 1:

\(\mathrm E(\mathrm f)=(-1;\;1)\)

Область значения тангенса и котангенса включает в себя все действительные числа:

\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)

Типы функций

При определении области значений функции необходимо учитывать ее фундаментальные особенности. Обозначенная выше классификация — не единственная. У математических функций есть некоторые параметры, которые влияют как на саму область значений, так и на выбор методики ее нахождения.

Важные свойства

К наиболее важным для поиска области значений функции относят следующие ее свойства:

1. Непрерывность. Непрерывной называется функция, на графике которой нет «точек разрыва». Таким точкам соответствуют значения переменной, при которых функция не имеет смысла, то есть — исключенные из области определения.
2. Монотонность. Монотонной называется функция, которая не возрастает или не убывает на всей области определения.
3. Четность. Четной называется функция, не меняющая своего значения при смене знака переменной. То есть, f(-x)=f(x). Соответственно, нечетная функция меняет значение. Выделяют также функции общего вида, которые не симметричны относительно центра или оси координат.
4. Периодичность. Периодическая функция повторяет свои значения через определенные равные интервалы значений переменной.

Методы нахождения

Поиск области значений функции несколько сложнее, чем определение ОДЗ. В зависимости от вида и типа функции, а также условий задачи для этого могут применяться различные методы.

Перебор значений

Самый простой и ограниченный способ. При его помощи можно находить область значений на небольшом промежутке целых чисел \(x\in(a;\;b)\). В таком случае заданные значения переменной поочередно подставляются в уравнение и вычисляются значения функции, соответствующие им.

Графический метод

Как ясно из названия способа, для его реализации необходимо построить график исследуемой функции. По внешнему виду кривой уже можно делать некоторые выводы. Если линия графика соответствует одному из видов элементарных функций, например, является параболой, то в качестве области значений берется промежуток, соответствующий данному графику.

2 имеет вид параболы с точкой перегиба с координатами (0, 0). Кривая непрерывна, то есть не имеет разрывов в области определения. Для того, чтобы определить область значений данной функции, достаточно построить ее график на ограниченном промежутке. Для примера возьмем \(x\in\lbrack-4;\;4\rbrack\):

 

Рисунок 1. Значение непрерывности и монотонности функции для области определения

На графике видно, что функция монотонно убывает на промежутке \(\lbrack-4;\;0\rbrack\) и монотонно возрастает на промежутке\( \lbrack0;\;4\rbrack\). Исходя из этого и непрерывности функции, можно экстраполировать данную закономерность на всю область определения. Так как минимальное значение данной функции равняется нулю, область значений будет следующей:

\(\mathrm E(\mathrm f)=\lbrack0;\;+\infty)\)

Производная, min и max

Описанные выше способы подходят не для всех ситуаций. В общем случае, задача по определению области значений функции всегда сводится к нахождению ее минимального и максимального значения или точек экстремума.

Определение

Согласно теореме Ферма, в точках локального экстремума производная исследуемой функции равняется нулю.

Важно понимать, что сами локальный экстремум не обязательно является максимумом или минимумом для функции в целом. Такие точки называются критическими или стационарными. Поэтому, кроме самих точек необходимо определять промежутки возрастания и убывания:

• если при переходе через критическую точку производная функции меняет знак с (+) на (-), то эта точка является максимумом;
• если при переходе через критическую точку производная меняет знак с (-) на (+), то такая точка является минимумом;
• если при переходе знак производной не меняется, то экстремума в данной точке нет.

Кроме того, экстремумы функции можно определять по второй производной. Предположим, при исследовании функции обнаружилась некая критическая точка x_1. Для нее справедливы следующие неравенства:

Если \(f»(x_1)>0\), то \(x_1\) — точка минимума. 2-5\) следующая:

\(E(y)=\lbrack-6;\;+\infty).\)

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Поиск по содержимому

Область определения и область значений функции. | Презентация к уроку по алгебре (9 класс) на тему:

Слайд 1

функция. Область определения функции. Область значений функции. Алгебра 9 класс

Слайд 2

Давайте вспомним: Какую зависимость называют функцией? Как читают запись y = f(x) ? Что называют аргументом функции? Что такое область определения функции? Что называют значением функции? Как читают запись f(2) = 6 и что она означает? Что называют областью значений функции?

Слайд 3

Определение функции. Обозначение функции. у( х ) — функция х — аргумент зависимая переменная независимая переменная

Слайд 4

Область определения функции. Область определения функции у(х) это все значения аргумента — Х Обозначение области определения — D( у )

Слайд 5

Область значений функции. Область значений функции у(х) это все значения — У _ Обозначение области значений — Е ( у )

Слайд 6

x — 4 — 3 — 2 — 1 0 1 2 3 y -8 — 6 — 4 — 2 0 2 4 6

Слайд 8

g(2) = g(- 2) = g(x) = 0 при x = g(x) = 1 при х = или х = D(g) = E(g) =

Слайд 9

f(-3) = f(- 1) = f(x) = — 1,5 при x = f(x) = 2 при х = х = , x = D(f) = E(f) =

Слайд 10

а) f(2) = ? б) D(f) = ? Решение: а) f( 16 ) = ? б) D(f) = ? Решение:

Слайд 11

График функции (х; у)- координаты точки в плоскости у( х )- функция х — аргумент у – ордината точки (координата оси ОУ ) х – абсцисса точки (координата оси ОХ )

Слайд 12

Область определения линейной функции y( х) = k x + b , k≠0 y x k > 0 y x k 0 х > 0 I ч. III ч. II ч. IV ч.

Слайд 13

Область значений линейной функции y( х ) = k x + b , k≠0 y x k > 0 y x k 0 у > 0 I ч. III ч. II ч. IV ч.

Слайд 14

Область определения линейной функции y( х) = k x + b , k= 0 y x y( х) = b y x y( х) = -b D( у ) = (-∞ ; + ∞) х Є (-∞ ; + ∞) -∞ + ∞ -∞ + ∞ О О х 0 х > 0 I ч.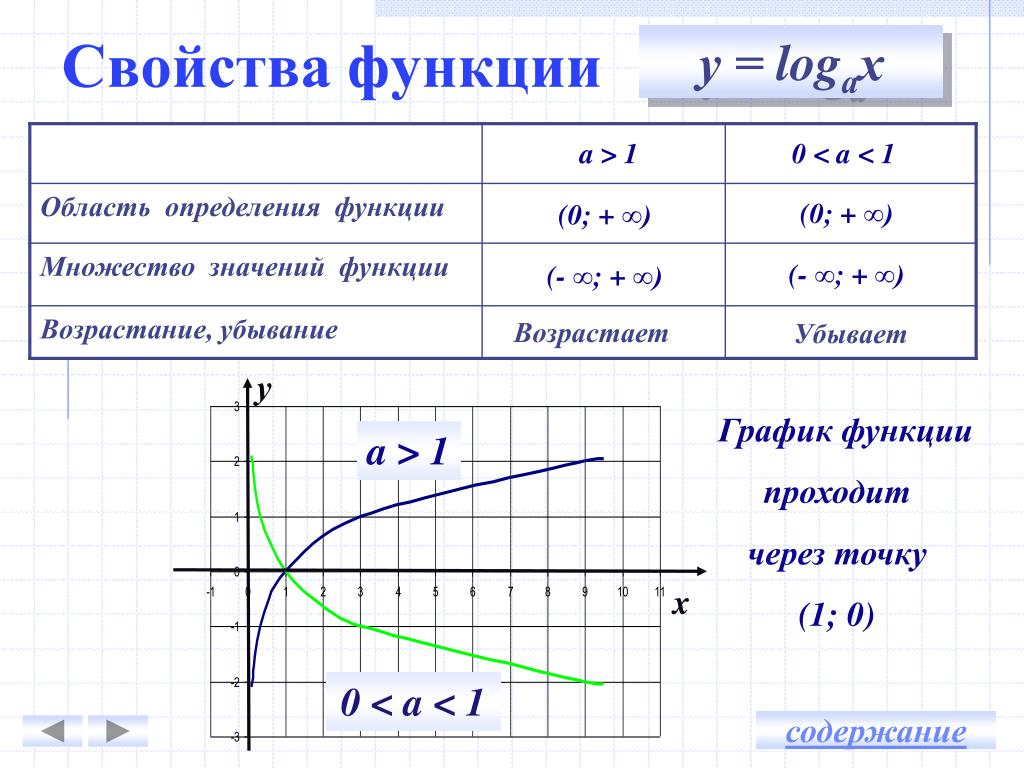 II ч. III ч. IV ч.

Слайд 15

Область значений линейной функции y( х) = k x + b , k= 0 y x y( х) = b y x y( х) = -b Е ( у ) = b -∞ + ∞ -∞ + ∞ О О I ч. II ч. III ч. IV ч. Е ( у ) = — b b -b

Слайд 16

Область определения прямой пропорциональности y( х) = k x y x k > 0 y x k 0 х > 0 I ч. III ч. II ч. IV ч.

Слайд 17

Область значений прамой пропорциональности y( х ) = k x y x k > 0 y x k 0 у > 0 I ч. III ч. II ч. IV ч.

Слайд 18

Область определения обратной пропорциональности , х≠0 y x k > 0 y x k 0 х > 0 I ч. III ч. II ч. IV ч.

Слайд 19

Область значений обратной пропорциональности , х≠0 y x k > 0 y x k 0 y > 0 I ч. III ч. II ч. IV ч.

Слайд 20

Область определения квадратичной функции , а≠0 y x а > 0 y x а 0 х > 0 I ч. III ч. II ч. IV ч.

Слайд 21

Область значений квадратичной функции , а≠0 y x а > 0 y x а 0 y

Слайд 22

Область определения функции , х ≥ 0 y x D( у ) = [0; + ∞) ; х Є [0; + ∞) + ∞ О х ≥ 0 I ч.

Слайд 23

Область значений функции , х ≥ 0 y x Е ( у ) = [0; + ∞) ; у(х) Є [0; + ∞) + ∞ О у ≥ 0 I ч.

Слайд 24

Область определения функции у = l х l _ y x D( у ) = (- ∞ ; + ∞) ; х Є (- ∞ ; + ∞) + ∞ О х

Слайд 25

Область значений функции у = l х l _ y x Е ( у ) = [ 0 ; + ∞) ; у(х) Є [ 0 ; + ∞) + ∞ О I ч. у ≥ 0 II ч.

Слайд 26

Область определения функции у = х³ y x D( у ) = (-∞ ; + ∞) ; х Є (-∞ ; + ∞) + ∞ О х ≥ 0 I ч. III ч. х

Слайд 27

Область значений функции у = х³ y x D( у ) = (-∞ ; + ∞) ; у(х) Є (-∞ ; + ∞) + ∞ О у ≥ 0 I ч. III ч. у

Слайд 28

Найдите по графику область определения функции — D( у ) -5 4 D( у )= [ -5 ; 4,5 ]

Слайд 29

Найдите по графику область значений функции — Е ( у ) -2 5 Е ( у )= [ -2 ; 5 ]

Слайд 30

По графику определите промежуток на котором определена данная функция -6 3 D( у )= [ -6 ; 3,5 ]

Слайд 31

По графику определите промежуток на котором определена данная функция -2 4 Е ( у )= [ -2 ; 4 ]

Слайд 32

Найдите по графику область определения функции -5 5 D( у )= [ -5 ; 5 ]

Слайд 33

Найдите по графику область определения функции -2 6 Е ( у )= [ -2 ; 6 ]

Слайд 34

Найдите область определения и значений функции -4 4 [ -4 ; 4) 3 ( — 1;3] а) б) в) г) д)

Слайд 35

Найдите область определения и значений функции 5 ( -1 ; 5 ] -3 4 [ — 3;4) а) б) в) г) д)

Слайд 36

Найдите область определения и значений функции -2 4 [ — 2;4) 4 [ — 1;4] а) б) в) г) д)

Слайд 37

Найдите область определения и значений функции б) в) г) — 4 2 [ -4 ; 2 ] 2 [ -1 ; 2 ] д) а)

Объяснение всех 4 областей действия JavaScript

Если вы написали хотя бы одну строку кода JavaScript, значит, вы использовали одну из четырех областей действия JavaScript, даже не подозревая об этом. Эти различные уровни области действия определяют, как будет работать ваш код, насколько легко ваш код будет писать/изменяться, а также многие другие факторы вашего кода, поэтому крайне важно знать все нюансы каждой отдельной области. В этой короткой статье я расскажу вам, что такое каждый уровень области видимости, как они взаимодействуют с вашим кодом и что вы можете сделать с этими знаниями, чтобы писать более чистый код.

Если вы предпочитаете учиться визуально, посмотрите видеоверсию этой статьи.

Что такое объем?

Первый вопрос, который нам нужно решить, это что такое масштаб. В JavaScript и практически в любом другом языке программирования ваш код выполняется в рамках заданной области. Эта область определяет, к каким переменным имеет доступ ваш код, как новые переменные будут взаимодействовать с остальной частью вашего кода и некоторые другие вещи. Лучший способ представить область действия — это раздел, который поможет вам отделить разные части кода друг от друга.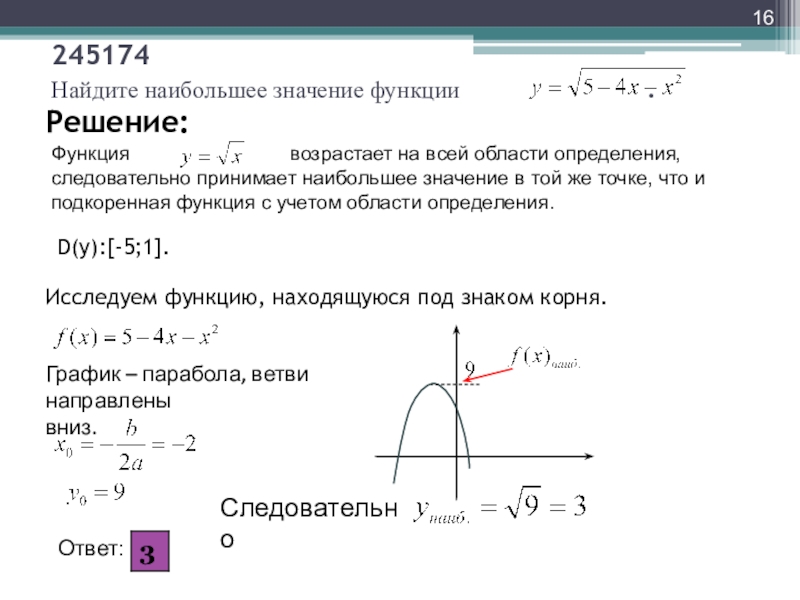

В приведенном выше примере у нас есть простой код, который определяет переменную вне функции и внутри функции. Затем мы записываем обе переменные в консоль как внутри, так и вне функции. Это прекрасно работает внутри функции, но вне функции наш журнал выдает ошибку, поскольку у нас нет доступа к внутренней переменной вне области действия функции.

В этом примере используются две из четырех областей видимости в JavaScript для разделения нашего кода таким образом, чтобы только определенные части кода имели доступ к определенным переменным. Это основная причина существования разных уровней охвата, поэтому давайте сейчас рассмотрим эти разные охваты.

Уровни охвата

Четыре различных уровня охвата:

1. Глобальный охват
2. Объем модуля
3. Блочный прицел
4. Область действия

Может показаться, что это слишком много для отслеживания, но на самом деле вы, вероятно, будете использовать область модуля и блока для 95% всего кода, который вы пишете, поэтому отслеживать его немного легче. Однако это не означает, что вы должны игнорировать другие области видимости, так как важно понимать, как они работают.

Глобальная область действия

Для начала мы поговорим о самой простой области действия, чтобы понять, какую область действия большинство разработчиков используют для всего своего кода, поскольку она просто игнорирует все ограничения, налагаемые другими областями. Чтобы понять глобальную область видимости, представьте, что у меня есть следующий HTML/JS.

Этот простой пример использует глобальную область видимости для определения своих переменных. Глобальная область действия работает так: каждый раз, когда вы определяете переменную на верхнем уровне файла (вне любой функции/фигурных скобок), она считается глобальной областью действия и к ней можно получить доступ ВЕЗДЕ во всем приложении. Этот глобальный доступ поначалу упрощает написание кода, поскольку вам не нужно беспокоиться о том, что переменные блокируются разными областями, но по мере того, как вы начинаете писать более сложный код, управлять этим быстро становится сложно. Эта проблема еще хуже, когда у вас есть несколько файлов.

Как вы можете видеть в приведенном выше примере, мы определили переменную в script-1.js и можем использовать эту переменную в script-2.js . Это потому, что переменная из script-1.js определяется глобально и может использоваться ВСЕГДА в вашем коде. Из-за этой особенности глобальной области видимости я стараюсь никогда не использовать глобальную область видимости ни в одном из своих приложений. Невероятно сложно отслеживать глобальную область действия по мере роста вашего приложения, поэтому я предпочитаю область действия модуля.

Область действия модуля

Область действия модуля очень похожа на глобальную область действия, но с одним небольшим отличием. Второстепенные переменные области доступны только в файле, в котором вы их определяете. Это означает, что их нельзя использовать в других файлах, что идеально, когда вы пытаетесь мысленно отслеживать все. Чтобы войти в область модуля, вам нужно использовать type="module" в тегах скрипта. Это гораздо больше, чем просто изменение области действия, поэтому, если вы не знакомы с модулями ES, вам следует ознакомиться с моим полным руководством по модулям ES.

С помощью этого единственного изменения мы устранили самую большую проблему, связанную с глобальной областью действия переменных, доступной в каждом файле, сохранив при этом преимущества возможности использования переменной в любом месте файла, в котором она определена. Из-за того, что область действия этого модуля является одной из двух областей видимости, которые я использую постоянно.

Область блока

Другая основная область, которую я постоянно использую, — это блочная область. Область блока — одна из самых простых для понимания областей, поскольку она соответствует фигурной скобке {} . По сути, каждый раз, когда у вас есть код внутри фигурных скобок, он считается собственной областью действия блока. Это означает, что такие вещи, как функции, операторы if, циклы for и т. д., создают собственную область действия блока.

В этом примере определяются две отдельные области блока. Каждая область блока определяется как код между фигурными скобками, и каждый блок имеет доступ ко всем переменным, которые находятся между фигурными скобками, кроме 9.0037 NOT в другом наборе фигурных скобок, а также во всех переменных его родительской области.

В нашем случае у нас есть два блока: функция test и оператор if . Наша область test имеет доступ ко всем переменным в функции test , которые не вложены в другой набор фигурных скобок, что означает, что у нее есть доступ к переменной funcVar . Наша тестовая область также будет иметь доступ к любым глобальным/модульным переменным уровня области, поскольку они являются родителями тест прицел.

Наша вторая область — это оператор if , и эта область имеет доступ к ifVar , а также ко всему, к чему имеет доступ область test , поскольку область test является родительской областью области if .

Важный вывод о блочной области: каждый раз, когда у вас есть фигурные скобки, вы создаете новую блочную область, которая имеет доступ ко всем областям, внутри которых она находится, но ни к одной из областей внутри нее. Это внутреннее/внешнее правило на самом деле верно для всех областей. Любая область будет иметь доступ к областям, в которых она находится, но у нее не будет доступа к областям внутри нее.

Вы даже можете добавить фигурные скобки в любом месте вашего кода, чтобы создать область видимости. Это не то, что я делаю часто, но это может быть полезно.

Область действия функции

Последняя область действия — это область действия функции, и мы надеемся, что вам никогда не придется об этом беспокоиться, поскольку она относится к ключевому слову var . Переменные, определенные с помощью ключевого слова var , имеют область действия на уровне функции, а не на уровне блока, что означает, что они заботятся только о фигурных скобках функции.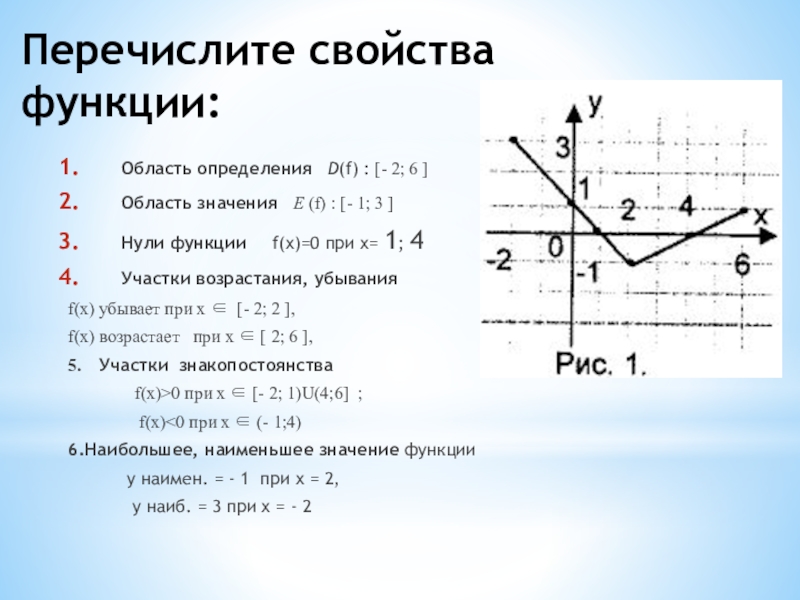

Этот код точно такой же, как код из примера уровня блока, но мы используем var вместо const для определения наших переменных. Вы увидите, что в этом примере наш код будет работать просто отлично, потому что ключевое слово var игнорирует область уровня блока, поэтому даже если ifVar определено в нашем блоке if , это не имеет значения для области действия функции.

Честно говоря, это довольно неинтуитивно, а var как ключевое слово вообще сложно использовать, поэтому я рекомендую никогда не использовать вар . Если вы хотите узнать больше о том, почему мне не нравится var и о различиях между var , let и const , ознакомьтесь с моим полным руководством var vs let vs const.

Несколько переменных с одним и тем же именем

Одна важная вещь, которую нужно понять об этой области видимости, — это то, как она работает, когда у вас есть несколько переменных с одним и тем же именем.

В этом примере у нас есть переменная a , определенная как внутри нашего проверить функцию и внутри нашего блока if . Когда мы выходим из системы и в блоке , если , мы получаем значение и из области , если , а когда мы регистрируем и вне блока , если , мы получаем значение и из области видимости , если . тест прицел.

Основной вывод из этого кода заключается в том, что когда у вас есть две переменные с одинаковыми именами, которые находятся в разных областях, они на самом деле являются двумя совершенно отдельными переменными. Они не имеют ничего общего друг с другом, они никогда не перезаписывают значения друг друга и работают точно так же, как две переменные с разными именами. Единственная разница в том, что если они имеют одно и то же имя, теперь невозможно получить доступ к значению переменной внешней области видимости после доступа к и всегда будут обращаться к самой доступной внутренней переменной области видимости.

Обычно я стараюсь не использовать одинаковые имена переменных при написании кода, но в некоторых случаях это может упростить написание кода, поэтому иногда это необходимо.

Заключение

Хотя наличие четырех разных областей видимости в JavaScript может показаться запутанным, на самом деле все немного проще, поскольку нас интересуют только две из четырех областей видимости. Понимание того, как работают эти области видимости, также имеет решающее значение для написания хорошего чистого кода.

Никто не говорил мне, что Scope и Scope Chain в JavaScript так легко понять | by Divyojyoti Ghosh

Изображение выше создано Divyojyoti Ghosh(me) на сайте www.canva.com с использованием различных элементов, доступных для создания дизайнов.

В области компьютерного программирования область видимости имеет дело с организацией переменных (где находится переменная?) и их присоединением (откуда можно получить доступ к переменной? ).

JavaScript имеет лексическую область видимости , что означает, что размещение блоков и функций в коде управляет областью видимости.

Перед тем, как начать с области действия и цепочки областей действия, нам нужно понять, что область действия и область действия переменной — это разные вещи в JavaScript. Итак, в чем именно разница? Область — это пространство или среда в коде, где была объявлена ​​конкретная переменная. Напротив, область действия переменной — это область в коде, где можно получить доступ к конкретной переменной.

Знание различных прицелов поможет нам лучше понять сам прицел. Есть три типа прицелов —

1. Глобальная область действия
2. Область действия функции
3. Область действия блока

Глобальная область действия

Область действия переменных, объявленных вне какой-либо функции или блока, является глобальной, т. е. к ним можно получить доступ в любом месте кода.

Все три переменные student_name , age и Minimum_marks имеют глобальную область действия и могут быть доступны в любом месте кода, поскольку все они объявлены вне какой-либо функции или блока.

Область действия

Все переменные, объявленные внутри функции, имеют область действия функции, т. е. к ним нельзя получить доступ где-либо за пределами функции. Все переменные, определенные в функции, объявлены ли они с использованием var , const или let , имеют область действия.

В приведенном выше фрагменте кода переменные minimum_marks , min_age_of_senior и max_marks имеют область действия функции, т. е. к ним можно получить доступ только внутри функции.

Область действия блока

Переменные, объявленные с помощью let или const в фигурных скобках { } (кроме функции), имеют область действия блока, т. е. доступ к этим переменным вне блока невозможен. Переменные, объявленные с помощью var в фигурных скобках, не могут быть блочными, т. е. к ним можно получить доступ и за пределами блока.

В приведенном выше фрагменте кода minimum_marks , определенные с помощью var в блоке if, доступны из любого места в коде, кроме maximal_marks , который определен с помощью let, заблокирован, поэтому он выдает ReferenceError, когда он вызывается вне блока.

В строгом режиме функции, объявленные с помощью let или const внутри блока, также являются заблокированными, даже именованные функции (не объявленные с использованием var, let или const) также являются заблокированными в строгом режиме.

В Javascript каждая область действия имеет доступ к переменным и функциям всех предковых/родительских областей. Во время выполнения, если JS-движок сталкивается с переменной, для доступа к переменной и ее значению он сначала ищет в локальной области видимости, если он не находит переменную в локальной области видимости, он ищет переменную в области своего родителя.

Поиск продолжается от одной области до ее родительской области до родительской области своего родителя, пока не будет найдена переменная. Вся эта концепция поиска переменной из внутренней области во внешнюю область известна как цепочка областей видимости. Последняя и самая внешняя область — это глобальная область, которая является конечной родительской областью.

Если переменная не найдена во всей этой цепочке областей видимости, механизм JS выдает ошибку ссылки и объявляет переменную не определенной.

В приведенном выше фрагменте кода последняя строка из Функция getGradYear() выдает ошибку ссылки, так как у функции нет доступа к переменной totalFees . Переменная totalfees отсутствует в локальной области действия функции или в какой-либо родительской функции функции getGradYear() , переменная определяется с помощью let в блоке if и, следовательно, ее область действия заблокирована.

Область блока if и область действия функции getGradYear являются дочерними элементами getDetailsOfStudent() область действия функции.