Свойства и графики тригонометрических функций. Базовый уровень 10 класс онлайн-подготовка на Ростелеком Лицей |
Тригонометрические функции числового аргумента
Основное отличие науки от искусства в том, что результат научного опыта, воспроизведенный разными людьми, будет одинаковым (если соблюдены основные условия проведения такого опыта). Произведение искусства каждый понимает по-своему, и единого правильного мнения о таком произведении быть не может.
Русский язык позволяет нам описать процессы, которые происходят вокруг: птица летит и машет крыльями, дерево согнулось под порывом ветра. Поэт может и более изящно воспользоваться языком: «…летят серебряные птицы, седые птицы – журавли…». Это описание помогает нам воспринимать окружающий мир, вдохновляться ним.
Но для более практичных вопросов такого описания недостаточно. Почему летит птица? Можем ли мы это использовать и построить аппарат для полетов? При каких условиях дерево сломается? Можно ли это предотвратить? Для ответа на эти вопросы нужен другой язык – математический.
Мы строим математическую модель процесса, описываем его на математическом языке. И в дальнейшем эти расчеты позволяют создавать самолеты и строить небоскребы, которые защищены от ураганов и землетрясений.
Множество процессов, которые окружают нас – периодически повторяющиеся. Это и различные колебания, о которых вы знаете из курса физики («Механические колебания», «Механические волны. Звук»), и периодические спады и подъемы в экономике.
Конечно, в реальном мире не существует идеальных периодических процессов. Да, зима наступает каждый год, но мы не можем предсказать заранее, в какой именно день выпадет снег, когда станет холодно и т. д. С другой стороны, зная, что зима все равно наступит, мы покупаем пальто, заготавливаем дрова на даче (не знаем, в какой именно день будем их сжигать, но знаем, что они, скорее всего, пригодятся). Тот же маятник обязательно затухает, если не сообщать ему дополнительную энергию.
Но, как мы уже знаем, точность решения задачи определяется целью.
Чтобы построить математическую модель всех этих повторяющихся событий, нужен определенный инструмент – тригонометрические функции. С этим инструментом мы уже немного знакомы: умеем вычислять значения тригонометрических функций и упрощать выражения, которые их содержат. Но чтобы полноценно использовать тригонометрические функции для построения математической модели периодических процессов, нам еще нужно изучить свойства и графики этих функций, а также научиться решать уравнения и неравенства, которые их содержат.
Об уравнениях речь пойдет позже, а сегодня мы займемся свойствами и графиками тригонометрических функций.
Мы определили тригонометрические функции как функции, которые ставят в соответствие углу поворота координаты (или их отношение) соответствующей точке на окружности (см. рис. 1):
Рис.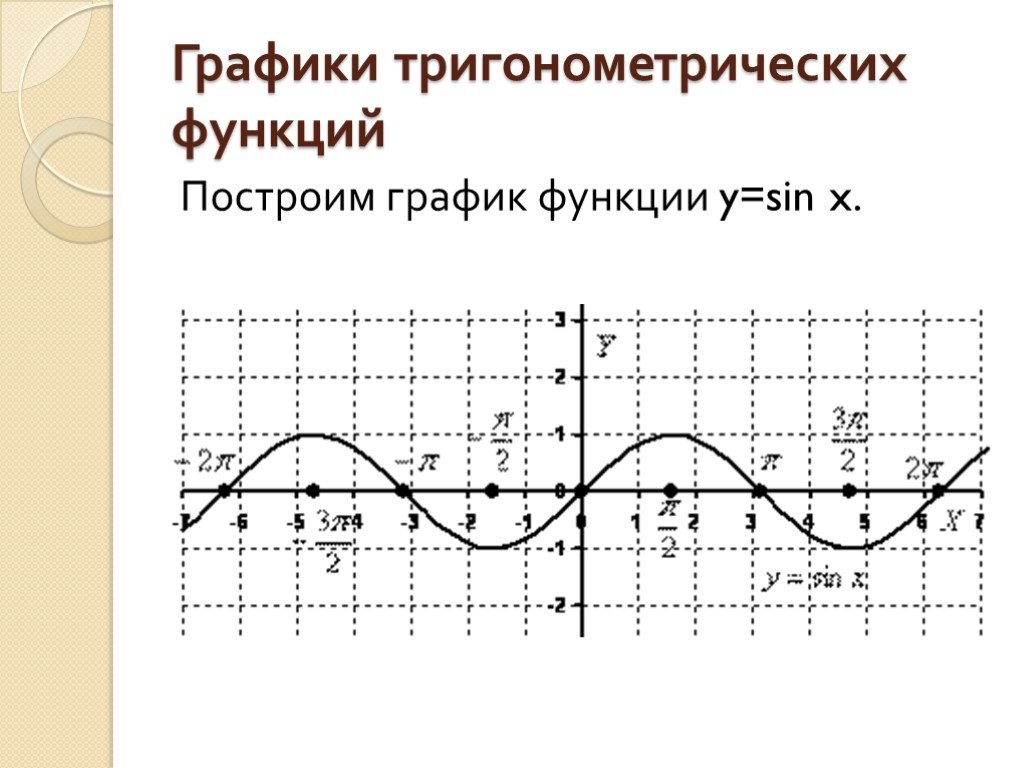
1. Единичная окружность
Понятно, что при повороте на полный оборот значения тригонометрических функций начинают повторяться (мы каждый день наблюдаем это на примере часов: прошло 12 часов, и стрелки снова на своих местах). Поэтому тригонометрические функции будут периодическими – их значения после изменения значения аргумента на определенное число будут повторяться. Периодических функций можно ввести много, самых разных. Мы рассмотрим свойства базовых, с помощью комбинаций которых можно выразить остальные. Звуки – это механические колебания, их вокруг нас великое множество. Но при этом все их с той или иной степенью точности можно математически описать с помощью набора базовых тригонометрических функций.
Мы выделили и изучили свойства некоторых видов функций: линейной, квадратичной, функции квадратного корня и других («Свойства функций. Базовые функции»). Воспользуемся готовой схемой изучения свойств функций для тригонометрических функций:
Правда, есть небольшая загвоздка: мы изучали числовые функции – в них числу ставится в соответствие число.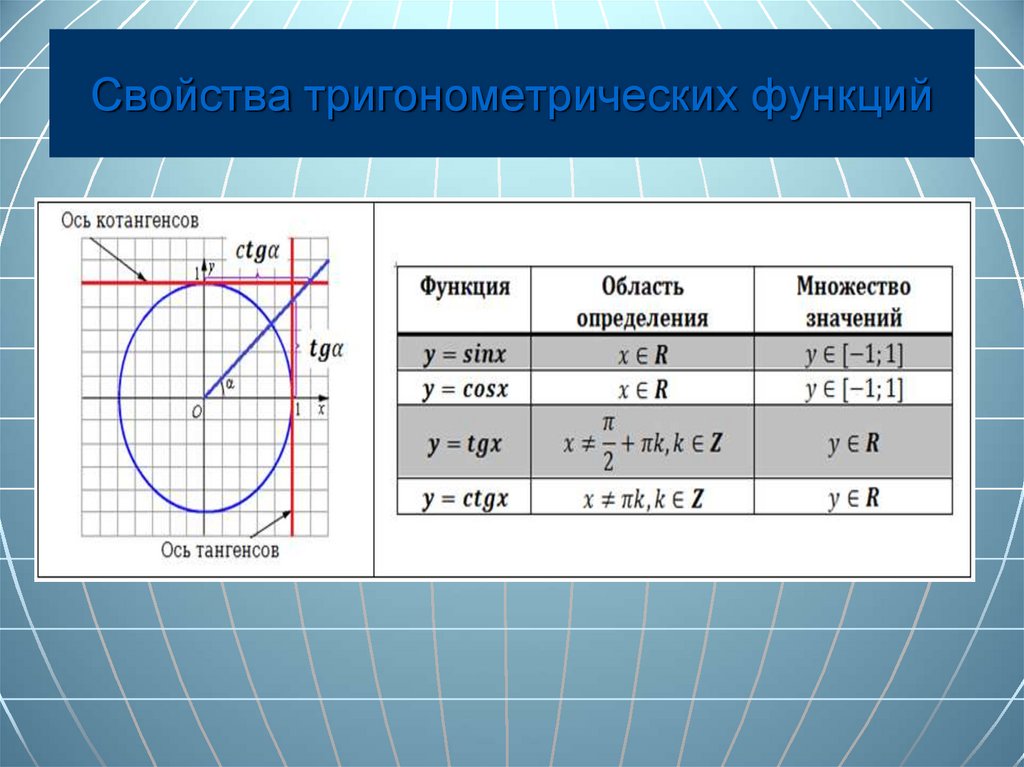
В тригонометрических же функциях мы говорили, что углу ставится в соответствие число. Разрешить эту ситуацию просто: будем брать величину угла, выраженную в радианах. Под записью будем понимать, что числу ставится в соответствие число . Причем так, что значение равно синусу радиан. Например,
Аналогично и для косинуса, тангенса и котангенса.
Как исследовать числовые функции, мы уже знаем. Можно построить их графики и рассмотреть различные характеристики:
- область определений и область значений;
- нули функции, промежутки знакопостоянства;
- промежутки монотонности: возрастания и убывания;
- четность;
- периодичность.
Про четность и периодичность тригонометрических функций, на самом деле, мы уже знаем. Вспомним, что функция называется четной, если для всех ее допустимых аргументов выполняется соотношение:
А для нечетных функций выполняется соотношение:
Мы знаем, что , а .
Соответственно, функция является четной функцией; – нечетной.
Для тангенса и котангенса выполнены следующие соотношения:
Значит, функции и также являются нечетными.
Теперь про периодичность. Вспомним, что функция называется периодической, если для всех ее аргументов выполняется соотношение:
Величина называется периодом функции. Мы знаем соотношения:
Значит, все тригонометрические функции являются периодическими. Причем синус и косинус имеют период , а тангенс и котангенс – период .
Об остальных свойствах и характеристиках тригонометрических функций, а также об их графиках мы поговорим далее в уроке.
Синус и косинус
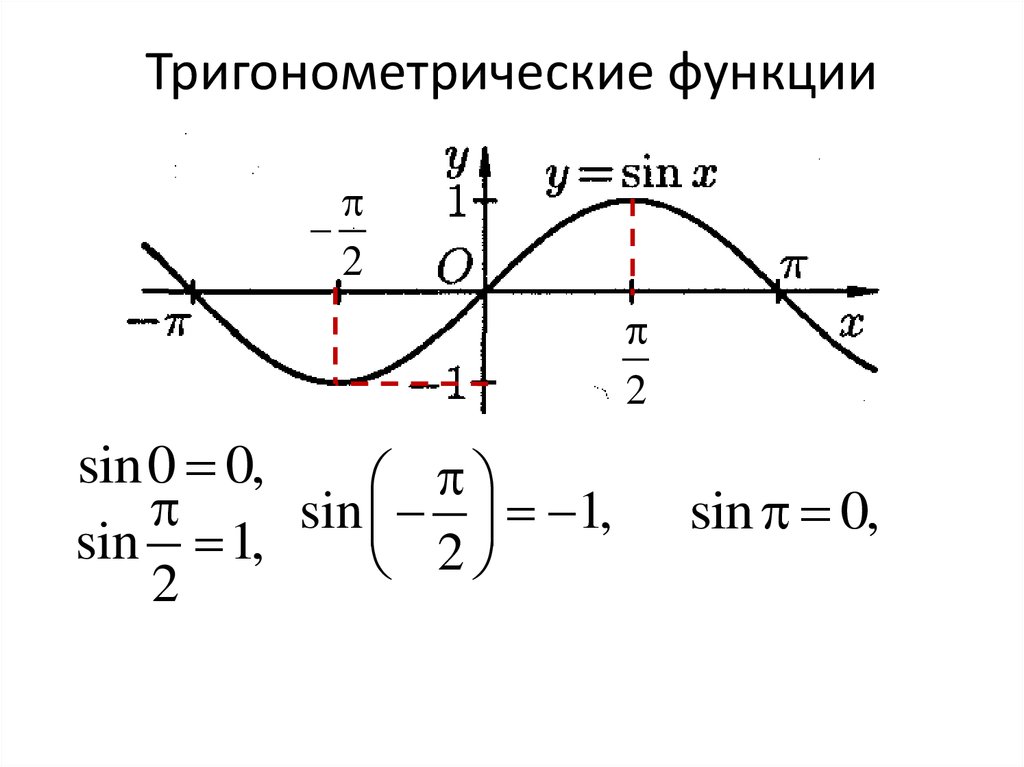
Начнем с построения графика функции синуса:
Мы знаем значения синуса для некоторых углов:
|
Градусы |
|||||
|
Радианы |
|||||
По ним мы можем составить таблицу значений для нашей функции.
Помним, что числовой аргумент функции – это величина угла в радианах. Поэтому получаем следующую таблицу:
Отметим эти точки на графике и соединим плавной линией (см. рис. 2).
Рис. 2. Соединенные точки
Обратите внимание на масштаб оси . Ранее мы изучали такие функции, в которых аргументом удобно было брать целые значения. Поэтому и цену деления было удобно брать целым числом. У тригонометрических же функций мы знаем значения для аргументов, пропорциональных . Поэтому и выбираем соответствующий масштаб.
Далее воспользуемся соотношением:
Его можно получить из формул приведения:
Это соотношение означает, что для аргументов, лежащих слева и справа от на равном расстоянии, значения синусов будут одинаковы. Получаем следующий график (см. рис. 3).
Рис. 3. Полученный график
Теперь воспользуемся тем, что синус – нечетная функция. Графики нечетных функций симметричны относительно начала координат. Отражаем график. Мы получили график функции на промежутке от (см.
рис. 4).
Рис. 4. График функции на промежутке от
Далее пользуемся периодичностью. Период синуса равен , значит, прибавив к аргументу , мы получим те же значения функции. Прибавляя еще или вычитая , мы будем получать те же значения. Наш кусочек функции будет как бы «копироваться» влево и вправо бесконечное количество раз. Полученная линия и будет являться графиком функции (см. рис. 5). Эту кривую еще называют синусоидой.
Рис. 5. График функции
Теперь отметим характеристики и свойства функции.
1. Областью определения являются все действительные числа:
Мы расширили понятие угла так, что его величина может быть любым числом. А величина угла в радианах – и есть аргумент функции.
2. Область значений:
Мы определяли синус как ординату точки на единичной окружности. Соответственно, значения синуса могут лежать только в пределах от до .
3. Нули функции – это решения уравнения .
4. Промежутки знакопостоянства также отметим по графику. От до функция принимает положительные значения; от до – отрицательные. Это же поведение мы видим и на других участках графика. В общем виде:
5. По графику также можно определить промежутки монотонности. От до функция возрастает; от до – убывает. На других участках графика то же самое. Тогда в общем виде:
Теперь перейдем к косинусу. Его график легко построить, воспользовавшись соотношением, которое мы уже сегодня доказывали:
Т. е. график функции совпадает с графиком функции . А этот график мы можем построить с помощью преобразования . Оно соответствует сдвигу графика на единиц влево. Значит, для построения график функции достаточно сдвинуть график синуса на влево.
Рис. 6. График функции
Видим, что область определения и область значений у косинуса такие же, как и у синуса:
А вот нули функции, промежутки знакопостоянства и монотонности сдвинутся вместе с графиком на влево. Нули:
Положительные и отрицательные значения:
Функция возрастает и убывает при:
Тангенс и котангенс
Теперь перейдем к тангенсу и котангенсу. Начнем строить график тангенса по точкам.
|
Радианы |
||||
Соответственно, таблица значений:
Тангенс не определен, ведь , а деление на ноль не определено.
Что же делать? Соединим уже имеющиеся точки и посмотрим, что будет происходить с графиком по мере приближения аргумента к (см. рис. 7).
Рис. 7. Соединенные точки
будет приближаться к , – приближаться к , а значение дроби будет становиться все больше и больше. Т. е. значение тангенса будет все расти и расти. Но график никогда не пересечет прямую , ведь при этом значении аргумента функция не определена. Подобную ситуацию мы видели на графике функции (см. рис. 8).
Рис. 8. График функции
При приближении аргумента к нулю значение функции неограниченно убывало. При этом график не пересекал прямую . Вспомним, что подобная прямая называется асимптотой графика. Соответственно, асимптотой графика будет прямая .
Мы построили часть графика тангенса. Теперь воспользуемся тем, что эта функция нечетная. Значит, график симметричен относительно начала координат. Далее пользуемся периодичностью функции. Период тангенса равен , значения функции будут повторяться через этот промежуток.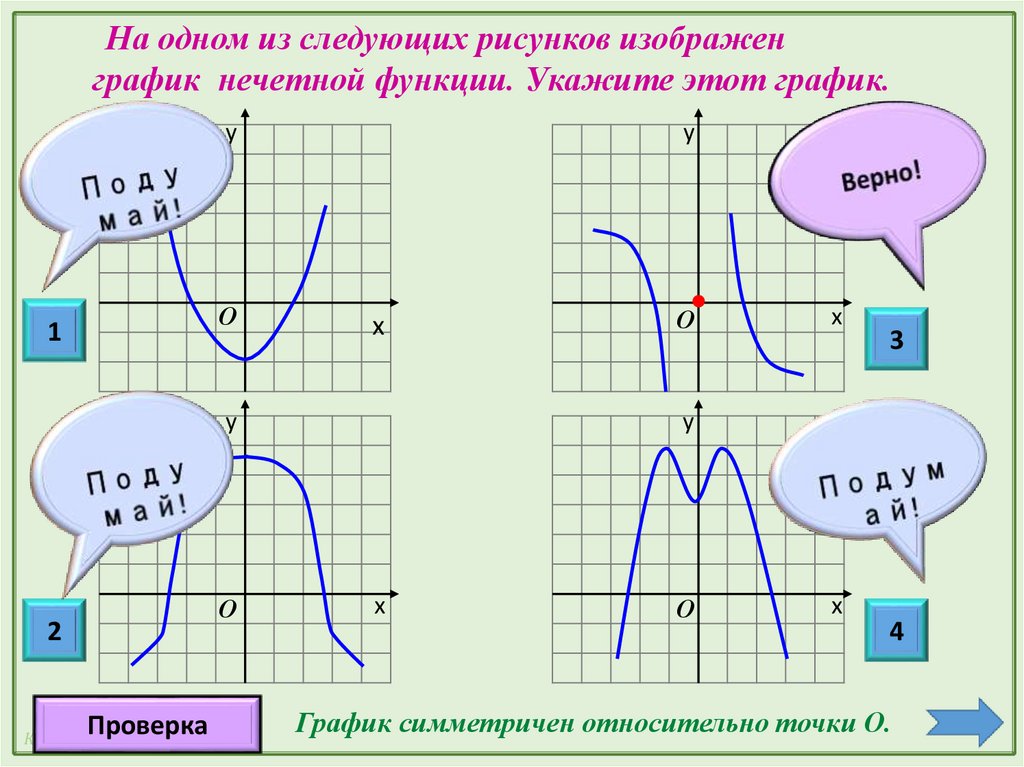
Получили график функции (см. рис. 9).
Рис. 9. График функции
Видим, что этот график имеет множество асимптот, уравнения которых в общем виде можно описать так:
Эти асимптоты разбивают график на отдельные части, которые еще называют ветками тангенса. Ветка, которая проходит через начало координат, называют главной веткой.
По графику определим характеристики функции.
1. Область определения:
2. Область значений:
3. Нули функции: . В общем виде все их можно описать так:
Несложно понять, почему они совпадают с нулями синуса, если вспомнить, что тангенс – отношение синуса и косинуса, а дробь равна только тогда, когда ее числитель равен .
4. В общем виде:
5. На каждой своей ветке функция возрастает:
При этом корректно говорить, что функция возрастает на каждом из этих интервалов. Но нельзя сказать, что она возрастает на всей области определения, ведь при переходе через асимптоту функция меняет значение с положительного на отрицательное.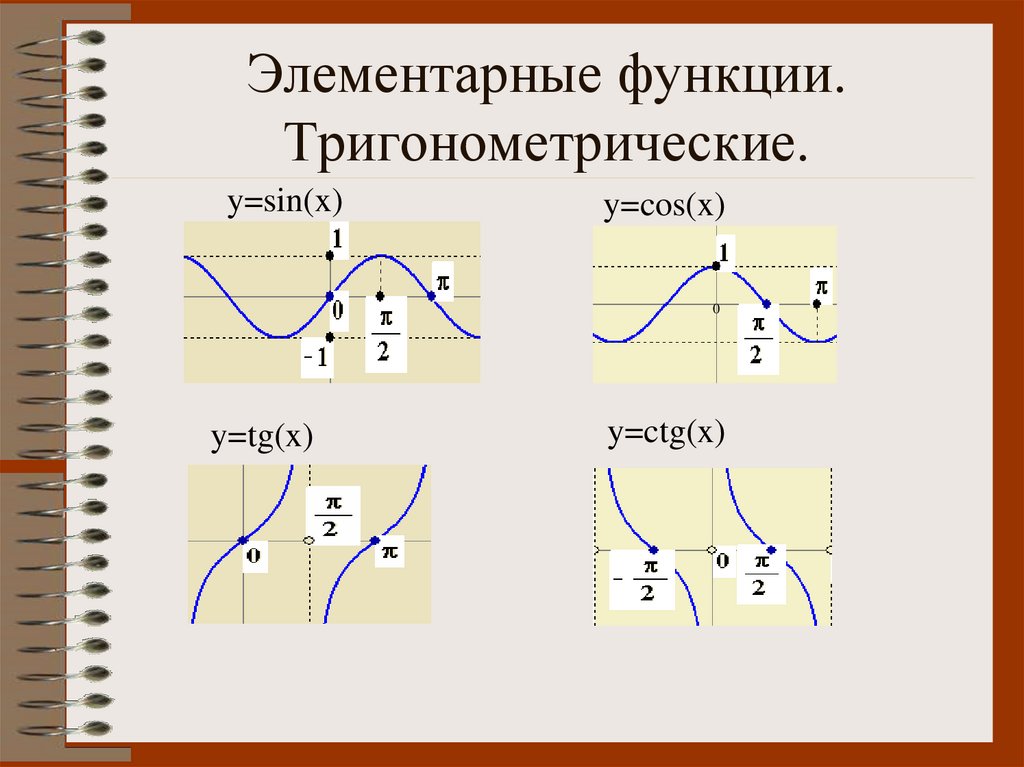
Т. е. значение уменьшается.
Теперь, наконец, рассмотрим функцию . Для ее построения удобно воспользоваться формулой приведения:
Т. е. нам достаточно построить график функции . В этом нам помогут преобразования графиков. Сначала строим – график тангенса отражается симметрично относительно оси . Затем сдвигаем его на влево. Получаем график функции , он же будет графиком функции .
Рис. 10. График функции
Отметим характеристики.
1. Область определения:
2. Область значений:
3. Нули функции (совпадают с нулями косинуса, объясните сами, почему):
4. В общем виде:
5. На каждой своей ветке функция убывает:
Преобразования графиков тригонометрических функций
Мы рассмотрели характеристики и графики тригонометрических функций , , и . Но при моделировании процессов обычно встречаются более сложные функции, например:
Чтобы исследовать подобные функции, достаточно применить преобразования графиков к уже изученным.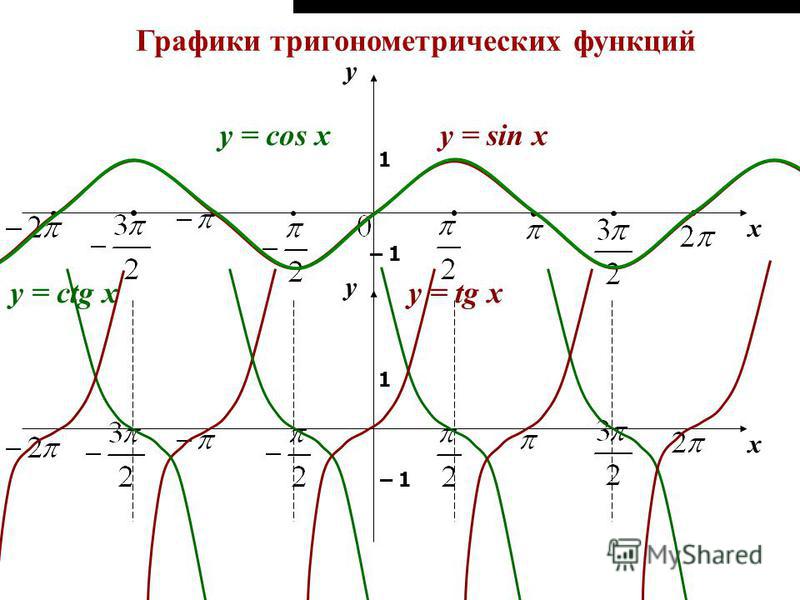
Вспомним эти преобразования (можете пересмотреть соответствующие уроки «Повторение и систематизация курса алгебры 7-9 класса. Функции», «Преобразование графиков функций»).
- Прибавление числа к функции сдвигает график вдоль оси .
- Прибавление числа к аргументу сдвигает график вдоль оси .
- Умножение значения функции на число растягивает или сжимает график вдоль оси . Если , то еще и симметрично отражает график относительно оси .
- Умножение аргумента на число растягивает или сжимает график вдоль оси x. Если , то еще и симметрично отражает график относительно оси .
Соответственно, чтобы построить график функции , необходимо:
1. Построить график функции (см. рис. 11).
Рис. 11. График функции
2. Сжать его вдоль оси в раз, получив график (см. рис. 12).
Рис. 12. График функции
3. Растянуть его вдоль оси (см. рис. 13), а затем симметрично отразить относительно оси .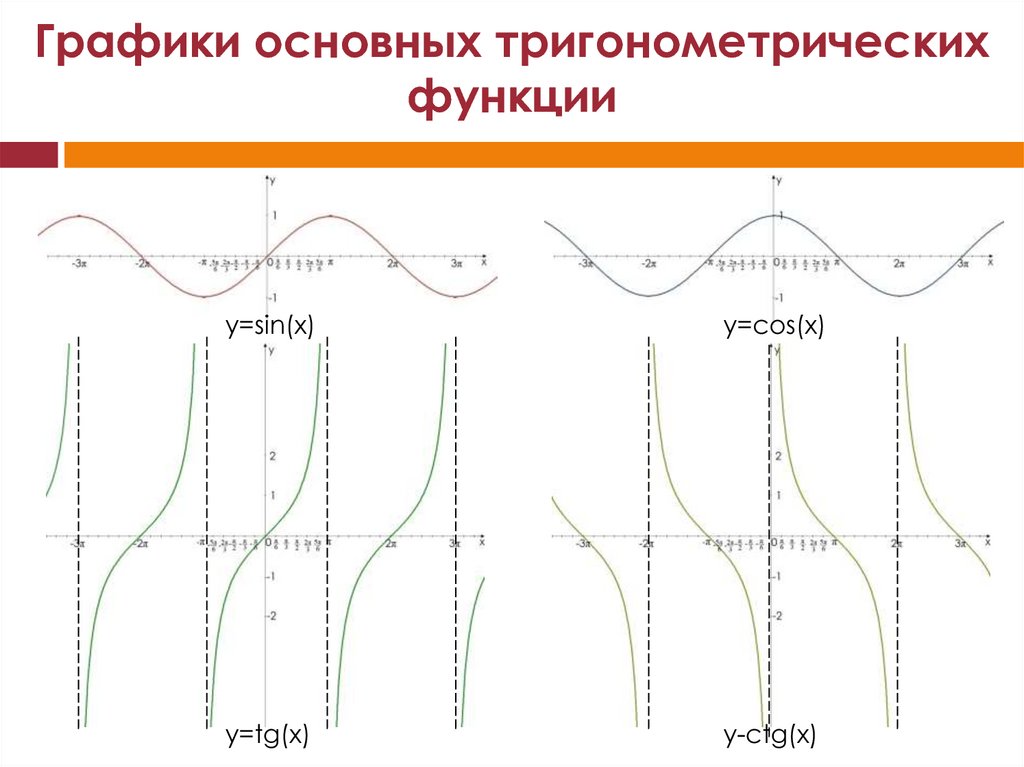
В итоге получим график функции (см. рис. 14).
Рис. 13. График функции
Рис. 14. График функции
По построенному графику функции можно указать все ее свойства. В частности, стоит обратить внимание, что у данной функции изменилась область значений и период по сравнению с функцией . Область значений данной функции: .
Период был , после сжатия вдоль оси он уменьшился в раз:
В общем случае про изменение области значений и периода функций можно сказать следующее.
- При преобразованиях вида и соответствующим образом изменяется область значений: сдвигается на или расширяется/сужается в раз.
- При преобразовании вида период функций увеличивается или уменьшается в раз.
- При преобразовании вида период функции и ее область значений остается прежней.
Итак, применяя различные преобразования графиков, мы можем исследовать тригонометрические функции вида , где – некоторые числа. Аналогично и для косинусов, тангенсов и котангенсов.
Но в математической модели могут встретиться и другие тригонометрические выражения. Например, при колебаниях математического маятника зависимость его скорости от времени выглядит следующим образом:
Тогда выражение для кинетической энергии принимает вид:
Константы и деление на можем объединить в одну положительную константу . Получим функцию кинетической энергии от времени: , где – некоторые числа. Как видите, здесь мы столкнулись с квадратом тригонометрической функции. Как же ее исследовать? Здесь нам поможет известный нам математический прием: свести нашу задачу к той, решение которой мы знаем.
Для начала перейдем к более привычным обозначениям:
Теперь используем формулу понижения степени:
Получаем:
А уже эту функцию мы уже знаем, как исследовать. Здесь нам помогут преобразования графиков. Базовая функция (см. рис. 15):
Рис. 15. График функции
Умножаем аргумент на :
При этом график сожмется вдоль оси в раз (см.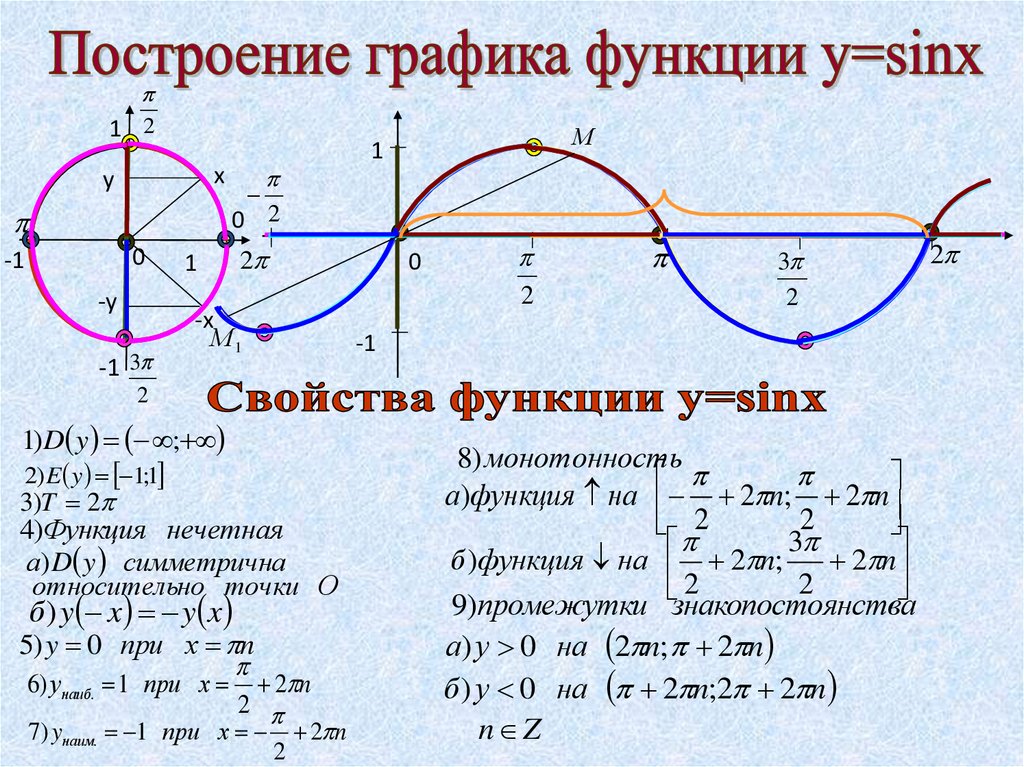
рис. 16).
Рис. 16. График функции
Период функции станет в раз меньше:
Далее умножаем функцию на :
График растягивается вдоль оси в раз и отражается симметрично относительно оси (см. рис. 17).
Рис. 17. График функции
При этом область значений расширяется в раз: было , станет:
И наконец, прибавляем :
График поднимается на (см. рис. 18).
Рис. 18. График функции
Область значений также смещается на :
Таким образом, мы смогли исследовать функцию, содержащую квадрат тригонометрической функции. Посмотрели, какой будет ее область значений и ее период.
Список литературы
- Алимов Ш.А., Колягин Ю.М., Ткачева М.В. Математика. Алгебра и начала математического анализа, геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
- Мордкович А.Г., Семенов П.В. Математика. Алгебра и начала математического анализа, геометрия. 10-11класс.
Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019. - Никольский С.М., Потапов М.К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – АО «Издательство “Просвещение”»
Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru
- Интернет-портал ru.solverbook.com
- Интернет-портал math34.ru
Домашнее задание
- Определить промежутки возрастания (убывания) функции на промежутке .
- Найти множество значений функции , если .
- Построить график функции:
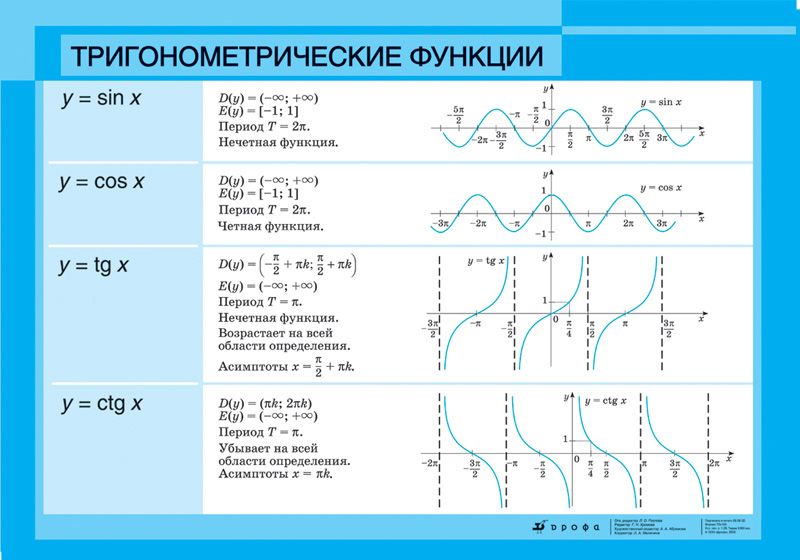
Тригонометрические функции, их свойства и графики.
Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим
функциям присуще понятие периодичности (повторяемости
значений функции при различных значениях
аргумента, отличных друг от друга на
величину периода ,
где Т —
период), поэтому, в список свойств
тригонометрических функций добавлен
пункт «наименьший
положительный период».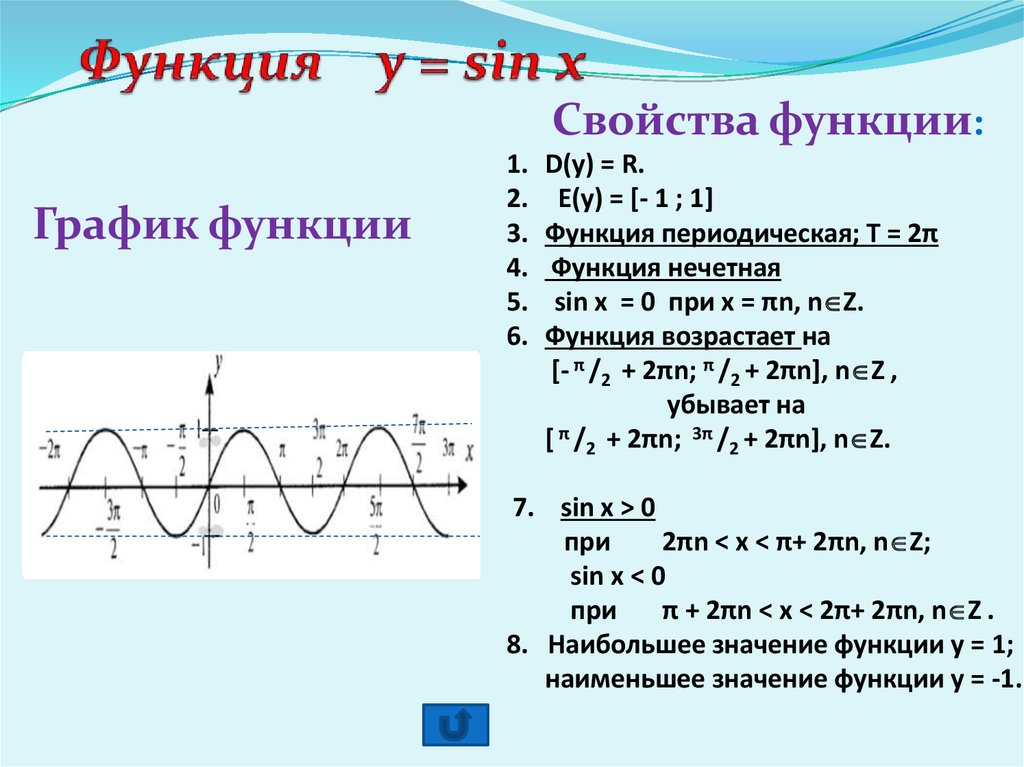
Также для каждой тригонометрической
функции мы укажем значения аргумента,
при которых соответствующая функция
обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
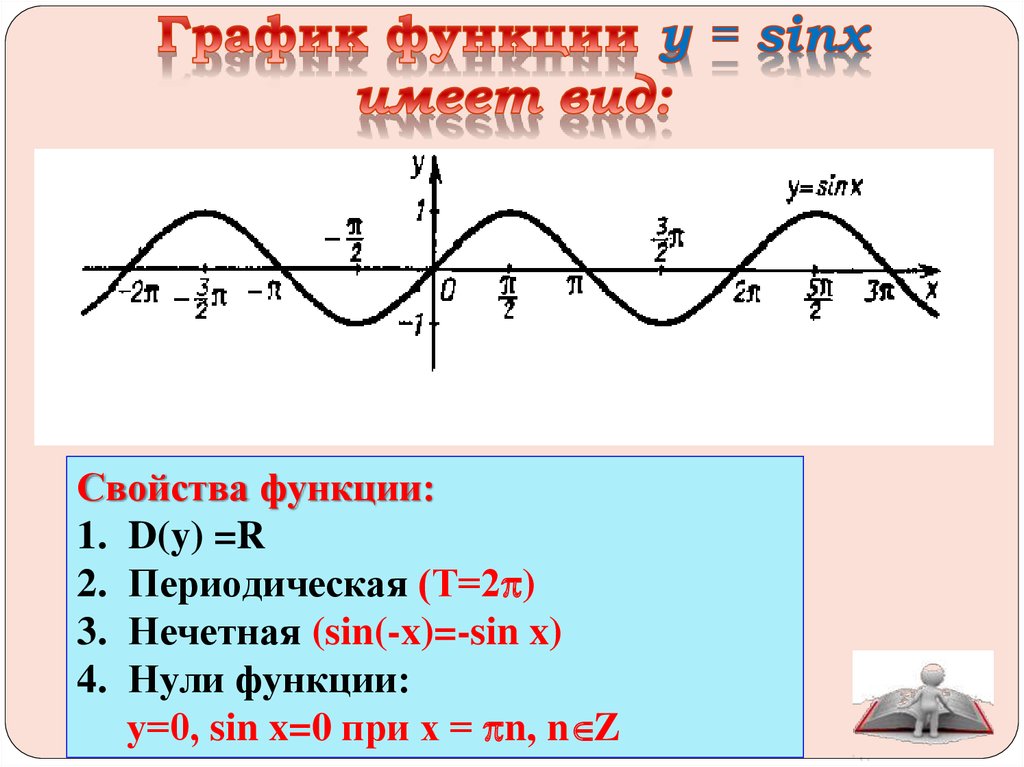
Функция синус y = sin(x).
Изобразим график функции синус, его называют «синусоида».
Свойства функции синус y = sinx.
Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при .
Наименьший положительный период функции синуса равен двум пи: .
Функция обращается в ноль при , где , Z – множество целых чисел.
Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть .
Функция синус — нечетная, так как .
Функция убывает при , возрастает при .
Функция синус имеет локальные максимумы в точках , локальные минимумы в точках .
Функция y = sinx вогнутая при , выпуклая при .
Координаты точек перегиба .
Асимптот нет.
Функция косинус y = cos(x).
График функции косинус (его называют «косинусоида») имеет вид:
Свойства функции косинус y = cosx.
Область определения функции косинус: .
Наименьший положительный период функции y = cosx равен двум пи: .
Функция обращается в ноль при , где , Z – множество целых чисел.
Область значений функции косинус представляет интервал от минус единицы до единицы включительно: .
Функция косинус — четная, так как .
Функция убывает при , возрастает при .
Функция y = cosx имеет локальные максимумы в точках , локальные минимумы в точках .
Функция вогнутая при , выпуклая при .
Координаты точек перегиба .
Асимптот нет.
Функция тангенс y = tg(x).
График функции тангенс (его называют «тангенсоида») имеет вид:
Свойства функции тангенс y = tgx.
Область определения функции тангенс: , где , Z – множество целых чисел. Поведение функции y = tgx на границе области определения Следовательно, прямые , где , являются вертикальными асимптотами.
Наименьший положительный период функции тангенс .
Функция обращается в ноль при , где , Z – множество целых чисел.
Область значений функции y = tgx: .
Функция тангенс — нечетная, так как .
Функция возрастает при .
Функция вогнутая при , выпуклая при .
Координаты точек перегиба .
Наклонных и горизонтальных асимптот нет.
Функция котангенс y = ctg(x).
Изобразим график функции котангенс (его называют «котангенсоида»):
Свойства функции котангенс y = ctgx.
Область определения функции котангенс: , где , Z – множество целых чисел. Поведение на границе области определения Следовательно, прямые , где являются вертикальными асимптотами.
Наименьший положительный период функции y = ctgx равен пи: .
Функция обращается в ноль при , где , Z – множество целых чисел.
Область значений функции котангенс: .
Функция нечетная, так как .
Функция y = ctgx убывает при .
Функция котангенс вогнутая при , выпуклая при .
Координаты точек перегиба .
Наклонных и горизонтальных асимптот нет.
5.2: Свойства графиков тригонометрических функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3336
- Майкл Коррал
- Schoolcraft College
В разделе 5.
1 мы видели, как графики тригонометрических функций повторяются через каждые \(2\pi \) радиан. В этом разделе мы обсудим это и другие свойства графиков, особенно для синусоидальных функций (синуса и косинуса).
Во-первых, напомним, что область определения функции \(f(x) \) — это множество всех чисел \(x \), для которых функция определена. Например, областью определения \(f(x) = \sin\;x\) является множество всех действительных чисел, тогда как областью определения \(f(x) = \tan\;x\) является множество все действительные числа, кроме \(x=\pm\,\frac{\pi}{2} \), \(\pm\,\frac{3\pi}{2} \), \(\pm\,\ frac{5\pi}{2} \), \(… \). диапазон функции \(f(x)\) — это набор всех значений, которые \(f(x)\) могут принимать в своей области определения. Например, диапазон \(f(x)=\sin\;x\) — это набор всех действительных чисел между \(-1 \) и \(1 \) (т. е. интервал \([-1, 1]\)), тогда как диапазон \(f(x) = \tan\;x \) представляет собой множество всех действительных чисел, как мы можем видеть из их графиков.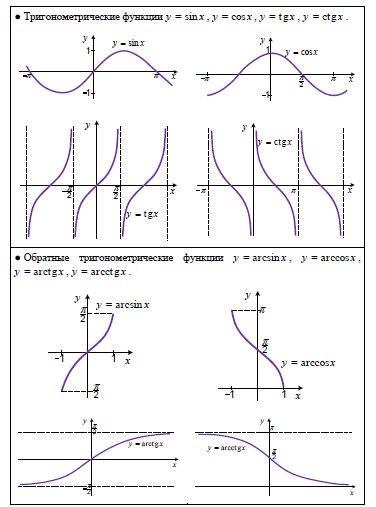
Функция \(f(x)\) является периодической , если существует число \(p>0\) такое, что \(x+p\) находится в области определения \(f(x)\) всякий раз, когда \(x \) есть, и если выполняется следующее соотношение:
\[\label{eqn:periodic} f(x+p) ~=~ f(x) \quad\text{для всех \(x\)} \]
Может быть много чисел \(p \), которые удовлетворяют вышеуказанным требованиям. Если существует наименьшее такое число \(p\), то мы называем это число периодом функции \(f(x)\).
Пример \(\PageIndex{1}\)
Функции \(\sin\;x \), \(\cos\;x \), \(\csc\;x \) и \(\sec \;x \) имеют одинаковый период: \(2\pi\) радиан. В разделе 5.1 мы видели, что графики \(y=\tan\;x \) и \(y=\cot\;x \) повторяются каждые \(2\pi \) радиан, но они также повторяются каждые \(\ пи\) радиан. Таким образом, функции \(\tan\;x \) и \(\cot\;x \) имеют период \(\pi \) радиан.
Пример \(\PageIndex{2}\)
Каков период \(f(x)=\sin\;2x\,\)?
Решение
График \(y=\sin\;2x \) показан на рисунке \(\PageIndex{1}\) вместе с графиком \(y=\sin\;x \) для сравнение на интервале \([0,2\pi] \).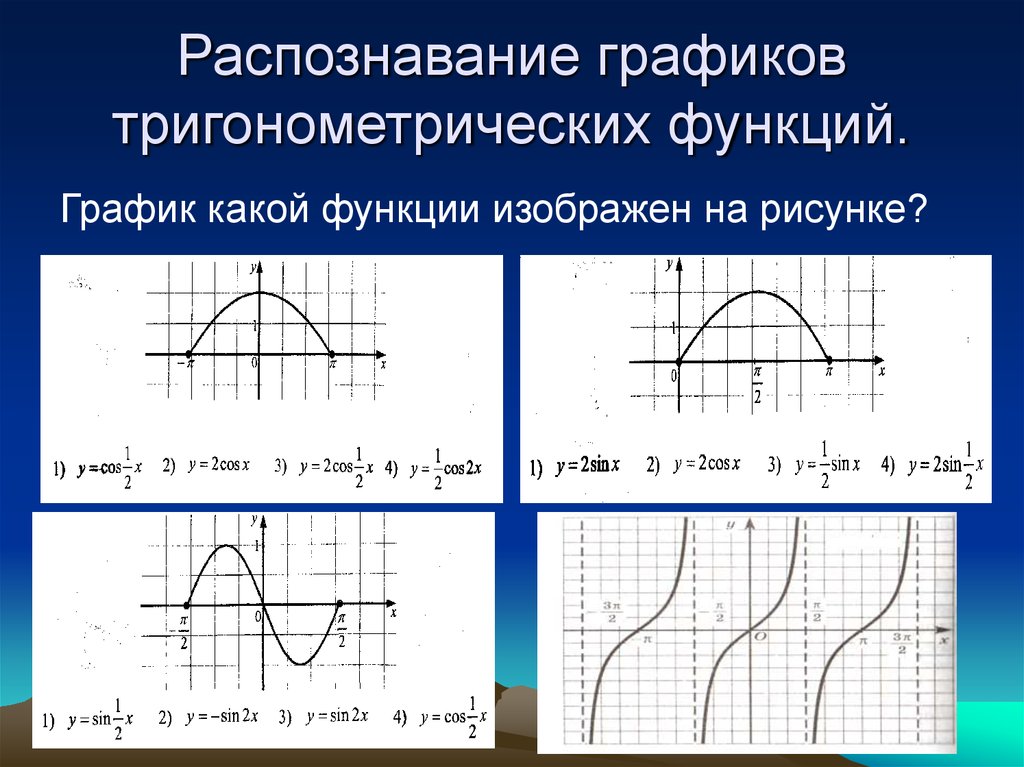
Обратите внимание, что \(\sin\;2x \) «работает в два раза быстрее», чем \(\sin\;x \).
Например, для \(x \) от \(0 \) до \(\frac{\pi}{2 } \), \(\sin\;x \) переходит из \(0 \) в \(1 \), но \(\sin\;2x\) может переходить из \(0 \) в \( 1 \) быстрее, как раз через интервал \([0,\frac{\pi}{4}] \). В то время как \(\sin\;x\) требуется полное \(2\pi \) радиан, чтобы пройти все цикл (самая большая часть графика, которая не повторяется), \(\sin\;2x \) проходит весь цикл всего за \(\pi \) радиан. Таким образом, период \(\sin\;2x\) равен \(\pi \) радианам.
В приведенном выше примере использовался график \(\sin\;2x \), но период можно найти аналитически. Поскольку \(\sin\;x \) имеет период \(2\pi \), мы знаем, что \(\sin\;(x+2\pi) = \sin\;x \) для всех \(x \ ). Поскольку \(2x\) является числом для всех \(x\), это означает, в частности, что \(\sin\;(2x+2\pi) = \sin\;2x\) для всех \(x \) . Теперь определите \(f(x)=\sin\;2x \).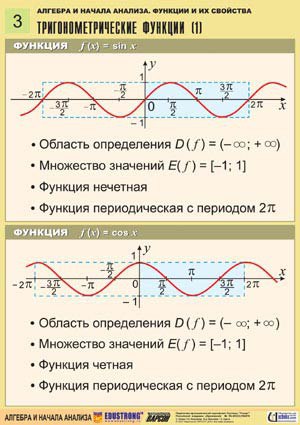
Затем
\[\nonumber \begin{align*}
f(x+\pi) ~&=~ \sin\;2\,(x+\pi)\\ \nonumber
&=~ \sin\;(2x+2 \pi)\\ \nonumber
&=~ \sin\;2x \quad\text{(как показано выше)}\\ \nonumber
&=~ f(x)
\end{align*} \nonumber \ ]
для всех \(x\), поэтому период \(p\) \(\sin\;2x\) равен не более \(\pi \), согласно нашему определению периода. Мы должны показать, что \(p>0 \) не может быть меньше, чем \(\pi \). Для этого воспользуемся доказательством от противного . То есть предположим, что \(0 \[\nonumber \begin{align*} для всех \(х\). Поскольку любое число \(u \) может быть записано как \(2x \) для некоторого \(x \) (т. Вышеупомянутое может показаться большой работой, чтобы доказать что-то, что было визуально очевидно из графика (и интуитивно очевидно из идеи «вдвое быстрее»). К счастью, нам не нужно выполнять всю эту работу для каждой функции. , поскольку аналогичный аргумент работает, когда \(\sin\;2x \) заменяется на \(\sin\;\omega x \) для любого положительного действительного числа \(\omega\): вместо деления \(2\pi \) на \(2\), чтобы получить период, делим на \(\omega \). Рассуждение работает и для других тригонометрических функций. Таким образом, мы получаем: Для любого числа \(\omega >0\): \[\nonumber \begin{alignat*}{4} Если \(\omega < 0 \), то используйте \(\sin\;(-A) = -\sin\;A \) и \(\cos\;(-A) = \cos\;A \ ) (например, \(\sin\;(-3x) = -\sin\;3x\)). Период \(y=\cos\;3x \) равен \(\frac{2\pi}{3} \), а период \(y= \cos\;\frac{1}{2}x \) равно \(4\pi \). Графики обеих функций показаны на рис. 5.2.2: Мы знаем, что \(\;-1 \le \sin\;x \le 1\; \) и \(\;-1 \le \cos\;x \le 1\; \) для все \(х\). Таким образом, для константы \(A \ne 0 \), \[ -|А| ~\le~ A\,\sin\;x ~\le~ |A| \quad\text{и}\quad для всех \(х\). В этом случае мы называем \(|A|\) амплитудой функций \(y=A\,\sin\;x\) и \(y=A\,\cos\;x\). В общем случае амплитуда периодической кривой \(f(x)\) равна половине разности наибольшего и наименьшего значений, которые может принимать \(f(x)\): \[ \text{Амплитуда \(f(x)\)} ~=~ \frac{\text{(максимум \(f(x)\))} ~-~ \text{(минимум \( f(x)\))}}{2} Другими словами, амплитуда — это расстояние от вершины или низа кривой до горизонтальной линии, которая делит кривую пополам, как показано на рис. Не все периодические кривые имеют амплитуду. Например, \(\tan\;x \) не имеет ни максимума, ни минимума, поэтому его амплитуда не определена. Точно так же \(\cot\;x\), \(\csc\;x\) и \(\sec\;x \) не имеют амплитуды. Поскольку амплитуда включает вертикальные расстояния, она не влияет на период функции, и наоборот. Найдите амплитуду и период \(y=3\,\cos\;2x \). Амплитуда равна \(|3| = 3 \), а период равен \(\frac{2\pi}{2}=\pi \). График показан на рисунке 5.2.4: Найдите амплитуду и период \(y=2 — 3\,\sin\;\frac{2\pi}{3}x \). Амплитуда \(-3\,\sin\;\frac{2\pi}{3}x \) равна \(|-3| =3 \). Добавление \(2 \) к этой функции для получения функции \(y=2 — 3\,\sin\;\frac{2\pi}{3}x \) не меняет амплитуду, даже если она изменяется максимум и минимум. До сих пор в наших примерах мы могли определить амплитуды синусоидальных кривых довольно легко Это не всегда будет так Найдите амплитуду и период \(y=3\,\sin\;x + 4\,\cos\;x \). Это иногда называют комбинацией синусоидальной кривой, поскольку она представляет собой сумму двух таких кривых. Период по-прежнему легко определить: поскольку \(\sin\;x\) и \(\cos\;x\) повторяются каждые \(2\pi \) радиан, то и комбинация \(3\, \sin\;x + 4\,\cos\;x \). Таким образом, \(y=3\,\sin\;x + 4\,\cos\;x \) имеет период \(2\pi \). График показывает, что амплитуда равна \(5 \), что может быть не сразу очевидным, просто взглянув на то, как определена функция. На самом деле, определение \(y=3\,\sin\;x + 4\,\cos\;x\) может натолкнуть вас на мысль, что амплитуда равна \(7\), поскольку наибольшая, чем \(3 \,\sin\;x \) может быть равно \(3\), а наибольшее значение \(4\,\cos\;x \) может быть равно \(4 \), так что наибольшая их сумма может быть равно \(3+4=7\). Однако \(3\,\sin\;x\) никогда не может равняться \(3\) для того же \(x\), что делает \(4\,\cos\;x\) равным \(4\ ) (почему?). Существует полезный метод (который мы обсудим далее в главе 6) для демонстрации того, что амплитуда \(y=3\,\sin\;x + 4\,\cos\;x\) равна \(5 \). Пусть \(\theta \) будет углом, показанным в прямоугольном треугольнике \[\nonumber \begin{align*} Таким образом, \(|y| = |5\, \sin\;(x+\theta)| = |5|\,\cdot\,|\sin\;(x+\theta)| \le (5)(1) = 5 \), поэтому амплитуда \( y=3\,\sin\;x + 4\,\cos\;x\) есть \(5\). Как правило, комбинация синусов и косинусов будет иметь период, равный наименьшему общему кратному периодов складываемых синусов и косинусов. В примере 5.9, \(\sin\;x \) и \(\cos\;x \) имеют период \(2\pi \), поэтому наименьшее общее кратное (которое всегда является целым числом , кратным ) равно \(1 \,\cdot\, 2\pi = 2\pi \). Найдите период \(y=\cos\;6x + \sin\;4x \). Период \(\cos\;6x \) равен \(\frac{2\pi}{6} = \frac{\pi}{3} \), а период \(\ sin\;4x\) равен \(\frac{2\pi}{4} = \frac{\pi}{2} \). Наименьшее общее кратное для \(\frac{\pi}{3} \) и \(\frac{\pi}{2} \) равно \(\pi\): \[\nonumber \begin{alignat*}{4} Таким образом, период \ (y=\cos\;6x + \sin\;4x \) равно \(\pi \). А как насчет амплитуды? К сожалению, мы не можем использовать технику из примера 5.9, так как мы берем косинус и синус одного и того же угла; мы берем косинус \(6x\), но синус \(4x\). При этом из графика видно, что максимум близок к \(2\), а минимум близок к \(-2\). В главе 6 мы опишем, как использовать программу численных вычислений, чтобы показать, что максимум и минимум равны \(\pm\,1,} \). Обратите внимание, что этот метод работает только тогда, когда угол \(\omega x \) одинаков как для синуса, так и для косинуса. Мы видели, как добавление константы к функции сдвигает весь график по вертикали. Теперь мы увидим, как сдвинуть весь график периодической кривой по горизонтали. Рассмотрим функцию вида \(y=A\,\sin\;\omega x \), где \(A \) и \(\omega \) — ненулевые константы. Для простоты будем считать, что \(A > 0 \) и \(\ omega > 0 \) (в общем случае любой из них может быть отрицательным). Теперь рассмотрим функцию \(y=A\,\sin\;(\omega x — \phi)\), где \(\phi \) — некоторая постоянный. Амплитуда по-прежнему \(A \), а период по-прежнему \(\frac{2\pi}{\omega} \), так как \(\omega x — \phi \) является линейной функцией \(x \). Кроме того, мы знаем, что синусоидальная функция проходит полный цикл, когда ее угол изменяется от \(0\) до \(2\pi \). Здесь мы берем синус угла \(\omega x — \phi \). Так как \(\omega x — \phi \) переходит от \(0 \) к \(2\pi \), весь цикл функции \(y=A\,\sin\;(\omega x — \phi) \) будет прослежена. Этот цикл начинается, когда \[\nonumber \omega x — \phi ~=~ 0 \quad \Rightarrow\quad x ~=~ \frac{\phi}{\omega} \nonumber \] и заканчивается, когда \[\nonumber \omega x — \phi ~=~ 2\pi \quad \Rightarrow\quad x ~=~ \frac{2\pi}{\omega}\;+\;\frac{\phi}{ \омега}~. \номер\] Таким образом, график \(y=A\,\sin\;(\omega x — \phi) \) есть просто график \(y=A\,\sin\;\omega x\), сдвинутый по горизонтали на \(\frac{\phi}{\omega} \), как на рис. Фазовый сдвиг определяется аналогично для других тригонометрических функций. Найдите амплитуду, период и фазовый сдвиг \(y=3\,\cos\;(2x — \pi) \). Амплитуда равна \(3 \), период равен \(\frac{2\pi}{2} = \pi \), фазовый сдвиг равен \(\frac{\pi}{2 } \). График показан на рис. 5.2.12: Обратите внимание, что график такой же, как график \(y=3\,\cos\;2x \), сдвинутый вправо на \(\frac{\pi}{2} \), количество фазы сдвиг. Найдите амплитуду, период и фазовый сдвиг \(y=-2\,\sin\;\left(3x + \frac{\pi}{2} \верно) \). Амплитуда равна \(2 \), период равен \(\frac{2\pi}{3} \), фазовый сдвиг равен \(\frac{-\frac{\pi}{ 2}}{3} = -\frac{\pi}{6} \). Ниже приводится сводка свойств тригонометрических графов: Для любых констант \(A \ne 0 \), \(\omega \ne 0 \) и \(\phi\): \[\nonumber \begin{align*} Эта страница под названием 5. Тригонометрические функции повторяются каждые 2 π радиан. В этом разделе мы обсудим это и другие свойства графиков, особенно для синусоидальных функций (синуса и косинуса). Во-первых, напомним, что домен функции f ( x ) представляет собой набор всех чисел x , для которых функция определена. Например, домен f ( x ) = sin x представляет собой набор всех действительных чисел, тогда как домен f ( x ) = tan x представляет собой набор всех действительных чисел. числа, кроме x = ± \(\frac{π}{2}\) , ± \(\frac{3π}{2}\), ± \(\frac{5π}{2}\),.. .. Диапазон функции f ( x ) — это набор всех значений, которые f ( x ) могут принимать в своей области. Функция f ( x ) является периодической если существует число p > 0 такое, что x + p находится в области f ( x ) всякий раз, когда есть x , и если выполняется следующее соотношение: $$f (x+ p) = ф (х) \; \text{для всех} \; Икс \; \; \; \; (1)$$ Может быть много чисел p , которые удовлетворяют вышеуказанным требованиям. Если существует наименьшее такое число p , то мы называем это число периодом функции f ( x ). 9Пример 1 Графики y = tan x и y = cot x повторяются каждые 2 π радиана, но они также повторяются каждые π радиана. Пример 2 Каков период f ( x ) = sin 2 x ? Решение : График y = sin 2 x показан на рис. 5.2.1 вместе с графиком y = sin x для сравнения на интервале [0,2 № ]. Обратите внимание, что sin 2 x «идет в два раза быстрее», чем sin x . Например, для x от 0 до \(\frac{π}{2}\) , sin x переходит от 0 к 1, но sin 2 x может переходить от 0 к 1 быстрее, как раз за интервал [0, \(\frac{π}{4}\)]. В то время как sin x занимает полные 2 π радиана, чтобы пройти через все цикла (самая большая часть графика, которая не повторяется), sin 2 x проходит весь цикл всего за π радиана. . Таким образом, период sin 2 x равен π радиан. В приведенном выше примере использовался график sin 2 x , но период можно найти аналитически. $$f(x+π) = sin 2(x+π)$$
$$= грех (2x+2π)$$
$$= грех 2x \; \text{ как показано выше}$$
$$= f(x) $$ для всех x , поэтому период p sin 2 x равен больше всего π , согласно нашему определению периода. Мы должны показать, что p > 0 не может быть меньше, чем π . Для этого воспользуемся доказательством от противного . То есть предположим, что 0 < p < π , затем покажем, что это приводит к некоторому противоречию и, следовательно, не может быть истинным. Итак, предположим, что 0 < p < π . $$sin 2x = f(x)$$
$$= f(x+p) (\text{ так как} \; p \text{ период} \; f(x))$$
$$= грех 2(х + р)$$
$$= sin (2x + 2p)$$ для всех x . Поскольку любое число u может быть записано как 2 х для некоторых х (т. е. u = 2( u /2)), это означает, что sin u = sin ( u + 2 p ) для всех вещественных чисел u , а значит период sin x максимально 2 p . Это противоречие. Почему? Потому что период sin x равен 2 π > 2 p . Следовательно, период p sin 2 x не может быть меньше π , поэтому период должен быть равен π . Вышеизложенное может показаться большой работой, чтобы доказать что-то, что было визуально очевидно из графика (и интуитивно очевидно из идеи «вдвое быстрее»). К счастью, нам не нужно выполнять всю эту работу для каждой функции, так как аналогичный аргумент работает, когда sin 2 x заменяется на sin ωx для любого положительного действительного числа ω : вместо деления 2 π на 2, чтобы получить период, разделите на ω . Для любого числа ω > 0: Если ω < 0, то используйте sin (− A ) = −sin A и cos (− A ) = cos A (например, sin (−3 x ) = −sin 3 x ). Пример 3 Период y = cos 3 x равен \(\frac{2π}{3}\) и период y = cos \(\frac{1}{2}\) x равно 4 π . Графики обеих функций показаны на рисунке 2: Мы знаем, что −1 ≤ sin x ≤ 1 и −1 ≤ cos x ≤ 1 для всех x . −| А | ≤ A sin x ≤ | А | и −| А | ≤ A cos x ≤ | А | для всех x . В этом случае мы называем | А | амплитуда функций y = A sin x и y = A cos x . В общем случае амплитуда периодической кривой f ( x ) составляет половину разности наибольшего и наименьшего значений, которые может принимать f ( x ): $$\text{Амплитуда}\ ; f(x) = \frac{(\text{максимум} f (x)) − (\text{минимум} f (x))}{2}$$ Другими словами, амплитуда – это расстояние от верхней или нижней части кривой до горизонтальной линии, которая делит кривую пополам, как показано на рис. 3. Не все периодические кривые имеют амплитуду. Например, tan x не имеет ни максимума, ни минимума, поэтому его амплитуда не определена. Пример 4 Найдите амплитуду и период y = 3 cos 2 x . Решение : Амплитуда |3| = 3, а период равен \(\frac{2π}{2}\) = π . График показан на рисунке 4: Пример 5 Найдите амплитуду и период y = 2−3 sin \(\frac{2π}{3}x\). Решение : Амплитуда −3 sin \(\frac{2π}{3}x\) равна |−3| = 3. Добавление 2 к этой функции для получения функции y = 2 − 3 sin \(\frac{2π}{3}x\) не меняет амплитуду, хотя и изменяет максимум и минимум. Он просто сдвигает весь график вверх на 2. Итак, в этом случае у нас есть $$\text{Амплитуда} = \frac{\text{max} — \text{min}}{2} = \frac{5 — (-1)}{2} = \frac{6}{2 } = 3$$ Период равен \(\frac{2π}{\frac{2π}{3}}x\) = 3. Пример 6 Найти амплитуда и период y = 2 sin ( x 2 ). Решение : Это не периодическая функция, поскольку угол, синус которого мы берем, x 2 , не равен линейная функция x , т.е. не имеет вида x + b для некоторых констант a и b . Вспомните, как мы утверждали, что sin 2 x «вдвое быстрее», чем sin x , так что его период равен π вместо 2 π . Можем ли мы сказать, что sin ( x 2 ) в несколько постоянных раз быстрее, чем sin x ? Нет. На самом деле мы видим, что «скорость» кривой продолжает увеличиваться до x становится больше, поскольку x 2 растет с переменной скоростью, а не с постоянной скоростью. Это можно увидеть на графике y = 2 sin ( x 2 ), показанном на рисунке 6. Обратите внимание, как кривая «ускоряется» по мере того, как x становится больше, создавая «волны» все уже и уже. Таким образом, y = 2 sin ( x 2 ) не имеет периода. Несмотря на это, оказывается, что функция имеет амплитуду, а именно 2. Чтобы понять почему, заметим, что, поскольку |sin 92)| ≤ 2 • 1 = 2 .$$ В упражнениях вам будет предложено найти значения x такие, что 2 sin ( x 2 ) достигает максимального значения 2 и минимального значения -2. Таким образом, амплитуда действительно равна 2. Примечание. Эта кривая по-прежнему синусоидальна, несмотря на то, что она не является периодической, поскольку общая форма по-прежнему напоминает «синусоиду», хотя и с переменным числом циклов . До сих пор в наших примерах мы могли довольно легко определить амплитуды синусоидальных кривых. Так будет не всегда. Пример 7 Найдите амплитуду и период y = 3 sin x +4 cos x . Решение : Это иногда называют комбинацией синусоидальной кривой, поскольку она представляет собой сумму двух таких кривых. Период по-прежнему легко определить: поскольку sin x и cos x повторяются каждые 2 π радиан, то и комбинация 3 sin x +4 cos x повторяется. Таким образом, y = 3 sin x +4 cos x имеет период 2 π . Мы можем видеть это на графике, показанном на рисунке 7: График предполагает, что амплитуда равна 5, что может быть неочевидно сразу, если просто посмотреть, как определена функция. На самом деле, определение y = 3 sin x +4 cos x может навести вас на мысль, что амплитуда равна 7, поскольку наибольшее значение, которое может быть при 3 sin x , равно 3, а наибольшее значение, которое может иметь 4 cos x может быть равно 4, так что наибольшая их сумма может быть 3 + 4 = 7. Однако 3 sin x никогда не может равняться 3 для того же x , что делает 4 cos x равным 4. Существует полезный способ показать, что амплитуда y = 3 sin x +4 cos x равна 5. Пусть θ будет углом, показанным в прямоугольном треугольнике на рис. 5.2.8. Тогда cos θ = \(\frac{3}{5}\) и sin θ = \(\frac{4}{5}\) . Мы можем использовать это следующим образом: $$y = 3 sin x + 4 cos x$$
$$= 5(\frac{3}{5}sin x + \frac{4}{5}cos x)$$
$$= 5(cos θ sin x + sin θ cos x)$$
$$= 5 sin (x+θ) \; \text{ (по формуле сложения синусов)} $$ Таким образом, |y| = |5 sin ( x + θ )| = |5| • |sin ( x + θ )| ≤ (5)(1) = 5, поэтому амплитуда y = 3 sin x +4 cos x равна 5. В общем случае комбинация синусов и косинусов будет иметь период, равный наименьшее общее кратное периодов синусов и косинусов. В примере 7 sin x и cos x имеют период 2 π , поэтому наименьшее общее кратное (которое всегда является целым числом , кратным ) равно 1 • 2 π = 2 π . Пример 8 Найдите период y = cos 6 x +sin 4 x . Решение : Период cos 6 x равно \(\frac{2π}{6}\) = \(\frac{π}{3}\), а период sin 4 x равен \(\frac{2π}{4}\) = \ (\ гидроразрыва {π} {2} \). Наименьшее общее кратное для \(\frac{π}{3}\) и \(\frac{π}{2}\) равно π: Таким образом, период y = cos 6 x + sin 4 x равно π . Мы можем видеть это на его графике на рисунке 9: А как насчет амплитуды? К сожалению, мы не можем использовать технику из примера 7, так как мы не берем косинус и синус одного и того же угла; мы берем косинус 6 x , но синус 4 x . Обобщающий пример 7, выражение формы 92}\). Обратите внимание, что этот метод работает только тогда, когда угол ωx одинаков как в синусоидальной, так и в косинусной форме. Мы видели, как добавление константы к функции сдвигает весь график по вертикали. Теперь мы увидим, как сдвинуть весь график периодической кривой по горизонтали. Рассмотрим функцию вида y = A sin ωx , где A и ω — ненулевые константы. Для простоты будем считать, что А > 0 и ω > 0 (в общем случае любой из них может быть отрицательным). Тогда амплитуда равна A , а период равен \(\frac{2π}{ω}\) . График показан на рисунке 10. Теперь рассмотрим функцию y = A sin ( ωx − φ ), где φ — некоторая константа. Амплитуда по-прежнему A , а период по-прежнему \(\frac{2π}{ω}\) , поскольку ωx − φ является линейной функцией x . $$ωx−\phi = 0 ⇒ x = \frac{\phi}{ω}$$ , и заканчивается, когда $$ωx−\phi = 2π ⇒ x = \frac{2π }{ω} + \frac{\phi}{ω}$$ Таким образом, график y = A sin ( ωx − φ ) — это просто график y = A sin ωx , сдвинутый по горизонтали на \(\frac{\phi}{ω}\), как на рисунке 11. График сдвинут вправо, когда φ > 0, и влево, когда φ < 0. Величина сдвига \(\frac{\phi}{ω}\) называется фазовым сдвигом графика. Фазовый сдвиг определяется аналогично для других тригонометрических функций. Пример 9 Найдите амплитуду, период и фазовый сдвиг y = 3 cos (2 x − π ). Решение : Амплитуда равна 3, период \(\frac{2π}{2}\) = π, а фазовый сдвиг равен \(\frac{π}{2}\). График показан на рисунке 12: Обратите внимание, что график такой же, как график y = 3 cos 2 x , сдвинутый вправо на \(\frac{π}{2}\), величина фазового сдвига. Пример 10 Найдите амплитуду, период и фазовый сдвиг y = −2 sin \(\left(3x + \frac{π}{2} \right)\). Решение : Амплитуда равна 2, период равен \(\frac{2π}{3}\), фазовый сдвиг равен \(\frac{-\frac{π}{2}}{3} \) = -\(\frac{π}{6}\) . Обратите внимание на отрицательный знак фазового сдвига, поскольку 3 x + π = 3 x −(− π ) имеет вид ωx − φ . График показан на рисунке 13: В технике говорят, что две периодические функции с одинаковым периодом равны вне фазы , если их фазовые сдвиги различаются.
\sin\;2x ~&=~ f(x)\\ \nonumber
&=~ f(x+p) \quad\text{(так как \(p \ ) является периодом \(f(x)\))}\\ \nonumber
&=~ \sin\;2(x+p)\\ \nonumber
&=~ \sin\;(2x+2p)
\конец{выравнивание*} \номер \]
е. \(u = 2(u/2)\)), это означает, что \(\sin\;u = \sin\;(u+2p)\) для всех действительных чисел \(u\), и, следовательно, период \(\sin\;x \) максимально равен \(2p \). Это противоречие. Почему? Потому что период \(\sin\;x\) равен \(2\pi > 2p\). Следовательно, период \(p \) функции \(\sin\;2x \) не может быть меньше \(\pi \), поэтому период должен быть равен \(\pi \).
\sin\;\omega x ~~&\text{имеет точку}~~ \frac{ 2\pi}{\omega}
\qquad\quad&\csc\;\omega x ~~&\text{имеет точку}~~ \frac{2\pi}{\omega}\\ \nonumber
\cos\ ;\omega x ~~&\text{имеет точку}~~ \frac{2\pi}{\omega}
\qquad\quad&\sec\;\omega x ~~&\text{имеет точку}~~ \ frac{2\pi}{\omega}\\ \nonumber
\tan\;\omega x ~~&\text{имеет период}~~ \frac{\pi}{\omega}
\qquad\quad&\cot \;\omega x ~~&\text{имеет точку}~~ \frac{\pi}{\omega}
\end{alignat*} \nonumber \]
Пример \(\PageIndex{3}\)
-|A| ~\le~ A\,\cos\;x ~\le~ |A|
\номер\]
\номер\]
5.2.3. Пример \(\PageIndex{4}\)
Решение
Пример \(\PageIndex{5}\)
Решение
Он просто сдвигает весь график вверх на \(2\). Итак, в данном случае у нас 92 ) \) достигает максимального значения \(2\) и минимального значения \(-2\). Таким образом, амплитуда действительно равна \(2\).
Примечание: эта кривая по-прежнему синусоидальна, несмотря на то, что она не является периодической, поскольку общая форма по-прежнему является формой «синусоидальной волны», хотя и с переменным числом циклов . Пример \(\PageIndex{7}\)
Решение
Мы можем видеть это на графике, показанном на рисунке 5.2.7:
на рис. 5.2.8. Затем \(\cos\;\theta = \frac{3}{5} \) и \(\sin\;\theta = \frac{4}{5} \). Мы можем использовать это следующим образом:
y ~&=~ 3\,\sin\;x ~+~ 4\,\cos\;x\\ \nonumber
& =~ 5\,\left( \tfrac{3}{5}\,\sin\;x ~+~ \tfrac{4}{5}\,\cos\;x \right)\\ \nonumber
&=~ 5\,( \cos\;\theta\;\sin\;x ~+~ \sin\;\theta\;\cos\;x )\\ \nonumber
&=~ 5\,\ sin\;(x+\theta)\quad\text{(по формуле сложения синуса)}
\end{align*} \nonumber \]
2.8 Пример \(\PageIndex{8}\)
Решение
1 \;\cdot\; \tfrac{\pi}{3} ~&=~ \tfrac{\pi}{3} \quad\quad\quad
&1 \;&\cdot\; \tfrac{\pi}{2} ~&=~ \tfrac{\pi}{2}\\ \nonumber
2 \;\cdot\; \tfrac{\pi}{3} ~&=~ \tfrac{2\pi}{3} \quad\quad\quad
&2 \;&\cdot\; \tfrac{\pi}{2} ~&=~ \pi\\ \nonumber
3 \;\cdot\; \tfrac{\pi}{3} ~&=~ \pi \quad\quad\quad &{} &{}\\ \nonumber
\end{alignat*} \nonumber \]
Это видно из его графика на рис. 5.2.9.:
Тогда амплитуда равна \(A \), а период равен \(\frac{2\pi}{\omega} \). График показан на рисунке 5.2.10.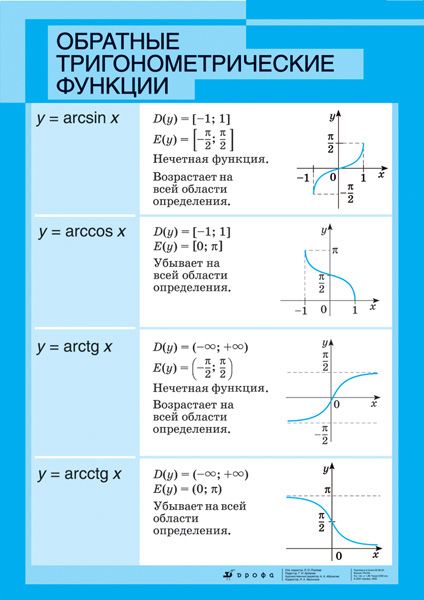
5.2.11. График сдвигается вправо, когда \(\phi >0 \), и влево, когда \(\phi <0 \). Величина \(\frac{\phi}{\omega} \) сдвига называется фазовый сдвиг графика. Пример \(\PageIndex{9}\)
Решение
Пример \(\PageIndex{10}\)
Решение
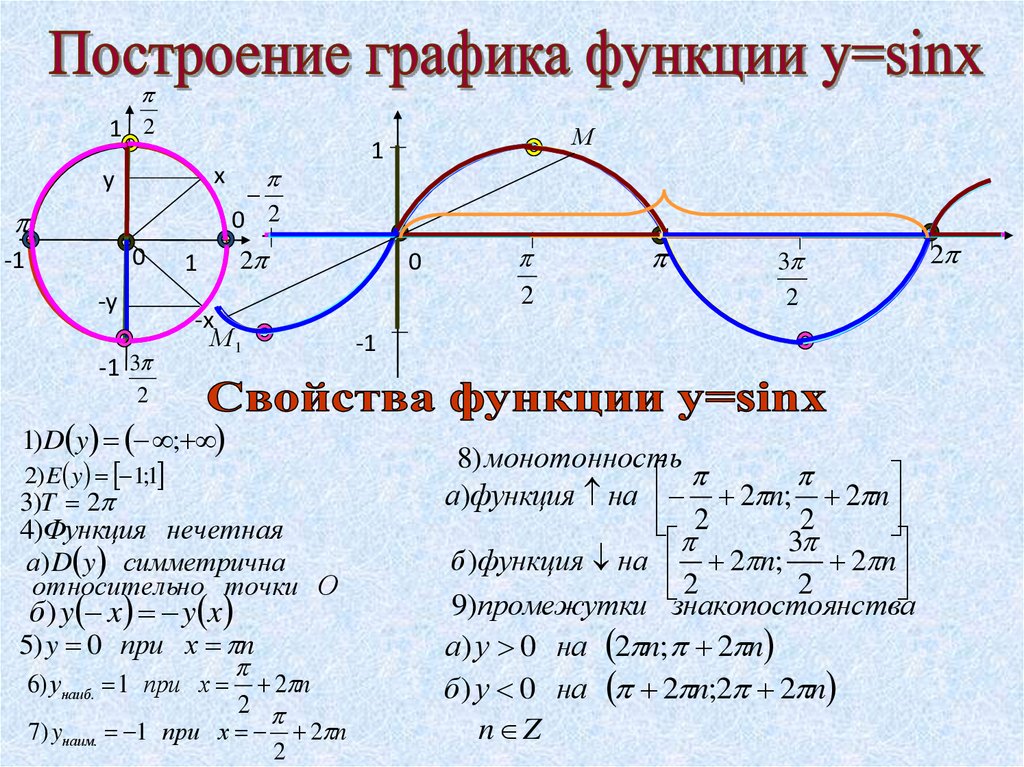Обратите внимание на отрицательный знак фазового сдвига, поскольку \(3x+\pi=3x-(-\pi)\) имеет вид \(\omega x — \phi\). График показан на рисунке 5.2.13: 9\circ\)) не совпадает по фазе, и \(\sin\;x \) можно сказать, что отстает от \(\sin\;\left( x — \frac{\pi}{6} \right) \ ) на \(\frac{\pi}{6} \) радиан, а \(\sin\;\left( x — \frac{\pi}{6} \right) \) отведения \( \sin \;x \) на \(\frac{\pi}{6} \) радиан. Периодические функции с одинаковым периодом и одинаковым фазовым сдвигом равны в фазе .
y = A\,\sin\;(\omega x — \phi) ~~&\text{имеет амплитуду \(|A| \), период \(\ tfrac{2\pi}{\omega} \), и фазовый сдвиг
\(\tfrac{\phi}{\omega}\)}\\ \nonumber
y = A\,\cos\;(\omega x — \phi) ~~&\text{имеет амплитуду \(|A| \), период \(\tfrac{2\pi}{\omega} \) и фазовый сдвиг
\(\tfrac{\phi}{ \omega}\)}\\ \nonumber
y = A\,\tan\;(\omega x — \phi) ~~&\text{имеет неопределенную амплитуду, период \(\tfrac{\pi}{\omega } \), и фазовый сдвиг
\(\tfrac{\phi}{\omega}\)}\\ \nonumber
y = A\,\csc\;(\omega x — \phi) ~~&\text{имеет неопределенную амплитуду, период \(\tfrac{2\pi}{\omega} \) и фазовый сдвиг
\ (\tfrac{\phi}{\omega}\)}\\ \nonumber
y = A\,\sec\;(\omega x — \phi) ~~&\text{имеет неопределенную амплитуду, период \(\ tfrac{2\pi}{\omega} \), и фазовый сдвиг
\(\tfrac{\phi}{\omega}\)}\\ \nonumber
y = A\,\cot\;(\omega x — \phi) ~~&\text{имеет неопределенную амплитуду, период \(\tfrac{\pi}{\omega} \) и фазовый сдвиг
\(\tfrac{\phi}{\omega}\)}
\end{align*} \nonumber \]
2: Свойства графиков тригонометрических функций распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом посредством исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
mecmath.net/trig/index.html Свойства графиков тригонометрических функций ‹ OpenCurriculum
Цели статьи
Например, диапазон f ( x ) = sin x представляет собой набор всех действительных чисел между -1 и 1 (т.е. интервал [-1,1]), тогда как диапазон f ( x ) = tan x — это множество всех действительных чисел, как видно из их графиков.
Таким образом, функции tan x и cot x имеют период π радиан.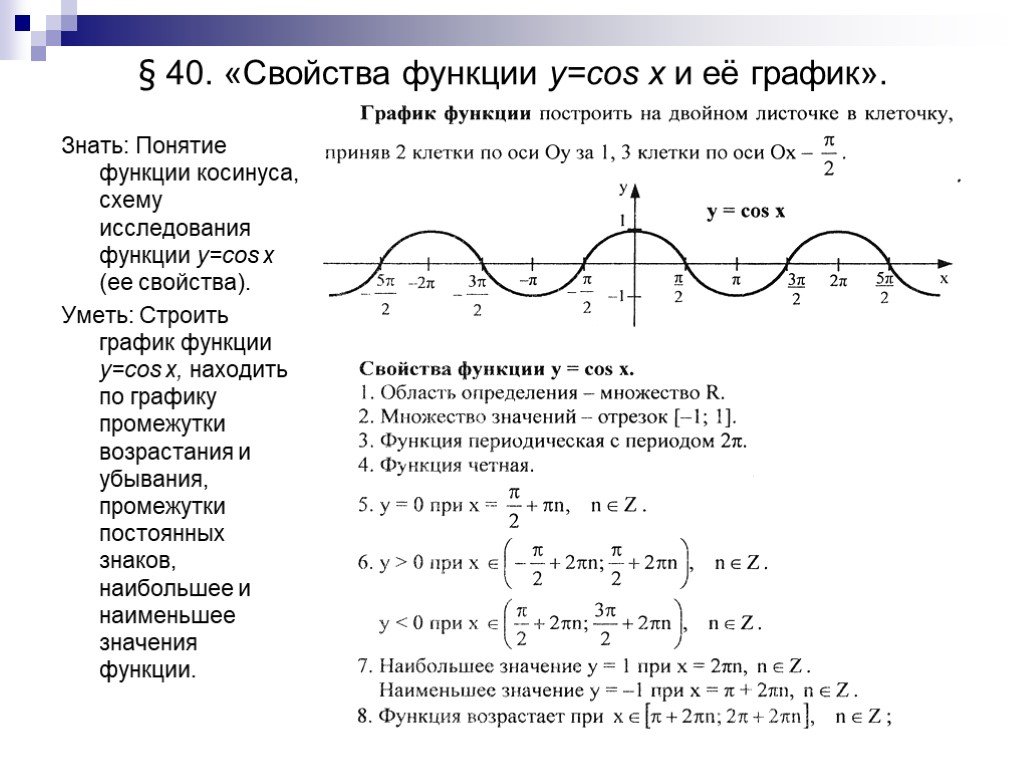
Поскольку sin x имеет период 2 π ,1 мы знаем, что sin ( x +2 π ) = sin x для всех x . Поскольку 2 x является числом для всех x , это означает, в частности, что sin (2 x +2 π = sin 2 x для всех x . Теперь определим f (3 ) = sin 2 x . Тогда
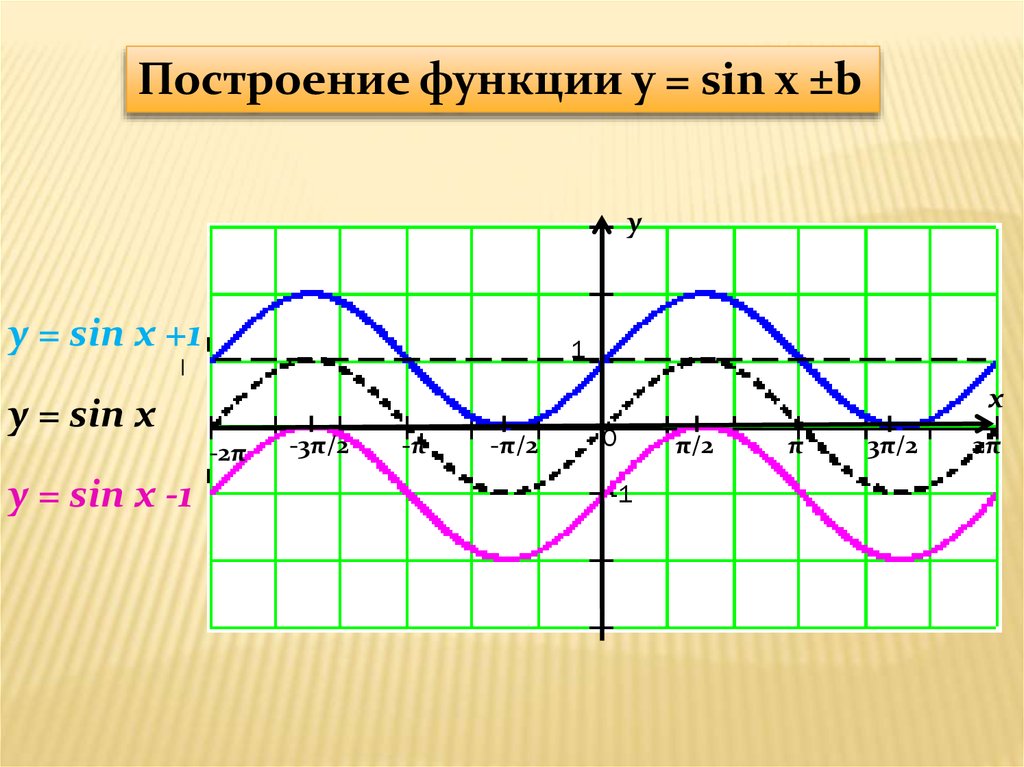Тогда 0 < 2 p < 2 π , и, следовательно,
И этот аргумент работает и для других тригонометрических функций. Таким образом, получаем: $$sin ωx \text{ имеет период} \frac{2π}{ω}$$ $$csc ωx \text{ имеет период} \frac{2π}{ω}$$ $$cos ωx \text{ имеет период} \frac{2π}{ω}$$ $$sec ωx \text{ имеет период} \frac{2π}{ω}$$ $$tan ωx \text{ имеет период} \frac{π}{ω}$$ $$ cot ωx \text{ имеет период} \frac{π}{ω}$$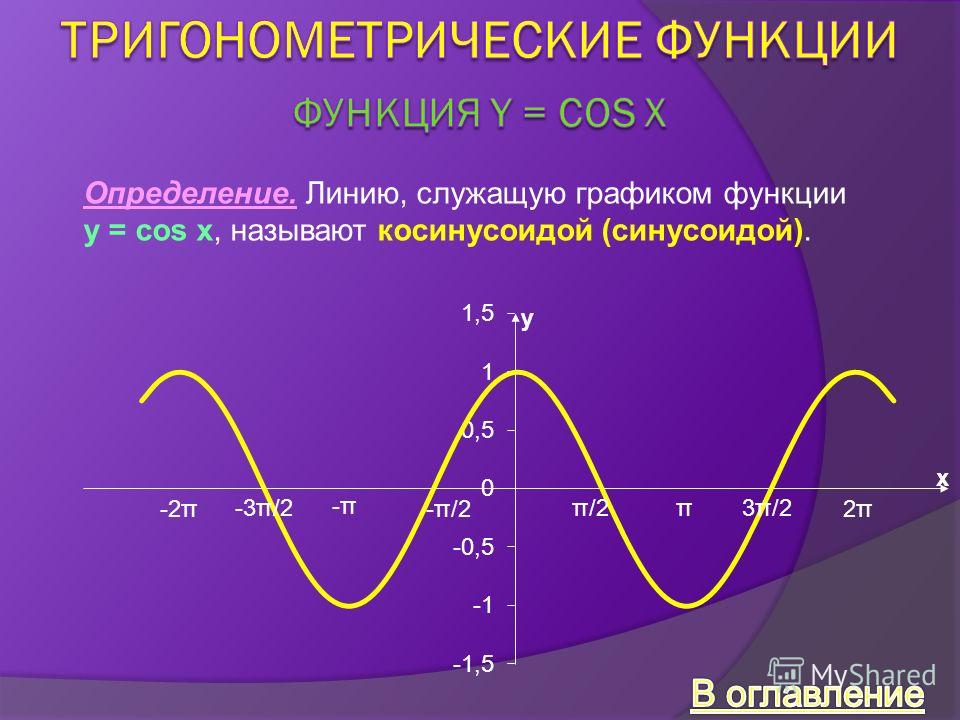 
Таким образом, для константы A \(\ne\) 0,
Точно так же cot x , csc x и sec x не имеют амплитуды. Поскольку амплитуда включает вертикальные расстояния, она не влияет на период функции, и наоборот.
График показан на рисунке 5:
(почему?).
$$\frac{π}{3} = \frac {π}{3}$$ $$\frac{π}{2} = \frac{π}{2}$$ $$\frac{π}{3} = \frac{2π {3}$$ $$\frac{π}{2} = π$$ $$\frac{π}{3} = π$$ $$\frac{π}{ 3} = π$$ 
В этом случае из графика видно, что максимум близок к 2, а минимум близок к -2.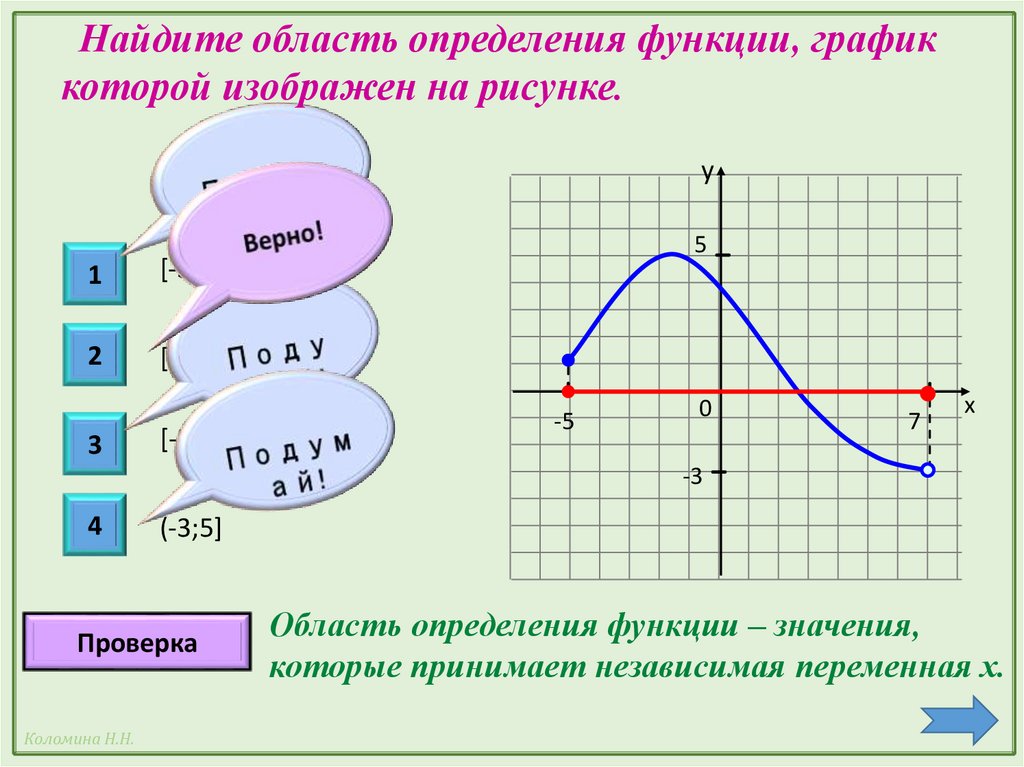
Кроме того, мы знаем, что синусоидальная функция проходит полный цикл, когда ее угол изменяется от 0 до 2 № . Здесь мы берем синус угла ωx − φ . Таким образом, при переходе ωx − φ от 0 до 2 π будет прослеживаться полный цикл функции y = A sin ( ωx − φ ). Этот цикл начинается, когда
