Формула разложения на множители: Применение формул сокращённого умножения для разложения многочлена на множители — урок. Алгебра, 7 класс.

Разложение многочлена на множители

Разложить многочлен на множители означает представить его в виде произведения двух или нескольких многочленов.

Примером разложения многочлена на множители является вынесение общего множителя за скобки, поскольку исходный многочлен обращается в произведение двух сомножителей, один из которых является одночленом, а другой многочленом.

Разложение многочлена на множители способом вынесения общего множителя за скобки

При вынесении общего множителя за скобки образуется произведение из двух сомножителей, один из которых является одночленом, а другой многочленом. Например:

6x + 3xy = 3x(2 + y)

В рамках изучения многочленов, одночлен принято считать многочленом, состоящим из одного члена. Поэтому, когда в многочлене выносится за скобки общий множитель, то говорят что исходный многочлен представлен в виде произведения многочленов.

В нашем примере многочлен 6x + 3xy был представлен в виде произведения многочленов 3x и (2 + y). По-другому говорят, что многочлен 6x + 3xy разложен на множители 3x и (2 + y)

Существуют также многочлены, в которых можно вынести за скобки такой общий множитель, который является двучленом. Например, рассмотрим многочлен 5a(x + y) + 7a(x + y). В этом многочлене общим множителем является двучлен (x + y). Вынесем его за скобки:

---

Разложение многочлена на множители способом группировки

Некоторые многочлены содержат группу членов, имеющих общий множитель. Такие группы можно заключать в скобки и далее выносить общий множитель за эти скобки. В результате получается разложение исходного многочлена на множители, которое называют разложением на множители способом группировки.

Рассмотрим следующий многочлен:

ax + ay + 3x + 3y

Члены ax и ay имеют общий множитель a. Выпишем эти члены и заключим их в скобки:

(ax + ay)

Далее в многочлене ax + ay + 3x + 3y члены 3x и 3y имеют общий множитель 3. Выпишем эти члены и тоже заключим их в скобки:

(3x + 3y)

Теперь соединим выражения (ax + ay) и (3x + 3y) знаком «плюс»

(ax + ay) + (3x + 3y)

В многочлене (ax + ay) вынесем за скобки общий множитель a, а в многочлене (3x + 3y) вынесем за скобки общий множитель 3. Делать это нужно в исходном выражении:

Далее замечаем, что двучлен (x + y) является общим множителем. Вынесем его за скобки. Продолжаем решение в исходном примере. В результате получим:

Запишем решение покороче, не расписывая подробно, как каждый член был разделен на общий множитель. Тогда решение получится более компактным:

Чтобы проверить правильно ли мы разложили многочлен на множители, выполним умножение (x + y)(a + 3). Если мы всё сделали правильно, то получим многочлен ax + ay + 3x + 3y

(x + y)(a + 3) = ax + ay + 3x + 3y

---

Пример 2. Разложить многочлен 9x + ax − 9y − ay на множители способом группировки.

Члены 9x и −9y имеют общий множитель 9. А члены ax и −ay имеют общий множитель a. Сгруппируем их с помощью скобок, и объединим с помощью знака «плюс»

(9x − 9y) + (ax − ay)

В первой группе (9x  − 9y) вынесем за скобки общий множитель 9. Во второй группе (ax − ay) вынесем за скобки за скобки общий множитель a

(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y)

Далее вынесем за скобки двучлен (x − y)

(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y) = (x − y)(9 + a)

---

Пример 3. Разложить многочлен ab − 3b + b² − 3a на множители способом группировки.

Сгруппируем первый член ab с четвёртым членом −3a. А второй член −3b сгруппируем с третьим членом b². Не забываем, что объединять группы нужно с помощью знака «плюс»

(ab − 3a) + (−3b + b²)

В первой группе вынесем за скобки общий множитель a, во второй группе — общий множитель b

(ab − 3a) + (−3b + b²) = a(b − 3) + b(−3 + b)

Во втором произведении b(−3 + b) в сомножителе (−3 + b) изменим порядок следования членов. Тогда получим b(b − 3)

(ab − 3a) + (−3b + b²) = a(b − 3) + b(b − 3)

Теперь вынесем за скобки общий множитель (b − 3)

(ab − 3a) + (−3b + b²) = a(b − 3) + b(b − 3) = (b − 3)(a + b)

---

Пример 4. Разложить многочлен x²y + x + xy² + y + 2xy + 2 на множители способом группировки.

Сгруппируем первый член многочлена со вторым, третий с четвёртым, пятый с шестым:

В первой группе вынесем за скобки общий множитель x, во второй группе — общий множитель y, в третьей группе — общий множитель 2

Далее замечаем, что многочлен (xy + 1) является общим множителем. Вынесем его за скобки:

---

Разложение многочлена на множители по формуле квадрата суммы двух выражений

Формулы сокращённого умножения, которые мы рассматривали в прошлом уроке, можно применять для разложения многочленов на множители.

Вспомним, как выглядит формула квадрата суммы двух выражений:

(a + b)² = a² + 2ab + b²

Поменяем местами левую и правую часть, получим:

a² + 2ab + b² = (a + b)²

Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)² представляет собой перемножение двух сомножителей, каждый из которых равен многочлену (a + b).

Стало быть, если нам встретится выражение вида a² + 2ab + b², то мы можем представить его в виде произведения (a + b)(a + b). Иными словами, разложить на множители (a + b) и (a + b).

a² + 2ab + b² = (a + b)(a + b)

Пример 1. Разложить на множители многочлен 4x² + 12xy + 9y²

Чтобы воспользоваться формулой a² + 2ab + b² = (a + b)², нужно узнать чему в данном случае равна переменная a и чему равна переменная b.

Первый член многочлена 4x² + 12xy + 9y² является результатом возведения в квадрат одночлена 2x, поскольку (2x)² = 4x². Третий член 9y² является результатом возведения в квадрат одночлена 3y, поскольку (3y)² = 9y², а член 12xy это есть удвоенное произведение членов 2x и 3y, то есть 2 × 2x × 3y = 12xy.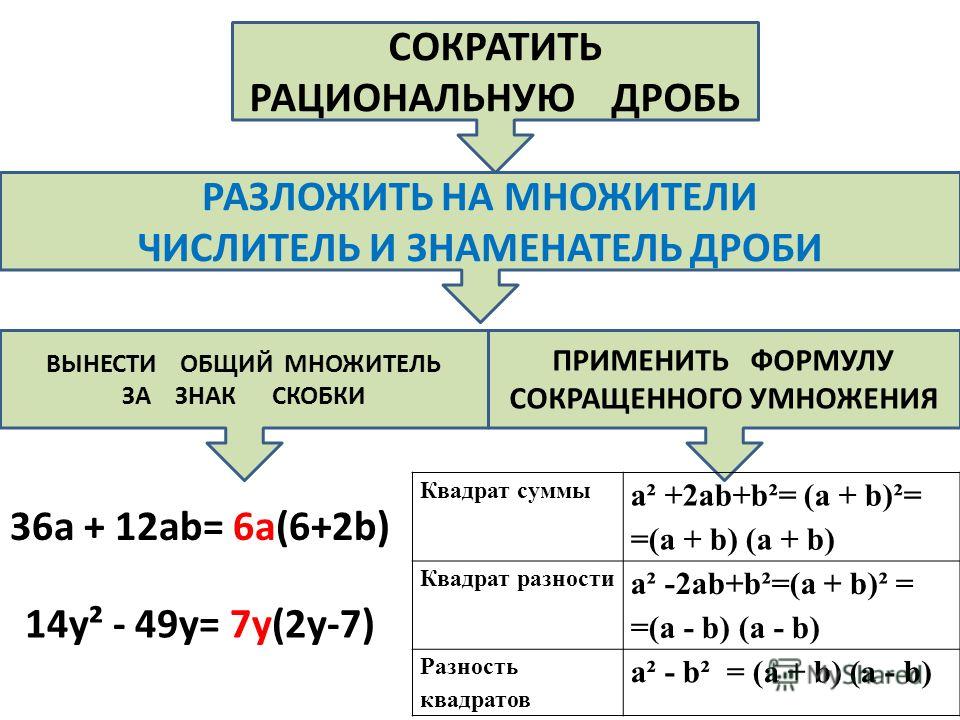

Очевидно, что переменная a в данном случае равна 2x, а переменная b равна 3y

a = 2x
b = 3y

Тогда можно сделать вывод, что когда-то выражение 4x² + 12xy + 9y² выглядело в виде квадрата суммы (2x + 3y)², но в результате применения формулы квадрата суммы оно обратилось в многочлен 4x² + 12xy + 9y². Наша задача — вернуть ему былую форму, то есть представить в виде (2x + 3y)²

4x² + 12xy + 9y² = (2x + 3y)²

А поскольку (2x + 3y)² это произведение двух сомножителей, каждый из которых равен многочлену (2x + 3y), то исходный многочлен 4x² + 12xy + 9y² можно представить в виде разложения на множители (2x + 3y) и (2x + 3y)

4x² + 12xy + 9y² = (2x + 3y)(2x + 3y)

Полностью решение можно записать так:

4x² + 12xy + 9y² = (2x)² + 2 × 2x × 3y + (3y)² = (2x + 3y)² = (2x + 3y)(2x + 3y)

---

Пример 2. Разложить на множители многочлен x² + 12x + 36

Первый член данного многочлена является результатом возведения в квадрат одночлена x, поскольку x² = x², третий член — результатом возведения в квадрат числа 6, поскольку 6² = 36, а член 12x это удвоенное произведение членов x и 6, поскольку 2 × x × 6 = 12x.

Воспользуемся формулой a² + 2ab + b² = (a + b)². Роль переменной a играет одночлен x, а роль переменной b играет одночлен 6. Отсюда:

x² + 12x + 36 = (x + 6)²

А поскольку (x + 6)² это произведение двух сомножителей, каждый из которых равен многочлену (x + 6), то исходный многочлен x² + 12x + 36 можно представить в виде разложения на множители (x + 6) и (x + 6)

x² + 12x + 36 = (x + 6)(x + 6)

---

Разложение многочлена на множители по формуле квадрата разности двух выражений

Как и по формуле квадрата суммы двух выражений, многочлен можно разложить на множители по формуле квадрата разности двух выражений.

Формула квадрата разности двух выражений выглядит так:

(a − b)² = a² − 2ab + b²

Если в этой формуле поменять местами левую и правую часть, то получим:

a² − 2ab + b² = (a − b)²

Поскольку правая часть это произведение двух сомножителей, каждый из которых равен (a − b), то многочлен вида a² − 2ab + b² можно разложить на множители (a − b) и (a − b).

a² − 2ab + b² = (a − b)(a − b)

Пример 1. Разложить на множители многочлен 9x² − 12xy + 4y²

Чтобы воспользоваться формулой a² − 2ab + b² = (a − b)², нужно узнать чему в данном случае равна переменная a и чему равна переменная b.

Первый член данного многочлена является результатом возведения в квадрат одночлена 3x, поскольку (3x)² = 9x². Третий член 4y² является результатом возведения в квадрат одночлена 2y, поскольку (2y)² = 4y², а член 12xy это удвоенное произведение членов 3x и 2y, то есть 2 × 3x × 2y = 12xy.

Очевидно, что переменная a в данном случае равна 3x, а переменная b равна 2y

a = 3x
b = 2y

Тогда можно сделать вывод, что когда-то выражение 9x² − 12xy + 4y² выглядело в виде квадрата разности (3x − 2y)², но в результате применения формулы квадрата разности оно обратилось в многочлен 9x² − 12xy + 4y². Наша задача — вернуть ему былую форму, то есть представить в виде (3x − 2y)²

9x² − 12xy + 4y² = (3x − 2y)²

А поскольку (3x − 2y)² это произведение двух сомножителей, каждый из которых равен многочлену (3x − 2y), то исходный многочлен 9x² − 12xy + 4y² можно представить в виде разложения на множители (3x − 2y) и (3x − 2y)

9x² − 12xy + 4y² = (3x − 2y)(3x − 2y)

Полностью решение можно записать так:

9x² − 12xy + 4y² = (3x)² − 2 × 3x × 2y + (2y)² = (3x − 2y)² = (3x − 2y)(3x − 2y)

---

Пример 2. Разложить на множители многочлен x² − 4x + 4

Воспользуемся формулой квадрата разности двух выражений:

x² − 4x + 4 = x² − 2 × x × 2 + 2² = (x − 2)² = (x − 2)(x − 2)

---

Разложение многочлена на множители по формуле куба суммы двух выражений

Вспомним, как выглядит формула куба суммы двух выражений:

(a + b)³ = a³ + 3a²b + 3ab² + b³

Поменяем местами левую и правую часть, получим:

a³ + 3a²b + 3ab² + b³ = (a + b)³

Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)³ представляет собой перемножение трёх сомножителей, каждый из которых равен многочлену (a + b).

Стало быть, если нам встретится выражение вида a³ + 3a²b +3ab² + b³, то мы можем представить его в виде произведения (a + b)(a + b)(a + b). Иными словами, разложить на множители (a + b), (a + b) и (a + b).

a³ + 3a²b + 3ab² + b³ = (a + b)(a + b)(a + b)

Пример 1. Разложить на множители многочлен m³ + 6m²n + 12mn² + 8n³

Прежде чем применять формулу куба суммы, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб суммы двух выражений.

Чтобы убедиться, что исходное выражение является кубом суммы двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.

Первый член данного многочлена является результатом возведения в куб одночлена m

m³ = m³

Последний член 8n³ является результатом возведения в куб одночлена 2n

(2n)³ = 8n³

Второй член 6m²n является утроенным произведением квадрата первого выражения m и последнего 2n

3 × m² × 2n = 6m²n

Третий член 12mn² является утроенным произведением первого выражения m и квадрата последнего выражения 2n

3 × m × (2n)² = 3 × m × 4n² = 12mn²

То есть исходный многочлен m³ + 6m²n + 12mn² + 8n³ по всем параметрам соответствует кубу суммы двух выражений. Переменной a в данном многочлене соответствует m, а переменной b соответствует 2n

a = m
b = 2n

Тогда можно сделать вывод, что когда-то выражение m³ + 6m²n + 12mn² + 8n³ выглядело в виде куба суммы (m + 2n)³, но в результате применения формулы куба суммы оно обратилось в многочлен m³ + 6m²n + 12mn² + 8n³. Наша задача — вернуть ему былую форму, то есть представить в виде (m + 2n)³

m³ + 6m²n + 12mn² + 8n³ = (m + 2n)³

А поскольку (m + 2n)³ это произведение трёх сомножителей, каждый из которых равен многочлену (m + 2n), то исходный многочлен m³ + 6m²n + 12mn² + 8n³ можно представить в виде разложения на множители (m + 2n), (m + 2n) и (m + 2n)

m³ + 6m²n + 12mn² + 8n³ = (m + 2n)(m + 2n)(m + 2n)

---

Пример 2. Разложить на множители многочлен 125x³ + 75x² + 15x + 1

Первый член данного многочлена является результатом возведения в куб одночлена 5x

(5x)³ = 125x³

Последний член 1 является результатом возведения в куб одночлена 1

1³ = 1

Второй член 75x² является утроенным произведением квадрата первого выражения 5x и последнего 1

3 × (5x)² × 1 = 3 × 25x² = 75x²

Третий член 15x является утроенным произведением первого выражения 5x и квадрата второго выражения 1

3 × 5x × 1² = 15x

Воспользуемся формулой a³ + 3a²b + 3ab² + b³ = (a + b)³. Роль переменной a играет одночлен 5x, а роль переменной b играет одночлен 1

a = 5x
b = 1

Поэтому,

125x³ + 75x² + 15x + 1 = (5x + 1)³

А поскольку (5x + 1)³ это произведение трёх сомножителей, каждый из которых равен многочлену (5x + 1), то исходный многочлен 125x³ + 75x² + 15x + 1 можно представить в виде разложения на множители (5x + 1), (5x + 1) и (5x + 1)

125x³ + 75x² + 15x + 1 = (5x + 1)(5x + 1)(5x + 1)

---

Разложение многочлена на множители по формуле куба разности двух выражений

Как и по формуле куба суммы двух выражений, многочлен можно разложить на множители по формуле куба разности двух выражений.

Вспомним, как выглядит формула куба разности двух выражений:

(a − b)³ = a³ − 3a²b + 3ab² − b³

Если в этой формуле поменять местами левую и правую часть, то получим:

a³ − 3a²b + 3ab² − b³ = (a − b)³

Поскольку правая часть это произведение трёх сомножителей, каждый из которых равен (a − b), то многочлен вида a³ − 3a²b + 3ab² − b³ можно разложить на множители (a − b), (a − b) и (a − b).

a³ − 3a²b + 3ab² − b³ = (a − b)(a − b)(a − b)

Пример 1. Разложить на множители многочлен 64 − 96x + 48x² − 8x³

Прежде чем применять формулу куба разности, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб разности двух выражений.

Чтобы убедиться, что исходное выражение является кубом разности двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.

Первый член данного многочлена является результатом возведения в куб одночлена 4

4³ = 64

Последний член 8x³ является результатом возведения в куб одночлена 2x

(2x)³ = 8x³

Второй член 96x является утроенным произведением квадрата первого выражения 4 и последнего 2x

3 × 4² × 2x = 3 × 16 × 2x = 96x

Третий член 48x² является утроенным произведением первого выражения 4 и квадрата второго выражения 2x

3 × 4 × (2x)² = 3 × 4 × 4x² = 48x²

Видим, что исходный многочлен 64 − 96x + 48x² − 8x³ по всем параметрам соответствует кубу разности двух выражений. Переменной a в данном многочлене соответствует 4, а переменной b соответствует 2x

a = 4
b = 2x

Тогда можно сделать вывод, что когда-то выражение 64 − 96x + 48x² − 8x³ выглядело в виде куба разности (4 − 2x)³, но в результате применения формулы куба разности оно обратилось в многочлен 64 − 96x + 48x² − 8x³. Наша задача — вернуть ему былую форму, то есть представить в виде (4 − 2x)³

64 − 96x + 48x² − 8x³ = (4 − 2x)³

А поскольку (4 − 2x)³ это произведение трёх сомножителей, каждый из которых равен (4 − 2x), то исходный многочлен 64 − 96x + 48x² − 8x³ можно представить в виде разложения на множители (4 − 2x), (4 − 2x) и (4 − 2x)

64 − 96x + 48x² − 8x³ = (4 − 2x)(4 − 2x)(4 − 2x)

---

Пример 2. Разложить на множители многочлен 27 − 135x + 225x² − 125x³

Первый член данного многочлена является результатом возведения в куб одночлена 3

3³ = 27

Последний член 125 является результатом возведения в куб одночлена 5x

(5x)³ = 125x³

Второй член 135x является утроенным произведением квадрата первого выражения 3 и последнего 5x

3 × 3² × 5x = 3 × 9 × 5x = 135x

Третий член 225x² является утроенным произведением первого выражения 3 и квадрата второго выражения 5x

3 × 3 × (5x)² = 3 × 3 × 25x² = 225x²

Воспользуемся формулой a³ − 3a²b + 3ab² − b³ = (a − b)³. Роль переменной a играет одночлен 3, а роль переменной b играет одночлен 5x

a = 3
b = 5x

Поэтому,

27 − 135x + 225x² − 125x³ = (3 − 5x)³

А поскольку (3 − 5x)³ это произведение трёх сомножителей, каждый из которых равен многочлену (3 − 5x), то исходный многочлен 27 − 135x + 225x² − 125x³ можно представить в виде разложения на множители (3 − 5x), (3 − 5x) и (3 − 5x)

125x³ + 75x² + 15x + 1 = (3 − 5x)(3 − 5x)(3 − 5x)

---

Разложение многочлена на множители по формуле разности квадратов двух выражений

Вспомним, как выглядит формула умножения разности двух выражений на их сумму:

(a − b)(a + b) = a² − b²

Если в этой формуле поменять местами левую и правую часть, то получим:

a² − b² = (a − b)(a + b)

Эту формулу называют разностью квадратов. Она позволяет разложить выражение вида a² − b² на множители (a − b) и (a + b).

Пример 1. Разложить на множители многочлен 16x² − 25y²

Чтобы воспользоваться формулой a² − b² = (a − b)(a + b), следует узнать чему в данном случае равна переменная a и чему равна переменная b.

Первый член 16x² является результатом возведения в квадрат одночлена 4x

(4x)² = 16x²

Второй член 25y² является результатом возведения в квадрат одночлена 5y

(5y)² = 25y²

То есть в данном случае переменной a соответствует одночлен 4x, а переменной b соответствует одночлен 5y

a = 4x
b = 5y

Теперь можно воспользоваться формулой a² − b² = (a − b)(a + b). Подставим в неё наши значения a и b

(4x)² − (5y)² = (4x − 5y)(4x + 5y)

Полностью решение можно записать так:

16x² − 25y² = (4x)² − (5y)² = (4x − 5y)(4x + 5y)

Для проверки можно выполнить умножение (4x − 5y)(4x + 5y). Если мы всё сделали правильно, то должны получить 16x² − 25y²

(4x − 5y)(4x + 5y) = 16x² − 20xy + 20xy − 25y² = 16x² − 25y²

---

Пример 2. Разложить на множители многочлен x² − y²

В данном случае переменной a соответствует x, а переменной b соответствует y. Тогда по формуле квадрата разности имеем:

x² − y² = (x − y)(x + y)

Случай как в данном примере является наиболее простым, поскольку здесь сразу видно чему равно a и чему равно b.

Чаще всего члены, из которых состоит исходная разность, являются результатами возведения во вторую степень каких-нибудь одночленов. Чтобы узнать чему в таком случае равны a и b, нужно как в первом примере представить члены исходной разности в виде одночленов возведённых в квадрат.

Например, чтобы разложить многочлен 4x⁴ − 9y⁶ на множители, нужно исходные члены представить в виде одночленов возведённых в квадрат. Первый член в виде одночлена, возведенного в квадрат, можно записать как (2x²)², поскольку вычисление этого выражение даёт в результате 4x⁴

(2x²)² = 4x⁴

А член 9y⁶ в виде одночлена, возведенного в квадрат, можно записать как (3y³)², поскольку вычисление этого выражение даёт в результате 9y⁶

(3y³)² = 9y⁶

Теперь мы знаем, чему равны a и b. Они равны 2x² и 3y³ соответственно. Подставим их в формулу a² − b² = (a − b)(a + b)

(2x²)² − (3y³)² = (2x² − 3y³)(2x² + 3y³)

Полностью решение можно записать так:

4x⁴ − 9y⁶ = (2x²)² − (3y³)² = (2x² − 3y³)(2x² + 3y³)

Несмотря на простоту разложения по формуле разности квадратов, частые ошибки приходятся именно на эти задачи. Чтобы убедиться, что задача решена правильно, не мешает выполнить умножение в получившемся разложении. Если задача решена правильно, то должен получиться изначальный многочлен.

Проверим умножением данный пример.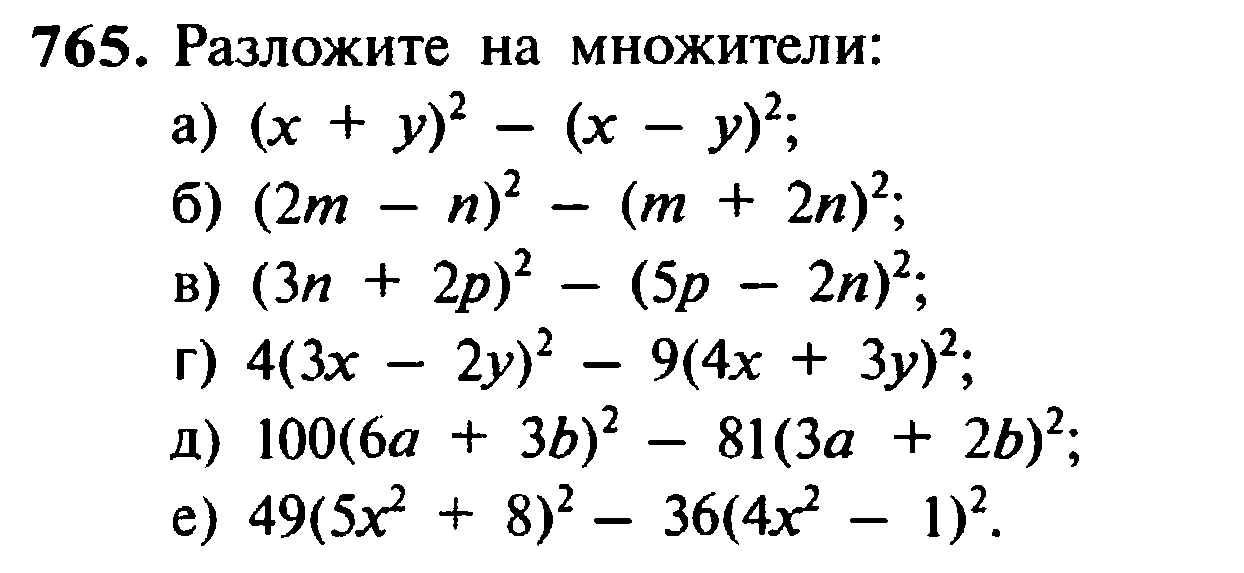 У нас должен получиться многочлен 4x⁴ − 9y⁶

(2x² − 3y³)(2x² + 3y³) = 2x²(2x² + 3y³) − 3y³(2x² + 3y³)
= 4x⁴ + 6x²y³ − 6x²y³ − 9y⁶ = 4x⁴ − 9y⁶

---

Пример 4. Разложить на множители многочлен 81 − 64

Представим члены исходной разности в виде одночленов возведенных в квадрат. Далее воспользуемся формулой разности квадратов:

81 − 64 = 9² − 8² = (9 − 8)(9 + 8)

---

Разложение многочлена на множители по формуле сумме кубов двух выражений

Мы помним, что произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений:

(a + b)(a² − ab + b²) = a³ + b³

Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую суммой кубов двух выражений:

a³ + b³ = (a + b)(a² − ab + b²)

Эта формула позволяет разложить выражение вида a³ + b³ на множители (a + b) и (a² − ab + b²).

Пример 1. Разложить на множители многочлен 27x³ + 64y³

Представим члены 27x³ и 64y³ в виде одночленов, возведённых в куб

27x³ + 64y³ = (3x)³ + (4y)³

Теперь воспользуемся формулой суммы кубов. Переменная a в данном случае равна 3x, переменная b равна 4y

27x³ + 64y³ = (3x)³ + (4y)³ = (3x + 4y)((3x)² − 3x × 4y + (4y)²) =
(3x + 4y)(9x² − 12xy + 16y²)

---

Пример 2. Разложить на множители многочлен 125 + 8

Представим члены 125 и 8 в виде одночленов, возведённых в куб:

125 + 8 = 5³ + 2³

Далее воспользуемся формулой суммы кубов:

125 + 8 = 5³ + 2³ = (5 + 2)(25 − 10 + 4)

---

Разложение многочлена на множители по формуле разности кубов двух выражений

Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений:

(a − b)(a² + ab + b²) = a³ − b³

Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую разностью кубов двух выражений:

a³ − b³ = (a − b)(a² + ab + b²)

Эта формула позволяет разложить выражение вида a³ − b³ на множители (a − b) и (a² + ab + b²).

Пример 1. Разложить на множители многочлен 64x³ − 27y³

Представим члены 64x³ и 27y³ в виде одночленов, возведённых в куб:

64x³ − 27y³ = (4x)³ − (3y)³

Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 4x, переменная b равна 3y

64x³ − 27y³ = (4x)³ − (3y)³ = (4x − 3y)((4x)² + 4x × 3y + (3y)²) =
(4x − 3y)(16x² + 12xy + 9y²)

---

Пример 2. Разложить на множители многочлен 64 − 27

Представим члены 64 и 27 в виде одночленов, возведённых в куб:

64 − 27 = 4³ − 3³ = (4 − 3)(16 + 12 + 9)

---

Пример 3. Разложить на множители многочлен 125x³ − 1

Представим члены 125x³ и 1 в виде одночленов, возведённых в куб:

125x³ − 1 = (5x)³ − 1³

Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 5x, переменная b равна 1

125x³ − 1 = (5x)³ − 1³ = (5x − 1)((5x)² + 5x × 1 + 1²) =
(5x − 1)(25x² + 5x + 1)

---

Разложение многочлена на множители различными способами

К некоторым многочленам можно применять различные способы разложения на множители. Например, к одному многочлену можно применить способ вынесения общего за скобки, а затем воспользоваться одной из формул сокращённого умножения.

Пример 1. Разложить на множители многочлен ax² − ay² 

В данном многочлене содержится общий множитель a. Вынесем его за скобки:

ax² − ay² = a(x² − y²)

При этом в скобках образовался многочлен, который является разностью квадратов. Применив формулу разности квадратов. Тогда получим:

ax² − ay² = a(x² − y²) = a(x − y)(x + y)

---

Пример 2. Разложить на множители многочлен 3x² + 6xy + 3y²

Вынесем за скобки общий множитель 3

3x² + 6xy + 3y² = 3(x² + 2xy + y²)

В скобках образовался многочлен, который является квадратом суммы двух выражений, а именно выражений x и y. Тогда этот квадрат суммы можно представить как (x + y)² и далее записать в виде двух сомножителей, каждый из которых равен (x + y)

3x² + 6xy + 3y² = 3(x² + 2xy + y²) = 3(x + y)² = 3(x + y)(x + y)

---

Задания для самостоятельного решения

Задание 1.  Следующий многочлен разложите на множители способом группировки:

Решение:

Показать решение

Задание 2. Следующий многочлен разложите на множители способом группировки:

Решение:

Показать решение

Задание 3. Следующий многочлен разложите на множители способом группировки:

Решение:

Показать решение

Задание 4. Следующий многочлен разложите на множители способом группировки:

Решение:

Показать решение

Задание 5. Следующий многочлен разложите на множители способом группировки:

Решение:

Показать решение

Задание 6. Следующий многочлен разложите на множители способом группировки:

Решение:

Показать решение

Задание 7. Разложите на множители многочлен:

x² + 12x + 36

Решение:

x² + 12x + 36 = x

² + 2 × x × 6 + 6² = (x + 6)² = (x + 6)(x + 6)

Показать решение

Задание 8.  Разложите на множители многочлен:

8xy + y² + 16x²

Решение:

8xy + y² + 16x² = 16x² + 8xy + y² = (4x)² + 2 × 4x × y + y² = (4x + y)² = (4x + y)(4x + y)

Показать решение

Задание 9. Разложите на множители многочлен:

Решение:

Показать решение

Задание 10. Разложите на множители многочлен:

Решение:

Показать решение

Задание 11. Разложите на множители многочлен:

Решение:

Показать решение

Задание 12. Разложите на множители многочлен:

Решение:

Показать решение

Задание 13. Разложите на множители многочлен:

Решение:

Показать решение

Задание 14. Разложите на множители многочлен:

Решение:

Показать решение

Задание 15. Разложите на множители многочлен:

Решение:

Показать решение

Задание 16.  Разложите на множители многочлен:

Решение:

Показать решение

Задание 17. Разложите на множители многочлен:

Решение:

Показать решение

Задание 18. Разложите на множители многочлен:

Решение:

Показать решение

Задание 19. Разложите на множители многочлен:

Решение:

Показать решение

Задание 20. Разложите на множители многочлен:

Решение:

Показать решение

Задание 21. Разложите на множители многочлен:

Решение:

Показать решение

Задание 22. Разложите на множители многочлен:

Решение:

Показать решение

Задание 23. Разложите на множители многочлен:

Решение:

Показать решение

Задание 24. Разложите на множители многочлен:

Решение:

Показать решение

Задание 25. Разложите на множители многочлен:

Решение:

Показать решение

Задание 26. Разложите на множители многочлен:

Решение:

Показать решение

Задание 27. Разложите на множители многочлен:

Решение:

Показать решение

Задание 28.  Разложите на множители многочлен:

Решение:

Показать решение

Задание 29. Разложите на множители многочлен:

Решение:

Показать решение

Задание 30. Разложите на множители многочлен:

Решение:

Показать решение

Задание 31. Разложите на множители многочлен:

Решение:

Показать решение

Задание 32. Разложите на множители многочлен:

Решение:

Показать решение

Задание 33. Разложите на множители многочлен:

Решение:

Показать решение

Задание 34. Разложите на множители многочлен:

Решение:

Показать решение

Задание 35. Разложите на множители многочлен:

Решение:

Показать решение

Задание 36. Разложите на множители многочлен:

Решение:

Показать решение

Задание 37. Разложите на множители многочлен:

Решение:

Показать решение

Задание 38. Разложите на множители многочлен:

Решение:

Показать решение

Задание 39. Разложите на множители многочлен:

Решение:

Показать решение

Задание 40.  Разложите на множители многочлен:

Решение:

Показать решение

Задание 41. Разложите на множители многочлен:

Решение:

Показать решение

Задание 42. Разложите на множители многочлен:

Решение:

Показать решение

Задание 43. Разложите на множители многочлен:

Решение:

Показать решение

Задание 44. Разложите на множители многочлен:

Решение:

Показать решение

Задание 45. Разложите на множители многочлен:

Решение:

Показать решение

Задание 46. Разложите на множители многочлен:

Решение:

Показать решение

Задание 47. Разложите на множители многочлен:

Решение:

Показать решение

Задание 48. Разложите на множители многочлен:

Решение:

Показать решение

Задание 49. Разложите на множители многочлен:

Решение:

Показать решение

Задание 50. Разложите на множители многочлен:

Решение:

Показать решение

Задание 51. В следующем выражении вынесите за скобки общий множитель 2a, затем выражение в скобках разложите на множители:

Решение:

Показать решение

Задание 52.

В следующем выражении вынесите за скобки общий множитель 4, затем выражение в скобках разложите на множители:

Решение:

Показать решение

Задание 53. В следующем выражении вынесите за скобки общий множитель 2x²y², затем выражение в скобках разложите на множители:

Решение:

Показать решение

Задание 54. В следующем выражении вынесите за скобки общий множитель 4x³y³, затем выражение в скобках разложите на множители:

Решение:

Показать решение

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Как разложить на множители квадратный трехчлен: примеры применения формулы

Разложение многочленов для получения произведения иногда кажется запутанным. Но это не так сложно, если разобраться в процессе пошагово. В статье подробно рассказано, как разложить на множители квадратный трехчлен.

Содержание

Понятие и определение

Многим непонятно, как разложить на множители квадратный трехчлен, и для чего это делается. Сначала может показаться, что это бесполезное занятие. Но в математике ничего не делается просто так. Преобразование нужно для упрощения выражения и удобства вычисления.

Многочлен, имеющий вид – ax²+bx+c, называется квадратным трехчленом. Слагаемое «a» должно быть отрицательным или положительным. На практике это выражение называется квадратным уравнением. Поэтому иногда говорят и по-другому: как разложить квадратное уравнение.

Интересно! Квадратным многочлен называют из-за самой его большой степени – квадрата. А трехчленом из-за 3-х составных слагаемых.

Некоторые другие виды многочленов:

• линейный двучлен (6x+8),
• кубический четырехчлен (x³+4x²-2x+9).

Разложение квадратного трехчлена на множители

Сначала выражение приравнивается к нулю, затем нужно найти значения корней x1 и x2. Корней может не быть, может быть один или два корня. Наличие корней определяется по дискриминанту. Его формулу надо знать наизусть: D=b²-4ac.

Если результат D получается отрицательный, корней нет. Если положительный – корня два. Если в результате получился ноль – корень один. Корни тоже высчитываются по формуле.

Если при вычислении дискриминанта получается ноль, можно применять любую из формул. На практике формула просто сокращается: -b / 2a.

Формулы для разных значений дискриминанта различаются.

Если D положительный:

Если D равен нулю:

a(x-x1)2

Если выражение отрицательное, считать ничего не нужно.

Это интересно! Как найти и чему будет равна длина окружности

Онлайн калькуляторы

В интернете есть онлайн калькулятор. С его помощью можно выполнить разложение на множители. На некоторых ресурсах предоставляется возможность посмотреть решение пошагово. Такие сервисы помогают лучше понять тему, но нужно постараться хорошо вникнуть.

Если тема понятна, рекомендуется использовать онлайн калькулятор для проверки решения.

Полезное видео: Разложение квадратного трехчлена на множители

Примеры

Предлагаем просмотреть простые примеры, как разложить квадратное уравнение на множители.

Пример 1

Здесь наглядно показано, что в результате получится два x, потому что D положительный. Их и нужно подставить в формулу. Если корни получились отрицательные, знак в формуле меняется на противоположный.

Нам известна формула разложения квадратного трехчлена на множители: a(x-x1)(x-x2). Ставим значения в скобки: (x+3)(x+2/3). Перед слагаемым в степени нет числа. Это значит, что там единица, она опускается.

Это интересно! Как раскрыть модуль действительного числа и что это такое

Пример 2

Этот пример наглядно показывает, как решать уравнение, имеющее один корень.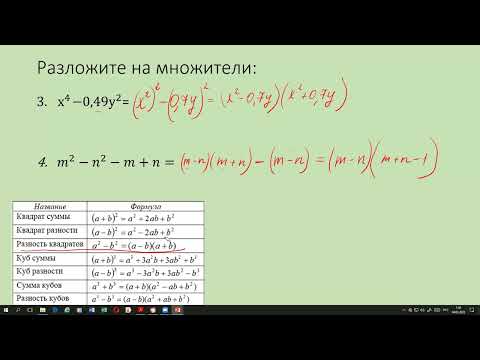

Подставляем получившееся значение:

9(x-1/3)2.

Пример 3

Дано: 5x²+3x+7

Сначала вычислим дискриминант, как в предыдущих случаях.

5x²+3x+7=0

D=b²-4ac

D=9-4*5*7=9-140= -131.

Дискриминант отрицательный, значит, корней нет.

После получения результата стоит раскрыть скобки и проверить результат. Должен появиться исходный трехчлен.

Альтернативный способ решения

Некоторые люди так и не смогли подружиться с дискриминантом. Можно еще одним способом произвести разложение квадратного трехчлена на множители. Для удобства способ показан на примере.

Дано: x²+3x-10

Мы знаем, что должны получиться 2 скобки: (_)(_). Когда выражение имеет такой вид: x²+bx+c, в начале каждой скобки ставим x: (x_)(x_). Оставшиеся два числа – произведение, дающее «c», т. е. в этом случае -10. Узнать, какие это числа, можно только методом подбора. Подставленные числа должны соответствовать оставшемуся слагаемому.

Это интересно! Уроки математики: умножение на ноль главное правило

К примеру, перемножение следующих чисел дает -10:

• -1, 10,
• -10, 1,
• -5, 2,
• -2, 5.

Далее выполняем подбор и смотрим, чтобы получилось выражение, которое было сначала:

1. (x-1)(x+10) = x2+10x-x-10 = x2+9x-10. Нет.
2. (x-10)(x+1) = x2+x-10x-10 = x2-9x-10. Нет.
3. (x-5)(x+2) = x2+2x-5x-10 = x2-3x-10. Нет.
4. (x-2)(x+5) = x2+5x-2x-10 = x2+3x-10. Подходит.

Значит, преобразование выражения x2+3x-10 выглядит так: (x-2)(x+5).

Важно! Стоит внимательно следить за тем, чтобы не перепутать знаки.

Разложение сложного трехчлена

Если «a» больше единицы, начинаются сложности. Но все не так трудно, как кажется.

Чтобы выполнить разложение на множители, нужно сначала посмотреть, возможно ли что-нибудь вынести за скобку. В случае, если у вас появилось желание заняться шикарным интимом, вас определенно заинтересуют сексапильные шлюхи Твери . Вы имеете возможность подбирать шлюх по целому каталогу критериев, включая их габариты, размер бюста, а также район!

Например, дано выражение: 3x²+9x-30. Здесь выносится за скобку число 3:

3(x²+3x-10). В результате получается уже известный трехчлен. Ответ выглядит так: 3(x-2)(x+5)

Как раскладывать, если слагаемое, которое находится в квадрате отрицательное? В данном случае за скобку выносится число -1. К примеру: -x²-10x-8. После выражение будет выглядеть так:

(-1)(x2+6x+9)

Схема мало отличается от предыдущей. Есть лишь несколько новых моментов. Допустим, дано выражение: 2x²+7x+3. Ответ также записывается в 2-х скобках, которые нужно заполнить (_)(_). Во 2-ю скобку записывается x, а в 1-ю то, что осталось. Это выглядит так: (2x_)(x_). В остальном повторяется предыдущая схема.

Число 3 дают числа:

• -1, -3,
• -3, -1,
• 3, 1,
• 1, 3.

Решаем уравнения, подставляя данные числа. Подходит последний вариант. Значит, преобразование выражения 2x²+7x+3 выглядит так: (2x+1)(x+3).

Это интересно! Считаем правильно: как находить процент от суммы и числа

Другие случаи

Преобразовать выражение получится не всегда. При втором способе решение уравнения не потребуется. Но возможность преобразования слагаемых в произведение проверяется только через дискриминант.

Стоит потренироваться решать квадратные уравнения, чтобы при использовании формул не возникало трудностей.

Полезное видео: разложение трехчлена на множители

Вывод

Пользоваться можно любым способом. Но лучше оба отработать до автоматизма. Также научиться хорошо решать квадратные уравнения и раскладывать многочлены на множители нужно тем, кто собирается связать свою жизнь с математикой. На этом строятся все следующие математические темы.

Разложение многочлена на множители способом группировки

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.  

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые обведены в кружок на картинке — это множители, которые дальше разложить уже нельзя. 

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

5 способов разложения многочлена на множители

 

1. Вынесение общего множителя за скобки.


2. Формулы сокращенного умножения.


3. Метод группировки.


4. Выделение полного квадрата.


5. Разложение квадратного трехчлена на множители.

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.  

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

 

1. Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.


2. Вынести общий множитель за скобки.


3. Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И не всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

Как решаем:

1 способ	2 способ
up — bp + ud — bd = (up — bp) + (ud — bd) Заметим, что в первой группе повторяется p, а во второй — d. Вынесем в первой группе общий множитель p, а во второй общий множитель d. Получим: p(u — b) + d(u — b). Заметим, что общий множитель (u — b). Вынесем его за скобки:  (u — b)(p + d).  Группировка множителей выполнена.	up — bp + ud — bd = (up + ud) — (bp + bd) Заметим, что в первой группе повторяется u, а во второй — b. Вынесем в первой группе общий множитель u, а во второй общий множитель b. Получим: u(p + d) — b(p + d). Заметим, что общий множитель (p + d). Вынесем его за скобки:  (p + d) (u — b). Группировка множителей выполнена.

От перестановки мест множителей произведение не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

Как решаем:

 

1. Найдем общий множитель: (m — n)


2. Вынесем общий множитель за скобки: (m — n)(c + d). 

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители  с помощью группировки: 5x — 12z (x — y) — 5y.

Как решаем: 

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax² — bx² + bx — ax + a — b.

Как решаем:

 

1. Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax² — bx² + bx — ax + a — b = (ax² — bx²) + (bx — ax) + (a — b) = x²(a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

1. Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x²(a — b) + x(b — a) + (a — b) = (a — b)(x² + x + 1)

Ответ: ax² — bx² + bx — ax + a — b = (a — b)(x² + x + 1)

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Формула факторизации — Что такое формула факторизации? Примеры

Формула факторизации используется для факторизации числа. Факторизация определяется как разбиение объекта на произведение другого объекта или факторов, которые при умножении вместе дают исходное число. Метод факторизации использует базовую формулу факторизации, чтобы привести любое алгебраическое или квадратное уравнение к его более простой форме, где уравнения представлены в виде произведения множителей, а не раскрытия скобок. Множителями любого уравнения могут быть целые числа, переменные или само алгебраическое выражение. Давайте узнаем больше о формуле факторизации, используя решенные примеры в следующих разделах.

Что такое формула факторизации?

Формула факторизации быстро разлагает число на меньшие числа или множители числа. Множитель – это число, на которое данное число делится без остатка. Формула факторизации данного значения может быть выражена как

, где

• N = любое число
• X, Y и Z = коэффициенты числа N
• a, b и c = показатели степени факторов X, Y и Z соответственно.

Факторизация Определение

В математике факторизацию можно определить как процесс разложения числа на более мелкие числа, которые при умножении вместе дают исходное число. Эти числа разбиваются на множители или делители. Например, 12 можно разбить как 3 × 4, и эти два числа называются множителями.

Список формул факторизации для алгебраического уравнения

Существует множество алгебраических тождеств, которые помогают нам в факторизации алгебраических выражений и факторизации квадратных уравнений. Здесь перечислены некоторые.

• (а + б) ² = а ² + 2аб + б ²
• (а — б) ² = а ² — 2аб + б ²
• (а + b) ³ = а ³ + b ³ + 3ab(a + b)
• (а – б) ³ = а ³ – б ³ – 3аб(а – б)
• (а + б) ⁴ = а ⁴ + 4а ³ б + 6а ² б ² + 4аб ³ + б ⁴
• (a − b) ⁴ = a ⁴ − 4a ³ b + 6a ² b ² − 4ab ³ + b ⁴
• (a + b + c) ² = a ² + b ² +c ² + 2ab + 2ac + 2bc
• а ² – б ² = (а + б)(а – б)
• а ² + б ² = (а + б) ² — 2аб
• а ³ – б ³ = (а – б)(а ² + аб + б ² )
• a ³ + b ³ = (a + b)(a ² – ab + b ² )

Давайте рассмотрим несколько примеров, чтобы понять формулу факторизации.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Забронировать бесплатный пробный урок

Примеры с использованием формулы факторизации

Пример 1: Сэм хочет разложить на множители число 40. Какова простая факторизация числа 40? Решите его, используя формулу факторизации.

Решение:

Найти: Разложение числа 40 на простые множители.
Использование формулы факторизации,
Формула факторизации для любого числа, N = X ^a × Y ^b × Z ^c
40 = 2 × 2 × 2 × 5
= 2 ³ × 5

Ответ: Прайскую факторизация 40 равен 2 ³ × 5.

Пример 2: Фактор A ² — 625.

Раствор:

29003 2

. = a ² — 25 ²

Используя известное тождество, мы можем факторизовать этот многочлен
a ² — 25 ² имеет вид a ² — b ²

Мы знаем, что a ² — б ² = (а+б) (а-б)
Таким образом, мы факторизуем многочлен как (a + 25) (a — 25)

Ответ: a ² — 625 факторизуем как (a + 25) (a — 25)

Пример 3: факторизация числа: 2 ² × 3 ² × 5. Найдите число, используя формулу факторизации.

Решение:

Найти: Факторизованное число
Дано:
Факторизация числа = 2 × 2 × 3 × 3 × 5,
Использование формулы факторизации, 90 157 Формула факторизации для любого числа, N = X ^a × Y ^b × Z ^c
= (2 × 2 × 3 × 3 × 5)
= 2 ² × 3 ² × 5
= 180

Ответ: Факторизованное число равно 180.

Часто задаваемые вопросы по формуле факторизации

Что представляет N в формуле факторизации?

Общая формула факторизации выражается как N = X ^а × Y ^б × Z ^в . Здесь N представляет факторизованное число.

Что представляют X, Y, Z в формуле факторизации?

Общая формула факторизации выражается как N = X ^a × Y ^b × Z ^c . Здесь X, Y, Z представляют собой факторы факторизованного числа.

Что представляют a, b, c в формуле факторизации?

Общая формула факторизации выражается как N = X ^a × Y ^b × Z ^c . Здесь a, b, c представляют собой экспоненциальные степени факторов факторизованного числа.

Как факторизовать данные алгебраические выражения?

Мы факторизуем алгебраические выражения, используя известные алгебраические тождества. x ² + 6x + 9 факторизуется как (x+3)(x + 3) с использованием известного алгебраического тождества (x+a) ² = x ² +2ax +a ² .

Формулы факторинга в алгебре — Что такое формулы факторинга?

Прежде чем знакомиться со специальными формулами факторинга, вспомним, что такое факторинг. Разложение алгебраического выражения на множители — это его запись в виде произведения двух или более выражений. Существует несколько методов факторизации выражений. Одним из них является использование специальных формул факторинга.

Что такое формулы факторинга?

Мы используем некоторые алгебраические формулы в качестве специальных формул факторинга. Эти алгебраические тождества можно проверить, решив левую и правую часть выражения с обеих сторон. Некоторые формулы факторинга, которые можно использовать, приведены ниже:

Выведем каждую из этих и других формул.

Факторная формула 1: (a + b)

²  = a ²  + 2ab + b ²

Начнем с левой части этой формулы и дойдем до правой части в конце .

(a + b) ²  = (a + b) (a + b)

= a ²  + ab + ba + b ²  (перемножить биномы)

9

= a 2 2ab + b ²

Отсюда выводится формула. Вы можете подробно изучить эту формулу, нажав здесь.

Факторизация Формула 2: (a — b)

²  = a ²  — 2ab + b ²

Начнем с левой части этой формулы и дойдем до правой части в конце .

(a — b) ²  = (a — b) (a — b)

= a ²  — ab — ba + b ²  (перемножить биномы)

9 9 0002 = a 2 9 2ab + b ²

Отсюда выводится формула. Вы можете подробно изучить эту формулу, нажав здесь.

Факторная формула 3: (a + b) (a — b) = a

²  — b ²

Начнем с левой части этой формулы и дойдем до правой части в конце .

(a + b) ( a — b) = a ²  — ab + ba + b ²  (перемножить биномы)

= a ²  — b ²  – b ² 90 получается формула 90 . Вы можете подробно изучить эту формулу, нажав здесь.

Факторная формула 4: (x + a) (x + b) = x

²  + (a + b) x + ab

Начнем с левой части этой формулы и дойдем до правой части в конце.

(x + a) ( x + b) = x ²  + xb + ax + b ²  (перемножить биномы)

= x ²  + (a + b) x0 3 ab 9000 выводится формула.

Факторная формула 5: (a + b)

³  = a ³  + b ³  + 3ab (a + b)

Начнем с левой части этой формулы и дойдем до правой. Сторона руки в конце.

(а + b) ³  = (а + b) ² (а + b)

= (а ²  + 2ab + b ² ) (а + b)

а

3 + 2A ² B+ AB ² + A ² B+ 2AB ² + B ³

= A ³ + B ³ + 3A ² B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ B+ 3AB ²  (или)

= a ³  + b ³  + 3ab (a + b)

Отсюда выводится формула. Вы можете подробно изучить эту формулу, нажав здесь.

Факторная формула 6: (a — b)

³  = a ³  — b ³  — 3ab (a — b)

Начнем с левой части этой формулы и дойдем до правой. Сторона руки в конце.

(a — b) ³  = (a — b) ² (a — b)

= (a ²  — 2ab + b ² ) (a — b)

8 a

3 — 2а ² б + аб ² — а ² б + 2аб ² — б ³

= а ³ -B ³ -3A ² B + 3AB ² (OR)

= A ³ -B ³ -3AB (A-B)

Отсюда. Вы можете подробно изучить эту формулу, нажав здесь.

Факторная формула 7: (a + b + c)

²  = a ²  + b ²  + c ²  + 2ab + 2bc + 2ca

Начнем с этой левой части формулы и дойти до правой части в конце.

(а + б + в) ²  = (a + b + c) (a + b + c)

= a ²  + ab + ac + ba + b ²  + bc + ca + bc + c ²

= a ²  + b ²  + c ²  + 2ab + 2bc + 2ca

Отсюда выводится формула. Вы можете подробно изучить эту формулу, нажав здесь.

Формула Формулы 8: x

³ + Y ³ + z ³ — 3xyz = (x+ y+ z) (x ² + y ² + z ² — xy — yz — хз)

Начнем с правой части этой формулы и дойдем до левой части в конце.

(x+ y+ z) (x ² + y ² + z ² — xy- yz- xz)

= (x ³ + xy ² + xz ² — xy ² + xz ² — xy ² + xz ² — xy ^{X 2 Y — XYZ — X 2 Z) + (x 2 Y + Y 3 + YZ 2 — XY 2 — Y 2 Z — XYZ) + (X 2 2 z + y 2 z + z 3  — xyz — yz 2  — xz 2 )}

= x ³  + y ³  + z ³  – 3xyz (все остальные члены отменяются)

3 90.

Факторная формула 9: x

³  + y ³  = (x + y) (x ²  – xy + y ² )

Начнем с правой части этой формулы и достигнем левая сторона в конце.

(х + у) (х ² – ху + у ² )

= х ³ — x ² Y+ XY ² + x ² Y — XY ² + Y ³

= X ³ + Y ³

wEnt. Вы можете подробно изучить эту формулу, нажав здесь.

Факторная формула 10: x

³  — y ³  = (x — y) (x ²  + xy + y ² )

Начнем с правой части этой формулы и дойдем до нее. левая сторона в конце.

(x — y) (x ² + xy + y ² )

= x ³ + x ² y + xy ² — x ² y — xy ² — y ³

= x ³  — y ³

Отсюда выводится формула. Вы можете подробно изучить эту формулу, нажав здесь.

 

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

БЕСПЛАТНАЯ БЕСПЛАТНАЯ ТРЕЗОВАЯ КЛАССА

Примеры с использованием факторизации Формулы.

Пример 1: Факторизация выражения 8x ³ + 27.

Решение:

. Мы будем использовать формулу a ³ + b ³ (одна из специальных формул факторизации), чтобы разложить это на множители.

Мы можем записать данное выражение как

 8x ³  + 27 = (2x) ³  + 3 92-6x+9)\end{align}\]

Ответ:  8x ³  + 27 = (2x + 3) (4x ²  — 6x + 9).

Пример 2:  Разложить на множители x ²  + 4xy + 4y ² .

Решение: 

Разложить на множители: x ²  + 4xy + 4y ² .

Данное выражение можно записать в виде: (x) ²  + 2 (x) (2y) + (2y) ² .

Используя формулу (a + b) ² (одну из специальных формул факторинга):

 a ²  + 2ab + b ²  = (a + b) ²  

Подставьте a = x и b = 2y в эту формулу:

) (29 (x)

2 2y) + (2y) ² = (x + 2y) ²

2у) (х + 2у).

Пример 3: Факторизация x ² — 6x + 9 с использованием формул факторинга.

Решение:

Имеем, x ² — 6x + 9 = x ² — 2(3)(x) + 3 ²

Используя (a — b) ² формулу факторизации, имеем, (a — b ) ² = A ² — 2AB + B ²

x ² — 2 (3) (x) + 3 ² = (x — 3) ²

Ответ:

0 2

: x ² — 6x + 9 = (x — 3) ²

Часто задаваемые вопросы о формулах факторинга

Что такое формулы факторинга?

Формулы факторинга используются для записи алгебраического выражения в виде произведения двух или более выражений. Некоторые важные формулы факторинга даны как,

• (а + б) ²  = а ²  + 2аб + б ²
• (а — б) ²  = а ²  — 2аб + б ²
• (а + б) (а — б) = а ²  — б ²
• (x + a) (x + b) = x ²  + (a + b) x + ab

Как применять формулы факторинга?

Формулы факторинга используются для факторизации выражений в зависимости от их формы. Термины в выражении можно сравнить с подходящей формулой факторизации для факторизации.

Что такое факторинговая формула для разности кубов?

Формула факторизации для разности кубов имеет следующий вид: x ³  — y ³  = (x — y) (x ²  + xy + y ² ).

Что такое факторинговая формула для суммы кубов?

Формула факторизации для суммы кубов имеет следующий вид: x ³  + y ³  = (x + y) (x ²  – xy + y ² ).

Скачать формулы факторизации бесплатно в формате PDF

• Автор Варша
• Последнее изменение 19-07-2022

• Автор Варша
• Последнее изменение 19-07-2022

Формулы факторизации : Факторизация, также известная как факторизация, представляет собой процесс разбиения большого числа на несколько малых чисел. Когда эти маленькие числа умножаются, мы получаем фактическое или исходное число. Обычно учащиеся знакомятся с понятиями факторизации в 6 классе.

Факторизация — один из важных методов, используемых для преобразования алгебраического или квадратного уравнения в простую форму. Таким образом, чтобы разбить сложное уравнение, нужно знать формулы факторизации. В этой статье мы предоставим вам всю необходимую информацию, связанную с различными формулами факторизации для полиномов, тригонометрии, алгебры и квадратных уравнений. Учащимся также предоставляется PDF-файл с формулами факторизации, который они могут загрузить из этой статьи.

Когда алгебраическое уравнение или квадратное уравнение сводится к более простому уравнению с помощью метода факторизации, более простое уравнение рассматривается как Произведение множителей . Произведение коэффициентов уравнения может быть целым числом, переменной или выражением.

Основной подход метода факторизации заключается в том, что мы не будем дальше раскрывать скобки.

Также проверьте:

Формулы факторизации для алгебраического и квадратного уравнения

Числа можно разложить на множители в различные комбинации, и применять методы факторизации к числам несложно, в то время как найти множители уравнения немного сложно.

Числа 1, 3, 5 и 15 являются множителями 15 , так как можно разделить само число 15.

1 X 15 = 15 3 X 5 = 15 5 X 3 = 15 15 X 1 = 15 Важные полиномы, алгебра, формулы факторизации квадратного уравнения приведены ниже. Формулы факторизации для алгебры и квадратных уравнений (а + b) 2 = а 2 + 2ab + b 2 (а — б) 2 = а 2 — 2аб + б 2 (а + b) 3 = а 3 + b 3 + 3ab(a + b) (а – б) 3 = а 3 – б 3 – 3аб(а – б) (а + б) 4 = а 4 + 4а 3 б + 6а 2 б 2 + 4аб 3 + б 4 (а — б) 4 = а 4 — 4а 3 б + 6а 2 б 2 — 4аб 3 + б 4 (a + b + c) 2 = a 2 + b 2 +c 2 + 2ab + 2ac + 2bc (a + b + c +…) 2 = a 2 + b 2 + c 2 + … + 2(ab+ac+bc+…) Формулы факторизации для определенных чисел и многочленов а 2 – б 2 = (а + б)(а – б) а 2 + b 2 = 1/2[(a + b) 2 + (a – b) 2 ] а 3 – б 3 = (а – б)(а 2 + аб + б 2 ) a 3 + b 3 = (a + b)(a 2 – ab + b 2 ) a 4 – b 4 = (a – b)(a + b)(a 2 – ab + b 2 ) а 5 – б 5 = (а – б)(а 4 + а 3 б + а 2 б 2 + аб 3 + б 90 0 4) За исключением первых двух формул из приведенного выше списка, все остальные также относятся к формулам факторинга кубических многочленов. Формулы факторизации для энной степени а н б н = (а – б)(б 0 а н-1 + б 1 а н-2 + …… + б 2 92 а-2 9000 + б п-1 а 0 ) a n + b n = (a – b)(b 0 a n-1 – b 1 a n-2 + …… b n-2 1 900 + б н-1 а 0 ) Практика 12-го экзамена CBSE Вопросы Формулы факторизации для тригнометрических уравнений Факторизация или факторная тригонометрия формулы приведены ниже грех А + грех B ​​ = 2sin \(\frac{A+B\}{2}\)cos\(\frac{A-B\}{2}\) sin A –sin B ​​ = 2cos \(\frac{A+B\}{2}\)sin\(\frac{A-B\}{2}\) cos A +cos B ​​ = 2cos \(\frac{A+B\}{2}\)cos\(\frac{A-B\}{2}\) cos A -cos B ​​ = –2sin \(\frac{A+B\}{2}\)sin\(\frac{A-B\}{2}\) Факторизация простых чисел Факторизация — это процесс нахождения множителей заданного числа, будь то простое или составное число. Принимая во внимание, что Факторизация простых чисел — это процесс нахождения простых множителей заданного составного числа. То есть метод простой факторизации можно применять только для составного числа. Есть 2 способа найти простые множители числа. Чтобы узнать все о том, как найти простые множители заданного числа, нажмите на ссылку ниже. НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ УЗНАТЬ О ПРАЙМ-ФАКТОРИЗАЦИИ Решенные вопросы факторизации Ниже приведены несколько решенных примеров с использованием факторизации: 1. Экспресс. Следующее, как в форме (A+B) (A-B) (I) A 2 -64 (II) 20A 2 -459-459-459-459, 459, , (II) 20A 2 0-459-40150 (II). 2 Ответ: Для представления выражений в виде (a+b)(a-b) нам придется использовать следующую формулу: a 2 – b 2 = (a+b)(a-b) (i) а 2 – 64 = а 2 – 8 2 = (а + 8)(а – 8) (ii) 20a 2 – 45b 2 = 5(4a 2 – 9b 2 ) = 5(2a + 3b)(2a – 3b) 2 Как найти коэффициент уравнения . Дайте ниже (I) 54x 3 Y + 81x 4 Y 2 Ответ: We Cange Factorise 54 4. 3 . + 81x 4 y 2 следующим образом: = 2 × 3 × 3 × 3 × x × x × x × y + 3 × 3 × 3 × 3 × x × x × x × x × y × у = 3 × 3 × 3 × x × x × x × y × (2 + 3 xy) = 27x 3 y (2 + 3 xy) 90 40 90 Квадратное уравнение методом факторизации (x + y) 2  – 4xy Ответ: 2  = х 2 + 2xy + y 2 (x + y) 2 — 4xy = x 2 + 2 y — 4xy = x 2 + 2 900 2 — 4x 2 — 2 — 2 2 — 4x 2 — 2 2 — 40150 . 2  + y 2  – 2xy Мы знаем, (x – y) 2  = x 2  + y 2  – 2xy Итак, факторизация x – y) 2 С помощью приведенных выше примеров вы получите представление о том, как факторизовать квадратные уравнения. ЗАГРУЗИТЬ ФАКТОРИЗАЦИЯ NCERT SOLUTIONS PDF ОТ ЗДЕСЬ Часто задаваемые вопросы о формулах факторизации Часто задаваемые вопросы о формулах факторизации приведены ниже: В. Что такое метод факторизации в математике? A. Факторизация обратна умножению. Сложные алгебраические, полиномиальные или квадратные уравнения разбиваются на более простые уравнения. Более простое уравнение при обратном умножении дает фактическое уравнение. Этот процесс известен как факторизация. Q. Дайте определение факторизации. A. Факторизация может быть определена как разложение сущности на множители таким образом, что при их перемножении получается исходная сущность. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт