Формула размещения с повторениями: Размещения с повторениями — урок. Алгебра, 11 класс.

Содержание

Формулы комбинаторики с повторениями. Перестановки

Чтобы в материале было легче ориентироваться, добавлю содержание данной темы:

Введение. Множества и выборки.

В этой теме рассмотрим основные понятия комбинаторики: перестановки, сочетания и размещения. Выясним их суть и формулы, по которым можно найти их количество.

Для работы нам понадобятся кое-какие вспомогательные сведения. Начнём с такого фундаментального математического понятия как множество. Подробно понятие множества было раскрыто в теме «Понятие множества. Способы задания множеств» .

Очень краткий рассказ про множества : показать\скрыть

Если вкратце: множеством именуют некую совокупность объектов. Записывают множества в фигурных скобках. Порядок записи элементов роли не играет; повторения элементов не допускаются. Например, множество цифр числа 11115555999 будет таким: $\{1,5,9 \}$. Множество согласных букв в слове «тигрёнок» таково: $\{т, г, р, н, к\}$. Запись $5\in A$ означает, что элемент 5 принадлежит множеству $A=\{1,5,9 \}$.

Количество элементов в конечном множестве называют мощностью этого множества и обозначают $|A|$. Например, для множества $A=\{1,5,9 \}$, содержащего 3 элемента, имеем: $|A|=3$.

Рассмотрим некое непустое конечное множество $U$, мощность которого равна $n$, $|U|=n$ (т.е. в множестве $U$ имеется $n$ элементов). Введём такое понятие, как выборка (некоторые авторы именуют её кортежем). Под выборкой объема $k$ из $n$ элементов (сокращённо $(n,k)$-выборкой) будем понимать набор элементов $(a_1, a_2,\ldots, a_k)$, где $a_i\in U$. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Две упорядоченные выборки, различающиеся лишь порядком элементов, являются различными. Если порядок следования элементов выборки не является существенным, то выборку именуют неупорядоченной.

Заметьте, что в определении выборки ничего не сказано про повторения элементов. В отличие от элементов множеств, элементы выборки могут повторяться.

Для примера рассмотрим множество $U=\{a,b,c,d,e\}$.

Множество $U$ содержит 5 элементов, т.е. $|U|=5$. Выборка без повторений может быть такой: $(a,b,c)$. Данная выборка содержит 3 элемента, т.е. объём этой выборки равен 3. Иными словами, это $(5,3)$-выборка.

Выборка с повторениями может быть такой: $(a,a,a,a,a,c,c,d)$. Она содержит 8 элементов, т.е. объём её равен 8. Иными словами, это $(5,8)$-выборка.

Рассмотрим ещё две $(5,3)$-выборки: $(a,b,b)$ и $(b,a,b)$. Если мы полагаем наши выборки неупорядоченными, то выборка $(a,b,b)$ равна выборке $(b,a,b)$, т.е. $(a,b,b)=(b,a,b)$. Если мы полагаем наши выборки упорядоченными, то $(a,b,b)\neq(b,a,b)$.

Рассмотрим ещё один пример, немного менее абстрактный:) Предположим, в корзине лежат шесть конфет, причём все они различны. Если первой конфете поставить в соответствие цифру 1, второй конфете — цифру 2 и так далее, то с конфетами в корзине можно сопоставить такое множество: $U=\{1,2,3,4,5,6\}$. Представьте, что мы наугад запускаем руку в корзинку с целью вытащить три конфеты. Вытащенные конфеты — это и есть выборка.

Так как мы вытаскиваем 3 конфеты из 6, то получаем (6,3)-выборку. Порядок расположения конфет в ладони совершенно несущественен, поэтому эта выборка является неупорядоченной. Ну, и так как все конфеты различны, то выборка без повторений. Итак, в данной ситуации говорим о неупорядоченной (6,3)-выборке без повторений.

Теперь подойдём с иной стороны. Представим себе, что мы находимся на фабрике по производству конфет, и на этой фабрике производятся конфеты четырёх сортов. Множество $U$ в этой ситуации таково: $U=\{1,2,3,4 \}$ (каждая цифра отвечает за свой сорт конфет). Теперь вообразим, что все конфеты ссыпаются в единый жёлоб, около которого мы и стоим. И, подставив ладони, из этого потока отбираем 20 конфет. Конфеты в горсти – это и есть выборка. Играет ли роль порядок расположения конфет в горсти? Естественно, нет, поэтому выборка неупорядоченная. Всего 4 сорта конфет, а мы отбираем двадцать штук из общего потока — повторения сортов неизбежны. При этом выборки могут быть самыми различными: у нас даже могут оказаться все конфеты одного сорта.

Следовательно, в этой ситуации мы имеем дело с неупорядоченной (4,20)-выборкой с повторениями.

Рассмотрим ещё пару примеров. Пусть на кубиках написаны различные 7 букв: к, о, н, ф, е, т, а. Эти буквы образуют множество $U=\{к,о,н,ф,е,т,а\}$. Допустим, из данных кубиков мы хотим составить «слова» из 5 букв. Буквы этих слов (к примеру, «конфе», «тенко» и так далее) образуют (7,5)-выборки: $(к,о,н,ф,е)$, $(т,е,н,к,о)$ и т.д. Очевидно, что порядок следования букв в такой выборке важен. Например, слова «нокфт» и «кфтон» различны (хотя состоят из одних и тех же букв), ибо в них не совпадает порядок букв. Повторений букв в таких «словах» нет, ибо в наличии только семь кубиков. Итак, набор букв каждого слова представляет собой упорядоченную (7,5)-выборку без повторений.

Еще один пример: мы составляем всевозможные восьмизначные числа из четырёх цифр 1, 5, 7, 8. Например, 11111111, 15518877, 88881111 и так далее. Множество $U$ таково: $U=\{1,5,7,8\}$. Цифры каждого составленного числа образуют (4,8)-выборку. {k}=\frac{n!}{(n-k)!} \end{equation}

Что обозначает знак «!»? : показать\скрыть

Запись «n!» (читается «эн факториал») обозначает произведение всех чисел от 1 до n, т.е.

$$ n!=1\cdot2\cdot 3\cdot \ldots\cdot n $$

По определению полагается, что $0!=1!=1$. Для примера найдём 5!:

$$ 5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120. $$

Пример №1

Алфавит состоит из множества символов $E=\{+,*,0,1,f\}$. Определим количество таких трёхсимвольных слов в этом алфавите, которые не содержат повторяющихся букв.

Под трёхсимвольными словами будем понимать выражения вида «+*0» или «0f1». В множестве $E$ пять элементов, поэтому буквы трехсимвольных слов образуют (5,3)-выборки. Первый вопрос: эти выборки упорядочены или нет? Слова, которые отличаются лишь порядком букв, полагаются различными, поэтому порядок элементов в выборке важен. Значит, выборка является упорядоченной. Второй вопрос: допускаются повторения или нет? Ответ на этот вопрос даёт условие: слова не должны содержать повторяющихся букв. {n}=\frac{n!}{(n-n)!}=\frac{n!}{0!}=\frac{n!}{1}=n! $$

Пример №3

В морозилке лежат пять порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения?

Пусть первому мороженому соответствует цифра 1, второму — цифра 2 и так далее. Мы получим множество $U=\{1,2,3,4,5\}$, которое будет представлять содержимое морозилки. Порядок съедения может быть таким: $(2,1,3,5,4)$ или таким: $(5,4,3,1,2)$. Каждый подобный набор есть (5,5)-выборка. Она будет упорядоченной и без повторений. Иными словами, каждая такая выборка есть перестановка из 5 элементов исходного множества. Согласно формуле (3) общее количество этих перестановок таково:

$$ P_5=5!=120. $$

Следовательно, существует 120 порядков выбора очередности съедения.

Ответ : 120.

Перестановки с повторениями

Перестановка с повторениями – упорядоченная $(n,k)$-выборка с повторениями, в которой элемент $a_1$ повторяется $k_1$ раз, $a_2$ повторяется $k_2$ раза так далее, до последнего элемента $a_r$, который повторяется $k_r$ раз. При этом $k_1+k_2+\ldots+k_r=k$.

Общее количество перестановок с повторениями определяется формулой:

\begin{equation}P_{k}(k_1,k_2,\ldots,k_r)=\frac{k!}{k_1!\cdot k_2!\cdot \ldots \cdot k_r!} \end{equation}

Пример №4

Слова составляются на основе алфавита $U=\{a,b,d\}$. Сколько различных слов из семи символов может быть составлено, если в этих словах буква «a» должна повторяться 2 раза; буква «b» — 1 раз, а буква «d» — 4 раза?

Вот примеры искомых слов: «aabdddd», «daddabd» и так далее. Буквы каждого слова образуют (3,7)-выборку с повторениями: $(a,a,b,d,d,d,d)$, $(d,a,d,d,a,b,d)$ и т.д. Каждая такая выборка состоит из двух элементов «a», одного элемента «b» и четырёх элементов «d». Иными словами, $k_1=2$, $k_2=1$, $k_3=4$. Общее количество повторений всех символов, естественно, равно объёму выборки, т.е. $k=k_1+k_2+k_3=7$. Подставляя эти данные в формулу (4), будем иметь:

$$ P_7(2,1,4)=\frac{7!}{2!\cdot 1!\cdot 4!}=105. $$

Следовательно, общее количество искомых слов равно 105.

{k}=\frac{n!}{(n-k)!\cdot k!} \end{equation}

Пример №5

В корзине размещены карточки, на которых написаны целые числа от 1 до 10. Из корзины вынимают 4 карточки и суммируют числа, написанные на них. Сколько различных наборов карточек можно вытащить из корзины?

Итак, в данной задаче исходное множество таково: $U=\{1,2,3,4,5,6,7,8,9,10\}$. Из этого множества мы выбираем четыре элемента (т.е., четыре карточки из корзины). Номера вытащенных элементов образуют (10,4)-выборку. Повторения в этой выборке не допускаются, так как номера всех карточек различны. Вопрос вот в чём: порядок выбора карточек играет роль или нет? Т.е., к примеру, равны ли выборки $(1,2,7,10)$ и $(10,2,1,7)$ или не равны? Тут нужно обратиться к условию задачи. Карточки вынимаются для того, чтобы потом найти сумму элементов. А это значит, что порядок карточек не важен, так как от перемены мест слагаемых сумма не изменится. Например, выборке $(1,2,7,10)$ и выборке $(10,2,1,7)$ будет соответствовать одно и то же число $1+2+7+10=10+2+1+7=20$.

{k}=\frac{(n+k-1)!}{(n-1)!\cdot k!} \end{equation}

Пример №6

Представьте себе, что мы находимся на конфетном заводе, — прямо возле конвейера, по которому движутся конфеты четырёх сортов. Мы запускаем руки в этот поток и вытаскиваем двадцать штук. Сколько всего различных «конфетных комбинаций» может оказаться в горсти?

Если принять, что первому сорту соответствует число 1, второму сорту — число 2 и так далее, то исходное множество в нашей задаче таково: $U=\{1,2,3,4\}$. Из этого множества мы выбираем 20 элементов (т.е., те самые 20 конфет с конвейера). Пригоршня конфет образует (4,20)-выборку. Естественно, повторения сортов будут. Вопрос в том, играет роль порядок расположения элементов в выборке или нет? Из условия задачи следует, что порядок расположения элементов роли не играет. Нам нет разницы, будут ли в горсти располагаться сначала 15 леденцов, а потом 4 шоколадных конфеты, или сначала 4 шоколадных конфеты, а уж потом 15 леденцов. Итак, мы имеем дело с неупорядоченной (4,20) выборкой с повторениями.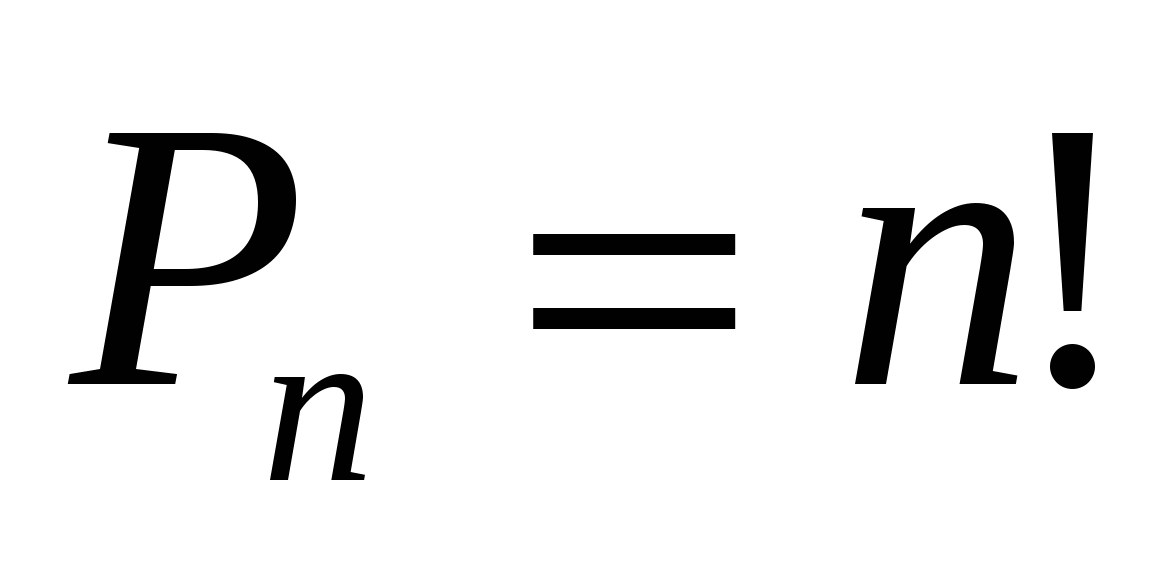

{20}=\frac{(4+20-1)!}{(4-1)!\cdot 20!}=\frac{23!}{3!\cdot 20!}=1771. $$

Следовательно, общее количество искомых комбинаций равно 1771.

Комбинаторикой называется раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Правило умножения (основная формула комбинаторики)

Общее число способов, которыми можно выбрать по одному элементу из каждой группы и расставить их в определенном порядке (то есть получить упорядоченную совокупность ), равно:

Пример 1

Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?

Решение

Первая монета имеет альтернативы – либо орел, либо решка. Для второй монеты также есть альтернативы и т.д., т.е. .

Искомое количество способов:

Правило сложения

Если любые две группы и не имеют общих элементов, то выбор одного элемента или из , или из , …или из можно осуществить способами.

Пример 2

На полке 30 книг, из них 20 математических, 6 технических и 4 экономических. Сколько существует способов выбора одной математической или одной экономической книги.

Решение

Математическая книга может быть выбрана способами, экономическая — способами.

По правилу суммы существует способа выбора математической или экономической книги.

Размещения и перестановки

Размещения – это упорядоченные совокупности элементов, отличающиеся друг от друга либо составом, либо порядком элементов.

Размещения без повторений , когда отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется последовательным выбором без возвращения, а его результат – размещением без повторений из элементов по .

Число различных способов, которыми можно произвести последовательный выбор без возвращения элементов из генеральной совокупности объема , равно:

Пример 3

Расписание дня состоит из 5 различных уроков. Определите число вариантов расписания при выборе из 11 дисциплин.

Решение

Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом, так и порядком следования. поэтому:

Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов. Число всех перестановок множества из элементов равно

Пример 4

Сколькими способами можно рассадить 4 человек за одним столом?

Решение

Каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:

Размещения с повторениями , когда отобранный элемент перед отбором следующего возвращается в генеральную совокупность. Такой выбор называется последовательным выбором с возвращением, а его результат — размещением с повторениями из элементов по .

Общее число различных способов, которыми можно произвести выбор с возвращением элементов из генеральной совокупности объема , равно

Пример 5

Лифт останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?

Чтобы решение задачи по теории вероятностей было максимально точным и верным, многие недорого заказывают контрольную работу на этом сайте. Подробно (как оставить заявку, цены, сроки, способы оплаты) можно почитать на странице Купить контрольную работу по теории вероятностей…

Решение

Каждый из способов распределения пассажиров по этажам представляет собой комбинацию 6 пассажиров по 7 этажам, отличающуюся от других комбинаций как составом, так и их порядком. Так как одном этаже может выйти как один, так и несколько пассажиров, то одни и те же пассажиры могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 7 элементов по 6:

Сочетания

Сочетаниями из n элементов по k называются неупорядоченные совокупности, отличающиеся друг от друга хотя бы одним элементом.

Пусть из генеральной совокупности берется сразу несколько элементов (либо элементы берут последовательно, но порядок их появления не учитывается). В результате такого одновременного неупорядоченного выбора элементов из генеральной совокупности объема получаются комбинации, которые называются сочетаниями без повторений из элементов по .

Число сочетаний из элементов по равно:

Пример 6

В ящике 9 яблок. Сколькими способами можно выбрать 3 яблока из ящика?

Решение

Каждый вариант выбора состоит из 3 яблок и отличается от других только составом, то есть представляет собой сочетания без повторений из 9 элементов:

Количество способов, которыми можно выбрать 3 яблока из 9:

Пусть из генеральной совокупности объема выбирается элементов, один за другим, причем каждый отобранный элемент перед отбором следующего возвращается в генеральную совокупность. При этом ведется запись, какие элементы появились и сколько раз, однако порядок их появления не учитывается. Получившиеся совокупности называются сочетаниями с повторениями из элементов по .

Число сочетаний с повторениями из элементов по :

Пример 7

На почте продают открытки 3 видов. Сколькими способами можно купить 6 открыток?

Это задача на отыскание числа сочетаний с повторениями из 3 по 6:

Разбиение множества на группы

Пусть множество из различных элементов разбивается на групп так, то в первую группу попадают элементов, во вторую — элементов, в -ю группу — элементов, причем . Такую ситуацию называют разбиением множества на группы.

Число разбиений на групп, когда в первую попадают элементов, во вторую — элементов, в k-ю группу — элементов, равно:

Пример 8

Группу из 16 человек требуется разбить на три подгруппы, в первой из которых должно быть 5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно сделать?

Решение

Здесь

Число разбиений на 3 подгруппы:

Излагается понятие геометрического закона распределения дискретной случайной величины и рассматривается пример решения задачи. Приведены формулы математического ожидания и дисперсии случайной величины, распределенной по геометрическому закону.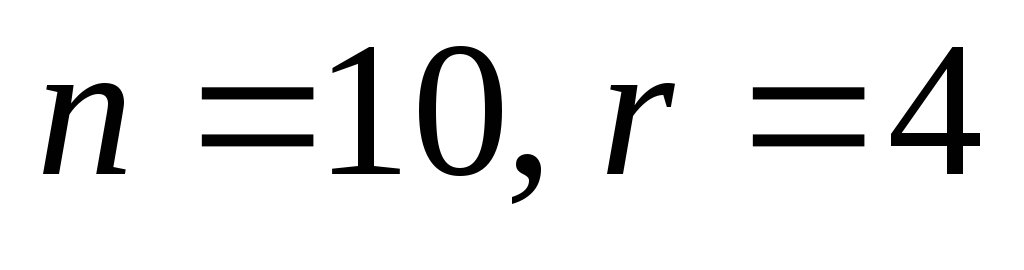

Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N , состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т.е. при изменении порядка переходим к другой m – выборке.

Сформулируем следующие определения:

Размещения без повторения

Размещением без повторения из n элементов по m N , содержащее m различных элементов .

Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы.

Теорема 3 . Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n . Записывают:

Перестановки без повторений

Перестановками из n элементов называются различные упорядочения множества N .

Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений.

Теорема 4 . Число различных перестановок без повторений вычисляется по формуле

Сочетания без повторений

Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N , содержащее m различных элементов.

Из определения следует, что два сочетания различаются только элементами, порядок не важен.

Теорема 5 . Число сочетаний без повторений вычисляют по одной из следующих формул:

Пример 1 . В комнате 5 стульев. Сколькими способами можно разместить на них

а) 7 человек; б) 5 человек; в) 3 человека?

Решение: а) Прежде всего надо выбрать 5 человек из 7 для посадки на стулья. Это можно сделать
способом. С каждым выбором конкретной пятерки можно произвести
перестановок местами.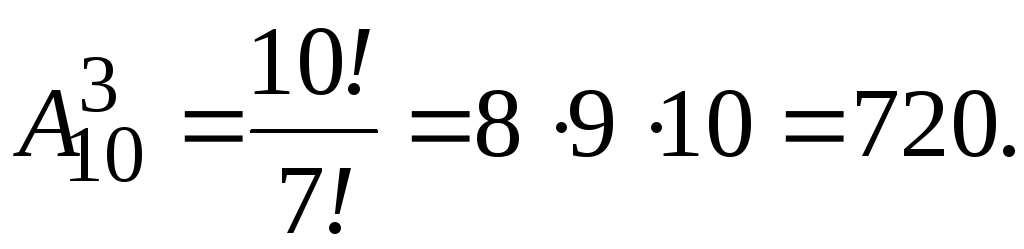 Согласно теореме умножения искомое число способов посадки равно.

Замечание: Задачу можно решать, используя только теорему произведения, рассуждая следующим образом: для посадки на 1-й стул имеется 7 вариантов, на 2-й стул-6 вариантов, на 3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов посадки 7 человек на 5 стульев равно . Решения обоими способами согласуются, так как

б) Решение очевидно —

в) — число выборов занимаемых стульев.

— число размещений трех человек на трех выбранных стульях.

Общее число выборов равно .

Не трудно проверить формулы
;

;

Число всех подмножеств множества, состоящего из n элементов.

Размещения с повторением

Размещением с повторением из n элементов по m называется всякое упорядоченное подмножество множества N , состоящее из m элементов так, что любой элемент ожжет входить в это подмножество от 1 до m раз, либо вообще в нем отсутствовать .

Число размещений с повторением обозначают и вычисляют по формуле, представляющей собой следствие из теоремы умножения:

Пример 2 . Пусть дано множество из трех букв N = {a, b, c}. Назовем словом любой набор из букв, входящих в это множество. Найдем количество слов длиной 2, которые можно составить из этих букв:
.

Замечание: Очевидно, размещения с повторением можно рассматривать и при
.

Пример 3 . Требуется из букв {a, b}, составить всевозможные слова длиной 3. Сколькими способами это можно сделать?

Ответ :

Цель занятия: уметь применять основные формулы комбинаторики и знать условия применения этих формул; знать свойства биномиальных коэффициентов и уметь определять разложение бинома при конкретных значениях n.

План занятия:

1. Число размещений.

2. Число перестановок.

3. Число сочетаний.

4. Повторения.

5. Бином Ньютона. Треугольник Паскаля.

Методические указания по изучению темы

Во многих практических случаях возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определенным условиям. Такие задачи называются комбинаторными. Разнообразие комбинаторных задач не поддается исчерпывающему описанию, но среди них есть целый ряд особенно часто встречающихся, для которых известны способы подсчета.

Комбинаторика – область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству. Термин «комбинаторика» происходит от латинского слова combina – сочетать, соединять.

Пусть есть некоторое множество из n элементов: x 1, x 2, x 3, …, x n .

Из этого множества можно образовать различные подмножества, то есть выборки, каждая из которых содержит m элементов (0 ≤ m ≤ n). Различают упорядоченные выборки (размещения), перестановки и неупорядоченные выборки (сочетания).

Размещения

Размещениями n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.

Число размещений из n элементов по m элементов обозначают (А – первая буква французского слова arrangement, что означает размещение, приведение в порядок) и вычисляют по формуле:

Понятие факториала

Произведение n натуральных чисел от 1 до n обозначается символом n ! (n факториал), то есть

Например, 2!=

5!=

Заметим, что удобно рассчитывать 0!, полагая по определению, 0!=1.

Примеры:

Из последних двух формул следует, что

Пример.

В однокруговом турнире по футболу участвуют 8 команд. Сколько существует вариантов призовой тройки?

Решение : Так как порядок команд в призовой тройке важен, то мы имеем дело с размещениями. Тогда

(вариантов).

Пример.

Сколькими способами можно выбрать три лица на три различные должности из десяти кандидатов?

Решение:

(способов).

Пример.

Сколько можно составить телефонных номеров из 5 цифр так, чтобы в каждом отдельно взятом номере все цифры были различными?

(телефонных номеров).

Перестановки

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.

Число всех возможных перестановок из n элементов обозначают P n (P – первая буква французского слова permutation, что означает перестановка) и вычисляют по формуле:

Пример.

В финальном забеге на 100 метров участвуют 8 спортсменов. Сколько существует вариантов протокола забега?

Решение:

В данном случае речь идёт обо всех перестановках из 8 элементов. Тогда (вариантов)

Пример.

Сколькими различными способами могут разместиться на скамейке10 человек?

Решение:

(способов)

Пример.

Сколькими способами можно разместить 7 лиц за столом, на котором поставлено 7 столовых приборов?

Решение:

(способов).

Сочетания

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом.

Число сочетаний вычисляют по формуле: (С — первая буква французского слова combinasion).

Пример.

Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов?

Решение :

(способов).

Пример.

Сколькими способами можно выбрать три детали из ящика, содержащего 15 деталей?

Решение:

(способов).

Другой вид формул числа размещений и числа сочетаний

; , то есть .

Свойства числа сочетаний:

При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В – k способами, то объект «либо А, либо В» можно выбрать n+k способами.

Правило произведения. Если некоторый объект А может быть выбран из совокупности объектов n способами и после каждого такого выбора другой объект В – k способами, то пара объектов (А, В) в указанном порядке может быть выбрана n×k способами.

Если некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.

Размещения с повторениями

Число размещений по m элементов с повторениями из n различных элементов равно n m ,то есть

Пример.

Из цифр 1,2,3,4,5 можно составить 5 3 =125 трехзначных чисел, если в одном и том же числе могут попадаться и одинаковые цифры.

Перестановки с повторениями

Если среди n элементов есть n 1 элементов одного вида, n 2 элементов другого вида и т.д., то число перестановок с повторениями

где

Пример.

Сколько различных перестановок букв можно сделать в слове «математика»?

Решение:

Сочетания с повторениями

Число сочетаний с повторениями из n различных элементов по m элементов равно числу сочетаний без повторений из (n +m -1) различных элементов по m элементов:

Пример.

Найти число сочетаний с повторениями из четырех элементов a , b , c , d по 3 элемента.

Решение:

Искомое число будет

Бином Ньютона

Для произвольного положительного целого числа n справедлива следующая формула:

Это бином Ньютона. Коэффициенты называются биномиальными коэффициентами.

При n = 2 получим формулу ;

При n = 3 получим формулу .

Пример. Определить разложение при n=4.

Решение:

Биномиальные коэффициенты обладают рядом свойств:

2. ;

Рассмотрим следующий треугольник:

………………………….

Строка под номером n содержит биномиальные коэффициенты разложения . Воспользовавшись свойством , можно заметить, что каждый внутренний элемент треугольника равен сумме двух элементов, расположенных над ним, а боковые элементы треугольника – единицы:

……………………….

Это треугольник Паскаля. Он позволяет быстро найти значения биномиальных коэффициентов.

В русскоязычной литературе перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются либо составом элементов, либо их порядком, обычно называют размещениями, а под перестановками понимают всю совокупность комбинаций, состоящих из одних и тех же n различных элементов и отличающихся только порядком их расположения. В этом смысле число всех возможных перестановок для множества из n различных элементов считается по формуле факториала Pn = n! или в Excel «=ФАКТР(N)» (см. рис. № 1)

Например, если ввести «=ПЕРЕСТ(3;2)», получим 6. Это 6 комбинации: (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).

А вот встроенная функция «=ЧИСЛКОМБ(N;K)» выдает комбинаторную формулу, называемую у нас «Число сочетаний». В русскоязычной литературе так именуют перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются только составом элементов, а порядок их выбора безразличен (см. рис, №4)

При использовании встроенных функций пользуйтесь «Справкой по этой функции». Например:

Задачи для самостоятельного решения

1. Вычислить:

2. Вычислить:

3. Вычислить:

4. Найти n , если 5С n 3 =

5. Найти n , если

6. Найти n , если

7. Найти n , если

8. Найти n , если , k n

9. Решить уравнение

10. Решить систему

11. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?

12. Сколькими способами можно выбрать четыре лица на четыре различные должности из девяти кандидатов?

13. Сколько можно составить телефонных номеров из 6 цифр так, чтобы в каждом отдельно взятом номере все цифры были различны?

14. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в один день?

15. Сколько можно записать четырёхзначных чисел, используя без повторения все 10 цифр?

16. Фирма производит выбор из девяти кандидатов на три различные должности. Сколько существует способов такого выбора?

17. В восьмом классе изучается 15 предметов. Сколькими способами можно составить расписание на среду, если известно, что в этот день должно быть 6 уроков?

18. В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?

19. Сколькими способами можно разместить 9 лиц за столом, на котором поставлено 9 приборов?

20. На собрании выступят 6 ораторов. Сколькими способами их фамилии можно расположить в списке?

21. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?

22. Сколькими различными способами можно расставить 10 различных книг на полке, чтобы определённые 4 книги стояли рядом?

23. В однокруговом турнире по футболу участвуют 8 команд. Сколько всего матчей будет сыграно?

24. Из 25 студентов нужно выбрать трех делегатов на конференцию. Сколькими способами это можно сделать?

25. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

26. В колоде 36 карт, из них 4 туза. Сколькими способами можно извлечь 6 карт так, чтобы среди них было 2 туза?

27. Комплексная бригада состоит из двух маляров, трёх штукатуров и одного столяра. Сколько различных бригад можно создать из рабочего коллектива, в котором 15 маляров, 10 штукатуров и 5 столяров?

28. В отборочном турнире за 3 путёвки на чемпионат мира участвуют 10 команд.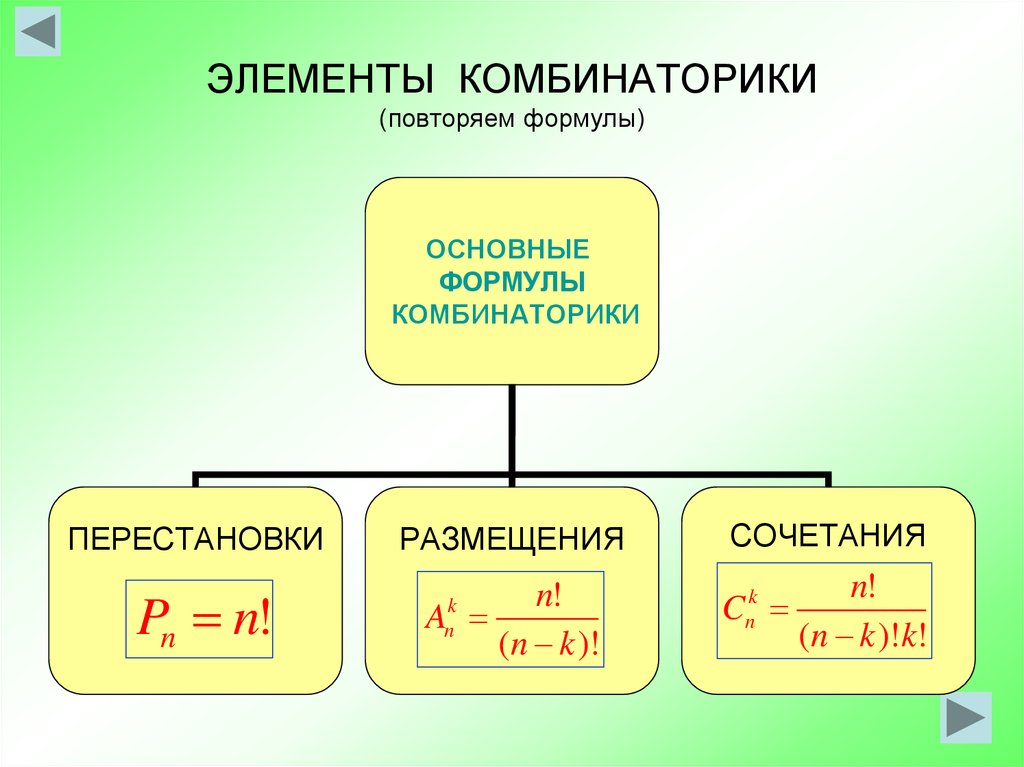 Сколько существует вариантов «счастливой тройки»?

29. Из 12 человек выбирают четверых для назначения на 4 одинаковые должности. Сколькими способами можно сделать такой выбор?

30. Сколькими различными способами можно составить разведывательную группу из 3-х солдат и одного командира, если имеется 12 солдат и 3 командира?

31. На плоскости дано n точек, из которых никакие три не лежат на одной прямой. Найти число прямых, которые можно получить, соединяя точки попарно.

32. Буквы азбуки Морзе образуются как последовательность точек и тире. Сколько различных букв можно образовать, если использовать 5 символов?

33. Сколько существует различных семизначных телефонных номеров?

34. Пусть буквы некоторой азбуки образуются как последовательность точек, тире и пробелов. Сколько различных букв можно образовать, если использовать 5 символов?

35. При игре в бридж между четырьмя игроками распределяется колода карт в 52 листа по 13 карт каждому игроку. Сколько существует различных способов раздать карты?

36. В почтовом отделении продаются открытки пяти видов. Определить число способов покупки семи открыток.

37. Два коллекционера обмениваются марками. Найти число способов обмена, если первый коллекционер обменивает 3 марки, а второй – 6 марок. (Обмен происходит по одной марке).

38. У одного студента 6 книг по математике, а у другого – 5. Сколькими способами они могут обменять 2 книги одного на 2 книги другого?

39. Сколько различных перестановок букв можно сделать в словах: «замок», «ротор», «обороноспособность», «колокол», «семинар»?

40. Сколькими различными способами можно разместить в 9 клетках следующие 9 букв: а, а, а, б, б, б, в, в, в?

41. В автомашине 6 мест. Сколькими способами 6 человек могут сесть в эту машину, если занять место водителя могут только двое из них?

42. Сколькими способами из колоды в 52 карты можно извлечь 6 карт, содержащих туза и короля одной масти?

43. Определить разложение при n=5.

44. Определить разложение при n=8.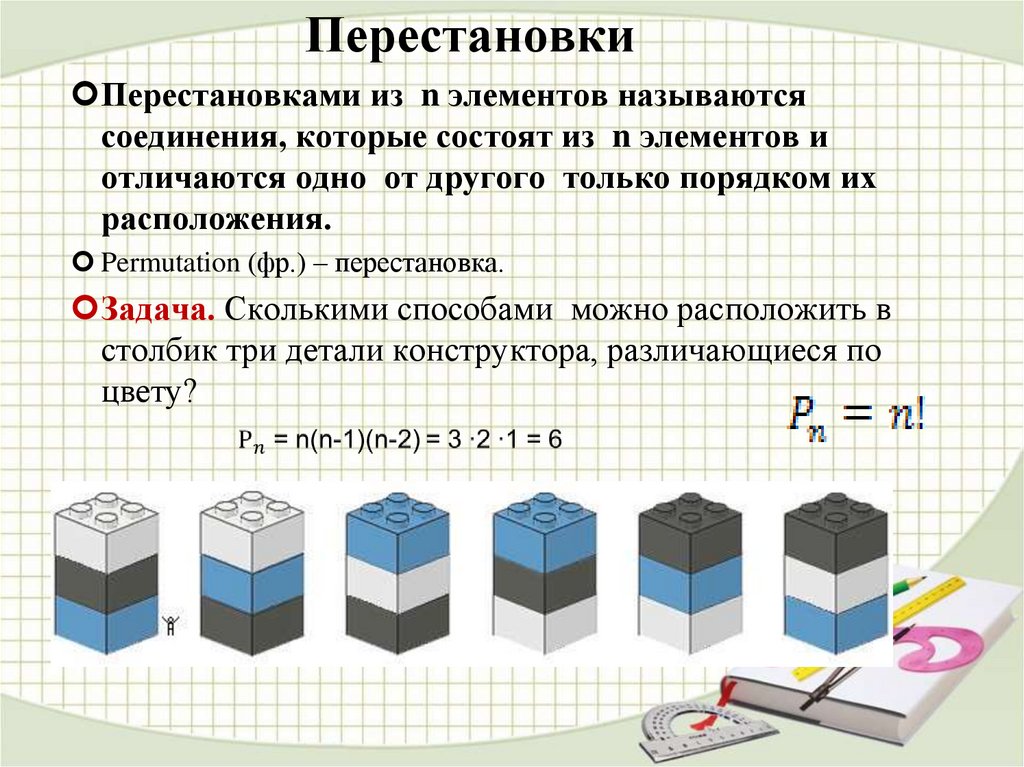

45. Найти член разложения , не содержащий x (то есть содержащий x в нулевой степени).

46. Найти шестой член разложения , если биномиальный коэффициент третьего от конца члена равен 45.

47. В разложении коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, то есть член разложения, не зависящий от x (членом, не зависящим от x, будет тот, который содержит x в нулевой степени).

48. В разложении бинома найти члены, не содержащие иррациональности.

49. Найти номер того члена разложения , который содержит a и b в одинаковых степенях.

Практическое занятие №2

(интерактивное занятие в малых группах)

Булевы функции

Цель занятия: уметь строить различные булевы функции, проверять эквивалентность булевых формул (используя таблицу истинности), определять существенные и фиктивные переменные.

План занятия:

1. Основные операции

2. Булевы функции от n переменных

3. Основные эквивалентности

В данной статье речь пойдет об особом разделе математики под названием комбинаторика. Формулы, правила, примеры решения задач — все это вы сможете найти здесь, прочитав статью до самого конца.

Итак, что же это за раздел? Комбинаторика занимается вопросом подсчета каких-либо объектов. Но в данном случае объектами выступают не сливы, груши или яблоки, а нечто иное. Комбинаторика помогает нам находить вероятность какого-либо события. Например, при игре в карты — какова вероятность того, что у противника есть козырная карта? Или такой пример — какова вероятность того, что из мешка с двадцатью шариками вы достанете именно белый? Именно для подобного рода задач нам и нужно знать хотя бы основы данного раздела математики.

Комбинаторные конфигурации

Рассматривая вопрос основных понятий и формул комбинаторики, мы не можем не уделить внимание комбинаторным конфигурациям. Они используются не только для формулировки, но и для решения различных Примерами таких моделей служат:

размещение;
перестановка;
сочетание;
композиция числа;
разбиение числа.

О первых трех мы поговорим более подробно далее, а вот композиции и разбиению мы уделим внимание в данном разделе. Когда говорят о композиции некого числа (допустим, а), то подразумевают представление числа а в виде упорядоченной суммы неких положительных чисел. А разбиение — это неупорядоченная сумма.

Разделы

Прежде чем мы перейдем непосредственно к формулам комбинаторики и рассмотрению задач, стоит обратить внимание на то, что комбинаторика, как и другие разделы математики, имеет свои подразделы. К ним относятся:

перечислительная;
структурная;
экстремальная;
теория Рамсея;
вероятностная;
топологическая;
инфинитарная.

В первом случае речь идет об исчисляющей комбинаторике, задачи рассматривают перечисление или подсчет разных конфигураций, которые образованы элементами множеств. На данные множества, как правило, накладываются какие-либо ограничения (различимость, неразличимость, возможность повтора и так далее). А количество этих конфигураций подсчитывается при помощи правила сложения или умножения, о которых мы поговорим немного позже. К структурной комбинаторике относятся теории графов и матроидов. Пример задачи экстремальной комбинаторики — какова наибольшая размерность графа, который удовлетворяет следующим свойствам… В четвертом пункте мы упомянули теорию Рамсея, которая изучает в случайных конфигурациях наличие регулярных структур. Вероятностная комбинаторика способна нам ответить на вопрос — какова вероятность того, что у заданного множества присутствует определенное свойство. Как нетрудно догадаться, топологическая комбинаторика применяет методы в топологии. И, наконец, седьмой пункт — инфинитарная комбинаторика изучает применение методов комбинаторики к бесконечным множествам.

Правило сложения

Среди формул комбинаторики можно найти и довольно простые, с которыми мы достаточно давно знакомы. Примером является правило суммы. Предположим, что нам даны два действия (С и Е), если они взаимоисключаемы, действие С выполнимо несколькими способами (например а), а действие Е выполнимо b-способами, то выполнить любое из них (С или Е) можно а+b способами.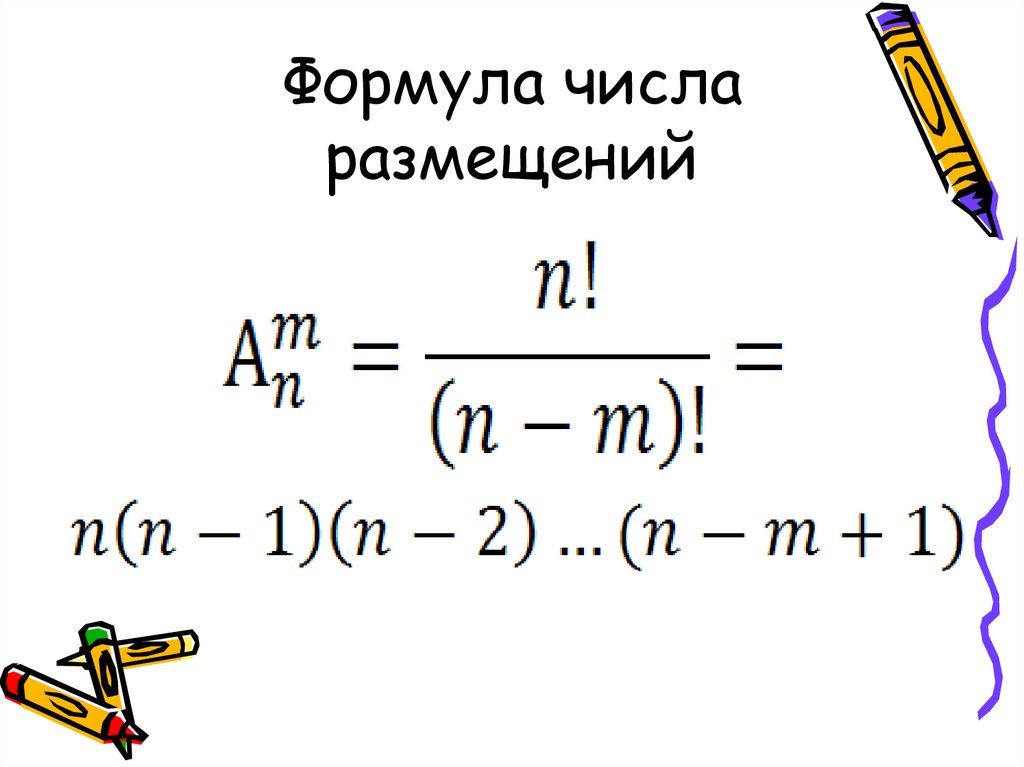

В теории это понять достаточно трудно, постараемся донести всю суть на простом примере. Возьмем среднюю численность учеников одного класса — допустим, это двадцать пять. Среди них пятнадцать девочек и десять мальчиков. Ежедневно в классе назначается один дежурный. Сколько есть способов назначить дежурного по классу сегодня? Решение задачи достаточно простое, мы прибегнем к правилу сложения. В тексте задачи не сказано, что дежурными могут быть только мальчики или только девочки. Следовательно, им может оказаться любая из пятнадцати девочек или любой из десяти мальчиков. Применяя правило суммы, мы получаем достаточно простой пример, с которым без труда справится школьник начальных классов: 15 + 10. Подсчитав, получаем ответ: двадцать пять. То есть существует всего двадцать пять способов назначить на сегодня дежурного класса.

Правило умножения

К основным формулам комбинаторики относится и правило умножения. Начнем с теории. Допустим, нам необходимо выполнить несколько действий (а): первое действие выполняется с1 способами, второе — с2 способами, третье — с3 способами и так далее до последнего а-действия, выполняемого са способами. Тогда все эти действия (которых всего у нас а) могут быть выполнены N способами. Как высчитать неизвестную N? В этом нам поможет формула: N = с1 * с2 * с3 *…* са.

Опять же, в теории ничего не понятно, переходим к рассмотрению простого примера на применение правила умножения. Возьмем все тот же класс из двадцати пяти человек, в котором учится пятнадцать девочек и десять мальчиков. Только на этот раз нам необходимо выбрать двух дежурных. Ими могут быть как только мальчики или девочки, так и мальчик с девочкой. Переходим к элементарному решению задачи. Выбираем первого дежурного, как мы решили в прошлом пункте, у нас получается двадцать пять возможных вариантов. Вторым дежурным может быть любой из оставшихся человек. У нас было двадцать пять учеников, одного мы выбрали, значит вторым дежурным может быть любой из оставшихся двадцати четырех человек. Наконец, применяем правило умножения и получаем, что двоих дежурных можно избрать шестью сотнями способов. Мы данное число получили умножением двадцати пяти и двадцати четырех.

Перестановка

Сейчас мы рассмотрим еще одну формулу комбинаторики. В данном разделе статьи мы поговорим о перестановках. Рассмотреть проблему предлагаем сразу же на примере. Возьмем бильярдные шары у нас их n-ое количество. Нам нужно подсчитать: сколько есть вариантов расставить их в ряд, то есть составить упорядоченный набор.

Начнем, если у нас нет шаров, то и вариантов расстановки у нас так же ноль. А если у нас шар один, то и расстановка тоже одна (математически это можно записать следующим образом: Р1 = 1). Два шара можно расставить двумя разными способами: 1,2 и 2,1. Следовательно, Р2 = 2. Три шара можно расставить уже шестью способами (Р3=6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. А если таких шаров не три, а десять или пятнадцать? Перечислять все возможные варианты очень долго, тогда нам на помощь приходит комбинаторика. Формула перестановки поможет нам найти ответ на интересующий нас вопрос. Pn = n *P (n-1). Если попытаться упростить формулу, то получаем: Pn = n* (n — 1) *…* 2 * 1. А это и есть произведение первых натуральных чисел. Такое число называется факториалом, а обозначается как n!

Рассмотрим задачу. Вожатый каждое утро выстраивает свой отряд в шеренгу (двадцать человек). В отряде есть три лучших друга — Костя, Саша и Леша. Какова вероятность того, что они будут стоять рядом? Чтобы найти ответ на вопрос, нужно вероятность «хорошего» исхода поделить на общее количество исходов. Общее число перестановок составляет 20! = 2,5 квинтиллиона. Как посчитать количество «хороших» исходов? Предположим, что Костя, Саши и Леша — это один сверхчеловек. Тогда мы имеем всего восемнадцать субъектов. Число перестановок в данном случае равняется 18 = 6,5 квадриллионов. При всем этом, Костя, Саша и Леша могут произвольно перемещаться между собой в своей неделимой тройке, а это еще 3! = 6 вариантов. Значит всего «хороших» расстановок у нас 18! * 3! Нам остается только найти искомую вероятность: (18! * 3!) / 20! Что равняется примерно 0,016. Если перевести в проценты, то это получается всего 1,6%.

Размещение

Сейчас мы рассмотрим еще одну очень важную и необходимую формулу комбинаторики. Размещение — это наш следующий вопрос, который предлагаем вам рассмотреть в данном разделе статьи. Мы идем на усложнение. Предположим, что мы хотим рассмотреть возможные перестановки, только не из всего множества (n), а из меньшего (m). То есть мы рассматриваем перестановки из n предметов по m.

Основные формулы комбинаторики стоит не просто заучивать, а понимать их. Даже несмотря на то, что они усложняются, так как у нас не один параметр, а два. Предположим, что m = 1, то и А = 1, m = 2, то А = n * (n — 1). Если далее упрощать формулу и перейти на запись при помощи факториалов, то получится вполне лаконичная формула: А = n! / (n — m)!

Сочетание

Мы рассмотрели практически все основные формулы комбинаторики с примерами. Теперь перейдем к заключительному этапу рассмотрения базового курса комбинаторики — знакомство с сочетанием. Сейчас мы будем выбирать m предметов из имеющихся у нас n, при этом всем мы будем выбирать всеми возможными способами. Чем же тогда это отличается от размещения? Мы не будем учитывать порядок. Этот неупорядоченный набор и будет являться сочетанием.

Сразу введем обозначение: С. Берем размещения m шариков из n. Мы перестаем обращать внимание на порядок и получаем повторяющиеся сочетания. Чтобы получить число сочетаний нам надо поделить число размещений на m! (m факториал). То есть С = А / m! Таким образом, способов выбрать из n шаров немножко, равняется примерно столько, сколько выбрать почти все. Этому есть логическое выражение: выбрать немножко все равно, что выкинуть почти все. Еще в данном пункте важно упомянуть и то, что максимальное число сочетаний можно достигнуть при попытке выбрать половину предметов.

Как выбрать формулу для решения задачи?

Мы подробно рассмотрели основные формулы комбинаторики: размещение, перестановка и сочетание. Теперь наша задача — облегчить выбор необходимой формулы для решения задачи по комбинаторике. Можно воспользоваться следующей довольно простой схемой:

Задайте себе вопрос: порядок размещения элементов учитывается в тексте задачи?
Если ответ нет, то воспользуйтесь формулой сочетания (С = n! / (m! * (n — m)!)).
Если ответ нет, то необходимо ответить на еще один вопрос: все ли элементы входят в комбинацию?
Если ответ да, то воспользуйтесь формулой перестановки (Р = n!).
Если ответ нет, то воспользуйтесь формулой размещения (А = n! / (n — m)!).

Пример

Мы рассмотрели элементы комбинаторики, формулы и некоторые другие вопросы. Теперь перейдем к рассмотрению реальной задачи. Представьте, что перед вами лежат киви, апельсин и банан.

Вопрос первый: сколькими способами их можно переставить? Для этого воспользуемся формулой перестановок: Р = 3! = 6 способов.

Вопрос второй: сколькими способами можно выбрать один фрукт? Это очевидно, у нас всего три варианта — выбрать киви, апельсин или банан, но применим формулу сочетаний: С = 3! / (2! * 1!) = 3.

Вопрос третий: сколькими способами можно выбрать два фрукта? Какие есть у нас вообще варианты? Киви и апельсин; киви и банан; апельсин и банан. То есть три варианта, но это легко проверить при помощи формулы сочетания: С = 3! / (1! * 2!) = 3

Вопрос четвертый: сколькими способами можно выбрать три фрукта? Как видно, выбрать три фрукта можно одним-единственным способом: взять киви, апельсин и банан. С = 3! / (0! * 3!) = 1.

Вопрос пятый: сколькими способами можно выбрать хотя бы один фрукт? Это условие подразумевает, что мы можем взять один, два или все три фрукта. Следовательно, мы складываем С1 + С2 + С3 =3 + 3 + 1 = 7. То есть у нас есть семь способов взять со стола хотя бы один фрукт.

Комбинаторика

Замечание 1

При решении многих практических задач часто приходится выбирать из некоторой совокупности объектов элементы, которым свойственны те или иные особенности, размещать элементы в некотором порядке, подсчитывать их количества и т.п. Поскольку в таких задачах речь идёт о комбинациях объектов, их называют комбинаторными.

Основные элементы комбинаторики, используемые при решении комбинаторных задач, таковы:

Правила суммы и произведения;
Перестановки без повторений;
Размещения без повторений;
Сочетания без повторений;
Перестановки с повторениями;
Размещения с повторениями;
Сочетания с повторениями.

Правило произведения

Если элемент a множества $A$ можно выбрать $m$ способами и при каждом из этих выборов элемент $b$ множества $B$ можно выбрать $n$ способами, то упорядоченную пару ($a$;$b$) можно выбрать $m$•$n$ способами.

Правило суммы

Если элемент $a$ из множества $A$ можно выбрать $m$ способами, а элемент $b$ из множества $B$ можно выбрать $n$ способами, то число способов, которыми можно осуществить выбор хотя бы одного элемента $a$ или $b$, равно сумме $m$+$n$.

Предполагается, что выборы $a$ и $b$ взаимно исключительны, то есть ни один из способов выбора элемента a не совпадает со способом выбора элемента $b$. При наличии таких совпадений результат выбора будет равен $m$+$n$-$p$,где $p$-количество совпадений.

Замечание 2

Правила суммы и произведения справедливы не только для двух, но и для любого числа объектов.

При выборе элементов по правилу суммы используется соединитель «или»‘ (выбираем элемент из первого конечного множества, или из второго, или из третьего и т.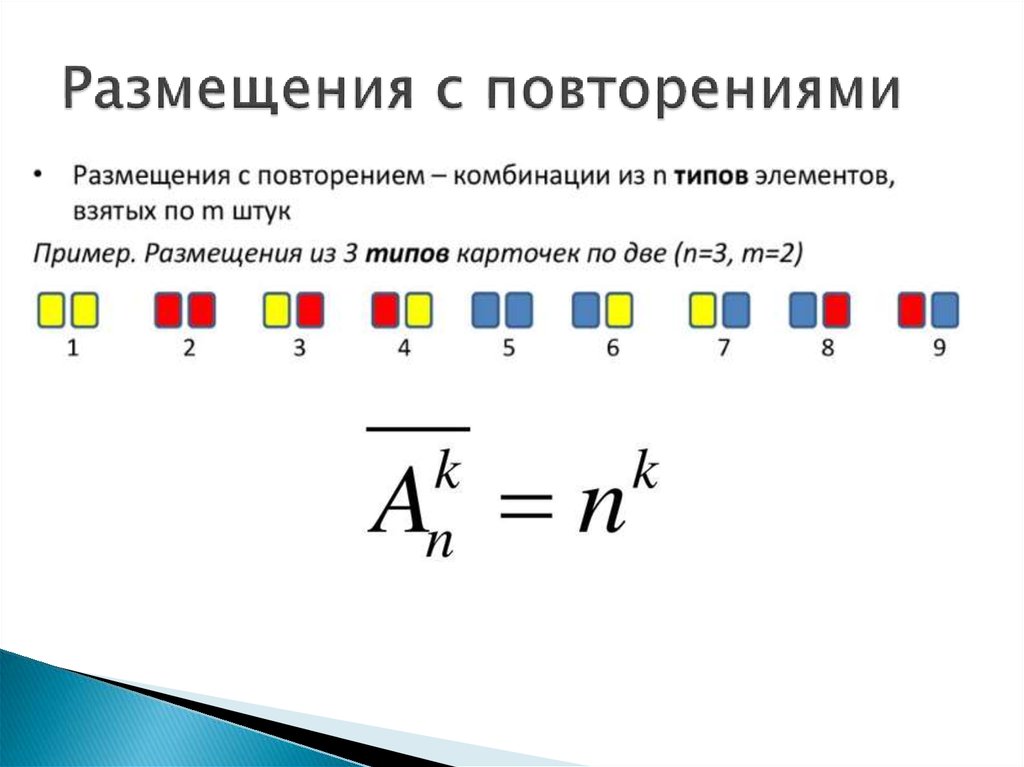 д.).

При образовании пары (тройки, четверки и т.д.) элементов по правилу произведения используется соединитель «и»‘ (из первого множества выбираем первый элемент и к нему присоединяем второй элемент из второго множества — образуется пара, и к паре присоединяем третий элемент из третьего множества — образуется тройка и т.д.).

Количество перестановок без повторений

Рассмотрим свойства сочетаний без повторений в комбинаторике. Разные последовательности, которые можно построить из элементов данного множества, взятых ровно по одному разу, называются перестановками. Эти последовательности отличаются друг от друга только порядком расположения элементов.

Например, из двухэлементного множества $M2$={$a$,$b$} можно образовать два упорядоченных двухэлементных множества: {$a$,$b$} или {$b$,$a$}.

Формула числа перестановок в комбинаторике: $Pn$ = $n$!

Комбинаторика: правило размещения без повторений

Подмножество, выбираемое из данного множества предметов, называют выборкой. {m} =\frac{\left(n+m-1\right)!}{m!\cdot \left(n-1\right)!} $.

Рассмотрим теперь как решать задачи на комбинаторику — ниже приведены различные примеры и задачи с сочетаниями, размещениями и перестановками.

Пример 1

Задание: химик использует семь ингредиентов для приготовления нужного состава. Сколькими способами можно осуществить порядок приготовления?

Решение. Давайте применим элементы комбинаторики и осуществим решение. Как известно, перестановками из $n$ элементов называются комбинации, состоящие из $n$ элементов и отличающиеся порядком расположения элементов.

Количество перестановок вычисляется по формуле $P_{n} =n!$.

Количество различных порядков вливания семи ингредиентов в сосуд — это число перестановок из семи элементов: $P_{7} =7!=1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7=5040$.

Разберём еще один пример задачи на размещение в комбинаторике с решением.

Пример 2

Задание: На собрании присутствуют 20 человек. {3} =\frac{10!}{\left(10-3\right)!} =\frac{10!}{7!} =8\cdot 9\cdot 10=720$.

1.8. Сочетания с повторениями

Пусть задано 5 различных элементов a, b, c, d, e (в достаточном количестве комплектов) и пусть требуется составить из этих пяти элементов по 3 элемента сочетания с повторениями.

Это значит, что каждое соединение должно содержать три элемента и одно от другого должно отличаться, по крайней мере, одним элементом.

Если бы сочетания составлялись без повторений, то они должны были быть различными:

abc abd abe acd ace ade bcd bce bde cde.

Сочетания же с повторениями по три элемента из заданных пяти элементов будут иметь вид:

aaa aab aac aad aae

abb abc abd abe

acb acd ace

add ade

aee

bbb bbc bbd bbe

bce bcd bce

bdd bde

bee

ccc ccd cce

cdd cde cee

ddd dde

dee

eee

Таким образом, сочетания же с повторениями из n элементов по m элементов (при 0≤ m ≤ n) может содержать любой элемент сколько угодно раз от до m включительно, или не содержать его совсем, т. е. каждое сочетание из n элементов по m элементов может состоять не только из m различных элементов, но и из m каких угодно и как угодно повторяющихся элементов.

Следует отметить, что если два соединения по m элементов отличаются друг от друга только порядком расположения элементов, то они не считаются различными сочетаниями.

Число сочетаний с повторениями из n элементов по m будем обозначать символом .

Существует формула для вычисления числа сочетаний с повторениями:

. (1.8.1)

Здесь m может быть и больше n.

Пример 1.8.1. В магазине продается видов тортов. Очередной покупатель выбил чек на три торта. Считая, что любой набор товаров равно-возможен, определить число возможных заказов.

Решение. Число равновозможных заказов по формуле (1. 8.1) равно

Ответ: 220.

2. Решение задач

2.1. Разные задачи

Лучший способ освоения комбинаторики – решение задач. Начинать естественно, надо с простейших. Именно о простых, типовых (и в тоже время важнейших) задачах и пойдет речь.

Пример 2.1.1. В студенческой группе человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?

Решение. Старостой может быть выбран любой из 20 человек, его заместителем – любой из оставшихся 19, а профоргом – любой из 18 студентов, т. е. n₁ = 20, n₂ = 19, n₃ = 18. По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно

n₁ · n₂· n₃ = 20 · 19 · 18 = 6 840 способов.

Ответ: 6 840.

Пример 2.1.2. Четыре юноши и четыре девушки садятся на 8 расположенных подряд стульев, причем юноши садятся на места с четными номерами, а девушки – на места с нечетными номерами. Сколькими способами это можно сделать?

Решение. Первый юноша может сесть на любое из четырех четных мест, второй – на любое из оставшихся трех мест, третий – на любое из оставшихся двух мест. Последнему юноше предоставляется всего одна возможность. Согласно правилу произведения, юноши могут занять четыре места 4 · 3 · 2 · 1 = 24 способами. Столько же возможностей имеют и девушки.

Таким образом, согласно правилу произведения, юноши и девушки могут занять все стулья 24 · 24 = 576 способами.

Ответ: 576.

Пример 2.1.3. В ящике 250 изделий. Известно, что 100 из них – первого, 120 – второго, а остальные – третьего сорта. Сколько способов выбора извлечения из ящика одной детали первого или третьего сорта?

Решение. Деталь первого сорта может быть извлечена n₁ = 100 способами, третьего сорта – n₂ = 30.

По правилу суммы существует n₁ + n₂= 100 + 30 + 130 способов извлечения одной детали первого или третьего сорта.

Ответ: 130.

Пример 2.1.4. В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?

Решение. Число разных способов распределения медалей равно

Ответ: 3 360.

Примечание. Необходимо различать сочетания и размещения. Например, в группе – 25 студентов, из них вышли из аудитории на перерыв. Студенты стоят вместе и беседуют. Тогда порядок, в котором они стоят, – не существенен. Число всех возможных групп из 25 человек по в этом случае – сочетания. Если же студенты отправились на перерыве в буфет или в кассу за стипендией, то тогда существенно, в каком порядке они стоят, т. е. кто из них первый, второй и т.д. В этой ситуации при подсчете возможных групп из 25 человек по необходимо составлять размещения.

Пример 2.1.5. У туриста есть семь консервных банок с ухой. В походе он будет находиться девять дней; из них какие-то семь дней будет есть уху, а три дня будет питаться всухомятку. Сколько у туриста есть способов выбрать дни с горячим питанием?

Решение. Число способов равно . Используя формулу (1.5.1), находим:

Ответ: 36.

Пример 2.1.6. В спортивной секции занимается баскетболистов. Сколько может быть организовано тренером разных спортивных пятерок?

Решение. Число разных спортивных пятерок равно . Используя формулу (1.5.1), находим:

Ответ: 792.

Пример 2.1.7. Из группы, состоящей из человек, выбирают троих для поездки на соревнование. Сколькими способами это может быть сделано?

Решение. Число способов равно . Используя формулу (1.5.1), находим:

Ответ: 2 300.

Пример 2.1.8. Для подарков ко дню 8 Марта молодой человек должен приобрести две броши и три браслета. В магазине ему предложили на выбор пять брошей и семь браслетов. Сколькими способами человек может сделать выбор?

Решение. Две броши из пяти можно выбрать числом способов, равным , а три браслета из семи – числом способов . Каждый из способов выбора броши нужно скомбинировать с каждым из способов выбора браслета. Следовательно, полное число способов, какими человек может выбрать две броши и три браслета, есть

Ответ: 350.

Пример 2.1.9. Восемь человек должны расположиться в двух комнатах, причем так, чтобы в каждой было не менее трех человек. Сколькими способами это можно сделать?

Решение. Есть два варианта. Первый вариант: в одной комнате три человека, а в другой пять. Второй: в каждой комнате по четыре человека.

В первом варианте количество способов расположения восьми человек в двух комнатах равно числу сочетаний трех из восьми (или пяти из восьми, что одно и то же), во втором варианте – числу сочетаний четырех из восьми .

Полное число способов расположения восьми человек в двух комнатах должно учитывать как первый, так и второй варианты:

Ответ: 126.

Пример 2.1.10. Группу из девяти человек надо разбить на три подгруппы: в одной два человека, в другой три, в третьей четыре. Сколькими способами можно выполнить такое разбиение?

Решение. Сначала выясняем, сколькими способами можно выбрать двух человек из девяти. Это число способов равно . После того, как этот выбор состоялся, осталось семь человек. Из них надо организовать подгруппы из трех и четырех человек. Это можно сделать числом способов, равным (или , что одно и то же). Итак, девять человек можно разбить на два, три и четыре следующим числом способов:

Примечание. Можно было бы сначала выяснить, сколькими способами можно выбрать трех человек из девяти. Тогда ответ на вопрос задачи дало бы произведение . А можно было бы сначала выяснить, сколько есть выборок четырех человек из девяти. Тогда ответ дало бы произведение . Докажите самостоятельно, что .

Ответ: 1260.

Пример 2.1.11. Сколькими способами можно из 40 человек, поступающих в вуз, создать 4 группы разных специальностей по 10 человек в каждой?

Решение. Первую группу можно создать способами. Вторую группу можно создать из оставшихся 30 человек способами. Третью группу можно создать из оставшихся 20 человек способами. Оставшиеся 10 человек составят четвертую группу. Итак, число всех различных способов составляет четырех групп из 40 человек равно

Ответ: .

Пример 2.1.12. Сколькими способами можно группу из 12 человек разбить на две подгруппы, в одной из которых должно быть не более пяти, а во второй – не более девяти человек?

Решение. Первая подгруппа может состоять либо из трех, либо из четырех, либо из пяти человек. Подгруппу из трех человек можно выбрать способами. Подгруппу из четырех человек можно выбрать способами, а подгруппу из пяти человек – способами. Учитывая, что выбор первой подгруппы первой подгруппы однозначно определяет вторую, найдем по правилу суммы искомое число способов: .

Ответ: 1 507.

Пример 2.1.13. Сколькими способами можно рассадить за столом пять гостей, если стол накрыт на семь персон?

Решение. Пять гостей из семи можно выбрать способами. Но это не ответ на поставленный в задаче вопрос, поскольку при рассаживании гостей за столом необходимо принимать во внимание также число перестановок пяти гостей (оно равно P₅). Ведь занявших те или иные пять стульев можно поменять местами. Таким образом, пять гостей можно рассадить за столом, накрытым на семь персон, числом способов, равным

Ответ: 2 520.

Пример 2.1.14. Десять команд участвуют в розыгрыше первенства по футболу, лучшие из которых занимают 1-е, 2-е и 3-е места. Две команды, занявшие последние места, не будут участвовать в следующем первенстве.

Сколько различных вариантов результата первенства может быть, если учитывать только положение первых трех и последних двух команд?

Решение. Задачу решим тремя способами.

Способ 1. Первые три места могут быть распределены способов. В результате останется семь команд, две из которых выбывают из следующего первенства.

Так как в этом случае порядок выбывших команд не важен, то это может произойти способами. Согласно правилу умножения получаем, что число различных результатов первенства равно .

Способ 2. Выберем без учета порядка пять команд из общего числа команд. В эту группу входят три команды, занявшие призовые места, и две выбывшие команды. Такую операцию можно выполнить способами. Из этих пяти команд без учета порядка выделим две команды, которые выбывают, что можно сделать способами. Для оставшихся трех команд распределение призовых мест возможно P₃ способами. По правилу умножения все три операции можно выполнить P₃ = 15 120.

Способ 3. Распределение всех 10 мест в первенстве возможно P₁₀= 10! способами.

Однако перестановки команд, занявших места с 4-го по 8-е, и перестановки команд, занявших 9-е и 10-е места, на результаты первенства не оказывают влияния. Число таких перестановок равно 5! · 2!, а число различных результатов первенства равно .

Ответ: 15 120.

Пример 2.1.15. Для освещения аудитории может быть включена каждая из имеющихся ламп. Сколько существует различных способов освещения аудитории?

Решение. Очевидно, что и число способов равно 2¹⁰ = 1 204. При этом учитывается и тот способ «освещения», при котором ни одна лампочка не горит.

Ответ: 1 024.

Пример 2.1.16. В кондитерском магазине продавались пирожные четырех видов: корзиночки, наполеоны, песочные и эклеры. Сколькими способами можно выбрать 7 пирожных?

Решение. В данной задаче подразумевается, что количество пирожных каждого сорта не ограничено. Для ответа на поставленный вопрос воспользуемся формулой сочетаний с повторениями (1.8.1):

Ответ: .

Пример 2.1.17. На конкурс представлено 10 студенческих работ. Денежные премии будут присуждаться по следующим номинациям: оригинальная научная идея; использование современного экономико-математи-ческого аппарата; применение компьютерного обеспечения; презентация результатов на научной конференции.

Сколько существует вариантов распределения премий, если по каждой комбинации установлены:

а) различные денежные премии;

б) одинаковые премии.

Решение

А. Каждый из вариантов распределения премий представляет собой комбинацию 4 работ из 10, отличающуюся от других комбинаций как самими работами, так и их порядком расположения по номинациям; причем одни и те же работы могут повторяться несколько раз, так как любая научная работа может получить премии как по одной, так и по нескольким (даже всем четырем) номинациям.

Число возможных вариантов распределения денежных премий представляет собой число размещений с повторениями из 10 элементов по 4 и определяется по формуле (1.8.1):

Б. Если по каждой номинации установлены одинаковые премии, то порядок следования работ в комбинации четырех премиальных работ значения не имеет. И тогда число вариантов распределения премий представляет собой число сочетаний с повторениями из 10 элементов по 4, определяемое по формуле (1.8.1):

Ответ: а) ; б) .

Формулы комбинаторики перестановки размещения сочетания примеры. Комбинаторика. Перестановки. Решение задач. Размещения с повторением

Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N , состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т. е. при изменении порядка переходим к другой m – выборке.

Сформулируем следующие определения:

Размещения без повторения

Размещением без повторения из n элементов по m N , содержащее m различных элементов .

Перестановки без повторений

Перестановками из n элементов называются различные упорядочения множества N .

Теорема 4 . Число различных перестановок без повторений вычисляется по формуле

Сочетания без повторений

Из определения следует, что два сочетания различаются только элементами, порядок не важен.

Теорема 5 . Число сочетаний без повторений вычисляют по одной из следующих формул:

Пример 1 . В комнате 5 стульев. Сколькими способами можно разместить на них

а) 7 человек; б) 5 человек; в) 3 человека?

б) Решение очевидно —

в) — число выборов занимаемых стульев.

— число размещений трех человек на трех выбранных стульях.

Общее число выборов равно .

Не трудно проверить формулы
;

;

Число всех подмножеств множества, состоящего из n элементов.

Размещения с повторением

Замечание: Очевидно, размещения с повторением можно рассматривать и при
.

Ответ :

Комбинаторные конфигурации

размещение;
перестановка;
сочетание;
композиция числа;
разбиение числа.

Разделы

перечислительная;
структурная;
экстремальная;
теория Рамсея;
вероятностная;
топологическая;
инфинитарная.

Правило сложения

Правило умножения

Перестановка

Размещение

Сочетание

Как выбрать формулу для решения задачи?

Задайте себе вопрос: порядок размещения элементов учитывается в тексте задачи?
Если ответ нет, то воспользуйтесь формулой сочетания (С = n! / (m! * (n — m)!)).
Если ответ нет, то необходимо ответить на еще один вопрос: все ли элементы входят в комбинацию?
Если ответ да, то воспользуйтесь формулой перестановки (Р = n!).
Если ответ нет, то воспользуйтесь формулой размещения (А = n! / (n — m)!).

Пример

Число размещений без повторений из n по k n k различными координатами.

Число размещений без повторений находится по формуле:

Пример: Сколькими способами можно построить 3-значное число с различными цифрами, не содержащее цифры 0?

Количество цифр
, размерность вектора с различными координатами

Число размещений с повторениями

Число размещений с повторениями из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k координатами, среди которых могут быть одинаковые.

Число размещений с повторениями находится по формуле:

Пример: Сколько слов длины 6 можно составить из 26 букв латинского алфавита?

Количество букв
, размерность вектора

Число перестановок без повторений

Число перестановок без повторений из n элементов – это число способов, сколькими можно расположить на n различных местах n различных элементов.

Число перестановок без повторений находится по формуле:

Замечание: Мощность искомого множества А удобно искать по формуле:
, гдех – число способов выбрать нужные места; у – число способов расположить на них нужные элементы; z – число способов расположить остальные элементы на оставшихся местах.

Пример. Сколькими способами можно расставить на книжной полке 5 различных книг? В скольких случаях две определенные книги А и В окажутся рядом?

Всего способов расставить 5 книг на 5-ти местах – равно = 5! = 120.

В задаче х – число способов выбрать два места рядом, х = 4; у – число способов расположить две книги на двух местах, у = 2! = 2; z – число способов расположить остальные 3 книги на оставшихся 3-х местах, z = 3! = 6. Значит
= 48.

Число сочетаний без повторений

Число сочетаний без повторений из n по k – это число способов, сколькими можно из n различных элементов выбрать k штук без учета порядка.

Число сочетаний без повторений находится по формуле:

Свойства:

1)
; 2)
; 3)
;

4)
; 5)
; 6)
.

Пример. В урне 7 шаров. Из них 3 белых. Наугад выбирают 3 шара. Сколькими способами это можно сделать? В скольких случаях среди них будет ровно один белый.

Всего способов
. Чтобы получить число способов выбрать 1 белый шар (из 3-х белых) и 2 черных шара (из 4-х черных), надо перемножить
и
Таким образом искомое количество способов

Упражнения

1. Из 35 учащихся класс по итогам года имели “5” по математике – 14 человек; по физике – 15 человек; по химии – 18 человек; по математике и физике – 7 человек; по математике и химии – 9 человек; по физике и химии – 6 человек; по всем трем предметам – 4 человек. Сколько человек имеют “5” по указанным предметам? Сколько человек не имеет “5” по указанным предметам? Имеет “5” только по математике? Имеет “5” только по двум предметам?

2. В группе из 30 студентов каждый знает, по крайней мере, один иностранный язык – английский или немецкий. Английский знают 22 студента, немецкий – 17. Сколько студентов знают оба языка? Сколько студентов знают немецкий язык, но не знают английский?

3. В 20 комнатах общежития института Дружбы Народов живут студенты из России; в 15 – из Африки; в 20 – из стран Южной Америки. Причем в 7 – живут россияне и африканцы, в 8 – россияне и южноамериканцы; в 9 – африканцы и южноамериканцы; в 3 – и россияне, и южноамериканцы, и африканцы. В скольких комнатах живут студенты: 1) только с одного континента; 2) только с двух континентов; 3) только африканцы.

4. Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике и астрономии. Три спецкурса посещают 10 студентов, по математике и физике – 30 студентов, по математике и астрономии – 25; спецкурс только по физике – 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике – 145, по астрономии – 100 студентов. Сколько студентов посещают спецкурс только по астрономии? Сколько студентов посещают два спецкурса?

5. Староста курса представил следующий отчет по физкультурной работе. Всего – 45 студентов. Футбольная секция – 25 человек, баскетбольная секция – 30 человек, шахматная секция – 28 человек. При этом, 16 человек одновременно посещают футбольную и баскетбольную секции, 18 – футбольную и шахматную, 17 – баскетбольную и шахматную, 15 человек посещают все три секции. Объясните, почему отчет не был принят.

6. В аквариуме 11 рыбок. Из них 4 красных, остальные золотые. Наугад выбирают 4 рыбки. Сколькими способами это можно сделать? Найти число способов сделать это так, чтобы среди них будет: 1) ровно одна красная; 2) ровно 2 золотых; 3) хотя бы одна красная.

7. В списке 8 фамилий. Из них 4 – женские. Сколькими способами их можно разделить на две равные группы так, чтоб в каждой была женская фамилия?

8. Из колоды в 36 карт выбирают 4 . Сколько способов сделать это так, чтобы: 1) все карты были разных мастей; 2) все карты были одной масти; 3) 2 красные и 2 черные.

9. На карточках разрезной азбуки даны буквы К, К, К, У, У, А, Е, Р. Сколько способов сложить их в ряд так, что бы получилось «кукареку».

10. Даны карточки разрезанной азбуки с буквами О, Т, О, Л, О, Р, И, Н, Г, О, Л, О, Г. Сколько способов сложить их так, что бы получилось слово «отолоринголог».

11. Даны карточки нарезной азбуки с буквами Л, И, Т, Е, Р, А, Т, У, Р, А. Сколько способов сложить их в ряд так, что бы получилось слово «литература».

12. 8 человек становятся в очередь. Сколько способов сделать это так, что бы два определенных человека А и Б оказались: 1) рядом; 2) на краях очереди;

13. 10 человек садятся за круглый стол на 10 мест. Сколькими способами это можно сделать так, чтоб рядом оказались: 1) два определенных человека А и Б; 2) три определенных человека А, Б и С.

14. Из 10 арабских цифр составляют 5-значный код. Сколькими способами это можно сделать так, чтобы: 1) все цифры были разными; 2) на последнем месте четная цифра.

15. Из 26 букв латинского алфавита (среди них 6 гласных) составляется шестибуквенное слово. Сколькими способами это можно сделать так, чтобы в слове были: 1) ровно одна буква «а»; 2) ровно одна гласная буква; ровно две буквы «а»; в) ровно две гласные.

16. Сколько четырехзначных чисел делятся на 5?

17. Сколько четырехзначных чисел с различными цифрами делятся на 25?

19. Брошены 3 игральные кости. В скольких случаях выпала: 1) ровно 1 «шестерка»; 2) хотя бы одна «шестерка».

20. Брошены 3 игральные кости. В скольких случаях будет: 1) все разные; 2) ровно два одинаковых числа очков.

21. Сколько слов с различными буквами можно составить из алфавита а, в, с, d. Перечислить их все в лексикографическом порядке: abcd, abcd….

Задача . Определить количество всех упорядоченных наборов длиныr , которые можно составить из элементов множестваX (
), если выбор каждого элемента
, производится из всего множестваX .

Упорядоченный набор
– это элемент декартова произведения
, состоящего изr одинаковых множителейX . По правилу произведения количество элементов множества
равно
. Мы вывели формулу
.

Пример . Сколько четырехзначных телефонных номеров можно составить, если использовать все десять цифр?

Здесь
, и количество телефонных номеров равно

2.1.5. Размещения без повторений

Задача . Сколько упорядоченных наборов
можно составить изn элементов множестваX , если все элементы набора различны?

Первый элемент можно выбратьn способами. Если первый элемент уже выбран, то второй элементможно выбрать лишь
способами, а если уже выбран
элемент
, то элементможно выбрать
способами (повторение уже выбранного элемента не допускается). По правилу произведения получаем

Эта формула записывается иначе с использованием обозначения
. Так как

Пример . Сколько может быть различных списков победителей олимпиады (первое, второе, третье место), если участвовало 20 человек?

Здесь
, искомым является число

2.1.6. Перестановки без повторений

Рассмотрим частный случай размещения без повторений: если
, то в размещении участвуют все элементы множестваX , т.е. выборки имеют одинаковый состав и отличаются друг от друга только порядком элементов. Такие выборки называютсяперестановками . Количество перестановок изn элементов обозначают:

Пример. Сколькими способами можно выстроить очередь в кассу, если хотят получить зарплату шесть человек?

2.1.7. Перестановки с повторениями

Пусть множество X состоит изk различных элементов:
.Перестановкой с повторениями состава
будем называть упорядоченный набор длины
, в котором элементвстречается раз
. Количество таких перестановок обозначается
.

Пример . Из букв
запишем перестановку с повторением состава
. Ее длина
, причем букваa входит 2 раза,b – 2 раза,c – один раз. Такой перестановкой будет, например,
или
.

Выведем формулу количества перестановок с повторениями. Занумеруем все одинаковые элементы, входящие в перестановку, различными индексами, т.е. вместо перестановки
получим
. Теперь все элементы перестановки различны, а количество таких перестановок равно
. Первый элемент встречается в выборкераз. Уберем индексы у первого элемента (в нашем примере получим перестановку
), при этом число различных перестановок уменьшится в раз, т.к. при изменении порядка одинаковых элементов наша выборка не изменится. Уберем индексы у второго элемента – число перестановок уменьшится в раз. И так далее, до элемента с номеромk – число перестановок уменьшится в раз. Получим формулу

Пример . Сколько различных “слов” можно получить, переставляя буквы слова “передача” ?

В этом слове буквы “е” и “а” встречаются два раза, остальные по одному разу. Речь идет о перестановке с повторением состава
длины. Количество таких перестановок равно

2.1.8. Сочетания

Задача . Сколько различных множеств изr элементов можно составить из множества, содержащегоn элементов?

Будем составлять вначале упорядоченные наборы по r элементов в каждом. Количество таких наборов (это размещения изn элементов поr ) равно
. Теперь учитываем, что порядок записи элементов нам безразличен. При этом изразличных размещений, отличающихся только порядком элементов, получим одно сочетание. Например, два различных размещения
и
из двух элементов соответствуют одному сочетанию
. Таким образом, число сочетанийвраз меньше числа размещений:

Пример . Количество способов, которыми мы можем выбрать из восьми дворников троих равно

Комбинаторика основные понятия и формулы, задачи с решением для начинающих, основы комбинаторики для чайников, свойства сочетания с повторениями

Математика

12. 11.21

11 мин.

Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни.

Оглавление:

Что такое комбинаторика в математике

Основные понятия

Правило произведения

Правило суммы

Сочетания с повторениями и без повторений

Размещения с повторениями и без повторений

Перестановки с повторениями и без повторений

Комбинаторные задачи с решениями

Заключение

Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека.

Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья.

Представители того научного мира пытались найти методы решения таких задач, их базовые правила и понятия, утвердить уникальные формулы и уравнения для тех, кто ещё не встречался с ними. Такая информация в наше время называется информацией «для чайников».

Попытаемся разобраться в аспектах этой области науки: каковы элементы, свойства, правила, методы и основное ее применение в нашей жизни? Конечно, всю область в одной статье невозможно охватить. Поэтому ниже будет представлено всё самое основное.

Что такое комбинаторика в математике

Суть этого термина дают книги прошлых лет: это раздел математики, занимающийся операциями со множеством элементов.

В интернете есть учебники по информатике и математике для детей, школьников, сборники материалов и задач для начинающих, где в доступном виде объяснена «занимательная» комбинаторика. Нужно твердо выяснить, как решать подобные задачи.

В младших классах задачи на эту тему решают на дополнительных кружках, а в школах с углубленным изучением математики — на основных уроках. К тому же, задачи по комбинаторике включены в олимпиады всех уровней.

Основные понятия

Их несколько:

Элемент – любой объект или явление, входящий в искомое множество.
Сочетание – подмножества, находящиеся в произвольном порядке в исходном множестве.
Перестановка – элементы во множестве находятся в строго определенном порядке.
Размещение – упорядоченные подмножества в исходном множестве.

Правило произведения

Является одним из основных правил при решении таких задач и звучит так:

При выборе элемента А из n способов и выборе элемента В из m способов верно утверждение, что выбрать пару А и В одновременно можно n*m способами.

Рассмотрим на конкретных примерах.

Задача №1.

В коробке лежит 2 мяча и 6 скакалок. Сколько существует способов достать 1 мяч и 1 скакалку?

Ответ прост: 2 * 6 = 12.

Задача №2.

Есть 1 кубик, 2 шарика, 3 цветка и 4 конфеты. Сколькими способами можно вытянуть кубик, шарик, цветок и конфету?

Решение аналогично: 1 * 2 * 3 * 4 = 24.

Причем левую часть можно записать гораздо проще: 4!

! в данном случае является не знаком препинания, а факториалом. С помощью него можно вычислить более сложные варианты и решать трудные задачи (существуют разные формулы, но об этом позже).

Задача №3.

Сколько двузначных чисел можно составить из 2 цифр?

Ответ: 2! = 2.

Задача №4.

Сколько десятизначных чисел можно составить из 10 цифр?

10! = 3628800.

Правило суммы

Тоже является базовым правилом комбинаторики.

Если А можно выбрать n раз, а В — m раз, то А или В можно выбрать (n + m) раз.

Задача №5.

В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш?

Ответ: 5 + 3 + 7 + 9 = 24.

Сочетания с повторениями и без повторений

Под этим термином понимают комбинации в произвольном порядке из множества n по m элементов.

Число сочетаний равно количеству таких комбинаций.

Задача №6.

В коробке находится 4 разных фрукта. Сколькими способами можно достать одновременно 2 разных фрукта?

Решение простое:

Где 4! – комбинация из 4 элементов.

С повторениями чуть сложней, комбинации считаются по такой формуле:

Задача №7.

Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку.

В этом случае:

Размещения с повторениями и без повторений

Под этим определением понимают набор m элементов из множества n элементов.

Задача №8.

Из 3 цифр надо выбрать 2, чтобы получались разные двузначные числа. Сколько вариантов?

Ответ прост:

А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз! В таком случае общая формула будет выглядеть следующим образом:

Задача №9.

Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона.

Решение:

Перестановки с повторениями и без повторений

Под этим термином понимают все возможные комбинации из n элементного множества.

Задача №10.

Сколько возможных пятизначных чисел можно составить из 5цифр? А шестизначных из 6 цифр? Семизначных из 7 цифр?

Решения, согласно вышеприведенной формуле, следующие:

5! = 120;

6! = 720;

7! = 5040.

А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше!

Задача №11.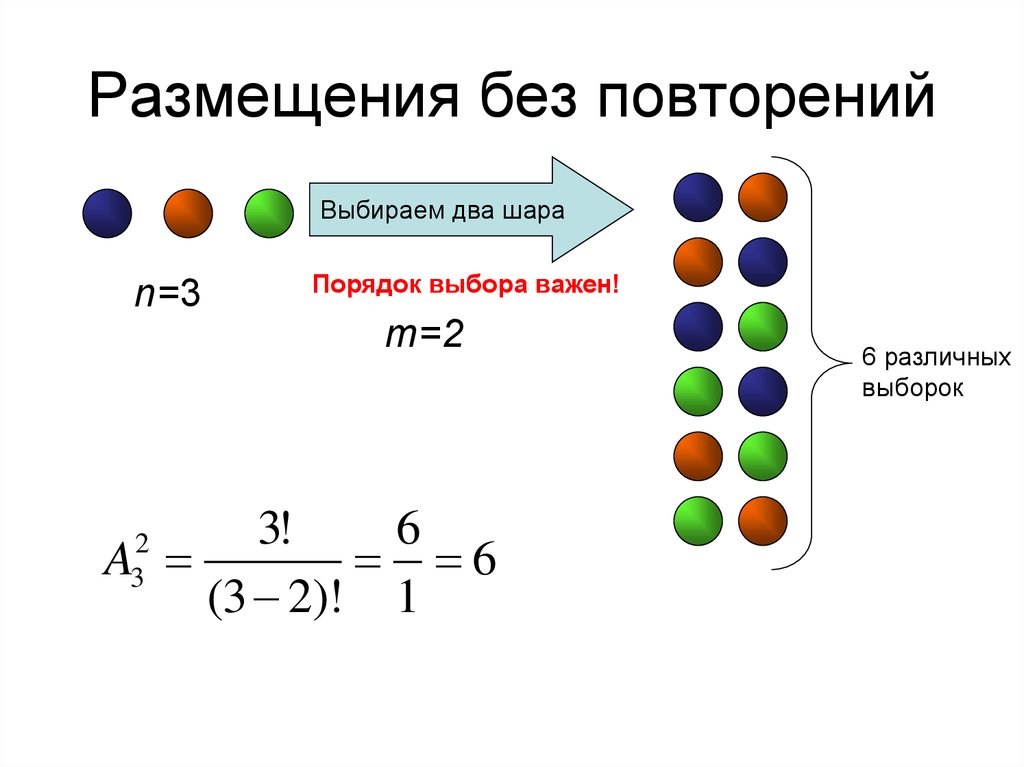

В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать?

Ответ прост: 4! / (3! * 1!) = 4.

Комбинаторные задачи с решениями

Примеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.

Типы задач	Что требуется найти	Методы решения
Магический квадрат	Фигура, в которой сумма чисел в рядах и столбцах должна быть одинакова (его разновидность – латинский квадрат).	Рекуррентные соотношения. Решается подобная же задача, но с гораздо меньшим множеством элементов по известным правилам и формулам.
Задача размещения	Стандартная производственная задача (например, в лоскутной технике) — найти возможные способы разложения количества продуктов в ячейки в определенном порядке.	Включения и исключения.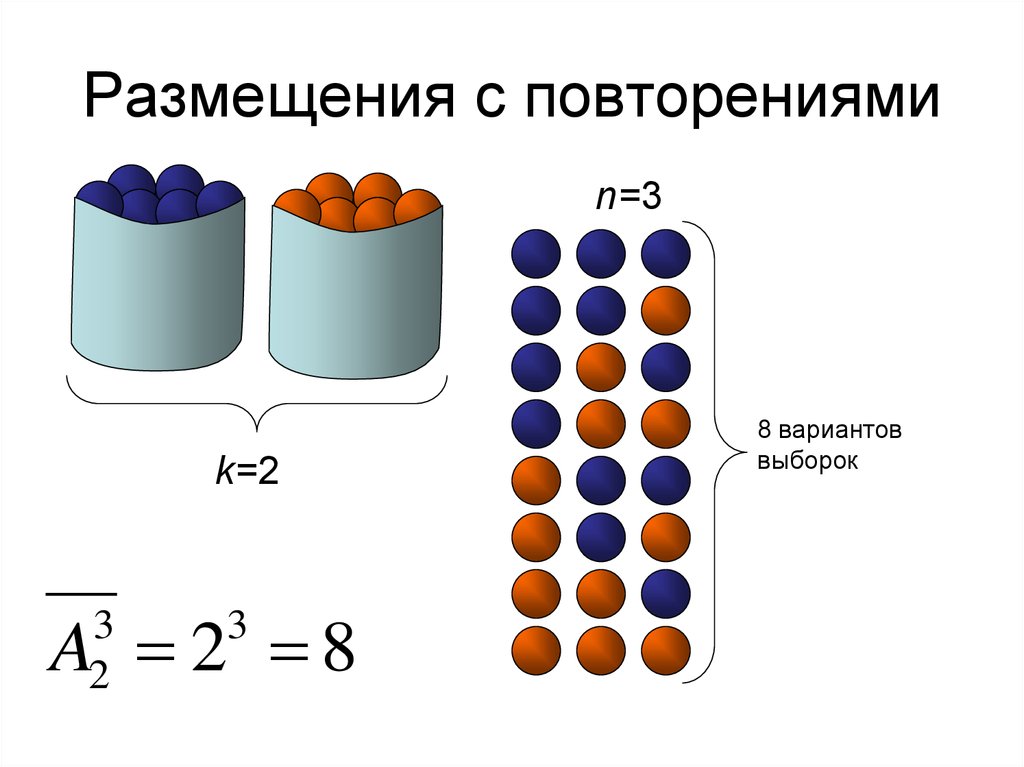 Как правило, применяется при доказательстве различных выражений.
Задачи про торговцев	Суть — найти все возможные пути прохождения людей из пункта А в пункт В.	Траектории. Для этого вида задач характерно геометрическое построение возможных способов решения.

Заключение

Стоит изучать эту науку, поскольку в век быстрой модернизации технологий потребуются специалисты, способные предоставить различные решения тех или иных практических задач.

Элементы комбинаторики. Формулы комбинаторики Размещения и теория вероятностей

КОМБИНАТОРИКА

Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Решение

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:

способами.

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Решение

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Решение

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение.

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Перестановки без повторений . Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Решение

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

Все N элементов, и ни один не повторяется, то это задача о количестве перестановок. Решение можно найти простым . На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).

В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы называются размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.

Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.

Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).

Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т. к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.

Основная формула комбинаторики

Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .

Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n 1 элементов, а вторая — из n 2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n 2 . Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n 2 . Так как в первой группе всего n 1 элемент, всего возможных вариантов будет n 1 *n 2 .

Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n 1 =6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.

В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.

Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.

Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .

Число размещений из n элементов по m

Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.

Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:

Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.

Пример 5 . Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т. к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:

Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 6 . Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.

Число сочетаний из n элементов по m

Число сочетаний обозначается C n m и вычисляется по формуле:

Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?

Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:

Перестановки из n элементов

Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.

Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.

Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?

Решение: эта задача о числе перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.

Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.

Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).

Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.

И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.

Пример 9. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.

Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.

Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Т.к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
На первом месте может стоять любая цифра кроме 0, т.е. 9 возможностей. На втором месте может стоять любая цифра, т.е. 10 возможностей. На третьем месте тоже может стоять любая цифра из, т.е. 10 возможностей. Четвертая и пятая цифры определены заранее, они совпадают с первой и второй, следовательно, число таких чисел 9*10*10=900.
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?

4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?

n = C 20 4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)=4845.
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
В первый конверт можно положить 1 из восьми писем, во второй одно из семи оставшихся, в третий одно из шесть т.д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?

Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.

Итак, предыстория.

Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.

Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?

Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся цифр»!! ! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).

Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.

Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999 (вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же! Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?

Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!

P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)

Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.

Описание алгоритма генерации под калькулятором.

Алгоритм

Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5 — последнее сочетание, так как все его элементы равны n — m + i.

Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.

Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.

Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.

Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.

Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).

Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.

Фактор	Пример	RockYou	iPhone	Опрос
*Даты*
ДДММ	2311	5. 26	1.38	3.07
ДМГГ	3876	9.26	6.46	5.54
ММДД	1123	10.00	9.35	3.66
ММГГ	0683	0.67	0.20	0.94
ГГГГ	1984	33.39	7.12	4.95
Итого		58.57	24.51	22.76
*Клавиатурный паттерн*
смежные	6351	1.52	4.99	—
квадрат	1425	0.01	0.58	—
углы	9713	0.19	1.06	—
крест	8246	0.17	0.88	—
диагональная линия	1590	0.10	1.36	—
горизонтальная линия	5987	0. 34	1.42	—
слово	5683	0.70	8.39	—
вертикальная линия	8520	0.06	4.28	—
Итого		3.09	22.97	8.96
*Цифровой паттерн*
заканчивается на 69	6869	0.35	0.57	—
только цифры 0-3	2000	3.49	2.72	—
только цифры 0-6	5155	4.66	5.96	—
повторяющиеся пары	2525	2.31	4.11	—
одинаковые цифры	6666	0.40	6.67	—
убывающая последовательность	3210	0.13	0.29	—
возрастающая последовательность	4567	3. 83	4.52	—
Итого		15.16	24.85	4.60
*Случайный набор цифр*		23.17	27.67	63.68

Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.

100 самых популярных PIN-кодов

0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.

P.S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:

перестановок с повторением | Superprof

Введение

Когда мы слышим в повседневной жизни слово «комбинация», мы сразу же думаем о коллекции вещей в виде комплекта или группы. Например, если кто-нибудь скажет, что в моей миске есть сочетание яблок, моркови и бананов, то мы сразу же подумаем, что в миске три предмета. Нас не интересует порядок, в котором эти три предмета были помещены в чашу.

В математике под комбинацией понимается количество способов, которыми различные объекты объединяются в набор. Порядок элементов в комбинации не важен. Мы всегда изучаем комбинацию с перестановкой в математике, потому что между этими двумя терминами есть много общего. Основное различие между комбинацией и перестановкой заключается в том, что 9Порядок 0007 имеет значение в перестановке , но не имеет значения в комбинации. Другими словами, мы можем сказать, что перестановка представляет собой упорядоченную комбинацию .

Вы уже читали выше пример простой комбинации, когда в миску кладут три вещи. Теперь давайте рассмотрим другой сценарий.

Гарри хочет составить пин-код, выбрав 4 цифры из набора первых пяти целых чисел (0,1,2,3,4). Предположим, что выбранный им пин-код — 4013. Может ли он переставить цифры как 3014 или 0143 и т. д.?

Конечно нет, важен порядок цифр. Если изменить порядок цифр, то пин-код не сработает. Это означает, что выбор кода из первых пяти целых чисел является примером перестановки.

Лучшие репетиторы по математике

Поехали

Типы перестановок

Существует два типа перестановок:

Перестановки с повторением
Перестановки без повторения

Перестановки с повторением

Мы знаем, что в перестановках важен порядок элементов. Перестановки с повторением означают, что мы можем выбрать один элемент дважды. Формула для вычисления перестановок с повторениями приведена ниже:

Здесь:

n = общее количество элементов в наборе

k = количество элементов, выбранных из набора

Рассмотрим следующий пример:

Из набора первых 10 натуральных чисел вас просят составить четырехзначное число. Сколько различных перестановок возможно?

Здесь, во-первых, нам нужно определить, можем ли мы выбрать цифру дважды или нет. У нас могут быть четырехзначные числа, такие как 1000, 1002, 3032 и 4044. Во всех этих числах одна цифра повторяется дважды или трижды. Следовательно, это означает, что это пример перестановок с повторением.

Общее количество элементов в наборе равно 10, а количество цифр, которые мы хотим выбрать из этого набора, равно 4. Следовательно, мы получим перестановки, подставив значения в следующую формулу:

Следовательно, Возможны 10000 перестановок, если мы хотим составить четырехзначное число из набора первых 10 натуральных чисел.

Иногда нам дают задачу, в которой идентичные элементы типа 1 повторяются «p» раз, типа 2 повторяются «q» раз, типа 3 повторяются «r» раз и т. д. . Возникает вопрос, что делать в этом случае? Что ж, ответ прост. Для вычисления перестановок в таких задачах существует отдельная формула.

Поскольку элементы повторяются, такие сценарии также являются примерами перестановок с повторением. Формула, которую следует использовать при вычислении перестановок в таких случаях, приведена ниже:

Давайте решим следующий пример с помощью приведенной выше формулы, чтобы сделать всю концепцию более ясной.

Сколько восьмизначных чисел можно составить из чисел 2, 2, 2, 3, 3, 3, 4, 4?

Здесь n = 8, p = 3, q = 3, r = 2,

В этом примере порядок элементов имеет значение, а цифры повторяются. Мы подставим вышеуказанные значения в формулу ниже:

Следовательно, возможно 560 перестановок.

Давайте решим еще несколько примеров ниже:

Пример 1

Сколькими способами можно расположить алфавиты слова ОТЛИЧНО ?

Решение

Общее количество элементов в слове = n = 9

E повторяется три раза, следовательно, p = 3

L повторяется 2 раза, следовательно, q = 2

. Подставьте эти значения в приведенную ниже формулу, чтобы получить количество способов, которыми можно расположить буквы этого слова:

Следовательно, буквы в слове ОТЛИЧНО можно расположить 30240 способами.

Пример 2

Решение

Здесь:

Общее количество флажков = n = 8

Количество красных флажков = p = 2

Количество синих флажков = q = 2

Количество зеленых флажков = r = 4

Это является примером перестановки с повторением, потому что элементы набора повторяются, и их порядок важен.

Поместите вышеуказанные значения в приведенную ниже формулу, чтобы получить количество перестановок:

Следовательно, флаги можно поднимать 420 способами.

Пример 3

Решение

Здесь:

Общее количество пар ботинок = n = 6

Количество красных ботинок = p = 2

Количество синих ботинок = q = 2

Количество задних ботинок = r = 2

Это пример перестановки с повторением, потому что элементы повторяются и важен их порядок.

Подставьте вышеуказанные значения в приведенную ниже формулу, чтобы получить количество перестановок:

Следовательно, обувь можно расположить на полке 90 способами.

Пример 4

Сколькими способами можно расположить алфавиты слова ЭЛЕКТРИЧЕСКИЙ ?

Решение

Общее количество элементов в слове = n = 8

E повторяется три раза, следовательно, p = 2

C повторяется 2 раза, следовательно, q = 2

Подставьте эти значения в приведенную ниже формулу, чтобы получить число

Следовательно, буквы в слове ЭЛЕКТРИЧЕСКИЙ можно расположить 10080 способами.

Пример 5

Человек должен выбрать трехзначное число из набора следующих семи чисел, чтобы составить трехзначное число.

{1, 2, 3, 4, 5, 6, 7}

Сколько различных вариантов расположения цифр возможно?

Решение

В трехзначном числе может быть 2 или 3 одинаковых числа. Точно так же в числе важен порядок цифр.

Дано, что человек может выбрать 3 цифры из набора 7 цифр. Следовательно, n = 7 и k = 3. Подставьте эти значения в приведенную ниже формулу, чтобы получить количество возможных комбинаций.

Следовательно, возможны 343 различных расположения.

комбинаторика — Как посчитать количество возможных комбинаций с повторениями?

Определения

Перестановка: каждый из нескольких возможных способов упорядочения или расположения объектов.
Комбинация: Каждый из нескольких возможных способов создания «коллекции» или «набора» объектов, выбранных из большего набора .

Это, мой друг, все.

Перестановки

Когда вы думаете о перестановках, слово, которое должно прийти на ум или появиться в вопросе, это порядок . В самом деле, в случае пароля порядок имеет значение, поскольку $LFKJ$ отличается от $FKLJ$ паролем.

В наборе $S$ из $k$ элементов, если нужно составить слов из $n$ букв, то порядок имеет значение, так как слова могут состоять из одинаковых букв и при этом отличаться друг от друга, как TEA и ел. 9n$ — это ответ, представьте, что вам нужно составить слово из $n$ букв. Сначала вы создаете $n$ пробелов, поэтому ситуация выглядит так: $$ \underbrace{-~-~-~\ldots -~-~-}_{ \mbox{n пробелов}} $$

Каждый пробел может быть заполнен любой из $k$ букв. Таким образом, у каждого пробела есть $k$ вариантов, и, поскольку повторений нет, пробелы можно обрабатывать независимо, т. е. мы можем заполнить пробел, не глядя на другие пробелы. Таким образом, ответ равен $k \times k\times . n$.

Комбинации

Теперь для комбинаций ключевое слово набор , или членство , если хотите.

Возьмем пример выбора комитета из пяти человек из набора из десяти кандидатов. В самом деле, не имеет значения, кто был выбран первым, кто вторым и т. д., поскольку комитет, в конце концов, один и тот же. То есть набор человек в комитет имеет значение, а не порядок их избрания.

Таким образом, контекст для комбинаций плохо сочетается с паролями, потому что здесь набора букв в пароле недостаточно для определения самого пароля: как с $LJKF$ и $FJLK$.

Но в наборах нет повторяющихся элементов , так при чем здесь это?

Теперь, что касается комбинаций с повторениями, что это вообще значит? Ведь мы говорим о множестве, так что случайное введение сложности в виде повторений не имеет смысла, не так ли?

Так и есть. Давайте зададим вопрос, где есть вопрос относительно порядка, а также относительно количества.

У вас есть три буквы $w,x,y$ и вам нужно составить повторяющихся комбинаций из трех букв. Это трехбуквенные слова, в которых имеет значение только раз, когда каждая буква встречается раз. Сколько их там?

Действительно, этот вопрос изначально кажется одним из перестановок, поскольку у нас есть задействованные слова, и они расположены по порядку.

Однако тот факт, что нас интересует только число появления букв, как бы убирает из этого угол перестановки.

Например, слова xyz и $yzx$ совпадают, потому что они содержат буквы $x,y,z$ ровно один раз. Однако $xxy$ и $xyy$ — это не одно и то же, потому что , хотя они содержат один и тот же набор букв, количество появлений каждой буквы в обеих буквах разное.

Таким образом, идею комбинаций с повторением следует рассматривать в соответствии с (любой из) следующих интерпретаций:

Количество слов из $n$ букв с повторениями, которые могут быть образованы из алфавита из $r$ букв, но в которых имеет значение только количество повторений каждой буквы.
Количество способов разместить $r$ одинаковых предметов в $n$ разных банках.
Количество решений уравнения $x_1 + … + x_n = r$, где $x_i \geq 0$ для всех $i$.

Время расчета: звезды и полосы

Расчет на самом деле довольно прост, мы делаем это с помощью техники, называемой звездами и полосами.

Вернемся к задаче выбора $k$ элементов из $n$ с повторениями. Вот что мы сделаем: сначала запишем $k$ звезд вот так: $$ \underbrace{*****….****}{\mbox{k звезд}} $$

Теперь поместите ровно $n-1$ перемычек между этими звездами так, чтобы перемычки разделили звезды на разные группы. Есть много способов сделать это. Как много? $$ **|****|******|*||**…|**|* $$ так что теперь у нас есть $n$ групп звезд, которые находятся между полосами. Например, в дивизионе выше первая группа имеет $2$ звезд, а вторая группа имеет $4$ звезд, третья – $6$, четвертая – $1$, пятая – ноль (такое возможно!), и так далее.

Теперь рассмотрим слово, в котором первый символ используется два раза, второй символ четыре раза, третий символ шесть раз, четвертый символ один раз, никогда не использует пятый символ и так далее. Это слово представляет собой комбинаций с повторением длины $k$ из $n$ символов.

Таким образом, каждая комбинация с повторением соответствует схеме из $n-1$ полос между $k$ звездочками, и наоборот .

Сколькими способами можно разместить $n-1$ звездочек среди $k$ полосок? Что ж, представьте ситуацию, когда вам доступны $n+k-1$ позиций. Вы заполняете звездочками ровно $k$ из них, а в остальных местах появляются полосы, что дает такую диаграмму. Следовательно, ответ $\binom{n+k-1}{k}$! 98$!

Заключение

Этот пост поможет вам понять разницу между перестановками, комбинациями и комбинациями с повторением, что является довольно запутанным понятием. Ключевым моментом являются различные толкования комбинаций с повторением, которые то и дело поднимают голову. С практикой вы сможете различать эти случаи.

Перестановки с повторением | Brilliant Math & Science Wiki

Мэй Ли, Александр Кац, Пи Хан Го, а также

способствовал

Содержимое

Перестановки с повторением
Основные примеры
Промежуточные примеры
Смотрите также

Для заданного набора nnn объектов, в котором имеется n1n_1n1 идентичных объектов типа 1, n2n_2n2 идентичных объектов типа 2, …\ldots… и nkn_knk идентичных объектов типа kkk, сколько различных перестановок объектов существует там? Обратите внимание, что в этом случае все объекты должны появиться в перестановке, и два порядка считаются разными, если два объекта в некоторой позиции iii не идентичны.

Если все объекты различны, то мы видели, что количество перестановок без повторения равно n!n!n!. Для каждой из этих перестановок мы можем переставить n1n_1n1 одинаковых объектов типа 1 в n1! н_1! п1! возможные пути; поскольку эти объекты считаются идентичными, расположение не меняется. Точно так же мы можем взять любой из n2! н_2! п2! перестановки n2n_2n2 одинаковых объектов типа 2 и получить такое же расположение. Продолжая этот аргумент, мы учитываем эти повторяющиеся аранжировки путем деления на количество повторений. Это дает следующий результат для общего количества перестановок:

Количество перестановок nnn объектов с n1n_1n1 идентичными объектами типа 1, n2n_2n2 идентичными объектами типа 2, … \ldots… и nkn_knk идентичными объектами типа kkk равно
n!n1!n2!⋯nk!. \frac{n!}{n_1! н_2! \cdots n_k!}.n1!n2!⋯nk!n!.

В случае, когда все объекты различны, имеем n1=n2=⋯=nd=1n_1 = n_2 = \cdots = n_d = 1n1=n2=⋯=nd=1, и приведенная выше теорема показывает, что количество перестановок

n!n1!n2!⋯nd!=n!1!1!⋯1!=n!, \frac{n!}{n_1! н_2! \cdots n_d!} = \frac{n!}{1! 1! \cdots 1!} = n!, n1!n2!⋯nd!n!=1!1!⋯1!n!=n!,

, который мы видели в «Перестановках без повторения». Обратите внимание, что мы предположили, что перестановка содержит все объекты в порядке. В случае, если мы хотим включить в порядок только некоторые объекты, см. Перестановки с ограничением.

В проработанных примерах перестановок без повторений мы видели, что если у Лизы есть nnn разных украшений, то она может расположить их в n!n!n! по-разному на ее мантии. Что произойдет, если вместо этого у Лизы будут одинаковые украшения? Сколькими способами Лиза может расположить украшения на своей мантии, если у нее есть 2 одинаковых украшения для кошек, 3 одинаковых украшения для собак, 1 кролик, 1 пингвин и 1 украшение для коалы?
Всего объектов 8, а если бы объекты считались различными, то их 8! 8! 8! способы их размещения на мантии. Для любой аранжировки мы можем взять любую из 2-х! 2! 2! перестановки кошачьих украшений и получить такое же расположение. Точно так же мы можем взять любой из 3! 3! 3! перестановки собачьих украшений и получить такое же расположение. Таким образом, чтобы учесть эти повторяющиеся расположения, мы делим на количество повторений, чтобы получить общее количество перестановок 8!3!2! \frac{8!}{3!2!} 3!2!8!. □_\квадрат□

Сколькими способами можно расположить буквы в имени РАМОНА?
Обратите внимание, что буква ААА встречается в слове дважды, а все остальные буквы — по одному разу. Если рассматривать ААА как отличные друг от друга (((скажем, A1 A_1 A1 и A2), A_2),A2), то существует 6!=720 6!= 720 6!=720 способов переставить буквы. Однако, поскольку буквы одинаковые, мы должны делить на 2! 2! 2! чтобы получить 7202!=360 \frac {720}{2!} = 360 2!720=360 способов. □_\квадрат□

Переставляя все буквы в слове МАТЕМАТИКА, сколько различных строк мы можем составить?

В стандартной колоде карт 52!52!52! различные перестановки карт. Если даны две одинаковые стандартные колоды карт, сколько существует различных перестановок?
Так как колоды карт идентичны, имеется по 2 одинаковых карты каждого типа (2 одинаковых туза пик, 2 одинаковых туза червей и т. д.). Тогда ni=2n_i=2ni=2 для каждого i=1,2,…,52i = 1, 2, \ldots, 52i=1,2,…,52. Тогда количество различных перестановок равно 9.{52} }.\ _\квадрат2!2!⋯2!(52+52)!=(2!)52104!. □

Сколько различных слов любой (ненулевой) длины можно составить, используя буквы KEPLER не более одного раза каждое?

Пояснение: В таком слове может быть две буквы E, но не может быть дубликатов любой другой буквы.

Назовем 666-значное число крутым , если каждая его цифра не меньше предыдущей. Сколько существует крутых 666-значных чисел?

Детали и предположения:

Перестановки

Процитировать как: Перестановки с повторением. Brilliant.org . Извлекаются из https://brilliant.org/wiki/permutations-with-repetition/

1.5 Выбор с повторением

Большинство задач на перестановку и комбинирование, с которыми мы сталкивались, учитывают варианты выбора. 3$. Если вытащено четыре шара, однако проблема становится другой.

Другой, возможно, более математический способ сформулировать такие проблемы. состоит в том, чтобы представить идею мультимножества . Мультимножество похоже на множество, за исключением того, что элементов может быть больше, чем однажды. Если $\{a,b\}$ и $\{b,c\}$ — обычные множества, говорят, что объединение $\{a,b\}\cup\{b,c\}$ равно $\{a,b,c\}$, а не $\{a,b,b,c\}$. Если мы интерпретировать их как мультимножества, однако мы пишем $\{a,b,b,c\}$ и считайте, что это отличается от $\{a,b,c\}$. Отличить мультимножества из множеств, и для сокращения выражения в большинстве случаев мы использовать повтор номер с каждым элементом. Например, мы напишем $\{a,b,b,c\}$ как $\{1\cdot a,2\cdot b,1\cdot c\}$. Написав $\{1\cdot a,1\cdot b,1\cdot c\}$ подчеркнем, что это мультимножество, хотя ни один элемент не появляется больше чем единожды. Мы также позволяем элементам быть включенными бесконечно количество раз, обозначенное $\infty$ для числа повторений, например $\{\infty\cdot a, 5\cdot b, 3\cdot c\}$. к$.

Теперь рассмотрим комбинации мультимножества, то есть подмножества: мультимножество, сколько в нем подмножеств заданного размера? Мы говорим что мультимножество $A$ является подмножеством $B$, если число повторений каждого элемента $A$ меньше или равно его числу повторений в $B$. Например, $\{20\cdot a, 5\cdot b, 1\cdot c\}$ — это подмножество $\{\infty\cdot a, 5\cdot b, 3\cdot c\}$. Мультимножество конечной, если она содержит только конечное число различных элементов, и все числа повторений конечны. Предположим снова, что $A=\{\infty\cdot a_1,\infty\cdot a_2,\ldots,\infty\cdot a_n\}$; как сколько у него конечных подмножеств размера $k$? Это сначала кажется довольно сложно, но при правильном оформлении получается знакомая проблема. Представьте, что у нас есть $k+n-1$ «пустых мест», например это:

Теперь мы размещаем маркеры $n-1$ в некоторых из этих мест:

Уникально идентифицирует подмножество: заполните все пробелы до сначала $\land$ с $a_1$, до второго с $a_2$ и так далее:

Таким образом, этот шаблон соответствует мультимножеству $\{1\cdot a_2,3\cdot a_3,\ldots, 1\cdot a_n\}$. Заполнение маркеров $\land$ во всех возможными способами производит все возможные подмножества размера $k$, поэтому существует есть $k+n-1\выберите n-1$ таких подмножеств. Обратите внимание, что это то же самое как $k+n-1\выберите k$; трудная часть на практике — помнить, что $-1$ идет с $n$, а не с $k$. 9к$. Количество комбинаций $n$ вещей, взятых за раз по $k$ без замены, равно ${n\choose k}$; количество комбинаций $n$ вещей, взятых $k$ за раз с замена ${k+n-1 \выберите k}$.

$$\пуля\четверка\пуля\четверка\пуля$$

Если $A=\{m_1\cdot a_1, m_2\cdot a_2,\ldots,m_n\cdot a_n\}$, аналогично вопросы могут быть довольно сложными. Вот более простой частный случай: сколько существуют ли перестановки мультимножества $A$? то есть сколько последовательности состоят из $m_1$ копий $a_1$, $m_1$ копий $a_2$ и скоро? Эта проблема поддается пересчету: предположим, для начала что мы можем различать разные копии каждого $a_i$; Oни например, могут быть окрашены по-разному: красный $a_1$, синий $a_1$, и так далее. n m_i$ элементы и перестановки $M!$. Теперь, если мы игнорируем цвета, так что все копии $a_i$ выглядят одинаково, мы обнаруживаем, что пересчитали желаемые перестановки. Перестановки, скажем, с элементами $a_1$ в одинаковые позиции выглядят одинаково, если мы игнорируем цвета $a_1$s. Как многие исходные перестановки обладают этим свойством? $m_1!$ перестановки будут казаться идентичными, если мы проигнорируем цвета $a_1$ элементов, так как существует $m_1!$ перестановок цветных $a_1$s в заданных $m_1$ позициях. Таким образом, после удаления дубликатов количество оставшихся перестановок равно $M!/m_1!$ (при условии, что другие $a_i$ все еще различимы). Тогда тот же аргумент применим к $a_2$s: существует $m_2!$ копий каждой перестановки, если мы игнорируем цвета $a_2$s, поэтому существует $\ds {M!\over m_1!\,m_2!}$ различных перестановок. Продолжая в том же духе, мы видим, что число различных перестановки после того, как все цвета игнорируются, $${M!\over m_1!\,m_2!\cdots m_n!}.$$ Это часто пишут $${M\выберите m_1\;\;m_2\;\ldots\; м_п},$$ называется полиномиальный коэффициент . Здесь во второй строке есть $n$ отдельных записей, а не одна запись о продукте. Обратите внимание, что если $n=2$ это

$\displaystyle{M\выберите m1\;\;m2}= \frac{M!}{m_1!\,m_2!}=\frac{M!}{m_1!\,(M-m_1)!}={M\выберите m_1}.$ (1.5.1)

Это легко увидеть комбинаторно: дано $\{m_1\cdot a_1, m_2\cdot a_2\}$ мы можем сформировать перестановку, выбрав $m_1$ мест, которые займет $a_1$, заполнив оставшиеся $m_2$ мест с $a_2$. Количество перестановок равно количество способов выбрать $m_1$ местоположений, т.е. $M\выберите m_1$.

Пример 1.5.1 Сколько решений имеет $\ds x_1+x_2+x_3+x_4=20$ в неотрицательных целых числах? то есть сколько Четверки $(m_1,m_2,m_3,m_4)$ неотрицательных целых чисел являются решениями задачи уравнение? Мы фактически решили эту проблему: Сколько подмножеств размера 20 имеется в мультимножестве $\{\infty\cdot a_1,\infty\cdot a_2,\infty\cdot a_3,\infty\cdot a_4\}$? Подмножество размера 20 имеет вид $\{m_1\cdot a_1,m_2\cdot a_2,m_3\cdot a_3,m_4\cdot a_4\}$ где $\sum m_i=20$, и они находятся в 1–1 соответствии с набор 4-х наборов $(m_1,m_2,m_3,m_4)$ неотрицательных целых чисел, таких что $\sum m_i=20$. n x_i = k$$ является $${k+n-1\выберите k}.$$ $\квадрат$

Это сразу наводит на некоторые обобщения: вместо общего количество решений, нам может понадобиться количество решений с переменные $x_i$ в определенных диапазонах, то есть мы могли бы потребовать, чтобы $m_i\le x_i\le M_i$ для некоторых нижних и верхних оценок $m_i$ и $M_i$.

С конечными верхними границами может быть трудно иметь дело; если мы требуем этого $0\le x_i\le M_i$, это то же самое, что подсчет подмультимножеств $\{M_1\cdot a_1,M_2\cdot a_2,\ldots,M_n\cdot a_n\}$. Нижние границы проще иметь дело.

Пример 1.5.2. Найдите количество решений $\ds x_1+x_2+x_3+x_4=20$ с $x_1\ge 0$, $x_2\ge 1$, $x_3\ge 2$, $x_4\ge -1$.

Мы можем преобразовать это к исходной задаче, в которой все нижние оценки равны 0. Решения, которые мы пытаемся посчитать, являются решениями этого измененное уравнение: $$ x_1+(x_2-1)+(x_3-2)+(x_4+1)=18.$$ Если мы установим $y_1=x_1$, $y_2=x_2-1$, $y_3=x_3-2$ и $y_4=x_4+1$, то $(x_1,x_2,x_3,x_4)$ является решением этого уравнения тогда и только тогда, когда $(y_1,y_2,y_3,y_4)$ — это решение $$ у_1+у_2+у_3+у_4=18,$$ и, кроме того, ограничения на $x_i$ выполняются тогда и только тогда, когда $y_i\ge 0$. Так как число решений последнего уравнения равно $18+4-1\выбрать 18$, это же количество решений задачи исходное уравнение. $\квадрат$

Пример 1.5.1 Предположим, в коробке 18 шаров, пронумерованных от 1 до 6, три шара с каждым номером. Когда 4 шара вынуты без возврата, сколько исходы возможны? Сделайте это двумя способами: предполагая, что порядок в имеет значение, какие шары вытянуты, а затем предположение о том, что порядок не важно.

Пример 1.5.2 Сколько перестановок букв в Миссисипи?

Пример 1.5.3 Сколько перестановок существует у мультимножества $\ds\{1\cdot a_1,1\cdot a_2,\ldots,1\cdot a_n\}$? 9{я}. $$ где сумма берется по всем $i_1,\ldots,i_m$ таким, что $i_1+\cdots+i_m=n$.

Пример 1.5.6 Найдите количество целочисленных решений $$x_1+x_2+x_3+x_4+x_5=50, x_1\ge -3, x_2\ge 0, x_3\ge 4, x_4\ge 2, x_5\ge 12.$$

Пример 1.5.7 Вы и ваш супруг принимаете по две мармеладные витаминки каждый день. день. Вы делите одну бутылку с 60 витаминами, 30 одного вкуса и 30 другого. Каждый из вас предпочитает разные вкусы, но это кажется ребячеством. выловить по две штуки каждого типа (но не принимать жевательные витамины). Так что вы просто возьмите первые четыре, которые выпадают, а затем разделите их в соответствии с вашими предпочтениями. Например, если их два вкус, вы и ваш супруг получаете витамины, которые вы предпочитаете, но если три вашего любимого вкуса, вы получаете два из тех, которые вам нравятся и ваш супруг получает по одному из каждого. Конечно, вы начинаете новый флакон каждые 15 дней. В среднем за 15-дневный период сколько витаминов вы принимаете вкус, который вы предпочитаете? (Из www.fivethirtyeight.com.)

Комбинаторный калькулятор, калькулятор комбинаций, вариаций, перестановок

Узнайте, сколькими способами можно выбрать k предметов из n предметов набора. С/без повторения, с/без порядка.

Расчет:

Ck(n)=(kn)=k!(n−k)!n! n=10 k=4 C4(10)=(410)=4!(10 −4)!10!=4⋅3⋅2⋅110⋅9⋅8⋅7=210

Количество комбинаций: 210

Вариантов

Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, образованная из множества n элементов. Элементы не повторяются и зависят от порядка элементов группы (поэтому расположены).

Количество вариаций можно легко подсчитать, используя комбинаторное правило произведения. Например, если у нас есть набор n = 5 чисел 1,2,3,4,5 и мы должны сделать вариации третьего класса, их V ₃ (5) = 5 * 4 * 3 = 60. Vk(n)=n(n−1)(n−2)…(n−k+1)=(n−k)!n! н! мы называем факториалом числа n, которое является произведением первых n натуральных чисел. Обозначение с факториалом только более понятное, эквивалентное. Для вычислений вполне достаточно использовать процедуру, вытекающую из комбинаторного правила произведения.

Перестановки

Перестановка является синонимом вариации n-го класса n-элементов. Таким образом, это любая упорядоченная группа из n элементов, состоящая из n элементов. Элементы не повторяются и зависят от порядка элементов в группе. P(n)=n(n−1)(n−2). ..1=n! Типичный пример: у нас есть 4 книги, и сколькими способами мы можем расположить их рядом на полке?

Вариации с повторением

Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, состоящая из множества n элементов, причем элементы могут повторяться и зависят от их порядка. Типичным примером является образование чисел из чисел 2,3,4,5 и нахождение их количества. Рассчитываем их количество по комбинаторному правилу произведения: Vk′(n)=n⋅n⋅n⋅n…n=nk

Перестановки с повторением

Повторяющаяся перестановка представляет собой упорядоченную группу k-элементов из n-элементов, при этом некоторые элементы повторяются в группе. Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок. Pk1k2k3…km′(n)=k1!k2!k3!…km!n! Типичный пример — узнать, сколько семизначных чисел образовано из чисел 2,2,2, 6,6,6,6.

Комбинации

Комбинация k-го класса из n элементов представляет собой неупорядоченную группу k-элементов, образованную из множества n элементов. Элементы не повторяются, и порядок элементов группы не имеет значения. В математике неупорядоченные группы называются множествами и подмножествами. Их количество является комбинационным числом и рассчитывается следующим образом: Ck(n)=(kn)=k!(n−k)!n! Типичный пример комбинаций: у нас 15 учеников, и мы должны выбрать троих. Сколько их будет?

Комбинации с повтором

Здесь мы выбираем k групп элементов из n элементов, независимо от порядка, и элементы могут повторяться. k логически больше n (иначе мы получили бы обычные комбинации). Их счет: Ck′(n)=(kn+k−1)=k!(n−1)!(n+k−1)! Пояснение к формуле — количество комбинаций с повторением равно количеству расположений n − 1 разделителей на n-1 + k местах. Типичный пример: мы идем в магазин, чтобы купить 6 шоколадок. Предлагают всего 3 вида. Сколько вариантов у нас есть? к = 6, п = 3.

Основы комбинаторики в текстовых задачах

Карточки
Игрок получает восемь карточек из 32. Какова вероятность того, что он выпадет а) все четыре туза б) хотя бы один туз
Футбольные команды
Нужно организовать футбольные команды. Есть три возрастные группы. Сколькими способами можно организовать десять команд для каждой возрастной группы? Это перестановка или комбинация?
Аккорды
Сколько четырехтональных аккордов (аккорд = одновременно звучащие разные тона) можно сыграть в пределах 7 тонов?
Футбольная команда
Футбольная команда имеет черные, фиолетовые и оранжевые футболки, бело-голубые шорты и полосатые и серые носки. Сколько разных нарядов могут начать игроки?
Пули вероятности
В мешочке шесть красных, пять зеленых, голубых и 11 желтых шаров. Какова вероятность того, что мы вытащим зеленую пулю?
Трехзначное число 2
Найдите количество всех трехзначных натуральных чисел, которые можно составить из цифр 1,2,3,4 и на которые распространяется одно и то же время, имеет следующие условия: на одной позиции стоит одно из цифры 1,3,4, на месте сотен 4 или 2.
Вероятность 40131
В классе IK3 28 учеников. Будут обследованы три ученика. Девятнадцать учеников готовы к экзамену. Какова вероятность того, что все трое окажутся неподготовленными?
Карты
Сколькими способами можно раздать 32 игральные карты 5 игрокам?
Чайка
Искусственно созданный остров в форме круга радиусом 50 м зарос травой. Единственным исключением является посадочная площадка для вертолетов в форме прямоугольника размером 15 м и 8 м. Какова вероятность того, что летящая чайка
Принимает решения
Решите расчетным путем, сколько кандидатов из общего числа 1000 кандидатов на должность генерального директора удовлетворяют квалификационным требованиям для достижения желаемых результатов на этой руководящей должности с вероятностью не менее 67% — при условии, конечно, что
Почетные ученики
Из 25 учеников в классе десять почетных. Сколькими способами мы можем выбрать из них пятерых учеников, если между ними должно быть ровно два знака отличия?
Парковка 72644
Сколькими способами десять автомобилей могут припарковаться рядом на стоянке?
Сапфиры 45461
Ювелир выбирает в кольцо три драгоценных камня. В нем есть рубины, изумруды и сапфиры. Сколько у него вариантов?
Делится на пять
Сколько различных трехзначных чисел, делящихся на пять, можно составить из цифр 2, 4 и 5? Мы можем повторять цифры в созданном номере.
C(6,3)
C(6,3) + 3 P(6,3)
Комбинации
Сколько различных комбинаций двузначного числа, кратного четырём, получается из цифр 3, 5 и 7?

Выучить формулы, типы, шаги для решения

При перестановке с повторением элементы могут повторяться. Перестановку с повторением определить проще всего. В этой статье мы узнаем о перестановке с повторением, объясненной с доказательством, формулами и решенными примерами, определением перестановки, типами, циклами и использованием перестановок.

Что такое перестановка?

Отдельные методы организации набора вещей в последовательном порядке называются перестановкой.

Например:

Порядок знаков, цифр, символов, алфавитов, букв и цветов.
Выбор первой, второй и третьей мест для победителей.

Математически перестановка связана с упорядочиванием всех данных набора в некоторой последовательности или порядке. Перестановки учитываются более или менее почти во всех областях математики. Для этого воспользуемся стандартной формулой перестановки. Помимо стандартной формулы, существуют различные свойства перестановок.

Узнайте здесь о различных концепциях биномиальной теоремы.

Перестановка с повторением

Проще всего определить перестановку с повторением. Рассмотрим, когда у куска есть n различных типов, и у каждого есть r вариантов каждый раз, тогда перестановки определяются как: n × n × … (r раз). Это означает, что существует n возможностей для первого выбора, за которыми следуют n возможностей для второго выбора, и так далее, каждый раз умножаясь.

Перестановка с повторением формулы

Количество перестановок n объектов, где p объектов одного типа, q объектов другого типа, а остальные, если они есть, другого типа, равно $\begin{align*}\frac{_nP_r }{p!q!}\end{align*}$

Прочтите эту статью о среднем арифметическом.

Как решить перестановку с повторением?

Рассмотрим слово ЗУБЫ. В слове 2 Е. Обе Е идентичны, и не имеет значения, в каком порядке мы пишем эти две Е, поскольку они одинаковы. Другими словами, если мы заменим «Е» на «Е», мы все равно напишем ЗУБЫ. То же самое верно и для T, так как в слове TEETH также есть 2 T. Сколькими способами можно расположить буквы в слове ЗУБЫ?

Мы должны учитывать тот факт, что эти 2 E идентичны и что 2 T идентичны. Делаем это по формуле:

$\frac{_nP_r}{x_1! x_2!}$, где x — количество повторений буквы.

$\begin{matrix}\frac{_nP_r}{x_1! x_2!} &= \frac{_5P_5}{2!2!}\\\frac{_5P_5}{2!2!} &= \frac {5 \times 4 \times 3 \times 2 \times 1}{2 \times 1 \times 2 \times 1}\\\frac{_5P_5}{2!2!} &= \frac{120}{4} \\\frac{_5P_5}{2!2!} &= 30\end{matrix}$

Также читайте об арифметических прогрессиях в этой статье. )\)

Определим количество различимых перестановок букв ЭЛЕМЕНТ.

Предположим, мы сделали все буквы разными, пометив буквы следующим образом.

$E_1LE_2ME_3NT$

Теперь все буквы отличаются друг от друга. В данном случае есть (7-1)! = 6! возможны различные круговые перестановки.

Давайте рассмотрим один такой случай круговой перестановки, где элементы расположены в следующем порядке:

$LE_1ME_2NE_3T$

Мы можем формировать новые сочетания перестановок из этого расположения, перемещая только буквы E. Ясно, что их 3! или 6 таких аранжировок. Мы перечисляем их ниже.

$\begin{matrix}LE_1ME_2NE_3\\LE_1ME_3NE_2\\LE_2ME_1NE_3T\\LE_2ME_3NE_1T\\LE_3ME_2NE_1T\\LE_3ME_1NE_2T\end{matrix}$

Поскольку буквы E не отличаются друг от друга, существует не только один вариант LEMENET . Это справедливо для любой перестановки.

Также узнайте о среднем отклонении.

Решенные примеры на перестановку с повторением

1. Найдите количество перестановок букв слова MICROSOFT.

A. Слово MICROSOFT состоит из 9 букв, в которых буква «О» повторяется два раза. Таким образом, количество перестановок букв слова MICROSOFT = ${9!\over{2!}}$ = 181440.

2. Сколько перестановок можно произвести с буквами слова КАЛЬКУЛЯТОР? В скольких из этих аранжировок гласные встречаются вместе?

A. Слово КАЛЬКУЛЯТОР состоит из 10 букв, в которых «C» повторяется два раза, «A» повторяется два раза, «L» повторяется два раза, а остальные все разные.
Следовательно, количество перестановок букв слова КАЛЬКУЛЯТОР = ${10!\over{2!2!2!}}$ = 453600
Слово КАЛЬКУЛЯТОР состоит из 4 гласных букв А, У, А, 0 Рассмотрим их как одну букву скажем P
Следовательно, теперь у нас есть 7 букв P, C, L, C, L, T, R, в которых «C» повторяется два раза, L повторяется два раза. Число расположения этих 7 букв равно 7!
дано ${7!\over{2!2!}}$ = 1260.

После этого 4 гласных (в которых ‘A’ повторяется 2 раза) можно расположить в ${4 !\over{2!}}$ = 12 способов
Следовательно, количество расстановок букв слова КАЛЬКУЛЯТОР, в которых гласные стоят вместе = 1260 x 12 = 15120.

3. Джон владеет шестицветными парами туфли (два красных, два синих и два черных). Он хочет поставить все эти пары обуви на полку для обуви. Сколько различных вариантов расположения обуви возможно? 9{2,2,2} _n = \frac {6!}{2!2!2!}\\= \frac{720}{8}\\= 90\\\end{matrix}\)
Следовательно, обувь можно расположить на обувной стойке 90 способами.

4. Человек должен выбрать три цифры из набора следующих семи чисел, чтобы составить трехзначное число.{1, 2, 3, 4, 5, 6, 7} Сколько различных комбинаций цифр возможный?

A. В трехзначном числе может быть 2 или 3 одинаковых числа. Точно так же в числе важен порядок цифр. Принято считать, что человек может выбрать 3 цифры из набора 7 цифр. Следовательно, n = 7 и k = 3. Подставьте эти значения в приведенную ниже формулу, чтобы получить количество возможных комбинаций. 93\)
= 343
Следовательно, возможны 343 различных расположения.

5. Если в коробке 4 шоколадных чипса, 2 овсяных и 2 двойных шоколадных печенья, в скольких различных порциях можно съесть все это печенье?

A:Общее количество печенья = 8, поэтому n = 8.
Мы хотим съесть все печенье; поэтому мы выбираем 8 объектов одновременно. Следовательно, r = 8.
В группе из 8 печений 4 шоколадных, 2 овсяных и 2 двойных шоколадных печенья. Мы едим группу печенья с повторяющимися вкусами. 9(3,2)_n = \frac{362880}{12}\\= 30240\end{matrix}\)
Следовательно, буквы в слове ОТЛИЧНО можно расположить 30240 способами.

Надеюсь, эта статья о перестановке с повторением была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!

Часто задаваемые вопросы о перестановке с повторением

В.1 Что такое перестановка с повторением?

Ответ 1 Это самые простые для определения. Рассмотрим, когда у фигуры есть n различных типов, и каждый раз у нее есть r вариантов выбора, тогда перестановки определяются следующим образом:
n × n × … (r раз)
Это означает, что существует n возможностей для первого выбора, за которыми следуют n возможностей для второго выбора, и так далее, каждый раз умножаясь.

Q.2 Что такое перестановка без повторения?

Ответ 2 В этом случае каждый раз количество вариантов уменьшается. Рассмотрим, когда кусок имеет n различных типов, и у каждого есть r вариантов каждый раз без повторения, перестановок будет:
n × (n-1) × (n-2)…
Это означает, что существует n возможностей для первого выбора, за которыми следует n-1 возможностей для второго выбора, и так далее, каждый раз умножая.

Q.3 Как найти количество перестановок с повторением?

Ответ 3 Рассмотрим слово ЗУБЫ. В слове 2 Е. Обе Е идентичны, и не имеет значения, в каком порядке мы пишем эти две Е, поскольку они одинаковы. Другими словами, если мы заменим «Е» на «Е», мы все равно напишем ЗУБЫ. То же самое верно и для T, так как в слове TEETH также есть 2 T. Сколькими способами можно расположить буквы в слове ЗУБЫ?
Мы должны учитывать тот факт, что эти 2 Е идентичны и что 2 Т идентичны. Делаем это по формуле:
$\frac{_nP_r}{x_1! x_2!}$, где x — количество повторений буквы.

В.4 Могут ли числа повторяться при перестановке?

Ответ 4 Да, элементы могут повторяться в перестановках.