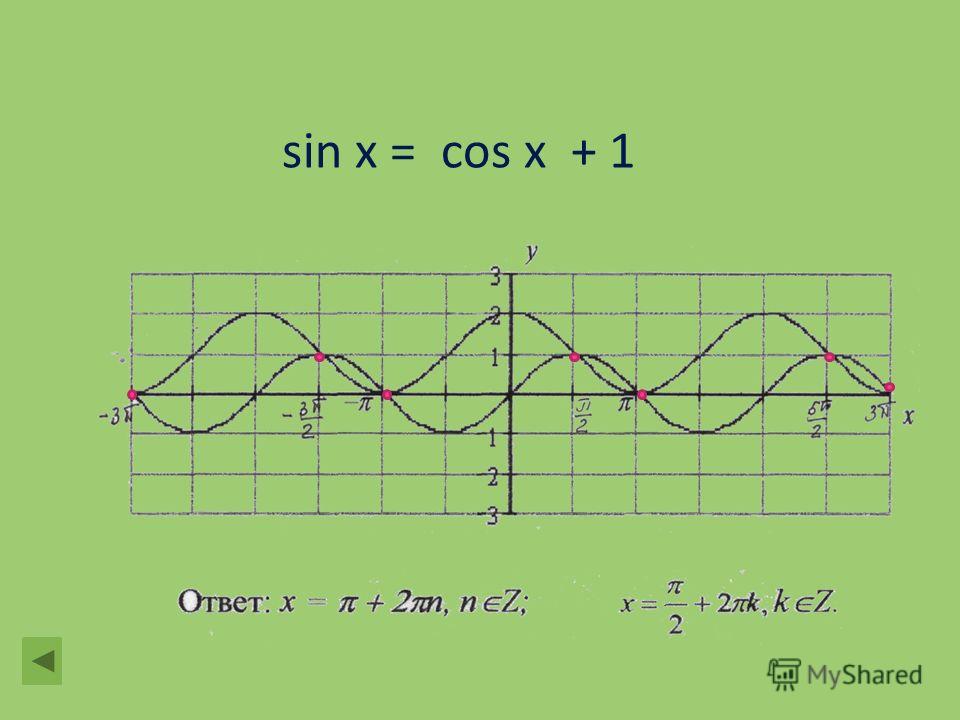График функции arccos x
Арксинус, arcsin
Определение и обозначения
Арксинус иногда обозначают так:
.
График функции арксинус
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
Арккосинус иногда обозначают так:
.
График функции арккосинус
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(– x ) = arcsin(–sin arcsin x ) = arcsin(sin(–arcsin x )) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(– x ) = arccos(–cos arccos x ) = arccos(cos(π–arccos x )) = π – arccos x ≠ ± arccos x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/ 2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 |
Формулы
Формулы суммы и разности
при или
при 0,,y>0 ;»> и 1″>
при и 1″>
при или
при 0,,y и 1″>
при 0 ;»> и 1″>
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:
Свойства функции арксинус y = arcsin(x).
· Областью определения функции арксинус является интервал от минус единицы до единицы включительно:
.
· Область значений функции y = arcsin(x):
.
· Функция арксинус — нечетная, так как
.
· Функция y = arcsin(x) возрастает на всей области определения, то есть, при
.
· Функция вогнутая при
, выпуклая при .
· Точка перегиба (0; 0), она же ноль функции.
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:
Свойства функции арккосинус y = arccos(x).
· Область определения функции арккосинус:
.
· Область значений функции y = arccos(x):
.
· Функция не является ни четной ни нечетной, то есть, она общего вида.
· Функция арккосинус убывает на всей области определения, то есть, при
.
· Функция вогнутая при
, выпуклая при .
· Точка перегиба
.
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:
Свойства функции арктангенс y = arctg(x).
· Область определения функции y = arctg(x):
.
· Область значений функции арктангенс:.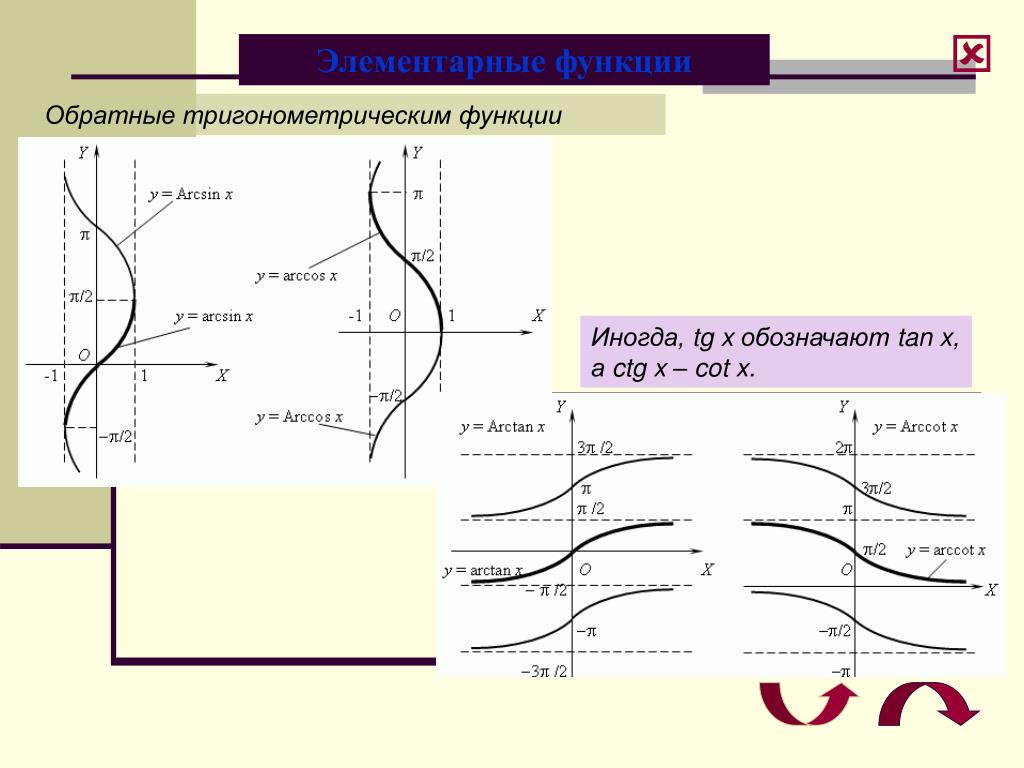
· Функция арктангенс — нечетная, так как
.
· Функция возрастает на всей области определения, то есть, при
.
· Функция арктангенс вогнутая при
, выпуклая при .
· Точка перегиба (0; 0), она же ноль функции.
· Горизонтальными асимптотами являются прямые
при и при . На чертеже они показаны зеленым цветом.
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:
Свойства функции арккотангенс y = arcctg(x).
· Областью определения функции арккотангенс является все множество действительных чисел:
· Область значений функции y = arcctg(x):
.
· Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
· Функция убывает на всей области определения, то есть, при
.
· Функция вогнутая при
, выпуклая при .
· Точка перегиба
.
· Горизонтальными асимптотами являются прямые
при (на чертеже показана зеленым цветом) и y = 0 при .
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8831 —
| 7545 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями.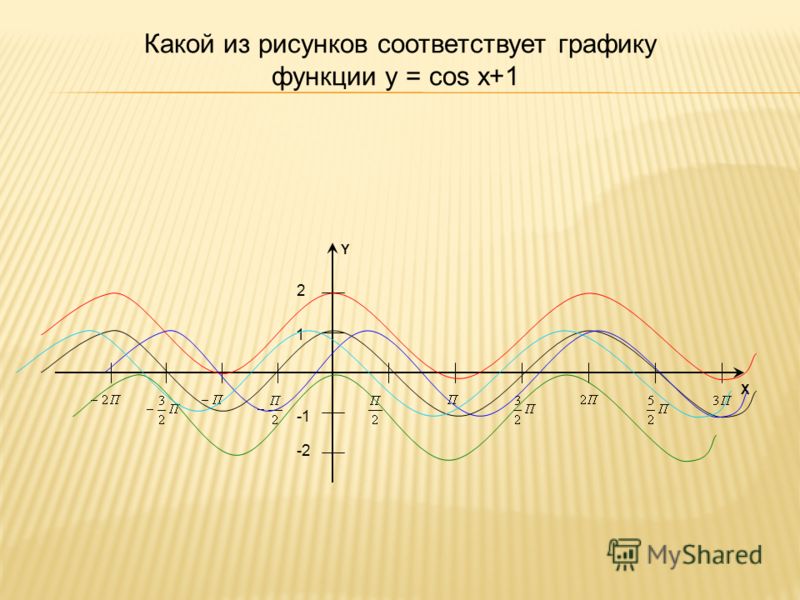 Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:
Свойства функции арксинус y = arcsin(x).
Областью определения функции арксинус является интервал от минус единицы до единицы включительно:
.
Область значений функции y = arcsin(x):
Функция арксинус — нечетная, так как
.
Функция y = arcsin(x) возрастает на всей области определения, то есть, при
.
Функция вогнутая при
, выпуклая при .
Точка перегиба (0; 0), она же ноль функции.
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:
Свойства функции арккосинус y = arccos(x).
Область определения функции арккосинус:
.
Область значений функции y = arccos(x):
.
Функция не является ни четной ни нечетной, то есть, она общего вида.
Функция арккосинус убывает на всей области определения, то есть, при
.Функция вогнутая при
, выпуклая при .
Точка перегиба
.
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:
Свойства функции арктангенс y = arctg(x).
Область определения функции y = arctg(x):
.
Область значений функции арктангенс:
.
Функция арктангенс — нечетная, так как
.
Функция возрастает на всей области определения, то есть, при
.
Функция арктангенс вогнутая при
, выпуклая при .
Точка перегиба (0; 0), она же ноль функции.
Горизонтальными асимптотами являются прямые
при
Свойства функции арккотангенс y = arcctg(x).
Областью определения функции арккотангенс является все множество действительных чисел:
.
Область значений функции y = arcctg(x):
.
Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
Функция убывает на всей области определения, то есть, при
.
Функция вогнутая при
, выпуклая при .
Точка перегиба
.
Горизонтальными асимптотами являются прямые
при (на чертеже показана зеленым цветом) и y = 0 при .
«>
График arccos. Тригонометрия. Обратные тригонометрические функции. Арксинус. Получение функции arcsin
Определение и обозначения
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
-1 ≤
x ≤ 1
и множество значений -π/2 ≤
y ≤ π/2
.
arcsin(sin x) = x .
Арксинус иногда обозначают так:
.
График функции арксинус
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
). Он имеет область определения -1 ≤
x ≤ 1
и множество значений 0 ≤
y ≤ π
.
cos(arccos
x)
= x
;
arccos(cos
x)
= x
.
Арккосинус иногда обозначают так:
.
График функции арккосинус
График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Функция арккосинус не является четной или нечетной:
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x ≠ ± arccos
x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | — 1 ≤ x ≤ 1 | — 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.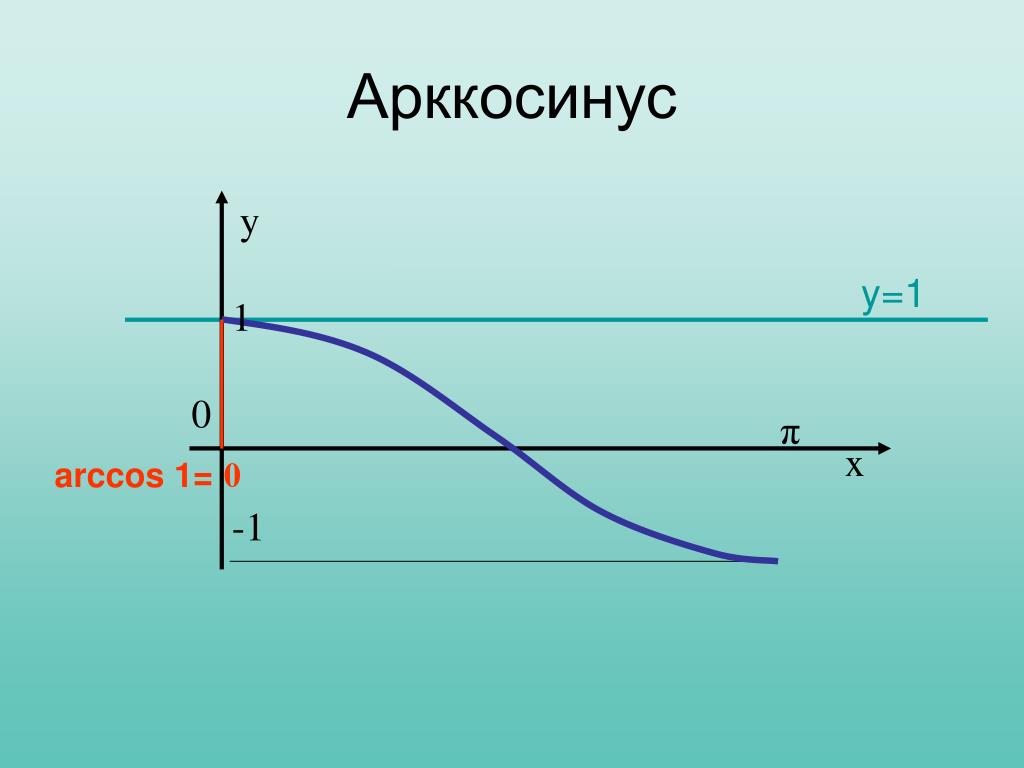
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| — 1 | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
См. также: Вывод формул обратных тригонометрических функций
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
См.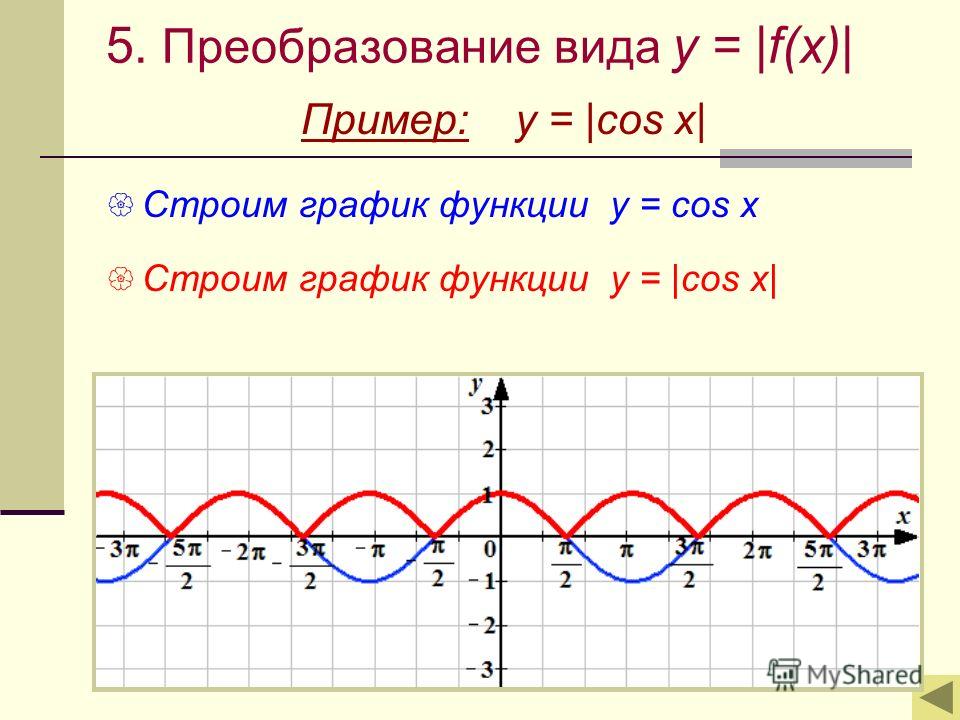 также:
Вывод формул
также:
Вывод формул
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков :
,
где — многочлен степени .
Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin
t
.
Интегрируем по частям, учитывая что -π/2
≤ t ≤ π/2
,
cos
t ≥ 0
:
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| ;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin
x)
= x
cos(arccos
x)
= x
.
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при .
Использованная литература:
И.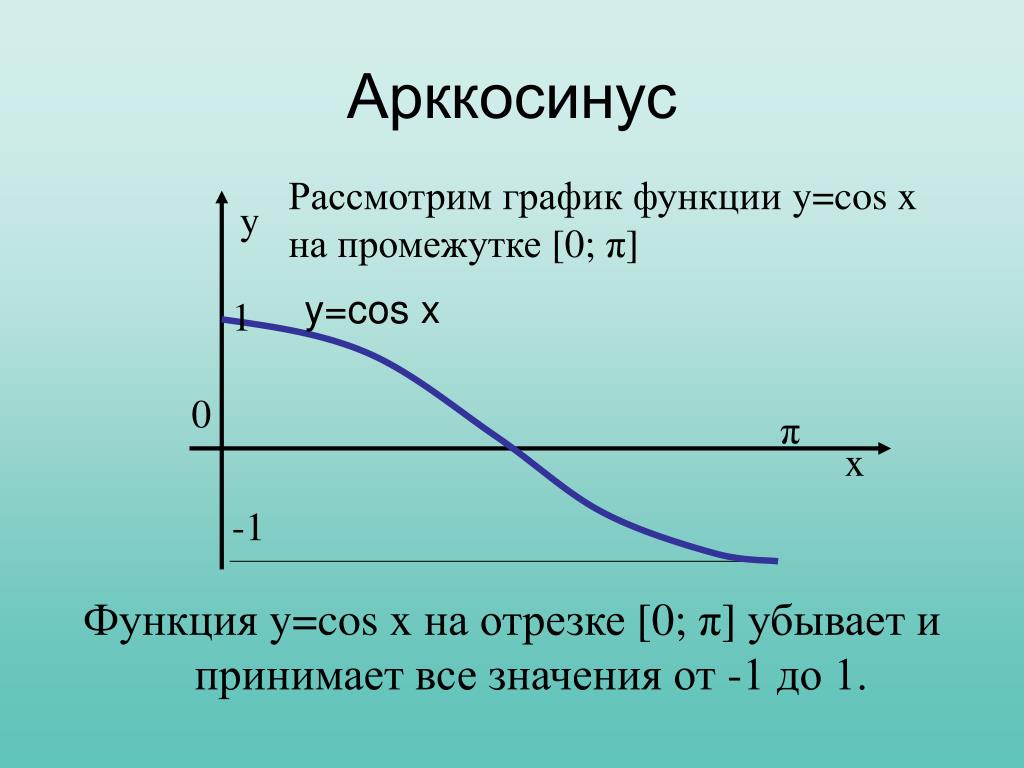 Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
См. также:
(круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям .
Арккосинус , обратная функция к cos (x = cos y), y = arccos x определен при и имеет множество значений . Другими словами возвращает угол по значению его cos .
Арккосинус (обозначение: arccos x ; arccos x — это угол , косинус которого равняется x и так далее).
Функция y = cos x непрерывна и ограничена на всей своей числовой прямой. Функция y = arccos x является строго убывающей.
Свойства функции arcsin .
Получение функции arccos .
Дана функция y = cos x . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является.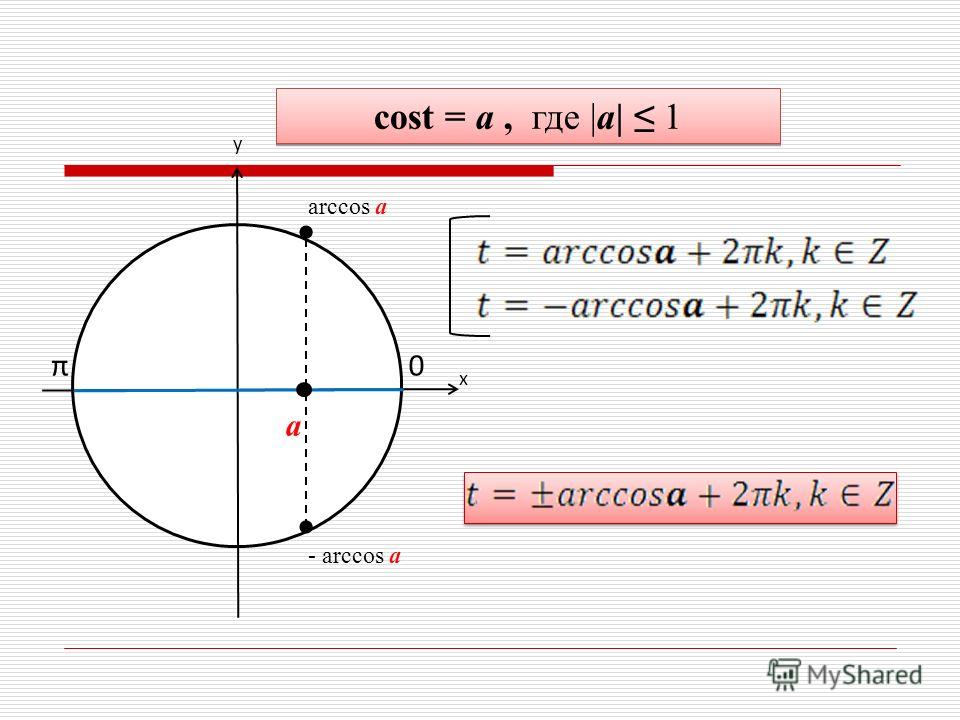 Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — . На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция y = arccos x , график которой симметричен графику y = cos x на отрезке относительно прямой y = x .
Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — . На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция y = arccos x , график которой симметричен графику y = cos x на отрезке относительно прямой y = x .
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn
(где n
целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
.
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
), имеющая область определения и множество значений .
Арктангенс (y = arctg
x
) — это функция, обратная к тангенсу (x = tg
y
), имеющая область определения и множество значений .
Арккотангенс (y = arcctg
x
) — это функция, обратная к котангенсу (x = ctg
y
), имеющая область определения и множество значений .
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус , Тангенс, котангенс .
y = arcsin x
y = arccos
x
y = arctg
x
y = arcctg
x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.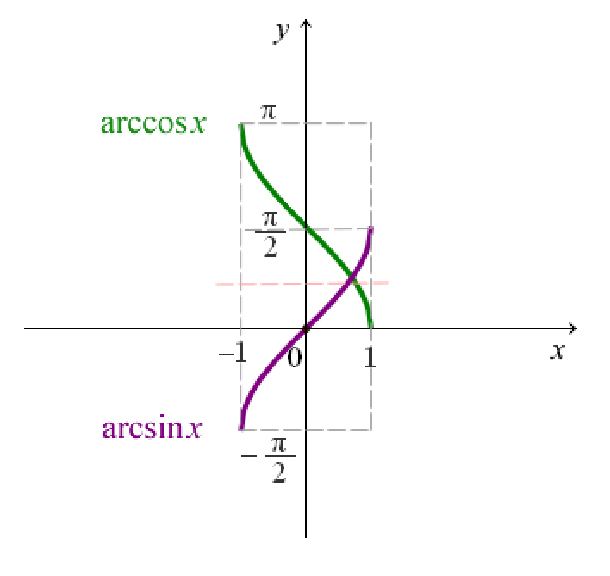
arcsin(sin
x)
= x
при
sin(arcsin
x)
= x
arccos(cos
x)
= x
при
cos(arccos
x)
= x
arctg(tg
x)
= x
при
tg(arctg
x)
= x
arcctg(ctg
x)
= x
при
ctg(arcctg
x)
= x
Формулы, связывающие обратные тригонометрические функции
См. также: Вывод формул обратных тригонометрических функций
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
при
при
при
при
при
при
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
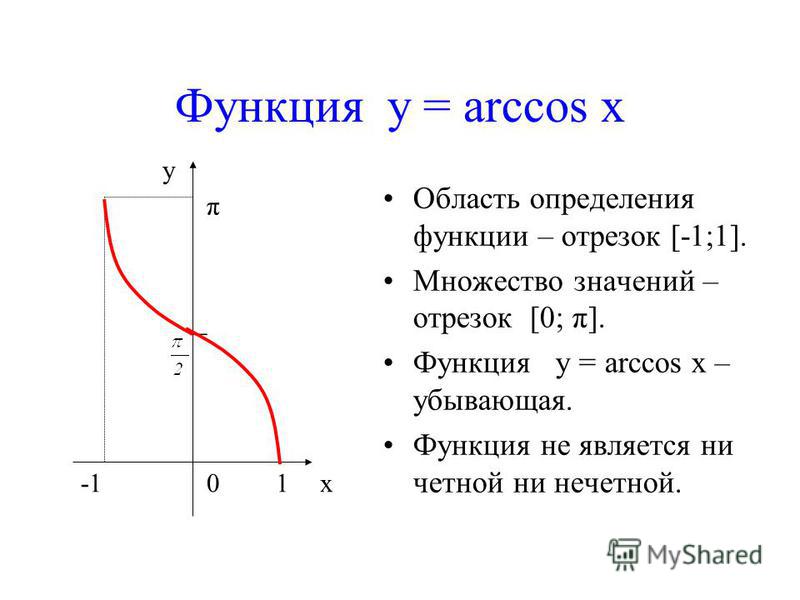
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .

- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.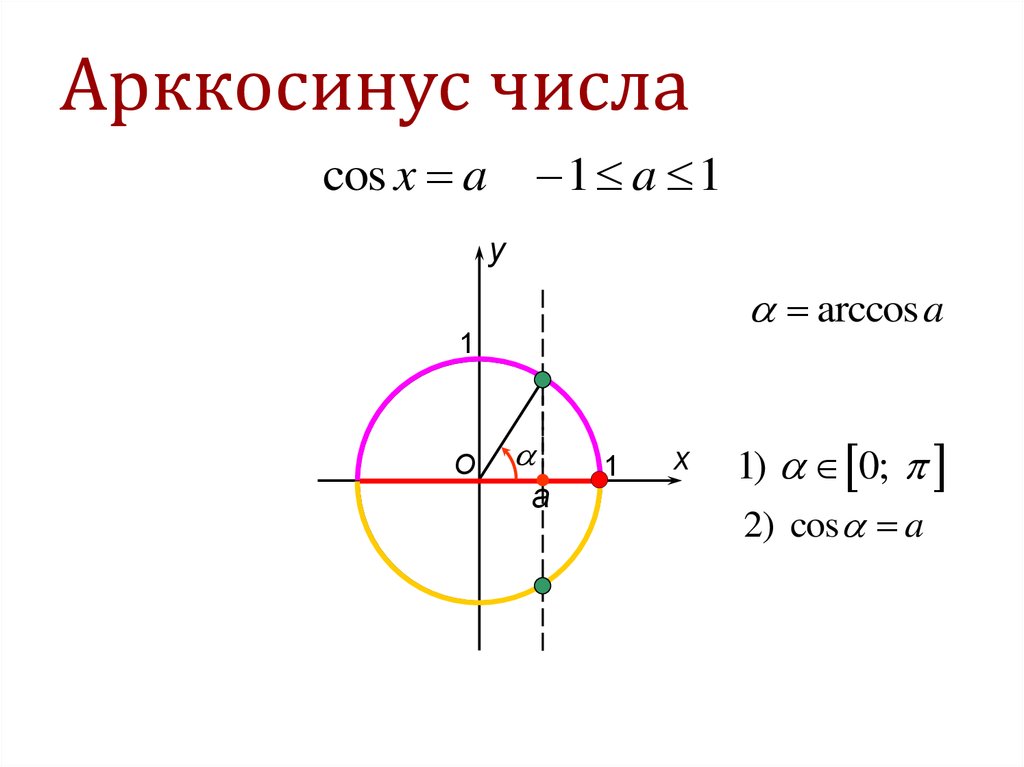
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям .
Арксинус (обозначается как arcsin x ; arcsin x — это угол, sin его равняется x ).
Арксинус (y = arcsin x ) — обратная тригонометрическая функция к sin (x = sin y ), которая имеет область определения и множество значений . Другими словами возвращает угол по значению его sin .
Функция y=sin x непрерывна и ограничена на всей своей числовой прямой. Функция y=arcsin x — строго возрастает.
Свойства функции arcsin .
График арксинуса.
Получение функции arcsin .
Есть функция y = sin x . На всей своей области определения она кусочно-монотонная, таким образом, обратное соответствие y = arcsin x не является функцией. Поэтому рассматриваем отрезок, на котором она только возрастает и принимает каждое значение области значений — . Т.к. для функции y = sin x на интервале все значения функции получается при только одном значении аргумента, значит, на этом отрезке есть обратная функция y = arcsin x , у которой график является симметричным графику функции y = sin x на отрезке относительно прямой y = x .
Arcsec что это
Обратные тригонометрические функции, их графики и формулы
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x , при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x . Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y .
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ), имеющая область определения и множество значений .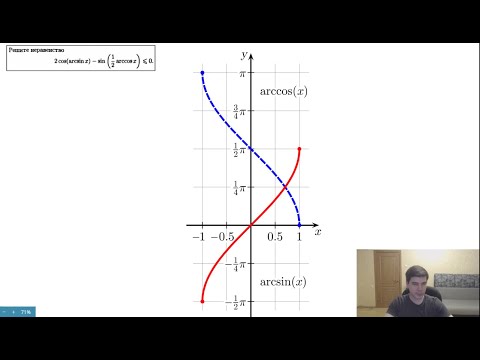
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ), имеющая область определения и множество значений .
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ), имеющая область определения и множество значений .
Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ), имеющая область определения и множество значений .
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус, Тангенс, котангенс.
y = arcsin x
y = arccos x
y = arctg x
y = arcctg x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin x ) = x при
sin(arcsin x ) = x
arccos(cos x ) = x при
cos(arccos x ) = x
arctg(tg x ) = x при
tg(arctg x ) = x
arcctg(ctg x ) = x при
ctg(arcctg x ) = x
Обратные тригонометрические функции
Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям.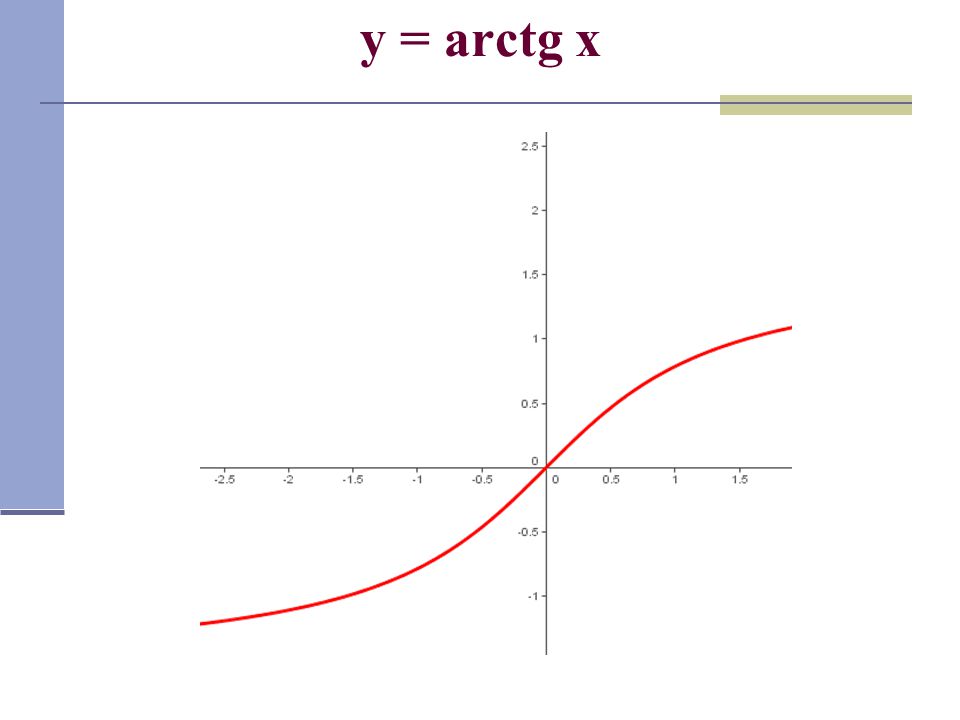 К обратным тригонометрическим функциям обычно относят шесть функций:
К обратным тригонометрическим функциям обычно относят шесть функций:
- аркси́нус (обозначение: arcsin)
- аркко́синус (обозначение: arccos)
- аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
- арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
- арксе́канс (обозначение: arcsec)
- арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin −1 для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1.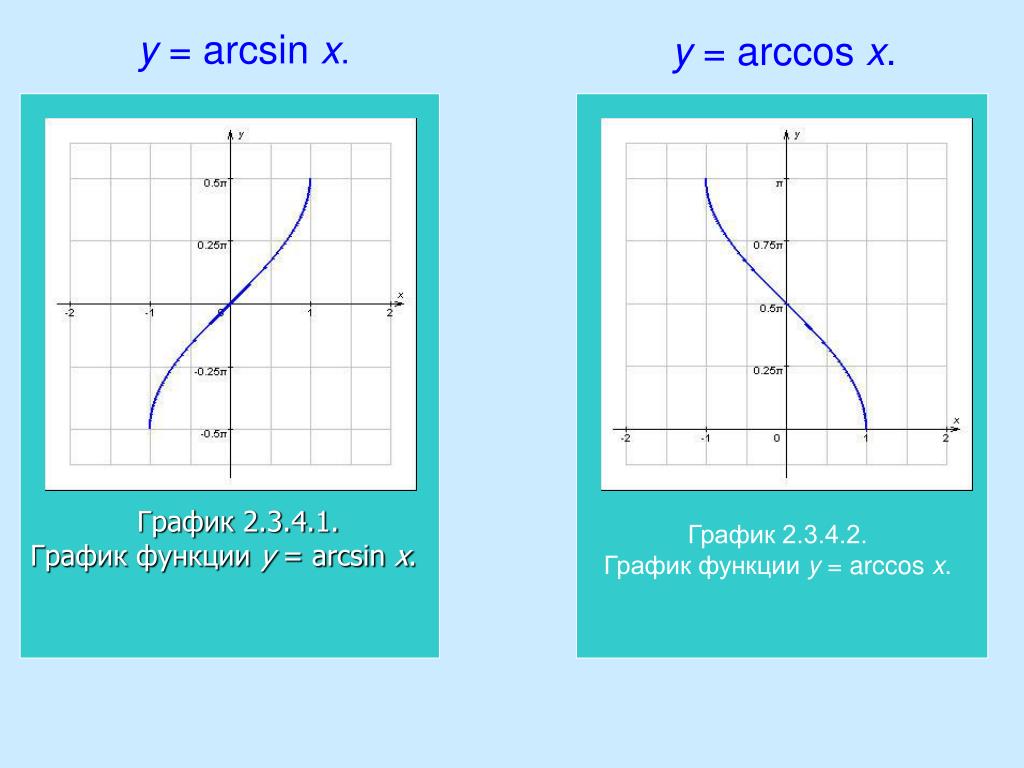
Содержание
Основное соотношение
График функции .
Арксинусом числа m называется такое значение угла x, для которого непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.
- при
- при (область определения),
- (функция является нечётной).
- при .
- при
- при
- На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — на интервале график которой симметричен графику функции на отрезке
Функция arccos
График функции .
Арккосинусом числа m называется такое значение угла x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.
- при
- при
- (область определения),
- (область значений).

Свойства функции arccos
- (функция центрально-симметрична относительно точки при
- при
- На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — На этом отрезке строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция график которой симметричен графику на отрезке относительно прямой
Функция arctg
График функции , для которого
Функция arcctg
Арккотангенсом числа m называется такое значение угла x, для которого
- . На этом отрезке существует обратная функция относительно прямой График симметричен к арктангенсу
Функция arcsec
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.

В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:
α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)
Связь с натуральным логарифмом
Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:
Тригонометрические функции sin arcsin x2. Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.

- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.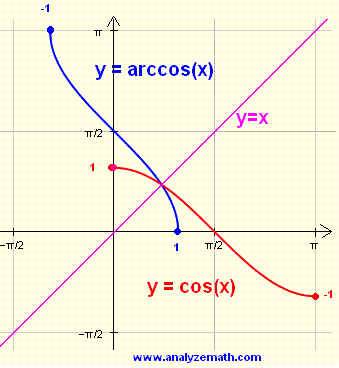
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей.
Определение обратных тригонометрических функций
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin
x
,
при заданном ,
имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x
такой корень, то и x + 2πn
(где n
целое) тоже будет корнем уравнения.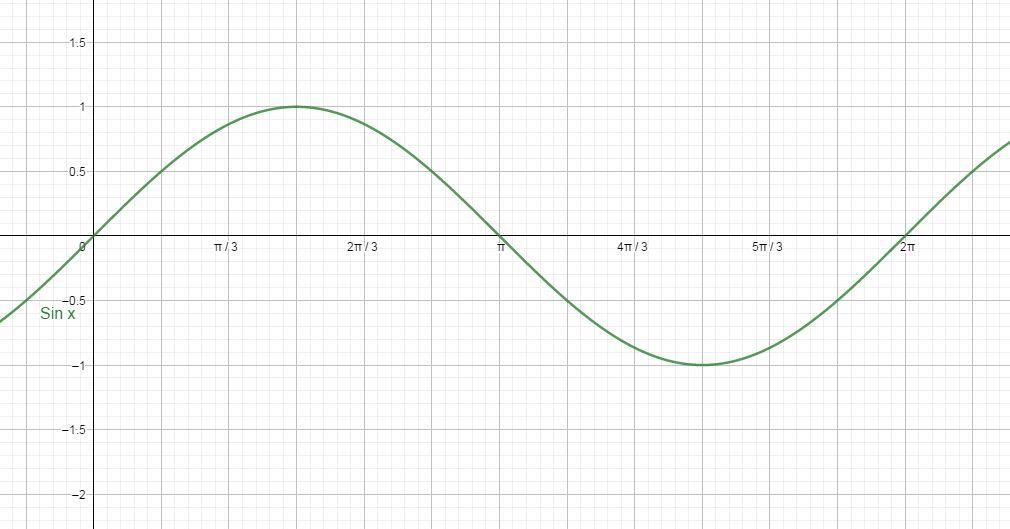 Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
.
Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin
x
.
Если ограничить аргумент x
интервалом ,
то на нем функция y = sin
x
монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin
y
.
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
Арксинус (y = arcsin x ) — это функция, обратная к синусу (x = sin y
Арккосинус (y = arccos x ) — это функция, обратная к косинусу (x = cos y ), имеющая область определения и множество значений .
Арктангенс (y = arctg x ) — это функция, обратная к тангенсу (x = tg y ), имеющая область определения и множество значений .
Арккотангенс (y = arcctg
x
) — это функция, обратная к котангенсу (x = ctg
y
), имеющая область определения и множество значений .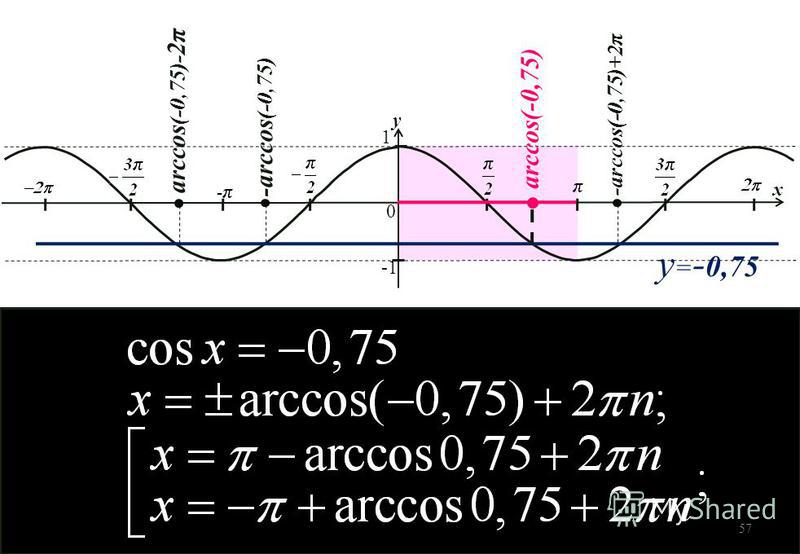
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус , Тангенс, котангенс .
y = arcsin x
y = arccos
x
y = arctg
x
y = arcctg
x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin
x)
= x
при
sin(arcsin
x)
= x
arccos(cos
x)
= x
при
cos(arccos
x)
= x
arctg(tg
x)
= x
при
tg(arctg
x)
= x
arcctg(ctg
x)
= x
при
ctg(arcctg
x)
= x
Формулы, связывающие обратные тригонометрические функции
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Урок и презентация на темы: «Арксинус.
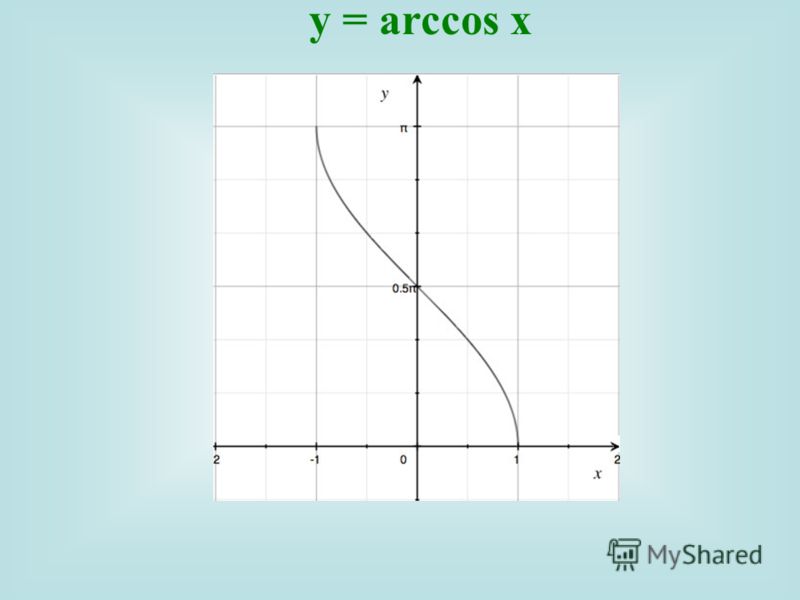 Таблица арксинусов. Формула y=arcsin(x)»
Таблица арксинусов. Формула y=arcsin(x)»Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Программная среда «1С: Математический конструктор 6.1»
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
Что будем изучать:
1. Что такое арксинус?
2. Обозначение арксинуса.
3. Немного истории.
4. Определение.
6. Примеры.
Что такое арксинус?
Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения.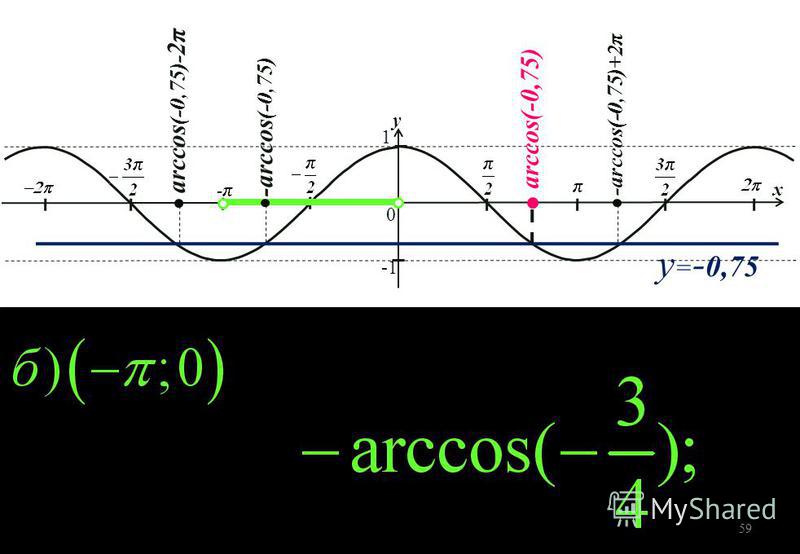 Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
а x2= 2π/3 + 2πk.
Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?
Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.
Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).
И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.
Немного истории арксинуса
История происхождения нашего символа совершенно такая же, как и у arccos.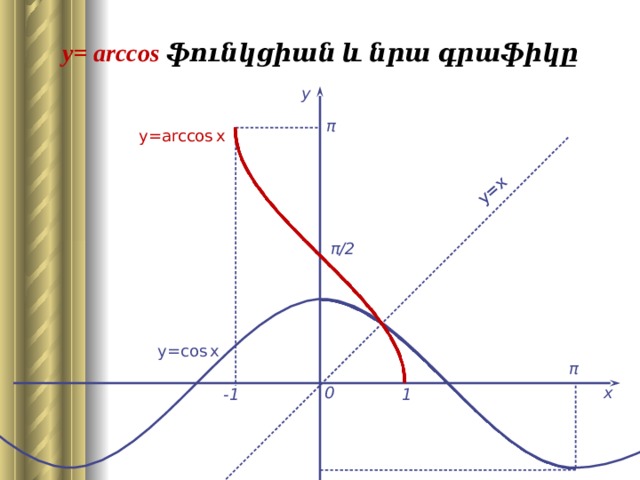 Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.
Определение арксинуса
Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.
Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πk
Перепишем:
x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).
Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.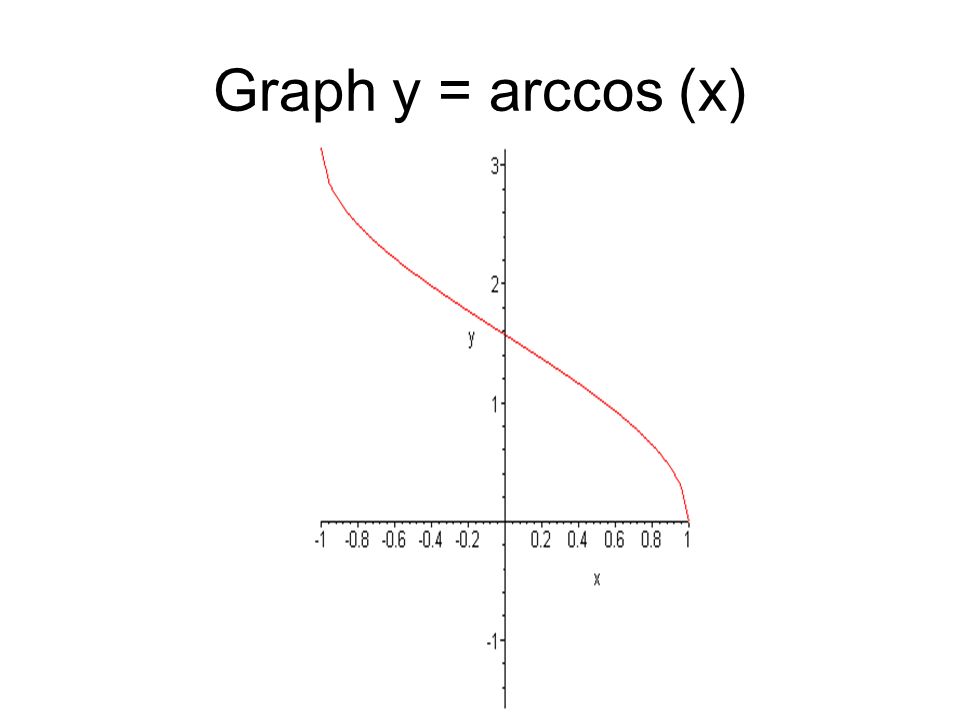
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:
Есть три случая, в которых предпочитают записывать решения более простым способом:
sin(x)=0, то x= πk,
sin(x)=1, то x= π/2 + 2πk,
sin(x)=-1, то x= -π/2 + 2πk.
Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).
Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.
Примеры
1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.
2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.
3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0.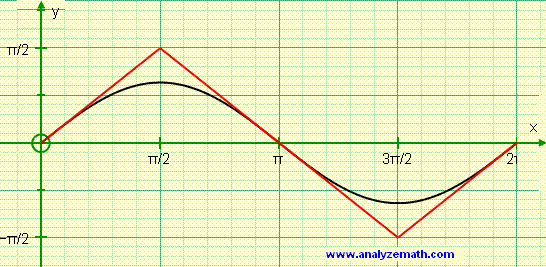 По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2.
Ответ: arcsin(0)=0.
4. Решить уравнение: sin(x) = -√2/2.
x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2)= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.
5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk
6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1) n — arcsin(3/5) + πk.
7. Решить неравенство sin(x)
Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Неравенству y
Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk
Задачи на арксинус для самостоятельного решения
1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0.25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно. ) Прямо здесь и сейчас вы в этом убедитесь.
) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.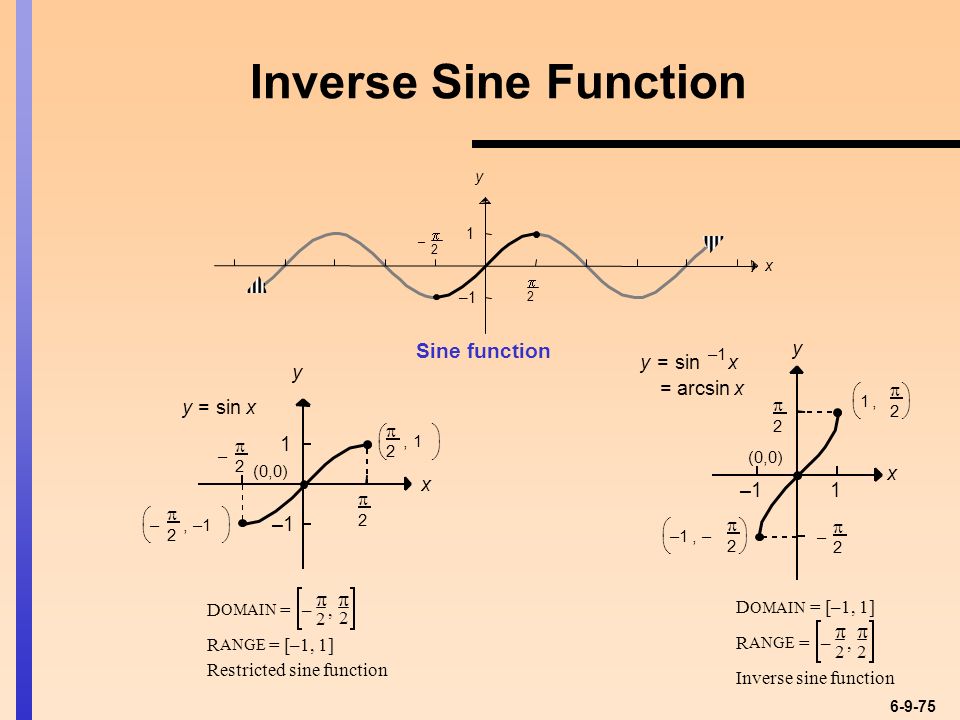 ) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите. ) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2. ) Что и является правильным ответом.
) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость. )
)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Представлен способ вывода формул для обратных тригонометрических функций. Получены формулы для отрицательных аргументов, выражения, связывающие арксинус, арккосинус, арктангенс и арккотангенс. Указан способ вывода формул суммы арксинусов, арккосинусов, арктангенсов и арккотангенсов.
Основные формулы
Вывод формул для обратных тригонометрических функций прост, но требует контроля за значениями аргументов прямых функций. Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых. Свойства обратных функций можно разбить на две группы.
Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых. Свойства обратных функций можно разбить на две группы.
В первую группу входят формулы, справедливые на всей области определения обратных функций:
sin(arcsin
x)
= x
cos(arccos
x)
= x
tg(arctg
x)
= x
(-∞ ctg(arcctg
x)
= x
(-∞
Во вторую группу входят формулы, справедливые только на множестве значений обратных функций.
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при
arctg(tg
x)
= x
при
arcctg(ctg
x)
= x
при
Если переменная x
не попадает в указанный выше интервал, то ее следует привести к нему, применяя формулы тригонометрических функций (далее n
— целое):
sin
x = sin(-
x-π)
;
sin
x = sin(π-x)
;
sin
x = sin(x+2
πn)
;
cos
x = cos(-x)
;
cos
x = cos(2
π-x)
;
cos
x = cos(x+2
πn)
;
tg
x = tg(x+πn)
;
ctg
x = ctg(x+πn)
Например, если известно, что то
arcsin(sin
x)
=
arcsin(sin( π — x ))
= π — x .
Легко убедиться, что при π — x попадает в нужный интервал. Для этого умножим на -1 : и прибавим π : или Все правильно.
Обратные функции отрицательного аргумента
Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.
arcsin(- x) = arcsin(-sin arcsin x) = arcsin(sin(-arcsin x)) = — arcsin x
Поскольку то умножив на -1
, имеем: или
Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.
Аналогично для остальных функций.
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x
arctg(- x) = arctg(-tg arctg x) = arctg(tg(-arctg x)) = — arctg x
arcctg(- x) = arcctg(-ctg arcctg x) = arcctg(ctg(π-arcctg x)) = π — arcctg x
Выражение арксинуса через арккосинус и арктангенса через арккотангенс
Выразим арксинус через арккосинус.
Формула справедлива при Эти неравенства выполняются, поскольку
Чтобы убедиться в этом, умножим неравенства на -1
: и прибавим π/2
:
или Все правильно.
Аналогично выражаем арктангенс через арккотангенс.
Выражение арксинуса через арктангенс, арккосинуса через арккотангенс и наоборот
Поступаем аналогичным способом.
Формулы суммы и разности
Аналогичным способом, получим формулу суммы арксинусов.
Установим пределы применимости формулы. Чтобы не иметь дела с громоздкими выражениями, введем обозначения: X = arcsin
x
,
Y = arcsin
y
.
Формула применима при
.
Далее замечаем, что, поскольку arcsin(-
x) = — arcsin
x,
arcsin(-
y) = — arcsin
y,
то при разных знаках у x
и y
,
X
и Y
также разного знака и поэтому неравенства выполняются. Условие различных знаков у x
и y
можно написать одним неравенством: .
То есть при формула справедлива.
Теперь рассмотрим случай x > 0
и y > 0
,
или X > 0
и Y > 0
.
Тогда условие применимости формулы заключается в выполнении неравенства: .
Поскольку косинус монотонно убывает при значениях аргумента в интервале от 0
,
до π
,
то возьмем косинус от левой и правой части этого неравенства и преобразуем выражение:
;
;
;
.
Поскольку и ;
то входящие сюда косинусы не отрицательные. Обе части неравенства положительные. Возводим их в квадрат и преобразуем косинусы через синусы:
;
.
Подставляем sin
X = sin arcsin
x = x
:
;
;
;
.
Итак, полученная формула справедлива при или .
Теперь рассмотрим случай x > 0, y > 0 и x 2 + y 2 > 1 . Здесь аргумент синуса принимает значения: . Его нужно привести к интервалу области значения арксинуса :
Итак,
при и.
Заменив x и y на — x и — y , имеем
при и.
Выполняем преобразования:
при и.
Или
при и.
Итак, мы получили следующие выражения для суммы арксинусов:
при или ;
при и ;
при и .
[Зачет 53] Обратные тригонометрические функции, их свойства и графики.
[Зачет 53] Обратные тригонометрические функции, их свойства и графики.
Обратные тригонометрические функции, их свойства и графики.
Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям.
Функция arcsin
График функции .
Арксинусом числа m называется такое значение угла x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.
- при
- при
- (область определения),
- (область значений).
[править]Свойства функции arcsin
- (функция является нечётной).
- при .
- при
- при
[править]Получение функции arcsin
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — . Так как для функции на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция график которой симметричен графику функции на отрезке относительно прямой
Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — . Так как для функции на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция график которой симметричен графику функции на отрезке относительно прямой
[править]Функция arccos
График функции .
Арккосинусом числа m называется такое значение угла x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.
- при
- при
- (область определения),
- (область значений).
[править]Свойства функции arccos
- (функция центрально-симметрична относительно точки ), является индифферентной.
- при
- при
[править]Получение функции arccos
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — На этом отрезке строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция график которой симметричен графику на отрезке относительно прямой
Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — На этом отрезке строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция график которой симметричен графику на отрезке относительно прямой
[править]Функция arctg
График функции .
Арктангенсом числа m называется такое значение угла , для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.
- при
- при
[править]Свойства функции arctg
- , при x > 0.
- , при x > 0.
[править]Получение функции arctg
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная , график которой симметричен графику на отрезке относительно прямой
Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная , график которой симметричен графику на отрезке относительно прямой
[править]Функция arcctg
График функции y=arcctg x
Арккотангенсом числа m называется такое значение угла x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.
- при
- при
[править]Свойства функции arcctg
- (график функции центрально-симметричен относительно точки
- при любых
[править]Получение функции arcctg
Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — . На этом отрезке строго убывает и принимает все свои значения только один раз, следовательно, на интервале существует обратная функция , график которой симметричен графику на отрезке относительно прямой График симметричен к арктангенсу
Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — . На этом отрезке строго убывает и принимает все свои значения только один раз, следовательно, на интервале существует обратная функция , график которой симметричен графику на отрезке относительно прямой График симметричен к арктангенсу
5.Обратные тригонометрические (аркфункции)
◦Функция арксинус y=arcsin(x)
Свойства функции y=arcsin(x).
◦Область определения арксинуса:
◦Область значений функции арксинус: .
◦Функция нечетная, так как .
◦Функция возрастает на всей области определения, то есть, при .
◦Функция вогнутая при , выпуклая при .
◦Точка перегиба (0; 0) , она же ноль функции.
◦Асимптот нет.
◦Функция арккосинус y=arccos(x)
Свойства функции y=arccos(x).
◦Область определения арккосинуса:
◦Область значений арккосинуса: .
◦Функция
не является ни четной ни нечетной, то
есть, она общего вида.
◦Функция убывает на всей области определения, то есть, при
◦Функция вогнутая при , выпуклая при
◦Точка перегиба .
◦Асимптот нет.
◦Функция арктангенс y=arctg(x)
Свойства функции y=arctg(x).
◦Область определения: .
◦Область значений: .
◦Функция арктангенс — нечетная, так как .
◦Функция возрастает на всей области определения, то есть, при .
◦Функция арктангенс вогнутая при , выпуклая при .
◦Точка перегиба (0; 0) , она же ноль функции.
◦Горизонтальными асимптотами являются прямые при и при . На чертеже они показаны зеленым цветом.
◦Функция арккотангенс y=arcctg(x)
Свойства функции y=arcctg(x).
◦Область определения: .
◦Область значений арккотангенса: .
◦Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
◦Функция
убывает на всей области определения,
то есть, при
.
◦Функция вогнутая при , выпуклая при .
◦Точка перегиба .
◦Горизонтальными асимптотами являются прямые при (на чертеже показана зеленым цветом) и y=0 при .
Преобразование графиков элементарных функций.
Три способа геометрических преобразований графика функции:
•Масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.
На необходимость масштабирования указывают коэффициенты k1 и k2 отличные от единицы, если , то происходит сжатие графика относительно oy и растяжение относительно ox , если , то производим растяжение вдоль оси ординат и сжатие вдоль оси абсцисс.
•Симметричное (зеркальное) отображение относительно координатных осей.
На
необходимость этого преобразования
указывают знаки «минус» перед
коэффициентами k1
(в этом случае симметрично отображаем
график относительно оси ox ) и k2
(в этом случае симметрично отображаем
график относительно оси oy ). Если знаков
«минус» нет, то этот шаг пропускается.
•Параллельный перенос (сдвиг) вдоль осей ox и oy .
Это преобразование производится В ПОСЛЕДНЮЮ ОЧЕРЕДЬ при наличии коэффициентов a и b , отличных от нуля. При положительном а график сдвигается влево на а единиц, при отрицательных а – вправо на а единиц. При положительном b график функции параллельно переносим вверх на b единиц, при отрицательном b – вниз на b единиц.
Пример (преобразование графика степенной функции).
С помощью преобразования графика функции построить
Решение.
Функция представляется в следующем виде:
Имеем k1=2, причем перед этим коэффициентом знак «минус»,
а=-1/2 , b=3 . Следовательно, получили цепочку геометрических преобразований графика: растяжение вдоль оси ординат вдвое, симметричное отображение относительно оси абсцисс, сдвиг вправо на 1/2 и сдвиг вверх на 3 единицы.
исходная степенная функция
растягиваем вдоль оси oy вдвое
отображаем симметрично относительно оси ox
сдвигаем вправо на 1/2
сдвигаем вверх на 3 единицы
Пример (преобразование графика показательной
функции).
Построить график показательной функции
Решение.
По свойствам степени преобразуем функцию:
Таким образом, имеем цепочку преобразований графика показательной функции :
исходная показательная функция
сжимаем вдоль оси oy вдвое
растягиваем вдвое вдоль оси ox
отображаем симметрично относительно оси ox
отображаем симметрично относительно оси oy
сдвигаем вверх на 8 единиц
Пример (геометрические преобразования графика логарифмической функции y=ln(x)).
Построить преобразованием графика функции
Решение.
Используем свойства логарифма:
Таким образом, имеем цепочку преобразований графика логарифмической функции:
график исходной функции натуральный логарифм
сжимаем вдоль оси oy втрое
растягиваем вдвое вдоль оси ox
отображаем симметрично относительно оси oy
сдвигаем вверх на 2 единицы
Преобразование
графиков тригонометрических функций подчиняется общей схеме геометрических
преобразований . Единственно хочется обратить внимание
на влияние коэффициента k2
на период тригонометрических функций.
При отличном от единицы коэффициенте
k2
период становится равным .
То есть, при растяжение графика функции вдоль оси
абсцисс соответствует увеличению
периода, а при сжатие графика соответствует уменьшению
периода. Коэффициент k1
влияет на амплитуду колебаний синусоиды
и косинусоиды.
Единственно хочется обратить внимание
на влияние коэффициента k2
на период тригонометрических функций.
При отличном от единицы коэффициенте
k2
период становится равным .
То есть, при растяжение графика функции вдоль оси
абсцисс соответствует увеличению
периода, а при сжатие графика соответствует уменьшению
периода. Коэффициент k1
влияет на амплитуду колебаний синусоиды
и косинусоиды.
Пример (геометрические преобразования синусоиды y=sinx).
С помощью преобразования графика функции y=sinx построить
Решение.
Приводим функцию к виду шаблона :
Имеем k1=3, k2=0,5, a=3, b=-2, причем перед коэффициентом k1 стоит знак «минус», перед k2 минуса нет.
Таким образом, цепочка преобразований графика функции y=sinx примет вид:
Поэтапное преобразование графика синусоиды. Графическая иллюстрация.
График
исходной синусоиды y=sin(x) . Наименьший
положительный период равен
. Максимумы находятся в точках
,
минимумы – в точках
.
Растягиваем вдоль оси ординат втрое (амплитуда колебаний при этом возрастает в три раза). Наименьший положительный период равен . Максимумы переходят в точки , минимумы – в точки .
Растягиваем вдоль оси абсцисс вдвое. Наименьший положительный период при этом вдвое увеличивается . Максимумы переходят в точки , минимумы – в точки .
Симметрично отображаем относительно оси абсцисс. Наименьший положительный период при этом не меняется . Максимумы переходят в точки , минимумы – в точки .
С двигаем график вправо на 3 единицы. Наименьший положительный период при этом не меняется . Максимумы переходят в точки , минимумы – в точки .
С двигаем график вниз на 2 единицы. Наименьший положительный период при этом не меняется . Максимумы переходят в точки минимумы – в точки
Э тим этапом задача преобразования графика тригонометрической функции y=sinx завершается.
Пример
(преобразование тригонометрической
функции y=cosx).
Построить график функции преобразованием косинусоиды y=cosx.
Решение.
Приводим функцию к виду шаблона :
Имеем , причем перед коэффициентом k2 стоит знак «минус», перед k1 минуса нет.
Таким образом, цепочка преобразований графика тригонометрической функции косинус примет вид:
Поэтапное преобразование графика косинусоиды. Графическая иллюстрация.
Исходный график y=cos(x) . Наименьший положительный период равен . Максимумы находятся в точках , минимумы – в точках .
Растягиваем вдоль оси ординат в 3/2 раза (амплитуда колебаний при этом возрастает в 3/2 раза). Наименьший положительный период равен . Максимумы переходят в точки , минимумы – в точки .
Сжимаем график вдоль оси абсцисс вдвое. Наименьший положительный период при этом вдвое уменьшается . Максимумы переходят в точки , минимумы – в точки .
Симметрично
отображаем относительно оси ординат. В силу четности функции график при этом
не изменится.
В силу четности функции график при этом
не изменится.
Сдвигаем график вправо на 1 единицу. Наименьший положительный период при этом не меняется . Максимумы переходят в точки , минимумы – в точки .
Сдвигаем график вверх на 1 единицу. Наименьший положительный период при этом не меняется . Максимумы переходят в точки , минимумы – в точки .
Этим этапом задача преобразования графика тригонометрической функции y=cosx завершается.
Пример (преобразование тригонометрической функции y=tgx ).
С помощью геометрических преобразований графика функции y=tgx построить
Решение.
Приводим функцию к виду шаблона :
Имеем , причем перед коэффициентами k1 и k2 стоит знак «минус».
Таким образом, цепочка преобразований графика тангенсоиды примет вид:
Поэтапное преобразование графика тангенсоиды. Графическая иллюстрация.
Исходный
график y=tg(x) . Наименьший положительный
период равен
. Область определения .
Область определения .
Производим сжатие вдоль оси ординат в 2 раза. Наименьший положительный период при этом не меняется . Область определения остается прежней .
Растягиваем график вдоль оси абсцисс в 3/2 раза. Наименьший положительный период при этом равен . Область определения изменяется на .
Симметрично отображаем относительно оси абсцисс. Период и область определения при этом не меняются.
Симметрично отображаем относительно оси ординат. Период и область определения при этом не меняются. Стоит заметить, что график в точности совпадает с графиком двумя шагами ранее. Это объясняется нечетностью функции тангенса. То есть, если к нечетной функции применить симметричное отображение относительно осей ox и oy , то получим исходную функцию.
Сдвигаем график вправо на (примерно на полторы единицы). Наименьший положительный период при этом не меняется Область определения изменяется на .
Сдвигаем
график вверх на (примерно на единицу). Период и область
определения при этом не меняются.
Период и область
определения при этом не меняются.
Этим этапом задача преобразования графика тригонометрической функции y=tgx завершается.
Пример (геометрические преобразования обратной тригонометрической функции y=arccosx).
Построить график функции преобразованием графика y=arccosx.
Решение.
Сначала от арккосинуса перейдем к арксинусу, используя соотношение обратных тригонометрических функций
Следовательно,
Таким образом, имеем цепочку преобразований арккосинуса в арксинус:
Поэтапное преобразование графика арккосинуса. Графическая иллюстрация.
Исходный график y=arccos(x) .
Отображаем симметрично относительно оси ox .
Сдвигаем вверх на .
Вот так перешли от арккосинуса к арксинусу
Теперь проводим геометрические преобразования графика арксинуса.
Имеем , причем перед коэффициентами k1и k2 знака минуса нет.
Таким образом, цепочка преобразований графика y=arcsinx примет вид:
Поэтапное
преобразование графика арксинуса. Графическая иллюстрация.
Графическая иллюстрация.
График функции y=arcsinx . Область определения . Область значений .
Растягиваем вдвое вдоль оси ординат. Область определения не меняется . Область значений становится .
Растягиваем вдоль оси абсцисс втрое. При этом область определения расширяется до . Область значений не меняется .
Сдвигаем график на единицу вправо. При этом область определения переходит в . Область значений не меняется .
Э тим этапом задача преобразования графика обратной тригонометрической функции завершается.
В чем разница между y = arccos x и y = cos-1 x?
Тригонометрия — это раздел математики, который устанавливает связь между сторонами и углами прямоугольного треугольника. Это помогает найти неизвестные стороны неизвестных углов треугольника. Углы измеряются либо в радианах, либо в градусах. Тригонометрическими отношениями или тригонометрическими функциями являются синус, косинус, тангенс и их обратные значения sec, cosec и cot. Тригонометрические функции вычисляются с помощью прямоугольного треугольника. Самая длинная сторона треугольника — гипотенуза, а противолежащие стороны — основание и высота. Тригонометрические функции используются для получения неизвестных углов и расстояний.
Тригонометрические функции вычисляются с помощью прямоугольного треугольника. Самая длинная сторона треугольника — гипотенуза, а противолежащие стороны — основание и высота. Тригонометрические функции используются для получения неизвестных углов и расстояний.
- Синус — отношение основания к гипотенузе
- Косинус — отношение высоты к гипотенузе
- Тангенс — отношение высоты к основанию
Обратная тригонометрическая функция получить углы из соотношений. Они также известны как «функции дуги». Инверсия применима к синусу, косинусу, тангенсу, косекансу, секансу и котангенсу. В этом домен и диапазон также инвертируются. Он представлен cos
-1 , sin -1 ,tan -1 и т. д. Они часто представляются как arccos, arcsin, arctan и т. д. Обратная функция также известна как антитригонометрическая функция. Эти функции полезны в инженерии, физике, математике и т. д. Ниже приведены некоторые формулы: ) = π/2В чем разница между y = arccos x и y = cos
-1 х?Ответ:
Как мы все знаем, cos любого угла определяется как отношение основания к гипотенузе.
cos -1 в основном является обратным cos x. Обратный cos обозначается как cos -1 (основание/гипотенуза). Следует отметить, что величина, обратная косинусу, не является обратной величиной косинуса. Обратная эта функция также известна как арккосинус или записывается как acos. Эта функция возвращает угол на основе значения. Домен — [-1,1], а диапазон — [0, π]. Поэтому acos и cos -1 совпадают. Следовательно, определение cos -1 или acos дается следующим образом:
Пусть y = cos x
Следовательно, cos -1 (y) = acos (y) = x
Пример: Найдите cos -1 (√3/2)
cos x= √3/2
cos x = cos π/6
x = π/6
Другие формулы,
- arc cos(1/x) = сек -1 (x)
- cos -1 (-x) = π -cos -1 (x)
- cos(cos -1 x) = x
- cos -1 x + cos -1 y= cos -1 (xy – √(1 – x 2 )√(1 – y 6 2) )
- cos -1 x – cos -1 y= cos -1 (xy + √(1-x 2 )√(1-y 2 )) 90 Аналогичные вопросы 6 90
Вопрос 1.
 Найдите арккосинус, если0040
Найдите арккосинус, если00401. Пусть y = cos x = 0
cos x = 0
x = arc cos(0)
x = π/2
1 cos = 4 0 2. Пусть
cos x = 1
x = arc cos (1)
x = 0
Вопрос 2: Найдите Arc Cos x, если sinx — 0,5
Решение:
. (x) + arcsin(x) = π/2
Следовательно, arccos(x) = π/2 – arcsin(0,5)
arccos(x) = π/3
Вопрос 3: Найдите домен и диапазон значений arccos(x). Отсюда найдите значение cos -1 (2)
Решение:
Диапазон arccos(x) равен [0,π], а область определения arccos(x) равна [-1,1 ].
Поскольку область определения арккосинуса равна [-1,1], следовательно, арккосинус не существует
Вопрос 4: Найдите значение cos(cos -1 0,5) и найдите значение cos -1 (-1/√2)
Решение:
Как мы все знаем, cos(cos -1 x) = x
Следовательно, значение равно 0,5
Как мы все знаем, диапазон равен [0,π] и cos -1 (-x) = π -cos -1 (x)
cos -1 (1/√2) = π/4
Значение π – π/4 = 3π/4, которое лежит в диапазон [0,π]
Вопрос 5: Найдите значение cos -1 (3/5) + cos -1 (7/25) через cos.

Решение:
Пусть A = cos-1 (3/5)
B= cos-1 (7/25)
Пусть
A + B = C
=> cos( A + B ) = cos C
=> cosAcosB – sinAsinB = cos C
=> 3/5 × 7/25 – 4/5 × 24/25 = cos C
=>cos C = -75/125
= >cos C = -3/5
Вопрос 6. Найдите значение cos -1 x – cos -1 y, если x = 3/5 y = 4/5
Решение:
Дано, x = 3/5 y = 4/5
Как известно, cos -1 x – cos -1 y = cos -1 (xy + √(1 – x 2) ) √(1 – y 2 ))
cos -1 ( 0,6 × 0,8 + 0,6 × 0,8) = cos -1 ( 0,96 )
7
М. Борна
В разделе Тригонометрические функции любого угла мы решали вопросы типа
«Найдите 2 угла, косинус которых равен 0,7.»
Нужна миллиметровка?
Значок миллиметровкиЗагрузить миллиметровку
Этот вопрос связан с использованием кнопки cos -1 на наших калькуляторах.
 Мы нашли cos -1 0,7, а затем рассмотрели квадранты, в которых косинус был положительным. Помните, что число, которое мы получаем при нахождении функции арккосинуса, cos -1 , представляет собой угол .
Мы нашли cos -1 0,7, а затем рассмотрели квадранты, в которых косинус был положительным. Помните, что число, которое мы получаем при нахождении функции арккосинуса, cos -1 , представляет собой угол .Теперь обратим внимание на все обратные тригонометрические функции и их графики. Хорошо иметь представление об этих графиках, чтобы знать, почему существуют ограничения на значения, которые мы находим в наших калькуляторах. 9-1`, когда речь идет о функции арккосинуса.]
Давайте сначала вспомним график `y = cos\ x` (который мы встречали в Графике y = a cos x), чтобы мы могли видеть, откуда берется график `y = arccos\ x`.
0,5ππ-0,5π0,511,522,5-0,5-1xyГрафик y = cos x .
Теперь мы выбираем часть этого графика от x = 0 до x = π , показанную здесь заштрихованной частью:
0.5ππ-0.5π0.511.522.53-0.5-1xyГрафик y = cos x с заштрихованной частью `0
График обратного косинуса x находится путем отражения выбранной части графика `cos x` через прямую `y = x`.
0,5ππ-0,5π0,511,522,53-0,5-1xyy = x
График y = cos x и линия `y=x`.
Теперь мы отразим каждую точку на этой части кривой `cos x` через линию y = x (я показал только несколько типичных точек, которые отражаются).0003 0,5ππ-0,5π123-1xy(π,−1)(−1,π)0,5π
Отражение точек на кривой через прямую `y=x`.
Результатом является график `y = arccos x`:
12-10,5ππxy(−1,π)Кривая `y=arccos x`.
См. анимацию этого процесса здесь: Анимация графика обратной тригонометрической функции.
Это все для графика — он не выходит за рамки того, что вы видите здесь. (Если бы это было так, то для каждого значения x было бы несколько значений и , и тогда у нас больше не было бы функции.) Я указал точки «начало» и «конец», `(-1 , pi)` и `(1,0)` с точками.
ПРИМЕЧАНИЕ 1: Метки осей также были отражены. То есть теперь по оси x идут обычные числа, а по оси y — кратные `0,5pi`.

ПРИМЕЧАНИЕ 2: Вы также можете встретить «arccos» в записи «acos», особенно в компьютерном программировании.
Домен (возможные значения x ) для arccos x равен
-1 ≤ x ≤ 1
Диапазон (из значений и для графика) для arccos x равен
0 ≤ arccos x ≤ π
Функция обратного синуса (арксинус)
Мы определяем функцию обратного синуса как
`y=arcsin\ x` для `-pi/2<=y<=pi/2`
, где y — это угол, синус которого равен x . Это означает, что
`х = грех у`
График
y = arcsin xДавайте сначала посмотрим на график y = sin x , а затем получим кривую y = arcsin x .
0.5ππ1.5π2π-0. 5π0.51-0.5-1xyОткрыть изображение на новой странице
5π0.51-0.5-1xyОткрыть изображение на новой страницеГрафик y = sin x , с выделенной частью от `-pi/2` до `pi/2`.
Как и раньше, если отразить указанную часть y = sin x (часть между `x=-pi/2` и `x=pi/2`) через строку y = x , получаем график y = arcsin x :
0,51-0,5-10,5π-0,5πxyОткрыть изображение на новой страницеГрафик y = arcsin x .
Еще раз: что видишь, то и получаешь. График не выходит за указанные границы x и y . Я указал точки «начало» и «конец» точками.
домен (возможные значения x ) arcsin х это
-1 ≤ x ≤ 1
Диапазон (из значений и для графика) для arcsin x равен
`-π/2 ≤ arcsin\ x ≤ π/2`
См. анимацию этого процесса здесь:
Анимация графика обратной тригонометрической функции.

Функция арктангенса (arctan)
Напомню, вот график y = tan x , который мы встречали ранее в Графиках tan, cot, sec и csc.
π2π−π-2π2468-2-4-6-8xyОткрыть изображение на новой страницеГрафик y = tan x .
Отразив заштрихованную часть графика (от `x=-pi/2` до `pi/2`) в строке y = x , мы получим график y = arctan x :
12345-1-2-3-4-50.5ππ-0.5π−πxyОткрыть изображение на новой страницеГрафик `y=»arctan»\ x`.
На этот раз график выходит за пределы того, что вы видите, как в отрицательном, так и в положительном направлении x , и он не пересекает пунктирные линии (асимптоты при `y=-pi/2` и `y=pi/2`).
Домен (возможные значения x ) arctan x равен
Все значения x
Диапазон (из значений и для графика) для arctan x равен
`-π/2
Числовые примеры arcsin, arccos и arctan
С помощью калькулятора в радианном режиме получаем следующее:
arcsin 0,6294 = sin -1 (0,6294) = 0,6808
arcsin (-0,1568) = sin -1 (-0,1568) = -0,1574
arccos (-0,8026) = cos -1 (-0,8026) = 2,5024
арктангенс (-1,9268) = тангенс -1 (-1,9268) = -1,0921
Обратите внимание, что калькулятор выдаст значения которые находятся в пределах определенного диапазона для каждой функции.

Ответов в каждом случае углов (в радианах).
Функция обратной секущей (угловые секунды)
График y = sec x , который мы встречали ранее в Графиках tan, cot, sec и csc:
π2π−π-2π2468-2-4-6-8xyОткрыть изображение на новой страницеГрафик y = сек x .
График y = угловых секунд x получается путем отражения заштрихованной части приведенной выше кривой в линии y = x :
: 12345-1-2-3-4-50.5ππ-0.5π−πxyОткрыть изображение на новой страницеГрафик `y=»arcsec»\ x`.
Кривая определена за пределами участка между −1 и 1. Я указал «начальные» точки `(-1,pi)` и `(1,0)` точками.
Домен `»дуг»сек\х` равен
Все значения x , кроме −1 < x < 1
Диапазон угловых секунд x равен
0 ≤ угловых секунд x ≤ π , `»угловых» секунд\ x ≠ π/2`
Функция обратного косеканса (arccsc)
График y = csc x , который мы встречали ранее в Графиках tan, cot, sec и csc, выглядит так:
π2π−π-2π2468-2-4-6-8xyОткрыть изображение на новой страницеГрафик y = csc x .

Обратите внимание, что нет значений y между −1 и 1.
Теперь для графика y = arccsc x , который мы получаем, отражая заштрихованную часть приведенной выше кривой в строке г = х :
12345-1-2-3-4-5π−πxy−π/2π/2Открыть изображение на новой страницеГрафик `y=»arccsc»\ x`.
График не определен между -1 и 1, но простирается в отрицательном и положительном x -направлениях оттуда.
Домен arccsc x равен
Все значения x , кроме −1 < x < 1
Диапазон arccsc x равен
`-π/2 ≤ «дуга»csc\ x ≤ π/2,` arccsc x ≠ 0
Функция арккотангенса (arccot)
График y = cot x , который мы встречали ранее в Графиках tan, cot, sec и csc, выглядит следующим образом:
π2π−π-2π246810-2-4-6-8-10xyОткрыть изображение на новой страницеГрафик y = кроватка x .

Взяв выделенную часть, как указано выше, и отразив ее в строке y = x , мы получим график y = дуга x :
2468-2-4-6-80.5ππ-0.5πxyОткрыть изображение на новой страницеГрафик `y=»arccot»\ x`.
График простирается в отрицательном и положительном x -направлениях (он не останавливается на -8 и 8, как показано на графике).
Итак, домен arccot x :
Все значения x
Диапазон arccot x равен
0 < арккот x < π
Альтернативный вид
Некоторые учебники по математике (и некоторые уважаемые математические программы, например, Mathematica) рассматривают следующее как область y = кроватка x , которую следует использовать:
π2π−π-2π246810-2-4-6-8-10xyОткрыть изображение на новой страницеГрафик y = кроватка x .

Это даст следующее при отражении в строке y = x :
24-2-40.5ππ-0.5π−πxyОткрыть изображение на новой страницеГрафик `y=»arccot»\ x`; альтернативный взгляд.
Опять же, график расширяется в отрицательном и положительном x -направлениях.
Домен arccot x также будет:
Все значения x
В этой версии диапазон для arccot x будет следующим:
`-π/2 х ≠ 0)
См. обсуждение этого вопроса по адресу:
.Какой правильный график arccot x?. 9(-1)(-1)=-pi/4`
`cos(-pi/4)=1/2sqrt(2)`
Калькулятор Arccos | cos(x)
Arccos Calculator
cos -1 (x)
Результат:
909 угол 5 дюймов:2 908 908 0 Угол в радианах: 0 Что такое arccos?
Арккосинус (или арккосинус) является обратной функцией косинуса.
 В прямоугольном треугольнике cos угла y определяется как отношение стороны, прилежащей к углу, к гипотенузе. Когда мы возьмем арккосинус этого отношения, мы получим меру угла y.
В прямоугольном треугольнике cos угла y определяется как отношение стороны, прилежащей к углу, к гипотенузе. Когда мы возьмем арккосинус этого отношения, мы получим меру угла y.Рассмотрим прямоугольный треугольник ниже.
В этом треугольнике прямой угол лежит при B. Cos угла y определяется как } = x$$
Чтобы найти угол y, когда известно отношение BC/AC, мы используем следующую формулу для арккосинуса. 9{-1} x$$
Выражение y = cos -1 x означает, что cos y = x , когда 0 ≤ y ≤ π и -1≤ x ≤ +1.
Арккосинус(x)=y определяется как множество всех углов, косинус которых равен x. Здесь следует отметить, что -1 не является показателем степени и, следовательно, cos -1 x ≠ 1 / cos x .
Свойства функции арккосинуса
Ниже приведены некоторые свойства функции арккосинуса.
Угол – Угол – это параметр, который рассчитывается, когда известен косинус (или арккосинус) угла. 9(-1)х. Это значение равно 0 ≤ y ≤ π радиан или 0 ≤ y ≤ +180 градусов.

Ниже приведен график функции арккосинуса.
На приведенном выше графике ось Y обозначает угол в радианах, а ось X обозначает арккосинус этого угла. Красная кривая обозначает функцию арккосинуса. Для любого значения x от -1 до +1 функция арккосинуса возвращает значение от 0 до π радиан (или от 0⁰ до 180⁰). Например, когда x=1, y=arccosine(x) возвращает y=0 радиан. Это означает, что cos (0) = 1,
Если сравнить график арккосинуса с графиком синуса, можно увидеть, что график арккосинуса можно получить из графика косинуса, просто поменяв местами горизонтальную и вертикальную оси.
Значения арксинуса(x)
Ниже приведены некоторые часто используемые значения арккосинуса(x).
y=cos -1 x в градусах y=cos -1 x в радианах х 0 0 1 30 $$π\over6$$ $$√3\более2$$ 45 $$π\over4$$ $$1\over√2$$ 60 $$π\over3$$ $$1\over2$$ 90 $$π\over2$$ 0 120 $$2π\over3$$ $$-1\over2$$ 135 $$3π\over4$$ $$-1\over√2$$ 150 $$5π\over6$$ $$-√3\over2$$ 180 $$π$$ -1 Значение арккосинуса(x) всегда положительное, даже если x отрицательное.
 Например, арккосинус (-1/2) = 120⁰ и арккосинус (1/2) = 60⁰ являются положительными. Это потому, что cos -1 (-x)=-cos -1 x.
Например, арккосинус (-1/2) = 120⁰ и арккосинус (1/2) = 60⁰ являются положительными. Это потому, что cos -1 (-x)=-cos -1 x.Это показано ниже.
На этом рисунке ось x обозначает значения арккосинуса, тогда как ось y обозначает угол θ. Арккосинус (x) будет положительным, когда 0 ≤ θ ≤ π/2 (в квадранте 1), и отрицательным, когда π/2
Мы также можем заметить, что
cos(cos -1 (x))=x, когда -1 ≤ x ≤ +1.
Например, cos(cos -1 (1/2)) = cos 60⁰ = 1/2.
Аналогично, cos -1 (cos x) = x, когда 0 ≤ x ≤ +π.
Например, cos -1 (cos π/4) = cos -1 (1/√2) = π/4.
Если нам нужно найти арккосинус косинуса угла, который не лежит между 0 и π, правильный угол можно найти, добавляя или вычитая 2π радиан, пока мы не получим угол в диапазоне от 0 до π, что является диапазоном функции арккосинуса. Это потому, что 2π — это период функции cos. 99\over9} + .
 ..)$$
..)$$Области применения
Тригонометрические функции, а также обратные тригонометрические функции широко используются в технике, геометрии и физике. В повседневной жизни косвенные измерения используются для поиска ответов на проблемы, которые не могут быть легко решены с помощью инструментов измерения. В таких случаях тригонометрические и обратные тригонометрические функции находят широкое применение для вычисления этих неизвестных измерений.
Они также используются для решения тригонометрических уравнений, описывающих реальные задачи.
В этом разделе мы рассмотрим несколько примеров задач, связанных с использованием формулы арккосинуса.
Ответ: Угол -6π/5 радиан не лежит между 0 и π, но его можно привести к этому диапазону, добавляя или вычитая 2π радиан, пока мы не получим угол в диапазоне от 0 до π радиан, что является диапазоном функции арккосинуса.
В этом случае -6π/5 радиан можно записать как -6π/5+2π=4π/5 радиан, что находится между 0 и π.

Следовательно, cos -1 (cos -6π/5) = cos -1 (cos(4π/5) ) = 4π/5
Ответ: Задачу можно визуализировать следующим образом.
В данном прямоугольном треугольнике стороны следующие. Нам нужно найти угол у.
AC указывает расстояние, пройденное человеком в северо-восточном направлении, а BC — расстояние от его начальной точки. Это можно представить в виде прямоугольного треугольника, как показано выше. Здесь AC= 28 миль, а BC= 8 миль.
9{-1}({2\over7}) ≈ 73,398⁰$$Следовательно, человек шел на 73,4⁰ к северу от востока.
См. также:
- Калькулятор арксинуса
- Калькулятор арктангенса
- Калькулятор синуса
- Калькулятор косинуса
- Калькулятор касательной
- Калькулятор тригнометрии
Делиться:
6.3E: Упражнения — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 18900
В этом разделе мы рассмотрим обратные тригонометрические функции.
 Обратные тригонометрические функции «отменяют» то, что «делает» исходная тригонометрическая функция, как и в случае с любой другой функцией и ее обратной функцией. Другими словами, область определения обратной функции — это диапазон исходной функции, и наоборот. 9{-1}(2)\). Объясните, как это можно сделать, используя функцию косинуса или функцию арккосинуса.
Обратные тригонометрические функции «отменяют» то, что «делает» исходная тригонометрическая функция, как и в случае с любой другой функцией и ее обратной функцией. Другими словами, область определения обратной функции — это диапазон исходной функции, и наоборот. 9{-1}(2)\). Объясните, как это можно сделать, используя функцию косинуса или функцию арккосинуса.5) Почему область определения функции синуса \(\sin x\) должна быть ограничена \(\left [ -\dfrac{\pi }{2},\dfrac{\pi }{2} \ справа ]\) для существования функции обратного синуса?
- Ответить
Для того чтобы любая функция имела обратную, функция должна быть взаимно однозначной и должна пройти тест горизонтальной линии. Обычная синусоидальная функция не является взаимно однозначной, если ее область определения каким-либо образом не ограничена. Математики согласились ограничить функцию синуса интервалом \(\left [ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right ]\), чтобы она была взаимно однозначной и имеет обратную.

6) Обсудите, почему это утверждение неверно: \(\arccos(\cos x)=x\) для всех \(x\).
7) Определите, верно или нет следующее утверждение, и объясните свой ответ: \(\arccos(-x)=\pi — \arccos x\)
- Ответ
Верно. Угол \(\theta _1\), равный \(\arccos(-x)\), \(x>0\), будет углом второго квадранта с опорным углом, \(\theta _2\), где \(\theta _2\) равно \(\arccos x\), \(x>0\). Поскольку \(\theta _2\) является опорным углом для \(\theta _1\), \(\theta _2=\pi — \theta _1\) и \(\arccos(-x)=\pi — \arccos х-\) 9{-1}(6)\)
- Ответ
\(1.41\)
В упражнениях 22-23 найдите угол \(\theta\) в данном прямоугольном треугольнике. Ответы округлить до сотых.
22)
23)
- Ответить
\(0,56\) радиан
Для упражнений 24-36 найдите точное значение, если возможно, без калькулятора.
 Если это невозможно, объясните, почему. 9{-1} х\)? Воспользуйтесь графическим калькулятором, чтобы приблизить ответ.
Если это невозможно, объясните, почему. 9{-1} х\)? Воспользуйтесь графическим калькулятором, чтобы приблизить ответ.Реальные приложения
53) Предположим, что \(13\)-футовая лестница прислонена к зданию и достает до низа окна второго этажа \(12\) футов над землей. Какой угол в радианах образует лестница со зданием?
- Ответить
\(0,395\) радиан
54) Предположим, вы проехали \(0,6\) мили по дороге, так что вертикальное расстояние изменилось от \(0\) до \(150\) футов. Какой угол подъема дороги?
55) Равнобедренный треугольник имеет две конгруэнтные стороны длиной \(9\) дюймов. Оставшаяся сторона имеет длину \(8\) дюймов. Найдите угол, который сторона в \(9\) дюймов образует со стороной в \(8\) дюймов.
- Ответить
\(1,11\) радиан
56) Не используя калькулятор, приблизительно вычислите значение \(\arctan (10,000)\). Объясните, почему ваш ответ является разумным.

57) Ферма для крыши дома строится из двух одинаковых прямоугольных треугольников. Каждый имеет основание \(12\) футов и высоту \(4\) футов. Найдите градусную меру острого угла, примыкающего к \(4\)-футовой стороне.
- Ответить
\(1,25\) радиан
58) Прямая \(y=\dfrac{3}{5}x\) проходит через начало координат в плоскости \(x,y\). Какова мера угла, который линия образует с положительной осью \(х\)?
59) Прямая \(y=\dfrac{-3}{7}x\) проходит через начало координат в плоскости \(x,y\). Какова мера угла, который линия образует с отрицательной осью \(x\)?
- Ответить
\(0,405\) радиан
60) Какой уклон должен иметь дорога, если угол подъема дороги составляет \(4\) градусов? (Уклон в процентах определяется как изменение высоты дороги на \(100\)-футовом горизонтальном расстоянии. Например, уклон \(5\%\) означает, что дорога поднимается на \(5\) футов на через каждые \(100\) футов горизонтального расстояния.
 )
)61) Лестница высотой \(20\) футов прислонена к стене здания так, что подошва лестницы находится в \(10\) футах от основания здания. Если спецификации требуют, чтобы угол подъема лестницы составлял от \(35\) до \(45\) градусов, соответствует ли размещение этой лестницы требованиям безопасности?
- Ответить
Нет. Угол, который образует лестница с горизонтом, составляет \(60\) градусов.
62) Предположим, лестница высотой \(15\) футов прислонена к стене дома так, что угол подъема лестницы составляет \(42\) градусов. На каком расстоянии от стены дома находится подножие лестницы?
6.3E: Упражнения распространяются под лицензией CC BY-NC-SA и были созданы, изменены и/или курированы LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Лицензия
- CC BY-NC-SA
- Показать страницу Оглавление
- нет
- Включено
- да
- Теги
- расчет: да
Дифференцирование обратных тригонометрических функций
Обзор
[Вернитесь к началу страницы]
обратная функция — это функция, которая обращает эффект применения функции, для которой она является обратной.
 Например, функция квадрата меняет действие функции извлечения квадратного корня и наоборот:
Например, функция квадрата меняет действие функции извлечения квадратного корня и наоборот:y = √ x , y 2 = x
Говоря более формально, две функции ƒ( x ) и g ( x ) являются обратными друг другу, если:
ƒ( г ( x )) = x и г (ƒ( x )) = x
Можно показать, что существует также связь между производными двух функций ƒ( x ) и g ( x ), которые являются обратными друг другу, которую мы можем записать как:
г ′( x ) = 1 ƒ′( г ( x )) Если вы изучали тригонометрию (вы должны, по крайней мере, иметь достаточное представление об основах, чтобы изучать исчисление), вы должны знать, что существует шесть наиболее часто используемых тригонометрических функций.
 Это функции синуса , косинуса , тангенса , секанса , косеканса и котангенса . Вы также должны знать, что каждой из этих функций соответствует обратная тригонометрическая функция . Это (соответственно) функции арксинус , арккосинус , арктангенс , арккотангенс , арксеканс и арккосеканс .
Это функции синуса , косинуса , тангенса , секанса , косеканса и котангенса . Вы также должны знать, что каждой из этих функций соответствует обратная тригонометрическая функция . Это (соответственно) функции арксинус , арккосинус , арктангенс , арккотангенс , арксеканс и арккосеканс .Каждая из шести обратных тригонометрических функций обращает действие соответствующей тригонометрической функции. Например, если мы применим функцию синуса к углу, мы получим синус этого угла в качестве вывода. Обратной функцией синуса является функция арксинуса. Если мы возьмем синус угла и применим к нему функцию арксинуса, результатом будет исходный угол. На самом деле это не совсем так. Из шести тригонометрических функций непрерывны только функция синуса и косинуса, но все тригонометрических функций являются периодическими .
 Это означает, что они повторно выдают один и тот же набор выходных значений через равные промежутки времени. Для большинства тригонометрических функций этот интервал равен 2π. Исключение составляют функции тангенса и котангенса, для которых интервал равен π.
Это означает, что они повторно выдают один и тот же набор выходных значений через равные промежутки времени. Для большинства тригонометрических функций этот интервал равен 2π. Исключение составляют функции тангенса и котангенса, для которых интервал равен π.Вследствие своей периодичности каждая тригонометрическая функция будет давать одно и то же выходное значение для бесконечного числа различных входных значений. Это вызывает проблему, потому что применение обратной функции к этому выходу даст только одно значение. Это означает, что наше определение отношения между двумя функциями, обратными друг другу, не работает. Например, если вы примените функцию синуса к углу π / 2 радиана (45°), на выходе вы получите 0,707. Если вы затем примените функцию синуса к углу 3 / 2 π радиан (135°), вы получите точно такой же результат. Очевидно, что применение функции арксинуса к 0,707 может дать только один результат, который будет π / 2 радиан (45°).

Чтобы обойти эту проблему, нам нужно 90 324 ограничить область определения 90 325 каждой из шести тригонометрических функций, чтобы у нас было однозначное отношение между входными и выходными значениями для каждой функции. Другими словами, мы выбираем домен для каждой функции таким образом, чтобы никакие два разных входных значения, переданных в функцию, не могли привести к одному и тому же результату.
На этой странице мы попытаемся объяснить, как была получена формула для нахождения производной каждой из обратных тригонометрических функций. Общая процедура практически одинакова в каждом случае. Начнем с арксинус функция.
Функция арксинуса
[Вернитесь к началу страницы]
Функция арксинуса является обратной функции синуса . Синусоидальная функция принимает угол в качестве входных данных и выдает синусоидальное значение угла в качестве выходных данных.
 При условии, что угол находится в пределах ограниченной области функции синуса, применение функции арксинуса к ее значению синуса даст нам исходный угол. На следующем рисунке показан график функции синуса. Как видите, график представляет собой непрерывный сигнал с периодом 2π радиан (360°).
При условии, что угол находится в пределах ограниченной области функции синуса, применение функции арксинуса к ее значению синуса даст нам исходный угол. На следующем рисунке показан график функции синуса. Как видите, график представляет собой непрерывный сигнал с периодом 2π радиан (360°).График синусоидальной функции
Чтобы функция арксинуса была истинно обратной функцией синуса, должно выполняться следующее утверждение:
sin (arcsin ( x )) = x и arcsin (sin ( x )) = x
Мы обеспечиваем это, ограничивая область определения функции отрезком [- π / 2 , π / 2 ], как видно из иллюстрации. Значение функции увеличивается в этой области по мере увеличения значения x , и каждое входное значение создает уникальное выходное значение. Синусоидальная функция теперь определяется следующим образом:
y = sin ( x ) for — π / 2 ≤ x ≤ π / 2
Давайте посмотрим, как получается производная функции арксинуса. Помните, что мы хотим дифференцировать функцию арксинуса по x , поэтому мы пытаемся найти:
Помните, что мы хотим дифференцировать функцию арксинуса по x , поэтому мы пытаемся найти:d (угловой синус ( x )) d x Первый шаг — установить y равными функции арксинуса:
y = arcsin ( x ) для — π / 2 ≤ y ≤ π / 2
- 3
- 3 Однако функция синуса обратна функции арксинуса, поэтому мы можем переписать это как:
sin ( y ) = x
Теперь мы воспользуемся неявным дифференцированием и найдем d y /d x , чтобы получить производную функции арксинуса через y (помните, наша конечная цель — получить производную от функция арксинуса с точки зрения x , но этот шаг приближает нас к этой цели). Сначала нам нужно продифференцировать обе части уравнения:
d (sin( y )) = d ( x ) d x d x Дифференцировать правую часть уравнения достаточно просто.
 Однако при дифференцировании левой части мы должны помнить, что y является функцией x , поэтому sin ( y ) на самом деле является составной функцией . Это означает, что мы должны применить 9Цепное правило 0324 . Цепное правило говорит нам, что производная составной функции получается путем умножения производной внешней функции на производную внутренней функции . В этом случае внешняя функция — sin ( y ), а внутренняя функция — y ( x ), поэтому мы получаем:
Однако при дифференцировании левой части мы должны помнить, что y является функцией x , поэтому sin ( y ) на самом деле является составной функцией . Это означает, что мы должны применить 9Цепное правило 0324 . Цепное правило говорит нам, что производная составной функции получается путем умножения производной внешней функции на производную внутренней функции . В этом случае внешняя функция — sin ( y ), а внутренняя функция — y ( x ), поэтому мы получаем:cos ( y )) · d y = 1 г x Давайте изменим это, чтобы получить d y /d x отдельно с левой стороны:
d y = 1 d x cos( y ) Поскольку мы знаем, что y равно arcsin ( x ), мы можем заменить y в левой части этого уравнения следующим образом:
D (ARCSIN ( x ) = 1 D x .  COSP ().
Теперь у нас есть формула (своего рода) для производной функции арксинуса, но нам все еще нужно переписать правую часть уравнения в терминах x . По сути, это означает, что нам нужно заменить термин cos ( y ) каким-либо термином, который включает только x . Помощь под рукой в виде тригонометрического тождества, известного как 9.0324 Тождество Пифагора , которое по существу дает нам теорему Пифагора в тригонометрических терминах. Пифагорейское тождество гласит:
COSP ().
Теперь у нас есть формула (своего рода) для производной функции арксинуса, но нам все еще нужно переписать правую часть уравнения в терминах x . По сути, это означает, что нам нужно заменить термин cos ( y ) каким-либо термином, который включает только x . Помощь под рукой в виде тригонометрического тождества, известного как 9.0324 Тождество Пифагора , которое по существу дает нам теорему Пифагора в тригонометрических терминах. Пифагорейское тождество гласит:cos 2 ( y ) + sin 2 ( y ) = 1
Переменная y в тождестве Пифагора представляет собой один из внутренних углов прямоугольного треугольника. Это также угол, который мы вводим в функцию синуса. Помните также, что мы уже установили этот грех ( y ) равно x . Если мы заменим x на sin ( y ) в тождестве Пифагора, мы получим:
cos 2 ( y ) + x 2 = 1
Отсюда получаем:
cos ( y ) = √(1 — x 2 )
Теперь мы можем переписать нашу формулу для производной функции арксинуса и привести ее к требуемому формату, заменив cos ( у ) следующим образом:
d (arcsin ( x )) = 1 d x √(1 — x 2 ) На приведенном ниже рисунке показан график функции арксинуса по всей области его определения, то есть на замкнутом интервале [-1, 1].
 Обратите внимание, что функцию можно дифференцировать только на открытом интервале (-1, 1). Открытый интервал, помните, делает , а не включают конечные точки. Хотя и минус один , и один входят в область определения функции арксинуса, функция не дифференцируема для этих значений x . Попробуйте подставить любой из них в формулу производной, и вы поймете, почему — вы получите ноль в знаменателе. Касательная к графику в любой из этих точек будет вертикальной линией, поэтому говорят, что наклон равен undefined .
Обратите внимание, что функцию можно дифференцировать только на открытом интервале (-1, 1). Открытый интервал, помните, делает , а не включают конечные точки. Хотя и минус один , и один входят в область определения функции арксинуса, функция не дифференцируема для этих значений x . Попробуйте подставить любой из них в формулу производной, и вы поймете, почему — вы получите ноль в знаменателе. Касательная к графику в любой из этих точек будет вертикальной линией, поэтому говорят, что наклон равен undefined .График y = arcsin ( x ) for — π / 2 ≤ y ≤ π / 2
17
17 Функция арккосинуса
[Вернитесь к началу страницы]
Функция арккосинуса является обратной функции косинуса . Функция косинуса принимает угол в качестве входных данных и выдает значение косинуса угла в качестве своего выхода.
 При условии, что угол находится в пределах ограниченной области функции косинуса, применение функции арккосинуса к ее значению косинуса даст нам исходный угол. На следующем рисунке показан график функции косинуса. Как и в случае с синусоидальной функцией, график представляет собой непрерывный сигнал с периодом 2π радиан (360°). Функция косинуса достигает своего максимального значения π / 2 радиана опережает синусоидальную функцию и, как говорят, опережает синусоидальную функцию на π / 2 радиан (90°).
При условии, что угол находится в пределах ограниченной области функции косинуса, применение функции арккосинуса к ее значению косинуса даст нам исходный угол. На следующем рисунке показан график функции косинуса. Как и в случае с синусоидальной функцией, график представляет собой непрерывный сигнал с периодом 2π радиан (360°). Функция косинуса достигает своего максимального значения π / 2 радиана опережает синусоидальную функцию и, как говорят, опережает синусоидальную функцию на π / 2 радиан (90°).График функции косинуса
Чтобы функция арккосинуса была истинно обратной функцией синуса, должно выполняться следующее утверждение:
cos (arccos ( x )) = x и arccos (cos ( x )) = x
Мы обеспечиваем это, ограничивая область определения функции закрытым интервалом [0, π], как вы можете видеть из иллюстрации.
 Значение функции уменьшается в этой области по мере увеличения значения x , и каждое входное значение создает уникальное выходное значение. Функция косинуса теперь определяется следующим образом:
Значение функции уменьшается в этой области по мере увеличения значения x , и каждое входное значение создает уникальное выходное значение. Функция косинуса теперь определяется следующим образом:y = cos ( x ) для 0 ≤ x ≤ π
Давайте посмотрим, как получается производная функции арккосинуса. Помните, что мы хотим дифференцировать функцию арккосинуса относительно x , поэтому мы пытаемся найти:
d (arccos( x )) d x Первый шаг — установить y равным функции арккосинуса:
y = arccos ( x ) для 0 ≤ y ≤ π
Однако функция косинуса обратна функции арккосинуса, поэтому мы можем переписать это как:
cos ( y ) = x
Мы будем использовать неявное дифференцирование и найдем d y /d x , чтобы получить производную функции арккосинуса через y .
 Дифференцируя обе части уравнения, получаем:
Дифференцируя обе части уравнения, получаем:d (cos( y )) = d ( x ) d x d x Помните, что cos ( y ) является составной функцией , поэтому нам нужно применить цепное правило. Внешняя функция — cos ( y ), а внутренняя функция — y ( x ), поэтому получаем:
-sin ( y ) · d y = 1 d x Давайте изменим это, чтобы получить d y /d x отдельно с левой стороны:
d y = -1 d x Поскольку мы знаем, что y равно arccos ( x ), мы можем заменить y в левой части этого уравнения следующим образом:
d (arccos( x )) = -1 d x sin y Теперь нам просто нужно переписать правую часть уравнения в терминах х .
 Пифагорейская идентичность снова приходит нам на помощь. Напомним, пифагорейское тождество дает нам следующее:
Пифагорейская идентичность снова приходит нам на помощь. Напомним, пифагорейское тождество дает нам следующее:cos 2 ( y ) + sin 2 ( y ) = 1
Мы уже установили, что cos( y ) равно x . Подстановка x вместо cos ( y ) в пифагорейском тождестве дает нам:
x 2 + sin 2 ( y ) = 1
Отсюда получаем:
sin ( y ) = √(1 — x 2 )
Теперь мы можем переписать нашу формулу для производной функции арккосинуса и привести ее в требуемый формат, заменив sin ( y ) следующим образом:
D (Arccos ( x ) = -1 D x √ (1 — x √ (1- x √ (9- x √ (9- x √ (9- x √ (9- x a Вы могли заметить, что эта формула почти идентична той, которую мы получили для функции арксинуса.  Отличие только в отрицательном знаке в числителе. На приведенном ниже рисунке показан график функции арккосинуса по всей ее области определения, которая снова является закрытым интервалом [-1, 1]. Как и в случае с функцией арксинуса, оба минус один и один входят в область определения функции арккосинуса, но функция не дифференцируема для этих значений x . Касательная к графику в любой из его конечных точек будет вертикальной линией, а наклон считается неопределенным.
Отличие только в отрицательном знаке в числителе. На приведенном ниже рисунке показан график функции арккосинуса по всей ее области определения, которая снова является закрытым интервалом [-1, 1]. Как и в случае с функцией арксинуса, оба минус один и один входят в область определения функции арккосинуса, но функция не дифференцируема для этих значений x . Касательная к графику в любой из его конечных точек будет вертикальной линией, а наклон считается неопределенным. График y = arccos ( x ) для 0 ≤ y ≤ π
Функция арктангенса
[Вернитесь к началу страницы]
Функция арктангенс является обратной функции тангенса . Функция тангенса принимает угол на вход и выдает значение тангенса угла на выходе. При условии, что угол находится в ограниченной области функции тангенса, применение функции арктангенса к его значению тангенса даст нам исходный угол.
 На следующем рисунке показан график функции тангенса. Функция тангенса отличается от функций синуса и косинуса тем, что ее график не является непрерывной формой волны и имеет период всего π радиан (180 °).
На следующем рисунке показан график функции тангенса. Функция тангенса отличается от функций синуса и косинуса тем, что ее график не является непрерывной формой волны и имеет период всего π радиан (180 °).График касательной функции
Чтобы функция арктангенса была истинно обратной функцией функции тангенса, должно выполняться следующее утверждение:
tan (arctan ( x )) = x и arctan (tan ( x )) = x
Мы обеспечиваем это, ограничивая область определения функции открытым интервалом (— π / 2 , π / 2 ), как видно из рисунка (обратите внимание, что функция тангенса не определена ни для x = — π / 2 , ни для = π / 2 ). Значение функции увеличивается в этой области по мере увеличения значения x , и каждое входное значение создает уникальное выходное значение.
 Функция тангенса теперь определяется следующим образом:
Функция тангенса теперь определяется следующим образом:y = tan ( x ) for — π / 2 < x < π /2
‘s 9000. Как и прежде, мы хотим дифференцировать функцию арктангенса относительно x , поэтому мы пытаемся найти следующее:
d (арктический( x )) d x Первый шаг — установить y равно функции арктангенса:
y = arctan ( x ) для — π / 2 < y < π / 2
Однако функция тангенса обратна функции арктангенса, поэтому мы можем переписать это как:загар ( y ) = x
Мы воспользуемся неявным дифференцированием и решим для d y /d x , чтобы получить производную функции арктангенса через y .
 Дифференцируя обе части уравнения, получаем:
Дифференцируя обе части уравнения, получаем:d (tan( y )) = d ( x ) d x d x Помните, что тангенс ( y ) — составная функция, поэтому нам нужно применить цепное правило. Внешняя функция tan ( y ), а внутренняя функция y ( x ), поэтому мы получаем:
SEC 2 ( Y ) · D Y = 1 D 8999999999999999999999999999999999999999999999999999999999999999999999999999898989ня 99999999999999999999999999999999999999999999999999999999999999999999999898979н. Давайте изменим это, чтобы получить d y /d x отдельно с левой стороны:
д г = 1 d x сек 2 ( y ) Поскольку мы знаем, что y равно арктангенсу ( x ), мы можем заменить y в левой части этого уравнения следующим образом:
d (arctan ( x )) = 1 d x sec 2 ( y ) Теперь нам нужно переписать правую часть уравнения в терминах x .
 На этот раз мы не будем использовать тождество Пифагора, но мы будем использовать тригонометрическое тождество, тесно связанное с ним. Разделив тождество Пифагора на cos 2 ( y ), мы получим следующее тригонометрическое тождество:
На этот раз мы не будем использовать тождество Пифагора, но мы будем использовать тригонометрическое тождество, тесно связанное с ним. Разделив тождество Пифагора на cos 2 ( y ), мы получим следующее тригонометрическое тождество:tan 2 ( y ) + 1 = sec 2 ( y )
Мы уже установили, что тангенс ( y ) равен x , поэтому мы можем переписать это новое тождество как:
x 2 + 1 = сек 2 ( y )
Теперь мы можем переписать нашу формулу для производной функции арктангенса и привести ее к нужному формату, заменив sec 2 ( y ), следующим образом:
d (arctan( x )) = 1 d x x 2 + 1 На рисунке ниже показан график функции арктангенса.
 В то время как области определения функций арксинуса и арккосинуса ограничены интервалом [-1, 1], область определения функции арктангенса состоит из всех действительных чисел. Функция также дифференцируема во всей своей области определения.
В то время как области определения функций арксинуса и арккосинуса ограничены интервалом [-1, 1], область определения функции арктангенса состоит из всех действительных чисел. Функция также дифференцируема во всей своей области определения.График y = arctan ( x ) for — π / 2 < y < π / 2
Функция арккотангенса
[Вернитесь к началу страницы]
Функция арккотангенса является обратной функцией котангенса . Функция котангенса принимает угол на вход и возвращает значение котангенса угла на выходе. При условии, что угол находится в пределах ограниченной области функции котангенса, применение функции арккотангенса к его значению котангенса даст нам исходный угол. На следующем рисунке показан график функции котангенса. Как и в случае функции тангенса, график функции котангенса не является непрерывной формой волны и имеет период всего π радиан (180 °).

График функции котангенса
Чтобы функция арккотангенса была истинно обратной функцией функции котангенса, должно выполняться следующее утверждение:
кроватка (arccot ( x )) = x и arccot (кроватка ( x )) = x
Мы обеспечиваем это, ограничивая область определения функции открытым интервалом (0, π), как видно из иллюстрации (обратите внимание, что функция котангенса не определена ни для х = 0 или х = π). Значение функции уменьшается в этой области по мере увеличения значения x , и каждое входное значение создает уникальное выходное значение. Функция котангенса теперь определяется следующим образом:
y = кроватка ( x ) для 0 < x < π
Давайте посмотрим, как получается производная функции арккотангенса.
 Мы хотим продифференцировать функцию арккотангенса по x , поэтому мы пытаемся найти:
Мы хотим продифференцировать функцию арккотангенса по x , поэтому мы пытаемся найти:d (arccot ( x )) d x Первый шаг — установить y равными функции арккотангенса:
y = arccot ( x ) для 0 < y < π
Однако функция котангенса является обратной функцией арккотангенса, поэтому мы можем переписать это как:
детская кроватка ( y ) = x
Мы воспользуемся неявным дифференцированием и найдем d y /d x , чтобы получить производную функции арккотангенса через y . Дифференцируя обе части уравнения, получаем:
d (кровать( y )) = d ( x ) 908 д х Помните, что кроватка ( y ) — составная функция, поэтому нам нужно применить цепное правило.
 Внешняя функция — это кроватка ( y ), а внутренняя функция — y ( x ), поэтому мы получаем:
Внешняя функция — это кроватка ( y ), а внутренняя функция — y ( x ), поэтому мы получаем:csc 2 ( y ) · d y = 1 d x Давайте изменим это, чтобы получить d y /d x отдельно с левой стороны:
d y = -1 d x csc 2 ( y ) Поскольку мы знаем, что y равно arccot ( x ), мы можем заменить y в левой части этого уравнения следующим образом:
d (arccot ( x )) = -1 d x csc 2 ( y ) Теперь нам нужно переписать правую часть уравнения в терминах x .
 На этот раз мы будем использовать другое тригонометрическое тождество, тесно связанное с тождеством Пифагора. Разделив тождество Пифагора на sin 2 ( y ), мы получим следующее тригонометрическое тождество:
На этот раз мы будем использовать другое тригонометрическое тождество, тесно связанное с тождеством Пифагора. Разделив тождество Пифагора на sin 2 ( y ), мы получим следующее тригонометрическое тождество:кроватка 2 ( y ) + 1 = csc 2 ( y )
Мы уже установили, что кроватка ( y ) равна x , поэтому мы можем переписать это новое тождество как:
x 2 + 1 = csc 2 ( y )
Теперь мы можем переписать нашу формулу для производной функции арктангенса и привести ее к нужному формату, заменив csc 2 ( y ), следующим образом:
d (arccot ( x )) = -1 d x x 2 + 1 На рисунке ниже показан график функции арккотангенса.
 Как и в случае с арктангенсом, область определения функции арккотангенса состоит из всех действительных чисел, и она дифференцируема во всей своей области определения. Вы также могли заметить, что производная функции арккотангенса является отрицательной производной функции арккотангенса.
Как и в случае с арктангенсом, область определения функции арккотангенса состоит из всех действительных чисел, и она дифференцируема во всей своей области определения. Вы также могли заметить, что производная функции арккотангенса является отрицательной производной функции арккотангенса.График y = arccot ( x ) для 0 < y < π
Функция арксеканс
[Вернитесь к началу страницы]
Функция арксеканс является обратной функции секанс . Функция секанса принимает угол в качестве входных данных и возвращает значение секущей угла в качестве выходных данных. При условии, что угол находится в пределах ограниченной области функции секущей, применение функции арксеканса к ее значению секанса даст нам исходный угол. На следующем рисунке показан график секущей функции. Как видите, график функции секущей не является непрерывной формой волны.
 Его период составляет 2π радиан (360°).
Его период составляет 2π радиан (360°).График секущей функции
Чтобы функция арксеканса была истинно обратной функцией функции секанса, должно выполняться следующее утверждение:
сек (угл.сек ( x )) = x и угл.сек (сек ( x )) = x
Мы обеспечиваем это, ограничивая область определения функции закрытым интервалом [0, π], как вы можете видеть из иллюстрации. Значение функции увеличится на x увеличивается, от один при x = 0 до некоторого числа, приближающегося к бесконечности , поскольку x приближается к π / 2 . Затем значение функции меняет знак, но продолжает увеличиваться по мере того, как x увеличивается от некоторого числа, приближающегося к отрицательной бесконечности близко к x = π / 2 до минус один при x = π.
 Каждое входное значение создает уникальное выходное значение, но обратите внимание, что функция не определена для х = π / 2 . Функция секущей определяется следующим образом:
Каждое входное значение создает уникальное выходное значение, но обратите внимание, что функция не определена для х = π / 2 . Функция секущей определяется следующим образом:y = сек ( x ) для 0 ≤ x ≤ π, кроме x = π / 2
2 Давайте посмотрим, как получается производная функции арксеканса. Как всегда, мы хотим дифференцировать функцию арксеканса относительно x , поэтому мы пытаемся найти:d (угловые секунды ( x )) d x Первый шаг — установить y равными функции арксеканс:
y = угл.сек ( x ) для 0 ≤ y ≤ π, кроме y = π / 2
Однако функция секущей обратна функции арксеканса, поэтому мы можем переписать это как:
сек ( y ) = x
Мы воспользуемся неявным дифференцированием и найдем d y /d x , чтобы получить производную функции арксеканса через y .
 Дифференцируя обе части уравнения, получаем:
Дифференцируя обе части уравнения, получаем:d (сек( y )) = d ( x ) 908 д х Помните, что sec ( y ) — составная функция, поэтому нам нужно применить цепное правило. Внешняя функция — это sec ( y ), а внутренняя функция — y ( x ), поэтому мы получаем:
sec( y ) · tan( y ) · d y = 1 d x Давайте изменим это, чтобы получить d y /d x отдельно с левой стороны:
d y = 1 d x sec( y ) · tan( y ) Поскольку мы знаем, что y равно угловой секунде ( x ), мы можем заменить y в левой части этого уравнения следующим образом:
d (arcsec ( x )) = 1 d x sec( y ) · tan( y ) Теперь нам нужно переписать правую часть уравнения в терминах x .
 Это выглядит сложнее, чем есть на самом деле, потому что теперь у нас есть произведение 90 324 двух различных тригонометрических функций 90 325 в знаменателе справа, обе принимают и в качестве аргумента. Однако мы все еще можем использовать тригонометрическое тождество — фактически то же самое, что мы использовали, чтобы помочь нам получить производную функции арктангенса — для решения проблемы. Вы можете вспомнить, что если мы разделим тождество Пифагора на cos 2 ( y ), мы получим следующее тригонометрическое тождество:
Это выглядит сложнее, чем есть на самом деле, потому что теперь у нас есть произведение 90 324 двух различных тригонометрических функций 90 325 в знаменателе справа, обе принимают и в качестве аргумента. Однако мы все еще можем использовать тригонометрическое тождество — фактически то же самое, что мы использовали, чтобы помочь нам получить производную функции арктангенса — для решения проблемы. Вы можете вспомнить, что если мы разделим тождество Пифагора на cos 2 ( y ), мы получим следующее тригонометрическое тождество:tan 2 ( y ) + 1 = sec 2 ( y )
Мы уже установили, что sec ( y ) равно x , поэтому мы можем переписать это новое тождество как:
загар 2 ( y ) + 1 = x 2
Подставив тангенс ( y ) в наше уравнение, мы получим:
D (ARCSEC ( x ) = 1 D x SEC394 D x SEC 2924).  0324 г ) — 1)
0324 г ) — 1)Но поскольку мы знаем, что sec ( y ) равно x , мы можем переписать это как:
d (угловые секунды( x )) = 1 d x Обратите внимание, что x 2 — 1 никогда не может быть отрицательным числом, так как функция арксеканс принимает результат функции секанса в качестве входных данных, и, как мы видели, значение sec ( x ) всегда будет ≤ -1 или ≥ 1. Также обратите внимание, что мы используем | х | в знаменателе, а не x , чтобы гарантировать, что d y /d x всегда будет положительным (на самом деле мы можем обосновать это с помощью тригонометрии, но мы не будем здесь вдаваться в подробности).
На приведенном ниже рисунке показан график функции арксеканса, и вы должны увидеть, что производная (которая представляет собой наклон касательной к графику в любой точке, просто напомню вам!) всегда будет положительной.
 Область определения функции состоит из всех действительных чисел, кроме открытого интервала (-1, 1), и функция дифференцируема для всех значений x , за исключением закрытого интервала [-1, 1]. Хотя и минус один , и один входят в область определения функции арксеканса, функция не дифференцируема для этих значений x . Попробуйте подставить любой из них в формулу производной, и вы поймете, почему — вы получите ноль в знаменателе. Касательные к графику в любой из этих точек будут вертикальными линиями, а их наклон будет равен undefined .
Область определения функции состоит из всех действительных чисел, кроме открытого интервала (-1, 1), и функция дифференцируема для всех значений x , за исключением закрытого интервала [-1, 1]. Хотя и минус один , и один входят в область определения функции арксеканса, функция не дифференцируема для этих значений x . Попробуйте подставить любой из них в формулу производной, и вы поймете, почему — вы получите ноль в знаменателе. Касательные к графику в любой из этих точек будут вертикальными линиями, а их наклон будет равен undefined .График y = угловая секунда ( x ) для 0 ≤ y ≤ π, кроме y = π / 2
Функция арккосеканса
[Вернитесь к началу страницы]
Функция арккосеканс является обратной функции косеканс . Функция косеканса принимает угол в качестве входных данных и возвращает значение косеканса угла в качестве выходных данных.
 При условии, что угол находится в пределах ограниченной области функции косеканса, применение функции арккосеканса к его значению косеканса даст нам исходный угол. На следующем рисунке показан график функции косеканса. Как видите, график функции косеканса не является непрерывной формой волны. Его период составляет 2π радиан (360°).
При условии, что угол находится в пределах ограниченной области функции косеканса, применение функции арккосеканса к его значению косеканса даст нам исходный угол. На следующем рисунке показан график функции косеканса. Как видите, график функции косеканса не является непрерывной формой волны. Его период составляет 2π радиан (360°).График функции косеканса
Чтобы функция арккосеканса была истинно обратной функцией функции косеканса, должно выполняться следующее утверждение:
csc (arccsc ( x )) = x и arccsc (csc ( x )) = x
Мы обеспечиваем это, ограничивая область определения функции отрезком [- π / 2 , π / 2 ], как видно из иллюстрации. Значение функции будет уменьшаться по мере увеличения x , от минус один при x = — π / 2 до некоторого числа, приближающегося к минус бесконечность , поскольку x становится ближе к 0.
 Значение функции становится ближе к 0. переключает знак, но продолжает уменьшаться по мере увеличения x от некоторого числа, приближающегося к до бесконечности , близкого к 0 до один в x = π / 2 . Каждое входное значение создает уникальное выходное значение, но обратите внимание, что функция не определена для x = 0. Функция косеканса определяется следующим образом:
Значение функции становится ближе к 0. переключает знак, но продолжает уменьшаться по мере увеличения x от некоторого числа, приближающегося к до бесконечности , близкого к 0 до один в x = π / 2 . Каждое входное значение создает уникальное выходное значение, но обратите внимание, что функция не определена для x = 0. Функция косеканса определяется следующим образом:y = csc ( x ) для — π / 2 ≤ x ≤ π / 2 5 x , 9 0 = 0
Давайте посмотрим, как получается производная функции арккосеканса. Как всегда, мы хотим продифференцировать функцию арккосеканса по x , поэтому мы пытаемся найти:
d (arccsc ( x )) d x Первый шаг — установить y равными функции арккосеканса:
y = arccsc ( x ) для — π / 2 ≤ y ≤ π / 3 = 5 9 9 0 4 9 1 7 8 2 ,
Однако функция косеканса обратна функции арккосеканса, поэтому мы можем переписать это как:
csc ( y ) = x
Мы воспользуемся неявным дифференцированием и найдем d y /d x , чтобы получить производную функции арккосеканса через y .
 Дифференцируя обе части уравнения, получаем:
Дифференцируя обе части уравнения, получаем:d (csc( y )) = d ( x ) d x d x Помните, что csc ( y ) является составной функцией , поэтому нам нужно применить цепное правило. Внешняя функция — это csc ( y ), а внутренняя функция — y ( x ), поэтому мы получаем:
-csc( у ) · cot( y ) · d y = 1 d x Давайте изменим это, чтобы получить d y /d x отдельно с левой стороны:
D Y = -1 D x CSC ().  0895
0895Поскольку мы знаем, что y равно arccsc ( x ), мы можем заменить y в левой части этого уравнения следующим образом:
d (arccsc ( x )) = -1 d x csc( y ) · cot( y ) Теперь нам нужно переписать правую часть уравнения через х . Опять же, это выглядит сложнее, чем есть на самом деле, потому что у нас есть произведение двух разных тригонометрических функций в знаменателе с правой стороны, обе принимают y в качестве аргумента. Как и в случае с функцией арксеканса, мы можем использовать тригонометрическое тождество, которое мы уже видели, чтобы помочь нам решить проблему. Это то же самое, что мы использовали, чтобы помочь нам получить производную функции арккотангенса. Вы можете вспомнить, что если мы разделим пифагорейское тождество на sin 2 ( y ), получаем следующее тригонометрическое тождество:
кроватка 2 ( y ) + 1 = csc 2 ( y )
Мы уже установили, что csc ( y ) равно x , поэтому мы можем переписать это новое удостоверение как:
кроватка 2 ( y ) + 1 = x 2
Замена детской кроватки ( y ) в нашем уравнении получаем:
d (arccsc( x )) = -1 d x csc ( y ) √( csc 2 ( y ) — 1) Но поскольку мы знаем, что csc ( y ) равно x , мы можем переписать это как:
d (arccsc( x )) = -1 г x | х | √( x 2 — 1) Обратите внимание, что x 2 — 1 никогда не может быть отрицательным числом, поскольку функция арккосеканса принимает результат функции косеканса в качестве входных данных, и, как мы видели, значение sec ( x ) всегда будет ≤ -1 или ≥ 1.
 Также обратите внимание, что мы снова используем | х | в знаменателе, а не x , чтобы гарантировать, что d y /d x всегда будет отрицательным (опять же, это можно обосновать с помощью тригонометрии, но мы не будем здесь вдаваться в подробности).
Также обратите внимание, что мы снова используем | х | в знаменателе, а не x , чтобы гарантировать, что d y /d x всегда будет отрицательным (опять же, это можно обосновать с помощью тригонометрии, но мы не будем здесь вдаваться в подробности).На приведенном ниже рисунке показан график функции арккосеканса, и вы должны увидеть, что производная (то есть наклон касательной к графику в любой точке) всегда будет отрицательной. Область определения функции состоит из всех действительных чисел, кроме открытого интервала (-1, 1), и функция дифференцируема для всех значений x , за исключением закрытого интервала [-1, 1]. Хотя и минус один , и один входят в область определения функции арккосеканса, функция не дифференцируема для этих значений x . Попробуйте подставить любой из них в формулу производной, и вы поймете, почему — вы получите ноль в знаменателе. Касательные к графику в любой из этих точек будут вертикальными линиями, а их наклон будет равен undefined .
 Вы также могли заметить, что производная функции арккосеканса является отрицательной производной функции арккосеканса.
Вы также могли заметить, что производная функции арккосеканса является отрицательной производной функции арккосеканса.График y = arccsc ( x ) для -π/2 ≤ y ≤ π/2, кроме y = 0
[Вернитесь к началу страницы]
Функции арксинуса, арккосинуса и арктангенса
Функции арксинуса, арккосинуса и арктангенсафункция арксинуса функция арккосинуса функция арктангенса
Функция арксинуса
Исходная информация: Функция арксинуса является обратной функцией синуса. (пока функция синуса ограничена определенной областью). Щелкните здесь для обзора обратных функций.Напомним, что функция синуса принимает угол x в качестве входных данных и возвращает синус этого угла в качестве выходных данных:
Например, если 30° — это вход, то 0,5 — это выход. Здесь мы хотим создать обратную функцию, которая будет принимать 0,5 в качестве входных данных и
возврат 30° в качестве выхода.
Но есть проблема. Обратите внимание, что существует много углов, синус которых равен 0,5: Мы говорим, что это отображение много к одному . Это означает, что обратная
отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арксинусом (с большой буквы и аббревиатурой арксинус) и функцией , называемой арксинусом
(со строчной буквой «а» и аббревиатурой arcsin). Вот как они определяются:
Здесь мы хотим создать обратную функцию, которая будет принимать 0,5 в качестве входных данных и
возврат 30° в качестве выхода.
Но есть проблема. Обратите внимание, что существует много углов, синус которых равен 0,5: Мы говорим, что это отображение много к одному . Это означает, что обратная
отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арксинусом (с большой буквы и аббревиатурой арксинус) и функцией , называемой арксинусом
(со строчной буквой «а» и аббревиатурой arcsin). Вот как они определяются:
Определение: Арксинус x , обозначаемый как Арксинус ( x ), определяется как « множество всех углов , синус которых равен x ». Это отношение один ко многим . Вот пример: Определение: Арксинус x , обозначаемый arcsin( x ), определяется как определяется как ‘ один угол между −π/2 и +π/2 радиан (или между −90° и +90°), синус которого равен х ’. Это функция «один к одному» . Вот пример: Определение: Из всех значений, возвращаемых отношением арксинуса,
тот, который совпадает со значением, возвращаемым функцией арксинуса
называется главным значением отношения арксинуса.
(Примером может служить значение 30°, показанное выше красным.)
Это функция «один к одному» . Вот пример: Определение: Из всех значений, возвращаемых отношением арксинуса,
тот, который совпадает со значением, возвращаемым функцией арксинуса
называется главным значением отношения арксинуса.
(Примером может служить значение 30°, показанное выше красным.)График: Красная кривая на графике справа — функция арксинуса. Обратите внимание, что для любых x между −1 и +1 возвращает одно значение между -π/2 и +π/2 радиан.
Если мы добавим серую кривую к красной кривой, мы получим график Отношение арксинуса. Вертикальная линия, нарисованная в любом месте между x = −1 и +1 касались бы этой кривой во многих местах, а это означает, что отношение арксинуса вернет много значений.
На этом графике угол y измерен в радианах. Если вы хотите измерить y в градусов тогда просто измените масштаб по вертикали так что и проходят от −360 ° до 360 °, а не от от -2π до 2π радиан; в остальном форма графика не меняется.

Если сравнить график арксинуса с графиком синуса тогда вы видите, что одно можно получить из другого, поменяв местами горизонтальная и вертикальная оси.
Домен и диапазон: Область определения функции арксинуса составляет от −1 до +1 включительно, а диапазон — от от −π/2 до π/2 радиан включительно (или от −9от 0° до 90°).
Функция арксинуса может быть распространяется на комплексные числа, в которых случай домен все комплексные числа.
Специальные значения функции арксинуса (Нажмите здесь для более подробной информации)
Решение уравнения sin( θ ) = c для θ с помощью арксинуса и арксинуса eПредположим, что угол θ неизвестен, но известен его синус быть с . Тогда нахождение этого угла требует решения этого уравнения для θ :
sin ( θ ) = с
Если это, скажем, простая задача о прямоугольном треугольнике и мы знаем , что угол θ должен быть где-то между 0 и 90°, тогда решение является единственным значением:θ = arcsin ( c )
С другой стороны, если это более сложная задача и нам нужно найти все возможные углы у которых синус равен c тогда решение это весь набор значений:θ = арксинус ( c )
Решения в этих двух случаях следуют непосредственно из определения функции арксинуса и отношения арксинуса. Обратите внимание, что если c больше 1 или меньше -1, то существуют
нет реальных решений. Однако есть комплексные решения.
Обратите внимание, что если c больше 1 или меньше -1, то существуют
нет реальных решений. Однако есть комплексные решения.
Оценка Arcsin( с )
Если c число, то весь набор значений Arcsin( c ) можно найти с помощью следующей процедуры. Обратитесь к графику справа где точки — желаемые значения.- Первое значение (главное значение), обозначенное как θ PV , находится по формуле вычисление arcsin( c ) с помощью калькулятора или с помощью тренера по алгебре.
- Второе значение, называемое θ 2 , находится по
используя симметрию кривой арксинуса. Обратите внимание, что две синие стрелки в
графы имеют одинаковую длину. Это означает, что θ 2 настолько меньше π, насколько θ PV больше нуля. В виде формулы:
θ 2 = π − θ PV
(Нажмите здесь, чтобы увидеть метод CAST для поиска θ 2 . )
) - Все остальные значения выше и ниже этих двух значений можно найти из этих двух значений, добавив или вычитание кратных 2π. Если мы используем целое число n для подсчета которое кратно другим значениям, можно получить по этой формуле: Например, если мы допустим n = −1, тогда мы получим значения для две нижние точки на графике.
- Если вы используете градусы вместо радианов, используйте следующие формулы вместо предыдущих:
Как использовать функцию арксинуса в программе Algebra Coach- Введите arcsin(x) в текстовое поле, где x — аргумент. Аргумент должен быть заключен в скобки.
- Установите соответствующие параметры:
- Установите arcsin, arccos и arctan опция.
(Настройка возвращает основное значение возвращает одно значение;
параметр не оценивать полезен, если вам нужны все значения
отношения Arc — но вам придется их вычислить самостоятельно.
 )
) - Установите параметр точная / с плавающей запятой. (Точный режим позволяет использовать специальные значения.)
- Установить режим градусов/радиан вариант.
- Установите параметр p, который соответствует или не соответствует параметру π. (Если вы хотите, чтобы арксинус возвращал специальные значения в радианном режиме затем включите это.)
- Включите комплексных чисел , если вы хотите иметь возможность оценивать арксинус комплексного числа или числа больше 1.
- Установите arcsin, arccos и arctan опция.
(Настройка возвращает основное значение возвращает одно значение;
параметр не оценивать полезен, если вам нужны все значения
отношения Arc — но вам придется их вычислить самостоятельно.
- Нажмите кнопку «Упростить».
Алгоритм для функции арксинусаНажмите здесь чтобы увидеть алгоритм, который компьютеры используют для вычисления функции арксинуса.
Функция арккосинуса
Исходная информация: Функция арккосинуса является обратной функцией косинуса. (пока функция косинуса ограничена определенной областью). Щелкните здесь для обзора обратных функций.
Щелкните здесь для обзора обратных функций.Напомним, что функция косинуса принимает угол х в качестве входных данных и возвращает косинус этого угла в качестве выходных данных:
Например, если 60° — вход, то 0,5 — выход. Здесь мы хотим создать обратную функцию, которая будет принимать 0,5 в качестве входных данных и вернуть 60 ° в качестве вывода. Но есть проблема. Обратите внимание, что существует много углов, косинус которых равен 0,5: Мы говорим, что это отображение много к одному . Это означает, что обратная отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы Требование «одно значение диапазона» чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арккосинусом (с большой буквы и аббревиатурой Arccos) и функцией , называемой арккосинусом (со строчной буквой «а» и аббревиатурой arccos). Вот как они определяются:
Определение: Арккосинус x , обозначаемый Arccos( x ), определяется как ‘ множество всех углов , косинус которых равен х ’. Это отношение один ко многим . Вот пример: Определение: Арккосинус x , обозначаемый как arccos( x ), определяется как
‘ один угол между 0 и π радиан
(или от 0° до 180°), косинус которого равен x ’.
Это функция «один к одному» . Вот пример: Определение: Из всех значений, возвращаемых отношением арккосинуса,
тот, который совпадает со значением, возвращаемым функцией арккосинуса
называется главное значение отношения арккосинуса.
(Примером может служить значение 60°, показанное выше красным.)
Это отношение один ко многим . Вот пример: Определение: Арккосинус x , обозначаемый как arccos( x ), определяется как
‘ один угол между 0 и π радиан
(или от 0° до 180°), косинус которого равен x ’.
Это функция «один к одному» . Вот пример: Определение: Из всех значений, возвращаемых отношением арккосинуса,
тот, который совпадает со значением, возвращаемым функцией арккосинуса
называется главное значение отношения арккосинуса.
(Примером может служить значение 60°, показанное выше красным.)График: Красная кривая на графике справа — функция арккосинуса. Обратите внимание, что для любого x между −1 и +1 он возвращает один значение между 0 и +π радиан.
Если мы добавим серую кривую к красной кривой, мы получим график Отношение арккосинуса. Вертикальная линия, нарисованная где-то между x = −1 и +1 касались бы этой кривой во многих местах, а это означает, что отношение арккосинуса вернет много значений.

На этом графике угол y измерен в радианах. Если вы хотите измерить y в градусах , то просто измените масштаб по вертикали так что и проходят от −360 ° до 360 °, а не от от -2π до 2π радиан; в остальном форма графика не меняется.
Если сравнить график арккосинуса с графиком косинуса тогда вы видите, что одно можно получить из другого, поменяв местами горизонтальная и вертикальная оси.
Домен и диапазон: Область определения функции арккосинуса составляет от −1 до +1 включительно, а диапазон — от От 0 до π радиан включительно (или от 0° до 180°).
Функция арккосинуса может быть распространяется на комплексные числа, в которых случай домен все комплексные числа.
Специальные значения функции арккосинуса (Нажмите здесь для более подробной информации)
Решение уравнения cos( θ ) = c для θ с помощью арккосинуса и Arccos ineПредположим, что угол θ неизвестен, но известен его косинус быть c .
 Тогда нахождение этого угла требует решения этого уравнения
для θ :
Тогда нахождение этого угла требует решения этого уравнения
для θ :потому что ( θ ) = с
Если это, скажем, простая задача о прямоугольном треугольнике и мы знаем , что угол θ должен быть где-то между 0 и 90°, то решение является единственным значением:θ = arccos ( c )
С другой стороны, если это более сложная задача и нам нужно найти все возможные углы , косинус которых равен c , тогда решение это весь набор значений:θ = Arccos ( c )
Решения в этих двух случаях следуют непосредственно из определения функции арккосинуса и соотношения арккосинуса. Обратите внимание, что если c больше 1 или меньше -1, то есть нет реальных решений. Однако есть комплексные решения.
Оценка Arccos( c )
Если c число, то весь набор значений Arccos( c ) можно найти с помощью следующей процедуры. Обратитесь к графику справа
где точки — желаемые значения.
Обратитесь к графику справа
где точки — желаемые значения.- Первое значение (главное значение), обозначенное θ PV , найдено оценка arccos( c ) с помощью калькулятора или с помощью тренера по алгебре.
- Второе значение, называемое θ 2 , находится по формуле
используя симметрию кривой арккосинуса. Обратите внимание, что две синие стрелки в
графы имеют одинаковую длину. Это означает, что θ 2 настолько меньше 2π, насколько θ PV больше нуля. В виде формулы:
θ 2 = 2 π − θ PV
(Нажмите здесь, чтобы увидеть метод CAST для поиска θ 2 .) - Все остальные значения выше и ниже этих двух значений
можно найти из этих двух значений, добавив или
вычитание кратных 2π. Если мы используем целое число n для подсчета
которое кратно другим значениям, можно получить по этой формуле: Например, если мы допустим n = −1, тогда мы получим значения для
две нижние точки на графике.

- Если вы используете градусы вместо радианов, используйте следующие формулы вместо предыдущих:
Как использовать функцию арккосинуса в Algebra Coach- Введите arccos(x) в текстовое поле, где x — аргумент. Аргумент должен быть заключен в скобки.
- Установите соответствующие параметры:
- Установите параметр arcsin, arccos и arctan . (Настройка возвращает основное значение возвращает одно значение; параметр не оценивать полезен, если вам нужны все значения отношения Arc — но вам придется их вычислить самостоятельно.)
- Установите параметр точная / с плавающей запятой. (Точный режим позволяет использовать специальные значения.)
- Установите параметр режима градусов/радиан.
- Установите параметр p, который соответствует или не соответствует параметру π.
 (Если вы хотите, чтобы арккосинус возвращал специальные значения в радианном режиме
затем включите это.)
(Если вы хотите, чтобы арккосинус возвращал специальные значения в радианном режиме
затем включите это.) - Включите комплексных чисел , если вы хотите иметь возможность оценивать арккосинус комплексного числа или числа больше 1.
- Нажмите кнопку «Упростить».
Алгоритм для функции арккосинусаНажмите здесь чтобы увидеть алгоритм, который компьютеры используют для вычисления функции арккосинуса.
Функция арктангенса
Исходная информация: Функция арктангенса является обратной функцией тангенса (пока функция тангенса ограничена определенной областью). Щелкните здесь для обзора обратных функций.Напомним, что функция тангенса принимает угол x в качестве входных данных и возвращает тангенс этого угла в качестве выходных данных:
Например, если 45° — вход, то 1.0 — выход. Здесь мы хотим создать обратную функцию, которая будет принимать 1.0 в качестве входных данных и
возврат 45° в качестве вывода.
Но есть проблема. Обратите внимание, что существует множество углов, тангенс которых равен 1,0: Мы говорим, что это отображение много к одному . Это означает, что обратная
отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арктангенсом (с большой буквы и аббревиатурой арктангенс) и функцией , называемой арктангенс
(со строчной буквой «а» и аббревиатурой arctan). Вот как они определяются:
Здесь мы хотим создать обратную функцию, которая будет принимать 1.0 в качестве входных данных и
возврат 45° в качестве вывода.
Но есть проблема. Обратите внимание, что существует множество углов, тангенс которых равен 1,0: Мы говорим, что это отображение много к одному . Это означает, что обратная
отображение было бы один-ко-многим и, следовательно, не удовлетворяло бы
Требование «одно значение диапазона»
чтобы отображение было функцией. Чтобы решить эту проблему, мы вводим как отношение называется арктангенсом (с большой буквы и аббревиатурой арктангенс) и функцией , называемой арктангенс
(со строчной буквой «а» и аббревиатурой arctan). Вот как они определяются:
Определение: Арктангенс x , обозначаемый Arctan ( x ), определяется как ‘ множество всех углов , тангенс которых равен х ’. Это отношение один ко многим . Вот пример: Определение: Арктангенс x , обозначаемый как arctan( x ), определяется как ‘ один угол между −π/2 и +π/2 радиан (или между −90° и +90°), тангенс которого равен x ’. Это один к одному функция . Вот пример: Определение: Из всех значений, возвращаемых отношением арктангенс,
тот, который совпадает со значением, возвращаемым функцией арктангенса
называется главным значением отношения арктангенса.
(Примером является значение 45°, показанное выше красным.)
Это один к одному функция . Вот пример: Определение: Из всех значений, возвращаемых отношением арктангенс,
тот, который совпадает со значением, возвращаемым функцией арктангенса
называется главным значением отношения арктангенса.
(Примером является значение 45°, показанное выше красным.)График: Красная кривая на графике справа — функция арктангенса. Обратите внимание, что для любых x возвращает одно значение между -π/2 и +π/2 радиан.
Если мы добавим серые кривые к красной кривой, то мы получим график Арктангенс отношения. Вертикальная линия, проведенная в любом месте будет касаться этого набора кривых во многих местах, а это означает, что отношение арктангенса вернет много значений.
На этом графике угол y измерен в радианах. Если вы хотите измерить y в градусах , то просто измените масштаб по вертикали так что y работает от −180° до 180° вместо от от -π до π радиан; в остальном форма графика не меняется.

Если сравнить график арктангенса с графиком касательной тогда вы видите, что одно можно получить из другого, поменяв местами горизонтальная и вертикальная оси.
Домен и диапазон: Область определения функции арктангенса — это все действительные числа, а диапазон — от От −π/2 до π/2 радиан без учета (или от −90° до 90°).
Функцию арктангенса можно распространяется на комплексные числа, в которых случай домен все комплексные числа.
Специальные значения функции арктангенса (Нажмите здесь для более подробной информации)
Решение уравнения tan( θ ) = c для θ с помощью арктангенса и арктангенсаПредположим, что угол θ неизвестен, но известен его тангенс быть с . Тогда нахождение этого угла требует решения этого уравнения для θ :
тангенс ( θ ) = с
Если это, скажем, простая задача о прямоугольном треугольнике и мы знаем , что угол θ должен быть где-то между 0 и 90°, тогда решение является единственным значением:θ = арктангенс ( c )
С другой стороны, если это более сложная задача и нам нужно найти все возможные углы , тангенс которых равен c , то решение это весь набор значений:θ = арктан ( c )
Решения в этих двух случаях следуют непосредственно из определений функции арктангенса и отношения арктангенса.
Оценка Arctan( c )
Если c число, то весь набор значений Arctan( c ) можно найти с помощью следующей процедуры. Обратитесь к графику справа где точки — желаемые значения.- Первое значение (главное значение), обозначенное как θ PV , находится по формуле оценка arctan( c ) с помощью калькулятора или с помощью тренера по алгебре.
- Все остальные значения выше и ниже этого значения можно найти с помощью
используя тот факт, что соседние значения удалены друг от друга на расстояние π.
Если мы используем целое число n для подсчета числа, кратного π, затем другого
значения можно получить по этой формуле:
θ = θ PV + π n
(Нажмите здесь, чтобы увидеть метод CAST для поиска θ 2 .) - Если вы используете градусы вместо радианов, используйте следующие формулы
вместо предыдущих:
θ = θ PV + 180°· n
Как использовать функцию арктангенса в программе Algebra Coach- Введите arctan(x) в текстовое поле, где x — аргумент.
 Аргумент должен быть заключен в скобки.
Аргумент должен быть заключен в скобки. - Установите соответствующие параметры:
- Установите параметр arcsin, arccos и arctan . (Настройка возвращает основное значение возвращает одно значение; не оценивать параметр полезен, если вы хотите получить все значения отношения Arc — но вам придется их вычислить самостоятельно.)
- Установите параметр точная / с плавающей запятой. (Точный режим позволяет использовать специальные значения.)
- Установите параметр режима градусов/радиан.
- Установите параметр p, который соответствует или не соответствует параметру π. (Если вы хотите, чтобы арктангенс возвращал специальные значения в радианном режиме затем включите это.)
- Включите комплексных чисел , если вы хотите иметь возможность оценивать арктангенс комплексного числа.
- Нажмите кнопку «Упростить».