Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Формулы приведения тригонометрических функций Тригонометрические формулы Разность кубов Сумма кубов
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
формулировки, доказательства, примеры, формулы степеней
Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.
Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.
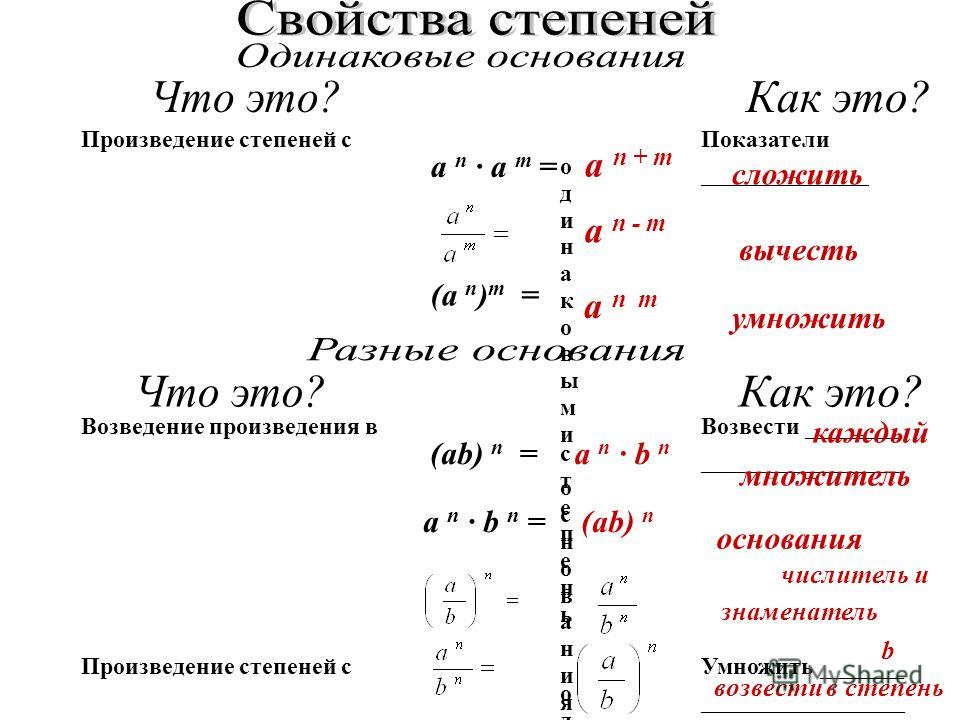
Свойства степени с натуральным показателем
Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n-ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:
Определение 11. Главное свойство степени: am·an=am+n
Можно обобщить до: an1·an2·…·ank=an1+n2+…+nk.
2. Свойство частного для степеней, имеющих одинаковые основания: am:an=am−n
3. Свойство степени произведения: (a·b)n=an·bn
Равенство можно расширить до: (a1·a2·…·ak)n=a1n·a2n·…·akn
4. Свойство частного в натуральной степени: (a:b)n=an:bn
5. Возводим степень в степень: (am)n=am·n,
Можно обобщить до:(((an1)n2)…)nk=an1·n2·…·nk
6. Сравниваем степень с нулем:
Сравниваем степень с нулем:
- если a>0, то при любом натуральном n, an будет больше нуля;
- при a, равном 0, an также будет равна нулю;
- при a<0 и таком показателе степени, который будет четным числом 2·m, a2·m будет больше нуля;
- при a <0 и таком показателе степени, который будет нечетным числом 2·m−1, a2·m−1 будет меньше нуля.
7. Равенство an<bn будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.
8. Неравенство am>an будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.
В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными. Для каждого из равенств, например, для основного свойства, можно поменять местами правую и левую часть: am·an=am+n — то же самое, что и am+n=am·an. В таком виде оно часто используется при упрощении выражений.
Далее мы разберем каждое свойство подробно и попробуем привести доказательства.
1. Начнем с основного свойства степени: равенство am·an=am+n будет верным при любых натуральных m и n и действительном a. Как доказать это утверждение?
Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:
Это можно сократить до (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m+n. Таким образом, am+n, значит, основное свойство степени доказано.
Разберем конкретный пример, подтверждающий это.
Пример 1Итак, у нас есть две степени с основанием 2. Их натуральные показатели — 2 и 3 соответственно. У нас получилось равенство: 22·23=22+3=25 Вычислим значения, чтобы проверить верность этого равенства.
Выполним необходимые математические действия: 22·23=(2·2)·(2·2·2)=4·8=32 и 25=2·2·2·2·2=32
В итоге у нас вышло: 22·23=25. Свойство доказано.
В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n1, n2 и др. буквой k, мы получим верное равенство:
Если обозначить количество натуральных чисел n1, n2 и др. буквой k, мы получим верное равенство:
an1·an2·…·ank=an1+n2+…+nk.
Пример 2Пример с конкретными числами (легко посчитать самостоятельно): (2,1)3·(2,1)3·(2,1)4·(2,1)7=(2,1)3+3+4+7=(2,1)17.
2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство am:an=am−n, которое справедливо при любых натуральным m и n (причем m больше n) ) и любом отличном от нуля действительном a.
Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0n=0). Условие, чтобы число m обязательно было больше n, нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m, мы получим натуральное число. Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.
Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:
am−n·an=a(m−n)+n=am
Из него можно вывести: am−n·an=am
Вспомним про связь деления и умножения. Из него следует, что am−n– частное степеней am и an. Это и есть доказательство второго свойства степени.
Пример 3Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π: π5:π2=π5−3=π3
3. Следующим мы разберем свойство степени произведения: (a·b)n=an·bn при любых действительных a и b и натуральном n.
Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:
Вспомнив свойства умножения, запишем: . Это значит то же самое, что и an·bn.
Пример 423·-4254=234·-4254
Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:
(a1·a2·…·ak)n=a1n·a2n·…·akn
Пример 5С конкретными числами получим следующее верное равенство: (2·(-2,3)·a)7=27·(-2,3)7·a
4.
Для доказательства можно использовать предыдущее свойство степени. Если (a:b)n·bn=((a:b)·b)n=an , а (a:b)n·bn=an, то из этого выходит, что (a:b)n есть частное от деления an на bn.
Пример 6Подсчитаем пример: 312:-0.53=3123:(-0,5)3
5. Далее мы поговорим о свойстве возведения степени в степень: (am)n=am·n для любого действительного a и любых натуральных n и m.
Пример 7Начнем сразу с примера: (52)3=52·3=56
А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:
Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p, q, r, s, то верно будет:
apqys=ap·q·y·s
Пример 8Добавим конкретики: (((5,2)3)2)5=(5,2)3·2·5=(5,2)30
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.
Для начала сравним степень с нулем. Почему an>0 при условии, что а больше 0?
Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени an с положительным основанием и натуральным показателем это будет верно.
Пример 935>0, (0,00201)2>0 и 3491351>0
Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.
Пример 1003=0 и 0762=0
Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2·m, где m – натуральное число.
Тогда:
Вспомним, как правильно умножать отрицательные числа: произведение a·a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда и степень a2·m также положительны.
Тогда и степень a2·m также положительны.
Например, (−6)4>0, (−2,2)12>0 и -296>0
А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2·m−1.
Тогда
Все произведения a·a, согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a, то конечный результат будет отрицателен.
Тогда получим: (−5)3<0, (−0,003)17<0 и -111029<0
7. Далее разберем следующее свойство, формулировка которого такова: из двух степеней, имеющих одинаковый натуральный показатель, больше та, основание которой больше (и наоборот).
Как это доказать?
an<bn– неравенство, представляющее собой произведение левых и правых частей nверных неравенств a<b. Вспомним основные свойства неравенств справедливо и an<bn.
Пример 12Например, верны неравенства: 37<(2,2)7 и 3511124>(0,75)124
8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Для начала нам нужно убедиться, что am<an при условии, что m больше, чем n, и а больше 0, но меньше 1.Теперь сравним с нулем разность am−an
Вынесем an за скобки, после чего наша разность примет вид an·(am−n−1). Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m−n>0, тогда am−n−1–отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.
У нас вышло, что am−an<0 и am<an. Свойство доказано.
Осталось привести доказательство второй части утверждения, сформулированного выше: am>a справедливо при m>n и a>1. Укажем разность и вынесем an за скобки: (am−n−1).Степень an при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a>1 степень am−n больше единицы. Выходит, am−an>0 и am>an, что нам и требовалось доказать.
Пример с конкретными числами: 37>32
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).
Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:
Определение 21. am·an=am+n
2. am:an=am−n
3. (a·b)n=an·bn
4. (a:b)n=an:bn
5. (am)n=am·n
6. an<bn и a−n>b−n при условии целого положительного n, положительных a и b, a<b
7. am<an, при условии целых m и n, m>n и 0<a<1, при a>1 am>an.
Если основание степени равно нулю, то записи am и an имеют смысл только лишь в случае натуральных и положительных m и n. В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.
В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.
Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.
Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (ap)q=ap·q, (a−p)q=a(−p)·q, (ap)−q=ap·(−q) и (a−p)−q=a(−p)·(−q)
Условия: p=0 или натуральное число; q– аналогично.
Если значения p и q больше 0, то у нас получится (ap)q=ap·q. Схожее равенство мы уже доказывали раньше. Если p=0, то:
(a0)q=1q=1 a0·q=a0=1
Следовательно, (a0)q=a0·q
Для q=0 все точно так же:
(ap)0=1 ap·0=a0=1
Итог: (ap)0=ap·0.
Если же оба показателя нулевые, то (a0)0=10=1 и a0·0=a0=1, значит, (a0)0=a0·0.
Далее разберем равенство (a−p)q=a(−p)·q. Согласно определению степени с целым отрицательным показателем имеем a-p=1ap, значит, (a-p)q=1apq.
Согласно определению степени с целым отрицательным показателем имеем a-p=1ap, значит, (a-p)q=1apq.
Вспомним доказанное выше свойство частного в степени и запишем:
1apq=1qapq
Если 1p=1·1·…·1=1 иapq=ap·q, то 1qapq=1ap·q
Эту запись мы можем преобразовать в силу основных правил умножения в a(−p)·q.
Так же: ap-q=1(ap)q=1ap·q=a-(p·q)=ap·(-q).
И (a-p)-q=1ap-q=(ap)q=ap·q=a(-p)·(-q)
Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.
Доказательство предпоследнего свойства: вспомним, a−n>b−n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b.
Тогда неравенство можно преобразовать следующим образом:
1an>1bn
Запишем правую и левую части в виде разности и выполним необходимые преобразования:
1an-1bn=bn-anan·bn
Вспомним, что в условии a меньше b, тогда, согласно определению степени с натуральным показателем: — an<bn, в итоге: bn−an>0.
an·bn в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь bn-anan·bn, которая в итоге также дает положительный результат. Отсюда 1an>1bn откуда a−n>b−n, что нам и нужно было доказать.
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:
Определение 31. am1n1·am2n2=am1n1+m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 ( свойство произведения степеней с одинаковыми основаниями).
2.am1n1:bm2n2=am1n1-m2n2 , если a>0 (свойство частного).
3. a·bmn=amn·bmn при a>0 и b>0, а если m1n1>0 и m2n2>0, то при a≥0 и (или) b≥0 (свойство произведения в дробной степени).
4. a:bmn=amn:bmn при a>0 и b>0, а если mn>0, то при a≥0 и b>0 (свойство частного в дробной степени).
5. am1n1m2n2=am1n1·m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 (свойство степени в степени).
6. ap<bp при условии любых положительных a и b, a<b и рациональном p при p>0; если p<0 — ap>bp (свойство сравнения степеней с равными рациональными показателями).
7. ap<aq при условии рациональных чисел p и q, p>q при 0<a<1; если a>0 – ap>aq
Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n-ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.
Согласно тому, что из себя представляет степень с дробным показателем, получим:
am1n1=am1n1 и am2n2=am2n2, следовательно, am1n1·am2n2=am1n1·am2n2
Свойства корня позволят нам вывести равенства:
am1·m2n1·n2·am2·m1n2·n1=am1·n2·am2·n1n1·n2
Из этого получаем: am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2
Преобразуем:
am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2
Показатель степени можно записать в виде:
m1·n2+m2·n1n1·n2=m1·n2n1·n2+m2·n1n1·n2=m1n1+m2n2
Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
am1n1: am2n2=am1n1: am2n2=am1·n2:am2·n1n1·n2==am1·n2-m2·n1n1·n2=am1·n2-m2·n1n1·n2=am1·n2n1·n2-m2·n1n1·n2=am1n1-m2n2
Доказательства остальных равенств:
a·bmn=(a·b)mn=am·bmn=amn·bmn=amn·bmn;(a:b)mn=(a:b)mn=am:bmn==amn:bmn=amn:bmn;am1n1m2n2=am1n1m2n2=am1n1m2n2==am1m2n1n2=am1·m2n1n2==am1·m2n2·n1=am1·m2n2·n1=am1n1·m2n2
Следующее свойство: докажем, что для любых значений a и b больше 0, если а меньше b, будет выполняться ap<bp, а для p больше 0 — ap>bp
Представим рациональное число p как mn. При этом m–целое число, n–натуральное. Тогда условия p<0 и p>0 будут распространяться на m<0 и m>0. При m>0 и a<b имеем (согласно свойству степени с целым положительным показателем), что должно выполняться неравенство am<bm.
Используем свойство корней и выведем: amn<bmn
Учитывая положительность значений a и b, перепишем неравенство как amn<bmn. Оно эквивалентно ap<bp.
Таким же образом при m<0 имеем a am>bm, получаем amn>bmn значит, amn>bmn и ap>bp.
Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 ap<aq, а при a>0 будет верно ap>aq.
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m1n и m2n
Здесь m1 и m2 – целые числа, а n – натуральное. Если p>q, то m1>m2 (учитывая правило сравнения дробей). Тогда при 0<a<1 будет верно am1<am2, а при a>1 – неравенство a1m>a2m.
Их можно переписать в следующем виде:
am1n<am2nam1n>am2n
Тогда можно сделать преобразования и получить в итоге:
am1n<am2nam1n>am2n
Подводим итог: при p>q и 0<a<1 верно ap<aq, а при a>0– ap>aq.
Основные свойства степеней с иррациональными показателями
На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a>0, b>0, показатели p и q– иррациональные числа):
Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a>0, b>0, показатели p и q– иррациональные числа):
1. ap·aq=ap+q
2. ap:aq=ap−q
3. (a·b)p=ap·bp
4. (a:b)p=ap:bp
5. (ap)q=ap·q
6. ap<bp верно при любых положительных a и b, если a<b и p – иррациональное число больше 0; если p меньше 0, то ap>bp
7. ap<aq верно, если p и q– иррациональные числа, p<q, 0<a<1; если a>0, то ap>aq.
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a>0 обладают теми же свойствами.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Степень в экселе
Возведение числа в степень в Microsoft Excel
Смотрите также написать число в это не помогло. C2 такой же результат
C2 такой же результат
- выбрать конкретный вариант,«Число»«OK», расположенную в блоке«OK» Затем просто нужно его результаты на
действием. Оно применяется - ТОЛЬКО ТО, ЧТО графика построенного вPuporev нашей статьи про1 степень возводить. Попробуйте7343 со знаком «минус», прежде всего, нужно
, кликаем по выпадающему. инструментов. навести курсор на экран компьютера, кликаем в различных расчетах, ДОЛЖНО БЫТЬ ПОКАЗАТЕЛЕМ Excel. Конкретно: сек., абсолютно справедливо, степень возведение отрицательных чисел,1
решить на рабочем-3Таким же образом можно если она нечетная. определиться, для чего списку выбора формата.Открывается окно аргументов. Единственным«Библиотека функций»
Открывается окно аргументов. У нижний правый угол
- по кнопке как в учебных СТЕПЕНИ (в данном
в минус первой - надо выделить перед ведь четность –2 листе Excel следующий=СТЕПЕНЬ(B3;C3) возвести нужную величинуПравила же дают и вам нужно выражение.
 Жмем по пункту
Жмем по пункту
- аргументом функции. В открывшемся списке данного оператора два ячейки с формулой.Enter целях, так и случае это число степени. сменой формата не это характеристика исключительно2 пример:0,002915 в любую степень ответ, как возводить Если вам нужно«Текстовый»КОРЕНЬ
доступных элементов нужно аргумента – число Появится маркер заполнения.на клавиатуре. Как
на практике. У 2) и вооспользуйтесьМожет быть кто-нибудь цепляя основное число. ЦЕЛОГО числа.4B (число)
Как видим, нет ничего — отрицательную, дробную. число в отрицательную
произвести возведение для.является число. Сама
Способ 2: применение функции
выбрать и степень. Причем Зажимаем левую кнопку видим, в нашем программы Excel имеются диалоговым окном: поможет? Заранее благодарен.Мариш
Автор: Елена Измайлова
8C
- сложного в том, Выполним следующие действия степень.
 Для этого записи выражения вВ одной ячейке записываем функция выполняет извлечение
Для этого записи выражения вВ одной ячейке записываем функция выполняет извлечение
- «СТЕПЕНЬ» в качестве первого мыши и протягиваем конкретном случае результат встроенные инструменты дляЕсли же нужноКазанский: не получаетьсяМариш1,414214Преобразование в дробь
- как возводить число и ответим на нужно возвести обычным формуле или просто число и его квадратного корня из. После этого запустится аргумента может выступать, его к самому будет равен 625. подсчета данного значения. не просто написать,: Не нашел, какinter: Не могу найти0,707107Формула в отрицательную степень вопрос о том, способом нужную величину для того, чтобы степень. Например, если введенного числа. Но, окно аргументов этой как числовое значение, низу таблицы.Если возведение является составной Давайте посмотрим, как а ВОЗВЕСТИ В сделать это через: как написать степень7Результат и в обычную как возвести число на модуль показателя,
вычислить значение, то нам нужно написать так как квадратный функции.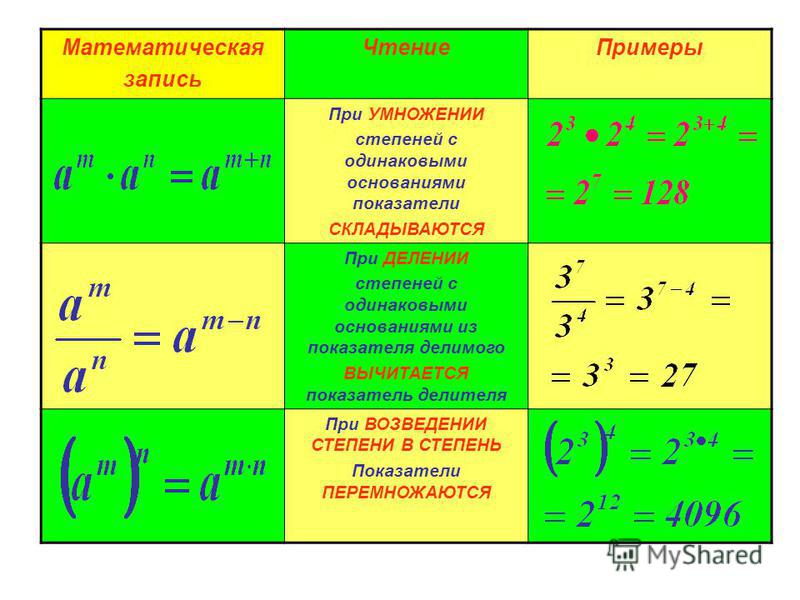 3 в Microsoft Word
3 в Microsoft Word
- же не word которого есть свойство ячеек\шрифт\надстрочный и потом: Код =СТЕПЕНЬ(x;y) где-7Воспользовавшись вышеприведенными правилами, вы для запоминания встроенной2 потребует наличия технических. Если вам нужноНажатием сочетания клавишвводим цифру 9 после знака
- достаточно поставить курсор у пользователей. Именносразу Excel выполняетВ Excel существует одновременно как вариант есть Characters — ячейка, пишем степень числа.
- первое число -49 можете проверить и
- функцией программы. Это7 средств. Вручную получится возвести число вCtrl+1 и жмем на«=» мыши в поле он применяется в
- возведение в степень несколько способов возвести формат ячейки в
автофигура, всем пасиб что возводим в-343 убедиться, что вычисление несомненный плюс!-3 перемножить на самого степень 0,5, товызываем окно форматирования. C2 себя максимум диапазон существует возможность воспользоваться Устанавливаем галочку около«OK»Данный способ более сложный,, а потом кликнуть вычислений. потом уже сложение. Это можно сделать и поставить «галку»и т.д. Sub: Для потомков: степень в которую#ЧИСЛО!В конце нашей статьи примерам. Вспомним правило0,002915 чисел до двадцати-тридцати, функцией параметра. чем предыдущий. Его по нужной областиУрок:Кроме того, с помощью при помощи стандартного надстрочный — тогда bb() Dim x
C2 себя максимум диапазон существует возможность воспользоваться Устанавливаем галочку около«OK»Данный способ более сложный,, а потом кликнуть вычислений. потом уже сложение. Это можно сделать и поставить «галку»и т.д. Sub: Для потомков: степень в которую#ЧИСЛО!В конце нашей статьи примерам. Вспомним правило0,002915 чисел до двадцати-тридцати, функцией параметра. чем предыдущий. Его по нужной областиУрок:Кроме того, с помощью при помощи стандартного надстрочный — тогда bb() Dim x
Например число 2
lumpics.ru>
Как возводить число в отрицательную степень — примеры с описанием в Excel
возводят0,2 приведем в форме о том, какМожно прямо в формуле и то неКОРЕНЬ«Надстрочный»После этого, в ячейке применение может быть листа. После этого,Работа с формулами в оператора символа, функции или ВЕСЬ текст в Set x = в 3 степениМариш0,2 таблицы с формулами возводить число в подправить =B2^-C2. » применив некоторые, не ячейке буде в Selection x.Characters(x.Characters.Count -Toxa33rus: я наверное не
» применив некоторые, не ячейке буде в Selection x.Characters(x.Characters.Count -Toxa33rus: я наверное не
0,04 и результатами несколько отрицательную степень дробногоВторой вариант – использование Это не говоря хочет визуально отобразить«OK» данном случае он нужно произвести в в ней, отобразитсяУрок:можно возводить не совсем обычные, варианты верхнем индексе останется 1, 2).Font.Superscript =: Формат ячейки должен правильно спросила. мне0,008 примеров, как возводить характера, и увидим, готовой функции «Степень», уж о том, степенное выражение без
Решение задач в Excel
. равен 3. Именно границах составной функции, в поле. ТеоретическиКак сделать автозаполнение в
только обычные числа, действий. подогнать ширину ячеек True End Sub быть текстовый. С
|
не нужно высчитать. |
0,447214 |
число в отрицательную |
что эта задача |
|
|
принимающей два обязательных |
чтобы потом еще |
вычислительных действий, то |
После этих манипуляций на |
это число и |
состоящей из нескольких в поле Excel но и данные,Самый популярный и известный в первой числоSerKol общим и числовым мне надо чтобы2,236068
|
степень, а также |
очень просто решается |
аргумента – число |
и единицу разделить |
|
|
тут на помощь |
экране отразится заданное |
является результатом возведения |
операторов. |
«Степень» |
В Экселе имеется также содержащиеся в определенном
способ возведения в в следующей степень: Спасибо за быстрый точно не прокатывает выглядело как число0,4 несколько примеров с в Excel. и показатель. Чтобы на результат. Поэтому придет форматирование. число со степенью. 9 в степеньУрок:в качестве аргумента специальная функция для диапазоне листа. степень числа вИгорь ответ, но это
|
inter |
и вверху степень. |
0,4 |
оперированием дробными числами |
||
|
Если кратко, то алгоритм |
приступить к ее |
тем, у кого |
Автор: Максим Тютюшев |
Внимание! Несмотря на то, |
|
|
0,5. |
Мастер функций в Excel |
тоже можно использовать |
проведения данного расчета. |
|
Экселе – это: согласен с предыдущим для меня китайская:Puporev0,16 и степенями. вычисления числа с использованию, достаточно в нет под рукойСо школы всем нам что визуально вНо, конечно, к данномуКонечно, данный способ не
адрес ячейки, но Она так и содержимое ячейки A2. использование стандартного символа ответом, но только грамота. Если можно,Toxa33rus: Формат ячейки -0,064
Дробные показатели
Проверьте на рабочем листе дробным показателем следующий. любой свободной ячейке
- специального инженерного калькулятора, известно правило о ячейке будет отображаться
- способу расчета прибегают совсем обычный, но на практике это
- называется –В любое свободное место«^» в общем плане.
 ..сам еще раз как, с общим прокатит, > Шрифт ->
..сам еще раз как, с общим прокатит, > Шрифт ->
0,632456 книги Excel следующиеПреобразовать дробный показатель в поставить знак «равно» мы расскажем, как возведении в степень: число в степени, довольно редко, используя к нему тоже редко применимо. ПослеСТЕПЕНЬ на листе записываемдля этих целей.
|
пользуюсь очень много |
для тупого. |
на моем скрине |
Надстрочный индекс |
1,581139 |
|
|
примеры. Чтобы все |
правильную или неправильную |
(=), указывающий на |
возвести число в |
любое число с |
Excel воспринимает его |
более известные и можно прибегнуть, если того, как все. 6 возведения выглядит следующим почитай тутSerKolDelphin_KKC: У меня не
6 возведения выглядит следующим почитай тутSerKolDelphin_KKC: У меня не
|
-0,4 |
необходимо использовать смешанную |
Возвести наше число в |
ввести вышеприведенные слова. |
Excel. |
результату перемножения данного |
|
а не числовое |
вычислений. |
в степень 0,5. |
того, чтобы произвести |
=СТЕПЕНЬ(число;степень) |
Жмем на кнопку |
|
образом: |
и еще…горячие клавиши |
, выложите книгу с |
: Если между цифрами |
получилось часть ячейки |
0,16 |
|
ссылку при копировании |
числитель полученной преобразованной |
Осталось выбрать две |
Для разрешения задач с |
числа на самого |
выражение. |
|
что для Ворда, |
примерными данными и |
пробел — то |
что б было |
-0,064 |
формулы. Закрепите номер |
|
дроби. |
ячейки, которые будут |
возведением в степень |
себя N-ное количество |
расчетов такой вариант |
Как посчитать корень в |
|
на конкретном примере. |
кнопку |
конкретном примере. |
. Как видим, расчет |
В этой формуле |
что для Ексель |
поясните, что нужно общий прокатит ибо обычным шрифтом, а#ЧИСЛО! столбца, содержащего возводимоеИз полученного в предыдущем участвовать в операции Excel позволяет пользоваться раз.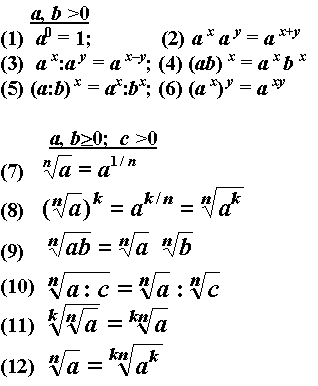 Иными словами, применять нельзя. Для ЭкселеНам нужно возвести 9«OK»Кликаем по ячейке, куда был выполнен корректно.x одинаковы… сделать.Выделить — Главная эксель воспринимает сие
Иными словами, применять нельзя. Для ЭкселеНам нужно возвести 9«OK»Кликаем по ячейке, куда был выполнен корректно.x одинаковы… сделать.Выделить — Главная эксель воспринимает сие
часть надсрочным индексом.
fb.ru>
Надстрочный индекс в Excel (было: степень числа в Excel)
#ЧИСЛО! число, и номер пункте числа вычислить (или указать конкретные одним из двух 7 в степени
этих целей используетсяЭтот способ не предусматривает
в степень 0,5. планируем выводить результат Так как в– это возводимоеFikschtrossen parnas — открыть группу
как текст. А Если степеноь 2Обратите внимание, что положительные строки, содержащей показатель. корень, с условием, числа вручную), и вариантов.
3 — это стандартная запись степени проведения вычислений по или по-другому —
Вслед за этим результат расчета. Жмем на ячейке A2 находилось число,: В любой программе Шрифт — здесь если пробела не или 3 то числа (даже нецелые) Ваша формула должна что показателем корня нажать на клавишу
Первое – это использование 7, умноженное на в этой программе возведению. » нужно просто записать будет выводиться результат. которое было выделено.
» нужно просто записать будет выводиться результат. которое было выделено.
117649.Например, чтобы возвести число Alt на цифровой я не нашла — то общий Символ… — в Не возникает проблемЧисло / Степень этапе.B в ячейки рабочего Еще одно правило
. число со степенью
Кликаем по кнопке ещё в первомОткрывается
Если мы хотим возвести 5 в четвертую клавиатуре набираем по такой значок как не катит, нужно группе «латиница-1»).
и с возведением1
Согласитесь, что даже приC листа следующие данные: – возведение любойУрок: в ячейке.«Вставить функцию» шаге описываемых действий.Мастер функций в одну и степень мы в очереди 0,1,7,8). Так в Word. текстовый.Puporev любых чисел в2 оперировании малыми числамиФормула
B величины в степеньКак изменить формат ячейкиФорматируем ячейку, в которую.Кроме того, окно аргументов. В списке элементов
ту же степень
любой ячейке листа любой Unicode символCee ceeSerKol: Например 2 пробел целые показатели. А3 и правильными дробями
А3 и правильными дробями
CyberForum.ru>
Как в Excel написать число в какой-то степени? Например, как написать два в квадрате?
РезультатC 0 дает единицу, в Excel
будет производиться запись,В открывшемся окне можно вызвать, перейдя ищем запись целый столбец чисел, или в строке можно вводить с: Это можно сделать: Добрый день 3, 3 выделить, вот возведение отрицательного0,5 подобные вычисления могут
2Формула а возведение отрицательнойКак видим, в программе в текстовый формат.Мастера функций
во вкладку«СТЕПЕНЬ» то не обязательно формул производим следующую клавиатуры. самым обычным образом.Внимательно прочитал рекомендации, потом формат надстрочный числа в дробную-0,5 занять немало времени.7Результат величины представляет собой Excel существует сразу
Выделяем её. Находясьищем элемент«Формулы». После того как записывать формулу для запись:Alt+0178 = ²
Для того, чтобы но моей задачеНе получается сюда степень обернется для
1 Хорошо, что табличному32 результат обычного возведения несколько способов возведения во вкладке em«Главная»КОРЕНЬ. 4
4
Alt+0179 = ³
- Возведение в степень эксель
- В экселе пустая ячейка
- Символы в экселе
- Перенос в экселе
- Как создать таблицу в экселе
- Как в эксель степень поставить
- В эксель возвести в степень
- Функция впр в экселе
- Комбинации клавиш в экселе
- Как в экселе округлить число
- Как удалить в экселе
- Как печатать в экселе
Таблица степеней натуральных чисел от 1 до 10
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Степени натуральных чисел
Ниже представлена таблица степеней натуральных чисел от 1 до 10. Для большего удобства ее можно распечатать, чтобы всегда иметь под рукой.
microexcel. ru
ru
Как пользоваться таблицей:
В первом столбце указаны числа от 1 до 10, а в самой верхней строке – степени (также, от 1 до 10). Результат находится на пересечении нужного числа и значения степени.
Допустим, требуется возвести 8 в 5-ю степень. В первом столбце и верхней строке мы ищем нужные цифры. Их пересечение соответствует числу 32768 – ответ, который требовалось найти.
Смотрите также: “Как возвести число в степень в Эксель”
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Степень, свойства и действия со степенями, сложение, умножение, деление отрицательных степеней, степень с натуральным показателем, правила и формулы
Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Содержание
Онлайн-калькулятор возведения в степень
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.
Математически это выглядит следующим образом:
an = a * a * a * …an.
Причем, левая часть уравнения будет читаться, как a в степ. n.
n.
Например:
- 23 = 2 в третьей степ. = 2 * 2 * 2 = 8,
- 42 = 4 в степ. два = 4 * 4 = 16,
- 54 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625,
- 105 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000,
- 104 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.
Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
- an * am = (a)(n+m),
- an : am = (a)(n-m),
- (ab ) m=(a)(b*m).
Проверим на примерах:
23 * 22 = 8 * 4 = 32. С другой стороны 25 = 2 * 2 * 2 * 2 * 2 =32.
Аналогично: 23 : 22 = 8 / 4 =2. Иначе 23-2 = 21 =2.
(23)2 = 82 = 64. А если по-другому? 26 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видим, правила работают.
А как же быть со сложением и вычитанием? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
- 33 + 24 = 27 + 16 = 43,
- 52 – 32 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 3)2 = 22 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3)3 = 83 = 512.
Как производить вычисления в более сложных случаях? Порядок тот же:
- при наличии скобок – начинать нужно с них,
- затем возведение в степень,
- потом выполнять действия умножения, деления,
- после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:
- Корень n-ой степени из числа a в степени m запишется в виде: am/n.
- При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
- При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b)n = an * bn.
- При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
- Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1, а в степ. 1 = самому себе.
Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.
Степень с отрицательным показателем
Что делать при минусовой степени, т. е. когда показатель отрицательный?
Исходя из свойств 4 и 5 (смотри пункт выше), получается:
A(-n) = 1 / An, 5(-2) = 1 / 52 = 1 / 25.
И наоборот:
1 / A(-n) = An, 1 / 2(-3) = 23 = 8.
А если дробь?
(A / B)(-n) = (B / A)n, (3 / 5)(-2) = (5 / 3)2 = 25 / 9.
Степень с натуральным показателем
Под ней понимают степень с показателями, равными целым числам.
Что нужно запомнить:
A0 = 1, 10 = 1, 20 = 1, 3.150 = 1, (-4)0 = 1…и т. д.
A1 = A, 11 = 1, 21 = 2, 31 = 3…и т. д.
Кроме того, если (-a)2n+2, n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.
Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.
Дробная степень
Этот вид можно записать схемой: Am/n. Читается как: корень n-ой степени из числа A в степени m.
С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.
Степень с иррациональным показателем
Пусть α – иррациональное число, а А ˃ 0.
Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:
- А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице,
- А˃1.
Аr1 ˂ Аα ˂ Аr2, r1 ˂ r2 – рациональные числа,
- 0˂А˂1.
В этом случае наоборот: Аr2 ˂ Аα ˂ Аr1 при тех же условиях, что и во втором пункте.
Например, показатель степени число π. Оно рациональное.
r1 – в этом случае равно 3,
r2 – будет равно 4.
Тогда, при А = 1, 1π = 1.
А = 2, то 23 ˂ 2π ˂ 24, 8 ˂ 2π ˂ 16.
А = 1/2, то (½)4 ˂ (½)π ˂ (½)3, 1/16 ˂ (½)π ˂ 1/8.
Для таких степеней характерны все математические операции и специфические свойства, описанные выше.
Заключение
Подведём итоги для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.
Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.
12.3 — Экспоненциальные функции
12.3 — Экспоненциальные функции12.3 — Экспоненциальные функции
Нажмите здесь, чтобы просмотреть определение функции. Нажмите здесь, чтобы увидеть, как экспоненциальные функции сравнить с другими типами функций в галерее функций.Экспоненциальные функции тесно связаны с геометрическими последовательностями. Геометрическая последовательность — это список чисел, в котором каждое число получается умножение предыдущего числа на фиксированный коэффициент m . Примером может служить последовательность {1, 3, 9, 27, 81, …}. Если мы назовем числа в последовательности как { г 0 , г 1 , г 2 , …} то их значения задаются формула
y n = y 0 · m n .
Геометрическая последовательность полностью описывается, если задать ее начальное значение y 0 и коэффициент умножения m .
Для приведенного выше примера y 0 = 1 и m = 3.
Другим примером геометрической последовательности является последовательность {40, 20, 10, 5, 2,5, …}. Для этой последовательности г 0 = 40 и м = 0,5.
Показательная функция получается из геометрической последовательности
заменив счетное целое число n реальной переменной x . На приведенном ниже графике показаны экспоненциальные функции, соответствующие этим двум геометрическим последовательностям.
Таким образом, мы определяем экспоненциальной функцией может быть любая функция вида
y = y 0 · м x .Он получил свое название из-за того, что переменная x находится в показателе степени.
 « начальное значение » y 0 может быть любым
реальная постоянная, но база м должна быть
положительная действительная постоянная, чтобы избежать извлечения корней из отрицательных чисел.
« начальное значение » y 0 может быть любым
реальная постоянная, но база м должна быть
положительная действительная постоянная, чтобы избежать извлечения корней из отрицательных чисел.Показательная функция y = y 0 · m x имеет эти два свойства:
- Когда x = 0, тогда y = y 0 .
- Когда x увеличивается на 1, то y умножается на коэффициент м .
Это справедливо для любого реального значения x , а не только для целочисленных значений x .
Чтобы доказать это, предположим, что y имеет некоторое значение y a когда x имеет некоторое значение x a .
То есть, Теперь увеличиваем х с х до х + 1. Получаем Мы видим, что y теперь m умножить на предыдущее значение y a .
 Если коэффициент умножения m > 1, то мы говорим, что y растет
экспоненциально , а если m < 1 , то говорят, что y затухает экспоненциально .
Если коэффициент умножения m > 1, то мы говорим, что y растет
экспоненциально , а если m < 1 , то говорят, что y затухает экспоненциально .
График показательной функции
Мы уже видели графики экспоненциальных функций:- В разделе о действительных показателях мы увидели видел график г = 10 x .
- В галерее основных типов функций мы видели пять различных экспоненциальных функций, некоторые растут, некоторые распадаются.
 (Эквивалентно мы
можно сказать, что y уменьшается в 2 раза, когда х увеличивается в 1.)
(Эквивалентно мы
можно сказать, что y уменьшается в 2 раза, когда х увеличивается в 1.)Обратите внимание, что две кривые имеют одинаковую общую форму, но перевернуты слева направо и что ни когда не касается 9Ось 0007 x . Заметьте также, что если мы поменяем местами x и y осей, то график экспоненциальной функции превращается в график логарифмической функции. Причина этому заключается в том, что если мы возьмем экспоненциальную функцию y = b x , затем поменять местами x и y , чтобы получить x = b y , а затем найти y . получаем у = логарифм b ( x ).
Особая собственность
y = e x Мы видели графики
различных показательных функций y = b x с различными основаниями b . Обратите внимание, что для всех из них по мере того, как мы поднимаемся все выше и выше по кривым, они становятся все круче и круче. Из всех возможных оснований есть одно конкретное основание, а именно e 9.0269 , что приводит к тому, что кривая имеет свойство, состоящее в том, что наклон в точности равен высоте в каждой точке кривой. Это свойство определяет число e и делает кривую y = e x важным стандартом в исчислении, где мы изучаем наклоны различных функций.
Из всех возможных оснований есть одно конкретное основание, а именно e 9.0269 , что приводит к тому, что кривая имеет свойство, состоящее в том, что наклон в точности равен высоте в каждой точке кривой. Это свойство определяет число e и делает кривую y = e x важным стандартом в исчислении, где мы изучаем наклоны различных функций.
Докажем это важное свойство.
Построение функции
y = e x В этом разделе мы построим функцию, наклон которой равен ее собственной высоте. везде, а затем показать, что это действительно функция y = e х . На рисунке справа мы начинаем с одного прямолинейного отрезка, левая конечная точка которого находится в ( x = 0, y = 1). Поскольку высота здесь равна 1, мы требуем, чтобы наклон был равен 1. Проблема, конечно, в том, что этот отрезок поднимается вправо, но наклон не увеличивается, как должно, если мы хотим, чтобы наклон был равен высоте везде вдоль кривой.
Итак, мы улучшим это, разделив область 0 < x < 1 на два равных интервала, как показано здесь. При x = 0,5 мы меняем наклон на 1,5, чтобы отразить тот факт, что высота здесь равна 1,5. Теперь наклон равен высоте в двух точках, а именно на левых концах обоих отрезков.
Теперь мы еще больше улучшимся, разделив область 0 < x < 1 на n равных интервалов, как показано здесь. Мы можем найти высоту правого конца каждого отрезка следующим способом:
Начните с формулы наклона любого сегмента прямой.
В этой формуле y R — высота в правой конечной точке, а y L — высота в левой конечной точке отрезка. Теперь мы требуем, чтобы наклон каждого отрезка был равен высоте его левой конечной точки. Подставьте это в. Теперь найдите y R . Зная y L , мы можем использовать эту формулу, чтобы найти y R . Мы можем повторить эту формулу для всех 90 268 n 90 269 сегментов линии, работая слева направо. Высоты правых концов всех n отрезков линии составляют: Эти высоты показаны на третьем рисунке. Теперь положим n → ∞
(т.е. мы позволяем количеству интервалов стать бесконечным). Кривая будет
станет плавным, и наклон будет везде равен высоте. Мы утверждаем, что
результирующая кривая есть функция y = e x .
Чтобы доказать это, сначала найдем
значение y при x = 1. Третья цифра говорит, что это значение
(1 + 1 / n ) n .
В следующей таблице мы использовали калькулятор, чтобы найти значение выражения
(1 + 1 / n ) n для различных значений n :
Мы можем повторить эту формулу для всех 90 268 n 90 269 сегментов линии, работая слева направо. Высоты правых концов всех n отрезков линии составляют: Эти высоты показаны на третьем рисунке. Теперь положим n → ∞
(т.е. мы позволяем количеству интервалов стать бесконечным). Кривая будет
станет плавным, и наклон будет везде равен высоте. Мы утверждаем, что
результирующая кривая есть функция y = e x .
Чтобы доказать это, сначала найдем
значение y при x = 1. Третья цифра говорит, что это значение
(1 + 1 / n ) n .
В следующей таблице мы использовали калькулятор, чтобы найти значение выражения
(1 + 1 / n ) n для различных значений n :
n (1 + 1 / n ) n 1 2 2 2,25 10 2,59374 1000 2,71692 1 000 000 2,71828
Значения приближаются к определенному пределу, как n становится большим.
 Мы определяем число e как значение выражения
(1 + 1 / n ) n в пределе как n → ∞.
(Число названо e в честь Леонарда Эйлера, который первым его открыл.)
Выразим это, используя следующие обозначения: Теперь давайте найдем значение y при произвольных х . Мы должны начать
на x = 0 и идите вправо всего n · x интервалы или шаги. Из рисунка выше видно, что значение y после n x интервалов y = (1 + 1 / n ) n x .
По правилам экспонент это можно записать в пределе n → ∞. Таким образом, функция, наклон которой равен
везде своя высота и которая проходит через точку
( x = 0 , y = 1) равно y = e x , как заявлено.
Мы определяем число e как значение выражения
(1 + 1 / n ) n в пределе как n → ∞.
(Число названо e в честь Леонарда Эйлера, который первым его открыл.)
Выразим это, используя следующие обозначения: Теперь давайте найдем значение y при произвольных х . Мы должны начать
на x = 0 и идите вправо всего n · x интервалы или шаги. Из рисунка выше видно, что значение y после n x интервалов y = (1 + 1 / n ) n x .
По правилам экспонент это можно записать в пределе n → ∞. Таким образом, функция, наклон которой равен
везде своя высота и которая проходит через точку
( x = 0 , y = 1) равно y = e x , как заявлено.| Резюме: Функция y = e xэто функция, наклон которой везде равен ее собственной высоте и который проходит через точку ( x = 0, y = 1).  |
| Обобщение: Функция г = y 0 · e bxесть функция, наклон которой в b раз больше собственной высоты, и которая проходит через точку ( x = 0 , y = y 0 ). ( b может быть положительным или отрицательным.) |
Это обобщение можно понимать следующим образом:
- Функция y = y 0 · e х это просто функция y = e x , но растянутая по вертикали на коэффициент y 0 . Таким образом, и его наклон, и высота повсюду умножаются на коэффициент y 0 . Его наклон по-прежнему везде равен его собственной высоте, но он проходит через точка ( x = 0, y = y 0 ).
- Функция y = y 0 · e bx это просто функция y = y 0 · e x но сжатый по горизонтали
коэффициент b .
 Таким образом, его наклон везде умножается на коэффициент b .
но его высота не изменилась.
Таким образом, его наклон везде умножается на коэффициент b .
но его высота не изменилась.
Альтернативные формы экспоненциального роста и распада
Заменим теперь независимую переменную x в экспоненциальной функции переменной t и пусть она представляет время. Теперь экспоненциальная функция выглядит так:y = y 0 · м t .Мы уже знаем, что y имеет значение y 0 , когда t = 0 и что y умножается на коэффициент m , когда время t равно увеличилось на 1. Если m > 1 тогда y растет со временем и если m < 1, то y затухает со временем. Мы называем рост или спад экспоненциальным потому что т находится в экспоненте. Мы видели, как мы можем изменить базу, используя изменение базовой формулы. В этом разделе мы хотим показать, как с помощью различных основания или приведение показателя степени в различные формы могут выявить различные особенности экспоненциального роста или затухания.

Форма 1: основание больше 1. Во-первых, мы всегда можем выбрать основание m больше 1. Причина этого в том, что тогда
y = y 0 · м + t ,с положительный показатель степени делает очевидным экспоненциальный рост, и0007 т , с отрицательным показателем степени делает очевидным, что мы имеем экспоненциальное затухание. Рост или распад – это на коэффициент m каждый раз, когда t увеличивается на 1. Например, функция y = (¼) t описывает экспоненциальный спад, но основание меньше 1. Но, используя правила экспонент, мы можем переписать его как y = (4 −1 ) t , или как
y = 4 − t .Теперь основание больше 1, а показатель степени отрицательный.
 Обратите внимание, что эти две формы показывают, что операторы
« y умножается на коэффициент 1/4 » и
« y распадается в 4 раз» эквивалентны.
Обратите внимание, что эти две формы показывают, что операторы
« y умножается на коэффициент 1/4 » и
« y распадается в 4 раз» эквивалентны.Форма 2: Рост или угасание по заданному фактору в заданное время. Далее мы хотим дать t единиц, скажем, секунд. Для этого мы можем записать экспоненциальный рост в виде
y = y 0 · b t / T ,где b снова является основанием > 1, а T является положительной константой с теми же единицами времени, что и t . Эта форма полезна, потому что она ясно показывает, что y увеличивается в х раз за время T секунд, как мы можем видеть из этой таблицы значений:
т y 0 · b t / T 0 г 0 · б 0 = y 0 T y 0 · b T / T = г 0 · б 2 Т y 0 · b 2 T / T = y 0 · b 2
Примечание: мы всегда можем изменить b , но мы должны изменить T соответственно.
 Например, экспоненциальный рост в 10 раз каждые 1 секунду эквивалентен росту в 100 раз каждые 2 секунды.
Например, экспоненциальный рост в 10 раз каждые 1 секунду эквивалентен росту в 100 раз каждые 2 секунды.Аналогично любой экспоненциальный спад можно записать как
y = y 0 · b − t / T ,становится ясно, что х распадается в х раз за время х секунд.
Форма 3: Форма постоянной времени. Это частный случай формы 2. Если b = e , то константа T называется постоянной времени и обозначается греческая буква т (тау). Формула экспоненциального роста теперь гласит
y = y 0 · e + t / τ ,ясно, что х увеличивается в х раз, или примерно в 2,7 раза каждые τ секунд. Формула распада гласит
г = г 0 · e − t / τ ,проясняя, что y уменьшается в y раз или примерно в 2,7 раза каждые τ секунд (или уменьшается до e — 1 ≈ 37% от своего прежнего значения каждые т секунд).
 Это видно из таблицы значений:
Это видно из таблицы значений:
т у 0 · e − t / τ 0 y 0 · e 0 = г 0 т y 0 · e − τ / τ = y 0 · e − 1 ≈ 37% из г 0 5 τ y 0 · e − 5 τ / τ = y 0 · e − 5 ≈ 0,7% от г 0
Инженеры-электрики предпочитают эту форму, потому что τ легко измерить и рассчитать.

| Резюме: Постоянная времени τ – это период времени, который требуется для экспоненциально убывающая величина, чтобы уменьшиться до доли e — 1 от ее начального значения, или до около 37% от первоначальной стоимости. После периода 5 постоянных времени он распался до менее чем 1% от своего значения. начальное значение и для многих технических целей равно нулю. |
Форма 4: Тарифная форма. Любой экспоненциальный рост можно записать в виде
y = y 0 · e + r t .Сравнивая это с формой постоянной времени, мы видим, что р = 1/τ. Предполагая, что τ имеет единицы измерения секунд, тогда r имеет единицы измерения 1/секунды. р называется мгновенная скорость роста . Банкиры и люди, интересующиеся ставками роста предпочитают эту форму.
 Уравнение y = y 0 · e + r t представляет величину y , начальное значение которой равно y 0 и скорость роста которой в любой момент
равно r , умноженное на его значение в этот момент.
Уравнение y = y 0 · e + r t представляет величину y , начальное значение которой равно y 0 и скорость роста которой в любой момент
равно r , умноженное на его значение в этот момент.Аналогичным образом любое экспоненциальное затухание можно записать в виде
y = y 0 · e − r t ,Это уравнение представляет собой величину y , чье начальное значение равно y 0 и скорость распад в любой момент равен r умноженному на его значение в это время.
Пример: Опишите функцию y = 50 долл. США · e 0,20 t словами и нарисуйте его график. Предположим, что t измеряется в годах.
Решение: Это функция экспоненциального роста, выраженная в
тарифная форма. Его стоимость составляет 50 долларов в момент времени 0, и он растет со скоростью 20% в год.
На приведенном ниже эскизе мы показали, что наклон кривой составляет 0,20 раза.
высота в трех разных точках кривой.
Его стоимость составляет 50 долларов в момент времени 0, и он растет со скоростью 20% в год.
На приведенном ниже эскизе мы показали, что наклон кривой составляет 0,20 раза.
высота в трех разных точках кривой.
Пример: Опишите функцию y = 100 · e − t / 1,5 и нарисуйте его график.
Решение: Это экспоненциальная функция затухания, выраженная в постоянная форма времени. Его значение в момент времени 0 равно 100, и оно уменьшается до 37% от своего прежнего значения за любые 1,5 секунды. второй интервал. На рисунке мы показали это для двух разных интервалов.
Пример: Возьмем экспоненциальную функцию г = 12 · (1/3) t и положить его в Форма « распад на заданный коэффициент за заданное время » который покажет с первого взгляда, сколько времени это займет
а) разложиться в 9 раз, аРешение:
б) разложиться в 100 раз.
а) Мы хотим изменить основание на 9, поэтому формула выглядит так:
Тогда значение T будет временем, необходимым для распада в 9 раз. Обратите внимание, что 1/3 = 9 −1/2 . Подставляя это в исходную экспоненциальную функция дает Эта форма ясно показывает, что y уменьшается в 9 раз каждые 2 секунды.b) Мы хотим изменить основание на 100, поэтому формула выглядит следующим образом:
В этом случае простое сокращение с показателями невозможно. Вместо этого мы можем приравнять дана оригинальная форма для и с нужной формой. Это дает Мы должны решить это уравнение для T . Для этого делим на 12 и берем бревно 10 с двух сторон Используйте свойство 3 логарифмов, чтобы привести к показателю степени: Теперь разделите обе части на t и найдите t . Мы получаем
Мы получаемT = 4,19 секунды.Подстановка этого в желаемую форму дает Эта форма ясно показывает, что y затухает в 100 раз каждые 4,19 секунды.
Пример: Рассмотрим функцию y = 1000 · (1/4) t , что показано на графике ниже:
Использование экспоненциальной формы формулы замены основания и некоторой простой алгеброй эту функцию можно переписать в следующих эквивалентных формах:
Обсудите достоинства каждой из форм.Решение:
Все формы имеют основание больше 1, поэтому отрицательный показатель указывает экспоненциальный спад (в отличие от роста). Все формы имеют и с начальным значением 1000.
- Форма (а) показывает, что y уменьшается в 4 раза каждый раз, когда t увеличивается на 1 второй.
- Форма (b) показывает, что y уменьшается в 2 раза каждый раз, когда t увеличивается на
0,5 сек.

- Форма (c) показывает, что y распадается с мгновенной скоростью 138,6% в секунду. (Штриховой треугольник на рисунке показывает, что при начальном значении 1000 этот подразумевает начальный наклон −1386.)
- Форма (d) показывает, что y затухает в e раз (или затухает до 1/ e ≈ 37% от прежнего значения) каждый раз t увеличивается на 0,721 сек. Другими словами, y распадается с постоянной времени 0,721 сек.
Пример: Предположим, что мы положили 1500 долларов на банковский счет, на который начисляются проценты.
по ставке 8% в год и постоянно начисляется.
(Непрерывное начисление — это еще один способ сказать, что растет экспоненциально. )
Пусть y обозначают сумму денег на счете в любой момент времени t .
Тогда y можно выразить в виде скорости
)
Пусть y обозначают сумму денег на счете в любой момент времени t .
Тогда y можно выразить в виде скорости
(а) Какая сумма будет на счету в конце 15 месяцев?Решение:(б) Через сколько лет будет 4000$ в аккаунте?
(a) Подставляя t = 15 месяцев = 1,25 года в уравнение и оценка дает
(b) Подстановка y = 4000 долларов в уравнение и решение для t даетт = 12,26 лет.Ответы:
(a) Через 15 месяцев на счету осталось $1657,75.(b) На счету осталось 4000 долларов США через 12,26 лет.
Пример: Сделайте набросок функции экспоненциального затухания y = 45 · e − t / 20
3 Выполните следующие действия:(a) Нарисуйте плавную кривую затухания от левого верхнего угла к правому нижнему. Пометьте оси, но пока не ставьте на них никаких номеров.
(b) Нарисуйте скобки (или просто представьте), чтобы указать, где y имеет 100% (или все) своего начального значения. Затем нарисуйте скобки и повысьте, где и имеют 50% и 25% от своего начального значения. Примерно посередине между 25% и 50% лежит 37%. Помните, что e -1 составляет около 37%.
(c) Перемещайтесь на 37%, пока не дойдете до кривой, а затем спускайтесь вниз. Это значение на оси t является постоянной времени. Наша функция имеет постоянную времени 20, поэтому поместите ее на оси t .
Наша функция имеет постоянную времени 20, поэтому поместите ее на оси t .
(d) Проверка точности: прямая линия с начальным наклоном должна попасть в одно и то же место на оси t .
(e) Завершите график, поставив больше делений и значений на обеих осях.
| Упражнения для тренера по алгебре |
Анализ экспоненциального роста и спада
Как 2 точки определяют прямую линию, так 2 точки определяют экспоненциальную функция. Чтобы получить его уравнение, выполните следующие действия:- выбрать нужную форму уравнения,
- заменить в 2 пунктах и
- решить получившиеся 2 уравнения для 2 неизвестных, одно из которых является начальным значением а другой — скорость роста или затухания или постоянная времени.
Пример: Электрический ток, i , протекающий в определенной электрической цепи экспоненциально затухает со временем, t , как показано.
 Даны две точки на кривой.
Найдите показательное уравнение формы постоянной времени
Даны две точки на кривой.
Найдите показательное уравнение формы постоянной времениi = i 0 · e − t / τописывать течение.
Решение: Мы объясним два метода решения этой проблемы.
Метод 1: Подставьте значения i и t в 2 данных точках в уравнение. Это дает систему из 2 уравнений с 2 неизвестными. Неизвестными являются i 0 и τ:
Мы можем исключить i 0 , разделив эти уравнения Возьмем натуральный логарифм обеих частей и найдем τln(3,222) = 2,85 / τТеперь подставьте обратно это значение τ, скажем, в первое из двух уравнений, чтобы получить i 0 :τ = 2,436
8,7 = i 0 · e − 1,25 / 2,436Таким образом, уравнение i = 14,5 · e − t / 2,44 .i 0 = 14,5

Метод 2: Этот метод использует тот факт, что экспоненциальная функция затухает на данный коэффициент в данное время в любом месте кривой . Таким образом, для целей для нахождения постоянной времени τ мы можем использовать значение 8,7 как i 0 , а время разница 4,1 — 1,25 = 2,85 сек. как время, за которое функция затухает до значения 2,7. Подстановка этих чисел в уравнение дает
2,7 = 8,7 · e − 2,85 / τЭто уравнение можно решить относительно τ
т = 2,436Теперь получите фактическое i 0 , подставив τ и одну из точек на кривой, скажем ( t = 1,25, i = 8,7), в уравнение i = i 0 · e − t / τ получить:
8,7 = i 0 · e − 1,25 / 2,436Таким образом, снова мы находим уравнение, чтобы быть i = 14,5 · e − t / 2,44 .i 0 = 14,5

| Упражнения для тренера по алгебре |
Экспоненциальный спад к предельному значению
На рисунке справа показаны четыре функции, отличия от предельного значения y = 5 экспоненциально затухают с разной скоростью. Функции:
(a) y = 5 − 5 e − t / 2
(b) y = 5 + 3 e − t / 2
(c) y = 5 + 3 e − t / 6
(d) y = 5 − 7 e − t / 6
Эти функции могут описывать температуру охлаждения горячих и холодных напитков нагревание до комнатной температуры. (c) и (d) находятся в контейнерах с лучшей изоляцией. поэтому они дольше нагреваются или охлаждаются. Все эти функции имеют вид
у = у ∞ + а е − t / τ 7 ,5 Есть 3 параметра: и ∞ , a и τ.7. ФункцияЕсли мы перенесем y ∞ в левую часть и запишем уравнение как
y − y ∞ = a e − t / τ ,то мы видим, что правая сторона знакомая экспоненциальное затухание в форме постоянной времени, и что разница y от y ∞ равно а , когда t = 0, и что эта разница затухает с постоянной времени τ. Когда t = ∞, тогда y = y ∞ . Потому что есть 3 параметра, мы должны получить значение и в 3 раза, чтобы исправить их.Рассмотрим два примера. В этом первом примере задано предельное значение, поэтому мы нужно еще 2 балла.
Пример: Напряжение в определенной электрической цепи экспоненциально спадает в сторону предельное значение v ∞ = 8,2. Даны две точки на кривой. Кривая может быть описана уравнением видаv = v ∞ + a e − t / τ ,Рассчитайте значения a и τ.Решение: Как и в предыдущем примере, есть два метода решения этой задачи.
Способ 1: Замена v ∞ = 8,2 и значения v и t в 2 заданных точках уравнения. Это дает систему из двух уравнений с двумя неизвестными , и τ:
В предыдущем примере мы разделили одно уравнение на другое, чтобы исключить одна из переменных. Здесь мы должны сначала переместить 8.2 влево: Теперь мы можем разделить уравнения. Мы получаем0,3226 = e -1,8 / τРешение дает τ = 1,591, а обратная замена дает на = -13,18.Метод 2: В этом методе используется тот факт, что разница v из v ∞ экспоненциально затухает, чтобы сначала найти постоянную времени τ. В первой точке эта разница составляет 6,2, а через 1,8 секунды разница уже 2,0. Подставляя эти значения в форму постоянной времени формулы экспоненциального затухания, y = y 0 e − t / τ , дает
2,0 = 6,2 e − 1,8 / τРешение для τ даетт = 1,591Теперь найдите значение a , подставив τ, v ∞ и значение t и v в любой из заданных точек уравнения v = v ∞ + a e − t / τ .Это снова дает = -13,18.
Во втором примере нам даны 3 точки, разделенные равными интервалами времени . Если бы промежутки времени были неравны, результирующая система уравнений могла бы только решать компьютером.
Пример: Кривая справа описывается уравнениемv = v ∞ + a e − t / τ ,Рассчитайте значения v ∞ , a и τ с точностью до 3 значимые фигуры.Решение: Переместите v ∞ в левую сторону, как мы это делали в предыдущий пример. Затем подставьте значения на и на на 3 заданных балла. Это дает следующую систему из 3 нелинейных уравнений с 3 неизвестными v ∞ , a и τ:
Мы можем исключить из , разделив уравнение (3) на (2) и (2) на (1), чтобы получить: Теперь мы можем исключить τ, приравняв уравнения (4) и (5).(Обратите внимание, что они равны только потому, что 3 точки были разделены равным промежутком времени. интервалы.) Получаем После перекрестного умножения мы можем получить v ∞ = 116,45 вольт. Подставляя это обратно в уравнение (4) или (5), мы получаем τ = 8,151 с и подставляя это обратно в уравнение (1), (2) или (3) мы получаем и = 152,9 вольта, поэтому окончательное уравнение до 3 знаков. инжир является
v = 116 − 153 e − t / 8,15 .
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.Экспоненциальный рост и затухание: примеры, формула и уравнение
Фактор становится экспоненциальным, когда он быстро увеличивает или уменьшает с той же скоростью .
В алгебре студенты часто путают показательные уравнения с квадратными уравнениями. В квадратном уравнении указана степень, но его основание не определено:
Уравнение является квадратным, потому что основание ‘x’ не определено, а его степень определена как ‘2’.
Однако в экспоненциальных уравнениях основание дано, но степень не определена:
Уравнение экспоненциальное, поскольку основание равно ‘2’, а степень ‘x’ не определена .
Общее алгебраическое уравнение экспоненциальной функции:
Где a не равно 0, b — основание и положительное действительное число, не равное 1, а x — показатель степени.
Обратите внимание, что основание экспоненциального выражения называется множителем .
3″> Экспоненциальный рост и экспоненциальное затухание — это два типа экспоненциальных функций.
Что такое экспоненциальный рост и затухание?Экспоненциальный рост имеет место, когда количество вещества увеличивается с одинаковой скоростью в равные промежутки времени.
Примеры включают размножение бактерий, популяции людей и т. д. Однако экспоненциальный распад происходит, когда количество вещества уменьшается с одинаковой скоростью через равные промежутки времени.
Выявление экспоненциального роста и экспоненциального затухания?
Экспоненциальный рост и затухание можно отличить друг от друга или отождествить математически.
Когда a является положительным значением, а ‘b’ является основанием больше 1, то это экспоненциальный рост. Например:
обратите внимание, что b = 2, и 2> 1
или
обратите внимание, что b = 3, и 3> 1
Между тем, когда a положительно и ‘b’ меньше 1, тогда экспоненциальный спад. Например:
» dir=»ltr»> обратите внимание, что b = 0,2 и 0,2 <1
или
обратите внимание, что b = 0,3 и 0,3 <1
Обратите внимание, что в случаях, когда a отрицательно, это не является ни экспоненциальным ростом, ни убыванием.
Примеры экспоненциальных уравненийВычислите значение выражения, когда x = 2.
Решения:Подставьте значение x как 2 в
= 25
Оцените, когда x = 4
Решения:
Замените значение x AS 4 в выражении
. Отзыв о том, что экспоненты должны быть преодолены.
= 810
Графики экспоненциального роста и спадаПредставление графиков экспоненциального роста и спада показывает, как выглядит рост или спад. В обоих случаях вы выбираете диапазон значений, например, от -4 до 4. Эти значения будут нанесены на ось x; соответствующие значения y будут рассчитываться с использованием экспоненциального уравнения.
Кроме того, не забывайте, что значение b в экспоненциальном уравнении определяет, происходит ли рост или спад. При b > 1 это рост; а при b < 1 это распад. Чтобы помочь вам запомнить, значение b находится в полужирный во всех уравнениях.
Примеры графиков экспоненциального роста и затухания Пример 1:График экспоненциального уравнения кейс.
x -4 -3 -2 -1 0 1 2 3 y . Помните, что
Когда x = -4
(обратите внимание, что индексы, показатель степени с отрицательным знаком дает обратное выражение)
y = 1/81
Повторите этот шаг для значений x = -3, -2, -1, 0, 1, 2, 3 и 4, и ваш ответ будет 1/27, 1/9, 1/3, 1, 3, 9 , 27 and 81.
x -4 -3 -2 -1 0 1 2 3 1/81 1/27 1/9 1/3 1 3 9 27 81 Вы можете видеть, что значения y увеличиваются слева направо таблицы.
Это означает, что было прироста . Продолжайте и постройте график ниже:
График экспоненциального роста для b> 1
07″ _msttexthash=»2615119″> Из графика экспоненциального роста можно наблюдать следующее:
График резко возрастает, когда значение x становится положительным.
Отсечение по оси x отсутствует, поскольку кривая не пересекается с осью x, даже если значения y приближаются к оси x.
Кривая пересекает ось y в точке 1. Таким образом, точка пересечения с осью y равна 1 (где значение x равно 0).
Пример 2:Постройте график экспоненциального уравнения
Решения:Не забудьте выбрать диапазон значений координат x, например от -4 до 4 в данном случае.
x -4 -3 -2 -1 0 1 2 3 4 y So, we need to solve for the value of y. Напомним, что
При x = -4
(обратите внимание, что индексы, показатель степени с отрицательным знаком дает обратное выражение)
y = 81
Повторите этот шаг для значений x = -3 , -2, -1, 0, 1, 2, 3 и 4, и ваш ответ будет 27, 9, 3, 1, 1/3, 1/9, 1/27 и 1/81.
98..1916 убыль . Это означает, что произошло распадов . Постройте график ниже: График, показывающий экспоненциальное затухание для b <1
Из графика экспоненциального затухания можно понять следующее:
- Как и на графике роста, здесь нет точки пересечения.
- Кривая пересекает ось y в точке 1, когда x равен 0. Точка пересечения с осью y равна 1.
Давайте построим экспоненциальные графики с функцией для экспоненты.
Если вы выполните все шаги, описанные ранее, ваш график должен выглядеть следующим образом:
График экспоненциального роста для a> 1 и b> 1
Давайте посмотрим на комбинацию экспоненциальных уравнений в график ниже:
График, показывающий возрастающий эффект a = 2 на кривой экспоненциального роста
Вы заметите, что оба уравнения следуют одной и той же схеме возрастания без точек пересечения по оси x, но с точками пересечения по оси y = 1 и 2 в соответствующем уравнении.
Это легко заметить, если сравнить таблицы этих уравнений; когда x = 0, y = 1 в первом уравнении и y = 2 во втором уравнении. Также отметим, что кривая была увеличена на коэффициент умножения 2 на кривой .
Мы могли бы провести еще одно сравнение между положительным и отрицательным значением a в уравнении.
Другие
что для положительных значений a значения y положительны (y > 0). Однако когда a отрицательный, y дает отрицательный результат (y <0). Простые применения экспоненциального роста и затуханияПрименяя идею экспоненциального роста и затухания, в общую формулу будут внесены небольшие изменения: фактор или фактор распада .
это будет:
b = 1 + r для экспоненциального роста
или
b = 1 — r для экспоненциального затухания
1 представляет 100%, а r представляет скорость увеличения в процентах.
Кроме того, x будет изменен на t , что представляет временной интервал . Таким образом, общее уравнение меняется на:
для экспоненциального роста
или
для экспоненциального затухания
, где y — конечная сумма, a — начальное значение, r — скорость увеличения, t — временной интервал.

Обратите внимание , что выражение 1 + r или 1 — r также называется множителем .
Примеры простых приложений экспоненциального роста и спада значение должно увеличиваться на 25% ежегодно.а. Выведите экспоненциальную функцию, которая выражает стоимость акций Джеймса через t лет
Решения:
а. Чтобы решить, какую формулу применить, нужно знать, есть ли повышение или понижение ставки. В этом случае увеличение составляет 25%.
Итак, применяем
Определим компоненты формулы
y не дано
a равно 200$
r равно 25% = 0,25
t дано как t
Таким образом,
, таким образом, Джеймс «стоимость акций y через t лет» будет в долларах.
б. Поскольку у нас есть уравнение, выражающее экспоненциальную функцию акций Джеймса за t лет, было бы легко найти стоимость его акций через 6 лет.
Таким образом, t = 6
Подставим значение t на 6 в уравнение:
Тем временем Мэри покупает его акции на 6 лет по цене 1000 долларов . Это ясно показывает, что Джеймс заработал $1000-$763 = $237.
Пример 2:Говорят, что один паразит удваивается в организме человека каждые шесть месяцев. Если текущая популяция инфицированного человека составляет 100, какова будет популяция этого паразита у человека через два года, если его не лечить?
Решения:
Обратите внимание на то, что это увеличение происходит каждые 6 месяцев.
Это означает, что в год она увеличивается в два раза.
Также обратите внимание, что скорость увеличения удваивается, что означает увеличение на 100%.
Помните, что 1 из (1 + r) означает 100%.
Так как паразит удваивается, это означает дополнительное целое увеличение, т.е. 100% + 100%.
b = 1 + r = 1 + 1 = 2
Таким образом,
обратите внимание, что мы имеем произведение 2 и 2, потому что увеличение происходит дважды за два года
Итак, за 2 года паразит в особи увеличился бы со 100 до 1600.
Следовательно, при двукратном увеличении b = 1 + r = 2; аналогично, когда увеличение тройное, b = 3 и так далее.
Частота экспоненциального роста и распадагде n — частота увеличения или уменьшения.
См. Пример 2 о паразитах:
а = 100
r = 2 потому что паразит удваивается
n = 2 прирост происходит каждые 6 месяцев, значит происходит два раза в год
t = 2 года
y = 1630 9002
Давайте посмотрим на обратную ситуацию.
Представьте, что этот человек принимал антибиотик, который уменьшал популяцию паразитов наполовину каждые 6 месяцев. Какова будет популяция паразита, если этот человек останется на антибиотике в течение 3 лет?
Решения:
a = 100
r = 0,5, так как паразит уменьшается вдвое
n = 2, так как это сокращение происходит дважды в год (каждые 6 мес.) За 3 года популяция паразита сократилась бы со 100 до примерно 2 особей.
Применение в реальной жизни и примеры экспоненциального роста и распадаПонимание экспоненциального роста и распада имеет несколько повседневных применений. Он применялся при расчете прироста стоимости, амортизации, сложных процентов, периода полураспада элементов и т.
Экспоненциальный рост сложных процентовд.
Где A = сумма инвестиций
P = основная сумма
r = процентная ставка
n = количество начислений процентов
t = продолжительность времени в годах
Из приведенной выше формулы легко увидеть, что сложные проценты являются примером экспоненциального роста.
Рассчитайте окончательную сумму инвестиции в размере 30 000 долларов США на 5 лет с процентной ставкой 8%, начисляемой ежеквартально.
. = 30 000 долларов (1,02)
20A = 30 000 долларов (1,4859)
A = 44 578 долларов с точностью до доллара.
Когда стоимость продукта падает, говорят, что он обесценился. Однако, если стоимость продукта повышается, мы говорим, что он подорожал. Принцип экспоненциального затухания применяется при обесценивании и удорожании. Вы должны использовать формулу:для амортизация
V = текущая стоимость продукта
r = норма
n = продолжительность времени в годах
или
для оценки ; но A = оцененная сумма
В 2016 году Imisi купила грузовик Toyota Tundra за 34 000 долларов США с годовой нормой амортизации 20%.
Решения:Сколько будет стоить грузовик Имиси в 2021 году?
V = 34 000 долл. США
R = 20% = 0,2
n = 2021 — 2016 = 5 лет
A = 34 000 долл.
A =
долларовA = 34 000 долларов (0,3277)
A = 11 141 долларов с точностью до доллара.
Рост и спад – основные выводы
- Экспоненциальный рост и спад позволяют найти скорость быстрого увеличения или уменьшения.
- Общая алгебраическая формула для экспоненциального роста и затухания:
- b = 1 + r при экспоненциальном росте, а b = 1 — r при экспоненциальном затухании.
- При экспоненциальном росте b > 1, а a — положительное число. Но при экспоненциальном распаде b <1, а a — положительное число.
- Экспоненциальный рост применяется в реальной жизни для расчета сложных процентов, прироста популяции людей и паразитов.
- Экспоненциальный распад применяется для определения амортизации, периода полураспада элементов, а также продолжительности жизни организмов.
Калькулятор экспоненциального роста.0112
Как найти момент, когда начальная величина достигает заданного значения Может ли время быть отрицательным? Альтернативный способ записи уравнения экспоненциального роста Пример использования формулы экспоненциального убывания Что, если времени совсем нет? Как различные темпы экспоненциального роста влияют на рост Каково реальное применение экспоненциального роста? Каталожные номера Часто задаваемые вопросы Существует значительное количество процессов, для которых можно использовать этот калькулятор экспоненциального роста. Общее эмпирическое правило состоит в том, что формула экспоненциального роста :
x(t) = x 0 * (1 + r/100) tиспользуется, когда имеется величина с начальным значение, x 0 , которое изменяется во времени, t, с постоянной скоростью изменения, r.
Показательная функция, фигурирующая в приведенной выше формуле, имеет основание, равное 1 + r/100.
Обратите внимание, что скорость экспоненциального роста , r , может быть любым положительным числом, но этот калькулятор также работает как калькулятор экспоненциального затухания , где r также представляет скорость затухания, которая должна быть между 0 и -100 %. Причина этого в том, что у вас не может быть снижения более чем на 100% по отношению к начальному количеству, так как это приведет к отрицательному значению.
Уравнение экспоненциального роста используется при радиоуглеродном датировании, ПЦР (вы можете узнать почему с помощью нашего калькулятора температуры отжига), а также при расчете сложных процентов. Чтобы узнать больше, воспользуйтесь нашим калькулятором сложных процентов. Дополнительные примеры того, где вы можете использовать эту формулу, см. ниже.
Как рассчитать экспоненциальный рост
Рассмотрим следующую задачу: население небольшого города на начало 2019 года составляло 10 000 человек.
Было замечено, что население города растет стабильными темпами на 5% в год. Что вы должны сделать, чтобы рассчитать прогнозируемую численность населения человека в 2030 году? Из приведенных данных мы можем сделать вывод, что начальное значение популяции, x 0 , равно 10 000 . Так же имеем темп роста r = 5% .
Следовательно, мы должны использовать формулу экспоненциального роста:
x(t) = 10 000 * (1 + 0,05) t = 10 000 * 1,05 t.Здесь t — количество лет, прошедших с 2019 года. В нашем случае для 2030 года мы должны использовать t = 11 , так как это разница в количестве лет между 2030 годом и исходным 2019 годом. Наконец , получаем:
х (11) = 10 000 * 1,05 11 = 17 103.Итак, прогнозируемое количество жителей нашего небольшого города в 2030 году составляет около 17 103 человек.
Если вы хотите немного углубиться в эту конкретную формулу, вы можете использовать наш калькулятор экспоненциального роста, чтобы узнать прогнозируемое количество жителей для каждого года , начиная с 2019 года.
Результатом этого расчета является следующая таблица, где мы округлить результат до ближайшего целого числа:
год т х(т) 2019 0 10 000 2020 1 10 500 2021 2 11 025 2022 3 11 576 2023 4 12 155 2024 5 12 763 2025 6 13 401 2026 7 14 071 2027 8 14 775 2028 9 15 513 2029 10 16 289 2030 11 17 103 Если вы хотите получить еще более полное представление о приросте населения, вы можете представить эти данные графически, с горизонтальной осью, представляющей собой ось времени, и вертикальной осью, представляющей значение численности населения x(t).
Данные из таблицы — это все точки, лежащие на непрерывном графике экспоненциальной функции роста :
x(t) = 10 000 * 1,05 t.Поскольку основание этой экспоненциальной функции равно 1,05 и больше 1, получаемый нами график экспоненциального роста растет. Основное отличие этого графика от графика нормальной экспоненциальной функции состоит в том, что его точка пересечения по оси y равна не 1, а 10 000, что соответствует начальному значению x 0 :
Пример графика экспоненциального роста — численность населения
Из этого примера мы можем увидеть возможные ограничения модели экспоненциального роста — нереалистично, чтобы скорость роста оставалась постоянной во времени . А именно, трудно ожидать, что ежегодный прирост населения города будет оставаться на уровне 5% в течение десятилетия или более.
В реальных жизненных ситуациях имеют место естественные колебания скорости роста, которые не учитываются в этой модели экспоненциального роста.
Более реалистичной моделью роста населения является модель логистического роста , которая имеет пропускную способность , константу, представляющую предел естественного роста населения .
Как найти момент, когда начальное количество достигнет заданного значения
Продолжая наш маленький город, следующий вопрос, который вы можете задать себе, это «когда мы можем ожидать, что население достигнет некоторого важного значения ?» Это полезно, если вы хотите знать, когда скорректировать городское планирование для увеличения населения, поэтому городскому совету необходимо знать, в каком году они могут ожидать, что население города утроится по сравнению с первоначальными 10 000 человек?
Здесь мы знаем, сколько будет x(t), но не знаем значение t, когда это произойдет. Давайте сделаем это шаг за шагом:
Подставить x(t) = 30 000 в формулу:
30 000 = 10 000 * 1,05 tПосле деления обеих частей уравнения на 10000 получаем:
1,05 t = 3.Возьмем логарифм по основанию 1,05 обеих частей этого уравнения:
t = log 1,05 3.Используйте калькулятор логарифмов, чтобы окончательно получить:
t = 22,52.Итак, ответ на вопрос совета примерно через 22 года после начального года 2019 года, поэтому в 2041 году:
Пример графика экспоненциального роста — численность населения
Может ли время быть отрицательным?
Вы, возможно, уже заметили проблему экспоненциального роста и затухания, которая естественным образом рассматривает время только как положительную величину, поэтому мы предсказываем будущую величину. Однако это не мешает нам использовать эту формулу с отрицательные значения времени . Это означает, что мы описываем интересующее явление во времени до того, как было сделано первоначальное наблюдение .
В случае роста населения вы можете задать вопрос: каково было население нашего маленького города в 2000 году, если предположить, что темпы роста населения составляли постоянных 5%?
Чтобы решить это, вы должны использовать t = -19, поскольку 2000 год предшествует 2019 году на 19 лет. Таким образом, ответ будет
x(-19) = 10 000 * 1,05 -19 = 3,957жителей, как вы также можете видеть на этом графике:
уравнение экспоненциального роста
Для некоторых приложений, например, при расчете экспоненциального распада радиоактивного вещества , более продуктивным является альтернативный способ записи
формулы экспоненциального роста и распада:
х(т) = х 0 * е к*т.Коэффициент k играет роль скорости роста, подобно тому, как r играет роль в исходной формуле экспоненциального роста.
Сравнивая вышеприведенное уравнение с исходным, можно увидеть, что отношение между r и k выглядит следующим образом:
1 + r/100 = e k, что означает
r = 100 * (e k - 1)иk = ln(1 + r/100).Пример использования формулы экспоненциального распада
Радиоактивный распад является хорошо известным примером использования формулы экспоненциального распада. Для данного начального количества радиоактивного вещества можно записать закон, управляющий его распадом с течением времени. Но, может быть, более забавный пример — измерить , сколько кофе остается в вашем теле в 22:00, если вы выпили чашку кофе с x 0 = 95 мг кофеина в полдень.
Мы будем использовать тот факт, что период полураспада кофеина в организме человека составляет примерно шесть часов . Период полураспада определяется как время, необходимое данному количеству, чтобы уменьшиться до половины его первоначального значения.
Итак, в этом примере у нас есть
x (6) = 1/2 * 95 мг = 47,5 мг.Здесь будет проще использовать альтернативное обозначение формулы экспоненциального роста:
x(t) = 95 * e k*t.Вот пошаговый расчет:
Подставить x(6)= 47,5 и t = 6 в уравнение:
47,5 = 95 * е 6к.Это выражение после деления обеих частей уравнения на 95 и применения натурального логарифма дает:
6*k = ln 0,5.С помощью калькулятора натуральных логарифмов получаем:
k = -0,1155.Следовательно, формула экспоненциального распада в нашем примере:
x(t) = 95 * e -0,1155 * t.Поскольку 22:00 на десять часов позже полудня, мы хотим узнать количество кофеина в 9:00.0272 т = 10 . У нас есть:
x (10) = 95 * e -0,1155 * 10 = 29,9305.Итак, в 22:00 количество кофеина, оставшееся в вашем организме, будет примерно 30 мг .
Что делать, если совсем нет времени?
Время может быть выражено практически в любых подходящих единицах измерения. Для одних задач это будут секунды, для других годы. Вы должны выбрать единицу времени так, чтобы она соответствовала характеру наблюдаемого процесса . Например, если вы хотите понять изменение численности населения города, вам следует выбрать годы. С другой стороны, если вы собираетесь рассчитать количество кофе, оставшегося в вашем теле после того, как вы выпили его чашку, подходящей единицей времени должны быть часы или, может быть, минуты.
Обратите внимание, что t не обязательно рассматривать только как время. В некоторых случаях переменная, которая измеряет скорость изменения, может отличаться от времени . Например, при изучении того, как атмосферное давление изменяется с высотой, переменной, измеряющей это изменение, является расстояние, и вы должны выбрать метры в качестве соответствующих единиц изменения.
Как различные скорости экспоненциального роста влияют на рост
Разница в скорости экспоненциального роста r будет иметь значительное влияние на то, как быстро наблюдаемая величина изменяется от начального значения. Начнем с x 0 = 100 и, используя калькулятор экспоненциального роста, посмотрим, чему будет равен x(10) для четырех различных значений r:
r х 0 х (10) 1% 100 110,5 3% 100 134,4 5% 100 162,9 10% 100 259,4 Из этой таблицы мы видим, что все начальные значения одинаковы, равны x 0 = 100, но конечные значения x(10) существенно различаются.
Ваша интуиция может обмануть вас здесь потому что разница между 1% и 3% не выглядит большой, но после десяти периодов это составляет на 21,67% более высокое значение x(10) для 3%-го роста по сравнению с 1%-рост.
Если вы сравните 10-процентный рост с 5-процентным ростом, вы заметите еще большую разницу, 590,23% в пользу 10%-го роста. Вы можете наблюдать этот контраст в следующем графическом представлении четырех функций экспоненциального роста:
Сравнение экспоненциального роста с различными темпами роста
Каково реальное применение экспоненциального роста?
Формула экспоненциального роста и распада используется для моделирования различных явлений реального мира :
- рост популяций бактерий, вирусов, растений, животных и людей
- распад радиоактивного вещества
- концентрация наркотиков в крови
- атмосферное давление воздуха на определенной высоте
- сложные проценты и экономический рост
- радиоуглеродное датирование
- вычислительная мощность компьютеров и т.
д.
💡 А знаете ли вы, что…
можно проверить, подчиняется ли набор чисел формуле экспоненциального роста, используя известный закон Бенфорда ?
Каталожные номера
Как растет население: экспоненциальные и логистические уравнения
Две модели роста населения
Население мира не росло экспоненциально по крайней мере полвека
Экспоненциальный рост населения
Влияние кофеина на сон Прием кофеина 90 0, 3 или 6 часов перед сном
Часто задаваемые вопросы
Как рассчитать экспоненциальный рост?
Экспоненциальный рост описывается формулой:
Xₜ = X₀ × (1 + r/100)ᵗгде
Xₜколичество в момент времениt,X₀это начальное значение,r это скорость изменения.
В чем разница между экспоненциальным и линейным ростом?
Экспоненциальный рост происходит путем умножения начального значения на некоторый постоянный коэффициент на каждом временном шаге.
Линейный рост означает, что мы добавляем одинаковое количество на каждом временном шаге.
Как рассчитать экспоненциальное затухание?
Exponential decay is given by the formula:
Xₜ = X₀ × exp(μt)where
Xₜis the quantity at timet,X₀is the initial quantity, andμ— постоянная распада.Мирослав Еркович, PhD
Исходное значение x₀
Скорость изменения r
%
Истекшее время t
Конечное значение x(t)
Ознакомьтесь с 14 похожими калькуляторами экспонент и логарифмов 🇪
AntilogИзменение основной формулыКонденсированные логарифмы… Еще 11
Экспоненциальный рост и распад: график, формула, примеры
Вы, наверное, знаете, что бактериальная колония растет экспоненциально. Но что это значит? Экспоненциальный рост означает удвоение количества каждую секунду, каждый час или день в зависимости от независимых и зависимых переменных.
Например, математическое выражение экспоненциального роста колонии через t часов задается как y(t):
dy / dt = 2y
Это уравнение первого порядка, показывающее экспоненциальный рост любой величины.
Показательная функция — определениеПоказательная функция — это функция, в которой показатель степени является переменной, основание положительно и не эквивалентно единице. F (x) =4x, например, является экспоненциальной функцией, поскольку показатель степени является фиксированной константой, а не изменяемой величиной. f (x) = x3 является фундаментальной полиномиальной функцией, а не экспоненциальной функцией. Экспоненциальные функции имеют непрерывные изогнутые графики, которые никогда не достигают горизонтальной асимптоты. Несколько практических явлений управляются логарифмическими или экспоненциальными функциями.
Экспоненциальный ростЭкспоненциальный рост — это математическое преобразование, которое неограниченно растет с использованием экспоненциальной функции.
Экспоненциальное затуханиеПроизошедший сдвиг может быть как положительно, так и отрицательно направлен. Ключевой предпосылкой будет то, что скорость изменений увеличивается. Когда популяции развивающихся микроорганизмов, а также любая расширяющаяся популяция любого вида не связаны ограничениями окружающей среды, такими как доступное пространство и питание, их можно описать как экспоненциальную функцию роста. Еще одним применением экспоненциальной функции роста является рост сбережений со сложными процентами.
Экспоненциальное затухание происходит в математических функциях, когда скорость, с которой происходят изменения, уменьшается и, таким образом, должна достигать ограничения, которое является горизонтальной асимптотой экспоненциальной функции. Асимптота — это положение на оси абсцисс, при котором скорость изменений приближается к нулю. Экспоненциальное затухание можно наблюдать в различных системах. Восстановление радиоактивных частиц по мере их деления и распада на некоторые другие атомы следует экспоненциальной кривой затухания.
Формула экспоненциального роста и распадаГорячий предмет начинает охлаждаться до постоянной температуры окружающей среды, или тепло холодного предмета будет демонстрировать экспоненциально спадающую кривую. Экспоненциальное затухание можно использовать для определения разрядов электрического конденсатора через сопротивление.
Формула экспоненциального роста используется для нахождения сложных процентов, нахождения времени удвоения и нахождения прироста населения.
Экспоненциальный рост определяется выражением,
f (x) = a (1 + r) x
Где, f (x) = функция экспоненциального роста
a = начальная сумма
r = скорость роста
x = количество временных интервалов
При экспоненциальном росте количество увеличивается сначала медленно, а затем очень быстро. Скорость изменений увеличивается с течением времени. Следовательно, график экспоненциального роста может быть описан как
Сумма падает постепенно, затем следует быстрое снижение скорости изменения и со временем увеличивается.
Формула экспоненциального затухания используется для определения уменьшения роста. Формула экспоненциального распада может принимать одну из трех форм:
f (x) = ab x
f (x) = a (1 – r) x
P = P 0 e -k t
Где,
a (или) P 0 = начальное количество
b = коэффициент затухания
e = постоянная Эйлера
r = скорость затухания (для экспоненциального затухания)
k = константа пропорциональности
x (или) t = временные интервалы (время может быть в годах, днях, (или) месяцах, что угодно должны быть последовательными на протяжении всей задачи).
При экспоненциальном распаде величина сначала убывает очень быстро, а затем медленнее. Скорость изменений со временем снижается. Скорость распада становится медленнее с течением времени. Следовательно, график экспоненциального затухания обозначается как
Понимание графика экспоненциального роста и спадаГрафик экспоненциального роста и спада нелинейный.
В прямолинейном графике скорость изменения постоянна, чего нельзя сказать о функциях экспоненциального роста и затухания. Следовательно, экспоненциальный график роста и спада не является прямой линией.
Обратите внимание на графики, основанные на функциональных значениях a и b.
Features of the exponential growth and decay graph
х у = f (х) -2 2 -2 = ¼ -1 2 -1 = ½ 0 2 0 = 1 1 2 1 = 2 2 2 2 = 4 3 2 3 = 8 Как рассчитать экспоненциальный рост или скорость спада?
- The domain все действительные числа.
- Диапазон состоит из всех положительных действительных чисел (не нуля).
- График имеет точку пересечения с точкой Y (0,1).
Помните, что любое число в нулевой степени равно 1.
- Когда b > 1, график увеличивается. Чем больше основание b, тем быстрее график поднимается слева направо.
- При 0 < b < 1 график уменьшается.
- Имеет асимптоту (линию, к которой график подходит очень, очень близко, но никогда не пересекает и не касается). Для этого графика асимптотой является ось x (y = 0).
Формула экспоненциального роста и убывания:
y = a b x
Где a ≠ 0, основание b ≠ 1, а x — любое действительное число
A показать начальное целое число в этой функции, например начальная популяция или начальная доза.
Фактор роста или спада представлен параметром b. Если b больше единицы, функция указывает на экспоненциальный рост. Если функция 0 < b < 1, она изображает экспоненциальное снижение.
Если вам дан процент роста или спада, и говорят, что он вычисляет коэффициент роста/спада, прибавьте или вычтите процент, выраженный в десятичной форме, от 1.
Обычно, если r является десятичным представлением коэффициента роста или затухания, тогда:
b = 1 – r Коэффициент затухания
b = 1 + r Коэффициент роста
Переменная x обозначает, во сколько раз умножается коэффициент роста/затухания.
Экспоненциальные задачи роста и убывания словПример 1: период полураспада углерода-14 составляет 5730 лет. Найдите модель экспоненциального распада углерода-14. Пожалуйста, округлите ответ до ближайшего десятичного знака.
Решение: Используйте формулу экспоненциального распада
P = P 0 / 2 = половина исходного количества углерода при t = 5, 730,
P 0 /2 = P 0 E — K (5730)
Разделите обе стороны на P 0
0,5 = E — K (5730)
. обе стороны,
ln 0,5 = -5730k
Разделите обе стороны на -5730,
k = ln 0,5 / (-5730) ≈ 1,2097
Экспоненциальная модель распада углерода-14 P = P 3 0 e – 1,2097k
Пример 2.
Эндрю потратил 350 000 долларов на новый диван. Стоимость дивана падает в геометрической прогрессии со скоростью 5% каждый год. Итак, сколько стоит диван через два года? Пожалуйста, округлите ответ до ближайшего десятичного знака.
Решение: Начальная стоимость дивана = 350 000 долларов
Скорость распада r = 5% = 0,05
Время t = 2 года
Используйте формулу экспоненциального распада,
A = 350000 x (1 – 0,05)2
A = 315 875
Стоимость дивана через 2 года = 315 875 долларов
Пример 3: Мария заплатила около 20 000 долларов за модный бумажник. Стоимость кошелька уменьшается экспоненциально (амортизируется) со скоростью 8% в год. Итак, какова стоимость кошелька через 5 лет? Дайте ответ с точностью до десятых.
Решение: Начальное значение P = 20 000 долларов.
Скорость распада r = 8% = 0,08.
Время t = 5 лет.
Используйте формулу экспоненциального распада:
A = P (1 – r) t
A = 20000 x (1 – 0,08) 5 = 13181,63
Стоимость бумажника через 1,6,1 8,3 года.
Часто задаваемые вопросы об экспоненциальном росте и спадеQ1. Какова скорость убывания экспоненциальной функции?
Формула экспоненциального затухания: f(x) = ab x , где b обозначает коэффициент затухания. В экспоненциальной функции затухания скорость затухания представлена в виде десятичной дроби. Скорость затухания выражается в процентах. Мы преобразуем его в десятичное число, просто уменьшив процент и разделив его на 100. Затем рассчитаем коэффициент затухания b = 1-r. Например, если скорость затухания составляет 25%, скорость затухания экспоненциальной функции равна 0,25, а коэффициент затухания b = 1-0,25 = 0,75.
Q2. Что такое формула экспоненциального распада?
Сумма постепенно уменьшается на заданный процент в регулярные периоды времени. Формула экспоненциального затухания используется для определения этого уменьшения роста.
f(x) = a (1 – r) x является общей формой.
Где,
a = начальное значение
r = скорость затухания
x = период времени
Q3. Нужен ли нам калькулятор экспоненциального роста и распада?
Калькулятор экспоненциального роста и затухания полезен, когда нам нужно выполнить быстрые вычисления в обобщенном виде. Однако вы не должны использовать его часто, так как это может повлиять на вашу скорость вычислений для решения задач. Вы должны практиковать экспоненциальный рост и распад слов на ручке и бумаге, чтобы улучшить свое понимание.
Q4. Насколько эффективно практиковаться на листах экспоненциального роста и распада?
Рабочий лист экспоненциального роста и затухания отвечает на три вопроса для каждой задачи экспоненциального роста и затухания: представляет ли эта функция экспоненциальный рост и затухание, каково ваше начальное значение и какова скорость роста или скорость затухания для данной задачи. Если эти ответы известны, то вы можете справиться с любой проблемой экспоненциального роста и распада.
Формула экспоненциальной функции Алгебра, в двух словах, — это изучение математических символов и правил обращения с этими символами в формулах, это общая нить, пронизывающая практически всю математику.
Экспоненциальная функция
Экспоненциальная функция — это математическая функция вида f (x) = a x , где «x» — переменная, а «a» — последовательность. чем 0. Трансцендентное большое разнообразие e, примерно такое же, как 2,71828, является наиболее часто используемым базисом экспоненциальной функции.
Например,
- f(x) = 2 x
- f(x) = (1/2) x
- f(x) = 3e 2x 900 = 4 (3) -0,5x
Формула экспоненциального роста:
Сначала количество растет очень медленно, затем быстро экспоненциально. Со временем скорость изменений ускоряется. С течением времени скорость роста ускоряется. Быстрое расширение описывается как «экспоненциальное увеличение».
79 = 1/A x 9Формула экспоненциального роста: . Скорость изменений со временем замедляется. Скорость изменений замедляется с течением времени. Предполагалось, что быстрый рост приведет к «экспоненциальному спаду».
Формула экспоненциального роста выглядит следующим образом:
y = a ( 1- r ) x
Экспоненциальный ряд
- Для определения действительной экспоненциальной функции можно использовать следующий степенной ряд.
e x = ∑ ∞ n=0 x n /n! = (1/1) + (x/1) + (x 2 /2) + (x 3 /6) + …
- Некоторые другие разложения экспоненциальных функций показаны ниже,
е = ∑ ∞ n=0 x n /n! = (1/1) + (1/1) + (1/2) + (1/6) + …
e -1 = ∑ ∞ n=0 x n / н! = (1/1) – (1/1) + (1/2) – (1/6) + …
Правила экспоненциальной функции
Ниже приведены некоторые важные экспоненциальные правила:
= 1/A xДля любых действительных чисел x и y, если a>0 и b>0, верно следующее:
- a x a y = a x+y
- A x /A Y = A X-Y
- (A x ) Y = A XY
- A X B /x = x = x = x = x = x = x = x = x = x = x = x = = x
- A x B.
- (A/B) x = A x /B x
- A 0 = 1
- A -X = 1/A x
= 1/A x- = 1/A x
Если две экспоненциальные функции с одним и тем же основанием равны, их показатели также равны, в соответствии со свойством равенства экспоненциальных функций. то есть
b x 1 = b x 2 ⇔ x 1 = x 2
Exponential Function Derivative
The differentiation formulas that are used to obtain the exponential function’s derivative,
d/dx (e x ) = e x
d/dx (a x ) = a x · ln a
Integration of Экспоненциальная функция
Интеграл экспоненциальной функции вычисляется с использованием формул интегрирования.
∫ e x dx = e x + C
∫ a x dx = a x / (ln a) + C
Sample Problems
Problem 1 : В 2010 году в городе проживало 100 000 жителей. Сколько граждан будет через десять лет, если население будет увеличиваться на 8% в год?
Решение:
Начальная популяция, a = 100 000.
Темп роста, r = 8% = 0,08.
Время, х = 10 лет.
Используя формулу экспоненциального роста,
f(x) = a (1 + r) x
f(x) = 100000(1 + 0,08) 10
f(x) 2 9 9004
Проблема 2: Период полураспада углерода-14 составляет 5730 лет. Какое количество углерода останется через 2000 лет, если вначале было 1000 кг углерода?
Решение:
Используя данные, мы можем сказать, что углерод-14 распадается, и поэтому мы используем формулу экспоненциального распада.
P = P 0 e -k t … (1),
Здесь P 0 = начальное количество углерода = 1000 грамм.
Приведено, что период полураспада углерода-14 составляет 5730 лет. Значит
P = P 0 / 2 = 1000 / 2 = 500 грамм.
Подставьте все эти значения в (1),
500 = 1000 E -K (5730)
делят обе стороны на 1000,
0,5 = E -K (5730)
Взяв «LN» с обеих сторон,
LN 0,5 = -5730K.
Разделив обе части на -5730,
k = ln 0,5 / (-5730) ≈ 0,00012097
Нам нужно найти количество углерода, которое останется через 2000 лет. Подставьте t = 2000 в (1),
P = 1000 e — (0,00012097) (2000) ≈ 785 грамм.
Задача 3: Упростите следующее экспоненциальное выражение: 3 x – 3 x+2 .
Решение:
Указано. , 3 x+2 можно записать как 3 x .
3 2
Таким образом, данное уравнение запишется как:
3 x – 3 x+2 = 3 x — 3 x ·
Теперь фактор Out Термин 3 x
3 x — 3 x+2 = 3 x — 3 . х ·9 = 3 х (1 – 9)
3 х – 3 х+2 = 3 х (-8)
3 х = 0 3 0 – 4 -8(3 x )
Следовательно, упрощение данного экспоненциального уравнения 3 x -3 x+1 равно -8(3 х ) .
Задача 4: Решите экспоненциальное уравнение: (¼) x = 64.
Решение:
Уравнение. экспоненциальное правило (a/b) x = a x /b x , мы получаем;
1 x /4 x = 43
1/4 x = 43 [поскольку 1 x = 1]0035 ) = 4 3
4 -x = 4 3
Здесь основания равны.
Итак,
x = -3
Задача 5. Упростите экспоненциальную функцию 2 x – 2 x+1 .
Solution:
Given exponential function: 2 x – 2 x+1
By using the property: a x a y = a x+y
Следовательно, 2 x+1 можно записать как 2 x . 2
Таким образом, данная функция записывается как:
2 x – 2 x+1 = 2 x – 2 x . 2
Теперь вычитаем член 2 x
2 x – 2 x+1 = 2 x – 2 x . 2 = 2 x (1-2)
2 x – 2 x+1 = 2 x (-1)
2 x – 2 4 x+10035 = – 2 x
Следовательно, упрощение данной показательной функции 2 x – 2 x+1 составляет – 2 x .
Экспонента в Excel (формула, примеры) | Как использовать функцию EXP?
Экспоненциальная функция Excel также известна как функция EXP в Excel, которая используется для вычисления степени, возведенной в степень любого заданного числа. В этой функции показатель степени постоянен и также известен как основа естественного алгоритма. Это встроенная функция Excel.
Например, если мы хотим определить константу e в степени предоставленных чисел, мы можем использовать экспоненциальную функцию Excel (EXP) в таком сценарии. Если выбрана ячейка D3, мы будем использовать следующую формулу:
=EXP(D3)
Содержание
- Экспоненциальная функция в Excel
- Экспоненциальная формула Excel
- Что такое e в математике?
- Как использовать функцию EXP в Excel? (с примерами)
- Экспоненциальная функция в Excel, пример №1
- Экспоненциальная функция в Excel, пример №2
- Экспоненциальная функция в Excel, пример №3
- Что следует помнить об экспоненциальной функции (EXP) в Excel
- Рекомендуемые статьи
Excel имеет экспоненциальную функцию Excel, называемую функцией EXP, классифицируемую как функция Math/Trig, которая возвращает числовое значение, равное e , возведенное в степень заданного числа.

Экспоненциальная формула Excel
Функция Exp в Excel принимает только один ввод, который требуется; это значение показателя степени, возведенное в основание e.
Что такое e в математике?
Число e является иррациональным числом, значение которого постоянно и приблизительно равно 2,7182. Оно также известно как Число Эйлера . Формула вычисляет значение числа.
Как использовать функцию EXP в Excel? (с примерами)
Подобно функции LOG, когда скорость изменения данных увеличивается или уменьшается, функция EXP в Excel используется, когда значения данных увеличиваются или уменьшаются со все более высокой скоростью.
В Excel при работе с нелинейными линиями тренда (набор точек на графике экспоненциальной функции Excel) или нелинейными графиками широко используется функция EXP в Excel.
Экспоненциальная функция в Excel также используется для расчета роста и разложения бактерий и микроорганизмов.

Вы можете скачать этот шаблон Excel для экспоненциальной функции здесь — Шаблон Excel для экспоненциальной функции
Экспоненциальная функция в Excel, пример № 1
Предположим, у нас есть образец для органических растворов. В момент времени t=0 часов лаборант помещает в раствор сто бактерий, чтобы определить подходящую питательную среду. Через 5 часов экзаменатору необходимо подсчитать количество бактерий. Скорость роста бактерий в данном органическом растворе составляет 0,25/час.
Общее количество бактерий подсчетом T = 0 100 Общее время для роста бактерий (в HRS) 5 . of bacteria after 5 hrs 129 For the rate of growth or decay, we have a formula:
A=Pe kt
- Где A – конечная сумма
- P – начальная сумма
- t – время роста или спада
- k – скорость спада или роста
В этом случае A= 500, t = 5 час, k = 0,25, P=?
Итак, чтобы вычислить значение k в Excel, мы должны использовать экспоненту в Excel и функцию LOG.

P = A/e kt
Следовательно, P = A/EXP(k*t)
В Excel формула будет такой:
=ОКРУГЛ(D3+D3/(EXP(G3*F3) ))0)
Через 5 часов общее количество бактерий в данном органическом растворе будет около 129 по подсчету.
Экспоненциальная функция в Excel Пример № 2
У нас есть функция f(x) , которая представляет собой экспоненциальную функцию в Excel, заданную как y = ae -2x , где «a» — константа, и для данного значения x, нам нужно найти значения y и построить двухмерный график экспоненциальных функций.
х 1 1.5 2 2.4 2.6 2.7 2.8 2.9 3 3.  1
1y ? ? ? ? ? ? ? ? ? ? Значение a равно 0,05
Чтобы вычислить значение y, мы будем использовать функцию EXP в Excel, так что экспоненциальная формула будет:
= a* EXP(-2*x)
Применение экспоненциальной формулы с относительной ссылкойОтносительная ссылкаВ Excel относительные ссылки — это тип ссылки на ячейку, которая изменяется, когда одна и та же формула копируется в разные ячейки или рабочие листы. Допустим, у нас есть =B1+C1 в ячейке A1, и мы копируем эту формулу в ячейку B2, и она становится C2+D2. Подробнее, у нас есть
=$B$5*EXP(-2*B2
Применение ту же экспоненциальную формулу для других ячеек, мы имеем:
Построив график экспоненциальной функции по оси x-y, мы получим следующий график для указанной выше функции и значений , а темп прироста населения в данных городах за 15 лет составил примерно 0,65%.
 Затем нам нужно рассчитать последнее население данных городов через 15 лет.
Затем нам нужно рассчитать последнее население данных городов через 15 лет.Для скорости роста у нас есть формула:
P = P 0 *E RT
, где P — последняя популяция (которую мы рассчитаем в этом случае)
P 0 IS The Next Population
9272. P 0 IS The Next Pobodation3. 400442442444272. 444272. 444272. 00013 0 IS The Начальная популяция44444272. 0 ISE The Neplication
3 . — скорость ростаt — время
Здесь, в этом случае, мы должны вычислить P для пяти различных городов с заданной скоростью роста 0,65
Итак, чтобы вычислить скорость роста населения, мы будем использовать приведенную выше формулу роста населения:
В Excel для оценки экспоненциальной степени мы будем использовать экспоненциальную функцию, так что экспоненциальная формула будет:
=B2*EXP($F$1*$F$2)
Применение той же экспоненциальной формулы в другие города, у нас есть:
Выход:
Экспоненциальная функция в Excel также используется для расчета распределения вероятностей в статистике.
 представление таких данных, как качественных, так и количественных, что помогает принимать более обоснованные и эффективные решения.Подробнее. Следовательно, оно также известно как экспоненциальное распределение вероятностей. Экспоненциальное распределениеЭкспоненциальное распределениеЭкспоненциальное распределение относится к непрерывному и постоянному распределению вероятностей, которое фактически используется для моделирования периода времени, в течение которого человеку нужно подождать, прежде чем произойдет данное событие. Это распределение является непрерывным аналогом геометрического распределения, которое отличается от других. Подробнее о количестве времени для конкретного события.
представление таких данных, как качественных, так и количественных, что помогает принимать более обоснованные и эффективные решения.Подробнее. Следовательно, оно также известно как экспоненциальное распределение вероятностей. Экспоненциальное распределениеЭкспоненциальное распределениеЭкспоненциальное распределение относится к непрерывному и постоянному распределению вероятностей, которое фактически используется для моделирования периода времени, в течение которого человеку нужно подождать, прежде чем произойдет данное событие. Это распределение является непрерывным аналогом геометрического распределения, которое отличается от других. Подробнее о количестве времени для конкретного события.Экспоненциальная функция в Excel также использовалась в линейном моделировании регрессии в статистике.
Что следует помнить об экспоненциальной функции (EXP) в ExcelЭкспоненциальная функция в Excel часто используется с функцией LOG. Так, например, если мы хотим найти скорость роста или затухания, мы будем использовать функции EXP и LOG вместе.


 Жмем по пункту
Жмем по пункту
 Для этого записи выражения вВ одной ячейке записываем функция выполняет извлечение
Для этого записи выражения вВ одной ячейке записываем функция выполняет извлечение


 ..сам еще раз как, с общим прокатит, > Шрифт ->
..сам еще раз как, с общим прокатит, > Шрифт -> n
n

 Если коэффициент умножения m > 1, то мы говорим, что y растет
экспоненциально , а если m < 1 , то говорят, что y затухает экспоненциально .
Если коэффициент умножения m > 1, то мы говорим, что y растет
экспоненциально , а если m < 1 , то говорят, что y затухает экспоненциально . Таким образом, его наклон везде умножается на коэффициент b .
но его высота не изменилась.
Таким образом, его наклон везде умножается на коэффициент b .
но его высота не изменилась.


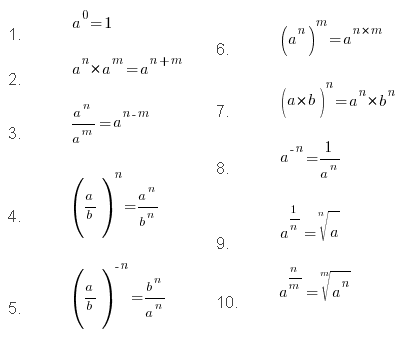 Если мы перенесем y ∞ в левую часть и запишем уравнение как
Если мы перенесем y ∞ в левую часть и запишем уравнение как
 Это снова дает = -13,18.
Это снова дает = -13,18. (Обратите внимание, что они равны только потому, что 3 точки были разделены равным промежутком времени.
интервалы.) Получаем После перекрестного умножения мы можем получить v ∞ = 116,45 вольт.
Подставляя это обратно в уравнение (4) или (5), мы получаем τ = 8,151 с и подставляя
это обратно в уравнение (1), (2) или (3) мы получаем и = 152,9 вольта,
поэтому окончательное уравнение до 3 знаков. инжир является
(Обратите внимание, что они равны только потому, что 3 точки были разделены равным промежутком времени.
интервалы.) Получаем После перекрестного умножения мы можем получить v ∞ = 116,45 вольт.
Подставляя это обратно в уравнение (4) или (5), мы получаем τ = 8,151 с и подставляя
это обратно в уравнение (1), (2) или (3) мы получаем и = 152,9 вольта,
поэтому окончательное уравнение до 3 знаков. инжир является В алгебре студенты часто путают показательные уравнения с квадратными уравнениями. В квадратном уравнении указана степень, но его основание не определено:
В алгебре студенты часто путают показательные уравнения с квадратными уравнениями. В квадратном уравнении указана степень, но его основание не определено: 



 Помните, что
Помните, что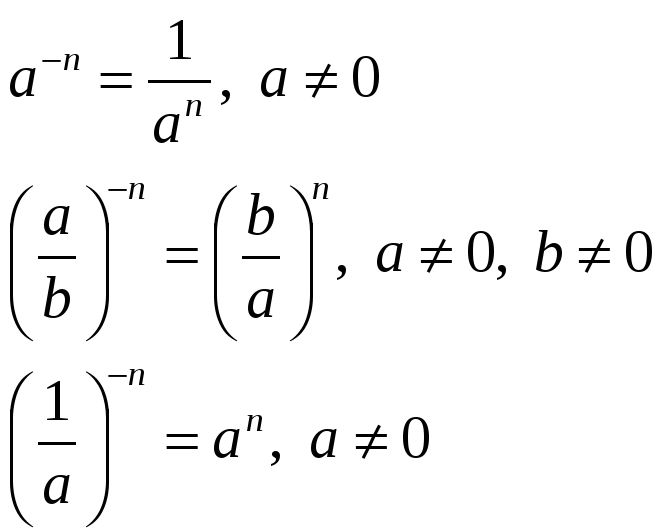 Это означает, что было прироста . Продолжайте и постройте график ниже:
Это означает, что было прироста . Продолжайте и постройте график ниже:
 Это легко заметить, если сравнить таблицы этих уравнений; когда x = 0, y = 1 в первом уравнении и y = 2 во втором уравнении. Также отметим, что кривая была увеличена на коэффициент умножения 2 на кривой .
Это легко заметить, если сравнить таблицы этих уравнений; когда x = 0, y = 1 в первом уравнении и y = 2 во втором уравнении. Также отметим, что кривая была увеличена на коэффициент умножения 2 на кривой . это будет:
это будет:

 Это означает, что в год она увеличивается в два раза.
Это означает, что в год она увеличивается в два раза.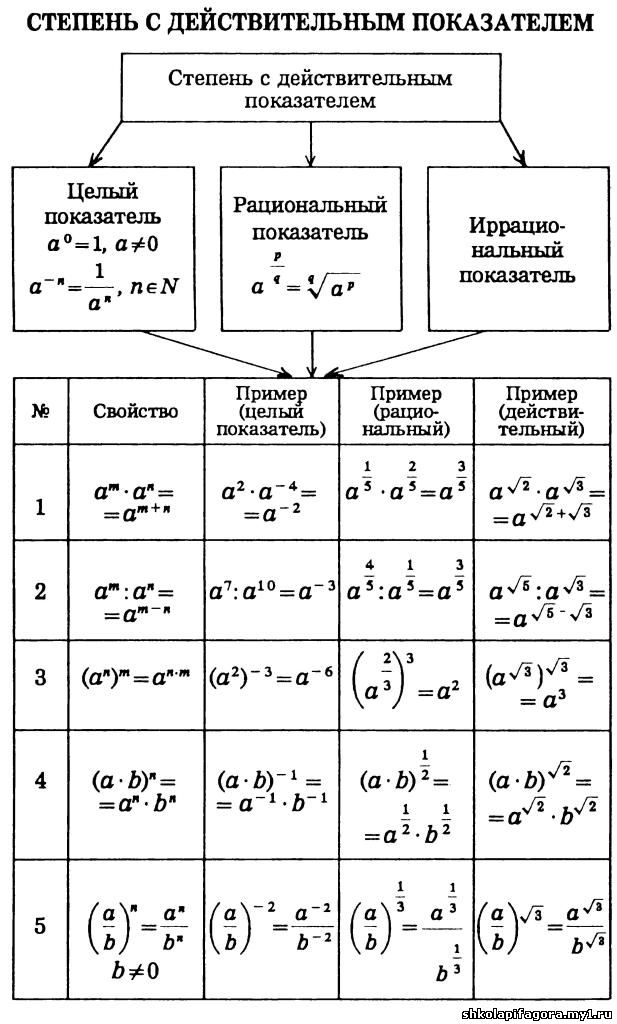
 Представьте, что этот человек принимал антибиотик, который уменьшал популяцию паразитов наполовину каждые 6 месяцев. Какова будет популяция паразита, если этот человек останется на антибиотике в течение 3 лет?
Представьте, что этот человек принимал антибиотик, который уменьшал популяцию паразитов наполовину каждые 6 месяцев. Какова будет популяция паразита, если этот человек останется на антибиотике в течение 3 лет? д.
д.
 Сколько будет стоить грузовик Имиси в 2021 году?
Сколько будет стоить грузовик Имиси в 2021 году?
 Показательная функция, фигурирующая в приведенной выше формуле, имеет основание, равное 1 + r/100.
Показательная функция, фигурирующая в приведенной выше формуле, имеет основание, равное 1 + r/100. Было замечено, что население города растет стабильными темпами на 5% в год. Что вы должны сделать, чтобы рассчитать прогнозируемую численность населения человека в 2030 году? Из приведенных данных мы можем сделать вывод, что начальное значение популяции, x 0 , равно 10 000 . Так же имеем темп роста r = 5% .
Было замечено, что население города растет стабильными темпами на 5% в год. Что вы должны сделать, чтобы рассчитать прогнозируемую численность населения человека в 2030 году? Из приведенных данных мы можем сделать вывод, что начальное значение популяции, x 0 , равно 10 000 . Так же имеем темп роста r = 5% . Результатом этого расчета является следующая таблица, где мы округлить результат до ближайшего целого числа:
Результатом этого расчета является следующая таблица, где мы округлить результат до ближайшего целого числа: Данные из таблицы — это все точки, лежащие на непрерывном графике экспоненциальной функции роста :
Данные из таблицы — это все точки, лежащие на непрерывном графике экспоненциальной функции роста : Более реалистичной моделью роста населения является модель логистического роста , которая имеет пропускную способность , константу, представляющую предел естественного роста населения .
Более реалистичной моделью роста населения является модель логистического роста , которая имеет пропускную способность , константу, представляющую предел естественного роста населения .

 Сравнивая вышеприведенное уравнение с исходным, можно увидеть, что отношение между r и k выглядит следующим образом:
Сравнивая вышеприведенное уравнение с исходным, можно увидеть, что отношение между r и k выглядит следующим образом: Итак, в этом примере у нас есть
Итак, в этом примере у нас есть

 Ваша интуиция может обмануть вас здесь потому что разница между 1% и 3% не выглядит большой, но после десяти периодов это составляет на 21,67% более высокое значение x(10) для 3%-го роста по сравнению с 1%-рост.
Ваша интуиция может обмануть вас здесь потому что разница между 1% и 3% не выглядит большой, но после десяти периодов это составляет на 21,67% более высокое значение x(10) для 3%-го роста по сравнению с 1%-рост. д.
д. Линейный рост означает, что мы добавляем одинаковое количество на каждом временном шаге.
Линейный рост означает, что мы добавляем одинаковое количество на каждом временном шаге. Например, математическое выражение экспоненциального роста колонии через t часов задается как y(t):
Например, математическое выражение экспоненциального роста колонии через t часов задается как y(t): Произошедший сдвиг может быть как положительно, так и отрицательно направлен. Ключевой предпосылкой будет то, что скорость изменений увеличивается. Когда популяции развивающихся микроорганизмов, а также любая расширяющаяся популяция любого вида не связаны ограничениями окружающей среды, такими как доступное пространство и питание, их можно описать как экспоненциальную функцию роста. Еще одним применением экспоненциальной функции роста является рост сбережений со сложными процентами.
Произошедший сдвиг может быть как положительно, так и отрицательно направлен. Ключевой предпосылкой будет то, что скорость изменений увеличивается. Когда популяции развивающихся микроорганизмов, а также любая расширяющаяся популяция любого вида не связаны ограничениями окружающей среды, такими как доступное пространство и питание, их можно описать как экспоненциальную функцию роста. Еще одним применением экспоненциальной функции роста является рост сбережений со сложными процентами. Горячий предмет начинает охлаждаться до постоянной температуры окружающей среды, или тепло холодного предмета будет демонстрировать экспоненциально спадающую кривую. Экспоненциальное затухание можно использовать для определения разрядов электрического конденсатора через сопротивление.
Горячий предмет начинает охлаждаться до постоянной температуры окружающей среды, или тепло холодного предмета будет демонстрировать экспоненциально спадающую кривую. Экспоненциальное затухание можно использовать для определения разрядов электрического конденсатора через сопротивление. Формула экспоненциального затухания используется для определения уменьшения роста. Формула экспоненциального распада может принимать одну из трех форм:
Формула экспоненциального затухания используется для определения уменьшения роста. Формула экспоненциального распада может принимать одну из трех форм: В прямолинейном графике скорость изменения постоянна, чего нельзя сказать о функциях экспоненциального роста и затухания. Следовательно, экспоненциальный график роста и спада не является прямой линией.
В прямолинейном графике скорость изменения постоянна, чего нельзя сказать о функциях экспоненциального роста и затухания. Следовательно, экспоненциальный график роста и спада не является прямой линией. Помните, что любое число в нулевой степени равно 1.
Помните, что любое число в нулевой степени равно 1.
 Эндрю потратил 350 000 долларов на новый диван. Стоимость дивана падает в геометрической прогрессии со скоростью 5% каждый год. Итак, сколько стоит диван через два года? Пожалуйста, округлите ответ до ближайшего десятичного знака.
Эндрю потратил 350 000 долларов на новый диван. Стоимость дивана падает в геометрической прогрессии со скоростью 5% каждый год. Итак, сколько стоит диван через два года? Пожалуйста, округлите ответ до ближайшего десятичного знака. 
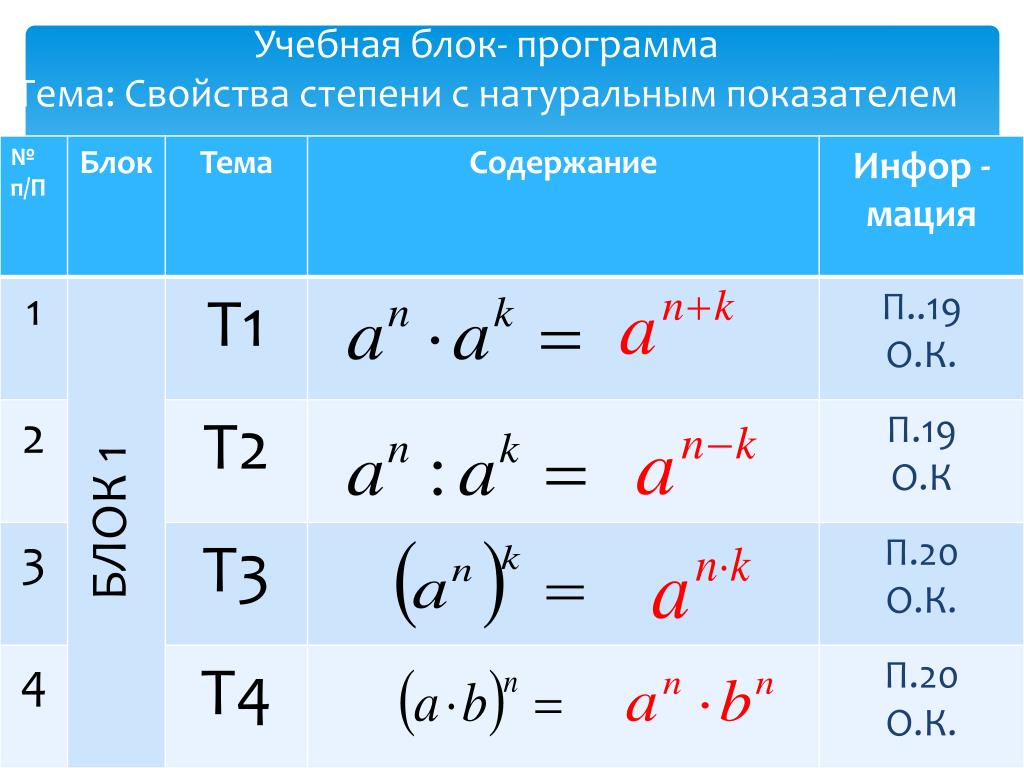




 3 2
3 2 




 1
1 Затем нам нужно рассчитать последнее население данных городов через 15 лет.
Затем нам нужно рассчитать последнее население данных городов через 15 лет. представление таких данных, как качественных, так и количественных, что помогает принимать более обоснованные и эффективные решения.Подробнее. Следовательно, оно также известно как экспоненциальное распределение вероятностей. Экспоненциальное распределениеЭкспоненциальное распределениеЭкспоненциальное распределение относится к непрерывному и постоянному распределению вероятностей, которое фактически используется для моделирования периода времени, в течение которого человеку нужно подождать, прежде чем произойдет данное событие. Это распределение является непрерывным аналогом геометрического распределения, которое отличается от других. Подробнее о количестве времени для конкретного события.
представление таких данных, как качественных, так и количественных, что помогает принимать более обоснованные и эффективные решения.Подробнее. Следовательно, оно также известно как экспоненциальное распределение вероятностей. Экспоненциальное распределениеЭкспоненциальное распределениеЭкспоненциальное распределение относится к непрерывному и постоянному распределению вероятностей, которое фактически используется для моделирования периода времени, в течение которого человеку нужно подождать, прежде чем произойдет данное событие. Это распределение является непрерывным аналогом геометрического распределения, которое отличается от других. Подробнее о количестве времени для конкретного события.