Mathway | Популярные задачи
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.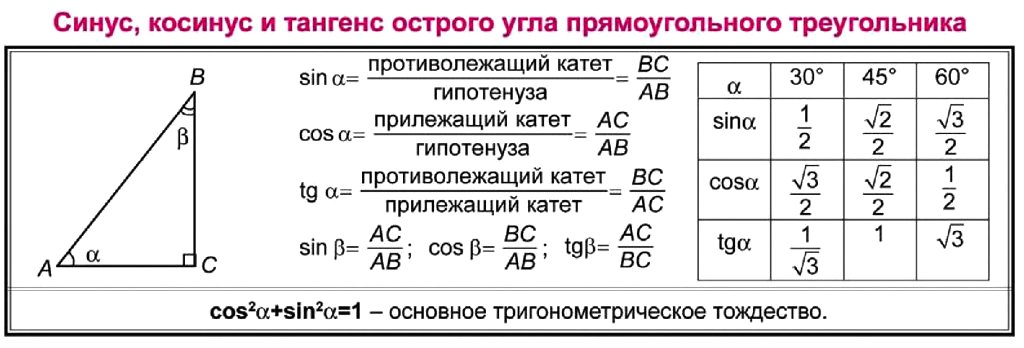 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.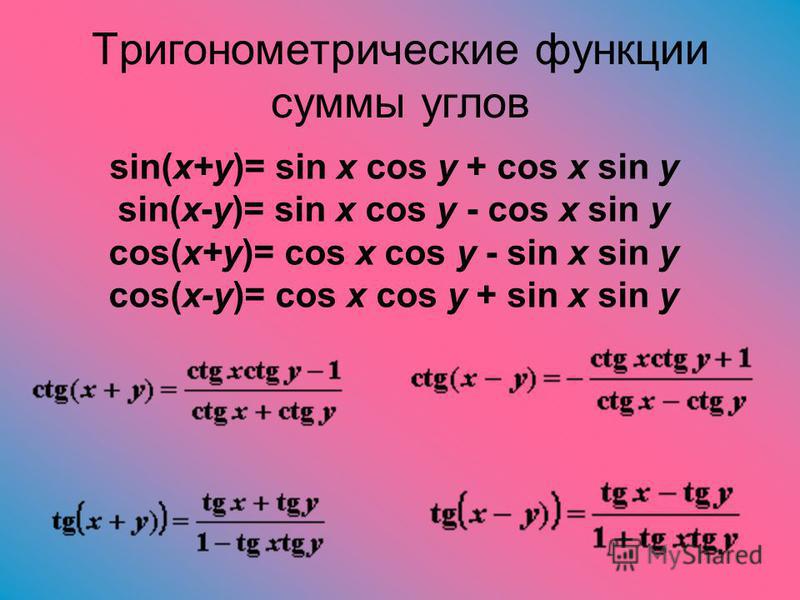 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.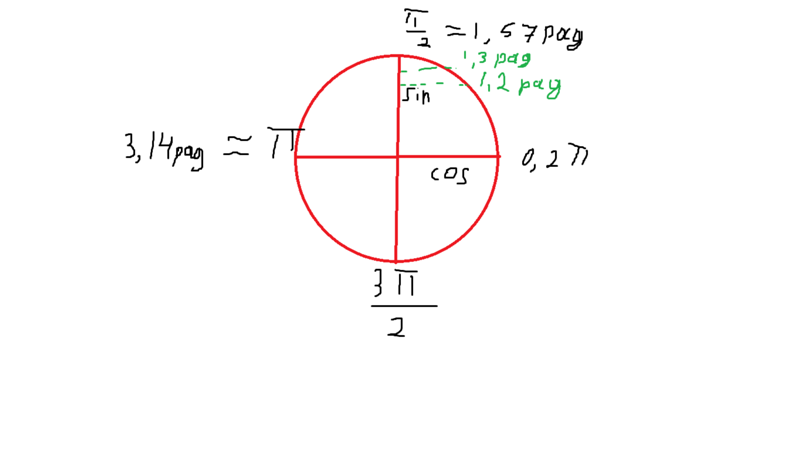 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
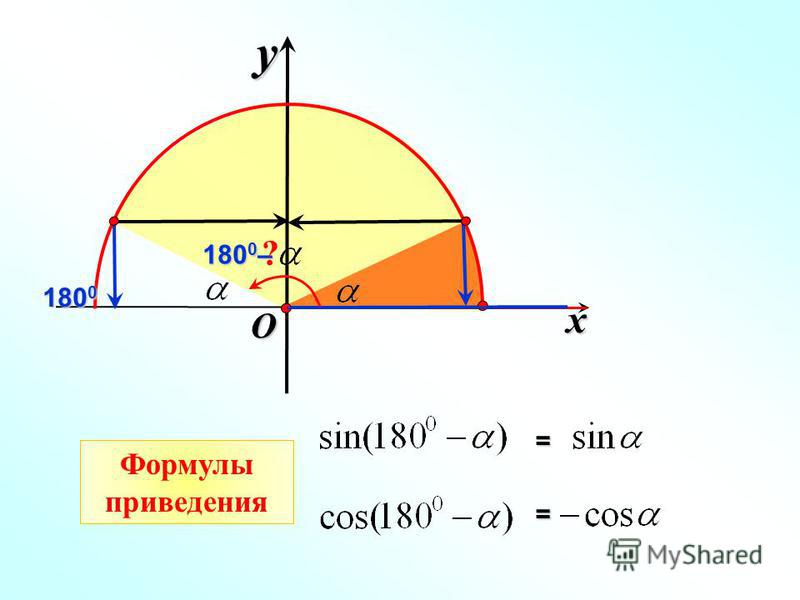
Формулы приведения. Знаки тригонометрических функций по четвертям
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.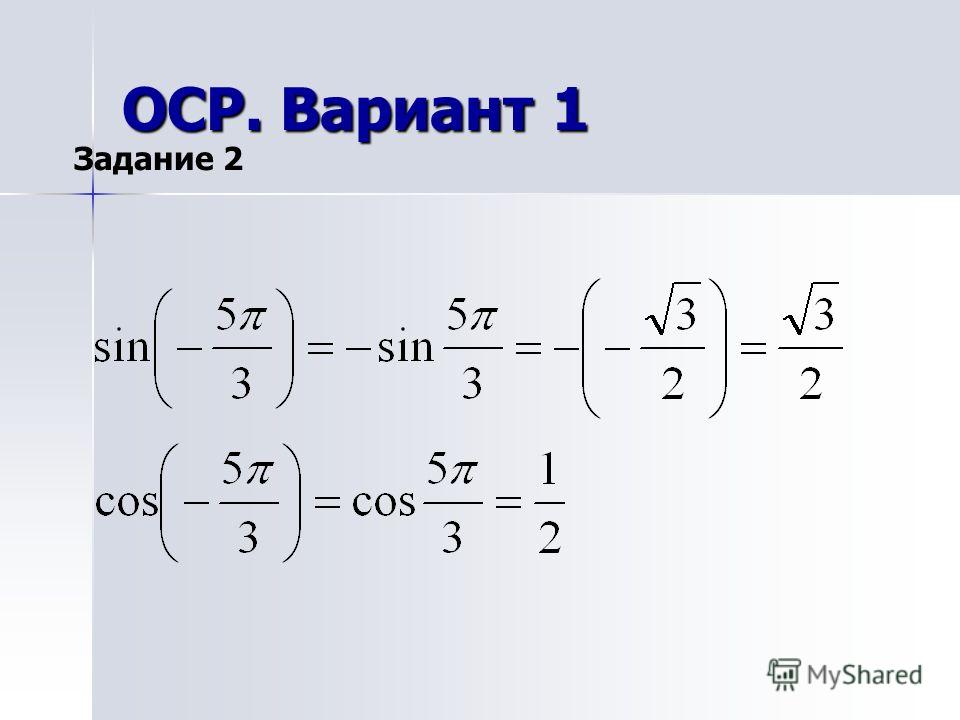 Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. ФОРМУЛЫ ПРИВЕДЕНИЯ
13.02.20221
2. Упростим выражение
3sin х cos х tg
x ctg 2 x
2
2
cos x sin 3 x
2
13.02.2022
2
3. Вспомним знаки тригонометрических функций по четвертям.
sin+ +
— —
cos
tg ; ctg
-+
-+
-+
+13.02.2022
3
13.02.2022
4
sin х sin х
cos х cos х
n x
tg 2 х tgх
ctg х ctgх
180
0
sin 3 х sin х
sin х sin cos x cos sin x sin x
cos 3 х cos х
tg 2 х tgх
ctg х ctgх
13.02.2022
5
sin х cos х
n
x, n нечётное
2
2
3
90
cos
х sin х
2
2
tg х ctgх
2
3
ctg
х tgх
2
3
ctg ctgx
270
1
ctgx
2
3
2
tg
х
ctgх
sin
х cos х
1
2 2 ctg
x 1 ctg ctgx
2
cos х sin х
2
13.
 02.2022
02.20222
6
7. ФОРМУЛЫ ПРИВЕДЕНИЯ
n xn
2
x, х-угол 1 четверти
n
2
x, n нечётное
2
180
0
sin n х
cos n x
13.02.2022
90
ФОРМУЛЫ
tg n x
ctg n x
n
sin
х
2
n
cos
x
2
3
270
2
n
tg
x
ПРИВЕДЕНИЯ
2
n
ctg
x
2
7
ФОРМУЛЫ ПРИВЕДЕНИЯ
13.02.2022
8
9. Мнемоническое правило для формул приведения
Мнемоническое правило для формулприведения
13.02.2022
9
• Итак, «лошадиное правило» звучит так:
• Если мы откладываем угол от вертикальной оси,
лошадь говорит «да» (киваем головой вдоль оси
OY) и приводимая функция меняет свое
название: синус на косинус, косинус на синус,
тангенс на котангенс, котангенс на тангенс.
• Если мы откладываем угол от горизонтальной
оси, лошадь говорит «нет» (киваем головой вдоль
оси OХ) и приводимая функция не меняет свое
название.

• Знак правой части равенства совпадает со
знаком приводимой функции, стоящей в левой
части равенства.
13.02.2022
10
11. ФОРМУЛЫ ПРИВЕДЕНИЯ ПРАВИЛО
0 22
3
2
• 1) Если под тригонометрической функцией
аргумент равен x; 2 x , то название
функции не меняется.
• 2) Если под тригонометрической функцией
3
x;
x , то название
аргумент равен
2
2
функции меняется (на родственное).
• 3) Перед полученной функцией ставят знак, который
имела бы в данной четверти исходная функция при
условии, что х — угол 1 четверти.
13.02.2022
11
12. Упростим выражение
3sin х cos х tg
x ctg 2 x
2
2
cos x sin 3 x
2
cos x cos x ctgx ctgx
0
sin x sin x
2
2
13.02.2022
3
2
12
• Рассмотрим применение формул приведения:
Пример 2:
3
2sin 7 cos
2
Упростите :
sin
3
2sin cos
2
2sin sin
Решение :
sin
sin
13.
 02.2022
02.20221
13
Пример 3:
Вычислите : sin160 cos110 sin 250 cos 340 tg110 tg 340
Решение : sin 180 20 cos 180 70
sin 270 20 cos 270 70
tg 90 20 tg 360 20
sin 20 cos 70 cos 20 sin 70
ctg 20 tg 20
sin 20 cos70 cos 20 sin 70 ctg 20 tg 20
sin 20 70 1 1 1 0
13.02.2022
14
Пример 3: (2 способ)
Вычислите : sin160 cos110 sin 250 cos 340 tg110 tg 340
Решение : sin 180 20 cos 90 20
sin 270 20 cos 360 20
tg 90 20 tg 360 20
sin 20 sin 20 cos 20 cos 20
ctg 20 tg 20
sin 2 20 cos 2 20 ctg 20 tg 20 1 1 0
13.02.2022
15
Пример 4:
5cos 29
Вычислите :
sin 61
5cos 29
5cos 29
5
Решение :
sin 90 29 cos 29
Решение :
13.02.2022
5cos 90 61
sin 61
5sin 61
5
sin 61
16
Пример 5:
3cos 54
Вычислите :
cos126
3cos 54
3cos54
3
Решение :
cos 180 54 cos 54
13.02.2022
17
Пример 6:
12
Вычислите : 2
2
sin 37 sin 127
12
Решение : 2
2
sin 37 sin 90 37
12
12
2
2
sin 37 cos 37
13.
 02.2022
02.202218
Пример 7:
7
Найдите : cos
,
2
если cos 0,8 и
2
Решение :
.
3
7
cos
cos
sin
2
2
sin 1 cos2 1 0, 64 0,36 0, 6
7
cos
0, 6
2
Ответ : 0, 6.
13.02.2022
19
20. Задания для закрепления изученного материала
№26.6Вычислите :5 1
а) cos
3 2
11
б ) sin
6
1
2
5
1
cos
cos 2 cos
3
3
3 2
11
sin
6
1
sin 2 sin
6
6 2
1
7
в ) sin
2
6
1
7
г ) cos
2
3
13.02.2022
20
21. Задания для закрепления изученного материала
№26.7Вычислите :3
в ) cos 4650 cos1050 cos330 cos 30
2
г )ctg 4110 ctg 510 ctg150 ctg 30 3
1
a) sin 3090
2
б )tg 2205 1
13.02.2022
21
22. Задания для закрепления изученного материала
№26.8Вычислите :а) cos 630 sin1470 ctg1125
cos 90 sin 30 ctg 45 1,5
31
7
б )2 cos
sin 7 tg
2 cos sin tg
3
4
3
4
1 0 1 2
49
г ) cos 9 2sin
6
13.
 02.2022
02.202221
сtg
4
1 1 1 1
22
23. Задания для закрепления изученного материала
№26.14Вычислите :11cos 287 25sin 557 11cos 287 25sin197
а)
sin17
sin17
11cos 270 17 25sin 180 17
sin17
11sin17 25sin17
sin17
13.02.2022
36
23
24. Задания для закрепления изученного материала
№26.14Вычислите :13sin 469 8cos 341
13sin109 8cos 19
б)
cos19
cos19
13sin 90 19 8cos19
cos19
13.02.2022
13cos19 8cos19
5
cos19
24
25. Задания для закрепления изученного материала
№26.18Вычислите :cos105 cos 5 sin105 cos85
а)
sin195 cos 5 cos195 sin185
cos105 cos 5 sin105 cos 90 5
sin195 cos 5 cos195 sin 180 5
cos105 cos 5 sin105 sin 5
sin195 cos 5 cos195 sin 5
cos 105 5
cos100 cos 90 10 sin10
1
sin 195 5 sin190 sin 180 10 sin10
13.02.2022
25
26. Задания для закрепления изученного материала
№26. 18Вычислите :
18Вычислите :sin 75 cos 5 cos 75 cos85
б)
cos 375 cos 5 sin15 sin 365
sin 75 cos 5 cos 75 cos 90 5
cos15 cos 5 sin15 sin 5
sin 75 cos 5 cos 75 sin 5
cos15 cos 5 sin15 sin 5
sin 75 5
sin 70 cos 20
1
cos 15 5 cos 20 cos 20
13.02.2022
26
Самостоятельно выполнить задание:
Вариант1: 26.9(а), 26.10(а), 26.11(а), 26.13(а), 26.16(а),
26.17(а), 26.19(а)
Вариант2: 26.9(б), 26.10(б), 26.11(б), 26.13(б), 26.16(б),
26.17(б), 26.19(б)
13.02.2022
27
28. СПАСИБО ЗА ВНИМАНИЕ.
13.02.202228
English Русский Правила
Белая функция или квадратичный косинус «наступает» / Хабр
Задача: Найти функцию для графика (бесконечного в обе стороны оси ОХ):
Ограничения: Должны использоваться только тригонометрические функции (любые прямые и обратные) и знаки операций плюс, минус, разделить, умножить, модуль. Решение должно быть представлено одной формулой.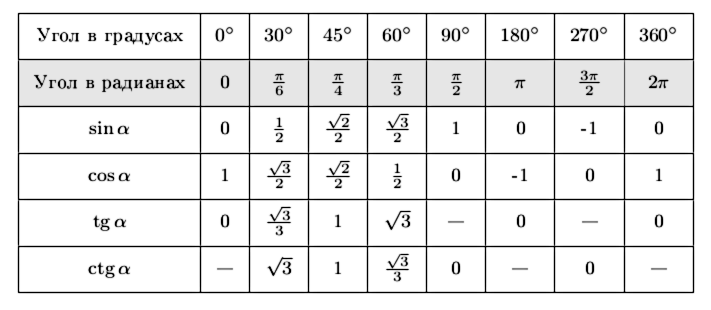
Подсказка: Раздумывая над этой задачей, мне попалось на глаза видео о так называемой квантовой запутанности фотонов. Я подумал, что фотон все же в большей мере волна, чем частица, поскольку частицей он определяется при определенных условиях, связанных с измерением состояния фотона, в остальных случаях — это волна. А где волна там обязательно должны быть тригонометрические функции косинуса и синуса, как минимум. Поэтому я подумал, что скорей всего вполне возможно, что есть вероятность создать «запутанную пару» от аргумента x для какой-то неизвестной функции с использованием только тригонометрических функций. Как ни странно, но именно поиск этой неизвестной функции, привел меня к решению поставленной выше задачи.
Решение задачи о поиске функции для квадратичного косинуса
Некоторые люди на форуме говорили мне, что решения этой задачи не может существовать, поскольку квадратное и круглое друг другом не представляется (как я это понял), но немного поэкспериментировав с построением графиков на WolframAlpha, решил, что это в корне неправильный подход.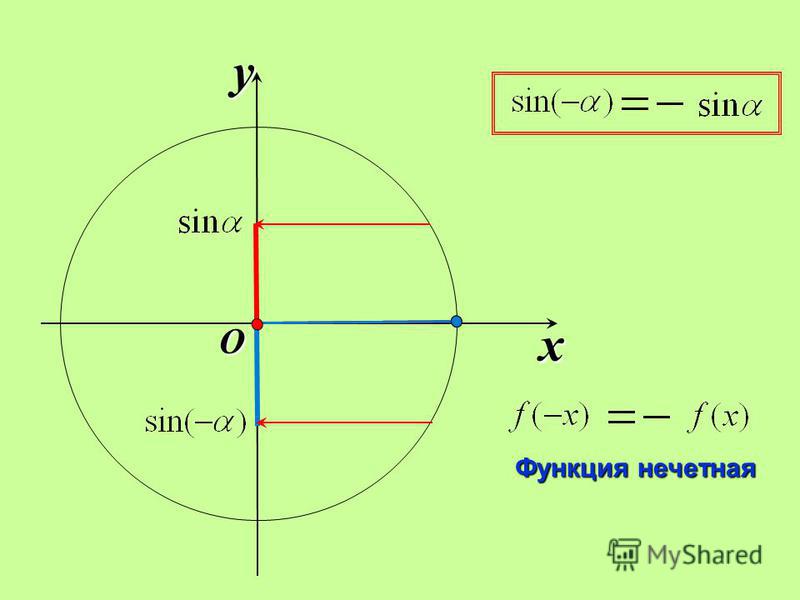 Как потом выяснилось, все дело как раз в «квантовой запутанности». Но обо всём по порядку.
Как потом выяснилось, все дело как раз в «квантовой запутанности». Но обо всём по порядку.
Как смоделировать запутанность? У нас есть прямые и обратные тригонометрические функции, есть переменная x-фотон и несколько тривиальных операций. Первое что приходит на ум (по крайне мере мне) это рассмотреть графики функций ArcSin[Cos[x]] и ArcCos[Sin[x]]:
Приведенные графики уже очень напоминают нужный нам «квадратичный косинус», но чего-то не хватает, оказывается не хватает «запутанности», то что мы сделали — это по сути запутанность первого уровня, но этого не достаточно, нужно эти две функции как-то скомпоновать, выйдя на запутанность второго уровня. После нескольких экспериментов с доступными тривиальными операциями я остановился на делении и вот что получилось (рис. 4):
Именно здесь я понял, что не потерялся в запутанности x-фотона и все как раз проясняется.
Казалось бы, наполовину задача решена и остается тупо скопировать решение в две формулы вида:
Но мне хотелось всё представить одно формулой и поиски продолжились…
Поэтому пришлось анализировать график, представленный на рис.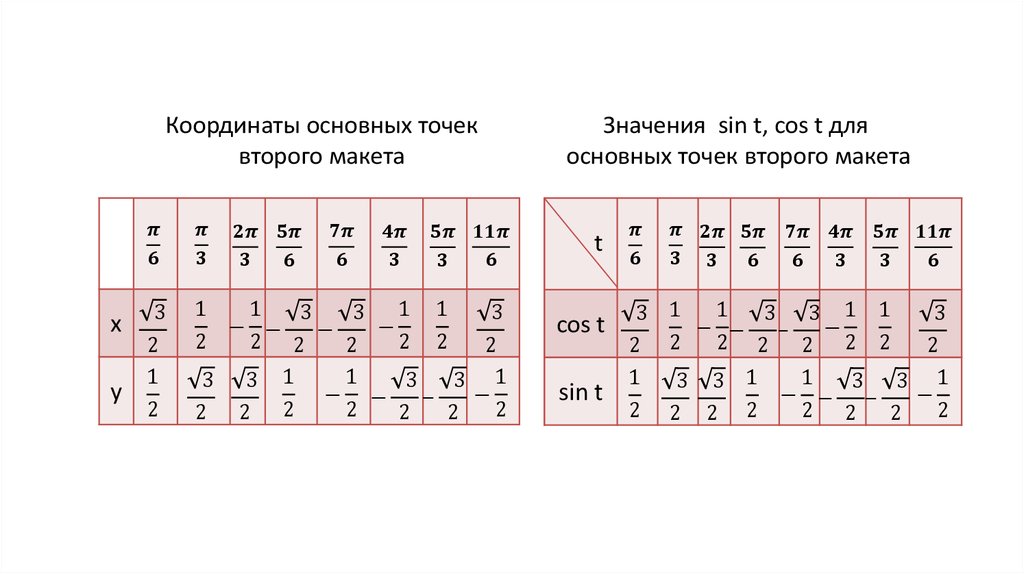 4. Что в нем примечательного?
4. Что в нем примечательного?
Во-первых, наполовину квадратичность присутствует, но нужно избавиться от этих восходящих линий. Как этого добиться? Только «аннигиляцией», то есть самоуничтожением противоположностей. И как раз здесь нам и понадобится модуль, чтобы у нас были симметричные плавно восходящие и нисходящии линии. Поэтому я рассмотрел такой график:
Казалось бы, маленькое отличие — модуль, но большая разница — теперь мы имеем симметричные (относительно начала координат) восходящие и нисходящии линии, которые достаточно «сложить» и они превратятся в квадрат… Но складывать их не нужно, достаточно еще одного модуля уровнем выше:
Что и требовалось доказать.
Эту функцию
y=ArcSin[Cos[x]]/ArcCos[Abs[Sin[x]]]
я назвал «
белая функция«, поскольку она настолько же идеальна и гармонична, как и белый цвет. Белая функция представляет собой сложную функцию-модель квантово-запутанной саму с собой пару от аргумента x. Белая функция к тому же определяет собой целый класс одноименных тригонометрических функций вида
Белая функция к тому же определяет собой целый класс одноименных тригонометрических функций вида
y=ArcSin[f1[x]]/ArcCos[Abs[f2[x]]]
, например, к этому виду можно также отнести функцию
y=ArcSin[1/Tan[x]]/ArcCos[Abs[Tan[x]]]
и т.д.
Исходники в формате Wolfram Mathematica — yadi.sk/d/3pl0lZMh4PzxCU
Оценка погрешности найденного решения
Для оценки точности я решил посчитать для белой функции площадь под графиком в окрестности точки Pi/2 с отрицательной стороны. И вот что получилось:
Evaluate[Integrate[
ArcSin[Cos[x]]/ArcCos[Abs[Sin[x]]], {x,
N[Pi, 100]/2 - 0.000000000000000000001`100, N[Pi, 100]/2}]]
Здесь я думаю меня сочтут полным профаном, но я всё таки скажу, что это означает.
Очевидно по результату в пределе действительная часть стремится к бесконечность, а мнимая к нулю то есть ∞+0. 0*i
0*i
Что это может означать? Какой смысл в действительной части и мнимой? Я думаю, что действительная часть пропорциональна точности
(в чем легко убедиться увеличивая количество нулей в формуле выше для приближения к точке Pi/2), а мнимая часть пропорциональна погрешности вычисления и эта погрешность стремиться к нулю в пределе.
Посему заключаем, что найденная формула белой функции делает возможным расчет с управляемой точностью, что не может не радовать. Но как такое возможно? Ответа у меня нет — думайте своей головой.
Проблема в комментариях рассматривается достаточно подробно, но особое место в вопросе белой функции занимает точка Pi/2, фольфрамальфа рисует это так:
Но нужно понимать, что это приближение, идеально в пределе там вертикальная линия и разрыва нет:
дорисовано красным то, что компьютер не может рассчитать!
Интересно, что в точках состыковки синего и красного y=+-Sqrt[2]/2
Другие способы решения
Abs[Cos[x]]/Cos[x]
с помощью ряда Фурье
Очевидно, эти способы не идут не в какое сравнение с найденным решением по точности и производительности, нет необходимости в сложении сотен косинусов, как это делает ряд Фурье. (I*x)]], которое с большой точностью даёт решение.
(I*x)]], которое с большой точностью даёт решение.
Разное
Моделирование форм с помощью найденной функции
Тривиальный пример, куб:
a[x_] := ArcSin[Cos[x]]/ArcCos[Abs[Sin[x]]]; (*белая функция*)
b[y_] := ArcSin[Cos[y]]/ArcCos[Abs[Sin[y]]]; (*белая функция*)
c[z_] := ArcSin[Cos[z]]/ArcCos[Abs[Sin[z]]]; (*белая функция*)
f[x_, y_] := a[x]*b[y];
time[t_] := c[t];
z = Table[
Plot3D[10*move*(1 + f[x, y]*time[move]), {x, -3*Pi/2,
3*Pi/2}, {y, -3*Pi/2, 3*Pi/2},
PlotRange -> {-50, 50}], {move, -Pi/2 + 0.1, Pi/2 - 0.1, Pi/100}];
z = Join[z, Reverse[z]];
Export["C:\\out.gif", z,
"AnimationRepetitions" -> Infinity]
Использование геометрии при решении тригонометрических задач
Геометрия является самым
могущественным средством
для изощрения наших умственных способностей и
дает нам возможность правильно мыслить и
рассуждать.
Г.Галлилей
Алгебра – не что иное, как записанная в
символах геометрия,
а геометрия — это просто алгебра, воплощенная в
фигурах
София Жермен
Многие тригонометрические задачи не решаются привычными для них методами или решаются очень сложно, а использование какого-нибудь геометрического приема дает короткое решение. Тригонометрические функции — это испытанный аппарат геометрии и их тоже нужно излагать, отправляясь от простых наглядных задач, как они практически и возникли — из решения треугольников
В школе мы начинаем изучать тригонометрию с вывода тригонометрических зависимостей из прямоугольного треугольника. Еще в 8-м классе, я начинаю работу по обучению детей тригонометрии, так как значительное число упражнений с аргументами из промежутка (0; ) выполняются геометрически. При таком подходе очевидны следующие плюсы.
Во-первых, раннее ознакомление учеников с
тригонометрическими заданиями способствует
раскрытию творческого потенциала учеников. Во-вторых,
расширению математического кругозора. В-третьих,
увеличению объема предметных умений. В-четвертых,
использование свойств равнобедренного и
прямоугольного треугольников, формул для
нахождения площадей фигур, теорем синусов и
косинусов приобретают устойчивость.
Во-вторых,
расширению математического кругозора. В-третьих,
увеличению объема предметных умений. В-четвертых,
использование свойств равнобедренного и
прямоугольного треугольников, формул для
нахождения площадей фигур, теорем синусов и
косинусов приобретают устойчивость.
В 10-м классе геометрический метод дает порой более легкий способ решения тригонометрических заданий. Геометрически можно показать интересные решения тригонометрических задач и проявить при этом смекалку и эрудицию.
Несколько примеров с использованием равнобедренного треугольника.
При решении используются следующие утверждения:
10 Высота равнобедренного треугольника, проведенная к основанию. Является медианой и биссектрисой.
20 Основание равнобедренного
треугольника равно удвоенному произведению
боковой стороны на косинус угла при основании.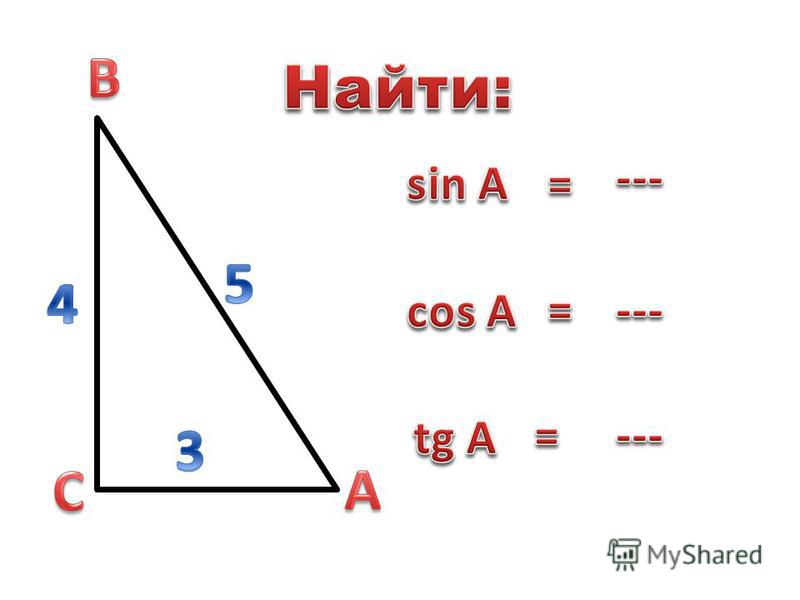
30 Биссектриса угла делит противоположную сторону треугольника на части пропорциональные прилежащим сторонам.
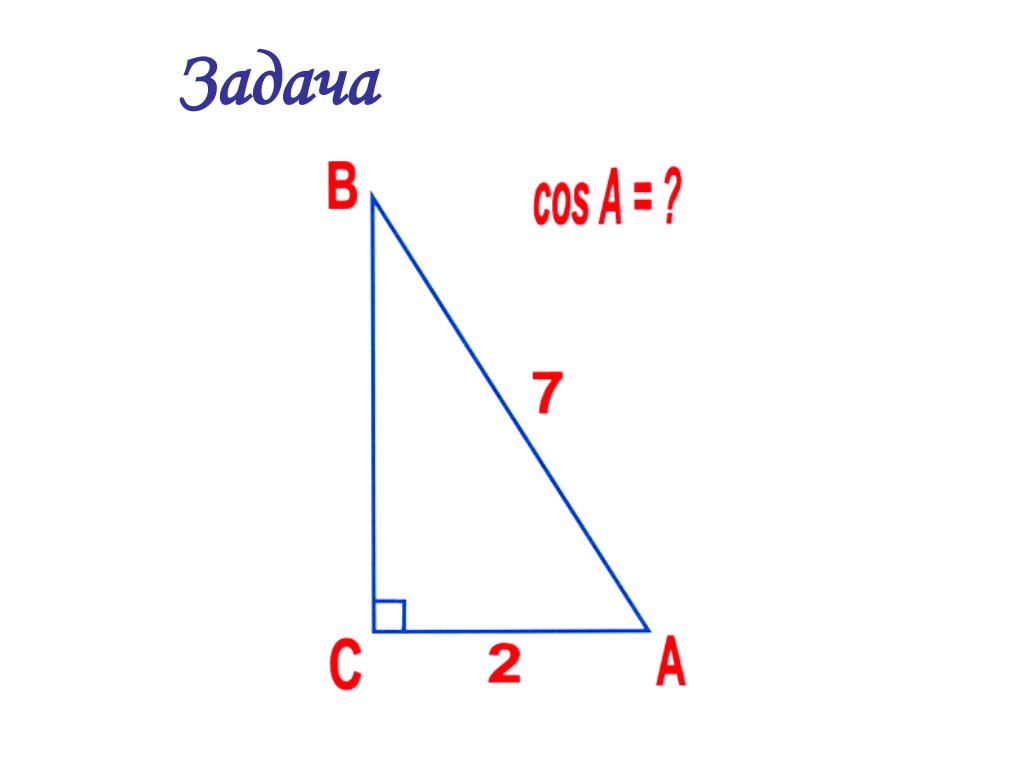
Задача 1. Вычислите cos15°.
В 10-м классе используется формула cos (45° – 30°)
В 8-м классе можно решить, используя равнобедренный треугольник
Для нахождения sin.cos. tg угла 22°30’ используем равнобедренный треугольник с углом против основания 45° далее аналогичное решение.
Задача 2. Найти sin 18°
В 10-м классе можно решить следующим образом.
sin 36°= cos 54°= cos (18° + 36°)
2 sin18° cos18° = cos18° cos36° – sin18° sin36°;
2 sin18° cos18°= cos18°(1 – 2sin218°) – 2sin218°cos18°
2 sin18° = 1 – 4sin218°, решаем квадратное уравнение и учтем, что sin18° > 0, получим
sin18° = .
Эту задачу можно решить геометрически
Строим равнобедренный треугольник АВС с АВ=ВС и
АВС=36°, тогда ВАС — ВСА = 72° (см рис. 2)
2)
Проведем AD биссектрису ВАС. Получим равнобедренные AВD и AСD. Обозначим AD=ВD=АС= а и АВ=b, тогда СD= а– b. Далее используем подобие треугольников или свойство биссектрисы угла и решим квадратное уравнение получим
Так как sin18° = cos72°. Рассмотрим AСD СD = 2АС·cos72° (свойство20) <–> cos = =
sin18° = cos
Рис. 2
При решении многих тригонометрических задач удобно применять прямоугольный треугольник
Задачи, связанные с обратными тригонометрическими функциями, решаются геометрически быстрее и проще
Задача 3. Вычислите Переформулируем задачу “Вычислить косинус суммы углов ”
Рис. 3
Построим углы . Из рисунка видно, что ANB = DSC (по двум катетам), следовательно т.е.
Задача 4. Вычислите
В 10-м классе можно решить задачу с помощью
формул, затратив на это немало усилий. Геометрически эта задача решается намного проще
Геометрически эта задача решается намного проще
Рис. 4
Обозначим . tg. Вычислим Построим прямоугольный АВС, где ВС=5n, АС=12n, тогда АВ=13n и ВАС = . Для угла строим ВСК, так, чтобы катет ВС был прилежащим к углу . В результате построения АВD равнобедренный, АВ=АD=13n . АВD= АDВ = , 2
0, т.е. = 0.
Задача 5. Решить уравнение: arcsin x + arcsin 2x =
Пусть arcsin x = , arcsin 2x = , где + = , тогда sin = x, sin = 2x.
Отметим, что x > 0 (иначе arcsin x < 0, arcsin 2x < 0, их сумма < 0).Построим прямоугольные треугольники, так чтобы + образовали прямой угол.
(рис. 5)
АВСD – прямоугольник.
Пусть АС = 1, тогда ВС = 1 · sin = sin = x, и CD = 1 · sin = sin = 2x.
По теореме Пифагора из треугольника АВС:
AB2 + BC2 = AC2,
(2x)2 + x2 = 1,
5x2 = 1,
x2 = ,
x = , x = –
– не подходит
по условию задачи.
Ответ: .
Задача 6. Решить уравнение: arcsin x + arcsin 2x = .
Пусть arcsin x = , arcsin 2x = , тогда + = .
x = sin , 2x = sin . Заметим, что x > 0.
РИС. 6
Построим АОМ = , АОВ = , МОВ = + = . АМОМ.
Пусть ОА = 1, тогда, из треугольника АОМ, АМ = 1 · sin = sin = 2x.
Проведём АКОВ. Из треугольника АОК АК = 1 · sin = sin = x.
Проведём КС ОМ. СКА = КОМ = – как углы с взаимно перпендикулярными сторонами.
Проведём АD КС. Из АDК KD = AK · cos 60° = x · = .
DC = AM = 2x. Значит, КС = KD + DC = + 2x = .
Из АОК по теореме Пифагора:
ОК = = .
Из ОКС: ОК · sin 60° = KC
Ответ: .
Примеры решения тригонометрических уравнений.
Задача 7. Решить уравнение cos x – sin x = 1.
cos x – sin x = 1
Разделим левую и правую часть уравнения на
корень квадратный из суммы квадратов
коэффициентов при cos x и sin x, т. е. на = :
е. на = :
Геометрическое решение:
Рис. 7
cos x – sin x = 1
ВС = 1 · sin x = sin x,
АС = 1 · cos x = cos x.
Следовательно, АС – ВС = 1. Но в АВС каждая сторона больше разности двух других сторон, т. е.
АВ > АС – ВС <=> АС – ВС < 1, т. к. АВ = 1. Но по условию задачи требуется, чтобы АС – ВС = 1. Это возможно только, если ABС превратится в отрезок, т.е.
если АС = 1, а ВС = 0, т.е. x1 = 0 + 2k, x1 = 2k, kZ
если АС = 0, а ВС = 1, т.е. x2 = –x2 = – + 2l, lZ
Ответ: 2k; – + 2l, kZ.
Задача 8 Решить уравнение , если х – острый угол
Геометрическое решение. Проведем BDAC.
Сумма двух отрезков равна 4 .Отрезки найдены по теореме косинусов
Многие математические задачи допускают
несколько вариантов решения. Часто первый
избранный бывает далеко не самым удачным. Нахождение “наиболее простых”, оригинальных
путей решения нередко является результатом
длительной и кропотливой работы. Умение решать
задачу различными способами является одним из
признаков хорошей математической подготовки
Нахождение “наиболее простых”, оригинальных
путей решения нередко является результатом
длительной и кропотливой работы. Умение решать
задачу различными способами является одним из
признаков хорошей математической подготовки
Решение тригонометрических задач методом, основанным на наглядно-геометрической интерпретации развивает логическое мышление и пространственное воображение
Литература
- А Г Мордкович. Алгебра и начала математического анализа. Учебник для 10 класса. Москва, “Мнемозина”, 2010.
- А.Ф. Бермант, Л.А. Люстерник. Тригонометрия. Москва, 1957.
- Савин А. Тригонометрия Квант, 1996. – №4.
Презентация
Сетевой фильтр Harper UCH-350 с блоком usb зарядки (черный)
Сетевой удлинитель вещь привычная и необходимая в каждом доме. А если туда добавить блок для зарядки устройств по USB, пользоваться им станет еще практичнее — можно зарядить смартфон, даже если заняты все розетки. Сегодня рассмотрим сетевой удлинитель с тремя розетками от компании Harper. Модель UCH-350 имеет три разъема usb общей мощностью 24 Вт и PD, кабель 1,5 м и выдерживает мощность до 4 кВт.
А если туда добавить блок для зарядки устройств по USB, пользоваться им станет еще практичнее — можно зарядить смартфон, даже если заняты все розетки. Сегодня рассмотрим сетевой удлинитель с тремя розетками от компании Harper. Модель UCH-350 имеет три разъема usb общей мощностью 24 Вт и PD, кабель 1,5 м и выдерживает мощность до 4 кВт.
Начнем обзор с заявленных характеристик продукта.
Технические характеристики
Тип устройства: сетевой фильтр (удлинитель)
Цвет: белый, черный
Материал корпуса: огнеупорный пластик до 850 °С
Длина кабеля: 1,5 м
Количество розеток: 3
Входное напряжение: AC 220-250В 50/60 Гц
Максимальная мощность нагрузки: 4000 Вт
Максимальный ток нагрузки: 16 А
Количество USB портов: 3
Количество Type-C портов: 1
Поддержка быстрой зарядки (Power Delivery 3.0): да, 20 Вт
Максимальная сила тока на 1 USB порт: 3 А
Суммарная сила тока для всех портов USB: 4,8 А
Размеры: 270х55х40 мм
Масса: 600 г.
Упаковка и комплектация
Удлинитель попадает к пользователю в картонной коробке с полиграфией. Характеристики приведены на разных языках, включая русский. Внутри есть дополнительная защита в виде воздухонаполненной пленки. Доступен черный и белый цвет корпуса.
Отмечу, отсутствие от пластика химического запаха.
Изготовлен удлинитель в Китае. Гарантия один год.
Комплект поставки изделия:
- Удлинитель с несъемным сетевым шнуром
- Руководство пользователя
- Гарантийный талон
Внешний вид
Сборка качественная. У корпуса глянцевые боковые поверхности, а поверхность, где расположены все интерфейсы, матовая. Блок с usb разъемами дополнительно выделен выборкой на корпусе. Указан ток для каждого разъема. Для быстрой зарядки доступно PD 20 Вт по разъему тип С.
Клавиша включения крупная, рядом индикаторы: сеть, заземление и индикация защиты от высоковольтных импульсов из сети.
Блок из трех «евро» розеток (тип СЕЕ 7/4): все под углом 45 градусов и с защитными шторками.
На задней части корпуса информация от производителя и два места для настенного монтажа:
Корпус собран на 6 винтов, их колодцы закрыты резиновыми заглушками. Заглушки служат нескользящими ножками, если удлинитель просто стоит.
Входной сетевой кабель несъемный, в корпус заводится через небольшую ПВХ втулку, для предотвращения изгиба. Кабель выглядит мощно, но достаточно гибкий, внутри три жилы по 1.5 мм², а диаметр по изоляции снаружи 8 мм. Изоляция матовая.
Оканчивается сетевой кабель угловой вилкой (16 А), на ее корпусе есть уступ для удобного извлечения из розетки.
Индикаторы светят тускло, отвлекать не будут:
Масса устройства:
Внутреннее устройство
Безопасность использования удлинителя определится его внутренним устройством. И можно сразу понять удлинитель это или действительно фильтр. Разбираем корпус на две половины. Винты со шлицом Y 3.0
Разбираем корпус на две половины. Винты со шлицом Y 3.0
Внутри UCH-350 медные кабели, пайка качественная. Кнопка включения двухполюсная, разрывает и фазу и нейтраль. Латунная полоска контактов розеток имеет толщину 0,5 мм.
Выключатель на 250 В 16 А с защитой от высоковольтных импульсов из сети варисторами (под термоусадкой):
Блок зарядки:
Тестирование
Для начала проверим потребление самого удлинителя от сети в холостом режиме:
Теперь посмотрим на возможности usb портов для зарядки гаджетов. Токоотдачу портов и протоколы проверим USB тестером FNB38 и регулируемой нагрузкой.
USB A (2 шт.) без протоколов быстрой зарядки. Без падения напряжения 5 В выдают по 2,5 А.
КПД при работе одного порта 83%
USB тип С оснащен быстрой зарядкой и PD:
А теперь совместная нагрузка портов 25 Вт:
Идет незначительная просадка напряжения 5 В.
Подключил на вечер к удлинителю Harper UCH-350 два обогревателя:
Корпус удлинителя не нагрелся, а кабель стал слегка теплым.
При заявленной 4 кВт общей мощности потребителей, можно смело подключать мощные бытовые потребители, например, фены, утюги или обогреватели.
Заключение
Harper UCH-350 — качественный удлинитель оснащенный современным зарядным блоком USB. Хороший вариант, когда не нужно много розеток (хотя у Harper есть подобные модели на 5 и даже на 8 розеток). Варисторная защита от импульсных помех из сети с индикацией несомненный плюс модели.
Спасибо за внимание. Удачных покупок!
Товар предоставлен для написания обзора магазином. Обзор опубликован в соответствии с п.18 Правил сайта.
Планирую купить +6 Добавить в избранное Обзор понравился
+37 +44
дайын үй жұмыстары Алгебра Абылкасымова 9 класс 2019 referatikz.
 com
comАлгебра 9 — сынып
Авторлары: Абылкасымова А., Кучер Т., Корчевский В., Жумагулова З. «Мектеп» баспасы 2019Упражнения для повторения курса алгебры 7—8 классов
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869
Глава I. УРАВНЕНИЯ, НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ И ИХ СИСТЕМЫ
§1. Нелинейные уравнения с двумя переменными
1.11.21.31.41.51.61.71.81.91.101.111.121.131.141.15
§2. Система нелинейных уравнений с двумя переменными
2.12.22.32.42.52.62.72.82.92.102.112.122.132.14
§3. Решение систем нелинейных уравнений с двумя переменными
3.13.23.33.43.53.63.73.83.93.103.113.123.133.143.153.163.173.183.193.203.21
3.223.233.243.253.263.273.283.293.303.313. 323.333.343.353.363.373.383.393.403.413.423.433.443.45
323.333.343.353.363.373.383.393.403.413.423.433.443.45
§4. Решение текстовых задач с помощью систем нелинейных уравнений с двумя переменными
4.14.24.34.44.54.64.74.84.94.104.114.124.134.144.154.164.174.184.194.204.214.224.234.244.254.264.274.284.29
§5. Неравенства с двумя переменными
5.15.25.35.45.55.65.75.85.95.105.115.125.135.145.155.165.175.185.19
§6. Системы нелинейных неравенств с двумя переменными
6.16.26.36.46.56.66.76.86.96.106.116.126.136.146.156.166.176.186.196.206.216.226.236.246.256.26
Проверь себя!
12345678910111213141516171819202122
2324252627
Глава II. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
§7. Основные понятия и правила комбинаторики (правило суммы и правило произведения)
7.17.27.37.47.57.67.77.87.97.107.117.127.137.147.157. 167.177.187.197.20
167.177.187.197.20
§8. Факториал числа. Перестановки и размещения
8.18.28.38.48.58.68.78.88.98.108.118.128.138.148.158.16
§9. Сочетания без повторений. Основные формулы комбинаторики
9.19.29.39.49.59.69.79.89.99.109.119.129.13
§10. Решение задач с использованием формул комбинаторики
10.110.210.310.410.510.610.710.810.910.1010.1110.1210.1310.1410.1510.1610.17
§11. Бином Ньютона и его свойства
11.111.211.311.411.511.611.711.811.911.1011.1111.1211.1311.1411.1511.16
Проверь себя!
12345678910
Глава III. ПОСЛЕДОВАТЕЛЬНОСТИ
§12. Числовая последовательность, ее виды, способы задания и свойства .
12.112.212.312.412.512.612.712.812.912.1012.1112.1212.1312.1412.1512.1612.1712.1812.1912.2012.2112.2212.23
12. 2412.2512.2612.2712.2812.2912.3012.31
2412.2512.2612.2712.2812.2912.3012.31
§13. Арифметическая прогрессия. Формула п-то члена арифметической прогрессии
13.113.213.313.413.513.613.713.813.913.1013.1113.1213.1313.1413.1513.1613.1713.1813.1913.2013.2113.2213.2313.2413.2513.2613.2713.2813.2913.3013.3113.3213.3313.3413.3513.36
§14. Формула для вычисления значения суммы первых n членов арифметической прогрессии
14.114.214.314.414.514.614.714.814.914.1014.1114.1214.1314.1414.1514.1614.1714.1814.1914.2014.2114.2214.2314.2414.2514.2614.2714.2814.2914.3014.3114.3214.3314.34
§15. Геометрическая прогрессия. Формула п-го члена геометрической прогрессии
15.115.215.315.415.515.615.715.815.915.1015.1115.1215.1315.1415.1515.1615.1715.1815.1915.2015.2115.2215.2315.2415.2515.2615.2715.2815.2915.3015.3115.3215.3315.3415.3515.3615.3715.3815.3915.40
§16. Формула для вычисления значения суммы первых n членов геометрической прогрессии
16. 116.2
116.2
16.316.416.516.616.716.816.916.1016.1116.1216.1316.1416.1516.1616.1716.1816.1916.2016.2116.2216.2316.2416.2516.2616.2716.2816.2916.3016.3116.3216.3316.3416.3516.3616.3716.3816.39
§17. Формула для вычисления значения суммы членов бесконечно убывающей геометрической прогрессии
17.117.217.317.417.517.617.717.817.917.1017.1117.1217.1317.1417.1517.1617.1717.1817.1917.2017.2117.2217.2317.2417.2517.2617.2717.2817.2917.3017.3117.3217.3317.3417.3517.3617.37
§18. Метод математической индукции
18.118.218.318.418.518.618.718.818.918.1018.1118.1218.1318.1418.1518.1618.1718.1818.1918.2018.2118.2218.2318.2418.2518.2618.2718.2818.2918.30
Проверь себя!
12345678910111213141516
17181920
Глава IV. ТРИГОНОМЕТРИЯ
§19. Градусная и радианная мера углов и дуг
19. 119.219.319.419.519.619.719.819.919.1019.1119.1219.1319.1419.1519.1619.1719.1819.1919.2019.2119.2219.2319.2419.25
119.219.319.419.519.619.719.819.919.1019.1119.1219.1319.1419.1519.1619.1719.1819.1919.2019.2119.2219.2319.2419.25
§20. Синус, косинус, тангенс и котангенс произвольного угла. Значения синуса, косинуса, тангенса и котангенса углов
20.120.320.420.520.620.720.820.920.1020.1120.1220.1320.1420.1520.1620.1720.1820.1920.2020.2120.2220.2320.2420.2520.2620.2720.2820.2920.3020.3120.3220.3320.3420.3620.3720.3820.3920.40
§21. Тригонометрические функции и их свойства
21.121.221.321.421.521.621.721.821.921.1021.1121.1221.1321.1421.1521.1621.1721.1821.1921.2021.2121.2221.2321.2421.2521.2621.2721.2821.2921.30
§22. Тригонометрические тождества
22.122.222.322.422.522.622.722.822.922.1022.1122.1222.1322.1422.1522.1622.1722.1822.1922.2022.2122.2222.23
22.2422.2622.2722.2922.3022.3122.32
§23. Формулы приведения
23. 123.223.323.423.523.623.723.823.923.1023.1123.1223.1323.1423.1523.1623.1723.1823.1923.2023.2123.2223.2323.2423.2523.2623.2723.2823.2923.3123.3223.33
123.223.323.423.523.623.723.823.923.1023.1123.1223.1323.1423.1523.1623.1723.1823.1923.2023.2123.2223.2323.2423.2523.2623.2723.2823.2923.3123.3223.33
§24. Формулы синуса и косинуса суммы и разности двух углов
24.124.224.324.424.524.624.724.824.924.1024.1124.1224.1324.1424.1524.1624.1724.1824.1924.2224.2624.28
§25. Формулы тангенса и котангенса суммы и разности двух углов
25.125.225.325.425.525.625.725.825.925.1025.1125.1225.1325.1425.1525.1625.1725.1825.1925.2025.21
§26. Формулы тригонометрических функций двойного и половинного углов
26.126.226.326.426.626.726.826.926.1026.1126.1226.1426.1526.1626.1726.1826.1926.2026.2126.2226.2426.29
Cos 54 градуса — Найти значение Cos 54 градуса
LearnPracticeDownload
Значение cos 54 градуса равно 0,5877852. . . . Cos 54 градуса в радианах записывается как cos (54° × π/180°), т. е. cos (3π/10) или cos (0,942477…). В этой статье мы обсудим способы нахождения значения cos 54 градусов на примерах.
е. cos (3π/10) или cos (0,942477…). В этой статье мы обсудим способы нахождения значения cos 54 градусов на примерах.
- Cos 54°: 0,5877852. . .
- Cos 54° в дробях: √(10 — 2√5)/4
- Cos (-54 градуса): 0,5877852. . .
- Cos 54° в радианах: cos (3π/10) или cos (0,9424777 . . .)
Каково значение Cos 54 градуса?
Значение cos 54 градуса в десятичной системе равно 0,587785252. . .. Cos 54 градуса также можно выразить с помощью эквивалента данного угла (54 градуса) в радианах (0,94247 . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/ 180°)
⇒ 54 градуса = 54° × (π/180°) рад = 3π/10 или 0,9424 . . .
∴ cos 54 ° = cos (0,9424) = √ (10 — 2 √ 5) / 4 или 0,5877852. . .
Объяснение:
Для cos 54 градуса угол 54° лежит между 0° и 90° (первый квадрант).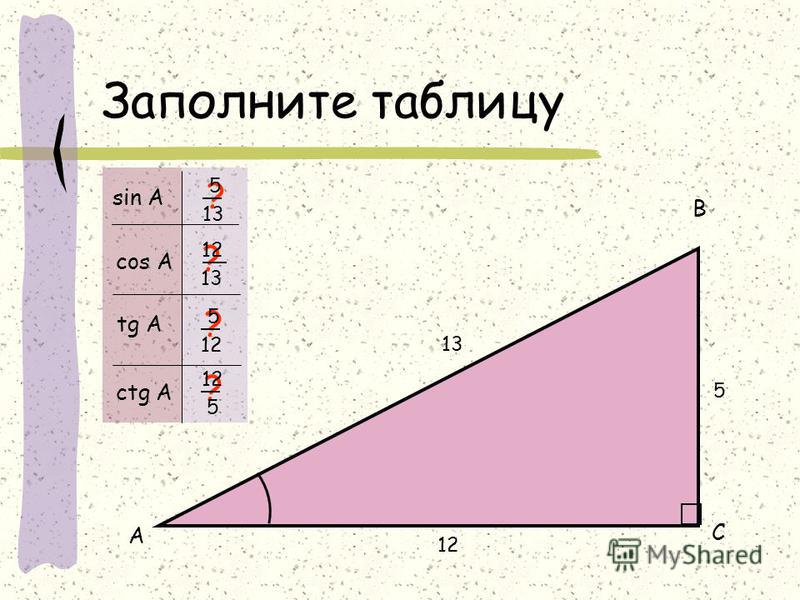 Поскольку функция косинуса положительна в первом квадранте, значение cos 54° = √(10 — 2√5)/4 или 0,5877852. . .
Поскольку функция косинуса положительна в первом квадранте, значение cos 54° = √(10 — 2√5)/4 или 0,5877852. . .
Поскольку функция косинуса является периодической функцией, мы можем представить cos 54° как cos 54 градуса = cos(54° + n × 360°), n ∈ Z.
⇒ cos 54° = cos 414° = cos 774° и так далее.
Примечание: Поскольку косинус — четная функция, значение cos(-54°) = cos(54°).
Методы определения значения косинуса 54 градуса
Функция косинуса положительна в 1-м квадранте. Значение cos 54° составляет 0,58778. . .. Мы можем найти значение cos 54 градуса по:
- Используя Unit Circle
- Использование тригонометрических функций
Cos 54 градуса с использованием единичной окружности
Чтобы найти значение cos 54 градуса с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 54° с положительной осью x.
- Cos 54 градусов равен координате x (0,5878) точки пересечения (0,5878, 0,809) единичной окружности и r.

Следовательно, значение cos 54° = x = 0,5878 (приблизительно)
Cos 54° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos 54 градуса как:
- ± √(1-sin² (54°))
- ± 1/√(1 + tan²(54°))
- ± кроватка 54°/√(1 + кроватка²(54°))
- ±√(косек²(54°) — 1)/косек 54°
- 1/сек 54°
Примечание. Поскольку 54° лежит в 1-м квадранте, окончательное значение cos 54° будет положительным.
Мы можем использовать тригонометрические тождества для представления cos 54° как
- -cos(180° — 54°) = -cos 126°
- -cos(180° + 54°) = -cos 234°
- sin(90° + 54°) = sin 144°
- sin(90° — 54°) = sin 36°
☛ Также проверьте:
- cos 270 градусов
- потому что 10 градусов
- потому что 210 градусов
- потому что 95 градусов
- потому что 71 градус
- потому что 57 градусов
Примеры использования Cos 54 градусов
Пример 1: Упростить: 3 (cos 54°/sin 144°)
Решение:
Мы знаем, что cos 54° = sin 144°
⇒ 3 cos 54°/sin 144° = 3 (cos 54°/cos 54°)
= 3(1) = 3Пример 2: Используя значение cos 54°, решите: (1-sin²(54°)).

Решение:
Мы знаем, (1-sin²(54°)) = (cos²(54°)) = 0,3455
⇒ (1-sin²(54°)) = 0,3455Пример 3. Найдите значение 2 cos(54°)/3 sin(36°).
Решение:
Используя тригонометрические тождества, мы знаем, что cos(54°) = sin(90° — 54°) = sin 36°.
⇒ cos(54°) = sin(36°)
⇒ Значение 2 cos(54°)/3 sin(36°) = 2/3
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронировать бесплатный пробный урок
Часто задаваемые вопросы о Cos 54 градуса
Что такое Cos 54 градуса?
Cos 54 градуса — значение тригонометрической функции косинуса для угла, равного 54 градусам. Значение cos 54° составляет √(10 — 2√5)/4 или 0,5878 (приблизительно)
Значение cos 54° составляет √(10 — 2√5)/4 или 0,5878 (приблизительно)
Каково значение Cos 54° в пересчете на Cosec 54°?
Поскольку функцию косинуса можно представить с помощью функции косеканса, мы можем записать cos 54° как [√(cosec²(54°) — 1)/cosec 54°]. Значение cosec 54° равно 1,23606.
Как найти косинус 54° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos 54° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(54°))
- ± 1/√(1 + tan²(54°))
- ± кроватка 54°/√(1 + кроватка²(54°))
- ± √(косек²(54°) — 1)/косек 54°
- 1/сек 54°
☛ Также проверьте: тригонометрическую таблицу
Каково значение Cos 54 градусов относительно Tan 54°?
Мы знаем, что, используя тригонометрические тождества, мы можем записать cos 54° как 1/√(1 + tan²(54°)). Здесь значение тангенса 54° равно 1,376381.
Как найти значение Cos 54 градуса?
Значение cos 54 градуса можно рассчитать, построив угол 54° с осью x и затем найдя координаты соответствующей точки (0,5878, 0,809) на единичной окружности. Значение cos 54° равно координате x (0,5878). ∴ cos 54° = 0,5878.
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядная программа
Mathway | Популярные проблемы
92| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найдите точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.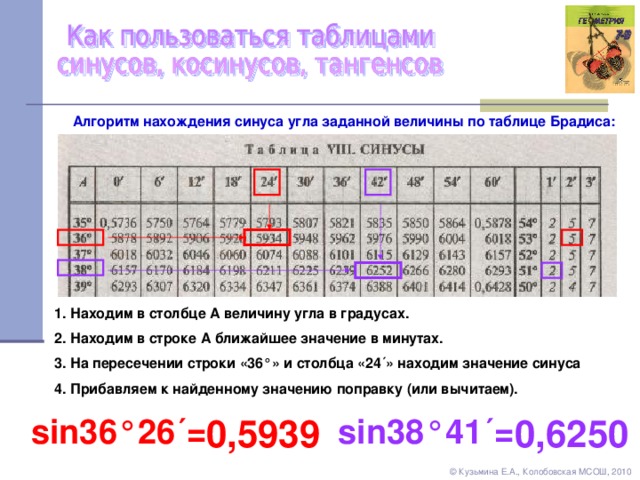 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек (60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт. )/4 )/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найдите точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | грех((2pi)/3) | |
| 88 | Найти точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найдите точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Значение Cos(54) — Косинус
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дом >> Площадь | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор — cos(54) — Solumaths
Cos, расчет онлайн
Резюме:
Тригонометрическая функция cos вычисляет cos угла в радианах, градусов или градианов.
cos online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить косинус ,
синус
и касательная
угла через одноименные функции.
Косинус тригонометрической функции отметил cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, грады и радианы, которые по умолчанию являются угловыми единицами.
- Расчет косинуса
- Специальные значения косинуса
- Основные свойства
- `cos(-x)= cos(x)`
- `cos(x+2*k*pi)=cos(x)`
- `cos(pi-x)=-cos(x) `
- `cos(pi+x)=-cos(x)`
- `cos(pi/2-x)=sin(x)`
- `cos(pi/2+x)=-sin(x) )`
- Производная косинуса
- Первообразная косинуса
- Свойства функции косинуса
- Уравнение с косинусом
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : грех. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
- Кто мы
- Бесплатные видео
- Лучшие учителя
- охваченных тем
- Членство
- О
- Математика
- Наука
- Английский
- Подготовка к тесту
- Колледж
- Войти
- Начните бесплатный пробный период
- Все
- 29 Предварительный расчет
- 22 Тригонометрия
- 3 Геометрия
Закон косинусов
Геометрия Базовая тригонометрия
Как определить и использовать закон косинусов.

закон косинусотношений треугольников
Закон косинусов
Тригонометрия Базовая тригонометрия
Как определить и использовать закон косинусов.
закон косинусотношений треугольников
Закон косинусов
Предварительный расчет Базовая тригонометрия
Как определить и использовать закон косинусов.

закон косинусотношений треугольников
Формулы сложения косинусов
Тригонометрия Расширенная тригонометрия
Как вывести косинус формулы разности.
единичный кругзакон косинусовформула расстояниякосинус разностной формулы
Формулы сложения косинусов
Предварительный расчет Расширенная тригонометрия
Как вывести косинус формулы разности.

единичный кругзакон косинусовформула расстояниякосинус разностной формулы
Определения синуса и косинуса
Тригонометрия Тригонометрические функции
Как мы определяем синус и косинус для всех мер угла, используя единичную окружность.
sinecosineопределение синуса и косинуса прямоугольного треугольника в стандартной позиции, определение синуса и косинуса окружности в единице измерения
Определения синуса и косинуса
Предварительный расчет Тригонометрические функции
Как мы определяем синус и косинус для всех мер угла, используя единичную окружность.

sinecosineопределение синуса и косинуса прямоугольного треугольника в стандартной позиции, определение синуса и косинуса окружности в единице измерения
Функция арккосинуса
Тригонометрия Расширенная тригонометрия
Как ограничить область определения косинуса, чтобы он имел обратную функцию.
обратные функции один к одному обратный косинус косинус
Функция арккосинуса
Предварительный расчет Расширенная тригонометрия
Как ограничить область определения косинуса, чтобы он имел обратную функцию.

обратные функцииодин к одномуобратный косинус/косинус
Найдите уравнение для синуса или косинуса
Тригонометрия Тригонометрические функции
Как определить график растянутой косинусной кривой.
синус, косинус, период, амплитуда, пересечение, точки поворота
г.
 Найдите уравнение для синуса или косинуса.
Найдите уравнение для синуса или косинуса.Предварительный расчет Тригонометрические функции
Как определить график растянутой косинусной кривой.
синус, косинус, период, амплитуда, пересечение, точки поворота
Оценка синуса и косинуса под другими специальными углами
Тригонометрия Тригонометрические функции
Как измерить синус и косинус числа 150.

sinecosineunit Окружность определения синуса и косинус угла в стандартном положении опорные углы
Оценка синуса и косинуса под другими специальными углами
Предварительный расчет Тригонометрические функции
Как измерить синус и косинус числа 150.
sinecosineunit окружность определения синуса и косинус угла в стандартном положении опорных углов
Вычисление синуса и косинуса под специальными острыми углами
Тригонометрия Тригонометрические функции
Как измерить синус и косинус числа пи/4?
sinecosineunit Окружность определения синусов и косинусов в стандартном положении
Вычисление синуса и косинуса под особыми острыми углами
Предварительный расчет Тригонометрические функции
Как измерить синус и косинус числа пи/4?
sinecosineunit Окружность определения синуса и косинус угла в стандартном положении
Тригонометрические соотношения: косинус
Геометрия Базовая тригонометрия
Как определить отношение косинусов и найти косинус угла в прямоугольном треугольнике.

отношение тригонометриипрямоугольного треугольникасинус SOHCATOA
Тригонометрические отношения: косинус
Тригонометрия Базовая тригонометрия
Как определить отношение косинусов и найти косинус угла в прямоугольном треугольнике.
отношение тригонометриипрямоугольного треугольникасинус SOHCAHTOA
Тригонометрические соотношения: косинус
Предварительный расчет Базовая тригонометрия
Как определить отношение косинусов и найти косинус угла в прямоугольном треугольнике.

отношение тригонометриипрямоугольного треугольникасинус SOHCATOA
г. Использование формул сложения синуса и косинуса для доказательства тождества
Тригонометрия Расширенная тригонометрия
Как использовать формулы сложения синуса и косинуса для доказательства тождества кофункций.
формулы сложения синусаформулы сложения синуса
Другие формы формулы косинуса двойного угла
Тригонометрия Расширенная тригонометрия
Как вывести еще две формулы косинуса двойного угла.

тождество Пифагораформулы косинуса двойного угла
- 1 Высшая национальная школа информатики, Laboratoire des Méthodes de Conception des Systèmes, BP 68M, 16309 Oued-Smar, Alger Алжир.

- 2 Лаборатория LIST Университета М’Хамеда Бугара Бумердес, проспект Независимости, 35000 Бумердес, Алжир.
- 3 Центр исследований и оптимизации искусственного интеллекта, Университет Торренса, Австралия, Fortitude Valley, Brisbane, QLD 4006 Australia.
- 4 Лаборатория LISV, Версальский университет Сен-Кантен-ан-Ивелин, 10-12 Авеню Европы, 78140 Велизи, Франция.
- PMID: 34092884
- PMCID: PMC8171367
- DOI: 10.1007/с10462-021-10026-у
- 1 Высшая национальная школа информатики, Laboratoire des Méthodes de Conception des Systèmes, BP 68M, 16309Уэд-Смар, Алжир Алжир.
- 2 Лаборатория LIST Университета М’Хамеда Бугара Бумердес, проспект Независимости, 35000 Бумердес, Алжир.

- 3 Центр исследований и оптимизации искусственного интеллекта, Университет Торренса, Австралия, Fortitude Valley, Brisbane, QLD 4006 Australia.
- 4 Лаборатория LISV, Версальский университет Сен-Кантен-ан-Ивелин, 10-12 Авеню Европы, 78140 Велизи, Франция.
- PMID: 34092884
- PMCID: PMC8171367
- DOI: 10.1007/с10462-021-10026-у
Гибридная стратегия Q-обучения на основе синуса и косинуса для решения проблемы минимизации комбинаторного набора тестов.
Замли К.З., Дин Ф., Ахмед Б.С., Бурес М. Замли КЗ и др. ПЛОС Один. 2018 17 мая; 13 (5): e0195675. doi: 10.1371/journal.pone.0195675. Электронная коллекция 2018. ПЛОС Один. 2018. PMID: 29771918 Бесплатная статья ЧВК.
Диспетчеризация экономической нагрузки с использованием меметического синус-косинусного алгоритма.

Аль-Бетар М.А., Авадаллах М.А., Зитар Р.А., Ассалех К. Аль-Бетар М.А. и соавт. J Ambient Intel Humaniz Comput. 2022 фев. 7:1-29. doi: 10.1007/s12652-022-03731-1. Онлайн перед печатью. J Ambient Intel Humaniz Comput. 2022. PMID: 35154502 Бесплатная статья ЧВК.
Новый мультисинусно-косинусный алгоритм для задач неограниченной оптимизации.
Рехман М.З., Хан А., Газали Р., Аамир М., Нави Н.М. Рехман М.З. и др. ПЛОС Один. 2021 6 августа; 16 (8): e0255269. doi: 10.1371/journal.pone.0255269. Электронная коллекция 2021. ПЛОС Один. 2021. PMID: 34358237 Бесплатная статья ЧВК.
Алгоритм арифметико-тригонометрической оптимизации с приложением для управления технологической установкой, работающей под давлением в реальном времени.

Деван П.А.М., Хуссин Ф.А., Ибрагим Р.Б., Бинги К., Нагараджапандян М., Ассаад М. Деван ПАМ и др. Датчики (Базель). 2022 13 января; 22 (2): 617. дои: 10.3390/s22020617. Датчики (Базель). 2022. PMID: 35062578 Бесплатная статья ЧВК.
Интеллектуальный тригонометрический фильтр частиц для визуального отслеживания.
Ненават Х., Ашвини К., Джатот Р.К., Мирджалили С. Ненават Х. и др. ИСА Транс. 2022, сен; 128 (часть A): 460–476. doi: 10.1016/j.isatra.2021.09.014. Epub 2021 24 сентября. ИСА Транс. 2022. PMID: 34610870
Обнаружение неисправностей редукторов ветряных турбин на основе IBOA-ERF.
Тан М.
 , Цао С., У Х., Чжу Х., Тан Дж., Пэн З., Ван Ю.
Тан М и др.
Датчики (Базель). 2022 9 сентября; 22 (18): 6826. дои: 10.3390/s22186826.
Датчики (Базель). 2022.
PMID: 36146174
Бесплатная статья ЧВК.
, Цао С., У Х., Чжу Х., Тан Дж., Пэн З., Ван Ю.
Тан М и др.
Датчики (Базель). 2022 9 сентября; 22 (18): 6826. дои: 10.3390/s22186826.
Датчики (Базель). 2022.
PMID: 36146174
Бесплатная статья ЧВК.Гибридные интеллектуальные модели на основе PCA для оценки предельной несущей способности стальных труб с бетонным заполнением, нагруженных в осевом направлении.
Хан К., Бисвас Р., Гудайниян Дж., Амин М.Н., Куреши Х.Дж., Араб АМА, Икбал М. Хан К. и др. Материалы (Базель). 2022 18 сентября; 15 (18): 6477. дои: 10.3390/ma15186477. Материалы (Базель). 2022. PMID: 36143788 Бесплатная статья ЧВК.
Классификация рака молочной железы с использованием оптимизированной системы трансферного обучения для кормления манта.
Багдади Н.
 А., Малки А., Магди Балаха Х., АбдулАзим Ю., Бадави М., Эльхосейни М.
Багдади Н.А. и соавт.
Компьютерные науки PeerJ. 2022 8 августа; 8:e1054. doi: 10.7717/peerj-cs.1054. Электронная коллекция 2022.
Компьютерные науки PeerJ. 2022.
PMID: 360
А., Малки А., Магди Балаха Х., АбдулАзим Ю., Бадави М., Эльхосейни М.
Багдади Н.А. и соавт.
Компьютерные науки PeerJ. 2022 8 августа; 8:e1054. doi: 10.7717/peerj-cs.1054. Электронная коллекция 2022.
Компьютерные науки PeerJ. 2022.
PMID: 360Бесплатная статья ЧВК.
Гибридная модель прогнозирования, основанная на SVR, для межфазной прочности сцепления ламинатов FRP с внешней связью на канавках с бетонными призмами.
Хан К., Икбал М., Бисвас Р., Амин М.Н., Али С., Гудайниян Дж., Алабдулла А.А., Араб АМА. Хан К. и др. Полимеры (Базель). 2022 29 июля; 14 (15): 3097. doi: 10.3390/polym14153097. Полимеры (Базель). 2022. PMID: 35956611 Бесплатная статья ЧВК.
Алгоритм оптимизации синтеза-деления (FuFiO).
Нухи Б.
 , Дараби Н., Сарех П., Баязиди Х., Дараби Ф., Талатахари С.
Нухи Б. и др.
Научный представитель 20 июля 2022 г .; 12 (1): 12396. doi: 10.1038/s41598-022-16498-4.
Научный представитель 2022.
PMID: 35859104
Бесплатная статья ЧВК.
, Дараби Н., Сарех П., Баязиди Х., Дараби Ф., Талатахари С.
Нухи Б. и др.
Научный представитель 20 июля 2022 г .; 12 (1): 12396. doi: 10.1038/s41598-022-16498-4.
Научный представитель 2022.
PMID: 35859104
Бесплатная статья ЧВК.- Абдель-Басет М., Чжоу Ю., Хезам И. Использование синусно-косинусного алгоритма в сочетании с методом Симпсона для численного интегрирования. Int J Math Oper Res. 2019;14(3):307–318. doi: 10.1504/IJMOR.2019.10020779. — DOI
- Abdel-Basset M, Mohamed R, Abouhawwash M, Chakrabortty RK, Ryan MJ (2021) EA-MSCA: эффективный многоцелевой модифицированный синусно-косинусный алгоритм с учетом энергии для планирования задач в реальном времени в многопроцессорных системах: методы и анализ.
 Экспертные системы с приложениями, стр. 114699
Экспертные системы с приложениями, стр. 114699
- Abdel-Basset M, Mohamed R, Abouhawwash M, Chakrabortty RK, Ryan MJ (2021) EA-MSCA: эффективный многоцелевой модифицированный синусно-косинусный алгоритм с учетом энергии для планирования задач в реальном времени в многопроцессорных системах: методы и анализ.
- Абдель-Фатах С., Эбид М., Камель С. (2019) Оптимальное распределение реактивной мощности с использованием модифицированного синусоидального алгоритма. In: 2019 Международная конференция по инновационным направлениям в вычислительной технике (ITCE). IEEE, стр. 510–514.
- Абдельсалам АА. Оптимальное распределение распределенных энергетических ресурсов для повышения надежности и экономической выгоды с использованием синус-косинусного алгоритма. Technol Econ Smart Grids поддерживает энергию. 2020;5(1):1–18. doi: 10.1007/s40866-020-00082-8. — DOI
- Абдельсалам А.

- Абдельсалам А.
Вычисление косинуса угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, вы должны сначала выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн от `pi/6`, введите cos(`pi/6`), после вычисления результат `sqrt(3)/2` возвращается.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и делать
расчеты со специальными связанными значениями в точной форме.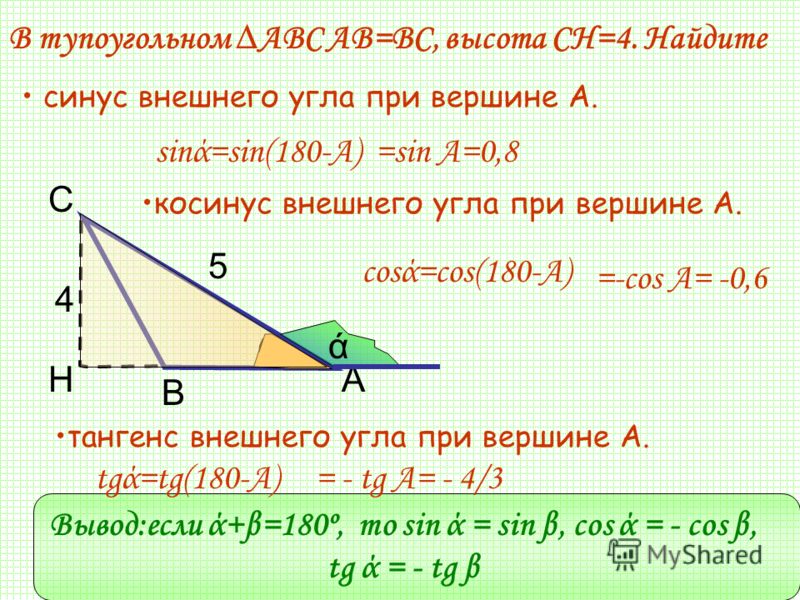
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 90, введите cos(90). возвращает 0.
Вычисление косинуса угла в градусах
Для вычисления косинуса угла в градианах необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 50, введите cos(50), после вычисления возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Косинус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список
специальные значения косинуса :
Вот список
специальные значения косинуса :
| cos(`2*pi`) | `1` | |||||||||||
| cos(`pi`) | `-1` | |||||||||||
| cos(`28 90 90 90` | ||||||||||||
| cos(`pi/4`) | `sqrt(2)/2` | |||||||||||
| cos(`pi/3`) | `1/2` | |||||||||||
| cos `) | `sqrt(3)/2` | |||||||||||
| cos(`2*pi/3`) | `-1/2` | |||||||||||
| cos(`3*pi/4`) | `-sqrt(2)/2` | |||||||||||
| cos(`5*pi/6`) | `-sqrt(3)/2` | |||||||||||
| cos(`0`) | `1` | |||||||||||
| cos(` pi`) | `1` | |||||||||||
| cos(`-pi`) | `-1` | |||||||||||
| cos(`pi/2`) | `09`488 pi/4`)
`AA x в RR, k в ZZ`, Производная косинуса равна -sin(x). Первообразная косинуса равна sin(x). Функция косинуса является четной функцией для каждого действительного x, `cos(-x)=cos(x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии. Калькулятор имеет решатель, который позволяет решать уравнение с косинусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или же `2*cos(x)=sqrt(2)` с этапами расчета. Синтаксис:cos(x), где x — мера угла в градусах, радианах или градах. Примеры:cos(`0`), возвращает 1 Производный косинус : Чтобы дифференцировать функцию косинуса онлайн,
можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса. Первообразная косинуса :Калькулятор первообразной позволяет вычислить первообразную функции косинуса. Первопроизводная от cos(x) есть первопроизводная(`cos(x)`)=`sin(x)` Предельный косинус :Калькулятор пределов позволяет вычислять пределы функции косинуса. предел cos(x) is limit(`cos(x)`) Обратная функция косинуса :обратная функция косинуса является функцией арккосинуса, отмеченной как arccos. Графический косинус:Графический калькулятор может отображать функцию косинуса в заданном интервале. Свойство функции косинуса:Функция косинуса является четной функцией. Расчет онлайн с косинусом См. также Список связанных калькуляторов: Напоминания о курсах, калькуляторы, упражнения и игры: тригонометрические функции, вещественные функции
косинус0012Вопросы? Обратная связь? работает на программном обеспечении для живого чата OlarkВсесторонний обзор алгоритма синус-косинуса: варианты и приложения. 2021;54(7):5469-5540. doi: 10.1007/s10462-021-10026-y. Epub 2021 2 июня. Асма Бенмессауд Габис 1 , Яссин Мераихи 2 , Сейедали Мирджалили 3 , Амар Рамдан-Шериф 4 ПринадлежностиБесплатная статья ЧВК Асма Бенмессауд Габис и др. Бесплатная статья ЧВК . 2021;54(7):5469-5540. doi: 10.1007/s10462-021-10026-y. Epub 2021 2 июня. АвторыАсма Бенмессауд Габис 1 , Яссин Мераихи 2 , Сейедали Мирджалили 3 , Амар Рамдан-Шериф 4 ПринадлежностиАбстрактный Синусно-косинусный алгоритм (SCA) — это новый метаэвристический алгоритм, основанный на свойствах тригонометрических синусоидальных и косинусоидальных функций. Ключевые слова: Метаэвристика; Оптимизация; популяционный алгоритм; Синус-косинусный алгоритм. © Автор(ы), по эксклюзивной лицензии Springer Nature B.V. 2021. Цифры
Рис. 1 Классификация метаэвристических алгоритмов
Рис. 1 Классификация метаэвристических алгоритмов рисунок 1Классификация метаэвристических алгоритмов
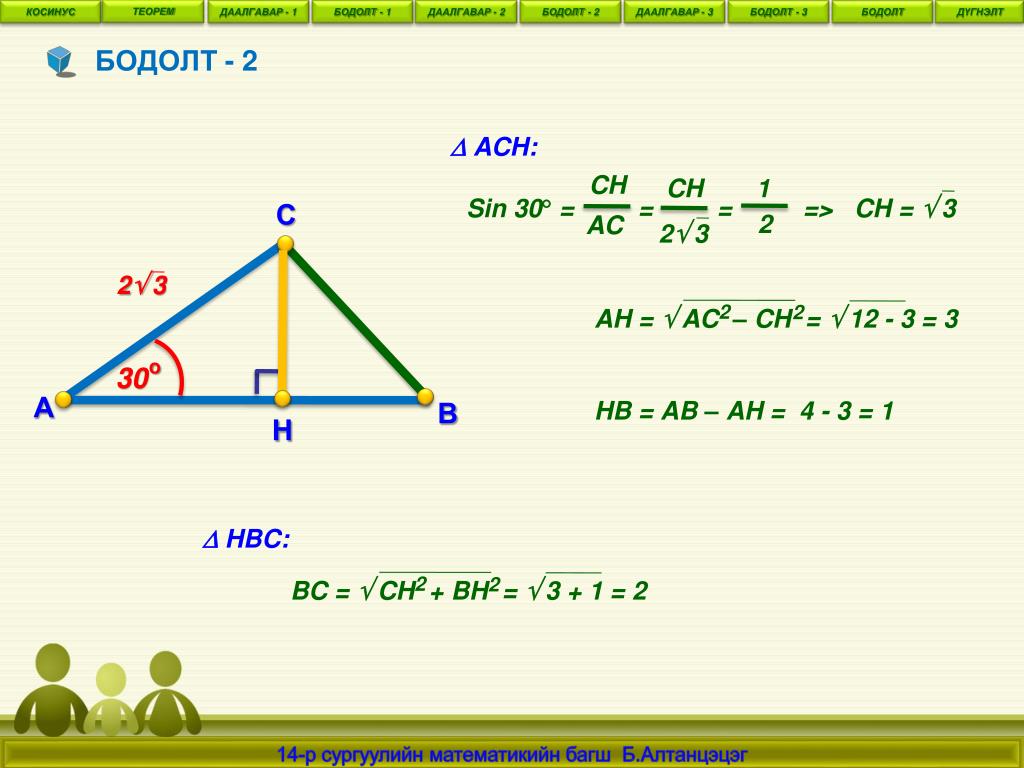
Рис. 2 Количество публикаций по SCA…
Рис. 2 Количество публикаций по SCA в научных базах данных Рис. 2Количество публикаций по SCA по научным базам данных
Рис. Количество публикаций по SCA…
Рис. 3 Количество публикаций по SCA в год Рис. 3Количество публикаций по SCA в год
Рис. 4 Топ-10 стран по…
Рис. 4 Топ-10 стран по количеству публикаций по алгоритму SCA Рис. 4Топ-10 стран по количеству публикаций по алгоритму SCA
Рис. 5 Топ-10 ключевых слов, связанных с SCA
Рис. Топ-10 ключевых слов, связанных с SCA Рис. 5Топ-10 ключевых слов, связанных с SCA
Рис. 6 Влияние синуса косинуса…
Рис. 6 Эффекты функций синуса косинуса в уравнениях. (1) и (2) на… Рис. 6Эффекты функций синуса и косинуса в уравнениях. (1) и (2) на следующей позиции (Mirjalili 2016b)
Рис. 7 Блок-схема синуса косинуса…
Рис. 7 Блок-схема алгоритма синус-косинуса Рис.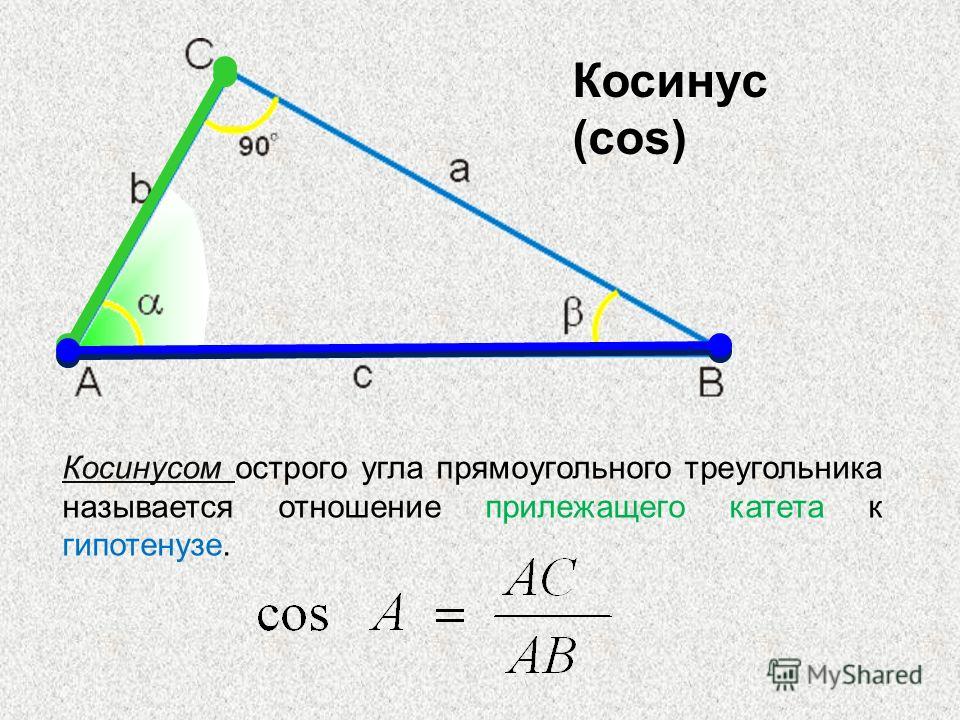 7 7 Блок-схема алгоритма синус-косинуса
Рис. 8 Варианты SCA
Рис. 8 Варианты SCA Рис. 8Варианты SCA
Рис. 9 Модифицированные версии SCA
Рис. 9 Модифицированные версии SCA Рис. 9Модифицированные версии SCA
Рис. 10 Модифицированные версии SCA
Рис. Модифицированные версии SCA Рис. 10Модифицированные версии SCA
Рис. 11 Гибридные версии SCA
Рис. 11 Гибридные версии SCA Рис. 11Гибридные версии SCA
Рис. 12 Гибридные версии SCA
Рис. 12 Гибридные версии SCA Рис. 12Гибридные версии SCA
Рис. Приложения SCA
Рис. 13 Приложения SCA Рис. 13Приложения SCA См. это изображение и информацию об авторских правах в PMC Похожие статьиПосмотреть все похожие статьи ЦитируетсяПросмотреть все статьи «Цитируется по» использованная литература |


 ..
.. ..
..
 ..
.. ..
..
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.

 Найдите уравнение для синуса или косинуса.
Найдите уравнение для синуса или косинуса.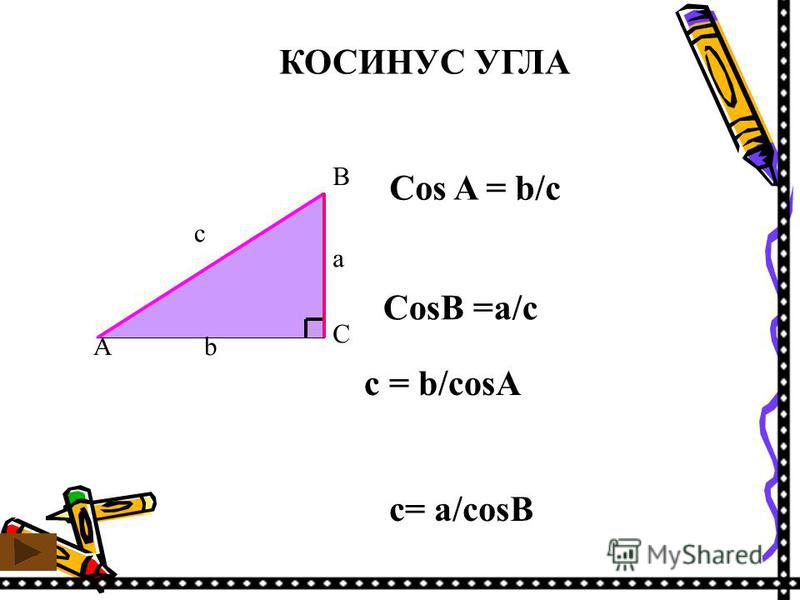



 Артиф Интелл Rev.
2021.
Артиф Интелл Rev.
2021.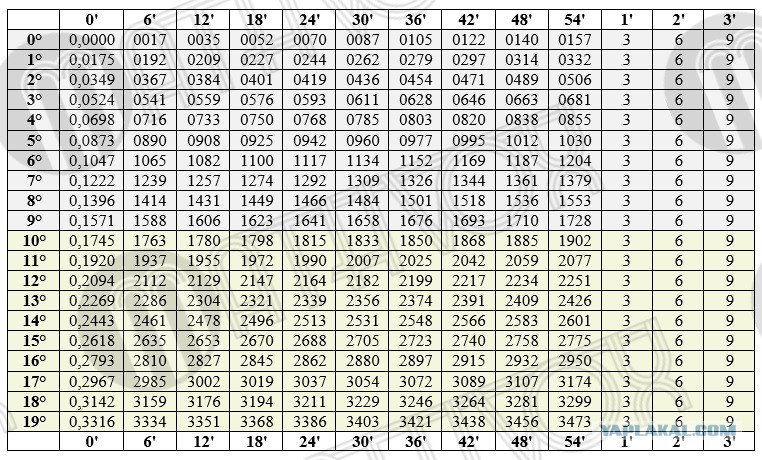
 С момента своего появления Мирджалили в 2016 году SCA привлекла большое внимание исследователей и широко использовалась для решения различных задач оптимизации в нескольких областях. Это внимание связано с его разумным временем выполнения, хорошей скоростью ускорения сходимости и высокой эффективностью по сравнению с несколькими хорошо известными алгоритмами оптимизации, доступными в литературе. В данной статье представлен краткий обзор базовой SCA и ее вариантов, разделенных на модифицированные, многокритериальные и гибридные версии. Кроме того, описаны приложения SCA в нескольких областях, таких как классификация, обработка изображений, планирование маршрута робота, планирование, радиальные распределительные сети и другие инженерные проблемы. Наконец, в документе рекомендованы некоторые потенциальные направления будущих исследований SCA.
С момента своего появления Мирджалили в 2016 году SCA привлекла большое внимание исследователей и широко использовалась для решения различных задач оптимизации в нескольких областях. Это внимание связано с его разумным временем выполнения, хорошей скоростью ускорения сходимости и высокой эффективностью по сравнению с несколькими хорошо известными алгоритмами оптимизации, доступными в литературе. В данной статье представлен краткий обзор базовой SCA и ее вариантов, разделенных на модифицированные, многокритериальные и гибридные версии. Кроме того, описаны приложения SCA в нескольких областях, таких как классификация, обработка изображений, планирование маршрута робота, планирование, радиальные распределительные сети и другие инженерные проблемы. Наконец, в документе рекомендованы некоторые потенциальные направления будущих исследований SCA.
 3
3 5
5 10
10 13
13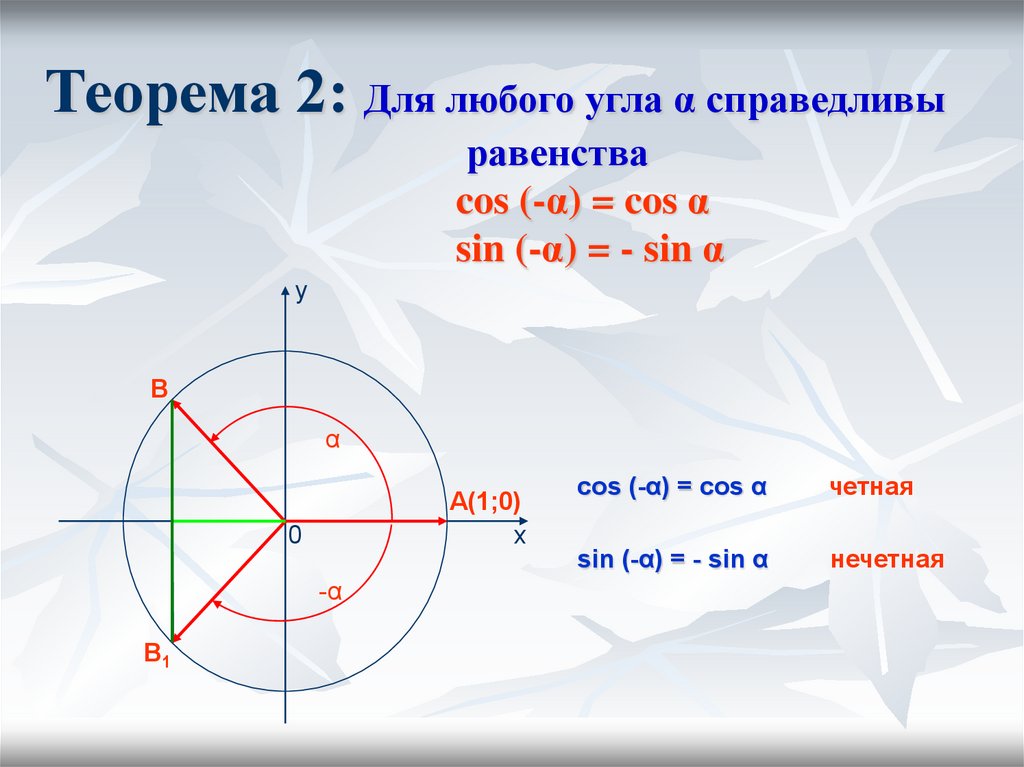

 , Цао С., У Х., Чжу Х., Тан Дж., Пэн З., Ван Ю.
Тан М и др.
Датчики (Базель). 2022 9 сентября; 22 (18): 6826. дои: 10.3390/s22186826.
Датчики (Базель). 2022.
PMID: 36146174
Бесплатная статья ЧВК.
, Цао С., У Х., Чжу Х., Тан Дж., Пэн З., Ван Ю.
Тан М и др.
Датчики (Базель). 2022 9 сентября; 22 (18): 6826. дои: 10.3390/s22186826.
Датчики (Базель). 2022.
PMID: 36146174
Бесплатная статья ЧВК. А., Малки А., Магди Балаха Х., АбдулАзим Ю., Бадави М., Эльхосейни М.
Багдади Н.А. и соавт.
Компьютерные науки PeerJ. 2022 8 августа; 8:e1054. doi: 10.7717/peerj-cs.1054. Электронная коллекция 2022.
Компьютерные науки PeerJ. 2022.
PMID: 360
А., Малки А., Магди Балаха Х., АбдулАзим Ю., Бадави М., Эльхосейни М.
Багдади Н.А. и соавт.
Компьютерные науки PeerJ. 2022 8 августа; 8:e1054. doi: 10.7717/peerj-cs.1054. Электронная коллекция 2022.
Компьютерные науки PeerJ. 2022.
PMID: 360 , Дараби Н., Сарех П., Баязиди Х., Дараби Ф., Талатахари С.
Нухи Б. и др.
Научный представитель 20 июля 2022 г .; 12 (1): 12396. doi: 10.1038/s41598-022-16498-4.
Научный представитель 2022.
PMID: 35859104
Бесплатная статья ЧВК.
, Дараби Н., Сарех П., Баязиди Х., Дараби Ф., Талатахари С.
Нухи Б. и др.
Научный представитель 20 июля 2022 г .; 12 (1): 12396. doi: 10.1038/s41598-022-16498-4.
Научный представитель 2022.
PMID: 35859104
Бесплатная статья ЧВК. Экспертные системы с приложениями, стр. 114699
Экспертные системы с приложениями, стр. 114699