правила применения формул сокращенного умножения
Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.
Формулы для квадратов применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.
Формулы для кубов не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.
Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.
Формулы для четвертого и пятого степени в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях.
Формулы для степени
n
расписаны
через биномиальные коэффициенты с использованием факториалов следующие
Пример 1. 7.
7.
Решение. Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты
Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад
Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7 ).
Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.
Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук. Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
И так вот они:
Первая х 2 — у 2 = (х — у) (х+у) .Чтобы рассчитать разность квадратов двух выражений надо перемножить разности этих выражений на их суммы.
Вторая (х + у) 2 = х 2 + 2ху + у 2 . Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Третья (х — у) 2 = х 2 — 2ху + у 2 . Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2 + у 3. Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
Пятая (х — у) 3 = х 3
— 3х 2 у + 3ху 2 — у 3 . Чтобы рассчитать куб разности двух выражений необходимо от куба первого выражения отнять утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.Шестая х 3 + у 3 = (х + у) (х 2 — ху + у 2) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.
Седьмая х 3 — у 3 = (х — у) (х 2 + ху + у 2) Чтобы произвести вычисление разности кубов двух выражений надо умножить разность первого и второго выражения на неполный квадрат суммы этих выражений.
Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).
О существовании этих закономерностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.
Разберем доказательство квадрата суммы (а + b) 2 = a 2 +2ab +b 2 .
Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения . Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).
Первая формула сокращенного умножения называется разность квадратов . Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.
а 2 — b 2 = (а — b)(a + b)
Разберем для наглядности:
22 2 — 4 2 = (22-4)(22+4)=18 * 26 = 468
9а 2 — 4b 2 c 2 = (3a — 2bc)(3a + 2bc)
Вторая формула о сумме квадратов . Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.
(а + b) 2 = a 2 +2ab + b 2
Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.
Так к примеру: квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544
Третья формула это квадрат разности . Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.
Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.
(а +b) 2 = а 2 — 2аb + b 2
где (а — b) 2 равняется (b — а) 2 . В доказательство чему, (а-b) 2 = а 2 -2аb+b 2 = b 2 -2аb + а 2 = (b-а) 2
Четвертая формула сокращенного умножения называется куб суммы . Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.
(а+b) 3 = а 3 + 3а 2 b + 3аb 2 + b 3
Пятая, как вы уже поняли называется куб разности . Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.
(а-b) 3 = а 3 — 3а 2 b + 3аb 2 — b 3
Шестая называется — сумма кубов . Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.
а 3 + b 3 = (а+b)(а 2 -аb+b 2)
По другому можно сказать сумму кубов можно назвать произведение в двух скобках.
Седьмая и заключительная, называется разность кубов (ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.
а 3 — b 3 = (а-b)(а 2 +аb+b 2)
И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.
Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!
Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке Интернет бизнес с Орифлейм . Там все очень подробно написано и показано. Будет интересно!
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Математика для самых маленьких. Детский сад — 7 класс. / / Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней.
| |||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||
Правила использования формул сокращенного умножения
В предыдущем уроке мы занимались факторизацией. Мы освоили два метода: вынос общего множителя за скобки и группировку. В этом уроке, следующий мощный метод: формулы сокращенного умножения . В краткой заметке — БСС.
Мы освоили два метода: вынос общего множителя за скобки и группировку. В этом уроке, следующий мощный метод: формулы сокращенного умножения . В краткой заметке — БСС.
Формулы сокращенного умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) необходимы во всех разделах математики. Они используются при упрощении выражений, решении уравнений, умножении полиномов, сокращении дробей, решении интегралов и т.д. и т.п. Словом, есть все основания иметь с ними дело. Понять, откуда они берутся, зачем нужны, как их запомнить и как применять.
Понятно?)
Откуда берутся формулы сокращенного умножения?
Равенства 6 и 7 записываются не совсем обычным образом. Как и наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее откуда ФСО.
Они взяты из умножения.) Например:
(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2
Вот так, никаких научных фокусов. Мы просто умножаем скобки и даем подобные. Вот так получается все формулы сокращенного умножения. сокращенное умножение потому, что в самих формулах нет умножения скобок и сокращения подобных. Сокращено.) Сразу выдается результат.
Мы просто умножаем скобки и даем подобные. Вот так получается все формулы сокращенного умножения. сокращенное умножение потому, что в самих формулах нет умножения скобок и сокращения подобных. Сокращено.) Сразу выдается результат.
пох надо знать наизусть. Без первой тройки о тройке и мечтать нельзя, без остальных — о четверке с пятеркой.)
Зачем нужны формулы сокращенного умножения?
Есть две причины выучить и даже запомнить эти формулы. Первое — готовый ответ на автомате резко снижает количество ошибок. Но это не основная причина. А вот и второй…
Кстати, у меня для вас есть еще парочка интересных сайтов.)
Можно потренироваться решать примеры и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Математические выражения (формулы) Сокращенное умножение (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) чрезвычайно незаменимы во многих областях точной наук. Эти 7 символов незаменимы при упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и многом другом. Так что будет очень полезно разобраться, как они получаются, для чего нужны, а главное, как их запомнить и потом применять. Затем применяя формулы сокращенного умножения на практике, самое сложное будет посмотреть что такое Х и что есть. Очевидно никаких ограничений на a и b нет, а значит это может быть любое числовое или буквальное выражение.
Эти 7 символов незаменимы при упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и многом другом. Так что будет очень полезно разобраться, как они получаются, для чего нужны, а главное, как их запомнить и потом применять. Затем применяя формулы сокращенного умножения на практике, самое сложное будет посмотреть что такое Х и что есть. Очевидно никаких ограничений на a и b нет, а значит это может быть любое числовое или буквальное выражение.
И так вот они:
Сначала х 2 — на 2 = (x — y) (x + y) .Чтобы вычислить разность квадратов двух выражений, надо умножить разности этих выражений по их суммам.
Секунда (x + y) 2 = x 2 + 2xy + y 2 . Чтобы найти сумму в квадрате двух выражений, нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Третий (x — y) 2 = x 2 — 2xy + y 2 . Чтобы вычислить разность в квадрате двух выражений, нужно из квадрата первого выражения вычесть удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Чтобы вычислить разность в квадрате двух выражений, нужно из квадрата первого выражения вычесть удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Четвертый (x + y) 3 = x 3 + 3x 2 y + 3x 2 + at 3. выражение, умноженное на произведение квадрата первого выражения на второе, умноженное на произведение квадрата первого выражения на второе, на произведение квадрата второго выражения, умноженное на три, и умноженное на куб второго выражения.
Пятый (х — у) 3 = х 3 — 3х 2 у + 3х 2 — по телефону 3 . Для вычисления куба разностей двух выражений необходимо из куба первого выражения вычесть троекратное произведение квадрата первого выражения на второе плюс троекратное произведение первого выражения на квадрат второго минус куб второго выражения.
шестой х 3 + у 3 = (х + у) (х 2 — ху + у 2) Чтобы вычислить сумму кубов двух выражений, нужно перемножить суммы первых а вторые выражения неполным квадратом разности этих выражений.
седьмой х 3 — при 3 = (х — у) (х 2 + ху + у 2) Чтобы произвести расчет куб разницы два выражения, надо разность умножить первого и второго выражений на неполный квадрат суммы этих выражений.
Нетрудно запомнить, что все формулы используются для выполнения расчетов в обратном направлении (справа налево).
О существовании этих закономерностей было известно около 4 тысяч лет назад. Их широко использовали жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и не использовали буквы в расчетах.
Давайте проанализируем сумму квадратов доказательств (a + b) 2 = a 2 + 2ab + b 2 .
Эту математическую закономерность доказал древнегреческий ученый Евклид, работавший в Александрии в 3 веке до н.э., для этого он использовал геометрический метод доказательства формулы, так как ученые древней Эллады не использовали буквы для обозначения чисел . Они везде употребляли не «а 2», а «квадрат на отрезке а», не «аб», а «прямоугольник, заключенный между отрезками а и Ь».
Формулы или правила сокращенного умножения используются в арифметике, а точнее в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами формулы выведены из существующих в алгебре правил умножения нескольких многочленов.
Использование этих формул обеспечивает достаточно быстрое решение различных математических задач, а также помогает упростить выражения. Правила алгебраических преобразований позволяют производить некоторые манипуляции с выражениями, следуя которым можно получить выражение в левой части равенства, которое в правой части, или преобразовать правую часть равенства (чтобы получить выражение в слева после знака равенства).
Удобно знать формулы сокращенного умножения по памяти, так как они часто используются при решении задач и уравнений. Основные формулы, включенные в этот список, и их названия приведены ниже.
квадрат суммы
Чтобы вычислить квадрат суммы, нужно найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения это правило записывается так: (a + c)² = a² + 2ac + c².
В виде выражения это правило записывается так: (a + c)² = a² + 2ac + c².
Квадрат разности
Для вычисления квадрата разности нужно вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятое с обратным знаком ) и квадрат второго числа. В виде выражения это правило выглядит так: (а — с)² = а² — 2ас + с².
Разность квадратов
Формула разности двух чисел в квадрате равна произведению суммы этих чисел на их разность. В виде выражения это правило выглядит так: а² — с² = (а + с) (а — с).
куб суммы
Чтобы вычислить куб суммы двух слагаемых, нужно вычислить сумму, состоящую из куба первого слагаемого, утроить произведение квадрата первого слагаемого и второго, утроить произведение первого члена на квадрат второго и куб второго члена. В виде выражения это правило выглядит так: (a + c)³ = a³ + 3a²c + 3ac² + c³.
Сумма кубов
Согласно формуле равна произведению суммы этих слагаемых на их неполный квадрат разности. В виде выражения это правило выглядит так: а³ + с³ = (а + с) (а² — ас + с²).
В виде выражения это правило выглядит так: а³ + с³ = (а + с) (а² — ас + с²).
Пример. Необходимо вычислить объем фигуры, которая образуется при сложении двух кубиков. Известны только величины их сторон.
Если значения сторон малы, то легко произвести расчеты.
Если длины сторон выражены громоздкими числами, то в этом случае проще применить формулу «Суммы кубов», что значительно упростит расчеты.
куб разности
Выражение для кубической разности звучит так: как сумму третьей степени первого члена утроить отрицательное произведение квадрата первого члена на второй утроить произведение первого члена на квадрат второго и отрицательный куб второго члена. В виде математического выражения куб разности выглядит так: (а — с)³ = а³ — 3а²с + 3ас² — с³.
Разность кубов
Формула разности кубов отличается от суммы кубов только одним знаком. Таким образом, разность кубов представляет собой формулу, равную произведению разности этих чисел на их неполный квадрат суммы. В виде математического выражения разность кубов выглядит так: а 3 — с 3 = (а — с) (а 2 + ас + с 2).
В виде математического выражения разность кубов выглядит так: а 3 — с 3 = (а — с) (а 2 + ас + с 2).
Пример. Необходимо рассчитать объем фигуры, который останется после вычитания желтой объемной фигуры, которая также является кубом, из объема синего куба. Известен только размер стороны малого и большого куба.
Если значения сторон небольшие, то расчеты достаточно просты. А если длины сторон выражены значащими числами, то стоит воспользоваться формулой под названием «Разность кубов» (или «Разностный куб»), которая значительно упростит расчеты.
При вычислении алгебраических полиномов для упрощения расчетов используем формулы сокращенного умножения . Всего таких формул семь. Их всех нужно знать наизусть.
Также следует помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.
Разность квадратов
Разность квадратов двух чисел равна произведению разности этих чисел на их сумму.
а 2 — б 2 = (а — б) (а + б)
сумма квадратная
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
(а + b) 2 = а 2 + 2ab + b 2
Обратите внимание, что с помощью этой сокращенной формулы умножения легко найти квадраты больших чисел без использования калькулятора или длинного умножения. Поясним на примере:
Найти 112 2 .
Разложим 112 на сумму чисел, квадраты которых мы хорошо помним.2
112 = 100 + 1
В скобках пишем сумму чисел и ставим над скобками квадрат.
112 2 = (100 + 12) 2
Воспользуемся формулой квадрата суммы:
112 2 = (100 + 12) 2 = 100 2 + 2 x 100 x 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544
Помните, что формула суммы квадратов также действительна. для любых алгебраических многочленов.
(8а + с) 2 = 64а 2 + 16ас + с 2
Внимание!!!
(a + b) 2 не равно a 2 + b 2
Квадрат разности
Квадрат разницы между двумя числами равен квадрату первого числа минус удвоенное произведение первого и второго плюс квадрат второго числа.
(а — б) 2 = а 2 — 2аб + б 2
Также стоит запомнить очень полезное преобразование:
(a — b) 2 = (b — a) 2
Приведенная выше формула доказывается простым раскрытием скобок:
(a — b) 2 = a 2 — 2ab + b 2 = b 2 — 2ab + a 2 = (b — a) 2
сумма куб
Куб суммы двух чисел равен кубу первого числа плюс умноженный на три квадрат первого числа умноженный на второе плюс умноженное на три произведение первого умноженное на квадрат второго плюс куб секунда.
(а + б) 3 = а 3 + 3а 2 б + 3аб 2 + б 3
Запомнить эту «ужасную» формулу довольно просто.
Узнай, что сначала идет 3.
Два полинома в середине имеют коэффициенты 3.
AПомните, что любое число в нулевой степени равно 1 (a 0 = 1, b 0 = 1). Легко видеть, что в формуле есть уменьшение степени а и увеличение степени b. Вы можете проверить это:
(a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3
Внимание!!!
(a + b) 3 не равно a 3 + b 3
куб разностей
Куб разности двух чисел равен кубу первого числа минус три умножения на квадрат первого числа и второго плюс утроенное произведение первого числа на квадрат второго минус куб второй.
(а — б) 3 = а 3 — 3а 2 б + 3аб 2 — б 3
Эта формула запоминается как и предыдущая, но только с учетом чередования знаков «+» и «-». Первому члену числа 3 предшествует «+» (по правилам математики мы его не пишем). Это означает, что перед следующим элементом будет стоять «-», затем снова «+» и т. д.
(а — б) 3 = + 3 — 3а 2б + 3аб 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Сумма кубов ( Не путать с кубом суммы!)
Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
а 3 + Ь 3 = (а + Ь)(а 2 — аб + Ь 2)
Сумма кубов равна произведению двух скобок.
Первая скобка представляет собой сумму двух чисел.
Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называется выражение:
A 2 — ab + b 2
Этот квадрат является неполным, так как в середине вместо двойного произведения стоит обыкновенное произведение чисел.
Куб Разностей (Не путать с Кубом Разностей!!!)
Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
а 3 — б 3 = (а — б) (а 2 + аб + б 2)
Будьте внимательны при написании символов. Следует помнить, что все приведенные выше формулы также используются справа налево.
Трудно запомнить формулы сокращенного умножения? Помочь делу легко. Нужно только помнить, как изображается такая простая вещь, как треугольник Паскаля. Тогда вы будете помнить эти формулы всегда и везде, вернее, не запоминать, а восстанавливать.
Что такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, входящих в разложение любой степени двучлена вида в многочлен.
Разобьем, например:
В этой записи легко запомнить, что в начале стоит куб первого числа, а в конце — куб второго числа. А вот то, что посередине, трудно вспомнить. И даже то, что в каждом следующем члене степень одного множителя все время уменьшается, а второго возрастает — это легко заметить и запомнить, труднее запомнить коэффициенты и знаки (плюс или минус?).
Итак, сначала шансы. Вам не нужно запоминать их! На полях тетради быстро рисуем треугольник Паскаля, и вот они — коэффициенты, уже перед нами. Начинаем рисовать с трех единиц, одну сверху, две снизу, справа и слева — ага, уже треугольник получается:
Первая строка, с одной единицей, нулевая. Затем идет первая, вторая, третья и так далее. Чтобы получить вторую строку, нужно снова поставить единицы по краям, а в центре записать число, полученное сложением над ним двух цифр:
Пишем третью строку: снова по краям единицы, и снова, чтобы получить следующую цифру в новой строке, добавляем цифры над ней в предыдущей:
Как у вас угадали, получаем в каждой строке коэффициенты от разложения двучлена в многочлен:
Ну и еще проще запомнить знаки: первый такой же, как и в развернутом двучлене (раскладываем сумма, что означает плюс, разность, что означает минус), и далее знаки чередуются!
Вот такая полезная штука — треугольник Паскаля. Наслаждаться!
Наслаждаться!
правила применения формул сокращенного умножения Как разложить куб суммы
Главная » Практические отчеты » Формулы сокращенного умножения. Куб разностей и кубы разностей: правила применения формул сокращенного умножения Как разложить куб суммы
В предыдущих уроках мы рассмотрели два способа разложения многочлена на множители: круглые скобки и группировка.
В этом уроке мы рассмотрим другой способ разложения многочлена на множители с использованием формул сокращенного умножения .
Мы рекомендуем прописывать каждую формулу не менее 12 раз. Для лучшего запоминания выпишите все формулы сокращенного умножения себе на небольшую шпаргалку.
Давайте вспомним, как выглядит формула разности кубов.
а 3 — б 3 = (а — б) (а 2 + аб + б 2)
Формулу разности кубиков не очень легко запомнить, поэтому мы рекомендуем использовать специальный способ ее запоминания.
Важно понимать, что любая формула сокращенного умножения работает и в обратную сторону.
(а — б) (а 2 + аб + б 2) = а 3 — б 3
Давайте рассмотрим пример. Необходимо учитывать разницу между кубами.
Обратите внимание, что «27a 3» равно «(3a) 3», что означает, что для формулы разности между кубами вместо «a» мы используем «3a».
Используем формулу разности кубов. На месте «а 3» имеем «27а 3», а на месте «б 3», как и в формуле, стоит «б 3».
Применение разности кубов в обратном направлении
Рассмотрим другой пример. Вы хотите преобразовать произведение многочленов в разность кубов, используя формулу сокращенного умножения.
Обратите внимание, что произведение полиномов «(х — 1) (х 2 + х + 1)» напоминает правую часть формулы разности кубов «», только вместо «а» стоит «х», а вместо «b» стоит «1»…
Используем для «(x — 1) (x 2 + x + 1)» формулу разности кубов в обратном направлении.
Рассмотрим более сложный пример. Требуется упростить произведение многочленов.
Требуется упростить произведение многочленов.
Если сравнить «(y 2 — 1) (y 4 + y 2 + 1)» с правой частью формулы разности кубов
« a 3 — b 3 = (a — b) (a 2 + ab + б 2)», тогда можно понять, что на месте «а» из первой скобки стоит «у 2», а на месте «б» стоит «1».
Формулы или правила сокращенного умножения используются в арифметике, точнее в алгебре, для более быстрого процесса вычисления больших алгебраических выражений. Сами формулы выведены из существующих в алгебре правил умножения нескольких многочленов.
Использование этих формул обеспечивает достаточно быстрое решение различных математических задач, а также помогает упростить выражения. Правила алгебраического преобразования позволяют производить некоторые манипуляции с выражениями, следуя которым можно получить выражение в левой части равенства в правой части, либо преобразовать правую часть равенства (получить выражение в левой части после знак равенства).
Удобно знать формулы сокращенного умножения по памяти, так как они часто используются при решении задач и уравнений. Ниже приведены основные формулы, входящие в этот список, и их названия.
Ниже приведены основные формулы, входящие в этот список, и их названия.
Сумма в квадрате
Чтобы вычислить квадрат суммы, нужно найти сумму, состоящую из квадрата первого слагаемого, удвоенного произведения первого слагаемого на второе и квадрата второго. В виде выражения это правило записывается следующим образом: (a + c)² = a² + 2ac + c².
Разность в квадрате
Для вычисления квадрата разности нужно вычислить сумму, состоящую из квадрата первого числа, удвоенного произведения первого числа на второе (взятого с обратным знаком) и квадрат второго числа. В виде выражения это правило выглядит так: (a — c)² = a² — 2ac + c².
Разность квадратов
Формула разности двух чисел в квадрате равна произведению суммы этих чисел на их разность. В виде выражения это правило выглядит следующим образом: а² — с² = (а + с) · (а — с).
Куб суммы
Для вычисления куба суммы двух слагаемых необходимо вычислить сумму, состоящую из куба первого слагаемого, утроенного произведения квадрата первого слагаемого и второго, утроенного произведение первого слагаемого на квадрат второго, а также куб второго слагаемого. В виде выражения это правило выглядит следующим образом: (a + c)³ = a³ + 3a²c + 3ac² + c³.
В виде выражения это правило выглядит следующим образом: (a + c)³ = a³ + 3a²c + 3ac² + c³.
Сумма кубов
По формуле приравнивается произведению суммы этих слагаемых на их неполный квадрат разности. В виде выражения это правило выглядит следующим образом: а³ + с³ = (а + с) · (а² — ас + с²).
Пример. Необходимо вычислить объем фигуры, которая образуется при сложении двух кубиков. Известны только размеры их сторон.
Если значения сторон небольшие, то расчеты несложные.
Если длины сторон выражены громоздкими числами, то в этом случае проще применить формулу «Сумма кубов», что значительно упростит расчеты.
Куб разности
Выражение для кубической разности следующее: как сумма третьей степени первого члена, утроить отрицательное произведение квадрата первого члена на второй, утроить произведение первого члена на квадрат второго и отрицательный куб второго члена. В виде математического выражения куб разности выглядит так: (a — c) ³ = a³ — 3a²c + 3ac² — c³.
Разность кубов
Формула разности кубов отличается от суммы кубов только одним знаком. Таким образом, разность кубов представляет собой формулу, равную произведению разности этих чисел на их неполный квадрат суммы. В виде разность кубов выглядит следующим образом: а 3 — с 3 = (а — с) (а 2 + ас + с 2).
Пример. Необходимо рассчитать объем фигуры, который останется после вычитания желтой объемной фигуры из объема синего куба, который тоже является кубом. Известен только размер стороны малого и большого куба.
Если значения сторон малы, то расчеты достаточно просты. А если длины сторон выражены значащими числами, то стоит воспользоваться формулой под названием «Кубы разности» (или «Куб разности»), которая значительно упростит расчеты.
Формулы сокращенного умножения.
Изучение формул сокращенного умножения: квадрат суммы и квадрат разности двух выражений; разность квадратов двух выражений; куб суммы и куб разности двух выражений; сумма и разность кубов двух выражений.
Применение формул сокращенного умножения при решении примеров.
Для упрощения выражений, факторизации многочленов и приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть .
Пусть a, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения .
(a + b) 2 = a 2 + 2ab + b 2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b) 2 = a 2 — 2ab + b 2
3. Разность квадратов двух выражений равна произведению разности этих выражений на их сумму.
а 2 — б 2 = (а -б) (а + б)
4. Куб суммы двух выражений равен кубу первого выражения плюс три умноженный на квадрат первого выражения и второй плюс умноженный на три произведения первого выражения на квадрат второго плюс куб второго выражения.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
5. Куб разности двух выражений равен кубу первого выражения минус утроенный квадрат первого выражение, а второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражений на неполный квадрат разности этих выражений.
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражений на неполный квадрат суммы этих выражений.
a 3 — b 3 = (a — b) (a 2 + ab + b 2)
Применение формул сокращенного умножения при решении примеров.
Пример 1.
Вычислить
а) Используя формулу квадрата суммы двух выражений, имеем
(40 + 1) 2 = 40 2 + 2 40 1 + 1 2 = 1600 + 80 + 1 = 1681
б) Используя формулу квадрата разности двух выражений, получаем
98 2 = (100 — 2) 2 = 100 2 — 2 100 2 + 2 2 = 10000 — 400 + 4 = 9604
Пример 2.




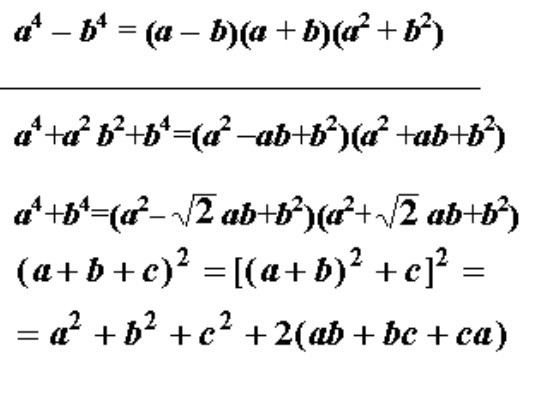
 Квадрат суммы и квадрат разности и куб суммы и куб разности.
Квадрат суммы и квадрат разности и куб суммы и куб разности.