Элементарная алгебра
Элементарная алгебра
ОглавлениеГлава I. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ§ 2. Понятия кольца и поля § 3. Упорядоченные поля § 4. Понятие функции и аналитического выражения § 5. Элементарные функции и их классификация § 6. Метод математической индукции Глава II. ОБЩИЕ СВЕДЕНИЯ ОБ УРАВНЕНИЯХ § 1. Понятие уравнения. Решения уравнения § 2. Классификация уравнений, изучаемых в элементарной математике § 3. Равносильность уравнений § 4. Преобразование уравнений при их решении Глава III. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ С ОДНИМ НЕИЗВЕСТНЫМ § 1. Алгебраические уравнения n-й степени с одним неизвестным § 2. Корни квадратного трехчлена § 3. Исследование квадратного трехчлена над полем действительных чисел § 4. Двучленные уравнения § 5. Трехчленные уравнения, приводящиеся к квадратным § 6. Симметрические уравнения § 7. Алгебраическое уравнение n-й степени с рациональными коэффициентами § 8. 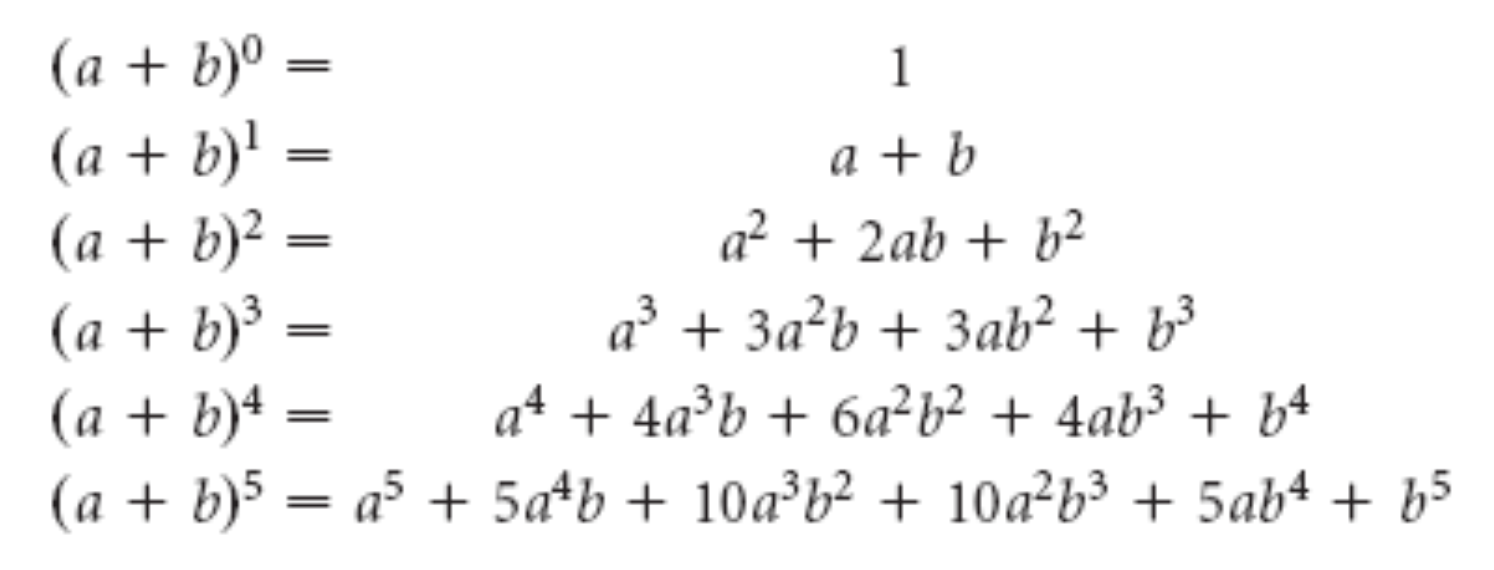 Частные приемы решения уравнений высших степеней§ 9. Дробно-рациональные уравнения Глава IV. ТЕОРИЯ СОЕДИНЕНИЙ § 2. Перестановки § 3. Сочетания § 4. Размещения § 5. Перестановки с повторениями § 6. Сочетания с повторениями § 7. Размещения с повторениями Глава V. БИНОМ НЬЮТОНА И ПОЛИНОМИАЛЬНАЯ ТЕОРЕМА § 1. Бином Ньютона § 2. Биномиальные коэффициенты и их основные свойства § 3. Треугольник Паскаля § 4. Полиномиальная теорема § 5. Вычисление сумм степеней первых n чисел натурального ряда Глава VI. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Многочлен от нескольких переменных и его каноническая форма § 2. Однородный многочлен от n переменных и число его членов § 3. Число членов в каноническом представлении многочлена от n переменных § 5. Тождественные преобразования многочленов. Тождество Лагранжа § 6. Применение метода неопределенных коэффициентов при выполнении алгебраических действий над многочленами Глава VII.  СИСТЕМЫ УРАВНЕНИЙ С НЕСКОЛЬКИМИ НЕИЗВЕСТНЫМИ§ 1. Понятие системы уравнений § 2. Равносильность систем уравнений § 3. Уравнения и системы уравнений, являющиеся следствием данной системы уравнений § 4. Основные элементарные методы решения систем уравнений § 5. Решение нелинейных систем алгебраических уравнений элементарными методами 1. Решение системы двух уравнений с двумя неизвестными, из которых одно—второй степени, а другое — первой. 2. Решение системы двух уравнений второй степени с двумя неизвестными, которые не имеют членов первой степени. 3. Решение системы двух уравнений второй степени с двумя неизвестными в общем виде. 4. Решение системы двух однородных уравнений с двумя неизвестными. 5. Решение системы двух уравнений с двумя неизвестными, одно из которых однородное, а второе не однородное. 7. Решение нелинейной системы алгебраических уравнений, в состав которой входят линейные уравнения. 8. Решение нелинейной системы алгебраических уравнений, левая часть одного из которых представляется в виде произведения.  § 6. Графическое решение нелинейных систем алгебраических уравнений с двумя неизвестными Глава VIII. НЕРАВЕНСТВА § 1. Основные свойства неравенств § 2. Тождественные неравенства § 3. Применение неравенств для определения наибольших и наименьших значений § 4. Решение неравенств § 5. Решение алгебраических неравенств с одним неизвестным первой и второй степени § 7. Применение неравенств для задания числовых и точечных множеств Глава IX. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 1. Корни с натуральными показателями в поле действительных чисел § 2. Тождественные преобразования иррациональных выражений в поле действительных чисел § 3. Решение иррациональных уравнений и систем, в состав которых входят иррациональные уравнения, в поле действительных чисел Глава X. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ В ПОЛЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 1.  Теоретические основы решения показательных и логарифмических уравнений§ 2. Решение показательных уравнений с одним неизвестным § 3. Решение логарифмических уравнений с одним неизвестным § 4. Решение трансцендентных уравнений, приводящихся к показательным и логарифмическим уравнениям § 5. Решение некоторых трансцендентных систем уравнений § 6. Графические способы решения трансцендентных уравнений и систем ЛИТЕРАТУРА |
Формулы сокращенного умножения
Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть.
Пусть а, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b)2 = a2 + 2ab + b2
2.
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b)2 = a2 — 2ab + b2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a2 — b2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a — b)3 = a3 — 3a2b + 3ab2 — b3
6.
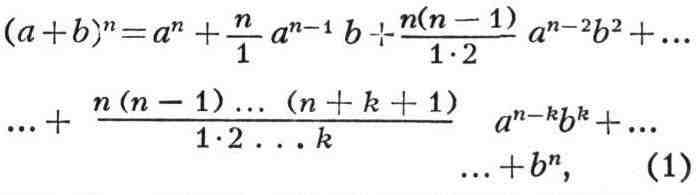
a3 + b3 = (a + b) (a2 — ab + b2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.
a3 — b3 = (a — b) (a2 + ab + b2)
8. Разность чисел в четвертой степени
(a — b)4 = a4 — 4a3b + 6a2b2 — 4ab3 + b4
9. Сумма чисел в четвертой степени
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
10. Разность чисел в пятой степени
(a — b)5 = a5 — 5a4b + 10a3b
11.
Сумма чисел в пятой степени
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
12. Квадрат трехчлена
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
13. Квадрат линейной формы
(a + b + c + … + u + v)2 = a2 + b2 + c2 + … + u2 + v2 + 2(ab + ac + … + au + av + bc + … + bu + bv + … + uv)
14. Куб трехчлена
(a + b + c)3 = a3 + b3 + c3 + 3a2b + 3ab2 + 3a2c + 3ac2 + 3b2c + 3bc2 + 6abc
Степени и степени
Обновлено 26 июня 2019 г. | Инфопожалуйста Персонал
в степени — это произведение , умножающее число само на себя.
Обычно степень представлена основанием, и показателем степени. Базовое число сообщает , какое число умножается. Показатель степени , небольшое число, написанное выше и справа от основного числа, говорит о сколько раз умножается основное число.
Например, «6 в 5-й степени» можно записать как «6 5 ». Здесь базовое число равно 6, а показатель степени равен 5. Это означает, что 6 умножается само на себя 5 раз: 6 х 6 х 6 х 6 х 6
6 х 6 х 6 х 6 х 6 = 7 776 или
| базовый номер | 2-я степень | 3-я степень | 4-я степень | 5-я степень 90 014 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 |
| 3 | 9 | 27 | 81 | 243 |
| 4 | 16 | 64 | 256 | 1024 |
| 5 | 25 | 125 | 625 | 3 125 |
| 6 | 36 | 216 | 1 296 | 7 776 |
| 7 | 49 | 343 | 2 ,401 | 16 807 |
| 8 | 64 | 512 | 4 096 | 32 768 |
| 9 | 81 | 729 | 6 561 | 59 049 |
| 10 | 100 | 1 000 9001 4 | 10 000 | 100 000 |
| 11 | 121 | 1 331 | 14 641 | 161 051 |
| 12 | 144 | 1 728 | 20 736 | 248 832 |
| Факториалы | Числа и формулы | 9001 3 Таблица умножения
Источники +
Наши общие источники
Видео с вопросами: Формулы множественных углов из формулы Эйлера
Стенограмма видео
Используйте формулу Эйлера, чтобы вывести формулу для cos 5 𝜃 и sin 5 𝜃 через sin 𝜃 и cos 𝜃.
Напомним, формула Эйлера говорит, что 𝑒 в степени 𝑖𝜃 равно cos 𝜃 плюс 𝑖 sin 𝜃. Итак, как мы применим это, чтобы вывести формулу для cos, равного пяти 𝜃, и sin, равного пяти 𝜃? Что ж, мы собираемся начать с возведения обеих частей этой формулы в пятую степень. Теперь мы можем сказать, что 𝑒 в 𝑖𝜃 все в пятой степени равно 𝑒 в пяти 𝑖𝜃. Но тогда, конечно, мы могли бы использовать формулу Эйлера, чтобы переписать это как cos пять 𝜃 плюс 𝑖 sin of Five 𝜃. Итак, у нас есть уравнение потому что пять 𝜃 плюс 𝑖 грех пяти 𝜃 равно косинусу 𝜃 плюс 𝑖 грех 𝜃 все в пятой степени. И теперь мы можем использовать биномиальную теорему, чтобы распределить эти скобки.
Это говорит о том, что 𝑎 плюс 𝑏 в 𝑛-й степени является суммой от 𝑘 равной нулю до 𝑛 из 𝑛 выберите 𝑘, умноженное на 𝑎 в степени 𝑛 минус 𝑘, умноженное на 𝑏 в 𝑘-й степени. Когда 𝑛 равно пяти, мы имеем 𝑎 плюс 𝑏 в пятой степени равно 𝑎 в пятой степени плюс пять выбрать один 𝑎 в четвертой степени 𝑏 плюс пять выбрать два раза 𝑎 в кубе умножить на 𝑏 в квадрате и так далее.
На самом деле, пять выбирают один и пять выбирают четыре равно пяти, а пять выбирают два и пять выбирают три равны 10. Итак, у нас есть следующая формула, которая поможет нам распределить скобки cos 𝜃 плюс 𝑖 sin 𝜃 в пятой степени. Первый член — это просто cos 𝜃 в пятой степени, а второй — пять cos 𝜃 в четвертой степени, умноженные на 𝑖 sin 𝜃.
Но на самом деле, давайте переместим 𝑖 вперед и запишем это как пять 𝑖 cos 𝜃 в четвертой степени sin 𝜃. Тогда третий член равен 10 кос в кубе 𝜃 умножить на 𝑖 грех 𝜃 в квадрате, что можно записать как 10 кос в кубе 𝜃 умножить на 𝑖 в квадрате умножить на квадрат греха 𝜃. Но мы знаем, что 𝑖 в квадрате равен минус единице. Таким образом, мы можем переписать это далее как отрицательные 10 cos в кубе 𝜃 sin в квадрате 𝜃. Тогда наш четвертый член равен 10 кос в квадрате 𝜃 умножить на 𝑖 грех 𝜃 в кубе. И если мы считаем 𝑖 в кубе равным 𝑖 умножить на 𝑖 в квадрате, мы увидим, что все это выражение можно переписать как минус 10 𝑖 умножить на кос в квадрате 𝜃 умножить на грех в кубе 𝜃.
Тогда у нас есть пять cos 𝜃 умноженных на 𝑖 sin 𝜃 в четвертой степени. А так как 𝑖 в четвертой степени равно 𝑖 в квадрате, это отрицательная единица в квадрате, то есть просто единица. И этот термин становится пятью cos 𝜃 sin 𝜃 в четвертой степени.
Наш последний термин равен 𝑖 sin 𝜃 в пятой степени. 𝑖 в пятой степени равно 𝑖 в четвертой степени, умноженное на 𝑖. Итак, мы имеем просто 𝑖 sin 𝜃 в пятой степени. Итак, наше уравнение теперь представляет собой кос пять 𝜃 плюс 𝑖 грех пять 𝜃 равно кос 𝜃 в пятой степени плюс пять 𝑖 cos 𝜃 в четвертой степени умножить на грех 𝜃 минус 10 кос в кубе 𝜃 грех в квадрате 𝜃 и так далее. И теперь мы готовы вывести формулу для пяти 𝜃. Мы делаем это, приравнивая или сравнивая действительные части с каждой стороны нашего уравнения. в левой части это просто кос пять 𝜃, тогда как в правой части у нас есть кос 𝜃 в пятой степени минус 10 куб куб 𝜃 квадрат греха 𝜃 плюс пять кос 𝜃 грех 𝜃 в четвертой степени.
Поскольку мы знаем, что действительные компоненты в каждой части нашего уравнения должны быть равны, мы создаем следующее уравнение.
И мы могли бы оставить это так. Но мы могли бы также вспомнить, что квадрат греха 𝜃 плюс квадрат квадрата 𝜃 равен единице. А затем, написав, что грех в квадрате 𝜃 равен единице минус косинус в квадрате 𝜃, мы находим косинус пять 𝜃 равно косинусу 𝜃 в пятой степени минус 10 косинус в кубе 𝜃 умноженный на один минус косинус в квадрате 𝜃 плюс пять косинусов 𝜃 умноженный на один минус косинус в квадрате 𝜃 в квадрате .
Наконец, мы распределяем скобки. И мы находим, что правая часть этого уравнения становится 16 cos 𝜃 в пятой степени минус 20 cos в кубе 𝜃 плюс пять cos 𝜃. Итак, мы получили нашу формулу для пяти 𝜃. Фактически, мы повторяем этот процесс для пяти 𝜃. На этот раз, однако, мы собираемся сравнить воображаемые части. В левой части у нас есть грех пять 𝜃, тогда как в правой части у нас есть пять кос 𝜃 в четвертой степени грех 𝜃 минус 10 кос в квадрате 𝜃 грех в кубе 𝜃 плюс грех 𝜃 в пятой степени. Таким образом, наше уравнение для греха пять 𝜃 становится грехом пять 𝜃 равно пяти, потому что 𝜃 в четвертой степени, грех 𝜃 минус 10, потому что в квадрате 𝜃 грех в кубе 𝜃 плюс грех 𝜃 в пятой степени.