формула, как найти q, сумма первых n чисел
Содержание:
- Что такое геометрическая прогрессия
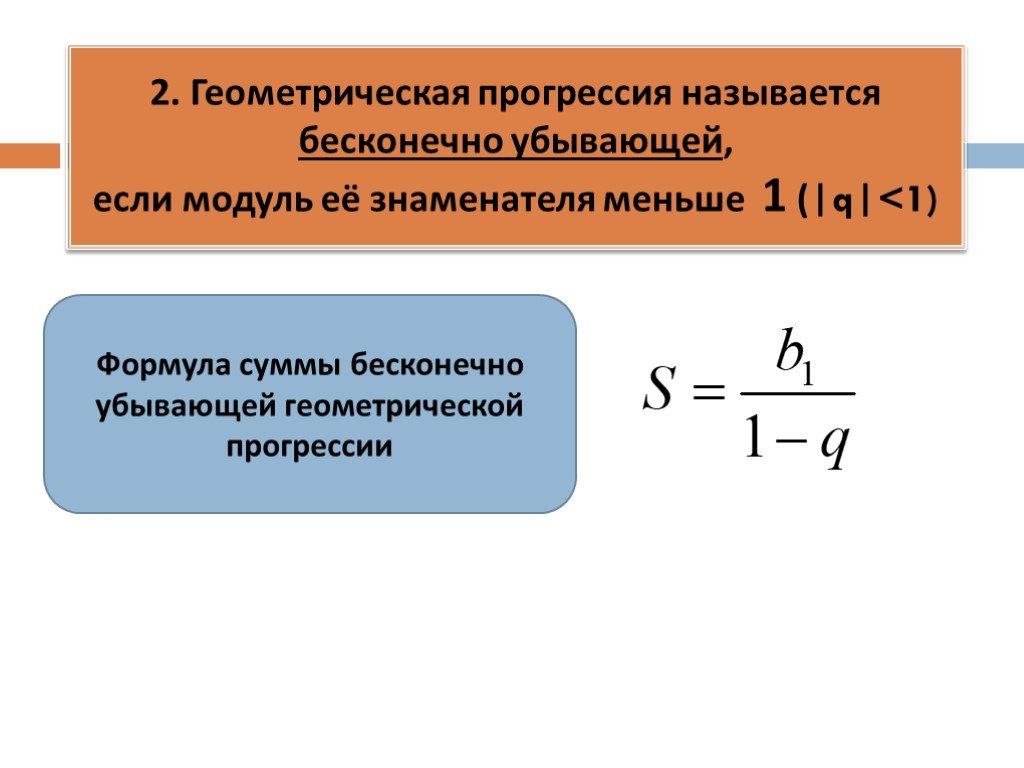
- Бесконечная убывающая геометрическая прогрессия — что из себя представляет
- Сумма первых n членов геометрической прогрессии
- Как найти q в геометрической прогрессии
- Примеры решения задач
Содержание
- Что такое геометрическая прогрессия
- Бесконечная убывающая геометрическая прогрессия — что из себя представляет
- Сумма первых n членов геометрической прогрессии
- Как найти q в геометрической прогрессии
- Примеры решения задач
Что такое геометрическая прогрессия
Геометрическая прогрессия являет собой последовательность чисел. Когда каждому натуральному числу n поставлено в соответствие число \(Xn\), то говорят, что представлена числовая последовательность. Она имеет вид: \(X_1, X_2\)
Когда каждому натуральному числу n поставлено в соответствие число \(Xn\), то говорят, что представлена числовая последовательность. Она имеет вид: \(X_1, X_2\)
,…,\(X_n\), или \({[X_n]}\). Для задания последовательности необходимо знать закон, по которому каждому натуральному числу n соответственно поставлено общее число последовательности \(f(n)=X_n.\)
Геометрическая прогрессия — последовательность с заданным первым членом \(b_1\), в которой каждый следующий, начиная со второго, получается умножением предыдущего на одно и то же число \(q\).
Числа \( b_1\) и q не могут равняться нулю, поскольку в таком случае все члены прогрессии, начиная со второго, будут равны нулю.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Геометрическую прогрессию определяют как произведение между ее знаменателем и n-м членом:
\(b_n=b_{n-1}\cdot q,\)
Где \(b_n\) — \(n-й\) член прогрессии, \(q\) — знаменатель прогрессии. 2=b_{n-1}\cdot b_{n+1}.\)
2=b_{n-1}\cdot b_{n+1}.\)
Если \(b_1 > 0\) и \(q > 1\) или \(b_1 < 0\) и \(0 < q < 1\), то для геометрической последовательности характерно возрастание.
Если \(b_1 > 0\) и 0 < \(q < 1\) или \(b_1 < 0\) и \(q > 1\), то для нее характерно убывание.
Примеры геометрических прогрессий в жизни:
- Размножение бактерий крайне велико и осуществляется по геометрической прогрессии: каждая клетка делится на две, новые — делятся еще на две и т.д. Знание принципов размножения бактерий находит свое применение в биотехнологии, пищевой промышленности, медицине и т.д.
- Зная формулу суммы геометрической прогрессии, можно находить площади и объемы геометрических фигур. Еще Архимед заметил связь между прогрессиями и вывел формулу для нахождения площади сегмента параболы через сумму бесконечно убывающей геометрической прогрессии.
- Возрастание скорости химических реакций происходит в геометрической прогрессии при увеличении температуры по арифметической прогрессии.
 2}\Rightarrow1+q=3\Rightarrow q=2.\)
2}\Rightarrow1+q=3\Rightarrow q=2.\)Ответ: \(q=2. \)
Насколько полезной была для вас статья?
Рейтинг: 1.00 (Голосов: 5)
Поиск по содержимому
Геометрическая прогрессия | umath.ru
Содержание
- Определение геометрической прогрессии
- Формула n-го члена геометрической прогрессии
- Сумма первых n членов геометрической прогрессии
- Формула суммы первых n членов геометрической прогрессии
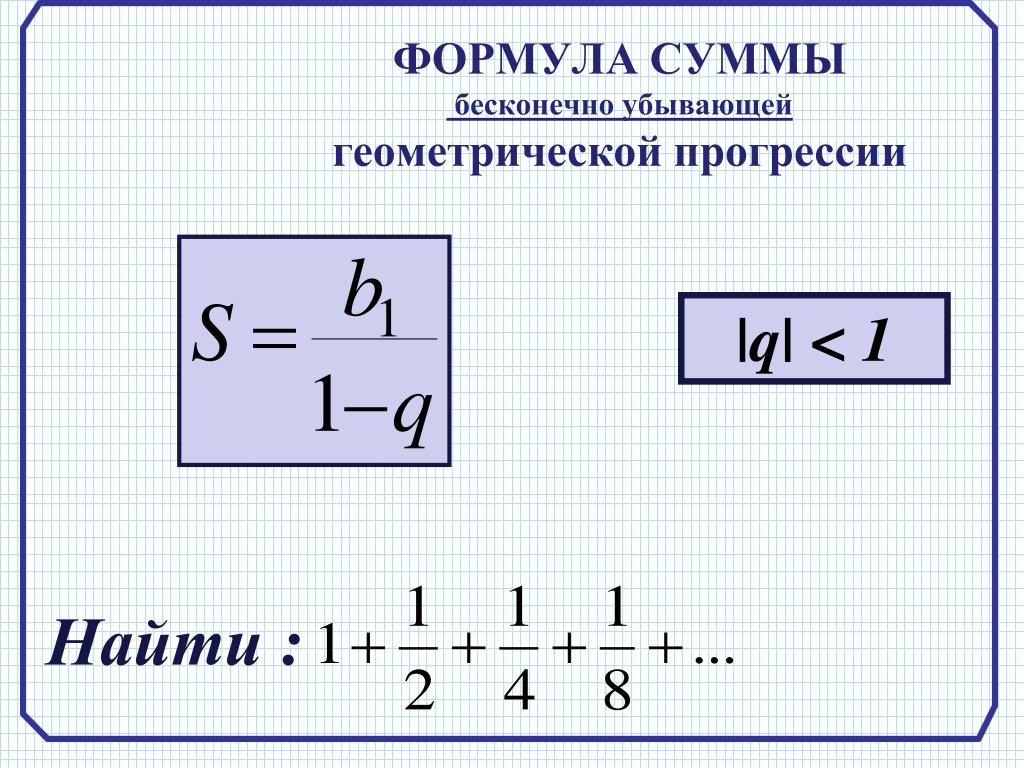
- Сумма бесконечно убывающей геометрической прогрессии
Определение геометрической прогрессии
Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число , называется геометрической прогрессией. Число называется знаменателем прогрессии.
То есть геометрическая прогрессия определяется рекуррентным соотношением
Примеры геометрических прогрессий.

- Последовательность — геометрическая прогрессия со знаменателем
- Последовательность — геометрическая прогрессия со знаменателем
- Последовательность — геометрическая прогрессия со знаменателем
Теорема 1. Пусть — геометрическая прогрессия со знаменателем Тогда для всех натуральных справедлива формула
Доказательство. Воспользуемся рекуррентным определением геометрической прогрессии:
Итак, для n-го члена геометрической прогрессии справедлива формула
Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:
Доказательство.
Из определения геометрической прогрессииСледовательно,
откуда
Обратное утверждение тоже верно. Если для всех членов последовательности начиная со второго, выполняется равенство то эта последовательность — геометрическая прогрессия.

Пример 1. Сумма первого и третьего членов геометрической прогрессии равна 10, а сумма второго и четвёртого членов — 30. Найдём первый член и знаменатель прогрессии.
Решение. По условию
Выразим члены геометрической прогрессии через и : Тогда система запишется в виде
Разделив второе уравнение системы на первое, получим Следовательно,
Сумма первых n членов геометрической прогрессии
Вычислим сумму первых n членов геометрической прогрессии знаменатель которой :
(1)
Умножим это равенство на :
или
(2)
Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим Отсюда, так как имеем
или
(3)
Так как то формулу (3) можно переписать в виде
(4)
Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.

Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии
По формуле (3) получаем
Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.
Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.
Наверное, вы спросите, чем же всё закончилось.
 Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.Сумма бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию Если её знаменатель то эта последовательность называется бесконечно убывающей геометрической прогрессией.
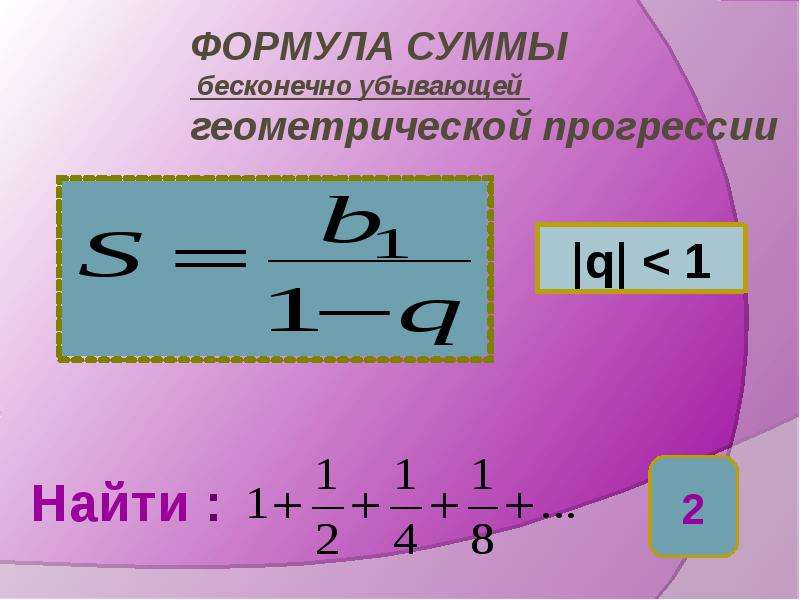
Сумма бесконечно убывающей геометрической прогресcии выражается формулой
(5)
Пример 3. Найдём сумму
Решение. — сумма бесконечно убывающей геометрической прогрессии с первым членом и знаменателем По формуле (5) получаем
То есть
summation — Сумма убывающего геометрического ряда целых чисел
Задавать вопрос
спросил
Изменено 7 лет, 10 месяцев назад
Просмотрено 4к раз
$\begingroup$
Я пытаюсь вычислить сумму целых чисел, которые делятся на два (при необходимости применяя функцию пола): $n\mapsto \lfloor \frac{n}{2}\rfloor$.

Пусть $S(n)=n+\lfloor\frac{n}{2}\rfloor+\left\lfloor\frac{\lfloor\frac{n}{2}\rfloor}{2}\right\rfloor+\ ldots$.
Например, $$ \начать{выравнивать*} S(100) &= 100 + 50 + 25 + 12 + 6 + 3 + 1 + 0 +\ldots\\ S(3) &= 3 + 1 + 0 + \ldots\\ S(1000) &= 1000 + 500 + 250 + 125 + 62 + 31 + 15 + 7 + 3 + 1 + 0 + \ldots\end{align*} $$
Я пытаюсь найти замкнутую форму для $S(n)$, где $n\in \mathbb N$. Есть идеи?
[Решение] Много хороших ответов. Спасибо! Вот моя реализация Java.
int вычислитьHalvesSum(int n) { вернуть 2 * n - Integer.bitCount(n) }- последовательности-и-ряды
- суммирование
- целые числа
$\endgroup$
2
$\begingroup$ 9к}\право\rэтаж $$
Расчет $\log_2$, вероятно, означает, что это не стоит реализовывать (вы добавили этот комментарий, пока я писал свой ответ).

$\endgroup$
$\begingroup$
Пусть $n$ — рассматриваемое число, а $m$ — количество единиц $1$ в двоичном представлении $n$. Например, если $n=100_{10}=1100100_2$, то $m=3$.
Тогда искомая сумма равна $$S(n)=2n-m$$
Это не постоянное время в $n$, но $O(\log n)$, что очень хорошо. Я сомневаюсь, что вы сможете сделать что-то лучше, так как просто запись ответа занимает $O(\log n)$ времени. 9{k+1}-1$ в $S(n)$.
Каждый взнос на единицу меньше, чем удвоенная стоимость его $1$. Таким образом, общий вклад равен $2n$ минус количество $1$s в двоичном представлении $n$.
$\endgroup$
Объяснение урока: Сумма бесконечной геометрической последовательности
В этом объяснителе мы научимся вычислять сумму бесконечной геометрической последовательности.
Геометрическая последовательность — это последовательность, имеющая общее отношение между последовательными элементами.
 Мы можем рассчитать значение обыкновенного отношения, разделив любой член на член, который ему предшествует.
Мы можем рассчитать значение обыкновенного отношения, разделив любой член на член, который ему предшествует.Например, следующая последовательность является геометрической: 1,3,9,27,81,….
Эта последовательность имеет знаменатель, равный 3, так как каждый член можно вычислить, умножив предыдущий член на 3. в следующей последовательности:
Посмотрите, что происходит, когда мы делим термин на предшествующий ему термин: 𝑇𝑟𝑇=𝑇𝑟𝑇𝑟=𝑟.
Независимо от того, какую пару терминов мы выбираем, их частное всегда равно 𝑟, знаменателю.
Давайте обобщим.
Определение:
Геометрическая последовательность — это последовательность, имеющая общее отношение между последовательными элементами. Общий член 𝑇 геометрической последовательности с первым членом 𝑇 и знаменателем 𝑟 определяется формулой 𝑇=𝑇𝑟.
Геометрический ряд представляет собой сумму заданного числа членов геометрической последовательности. Ряд может быть конечным или бесконечным.

Определение:
Обычное отношение 𝑟 геометрической последовательности, 𝑛-й член которой равен 𝑇, определяется как 𝑟=𝑇𝑇.
В качестве альтернативы, оно также может быть задано как 𝑟=𝑇𝑇.
Теперь вернемся к нашему предыдущему примеру геометрической последовательности: 1,3,9,27,81,….
Мы замечаем, что по мере увеличения числа членов 𝑛 значение самого члена 𝑇 растет экспоненциально. Тогда мы могли бы заключить, что если бы нам нужно было вычислить сумму большого числа членов, наш результат был бы особенно велик. На самом деле, когда 𝑛 приближается к бесконечности для этой последовательности, сумма членов 𝑆 также будет стремиться к бесконечности.
Однако это не всегда так. На самом деле, как это ни парадоксально, некоторые бесконечные геометрические последовательности от 90 115 до 90 116 имеют конечную сумму. Мы можем увидеть такие последовательности при рассмотрении фрактальной геометрии, например, при вычислении площади снежинки Коха

Когда бесконечная геометрическая последовательность имеет конечную сумму, мы говорим, что ряд (это просто сумма всех членов) равен сходящийся . Чтобы геометрический ряд сходился, нам нужно, чтобы последовательные члены становились экспоненциально меньшими, пока не приблизились к нулю. Для этого обыкновенное отношение должно находиться в интервале ]−1,1[.
Например, следующая последовательность имеет обыкновенное отношение 12 и является сходящейся; когда 𝑛 приближается к бесконечности, 𝑇 приближается к нулю, то есть мы можем найти сумму бесконечной последовательности: 8,4,2,1,12,….
Определение:
Бесконечный геометрический ряд называется сходящимся, если абсолютное значение знаменателя 𝑟 меньше 1: |𝑟|1.
Чтобы найти формулу суммы членов бесконечной геометрической последовательности, давайте сначала рассмотрим конечный геометрический ряд с первым членом 𝑇 и знаменателем 𝑟 с членами 𝑛: 𝑆=𝑇+𝑇𝑟+𝑇𝑟+𝑇𝑟+⋯+𝑇𝑟 .
Умножение этого уравнения на 𝑟 дает 𝑟𝑆=𝑇𝑟+𝑇𝑟+𝑇𝑟+𝑇𝑟+⋯+𝑇𝑟.
 0003
0003Теперь мы можем вычесть второе уравнение из первого и полностью разложить на множители. . Обратите внимание, что когда мы вычитаем слагаемые в правой части, большинство слагаемых становятся равными нулю:0003
Разделив обе части этого уравнения на 1−𝑟, получим формулу суммы первых 𝑛 членов геометрического ряда с первым членом 𝑇 и знаменателем 𝑟: 𝑆=𝑇(1−𝑟)1−𝑟.
Ранее мы утверждали, что для сходящегося геометрического ряда −1𝑟1.
Это означает, что по мере того, как 𝑛 приближается к бесконечности, 𝑟 должно стремиться к нулю.
Другими словами, если |𝑟|1, то lim→∞𝑟=0.
Мы можем рассмотреть, что происходит с нашим сходящимся геометрическим рядом, когда 𝑛 приближается к бесконечности. Для |𝑟|1 lim→∞𝑇(1−𝑟)1−𝑟=𝑇(1−0)1−𝑟=𝑇1−𝑟.
Иногда это называют суммой до бесконечности геометрического ряда.
Определение: сумма бесконечной геометрической последовательности
Если обыкновенное отношение 𝑟 удовлетворяет условию |𝑟|1, то сумма бесконечного геометрического ряда с первым членом 𝑇 равна 𝑆=𝑇1−𝑟.
 ∞
∞Давайте теперь рассмотрим вопрос, который требует от нас применения наших знаний об общих соотношениях в геометрических последовательностях и условиях сходимости этих рядов, а также вычислить значение сходящегося бесконечного геометрического ряда.
Пример 1. Нахождение суммы бесконечного геометрического ряда
Нахождение суммы геометрического ряда 132+134+138+⋯.
Ответ
Мы знаем, что если знаменатель 𝑟 удовлетворяет условию |𝑟|1, то сумма бесконечной геометрической последовательности с первым членом 𝑇 равна 𝑆=𝑇1−𝑟.∞
Мы видим, что первый член равно 132, поэтому нам нужно рассчитать обыкновенное отношение 𝑟. Мы находим это, разделив термин на предшествующий ему термин, поэтому мы будем использовать первые два термина: 𝑟=134÷132=12.
Мы видим, что абсолютное значение обыкновенного отношения меньше 1, поэтому мы можем найти сумму этого ряда, полагая 𝑇=132 и 𝑟=12: 𝑆=1−=132÷12=13.∞
Сумма ряда равна 13.
В нашем следующем примере мы увидим, как применять эту технику при работе с радикальными отношениями.

Пример 2. Определение знаменателя бесконечной геометрической последовательности и нахождение ее суммы, если она существует
Рассмотрим ряд 160+160√2+80+80√2+40+40√2+⋯.
Ряд геометрический. Каково его обыкновенное отношение?
Сходится ли этот ряд? Если да, то какова его сумма?
Ответ
Часть 1
Обычное отношение в геометрической последовательности 𝑟 находится путем деления члена ряда на член, который ему предшествует. Выберем первые два члена: 160√2÷160=1√2.
Обычное отношение равно 1√2.
Заметьте, мы получили бы тот же результат, если бы разделили третий член на второй или даже любой член на член, который ему предшествует!
Часть 2
Геометрический ряд сходится, если |𝑟|1 или −1𝑟1.
В данном случае −11√21, что означает, что этот ряд сходится. Таким образом, мы можем найти сумму ряда с первым членом 𝑇 и знаменателем 𝑟, применяя формулу 𝑆=𝑇1−𝑟∞ с 𝑇=160 и 𝑟=1√2: 𝑆=1601−.∞√
упрощая 1−1√2, мы создаем общий знаменатель √2: 1−1√2=√2√2−1√2=√2−1√2.

Сумма ряда теперь равна 𝑆=160=160×√2√2−1=160√2√2−1.∞√√
Чтобы закончить, мы должны не забыть рационализировать знаменатель умножить на сопряжено с из √2−1. Сопряжение находится путем изменения знака между двумя терминами: +1=320+160√21.∞
Факторизуя это выражение, мы находим 𝑆=1602+√2.∞
Да, ряд сходится, с бесконечной суммой 1602+√2 .
В наших предыдущих двух примерах мы установили существование суммы и вычислили эту сумму на основе нескольких первых членов ряда. Мы также можем использовать формулу для 𝑛-го члена геометрической прогрессии, чтобы получить тот же результат.
Пример 3. Нахождение суммы бесконечного числа членов геометрической последовательности по заданному ее общему члену .
Ответ
Общий член геометрического ряда с первым членом 𝑇 и знаменателем 𝑟 равен 𝑇=𝑇𝑟.
Сравнивая это с нашей последовательностью, мы видим, что они не совсем совпадают. Вместо этого мы можем использовать формулу 𝑛-го члена, которую нам дали, чтобы сгенерировать первые два члена.

Когда 𝑛=1, 𝑇=3×14=3×14=3.
Когда 𝑛=2, 𝑇=3×14=3×14=314.
Таким образом, первый член равен 3, а обыкновенное отношение равно 314÷3=114.
Поскольку знаменатель находится в интервале (−1,1), ряд сходится, поэтому мы можем найти его сумму, используя формулу 𝑆=𝑇1−𝑟∞ с 𝑇=3 и 𝑟=114: 𝑆=31 −=3÷1314=4213.∞
Как упоминалось ранее, применение этого процесса выходит за рамки только данного ряда. На самом деле мы можем представить повторяющееся десятичное число как дробь, представляя десятичное число как геометрическую серию.
Пример 4: Повторяющиеся десятичные дроби
Найдя сумму бесконечной геометрической прогрессии, выразите 0,̇37̇5 в виде обыкновенной дроби.
Ответ
Повторяющееся десятичное число 0.̇37̇5=0.375375375375….
Это означает, что мы можем разделить его на 0,375+0,000375+0,000000375+⋯, а затем записать каждый член в виде дроби: 0,̇37̇5=3751000+3751000000+3751000000000+⋯.
Это геометрический ряд с первым членом 3751000 и знаменателем 11000.
 Поскольку знаменатель находится в интервале ]−1,1[ мы можем сказать, что этот ряд сходится, и таким образом найти его сумму.
Поскольку знаменатель находится в интервале ]−1,1[ мы можем сказать, что этот ряд сходится, и таким образом найти его сумму.Использование формулы 𝑆=𝑇1−𝑟∞ с 𝑇=3751000 и 𝑟=11000 дает 𝑆=1−=3751000÷9991000=375999.∞
Полностью упрощая, мы видим, что повторяющееся десятичное число 0.̇37̇5 эквивалентно 125333.
Давайте теперь рассмотрим, как этот процесс будет отличаться для повторяющегося десятичного числа, цифры которого не повторяются все .
Пример 5: Повторяющиеся десятичные дроби
Найдя сумму бесконечной геометрической последовательности, выразите 0,4̇3 в виде обыкновенной дроби.
Ответ
Повторяющееся десятичное число 0,4̇3=0,4333333….
Это означает, что мы можем разделить его на 0,4+0,0̇3=0,4+0,03+0,003+0,0003+⋯.
Рассматривая сумму 0,03+0,003+0,0003+⋯, мы видим, что имеем геометрический ряд с первым членом 𝑇=0,03. Обычное отношение 0,0030,03=110.
Поскольку абсолютное значение этого знаменателя меньше 1, этот ряд сходится, поэтому мы можем найти его сумму.

Использование формулы 𝑆=𝑇1−𝑟∞ с 𝑇=0,03 и 𝑟=110 дает 𝑆=0,031−=0,03÷910=390.∞
Полностью упрощая, мы видим, что повторяющееся десятичное число 0,0̇3 эквивалентно 130.
Это означает, что 0,4̇3=0,4+130=1330.
Как обыкновенная дробь, 0,4̇3 равно 1330.
В нашем следующем примере мы рассмотрим, как найти бесконечную сумму геометрической прогрессии, зная значение двух ее членов. Это будет включать применение формулы для общего члена геометрической последовательности, а затем вычисление значения обыкновенного отношения в обратном направлении.
Пример 6. Нахождение суммы бесконечной геометрической последовательности по значениям двух членов
Найдите сумму бесконечной геометрической последовательности, если первый член равен 171, а четвертый член равен 17164.
Ответ
Геометрический ряд сходится, если |𝑟|1 или −1𝑟1, где 𝑟 — знаменатель.
В этом случае сумма бесконечной геометрической последовательности с первым членом 𝑇 равна 𝑆=𝑇1−𝑟.
 ∞
∞Обратите внимание, что нам дано значение первого и четвертого членов, поэтому нам нужно будет использовать эту информацию для расчета обыкновенного отношения.
Используем формулу для 𝑛-го члена геометрической прогрессии с 𝑇=171 и 𝑇=17164: 𝑇=𝑇𝑟17164=171𝑟17164=171𝑟. 9 0003
Чтобы найти 𝑟, мы будем разделите на 171 и найдите кубический корень из обеих частей уравнения: 164=𝑟𝑟=14.
Поскольку абсолютное значение этого знаменателя меньше 1, этот ряд сходится, и мы можем найти его сумму.
Использование формулы 𝑆=𝑇1−𝑟∞ с 𝑇=171 и 𝑟=14 дает 𝑆=1711−=171÷34=228,∞
Сумма бесконечной геометрической прогрессии равна 228,
В нашем последнем примере мы рассмотрим, как можно применить формулу бесконечной суммы геометрического ряда для вычисления первого члена.
Пример 7. Нахождение первого члена бесконечной геометрической последовательности по ее знаменателю и сумме членов
Найдите первый член бесконечной геометрической последовательности, знаменатель которой равен 14, а сумма равна 9867.

- Определение геометрической прогрессии

 2}\Rightarrow1+q=3\Rightarrow q=2.\)
2}\Rightarrow1+q=3\Rightarrow q=2.\)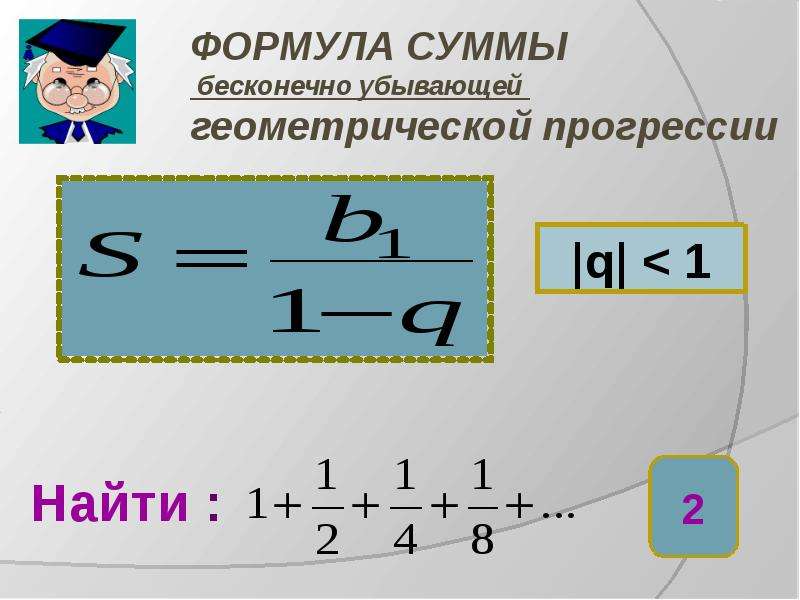

 Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.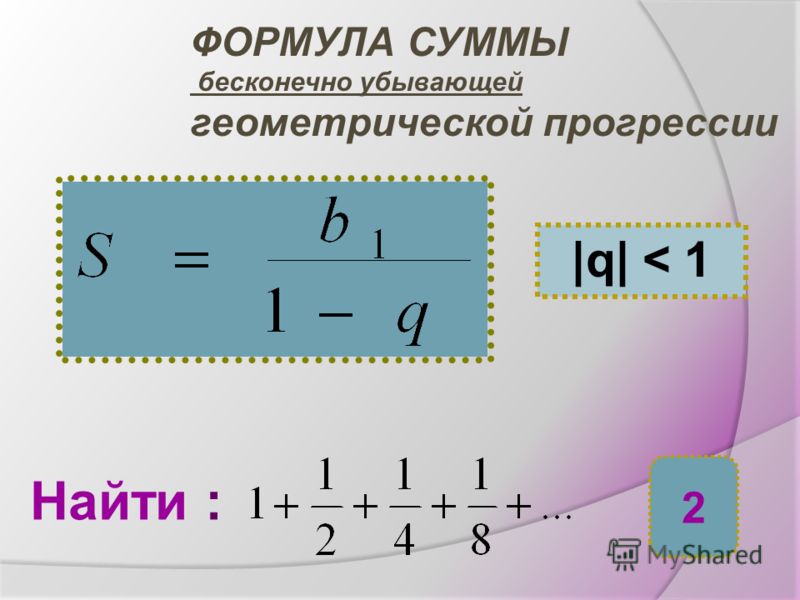

 Мы можем рассчитать значение обыкновенного отношения, разделив любой член на член, который ему предшествует.
Мы можем рассчитать значение обыкновенного отношения, разделив любой член на член, который ему предшествует.

 0003
0003 ∞
∞


 Поскольку знаменатель находится в интервале ]−1,1[ мы можем сказать, что этот ряд сходится, и таким образом найти его сумму.
Поскольку знаменатель находится в интервале ]−1,1[ мы можем сказать, что этот ряд сходится, и таким образом найти его сумму.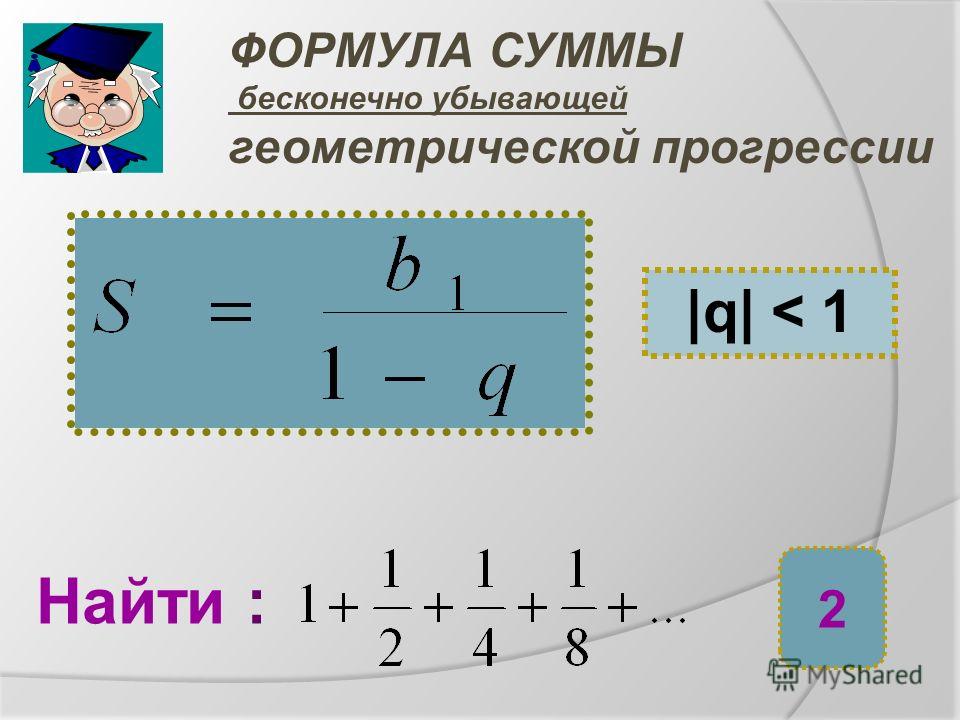
 ∞
∞