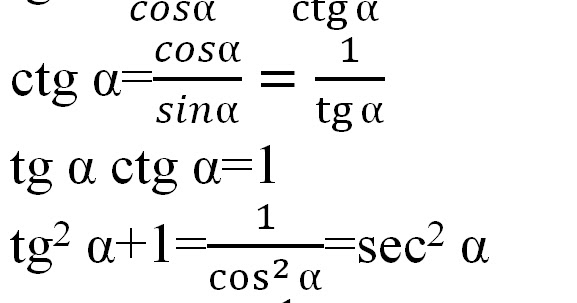Основные тригонометрические формулы
В самом начале этой статьи мы с Вами рассмотрели понятие тригонометрических функций. Основное назначение их назначение – это изучение основ тригонометрии и исследование периодических процессов. И тригонометрический круг мы не зря рисовали, потому что в большинстве случаев тригонометрические функции определяются, как отношение сторон треугольника или его определенных отрезков в единичной окружности. Так же я упоминал о неоспоримо огромном значении тригонометрии в современной жизни. Но наука не стоит на месте, в результате мы можем значительно расширить область применения тригонометрии и перенести ее положения на вещественные, а иногда и на комплексные числа.
Формулы тригонометрии бывают нескольких видов. Рассмотрим их по порядку.
Соотношения тригонометрических функций одного и того же угла
Выражения тригонометрических функций друг через друга
(выбор знака перед корнем определяется тем, в какой из четвертей круга расположен угол ?)
Далее следуют формулы сложения и вычитания углов:
Формулы двойных, тройных и половинных углов.
Замечу, что все они проистекают из предыдущих формул.

Формулы преобразования тригонометрических выражений:
Здесь мы подошли к рассмотрению такого понятия как основные тригонометрические тождества.
Тригонометрическое тождество — это равенство, которое состоит из тригонометрических соотношений и которое выполняется для всех значений величин углов, которые входят в него.
Рассмотрим наиболее важные тригонометрические тождества и их доказательства:
Первое тождество вытекает из самого определения тангенс.
Возьмем прямоугольный треугольник, в котором имеется острый угол х при вершине А.
Для доказательства тождеств необходимо воспользоваться теоремой Пифагора:
(ВС) 2 + (АС) 2 = (АВ) 2
Теперь разделим на (АВ) 2 обе части равенства и припомнив определения sin и cos угла, мы получаем второе тождество:
(ВС) 2/(AB) 2 + (AC) 2/(AB) 2 = 1
sin x = (BC)/(AB)
cos x = (AC)/(AB)
sin2 x + cos2 x = 1
Для доказательства третьего и четвертого тождеств воспользуемся предыдущим доказательством.
Для этого обе части второго тождества разделим на cos2 x:
sin2 x/ cos2 x + cos2 x/ cos2 x = 1/ cos2 x
sin2 x/ cos2 x + 1 = 1/ cos2 x
Исходя из первого тождества tg x = sin х /cos x получаем третье:
1 + tg2 x = 1/cos2 x
Теперь разделим второе тождество на sin2 x:
sin2 x/ sin2 x + cos2 x/ sin2 x = 1/ sin2 x
1+ cos2 x/ sin2 x = 1/ sin2 x
cos2 x/ sin2 x есть не что иное, как 1/tg2 x, поэтому получаем четвертое тождество:
1 + 1/tg2 x = 1/sin2 x
Пришла пора вспомнить теорему о сумме внутренних углов треугольника, которая гласит, что сумма углов треугольника = 180
Опять вспомним определения для sin и cos и получаем пятое и шестое тождества:
sin x = (BC)/(AB)
cos(900– x ) = (BC)/(AB)
cos(900– x ) = sin x
Теперь выполним следующее:
cos x = (AC)/(AB)
sin(900– x ) = (AC)/(AB)
sin(900– x ) = cos x
Как видите – здесь все элементарно.
Существуют и другие тождества, которые используются при решении математических тождеств, я приведу их просто в виде справочной информации, потому как все они проистекают из вышерассмотренных.
sin 2х =2sin х*cos х
cos 2х =cos2х -sin2х =1-2sin2х =2cos2х -1
tg 2x = 2tgx/(1 — tg2 x)
сtg 2x = (сtg2 x — 1) /2сtg x
sin3х =3sin х — 4sin3х
cos3х =4cos3х — 3cos х
tg 3x = (3tgx – tg3 x) /(1 — 3tg2 x)
сtg 3x = (сtg3x – 3сtg x) /(3сtg2 x — 1)
Когда-то, будучи школьником, я с удовольствием применял эти формулы для решения различного рода задач, как то упростить выражение или решить уравнение. Главное разглядеть — куда и какую формулу необходимо применить, и тогда многоярусная конструкция превращается в обычное числовое выражение.
Формулы двойного угла в тригонометрии: синус косинус двойного угла
Основные понятия. Тригонометрия довольно древняя наука, и ее первые упоминания связаны с необходимостью в практичной жизни, в земледелии, астрономии и строительстве. Впервые именно астрономы вывели такие понятия как отношение сторон треугольника. А официальные названия функций стали появляться позже, например, синус, который получил свое название первым, получил свое название от греческих математиков уже в третьем веке до н.э.. а косинус является относительно молодым, и был выведен как дополнение к синусу. История тригонометрии обширна и интересна, из древней науки о треугольниках она перешла в известную нам науку о тригонометрических функциях. Для того чтобы разобраться в формулах двойного угла, необходимо вспомнить основные понятия тригонометрии.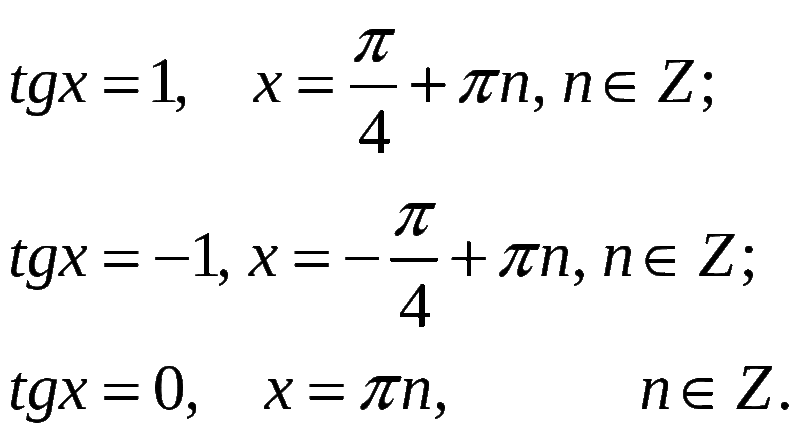
Данные примеры будут использоваться далее по тексту. Мы можем посмотреть их значение на окружности на рисунке ниже.
Основное тождество в тригонометрии, звучит так:
- Синус в квадрате угла плюс косинус в квадрате угла равны единице;
- Произведение тангенса и котангенса угла равно единице;
- Тангенс угла равен, делению, синуса этого угла на косинус, а котангенс наоборот косинуса на синус.
Данные тождества также будут применены для выведения формул двойного, тройного и т.д. углов.
Формулы двойного угла в тригонометрии
Формулы двойного угла тригонометрических функций, необходимы для того чтобы выразить их, при этом угол должен иметь значение 2а, а также используя ТФ этого угла. Для отражения её на графике используют координаты с окружностью.
Список формул двойного угла
Прежде чем преступить к образованию формул двойного угла тригонометрии, давайте вспомним, что в тригонометрии углы принято писать в виде na, в такой записи п — обозначение натурального числа, а а — угол альфа. {*} \operatorname{ct} a}
\]
{*} \operatorname{ct} a}
\]
Стоит не забывать, что выше приведённые формулы sin и cos, можно применять для любого значения угла. А вот если рассмотреть, формулы для тангенса, то при любых альфа где, tg 2a , имеет смысл, то есть при \[a \neq \frac{\pi}{4}+\frac{\pi}{2} \cdot z\], где z любое целое число. Что же касается формулы двойного угла котангенса, то при любом a, где ctg 2α определён на α ≠ 2 * z .
Как мы видим косинус с таким видом угла, наделён тремя вариантами записи формул, все они равноправны, а это значит, что результат их применения будет абсолютно одинаковым.
Доказательство формул двойного угла
Для того чтобы, формулы двойного угла были доказаны, вернёмся к истокам, формулам сложения. Сначала рассмотрим формулу синуса суммы, которая выглядит следующим образом:
\[ \operatorname{Sin}(a+b)=\operatorname{Sin} a * \cos b+\cos a * \sin b \]
Косинуса суммы:
\[ \operatorname{Cos}(a+b)=\cos a * \cos b-\sin a * \sin b \]
Если считать что a = b, тогда выходит:
\[ \operatorname{Sin}(a+a)=\sin a * \cos a+\cos a * \sin a=2 * \cos a * \sin a \]
И также для косинуса:
\[ \cos (a+a)=\cos a * \cos a-\sin a * \sin a=\cos ^{2} \alpha-\sin ^{2} \alpha \]
Таким способом мы доказали формулы синуса и косинуса двойного угла.
Формулы которые остались: cos 2α = 1 − 2 * sin2α , cos 2α = 2 * cos2α−1, выразили в таком виде благодаря приведению вместо единицы тождества суммы квадратов, cos2α +sin2α = 1. Поэтому вышло следующее:
Формулы приведения двойного угла: 1 − 2 * sin2α = cos2α +sin2α — 2 * sin2α = cos2α — sin2α.
И так же с третьих примеров формулы двойного угла.
2 * cos2α−1 = 2 * cos2α -( cos2α +sin2α ) = cos2α — sin2α.
Для того, чтобы выполнить доказательство формул для тангенса и котангенса двойного угла тоже применяется равенство следующего вида:
\[ \operatorname{tg} 2 \alpha=\frac{\sin 2 \alpha}{\cos 2 \alpha} \text { и } \operatorname{ctg} 2 \alpha=\frac{\cos 2 \alpha}{\sin 2 \alpha} . \]
Сделав замену на данные равенства получим следующие выражения:
\[ \operatorname{tg} 2 \alpha=\frac{\sin 2 \alpha}{\cos 2 \alpha}=\frac{2 \cdot \sin \alpha \cdot \cos \alpha}{\cos ^{2} \alpha-\sin ^{2} \alpha} \text { и } \operatorname{ctg} 2 \alpha=\frac{\cos 2 \alpha}{\sin 2 \alpha}=\frac{\cos ^{2} \alpha-\sin ^{2} \alpha}{2 \cdot \sin \alpha \cdot \cos \alpha} \]
Представленные выше выражения мы разделим на cos2α, при котором cos2α ≠ 0, а альфа имеет любое значение, когда тангенс угла альфа определён. {\circ}}
\]
{\circ}}
\]
Так как мы знаем, что синус тридцати градусов равен одной второй, косинус этого угла, равен корню из трёх, который поделен на два, тангенс заданного угла это корень из трёх на три, котангенс корень из трёх.
Получается, что синус двойного угла, то есть шестидесяти градусов, равен корню из трёх, который поделен на два; косинус — одной второй; тангенс корню из трёх; а котангенс корню из трёх делённому на три.
Получаем следующие выражения:
Сделав все операции по вычислению, можно прийти к выводу, что справедливость для угла альфа тридцати градусов, подтверждена.
Теперь мы понимаем, что применение формул тригонометрии двойного угла, это видоизменение тригонометрических выражений. Стоит также рассмотреть пример применения формул двойного угла, в случае, когда угол не равен 2a. К примеру возьмём значение \[\frac{5 \pi}{6}\]. Имея такое значение, для решения задания, его необходимо преобразовать, поэтому получаем следующее:
\[a=\frac{5 \pi}{6}: 2=\frac{5 \pi}{12}\], применив данное выражение формула двойного угла для косинуса получит следующий вид:
\[ \cos \frac{5 \pi}{6}=\cos ^{2} \frac{5 \pi}{12}-\sin ^{2} \frac{5 \pi}{12} \]
Пример:
Необходимо, через тригонометрические функции представить \[\sin \frac{2 a}{3} \text { при } \frac{a}{6}\].
Решение:
Так как в условии уже \[\frac{2 a}{3}=4 * \frac{a}{6}\], то применив дважды выше обозначенную формулу удвоенного угла, что выражая \[\sin \frac{2 a}{3}\], через функции угла \[\frac{a}{6}\], с применением формулы двойного угла, выходит , \[\sin \frac{2 a}{3}=2 * \sin \frac{a}{3} * \cos \frac{a}{3}\], затем к \[\sin \frac{a}{3} \text { и } \cos \frac{a}{3}\]в данном примере подставим снова данную формулу удвоенного угла и получим следующее выражение:
Формулы тройного угла и более углов
Так как зачастую в тригонометрии возникает необходимость вычисления не только двойного угла, но и больше, например тройного, четверного и тд. Стоит рассмотреть примеры их вычисления. Выведение их формул аналогично с выведением формул двойного угла, но для этого будем применять формулы сложения (суммы) двойного угла.
Пример:
sin 3α = sin ( 2 α + α ) = sin 2α * cos α + cos 2 α * sin α = 2 * sin α ⋅ cos α * cos α + ( cos2α — sin2α ) * sin α =
=3 * sin α * cos2α — sin3α
Заменим cos2α, на выражение 1 — sin2α, и теперь получившаяся ранее формула тройного угла sin 3α =3 * sin α * cos2α — sin3α, примет следующий вид: sin 3α = 3 * sin α * cos2α — sin3α = 3 *sin α — 4* sin3α
Аналогично поступим и с формулами cos тройного угла:
cos 3α = cos ( 2 α + α ) = cos 2α * cos α − sin 2α *sin α = ( cos2α — sin2α ) * cos α − 2* sin α * cos α * sin α =
= cos3α − 3* sin2α * cos α
Заменяем sin2α на выражение разности единицы и косинуса, 1 — cos2α, выходит следующая формула : cos 3α =
= -3 * cos α + 4* cos3α
Так как теперь у нас есть формулы тройного угла синуса и косинуса, мы можем вывести формулы тройного угла для тангенса и котангенса, подставив полученные выражения в первичные формулы:
И так далее…
К примеру, чтобы привести формулу угла четыре альфа, для удобства лучше 4а представить, как 2 * 2а, и в результате мы получим, что для выведения формулы для 4а, нужно использовать две формулы двойного угла.
А для выведения формулы угла пятой степени, 5а, необходимо выполнить 5а как сумму тройного и двойного угла, то есть 2а+3а.
В результате мы получим выражение из суммы двух формул двойного и тройного угла. Стоит отметить, что такое же правило будет действовать если необходимо вывести формулу половинного угла.
Область применения
Для того чтобы найти значение тригонометрических функций, берётся окружность на оси координат, у которой радиус равен единице, а диаметры у неё находятся в перпендикулярном положении.
Для такого вычисления нам понадобится отложить от точки, которая принадлежит окружности различные дуги, любой длины. Соответственно если мы отложим их против часовой стрелки они примут положительное значение, а если по часовой, то отрицательное.
Допустим конец дуги имеет некую длину s, в таком случае проекция радиуса в любом выбранном значении диаметра станет значением косинуса данной дуги. Выбранная длина s, или радианная мера угла, будет считаться числом аргумента. А если этот самый аргумент, это тригонометрическая функция угла, то мы знаем, что значение может быть и в градусах.
А если этот самый аргумент, это тригонометрическая функция угла, то мы знаем, что значение может быть и в градусах.
Мы знаем, что острый угол имеет значения больше нуля, но меньше п\2. В таком случае тригонометрическая функция рассматривается как катет делённый на гипотенузу. Такие названия сторон связаны с прямоугольным треугольником, в котором величина угла равна 90 градусов.
Чтобы решить задачи с функциями тригонометрии, используют теорему Пифагора. Такая теорема основана на свойствах того самого прямоугольного треугольника, в котором квадрат гипотенузы равен сумму квадратов катетов.
Так как дуга делит окружность на несколько частей, то мы можем увидеть, что углы лежащие в первой четверти больше нуля. А во второй синус меньше, а косинус больше нуля, а в третьей все функции будут меньше нуля, то есть отрицательными, четвёртая имеет значения противоположные второй. Не стоит забывать, что для построения окружности вам понадобится циркуль.
Как мы видим формулы двойного угла, не так трудно вывести, для этого необходимо знать основные тригонометрические тождества и разобраться в единичной окружности на оси координат.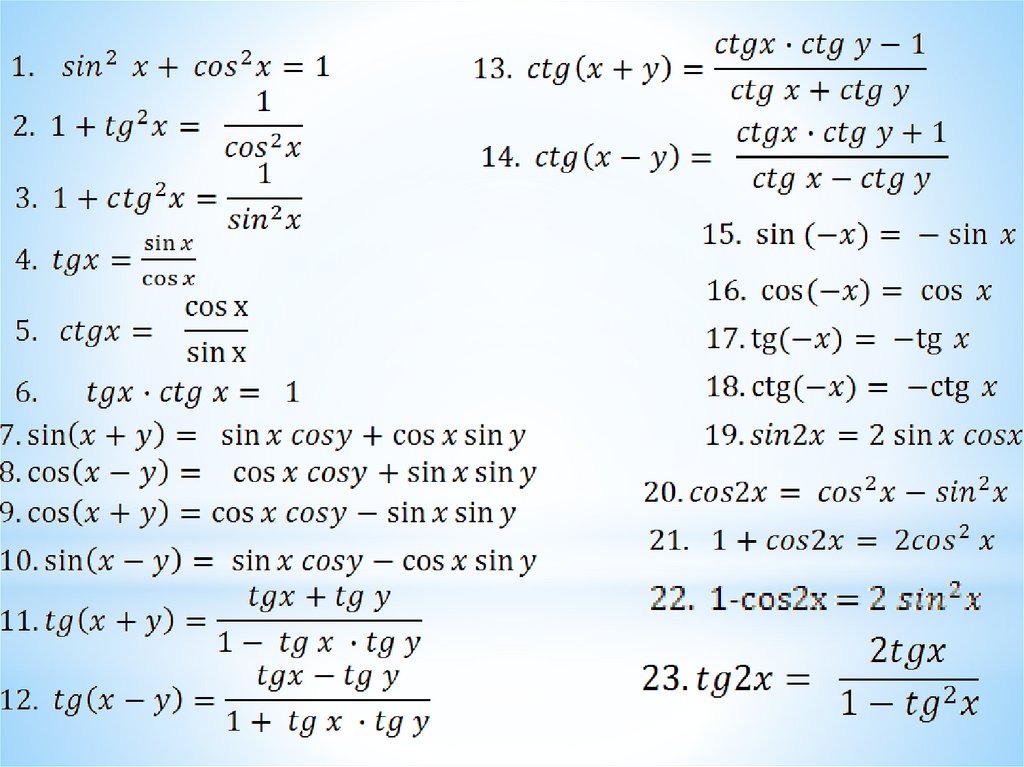 Также необходимо отметить, что формулы двойного угла, как и другие формулы тригонометрии используются в разных сферах жизни:
Также необходимо отметить, что формулы двойного угла, как и другие формулы тригонометрии используются в разных сферах жизни:
- В астрономии, учёные с помощью формул вычисляют положение небесных тел, а также расстояние до них;
- Для различного вида навигации, к примеру, морской и воздушной;
- В медицине и биологии, при построении биоритма живых организмов, а также тригонометрия служит основой работы некоторой медицинской техники;
- Архитекторам она важна при создании планов строений;
- но и это не всё, тригонометрия важна и для экономики, в производстве и создании электроники, в различных аналитических вычислениях, акустических построениях и многом другом.
Tan2x — формула, идентичность, примеры, доказательство
Tan2x — важная тригонометрическая функция. Формула Tan2x является одной из наиболее часто используемых тригонометрических формул двойного угла и может быть выражена через различные тригонометрические функции, такие как tan x, cos x и sin x.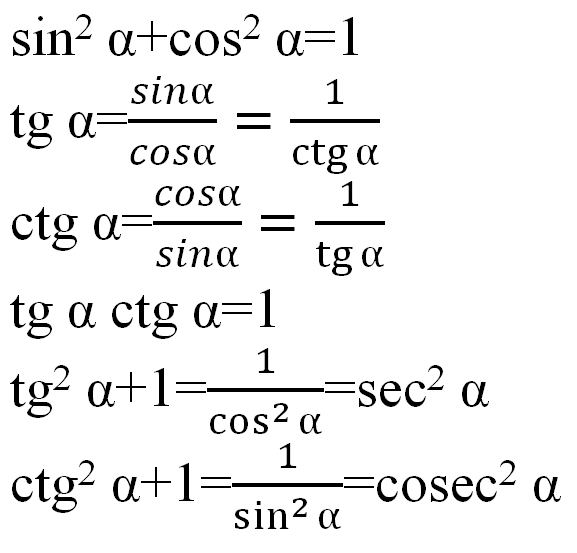 2x, их доказательство и выразим их в терминах различных тригонометрических функций. Мы также изучим график tan2x и его период вместе с концепцией тангенса квадрата x и решим примеры для лучшего понимания. 92x Формула
2x, их доказательство и выразим их в терминах различных тригонометрических функций. Мы также изучим график tan2x и его период вместе с концепцией тангенса квадрата x и решим примеры для лучшего понимания. 92x Формула
Что такое Tan2x в тригонометрии?
Tan2x является тригонометрической функцией и имеет формулу, которая используется для решения различных задач в тригонометрии. Tan2x — важная формула двойного угла, то есть формула тригонометрии, в которой угол удваивается. Его можно выразить через тангенс х, а также как отношение sin2x и cos2x. Поскольку величина, обратная tan x, равна cot x, поэтому мы можем записать tan2x как обратную величину cot 2x, то есть tan2x = 1/cot2x. Давайте посмотрим на формулу tan2x:
Tan2x Формула
Мы можем выразить формулу tan2x в двух различных формах. Это может быть выражено только в терминах функции тангенса и как комбинация функции синуса и функции косинуса. Формула для идентичности tan2x задается как:
Это может быть выражено только в терминах функции тангенса и как комбинация функции синуса и функции косинуса. Формула для идентичности tan2x задается как:
- tan2x = 2tan x / (1−tan 2 x)
- tan2x = sin 2x/cos 2x
Формула Tan2x Proof
Формулу Tan2x можно получить двумя разными способами. Во-первых, мы будем использовать формулу сложения углов для функции тангенса, чтобы получить тождество tan2x. Обратите внимание, что мы можем записать двойной угол 2x как 2x = x + x. Мы будем использовать следующую тригонометрическую формулу, чтобы доказать формулу для tan2x:
- tan (a + b) = (tan a + tan b)/(1 — tan a tan b)
Имеем
tan2x = tan (x + x)
= (tan x + tan x)/(1 — tan x tan x)
= 2 tan x/(1 — tan 2 x)
Следовательно, мы получили формулу tan2x, используя формулу суммы углов функции тангенса.
Подтверждение подлинности Tan2x с использованием Sin и Cos
Теперь мы выведем формулу tan2x, выразив tan как отношение sin и cos. Мы будем использовать следующие тригонометрические формулы:
Мы будем использовать следующие тригонометрические формулы:
- тангенс x = sin x/ cos x
- sin 2x = 2 sin x cos x
- cos 2x = cos 2 x — sin 2 x
Используя приведенные выше формулы, мы имеем
tan2x = sin 2x/cos 2x
= 2 sin x cos x/(cos 2 x — sin 2 x)
Разделить числитель sin2 на знаменатель x cos x/(1 — 2 sin 2 x) by cos 2 x
tan2x = [2 sin x cos x/cos 2 x]/[(cos 2 x — sin 2 x)/cos 2 x]
= (2 sin x/cos x)/(1 — sin 2 x/cos 2 x)
= 2
= 2
= 2 2 x/cos x/(1 — tan 2 x)
Следовательно, мы получили формулу tan2x, представив ее как отношение sin 2x и cos 2x.
График Tan2x
График tan2x похож на график tan x. Мы знаем, что период тангенса x равен π. Поскольку период tan bx определяется как π/|b|, период tan2x равен π/2. Ниже приведен график tan2x, и, как видно из графика, значение tan2x повторяется через каждые π/2 радиана. Кроме того, значение tanx равно нулю всякий раз, когда x является целым числом, кратным π, поэтому tan2x равно нулю, когда 2x = nπ, где n — целое число, что означает, что на приведенном ниже графике есть точки пересечения x при x = nπ/2. . 92x ⇒ желтовато-коричневый 2 x = 1/кровать 2 x
Ниже приведен график tan2x, и, как видно из графика, значение tan2x повторяется через каждые π/2 радиана. Кроме того, значение tanx равно нулю всякий раз, когда x является целым числом, кратным π, поэтому tan2x равно нулю, когда 2x = nπ, где n — целое число, что означает, что на приведенном ниже графике есть точки пересечения x при x = nπ/2. . 92x ⇒ желтовато-коричневый 2 x = 1/кровать 2 x
Tan2x в пересчете на Cos
Мы можем вывести формулу tan2x через cos. Мы будем использовать следующие тригонометрические формулы, чтобы выразить tan2x через cos x.
- тангенс x = sin x/cos x
- sin 2x = 2 sin x cos x
- cos 2x = 2 cos 2 x — 1
- sin x = √(1 — cos 2 x)
Используя приведенные выше формулы, мы имеем
tan2x = sin 2x/ cos 2x
= 2 sin x cos x/(2 cos 2 x — 1)
= [2 √(1 — cos 2 x) cos x/(2 cos 2 x — 1)]
Точно так же мы можем записать tan2x через грех, используя тригонометрические тождества.
tan2x = [2 sin x/(1 — 2 sin 2 x)]√(1 — sin 2 x)
Важные замечания по формуле Tan 2x
- tan2x = 2tan x1 ( − желто-коричневый 2 х)
- tan2x = sin 2x/cos 2x
- Производная tan2x равна 2 с 2 (2x)
- Интеграл от tan2x равен (-1/2) ln |cos 2x| + C или (1/2) ln |sec 2x| + с.
☛ Статьи по теме:
- Формулы касательной
- Кос 2x
Часто задаваемые вопросы по Tan2x Formula
Что такое Tan2x в тригонометрии?
Формула Tan2x является одной из наиболее часто используемых тригонометрических формул двойного угла и может быть выражена через различные тригонометрические функции, такие как tan x, cos x и sin x. Обычно используемая формула для tan2x: tan2x = 2tan x / (1 − tan 2 х).
Что такое формула Tan2x?
Формула Tan2x может быть выражена различными способами, например:
- tan2x = 2tan x / (1 − tan 2 x)
- tan2x = sin 2x/cos 2x
- tan2x = [2 cos x/(2 cos 2 x — 1)]√(1 — cos 2 x)
- tan2x = [2 sin x/(1 — 2 sin 2 x)]√(1 — sin 2 x)
Что такое домен и диапазон Tan2x?
Домен tan2x состоит из всех вещественных чисел, кроме тех, для которых tan2x не определен. Итак, область определения tan 2x есть R — {(2n + 1)π/4, n ∈ Z}. Диапазон tan2x — это все действительные числа, то есть R.
Итак, область определения tan 2x есть R — {(2n + 1)π/4, n ∈ Z}. Диапазон tan2x — это все действительные числа, то есть R.
Как найти производную Tan2x?
Производная tan2x может быть рассчитана с использованием различных методов, таких как цепное правило и частное правило. Производная tan2x равна 2 с 2 (2x).
Что такое интеграл Tan2x?
Интеграл от tan2x определяется выражением (-1/2) ln |cos 2x| + C или (1/2) ln |sec 2x| + C.
Что представляет собой формула Tan2x с точки зрения Cos x и Sin x?
Формула Tan2x с точки зрения sin x и cos x определяется как tan2x = 2 sin x cos x /(cos 92x всегда неотрицательно, так как квадрат числа никогда не бывает отрицательным.
Тканевая трансглютаминаза (TG2)-субстрат-пептид T26 — Анализы и субстраты — Продукты
Ссылка Вир. Лицензионное соглашение с Zedira и Dr. Falk Pharma для разработки первой в своем классе терапии целиакии
Ссылка Кооперация и лицензирование для zwischen Takeda, Zedira и Dr.