Формула векторов: Векторы — основные понятия и формулы

Аналитическая геометрия

Аналитическая геометрия

Привалов И.И. Аналитическая геометрия. М.: Наука, 1966. — 272 с. Учебник для студентов высших технических заведений. Содержит разделы: Аналитическая геометрия на плоскости, Аналитическая геометрия в пространстве. Много решенных примеров и задач. Оглавление ВВЕДЕНИЕ ЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций. § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 6. Построение прямой линии по ее уравнению. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости. § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры. § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии. Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. Упражнения ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ § 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой. § 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова. Упражнения Ответы

Найти вектор скорости и ускорения точки, примеры решений

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.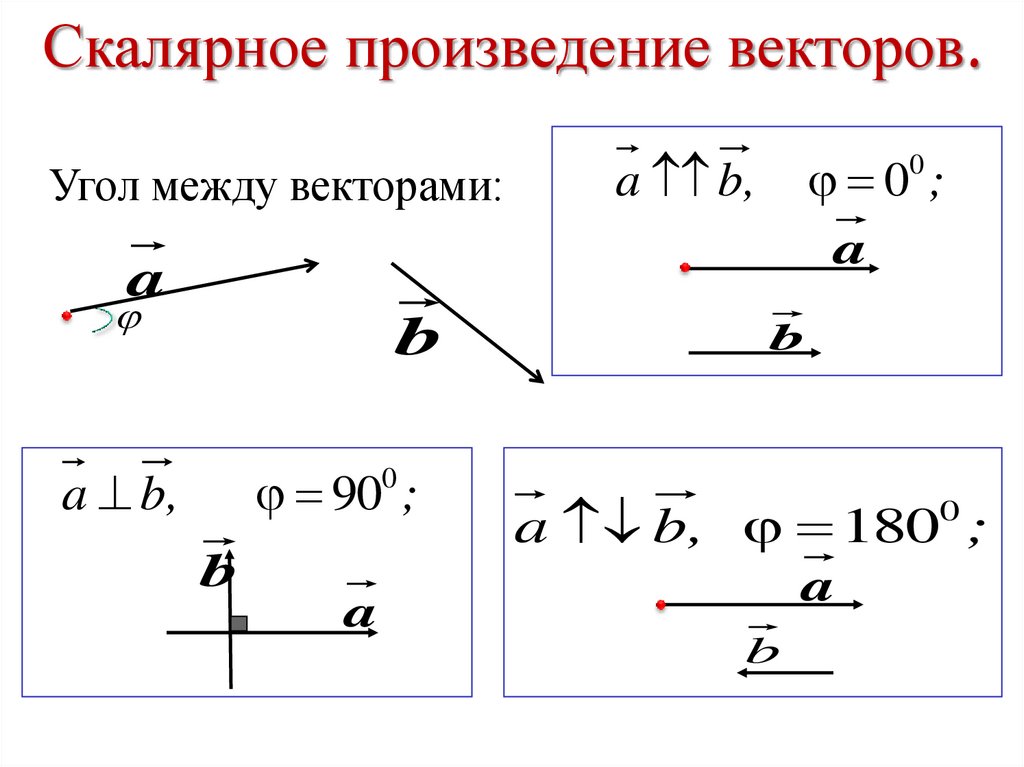

 

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Объяснение урока: Момент силы относительно точки в 2D: векторы

В этом объяснении мы узнаем, как найти момент плоской системы сил, действующих на тело относительно точки, как вектор.

Мы знаем, что сила или система сил может оказывать вращательное действие на тело, которое описывается моментом сила или система сил относительно точки. Напомним, что при плоском движении момент 𝑀 силы ⃑𝐹 о точке определяется как скаляр, величина которого определяется выражением |𝑀|=‖‖⃑𝐹‖‖𝑑,⟂ где 𝑑⟂ — перпендикулярное расстояние между точкой и линией действия силы ⃑𝐹. Затем мы можем определить знак момента, рассмотрев, является ли эффект вращения идет по часовой стрелке или против часовой стрелки. По соглашению мы определяем момент с действием против часовой стрелки как положительный, что означает, что момент с эффектом вращения по часовой стрелке определяется как отрицательный.

Хотя это определение хорошо подходит для плоского движения, оно недостаточно, когда мы рассматриваем движение с трехмерным пространство, потому что понятие записи по часовой стрелке или против часовой стрелки здесь не работает. Следовательно, мы хотели бы расширить определение момента для трехмерного движения из скалярного момента, определенного для плоского движения. Чтобы сохранить понятия ориентации вращения, мы определяем момент как вектор следующим образом.

Определение: момент силы

Момент силы ⃑𝐹, действующей на тело относительно точки 𝑂, определяется выражением 𝑀=⃑𝑟×⃑𝐹, где 𝑟 — вектор положения 𝐴, точки приложения силы ⃑𝐹.

В этом определении мы видим, что система координат выбрана так, что ее начало совпадает с точкой около что мы принимаем момент. Если бы мы хотели вычислить момент силы ⃑𝐹 относительно точки 𝑃 это не источник, то мы просто заменим ⃑𝑟 на 𝑃𝐴: 𝑀=𝑃𝐴×⃑𝐹.

Буква 𝑃 была добавлена ​​в качестве нижнего индекса к 𝑀, чтобы указать, что момент взят около точки 𝑃.

В нашем первом примере мы будем использовать эту формулу для вычисления векторного момента силы на плоскости относительно точки.

Пример 1. Нахождение момента вектора силы относительно точки

Если на точку действует сила ⃑𝐹=−5⃑𝑖+𝑚⃑𝑗 𝐴(7,3), определить момент ⃑𝐹 относительно точки 𝐵(7,−2).

Ответ

В этом примере нам нужно найти момент плоской силы относительно точки. Напомним, что векторный момент силы ⃑𝐹, действующий в точке 𝐴 относительно точки 𝐵, определяется выражением 𝑀=𝐵𝐴×⃑𝐹.

Начнем с нахождения вектора 𝐵𝐴: 𝐵𝐴=(7,3,0)−(7,−2,0)=(0,5,0).

Мы можем написать ⃑𝐹 как ⃑𝐹=−5⃑𝑖+𝑚⃑𝑗+0⃑𝑘=(−5,𝑚,0).

Взяв векторное произведение, 𝐵𝐴×⃑𝐹=||||⃑𝑖⃑𝑗⃑𝑘050−5𝑚0||||=(5×0−0×𝑚)⃑𝑖−(0×0−0×(−5))⃑𝑗+(0×𝑚−5×( −5))⃑𝑘=25⃑𝑘.

Заметим, что неизвестная константа 𝑚 в силе ⃑𝐹 сокращалась, когда мы вычислили перекрестное произведение. Следовательно, момент ⃑𝐹 относительно точки 𝐵 равен 25⃑𝑘.

В предыдущем примере мы вычислили векторный момент плоской силы относительно точки по формуле 𝑀=⃑𝑟×⃑𝐹.

Мы видим, что результирующий вектор векторного произведения содержит только компонент ⃑𝑘, а компоненты ⃑𝑖 и ⃑𝑗 исчезли. Это не удивительно, если мы рассмотрим геометрическое свойство перекрестного произведения. Напомним, что вектор, полученный в результате перекрестного произведения двух векторов должны быть перпендикулярны двум векторам. Поскольку 𝑀 определяется как крест произведение векторов ⃑𝑟 и ⃑𝐹, оно должно быть перпендикулярно обоим векторы. Мы знаем, что ⃑𝑟 и ⃑𝐹 оба лежат на 𝑥𝑦-плоскость, поэтому 𝑀 должна быть перпендикулярна 𝑥𝑦-плоскости. Вектор, перпендикулярный плоскости 𝑥𝑦, должен быть параллелен единичному вектору ⃑𝑘 в трехмерной системе координат. Это означает ⃑𝑟×⃑𝐹=𝑐⃑𝑘 для некоторого скаляра 𝑐. Поскольку это всегда так, мы можем упростить вычисление этого перекрестного произведения на используя двумерное перекрестное произведение.

Определение: двумерное перекрестное произведение

Для двух двумерных векторов (𝑎,𝑏) и (𝑐,𝑑), двумерное перекрестное произведение определяется как (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Как мы видим, двумерное перекрестное произведение вычисляется быстрее. Мы будем использовать эту формулу для вычисления перекрестного произведения двухмерных векторы для оставшейся части этого объяснения.

Далее обсудим величину момента, которая равна величине векторного произведения: ‖‖𝑀‖‖=‖‖⃑𝑟×⃑𝐹‖‖.

Напомним, что перекрестное произведение двух векторов дает площадь параллелограмма, две смежные стороны которого образованы два вектора. Проследим это, используя следующую схему.

На приведенной выше диаграмме площадь выделенной области представляет собой величину векторного произведения ⃑𝑟×⃑𝐹 и, следовательно, величину момента 𝑀. Мы также можем найти площадь этого параллелограмма геометрически, используя геометрическую формулу длина основанияперпендикулярвысота×.

На схеме основание этого параллелограмма образовано вектором ⃑𝐹, а высота равна перпендикулярное расстояние от начала координат до линии действия ⃑𝐹, которое обозначается 𝑑⟂.

Это приводит к следующей формуле для величины векторного момента для двумерной силы относительно точки.

Свойство: Величины векторного момента силы

Величина векторного момента плоской силы ⃑𝐹 относительно точки определяется выражением ‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝑑,⟂ где 𝑑⟂ — перпендикулярное расстояние между точкой и линией действия силы ⃑𝐹.

Мы видим, что приведенная выше величина векторного момента равна величине скалярного момента. Следовательно, величина векторного момента согласуется с величиной скалярного момента для плоского движения.

Когда мы переформулируем это уравнение, мы получим полезную формулу для вычисления перпендикулярного расстояния между точкой и линией действия силы.

Формула: Расстояние по перпендикуляру между точкой и линией действия

Пусть 𝑀 векторный момент силы или системы сил на плоскости относительно точки. Тогда перпендикулярное расстояние между точкой и линией действия силы определяется выражением 𝑑=‖‖𝑀‖‖‖‖⃑𝐹‖‖.⟂

В следующем примере мы вычислим момент плоской силы относительно точки, а затем воспользуемся этой формулой, чтобы найти перпендикулярное расстояние между точкой и линией действия силы.

Пример 2. Нахождение вектора момента силы, действующей в точке, и перпендикуляра между моментом и линией Действие Силы

Учитывая, что сила ⃑𝐹=4⃑𝑖−3⃑𝑗 действует через точки 𝐴(3,6), определить момент 𝑀 относительно происхождение 𝑂 силы ⃑𝐹. Кроме того, вычислить перпендикуляр расстояние 𝐿 между 𝑂 и линией действия силы.

Ответ

В этом примере сначала нужно найти момент 𝑀 относительно 𝑂 силы ⃑𝐹, а затем рассчитайте перпендикулярное расстояние между 𝑂 и линией действие ⃑𝐹. Начнем с поиска момента. Напомним, что векторный момент силы ⃑𝐹, действующий в точке 𝐴 относительно начала координат 𝑂, определяется выражением 𝑀=𝑂𝐴×⃑𝐹.

Нам даны координаты 𝐴, значит, 𝑂𝐴 — это позиция вектор, заданный 𝑂𝐴=(3,6).

Мы можем записать ⃑𝐹 в компонентной форме как ⃑𝐹=4⃑𝑖−3⃑𝑗=(4,−3).

Теперь мы готовы вычислить перекрестное произведение 𝑂𝐴×⃑𝐹. Напомним, что векторное произведение двумерных векторов определяется формулой (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Применяя эту формулу, получаем 𝑂𝐴×⃑𝐹=(3,6)×(4,−3)=(3×(−3)−6×4)⃑𝑘=−33⃑𝑘.

Следовательно, момент ⃑𝐹 относительно начала координат равен −33⃑𝑘.

Далее найдем перпендикулярное расстояние между началом координат и линией действия для ⃑𝐹. Напомним, что модуль векторного момента плоской силы ⃑𝐹 относительно точки определяется выражением ‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝐿, где 𝐿 — перпендикулярное расстояние между точкой и линией действия силы ⃑𝐹. Мы можем изменить это уравнение, чтобы написать 𝐿=‖‖𝑀‖‖‖‖⃑𝐹‖‖.

Поскольку мы знаем, что 𝑀=−33⃑𝑘, мы можем получить ‖‖𝑀‖‖=33. Найдем ‖‖⃑𝐹‖‖: ‖‖⃑𝐹‖‖=4+(−3)=√25=5.

Подставив эти значения в формулу для 𝐿, получим 𝐿=335=6,6.

Следовательно, 𝑀=−33⃑𝑘,𝐿=6.6.lengthunits

Мы отметили, что момент силы относительно точки приводит к вектору, параллельному единичному вектору ⃑𝑘. Другими словами, существует некоторый скаляр 𝑐 такой, что 𝑀=𝑐⃑𝑘.

Кроме того, мы заметили, что величина момента равна величине скалярного момента |𝑀|. Это означает, что либо 𝑐=𝑀, либо 𝑐=−𝑀. Чтобы определить, какой из них верен, нам нужно проверить, соответствует ли знак 𝑐 знаку скалярного момента. 𝑀.

Свойства векторного произведения позволяют нам сначала заключить, что 𝑀 является вектором, перпендикулярным плоскость, определяемая ⃑𝑟 и ⃑𝐹. Направление 𝑀 определяется по правилу правой руки. Это правило иногда объясняют ссылкой на вращение винта: направление вектора ⃑𝐴×⃑𝐵 соответствует направление движения (вверх или вниз) крышки бутылки или гайки, которое можно было бы повернуть в том же направлении вращения, что и при переходе от от ⃑𝐴 до ⃑𝐵, как показано на следующей диаграмме.

Помните, что у нас есть 𝑀=⃑𝑟×⃑𝐹=𝑐⃑𝑘.

Если 𝑐>0, вектор момента будет выходить из плоскости (вверх), что соответствует направлению против часовой стрелки вращение в соответствии с рисунком выше. Если 𝑐0, то вектор момента ушел бы в плоскость (вниз), что указывает на вращение по часовой стрелке. Напомним, что для скалярного момента 𝑀 ориентация против часовой стрелки соответствует к положительному знаку, а вращение по часовой стрелке приводит к отрицательному знаку. Это говорит нам о том, что знак скалярного момента 𝑀 согласуется со знаком скаляра 𝑐. Таким образом, мы показали, что 𝑐=𝑀.

Свойство: двумерный векторный момент силы

Пусть 𝑀 и 𝑀 будут скалярным и векторным моментами силы или системой сил, на плоскости около точки. Затем, 𝑀=𝑀⃑𝑘.

Это свойство твердо устанавливает, почему этот векторный момент является разумным расширением скалярного момента для плоской силы. Кроме того, векторный момент можно обобщить, чтобы представить момент общей трехмерной силы относительно точки, поскольку он получен используя перекрестное произведение.

Из этого свойства можно сделать несколько полезных выводов. Во-первых, мы знаем, что скалярный момент не зависит от положение точки, на которую действует сила, если точка лежит на одной линии действия силы. Это потому что скалярный момент получается только с использованием величины силы ‖‖⃑𝐹‖‖ и перпендикулярное расстояние 𝑑⟂. Это означает, что векторный момент также не зависит от местоположения точки, на которую действует сила. Мы сможем понять это лучше, если сравним величину момента, когда мы переместите эту точку вдоль линии действия.

Мы видим, что площади обоих параллелограммов равны, так как длина основания ‖‖⃑𝐹‖‖ и высота 𝑑⟂ одинаковы для обоих параллелограммы. Это говорит нам о том, что величина момента для этих двух систем одинакова. Кроме того, мы можем видеть что обе системы будут вызывать вращение по часовой стрелке вокруг начала координат, а это означает, что знак момента будет одинаковым для обе системы. Следовательно, векторный момент одинаков для этих двух систем. Это приводит к следующему полезному свойству.

Свойство: Векторный момент силы

Векторный момент 𝑀 силы относительно точки не зависит от точки, в которой сила действует до тех пор, пока точка лежит на одной линии действия.

В следующем примере мы найдем векторный момент плоской силы относительно точки, когда начальная точка 𝐴 не дается.

Пример 3. Определение момента вектора силы, действующего в точке

Конец 𝐴 из 𝐴𝐵 находится в точке (−6,7) и 𝐴𝐵 имеет середину 𝐷(−7,1). Если линия действия силы ⃑𝐹=−2⃑𝑖−6⃑𝑗 делит пополам 𝐴𝐵, определить момент ⃑𝐹 относительно точки 𝐵.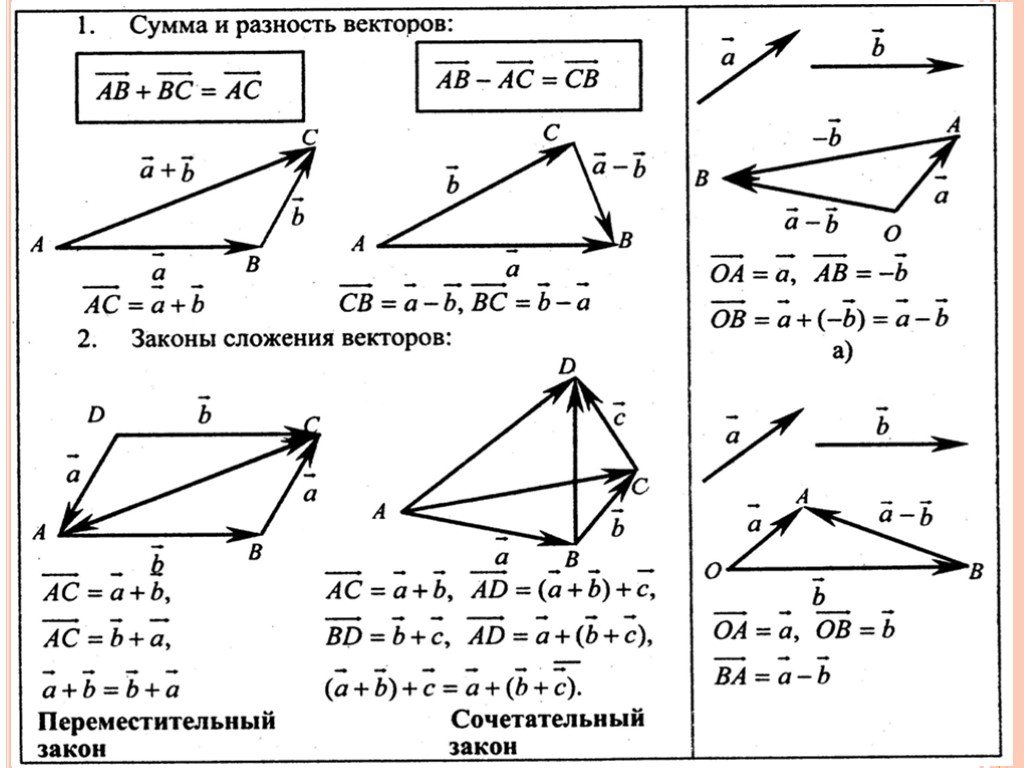

Ответ

В этом примере нам нужно найти момент плоской силы относительно точки. Напомним, что векторный момент силы ⃑𝐹, действующий в точке 𝑃 относительно точки 𝑂, определяется выражением 𝑀=𝑂𝑃×⃑𝐹.

Хотя нам не известна точка, в которой действует сила, нам известно, что линия действия силы ⃑𝐹 делит 𝐴𝐵 пополам. Это означает, что линия действия проходит через середину 𝐷 отрезка 𝐴𝐵. Напомним, что векторный момент 𝑀 силы, приложенной к точке, не зависит от начальной точки, если точка лежит в той же линии действия. Следовательно, мы можем вычислить момент, считая, что начальная точка находится в точке 𝐷(−7,1). Это означает, что момент ⃑𝐹 о 𝐵 дается 𝑀=𝐵𝐷×⃑𝐹.

Начнем с поиска вектора 𝐵𝐷. Так как 𝐷 является серединой 𝐴, мы знаем, что ‖‖𝐴𝐷‖‖=‖‖𝐵𝐷‖‖.

Также эти векторы имеют противоположное направление, а значит 𝐵𝐷=−𝐴𝐷.

Мы можем найти 𝐴𝐷, используя координаты точек 𝐴 и 𝐷: 𝐴𝐷=(−7,1)−(−6,7)=(−1,−6).

Следовательно, 𝐵𝐷=-(-1,-6)=(1,6).

Теперь мы готовы вычислить векторное произведение 𝐵𝐷×⃑𝐹. Напомним, что векторное произведение двумерных векторов определяется формулой (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Применяя эту формулу, получаем 𝐵𝐷×⃑𝐹=(1,6)×(−2,−6)=(1×(−6)−6×(−2))⃑𝑘=6⃑𝑘.

Следовательно, момент ⃑𝐹 относительно точки 𝐵 равен 6⃑𝑘.

В следующем примере мы найдем момент системы плоских сил, действующих в одной точке относительно другой точки, сначала найти равнодействующую сил.

Пример 4: Расчет момента трех сил, действующих на одну точку относительно данной точки, и расстояния между точками

Учитывая, что ⃑𝐹=−2⃑𝑖+2⃑𝑗, ⃑𝐹=−3⃑𝑖−⃑𝑗, и ⃑𝐹=⃑𝑖−4⃑𝑗 действуют в точке 𝐴(2,3), определить момент ⃑𝑚 равнодействующей сил относительно точки 𝐵(−2,−1) и вычислить длину перпендикулярной линии 𝐿 соединение точки 𝐵 с результирующей линией действия.

Ответ

В этом примере нам дана система плоских сил, действующих в одной и той же точке. Начнем с нахождения равнодействующей силы. Напомним, что равнодействующая системы сил, действующих в одной точке, равна сумме всех векторов сил в система. Следовательно, результирующая ⃑𝐹 определяется выражением ⃑𝐹 = ⃑𝐹+⃑𝐹+⃑𝐹 =  -2⃑𝑖+2⃑𝑗+ -3⃑𝑖 — ⃑𝑗+⃑𝑖 -4⃑𝑗 =  -2⃑𝑖 -3⃑𝑖+⃑𝑖+2⃑𝑗 -4⃑𝑗 = −4⃑𝑖 -3⃑𝑗. 

Это говорит нам о том, что равнодействующая сил равна ⃑𝐹=−4⃑𝑖−3⃑𝑗. Далее найдем момент ⃑𝑚 равнодействующей около точки 𝐵(−2,−1). Напомним, что векторный момент силы ⃑𝐹, действующей в точке 𝐴 о точке 𝐵 дается 𝑀=𝐵𝐴×⃑𝐹.

Используя координаты 𝐴 и 𝐵, мы можем найти 𝐵𝐴=(2,3)−(−2,−1)=(4,4).

Теперь мы готовы вычислить перекрестное произведение 𝐵𝐴×⃑𝐹. Напомним, что перекрестное произведение двумерных векторов определяется выражением (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Это приводит к 𝐵𝐴×⃑𝐹=(4,4)×(−4,−3)=(4×(−3)−4×(−4))⃑𝑘=4⃑𝑘.

Следовательно, момент равнодействующей сил относительно точки 𝐵 равен 4⃑𝑘.

Далее найдем длину перпендикуляра 𝐿, соединяющего точку 𝐵 с результирующая линия действия. Эта длина 𝐿 также известна как перпендикулярное расстояние между точкой 𝐵 и результирующая линия действия. Чтобы вычислить эту длину, вспомним, что величина векторный момент плоской силы ⃑𝐹 относительно точки определяется выражением ‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝐿, где 𝐿 — перпендикулярное расстояние между точкой и линией действия для ⃑𝐹. Мы можем изменить это уравнение, чтобы написать 𝐿=‖‖𝑀‖‖‖‖⃑𝐹‖‖.

Поскольку мы знаем, что 𝑀=4⃑𝑘, мы можем получить ‖‖𝑀‖‖=4. Найдем ‖‖⃑𝐹‖‖: ‖‖⃑𝐹‖‖=(−4)+(−3)=√25=5.

Подставляя эти значения в формулу для 𝐿, получаем 𝐿=45=0,8.

Следовательно, 𝑀=4⃑𝑘,𝐿=0,8.lengthunit

В предыдущем примере мы нашли момент системы плоских сил, действующих в той же точке относительно другой точки. Мы можем отметить что процесс нахождения момента для системы сил такой же, как и для одной силы, если силы действуют в тот же пункт.

Рассмотрим теперь задачу нахождения момента системы плоских сил, когда силы не действуют в одной и той же точке.

Определение: Момент системы плоских сил

Рассмотрим систему сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹, действующий в 𝐴, 𝐴, …, и 𝐴 соответственно. Чтобы найти момент этой системы сил относительно точки 𝑂, найдем нужно найти моменты 𝑀, 𝑀, …, и 𝑀 сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹 о пункте 𝑂. Тогда, момент система 𝑀 относительно точки 𝑂 задается формулой 𝑀=𝑀+𝑀+⋯+𝑀.

Это определение говорит нам, что момент системы сил равен сумме отдельных моментов каждой силы в система примерно в том же месте.

В нашем последнем примере мы найдем неизвестные константы сил в системе, действующей в разных точках, когда нам задано момент системы сил относительно двух различных точек.

Пример 5. Нахождение неизвестных компонентов двух сил по сумме их моментов относительно двух точек ⃑𝐹 — две силы, действующие в точках 𝐴(3,1) и 𝐵(−1,−1) соответственно. Сумма моментов относительно точки начала равна нулю.

сумма моментов относительно точки 𝐶(1,2) также равна нулю. Определите значения 𝑚 и 𝑛.

Ответ

В этом примере нам нужно найти неизвестные константы 𝑚 и 𝑛 в силах ⃑𝐹 и ⃑𝐹, когда нам известно, что сумма моменты двух сил относительно начала координат, а также относительно точки 𝐶 равны нулю. Мы можем найти неизвестные константы путем идентификации пары одновременных уравнений с участием 𝑚 и 𝑛. Мы получим первое уравнение, вычислив сумму моментов ⃑𝐹 и ⃑𝐹 о происхождении и приравнивании их к нулю.

Напомним, что векторный момент силы ⃑𝐹, действующей в точке 𝑃 относительно точка 𝑄 задается 𝑀=⃑𝑟×⃑𝐹, где ⃑𝑟 — вектор из точки 𝑄 в точку 𝑃. Позволь нам сначала найдите момент ⃑𝐹 о происхождении. С ⃑𝐹 действует в точке 𝐴, мы можем написать ⃑𝑟=𝑂𝐴=(3,1).

Мы можем записать ⃑𝐹 в компонентной форме как ⃑𝐹=𝑚⃑𝑖+⃑𝑗=(𝑚,1).

Теперь мы готовы вычислить перекрестное произведение 𝑂𝐴×⃑𝐹. Напомним, что перекрестное произведение двумерных векторов определяется выражением (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.

Это приводит к ⃑𝑟×⃑𝐹=(3,1)×(𝑚,1)=(3×1−1×𝑚)⃑𝑘=(3−𝑚)⃑𝑘.

Далее найдем момент ⃑𝐹 относительно начала координат . С ⃑𝐹 действует в точке 𝐵, мы можем написать ⃑𝑟=𝑂𝐵=(−1,−1).

Мы можем записать ⃑𝐹 в компонентной форме как ⃑𝐹=𝑛⃑𝑖−5⃑𝑗=(𝑛,−5).

Взяв векторное произведение, ⃑𝑟×⃑𝐹=(−1,−1)×(𝑛,−5)=(−1×(−5)−(−1)×𝑛)⃑𝑘=(5+𝑛)⃑𝑘.

Тогда сумма этих двух моментов относительно начала координат равна (3−𝑚)⃑𝑘+(5+𝑛)⃑𝑘=(8−𝑚+𝑛)⃑𝑘.

Так как нам дано, что сумма этих моментов должна равняться нулю, то получаем

8−𝑚+𝑛=0.

(1)

Это дает нам одно уравнение, включающее 𝑚 и 𝑛. Мы можем повторить это вычисление на данный момент о точке 𝐶, чтобы получить другое уравнение, но мы также можем найти второе уравнение, используя свойства моменты. Найдем момент ⃑𝐹 относительно точки 𝐶: ⃑𝑟=𝐶𝐴=(3,1)−(1,2)=(2,−1).

Взяв векторное произведение, ⃑𝑟×⃑𝐹=(2,−1)×(𝑚,1)=(2×1−(−1)×𝑚)⃑𝑘=(2+𝑚)⃑𝑘.

Далее, на момент ⃑𝐹 о 𝐶, ⃑𝑟=𝐶𝐵=(−1,−1)−(1,2)=(−2,−3).

Взяв векторное произведение, ⃑𝑟×⃑𝐹=(−2,−3)×(𝑛,−5)=(−2×(−5)−(−3)×𝑛)⃑𝑘=(10+3𝑛)⃑𝑘.

Суммируя эти два моменты про 𝐶, (2+𝑚)⃑𝑘+(10+3𝑛)⃑𝑘=(12+𝑚+3𝑛)⃑𝑘.

Так как нам дано, что сумма этих моментов должна равняться нулю, то получаем

12+𝑚+3𝑛=0.

(2)

Теперь, когда мы получили два уравнения для 𝑚 и 𝑛, напишем уравнения (1) и (2) здесь: 8−𝑚+𝑛=0,12+𝑚+3𝑛=0.

Мы можем сложить два уравнения, чтобы исключить 𝑚. Это ведет к 20+4𝑛=0.

Преобразование этого уравнения таким образом, что 𝑛 является субъектом, дает нам 𝑛=−5. Мы можем заменить это значение в уравнение (1), чтобы записать 8−𝑚−5=0.

Преобразование этого уравнения таким образом, что 𝑚 является субъектом, приводит к 𝑚=3. Следовательно, у нас есть 𝑚=3,𝑛=−5.

Давайте закончим повторением нескольких важных понятий из этого объяснения.

Ключевые точки

• Вектор момента силы ⃑𝐹, действующей в точке 𝐴 относительно точки 𝑂 дается 𝑀=⃑𝑟×⃑𝐹, где ⃑𝑟 — вектор из точки 𝑂 в точку 𝐴.
• Величина векторного момента плоской силы ⃑𝐹 относительно точки определяется выражением ‖‖𝑀‖‖=‖‖⃑𝐹‖‖𝑑,⟂ где 𝑑⟂ — перпендикулярное расстояние между точкой и линией действия силы ⃑𝐹.
• Векторный момент 𝑀 силы относительно точки не зависит от начальной точки, пока точка лежит на одной линии действия.
• Пусть 𝑀 и 𝑀 — скалярный и векторный моменты силы, или система сил на плоскости относительно точки. Затем, 𝑀=𝑀⃑𝑘.
• Вычисление перекрестного произведения ⃑𝑟×⃑𝐹 для вычисления момент 𝑀 плоской силы относительно точки можно упростить, используя двумерное перекрестное произведение, которое определяется формулой (𝑎,𝑏)×(𝑐,𝑑)=(𝑎𝑑−𝑏𝑐)⃑𝑘.
• Рассмотрим систему сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹 действующие в 𝐴, 𝐴, … и 𝐴 соответственно. Чтобы найти момент этой системы сил относительно точки 𝑂, нужно найти моменты 𝑀, 𝑀, … и 𝑀 сил ⃑𝐹, ⃑𝐹, …, и ⃑𝐹 о пункте 𝑂. Тогда, момент система 𝑀 относительно точки 𝑂 задается формулой 𝑀=𝑀+𝑀+⋯+𝑀. 92 }\\ d = \sqrt{ 11 } \end{align}

  Следовательно, расстояние между точками $P$ и $Q$ равно $\sqrt{11}$.

  Предположим, что у нас есть вектор $\vec{u}$. Если этот вектор умножить на скаляр $k$, то норма вектора $k\vec{u}$ будет в k раз больше, чем $k$. Однако есть проблема. Мы определяем норму как величину или длину вектора, поэтому норма должна быть положительной. Отсюда получаем следующее соотношение:

  (4)

  \begin{align} \| к \vec{u} \| = \ середина к \ середина \ | \vec{и} \| \end{выравнивание}

  Заметим, что $\mid k \mid$ представляет абсолютное значение k , то есть:

  (5)

  \begin{align} \mid k \mid = \left\{\begin{matrix} k & \mathrm{if \: k >0}\\ -k & \mathrm{if \: k < 0} \ конец{матрица}\справа.

  No related posts.