Точки пересечения графика функции с осями координат онлайн: Пересечение с осями онлайн

Точки пересечения графиков в Excel

Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.

Строим графики с точками пересечений

Имеются две функции, по которым нужно построить графики:

Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:

1. Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
2. Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.

Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.



Находим точку пересечения графиков в Excel

В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.

Первый способ. Найти общие значения в рядах данных для указанных функций.

В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.

Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.

Изменим график, добавив новые данные. Получим две пересекающиеся линии.

Второй способ.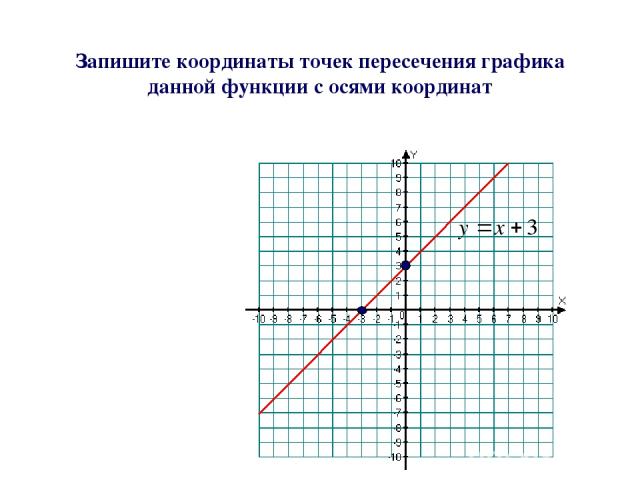 Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».

Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.

Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.

Нажимаем «Выполнить» — инструмент предлагает решение уравнений.

Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.

Точки пересечения для трех показателей

Существует три показателя, которые измерялись во времени.

По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).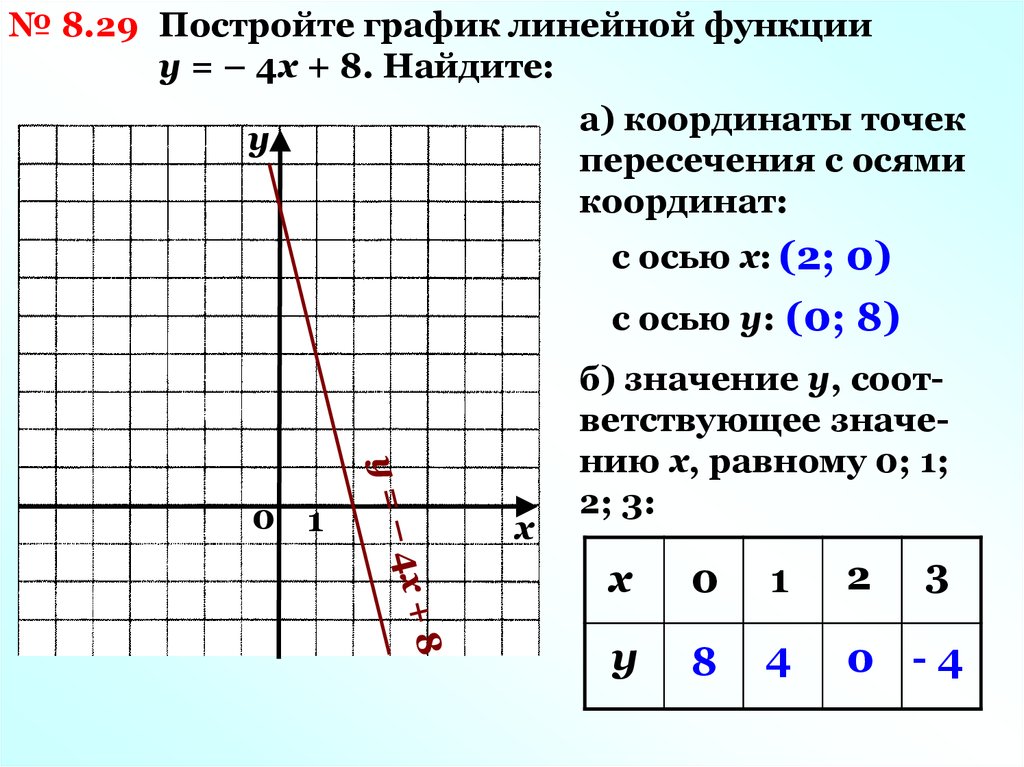

Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.

Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:

На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.

Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:

На основе новых данных построим точечные диаграммы на том же поле (где наши графики).

Получается такой рисунок:

Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:

Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.

Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.

Квадратичная и кубическая функции и их графики 7 класс онлайн-подготовка на Ростелеком Лицей

Тема 4: Целые выражения

• Видео
• Тренажер
• Теория

Заметили ошибку?

84. Функции у = х² и у = х³ и их графики

Начнем с функции у = х². Самый простой пример зависимости, которую может выражать эта функция – это зависимость площади квадрата от его стороны.

Построим график этой функции по точкам.

х	-3	-2	-1	0	1	2	3
у	9	4	1	0	1	4	9

Отметим точки на координатной плоскости и соединим их плавной кривой.

Получился график, который называется квадратичная парабола. Исследуем его.

1. Область определения D(y) = (- ∞;∞).
2. Область значений Е(у) = [0;∞).
3. Точки пересечения с осями координат х = 0, у =0 ² =0. Единственная точка пересечения с осями – (0;0).
4. Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞).
5. График функции у=х² симметричен относительно оси у.

Рассмотрим функцию y=x³ Приведите пример зависимости, которую может выражать эта функция. Простой пример такой зависимости – зависимость объема куба от длины ребра.

Построим график функции по точкам.

х	-3	-2	-1	0	1	2	3
у	-27	-8	-1	0	1	8	27

График этой функции тоже называется параболой.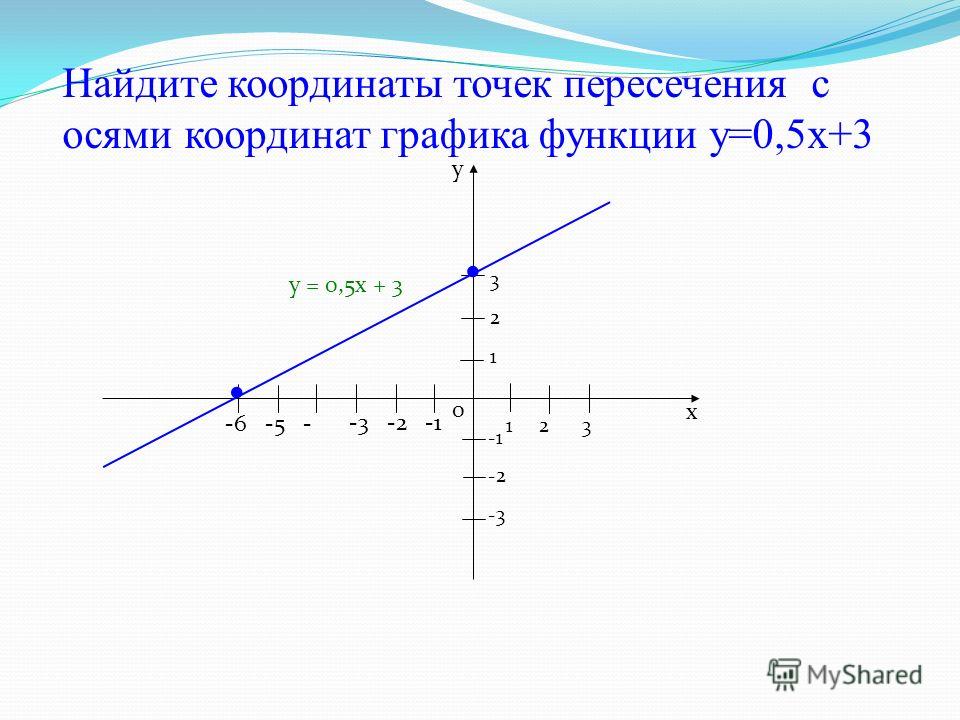 Это кубическая парабола.

Исследуем его

1. Область определения. D(y) = (- ∞;∞).
2. Область значений Е(у) = (- ∞;∞).
3. Точка пересечения с осями координат, как и в случае с графиком у=х², одна – (0;0).
4. График функции возрастает на всей области определения.
5. При х0 y>0.
6. График функции симметричен относительно начала координат.

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Калькулятор точки пересечения (линия или кривая в 2D-плоскости) Онлайн

Поиск инструмента

Поиск инструмента в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Точка пересечения

Инструмент для нахождения точки (точек) пересечения двух линий или кривых путем расчета из соответствующих уравнений (пересечение в 2D-плоскости) .

Результаты

Точка пересечения — dCode

Теги: Функции

Поделиться

dCode и другие

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Найти точку пересечения двух линий

Уравнение прямой 1
Уравнение прямой 2
Переменная (ось X)
Переменная (ось Y)

См. также: Линейное уравнение — Решатель уравнений

Найти точку (точки) пересечения 2 кривых

Кривые означают любой тип геометрической функции, включая линии.

Уравнение кривой 1
Уравнение кривой 2
Переменная (ось X)
Переменная (ось Y)

См. также: Equation Solver

Ответы на вопросы (FAQ)

Что такое точка пересечения? (Определение)

Точка пересечения двух элементов/чертежей/графиков/кривых в 2D-плоскости – это место пересечения/наложения двух элементов.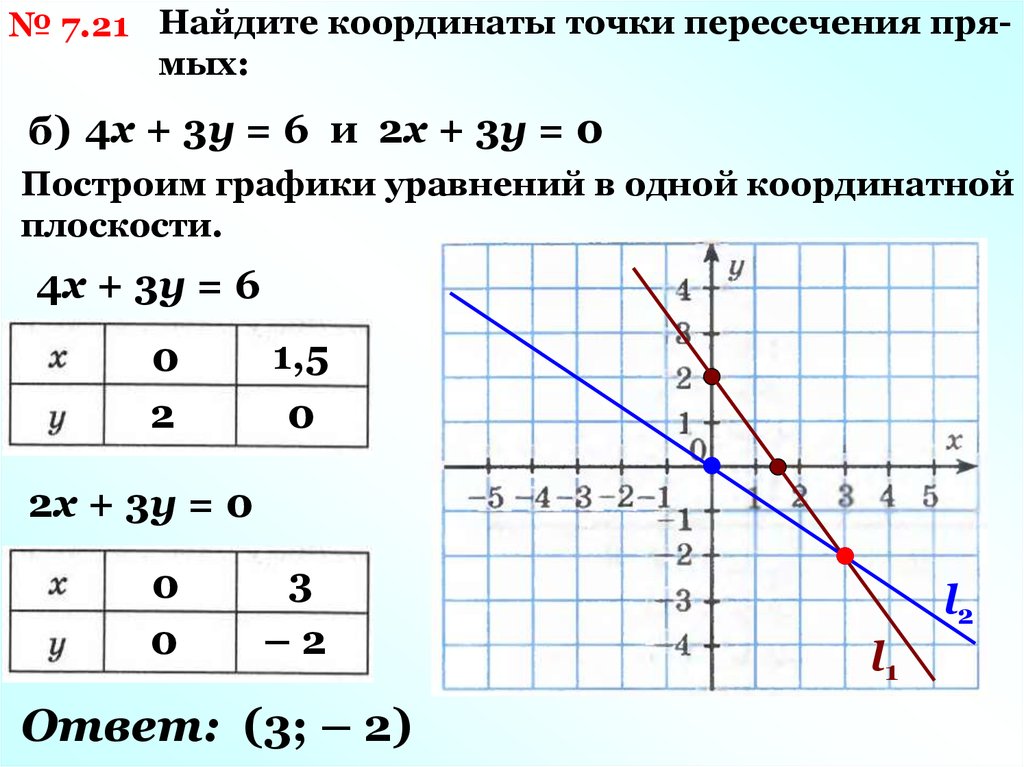

Как рассчитать точку пересечения двух линий?

Из уравнений 2-х линий 2D-плоскости можно вычислить точку пересечения (если она существует) путем решения соответствующей системы уравнений. Полученные значения (как правило, для $x$ и $y$) соответствуют координатам $(x,y)$ точки пересечения.

Пример: Строки соответствующих уравнений $ y = x + 2 $ и $ y = 4-x $ образуют систему уравнений $ \begin{cases} y = x+2 \\ y = -x+4 \end{cases} $ которое имеет для решения $ \begin{cases} x = 1 \\ y = 3 \end{cases} $ поэтому точкой пересечения двух прямых является точка с координатами $ (1,3) $

Как рассчитать точку пересечения 2-х кривых?

Расчет точки (или точек) пересечения 2-х кривых требует решения соответствующей системы уравнений. 92 \\ y = 1 \end{cases} $, которое имеет 2 решения $ \begin{cases} x = 1 \\ y = 1 \end{cases} $ и $ \begin{cases} x = -1 \\ y = 1 \end{cases} $ и поэтому функция квадрата имеет 2 точки пересечения с горизонтальной прямой в точках координат $(x,y)$: $(-1,1)$ и $(1,1)$

Исходный код

dCode сохраняет за собой право собственности на исходный код «Точки пересечения». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Точка пересечения», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Точки пересечения» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или API-доступ для «Точки пересечения» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении для Android!

Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Точка пересечения» или любых ее результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Точка пересечения на dCode. fr [онлайн-сайт], получено 26 ноября 2022 г.,

https://www.dcode.fr/intersection-point

Сводка

• Найти точку пересечения 2-х линий
• Найти точку(-и) пересечения 2-х кривых
• Что такое точка пересечения? (Определение)
• Как рассчитать точку пересечения двух линий?
• Как рассчитать точку пересечения двух кривых?

Similar pages

• Equation Solver
• Linear Equation
• Inverse Fourier Transform
• Function Calculator (Table of Values)
• Stationary Point of a Function
• Period of a Function
• Critical Point of a Function
• Список инструментов Dcode

Поддержка

• PayPal
• Patreon
• Подробнее

Форум/Справка

Ключевые слова

Интерсекция, точка, координата, линия, линия, линия, Связанная линия, Связация

.

▲

функций — Как найти пересечение с осью $x$ или $y$

спросил 9 лет, 8 месяцев назад

92-x-1$, как найти пересечение осей $x$ и $y$.

На данный момент я знаю только, что когда мы ищем пересечение с $x$, мы получаем $y=0$, а когда мы ищем $y$, мы получаем $x=0$.

Однако, если пересечение с осью $y$, $x=0$, то мы получаем, $f(x)=0+0-0-1$, следовательно, будет, $(0,-1 )$, но когда мы ищем ось $x$, $y=0$, на что менять $0$? В функции нет $y$.

• функции

$\endgroup$ 92-x-1=0$. Для этого сначала проверьте красивые числа, такие как маленькие (по абсолютной величине) целые числа.

Ниже приведен график для вашей функции (хотя, вероятно, это то, что вы пытаетесь найти, я использую его просто как иллюстративный пример, я мог бы выбрать другую функцию).

Когда график пересекает ось $y$? Именно тогда, когда $x=0$. И когда он пересекает ось $x$? Именно тогда, когда $f(x)=0$.

Также обратите внимание на полезный комментарий Брайана М. Скотта ниже.

Глядя на график, вы можете обнаружить, что точки, в которых график пересекает ось $x$, равны $(-1,0)$ и $(1,0)$ (обратите внимание, что $y$ координата просто должна была быть $0$, иначе она не пересекала бы ось $x$.