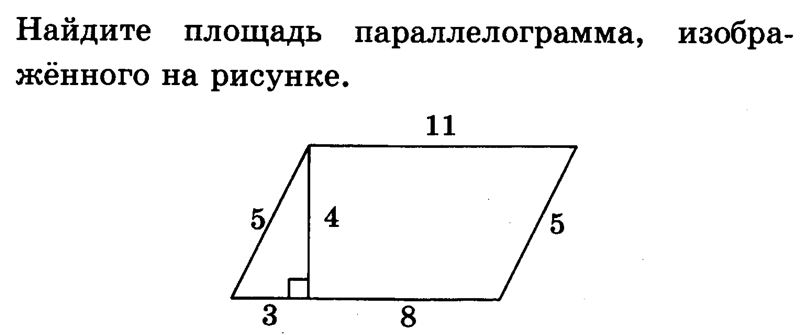
Площадь параллелограмма
Для полной функциональности сайта желательно включить JavaScript в настройках Вашего браузера.
Главная
→
Геометрия
→
Площадь параллелограмма
Площадь параллелограмма, формулы и калькулятор для вычисления площади в режиме онлайн.
Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади в режиме онлайн.
Площадь параллелограмма – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.
Таблица с формулами площади параллелограмма (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
Площадь параллелограмма по основанию и высоте параллелограмма
. .. подготовка …
.. подготовка …
a — сторона
h — высота
2
Площадь параллелограмма по стороне и высоте, опущенной на эту сторону
… подготовка …
b — сторона
hb — высота
3
Площадь параллелограмма по двум сторонам и углу между ними
… подготовка …
a — сторона
b — сторона
α° — угол между сторонами
4
Площадь параллелограмма по двум диагоналям и углу между этими диагоналями
… подготовка …
d1 — диагональ
d2 — диагональ
α° — угол между диагоналями
5
Площадь параллелограмма по вписанной окружности и стороне
Данная формула применима только для параллелограммов, в которые можно вписать окружность.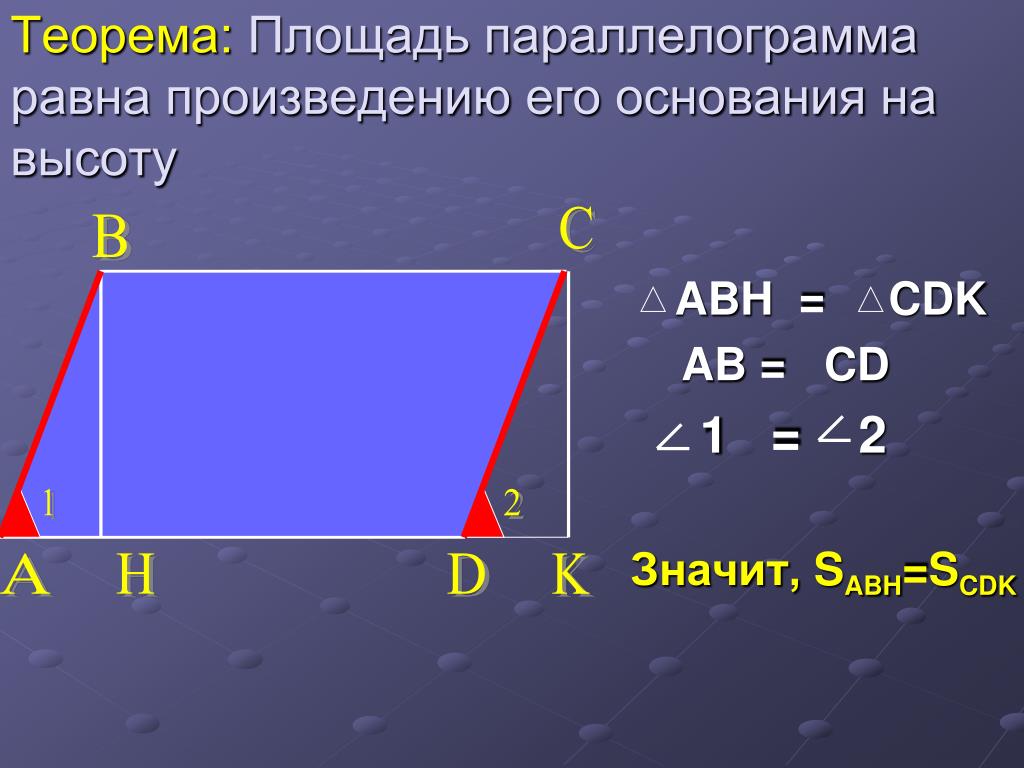 Таким параллелограммом может являться только ромб.
Таким параллелограммом может являться только ромб.
… подготовка …
a — сторона
r — радиус вписанной окружности
6
Площадь параллелограмма по вписанной окружности и углу между сторонами
Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.
… подготовка …
r — радиус вписанной окружности
α° — угол между сторонами
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади параллелограмма
| исходные данные (активная ссылка для перехода к калькулятору) |
эскиз | формула | |
| 1 | основание и высота | ||
| 2 | сторона и высота, опущенная на эту сторону |
||
| 3 | две стороны и угол между ними | ||
| 4 | диагонали и угол между ними | ||
| 5 | вписанная окружность и сторона | ||
| 6 | вписанная окружность и угол между сторонами |
Определения
Параллелограмм — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.
Высота параллелограмма – это отрезок проведенный из вершины параллелограмма к противоположной стороне под углом в 90 градусов.
Некоторые свойства параллелограмма:
- Сумма углов параллелограмма равна 360 градусов
- Сумма углов, прилегающих к любой из сторон равна 180 градусов
- Противоположные стороны параллельны и имеют одинаковую длину
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Как найти площадь параллелограмма? Ответ на webmath.ru
Содержание:
- Формулы
- Примеры вычисления площади параллелограмма
Формулы
Первый способ. Чтобы найти площадь параллелограмма (рис. 1), нужно найти произведение стороны $a$ параллелограмма на высоту $h_a$, проведенную к этой стороне, то есть
$$S=ah_{a}$$
Второй способ. Чтобы найти площадь параллелограмма, надо найти произведение двух его смежных сторон
$a$ и $b$, умноженное на синус угла
$\alpha$ между ними (рис. 2):
Чтобы найти площадь параллелограмма, надо найти произведение двух его смежных сторон
$a$ и $b$, умноженное на синус угла
$\alpha$ между ними (рис. 2):
$$\mathrm{S}=a b \sin \alpha$$
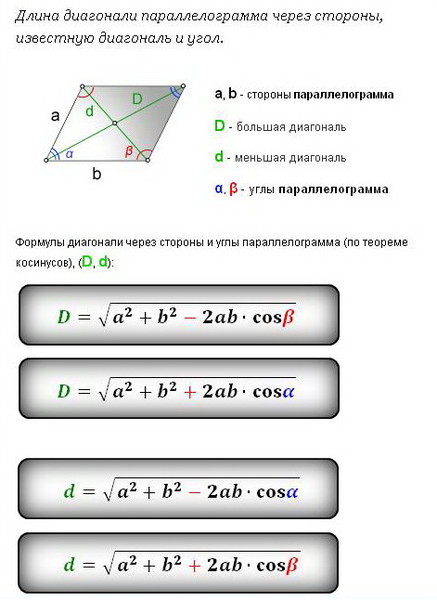
Третий способ. Чтобы найти площадь параллелограмма, надо найти полупроизведение его диагоналей $d_1$ и $d_2$ на синус угла $\beta$ между ними (рис. 3):
$$\mathrm{S}=\frac{1}{2} d_{1} d_{2} \sin \beta$$
Примеры вычисления площади параллелограмма
Пример
Задание. Найти площадь параллелограмма, если его сторона равна 2 см, а высота, проведенная к этой стороне — 3 см.
Решение. Искомая площадь равна
$S=2 \cdot 3 = 6$ (см2)
Ответ. $S=6$ (см2)
Все формулы площади Калькулятор площади параллелограмма
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. {\circ}=28 \cdot \frac{\sqrt{3}}{2}=14 \sqrt{3}$ (см2)
{\circ}=28 \cdot \frac{\sqrt{3}}{2}=14 \sqrt{3}$ (см2)
Ответ.
Остались вопросы?
Здесь вы найдете ответы.
Каким образом можно доказать утверждение о том, что площадь параллелограмма есть число, получаемое в результате умножения длин двух его сторон, являющихся смежными, и синуса угла, который образуется между ними?
Параллелограмм следует расположить по горизонтали. Обозначим его верхнее основание как АВ, а противоположное ему основание – как CD. Из точек ВЕ и AF проведем перпендикулярные прямые на нижнее основание фигуры. В результате получится прямоугольник ABEF. Площадь образовавшейся прямоугольной фигуры равна площади параллелограмма по той причине, что параллелограмм ABCD и фигура с прямыми углами ABEF являются равносоставленными, о чем свидетельствует равенство треугольников ВEC и DAF.
Площадь (S) прямоугольника представляет собой произведение длин сторон EF и FA, которое, в свою очередь, равно:
CD*AD*sin(CDA)
Именно это и требовалось доказать.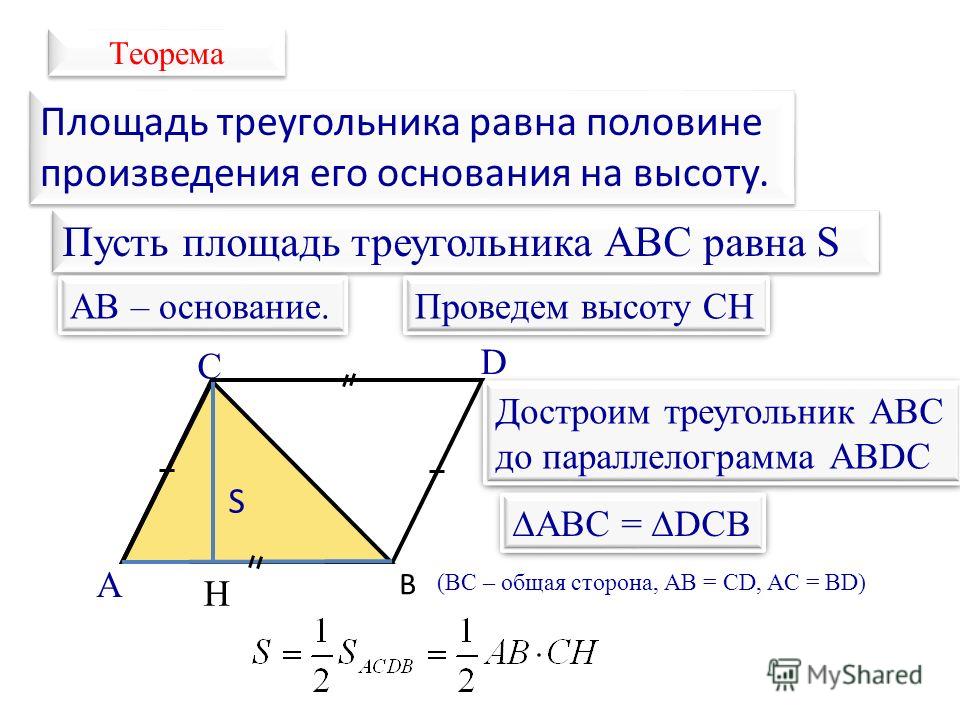
Параллелограмм имеет смежные стороны длиной 26 см и 32 см. Один из углов данной фигуры равен 150 градусам. Каким способом можно вычислить площадь параллелограмма?
Обозначим имеющийся параллелограмм как АВСD. Тогда одна его сторона АВ равна 26 см, а другая АD – 32 см. Угол АВС параллелограмма составляет 150 градусов.
Принимая во внимание тот факт, что сумма внутренних односторонних углов параллелограмма равна 180 градусов, можно говорить о том, что его угол ВАD составляет 30 градусов. Проведем высоту ВК, и в итоге получим треугольник АВК с прямым углом. Длина опущенной высоты как катета, расположенного противоположно углу в 30 градусов, равна 13 см. Площадь (S) параллелограмма есть число, полученное в результате умножения длины высоты на длину стороны. Это значит, что:
S (АВСD) = 13 *32 = 416 см кв.
Ответ: Площадь параллелограмма равна 416 см кв.
Прямая АС проведена через середины двух сторон параллелограмма, которые
являются смежными.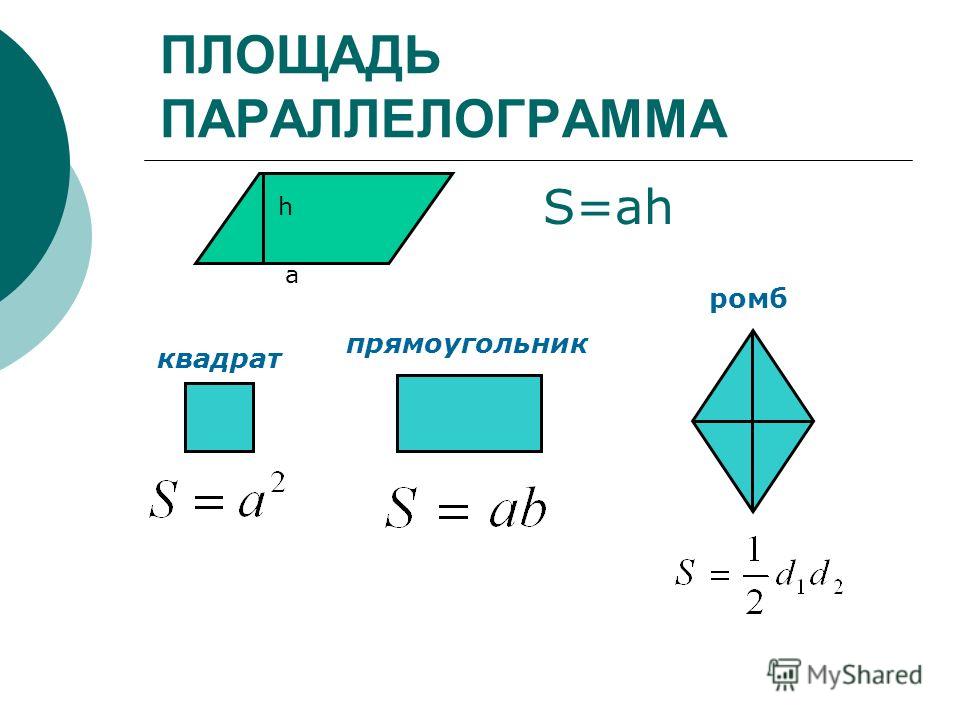 Данная прямая отсекает от параллелограмма два
треугольника – FMD и АDС. Площадь одного из отсеченных треугольников
составляет 32 см кв. Как высчитать площадь параллелограмма?
Данная прямая отсекает от параллелограмма два
треугольника – FMD и АDС. Площадь одного из отсеченных треугольников
составляет 32 см кв. Как высчитать площадь параллелограмма?
Прямая АС представляет собой диагональ биссектрисы. В этом случае образовавшиеся посредством ее проведения треугольники FMD и АDС являются подобными по причине наличия общего угла А и равенства сторон. На основании этого можно говорить о том, что:
SADC=1/2*ab*sin a
SFDM=1/2 *2a*2b sin a
SADC / SFDM= 32/x
1/4=32/x
x=128
Теперь можно рассчитать площадь параллелограмма (S), которая будет равна 2*х:
S = 128*2 = 256 см кв.
Ответ: Площадь параллелограмма равна 256 см кв.
Параллелограмм имеет стороны, длины которых составляют 10 см и 6 см. Данные стороны образуют угол, равный 150 градусам. Как рассчитать площадь параллелограмма в этом случае?
Обозначим угол в 150 градусов буквой В. Зная о том, что внутренние
односторонние углы параллелограмма в сумме дают 180 градусов, можно
вычислить второй угол А. Он будет равен:
Он будет равен:
∠А = 180-150 = 30 градусов.
Теперь следует провести высоту ВВ1, которая образует треугольник АВВ1, являющийся прямоугольным. Длина ВВ1 будет равна половине длины стороны, равной 6 см:
ВВ1 = 6/2 = 3 см.
Тогда площадь (S) параллелограмма можно рассчитать, умножив длину ВВ1 на 10 см (длина смежной стороны):
S = 3*10 = 30 см кв.
Ответ: Площадь параллелограмма равна 30 см кв.
Проведенные диагонали делят параллелограмм на четыре треугольных фигуры. Площадь одной из них равна 7 м кв. Каким образом можно найти площадь параллелограмма?
Обозначим имеющийся параллелограмм как ABCD. Точкой пересечения его
диагоналей является точка О. Образованные диагоналями треугольные фигуры
ABO, BCO, CDO, DAO являются одинаковыми по площади. Об этом
свидетельствует тот факт, что диагонали параллелограмма делятся ровно
пополам в точке их пересечения. Свидетельством того, что все четыре
треугольника имеют одинаковые площади, выступает равенство синусов смежных
углов. Площадь является ½ числа, которое получено в результате умножения
длин сторон треугольника и синуса угла, образованного между ними.
Параметры, которые отвечают вычислению площадей треугольников, равны, а
это означает равенство и самих площадей.
Площадь является ½ числа, которое получено в результате умножения
длин сторон треугольника и синуса угла, образованного между ними.
Параметры, которые отвечают вычислению площадей треугольников, равны, а
это означает равенство и самих площадей.
Если площади всех четырех треугольных фигур равны, то площадь самого параллелограмма будет в четыре раза превышать площадь любого из них. Это значит, что площадь (S) параллелограмма может быть вычислена следующим образом:
S = 4*7 = 28 м кв.
Ответ: Площадь параллелограмма равна 28 м кв.
Дан параллелограмм ABCD, на одной из сторон которого АВ поставлена точка М. Известно, что площадь треугольника MCD составляет 38 см кв. Как найти площадь параллелограмма?
Площадь (S) параллелограмма рассчитывается путем умножения длины его основания на длину его высоты.
Прямые МС и МD, проведенные из точки М, делят параллелограмм на треугольники. Площадь первого из них вычисляется как:
S₁ = 1/2 * a * h = 38 см кв.
Формула для расчета площади второго треугольника выглядит так:
S₂ = 1/2 * a₁* h
Площадь третьего треугольника можно найти следующим образом:
S₃ = 1/2 *a₃* h,
где а =а₁ + а₂
Теперь через площади образованных треугольников можно вычислить площадь параллелограмма:
S = S₁ + S₂ + S₃ = 1/2 *(a * h +a₁ * h +a₂ * h) = 1/2 * (a * h + h(a₁ + a₂)) = 1/2 * (a * h + a * h) = 2 * 38 = 76 см. кв.
Ответ: Площадь параллелограмма равна 76 см кв.
Длина основания параллелограмма составляет 5 см, а его высота равна 3 см. Как найти площадь параллелограмма?
Формула расчета площади параллелограмма (S) включает длину его высоты и длину его основания. Данные элементы нужно перемножить, для того чтобы вычислить площадь фигуры:
S = a*h= 5*6=30 см кв.
Ответ: Параллелограмм имеет площадь 30 см кв.
Имеется параллелограмм ABCD. Посередине его стороны АВ поставлена точка Е,
из которой проведена прямая, образующая треугольник CDE площадью 36 см кв. Каким образом можно найти площадь параллелограмма?
Каким образом можно найти площадь параллелограмма?
На продолжение стороны CD опустим перпендикуляр ЕН из точки Е. Он представляет собой высоту для параллелограмма ABCD и треугольника CDE.
Известно, что площадь (S) параллелограмма является произведением длины его стороны и высоты, которая на нее опущена. Площадь треугольника представляет собой ½ от числа, которое получилось в результате умножения длины стороны на высоту, опущенную на нее. На основании этого можно сделать вывод о том, что:
S(ABCD) = EH*CD
S(∆CDE) = ½*EH*CD => 2*S(∆CDE) = EH*CD.
Из этого следует, что:
2*S(∆CDE) = S(ABCD) = 2*36 ед² = 72 ед. кв.
Ответ: Площадь параллелограмма составляет 72 кв. ед.
В каком виде представлена формула, которая предназначена для вычисления площади параллелограмма?
Для получения возможности рассчитать, чему равна площадь (S)
параллелограмма, нужно располагать сведениями о длине его основания (а) и
высоты (h). В этом случае площадь можно высчитать при помощи следующей
формулы:
В этом случае площадь можно высчитать при помощи следующей
формулы:
S = а* h.
Как найти площадь параллелограмма через синус, если известно, что длины его сторон равны 8 см и 10 см, а синус одного из его углов составляет 0,05?
Формула, которая предназначена для вычисления площади параллелограмма (S) через синус, выглядит следующим образом:
S = a × b × sin A
В данной формуле буквами a и b обозначены стороны параллелограмма, являющиеся смежными, а А означает угол, который образован между этими сторонами.
Доказано, что синусы смежных углов являются равными. Это значит, что синус тупого угла равен синусу острого угла.
Площадь параллелограмма вычисляем следующим образом:
S = 8 × 10 × 0,05 = 4 см кв.
Ответ: Параллелограмм имеет площадь, равную 4 см кв.
Имеется параллелограмм ABCD, в котором опущена высота на его сторону АВ. Ее
длина равна 12 см. При этом длина AD составляет 24 см. Каким образом можно
высчитать значение синуса угла А?
Каким образом можно
высчитать значение синуса угла А?
Высота, опущенная на сторону АВ параллелограмма, обозначена как СК. Полученный в результате треугольник КВС имеет прямой угол.
Sin B=АВ/ВС.
В этом случае ВС=AD=24 см. Так, синус угла В равен:
sinВ=12/24=1/2, что соответствует углу 30 градусов.
В параллелограмме проведены диагонали, длины которых равны 5 см и 28 см. Между ними образован угол, составляющий 30 градусов. Как можно найти площадь параллелограмма через синус в данном случае?
Площадь любой из четырехугольных фигур может быть вычислена, если известны длины ее диагоналей и синус угла, образованного между ними. Для этого нужно произвести умножение упомянутых величин, а затем разделить полученное число на 2. В случае с параллелограммом, обозначенным как ABCD, площадь рассчитывается по этой же формуле:
S = 1/2 AC*BD*sin∠AOB = ½*28*5*sin30° = 14*5*1/2 = 7*5 = 35 кв. см.
Ответ: Площадь параллелограмма равна 35 см кв.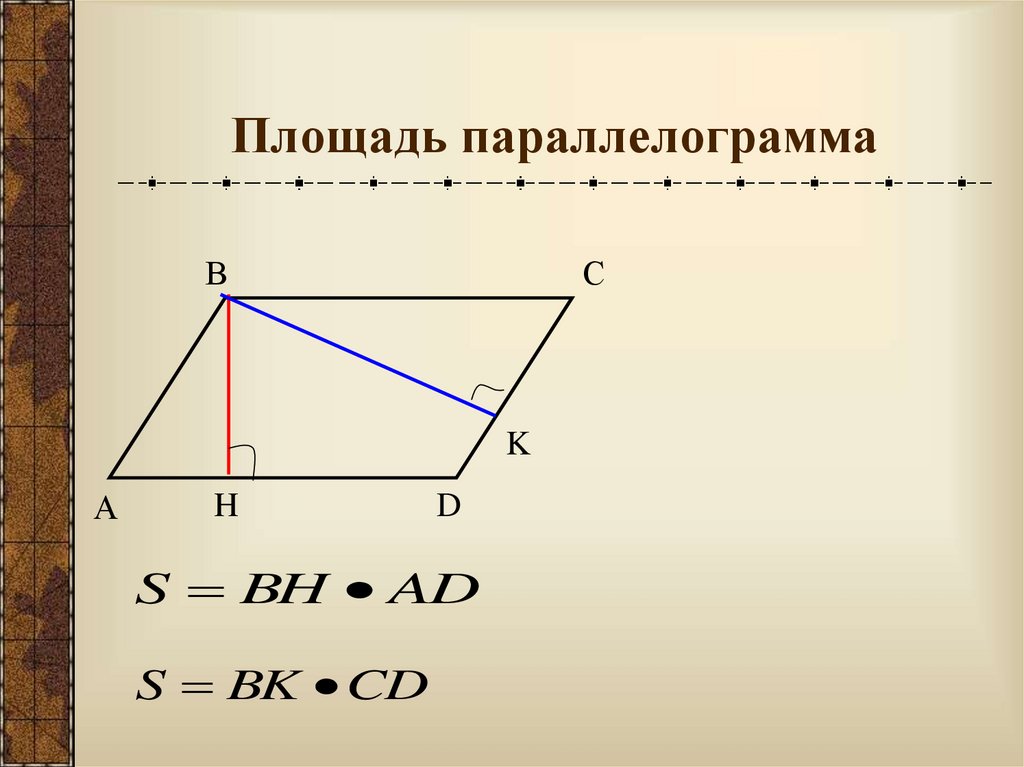
Представляется ли возможным высчитать площадь параллелограмма при условии, что длины двух его диагоналей и образованный в месте их пересечения угол являются известными величинами?
Площадь параллелограмма (S) представляет собой половину числа, полученного после умножения друг на друга длин проведенных в нем диагоналей, которое умножено на синус образовавшегося в итоге их пересечения угла:
S = ½*d 1*d 2*sin α
Возможно ли рассчитать площадь параллелограмма по диагоналям, длины которых равны 6 см и 4 см? При этом известно, что образованный ими угол является прямым.
Для определения площади параллелограмма через известные длины проведенных в нем диагоналей применяется приведенная ниже формула:
S = ½*d 1*d 2*sin α,
где диагонали фигуры обозначены как d 1 и d 2, а синус образованного в результате их пересечения угла — sin α.
Подставим в указанное равенство величины, приведенные в задании:
S = 1/2 * 4 см * 6 см * sin 90° = 12 см кв.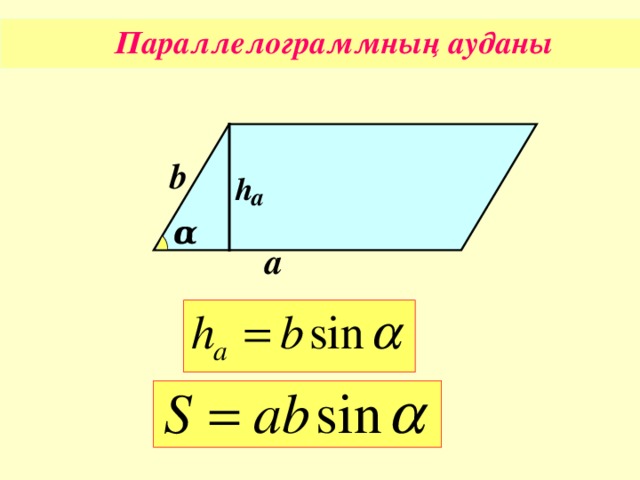
Ответ: Площадь параллелограмма, вычисленная через диагонали, равна 12 см кв.
На одной из сторон параллелограмма ABCD, обозначенной как ВС, отмечена точка М. Чему будет равна площадь параллелограмма при условии, что площадь треугольника МАD составляет 21 см кв.?
Под площадью параллелограмма (S) понимается величина, полученная в результате умножения длины его стороны (b) на высоту (h), которая опущена к ней. В виде формулы это выглядит следующим образом:
S =b*h
Площадь треугольной фигуры представляет собой ½ числа, полученного произведением длины стороны на высоту, которая к ней проведена:
S=1/2*b*h,
Отсюда получаем, что:
b*h=2Sт=2*21=42 см кв.
Если говорить о треугольнике МАD, то в нем сторона АD представлена в
качестве стороны b, как и в случае с параллелограммом. Высота указанного
треугольника будет также представлять собой высоту параллелограмма. Это
обусловлено тем, что точка М расположена на стороне, которая
противоположна стороне ВС. Из этого следует, что площадь параллелограмма
равна 42 см кв.
Из этого следует, что площадь параллелограмма
равна 42 см кв.
Ответ: Площадь параллелограмма равна 42 см кв.
Параллелограмм ABCD имеет стороны длиной 10 см и 14 см, а также острый угол в 60 градусов. Каким образом можно вычислить площадь параллелограмма?
В параллелограмме ABCD нужно провести высоту ВН на сторону AD. После этого получается треугольник АВН с углом в 90 градусов. Можно рассчитать, чему равен еще один угол данного треугольника:
АВН = 90-60 = 30
ВН = АВ*sin60 = 10*корень3/2 = 5*корень3
Таким образом, можно узнать, чему будет равна площадь параллелограмма:
S = AD*ВН = 14*5*√3 = 70*√3 см кв.
Ответ: Площадь параллелограмма составляет 70*√3 см кв.
Дан параллелограмм, через середины пары смежных сторон которого проведена прямая. Она отсекает треугольную фигуру площадью 32 см кв. Чему в данном случае равна площадь параллелограмма?
АС представляет собой диагональ биссектрисы. В этом случае оба
треугольника FMD и ADC являются подобными по той причине, что они имеют
общий угол А и их стороны равны. Из этого следует, что:
В этом случае оба
треугольника FMD и ADC являются подобными по той причине, что они имеют
общий угол А и их стороны равны. Из этого следует, что:
S ADC = 1/2*ab*sina
S FDM=1/2 *2a*2bsina
Отношение площадей двух треугольников выглядит как:
S ADC / S FDM= 32/x
1/4=32/x
x=128
Теперь можно высчитать площадь параллелограмма:
S = 128*2 = 256 см кв.
Читать дальше: как найти площадь трапеции.
2 формулы вычисления площади параллелограмма. Площадь параллелограмма
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. Указанные величины и формулы для их вычисления будут приведены ниже.
Свойства параллелограмма
Противоположные стороны параллелограмма как и противоположные углы равны между собой:
AB=CD, BC=AD
,
Диагонали параллелограмма в точке пересечения делятся на две равные части:
АО=OC, OB=OD.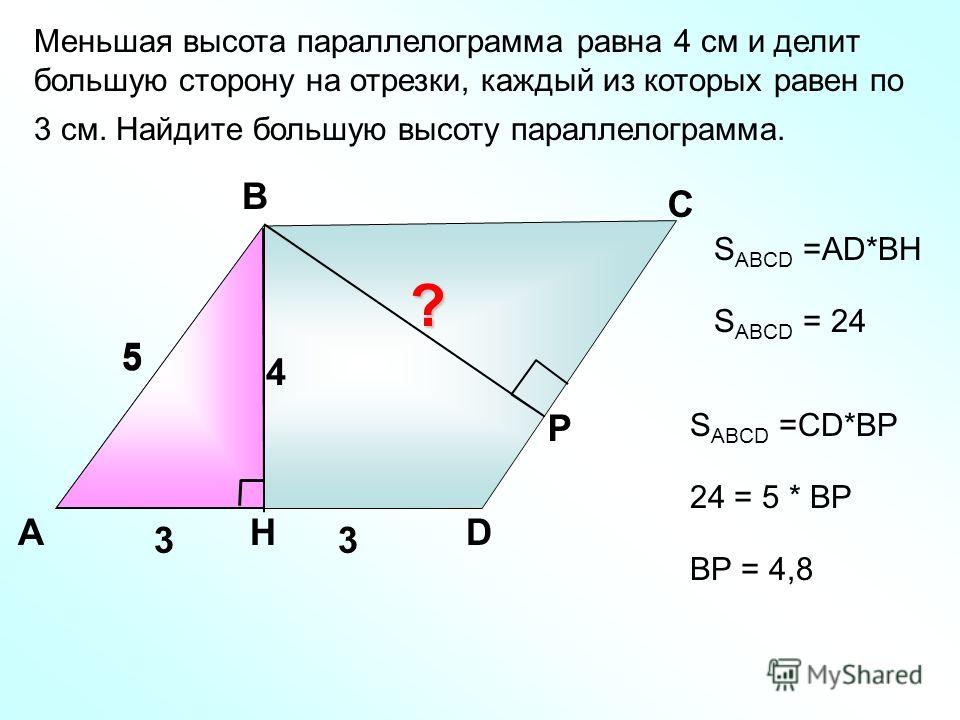 2)
.
2)
.
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов (прилегающие к одной стороне) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма
— это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.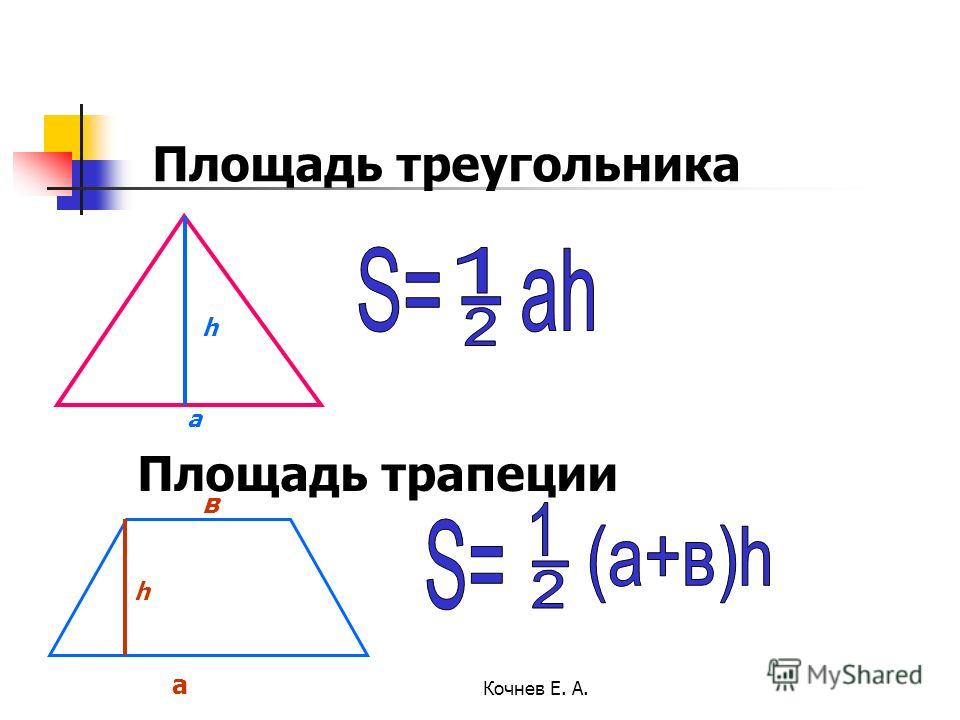
Формула площади параллелограмма
Площадь параллелограмма
равна произведению стороны на высоту проведенную к ней. Формула площади следующая
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Параллелограмм представляет собой четырехугольную фигуру, у которой противолежащие стороны попарно параллельны и попарно равны. Равны у него также и противоположные углы, а точка пересечения диагоналей параллелограмма делит их пополам, являясь при этом центром симметрии фигуры. Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Ключевой характеристикой параллелограмма, очень часто используемой при нахождении его площади, является высота. Высотой параллелограмма принято называть перпендикуляр, опущенный из произвольной точки противоположной стороны к отрезку прямой, образующей данную сторону.
- В самом простом случае площадь параллелограмма определяется как произведение его основания на высоту.
S = DC ∙ h
где S — площадь параллелограмма;
a — основание;
h — высота, проведенная к данному основанию.Данную формулу очень легко понять и запомнить, если взглянуть на следующий рисунок.
Как видно из данного изображения, если слева от параллелограмма отрезать воображаемый треугольник и присоединить его справа, то в результате мы получим прямоугольник.
 А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону. - Площадь параллелограмма может быть также найдена в результате перемножения длин двух смежных оснований и синуса угла между ними:
S = AD∙AB∙sinα
где AD, AB — смежные основания, образующие точку пересечения и угол а между собой;
α — угол между основаниями AD и AB. - Также площадь параллелограмма можно найти разделив пополам произведение длин диагоналей параллелограмма на синус угла между ними.
S = ½∙AC∙BD∙sinβ
где AC, BD — диагонали параллелограмма;
β — угол между диагоналями. - Существует также формула для нахождения площади параллелограмма через радиус вписанной в него окружности. Она записывается следующий образом:
Параллелограмм – это четырехугольник, у которого стороны попарно параллельны.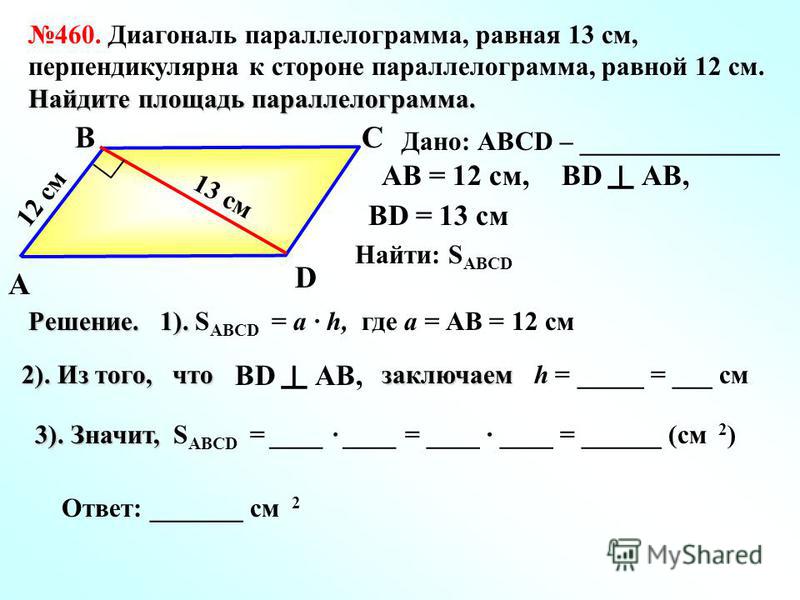
В этой фигуре противоположные стороны и углы равны между собой. Диагонали параллелограмма пересекаются в одной точке и делятся ей пополам. Формулы площади параллелограмма позволяют найти значение через стороны, высоту и диагонали. Параллелограмм также может быть представлен в частных случаях. Ими считаются прямоугольник, квадрат и ромб.
Для начала рассмотрим пример расчета площади параллелограмма по высоте и стороне, к которой она опущена.
Этот случай считается классическим и не требует дополнительного разбирательства. Лучше рассмотрим формулу вычисления площади через две стороны и угол между ними. Этот же способ применяется в расчете . Если даны стороны и угол между ними, то площадь рассчитывается так:
Допустим, дан параллелограмм со сторонами a
= 4 см, b
= 6 см. Угол между ними α
= 30°. Найдем площадь:
Площадь параллелограмма через диагонали
Формула площади параллелограмма через диагонали позволяет быстро найти значение.
Для вычислений понадобится величина угла, расположенного между диагоналями.
Рассмотрим пример расчета площади параллелограмма через диагонали. Пусть дан параллелограмм с диагоналями D
= 7 см, d
= 5 см. Угол, лежащий между ними α
=30°. Подставим данные в формулу:
Пример расчета площади параллелограмма через диагональ дал нам прекрасный результат – 8,75.
Зная формулу площади параллелограмма через диагональ можно решать множество интересных задач. Давайте рассмотрим одну из них.
Задача: Дан параллелограмм с площадью 92 кв. см. Точка F
расположена на середине его стороны ВС
. Давайте найдем площадь трапеции ADFB
, которая будет лежать в нашем параллелограмме. Для начала нарисуем все, что получили по условиям.
Приступаем к решению:
По нашим условиям ah
=92, а соответственно, площадь нашей трапеции будет равняться
Площадь параллелограмма. В очень многих задачах по геометрии связанных с вычислением площадей, в том числе и заданиях на ЕГЭ, используются формулы площади параллелограмма и треугольника. Их существует несколько, здесь мы их с вами рассмотрим.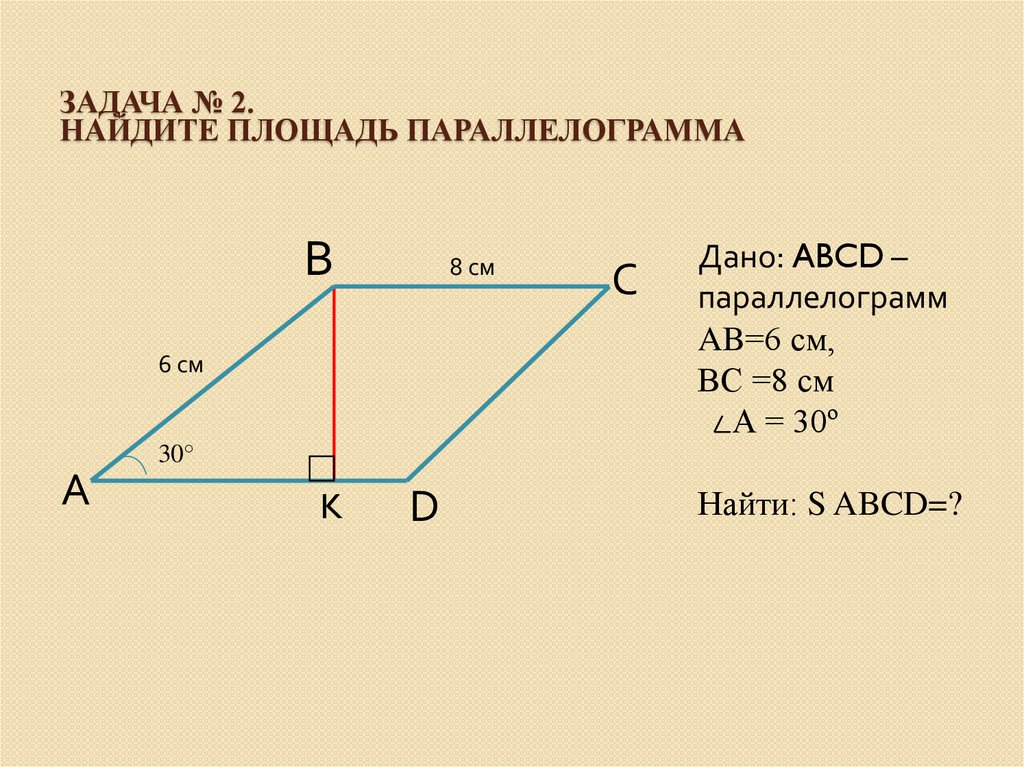
Перечислять эти формулы было бы слишком просто, этого добра и так хватает в справочниках и на различных сайтах. Мне хотелось бы донести суть — чтобы вы их не зубрили, а понимали и легко могли вспомнить в любой момент. После изучения материала статьи вы поймёте, что формулы эти учить совсем не нужно. Объективно говоря, они так часто встречаются при решениях, что откладываются в памяти надолго.
1. Итак, давайте рассмотрим параллелограмм. Определение гласит:
Почему так? Всё просто! Чтобы показать наглядно в чём смысл формулы, выполним некоторые дополнительные построения, а именно построим высоты:
Площадь треугольника (2) равна площади треугольника (1) — второй признак равенства прямоугольных треугольников «по катету и гипотенузе». Теперь мысленно «отрежем» второй и перенесём его наложив на первый — получим прямоугольник, площадь которого будет равна площади исходного параллелограмма:
Площадь прямоугольника, как известно, равна произведению его соседних сторон. Как видно по эскизу, одна сторона полученного прямоугольника равна стороне параллелограмма, а другая его высоте параллелограмма. Поэтому и получаем формулу площади параллелограмма S = a∙h
a
Как видно по эскизу, одна сторона полученного прямоугольника равна стороне параллелограмма, а другая его высоте параллелограмма. Поэтому и получаем формулу площади параллелограмма S = a∙h
a
2. Продолжим, ещё одна формула его площади. Имеем:
Площадь параллелограмма формула
Обозначим стороны как a и b, угол между ними γ «гамма», высота h a. Рассмотрим прямоугольный треугольник:
Формула вычисления площади параллелограмма. Как найти площадь параллелограмма
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. Указанные величины и формулы для их вычисления будут приведены ниже.
Свойства параллелограмма
Противоположные стороны параллелограмма как и противоположные углы равны между собой:
AB=CD, BC=AD
,
Диагонали параллелограмма в точке пересечения делятся на две равные части:
АО=OC, OB=OD. 2)
.
2)
.
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов (прилегающие к одной стороне) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма
— это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
Формула площади параллелограмма
Площадь параллелограмма
равна произведению стороны на высоту проведенную к ней. Формула площади следующая
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Площадь параллелограмма. В очень многих задачах по геометрии связанных с вычислением площадей, в том числе и заданиях на ЕГЭ, используются формулы площади параллелограмма и треугольника. Их существует несколько, здесь мы их с вами рассмотрим.
Их существует несколько, здесь мы их с вами рассмотрим.
Перечислять эти формулы было бы слишком просто, этого добра и так хватает в справочниках и на различных сайтах. Мне хотелось бы донести суть — чтобы вы их не зубрили, а понимали и легко могли вспомнить в любой момент. После изучения материала статьи вы поймёте, что формулы эти учить совсем не нужно. Объективно говоря, они так часто встречаются при решениях, что откладываются в памяти надолго.
1. Итак, давайте рассмотрим параллелограмм. Определение гласит:
Почему так? Всё просто! Чтобы показать наглядно в чём смысл формулы, выполним некоторые дополнительные построения, а именно построим высоты:
Площадь треугольника (2) равна площади треугольника (1) — второй признак равенства прямоугольных треугольников «по катету и гипотенузе». Теперь мысленно «отрежем» второй и перенесём его наложив на первый — получим прямоугольник, площадь которого будет равна площади исходного параллелограмма:
Площадь прямоугольника, как известно, равна произведению его соседних сторон.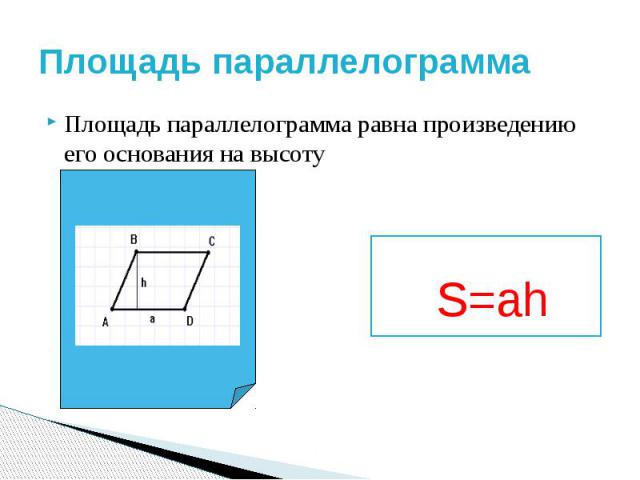 Как видно по эскизу, одна сторона полученного прямоугольника равна стороне параллелограмма, а другая его высоте параллелограмма. Поэтому и получаем формулу площади параллелограмма S = a∙h
a
Как видно по эскизу, одна сторона полученного прямоугольника равна стороне параллелограмма, а другая его высоте параллелограмма. Поэтому и получаем формулу площади параллелограмма S = a∙h
a
2. Продолжим, ещё одна формула его площади. Имеем:
Площадь параллелограмма формула
Обозначим стороны как a и b, угол между ними γ «гамма», высота h a. Рассмотрим прямоугольный треугольник:
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Параллелограмм – это четырехугольник, у которого стороны попарно параллельны.
В этой фигуре противоположные стороны и углы равны между собой. Диагонали параллелограмма пересекаются в одной точке и делятся ей пополам. Формулы площади параллелограмма позволяют найти значение через стороны, высоту и диагонали. Параллелограмм также может быть представлен в частных случаях. Ими считаются прямоугольник, квадрат и ромб.
Для начала рассмотрим пример расчета площади параллелограмма по высоте и стороне, к которой она опущена.
Этот случай считается классическим и не требует дополнительного разбирательства. Лучше рассмотрим формулу вычисления площади через две стороны и угол между ними.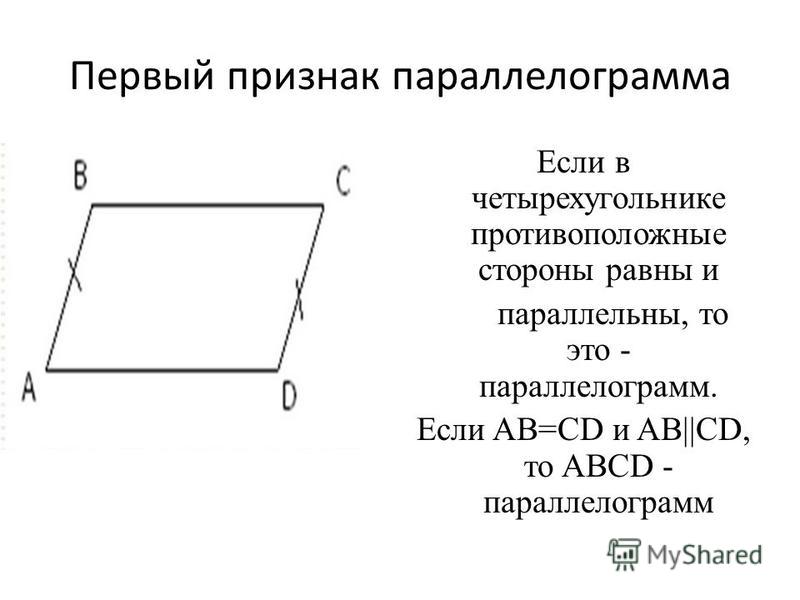 Этот же способ применяется в расчете . Если даны стороны и угол между ними, то площадь рассчитывается так:
Этот же способ применяется в расчете . Если даны стороны и угол между ними, то площадь рассчитывается так:
Допустим, дан параллелограмм со сторонами a
= 4 см, b
= 6 см. Угол между ними α
= 30°. Найдем площадь:
Площадь параллелограмма через диагонали
Формула площади параллелограмма через диагонали позволяет быстро найти значение.
Для вычислений понадобится величина угла, расположенного между диагоналями.
Рассмотрим пример расчета площади параллелограмма через диагонали. Пусть дан параллелограмм с диагоналями D
= 7 см, d
= 5 см. Угол, лежащий между ними α
=30°. Подставим данные в формулу:
Пример расчета площади параллелограмма через диагональ дал нам прекрасный результат – 8,75.
Зная формулу площади параллелограмма через диагональ можно решать множество интересных задач. Давайте рассмотрим одну из них.
Задача: Дан параллелограмм с площадью 92 кв. см. Точка F
расположена на середине его стороны ВС
. Давайте найдем площадь трапеции ADFB
, которая будет лежать в нашем параллелограмме.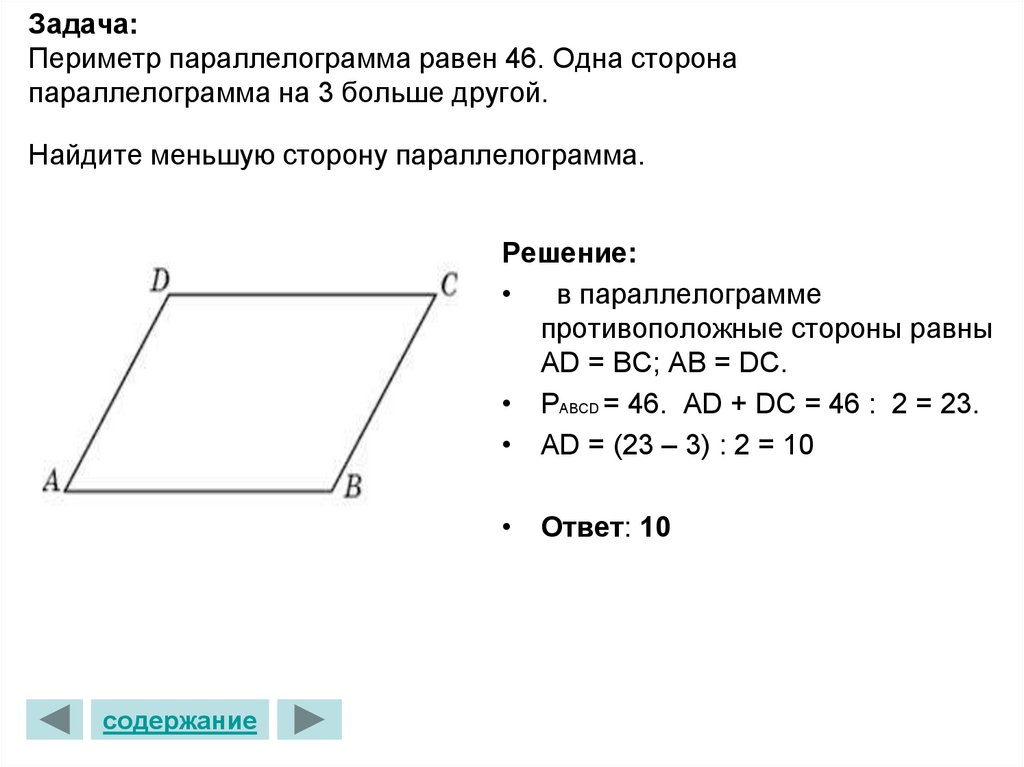 Для начала нарисуем все, что получили по условиям.
Для начала нарисуем все, что получили по условиям.
Приступаем к решению:
По нашим условиям ah
=92, а соответственно, площадь нашей трапеции будет равняться
Площадь параллелограмма — формула, методика и примеры вычисления » Kupuk.net
Задачи на нахождение площади параллелограмма довольно часто встречаются в геометрии при выполнении контрольных работ, написании зачетов и решении практических заданий экзаменационных билетов. Для получения отличных оценок необходимо знать доказательства теорем, основные соотношения и методику их нахождения, а также уметь применять знания, полученные в процессе обучения, на практике.
Общие сведения
Перед обучением решению задач специалисты рекомендуют изучить теорию и разобраться в ней. Параллелограмм — геометрическая фигура, состоящая из четырех вершин и взаимно-параллельными, а также равными между собой противоположными сторонами. Высота — часть прямой (отрезок), исходящая из вершины на противоположную сторону и образующая с последней прямой угол.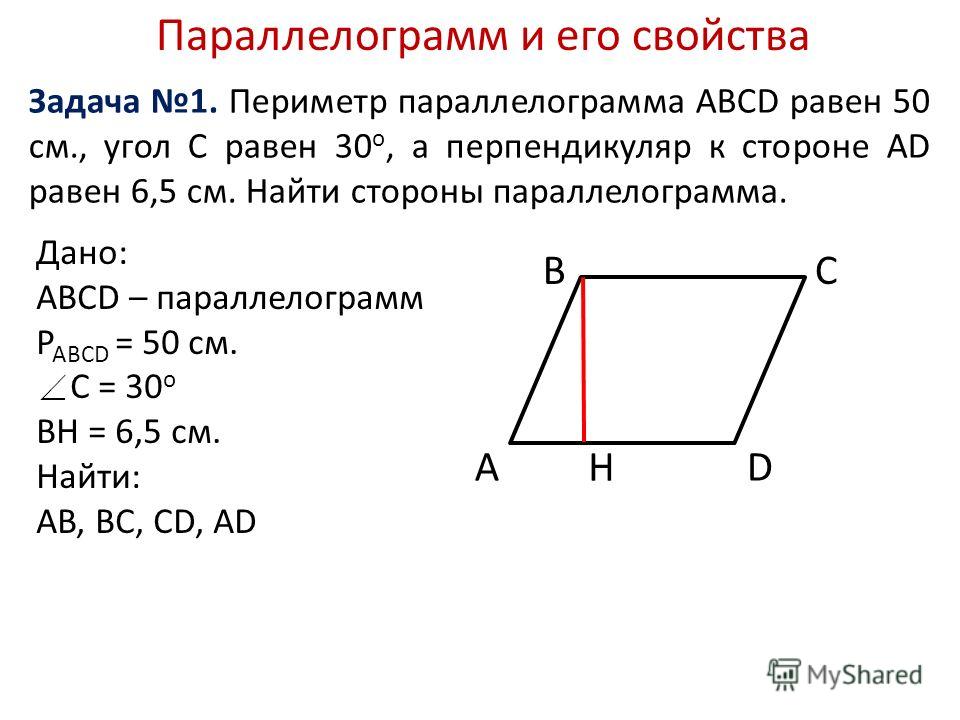
Диагонали не равны между собой. Для удобства их обозначают литерами F и f (большая и малая соответственно). Однако у квадрата и прямоугольника они эквивалентны. Специалисты рекомендуют на начальных этапах обучения правильно определять геометрическую фигуру. Для этой цели существуют признаки параллелограмма.
Признаки параллелограмма
Признаки — набор критериев и правил, при помощи которых определяется тип геометрического тела. В некоторых задачах с повышенной сложностью дается четырехугольник с определенными исходными данными. Далее необходимо найти один из его параметров по формуле. Для этого следует правильно идентифицировать фигуру, чтобы воспользоваться необходимым соотношением.
Вот на этом этапе будут полезны признаки, позволяющие отнести геометрическое тело к классу параллелограммов. К ним относятся следующие:
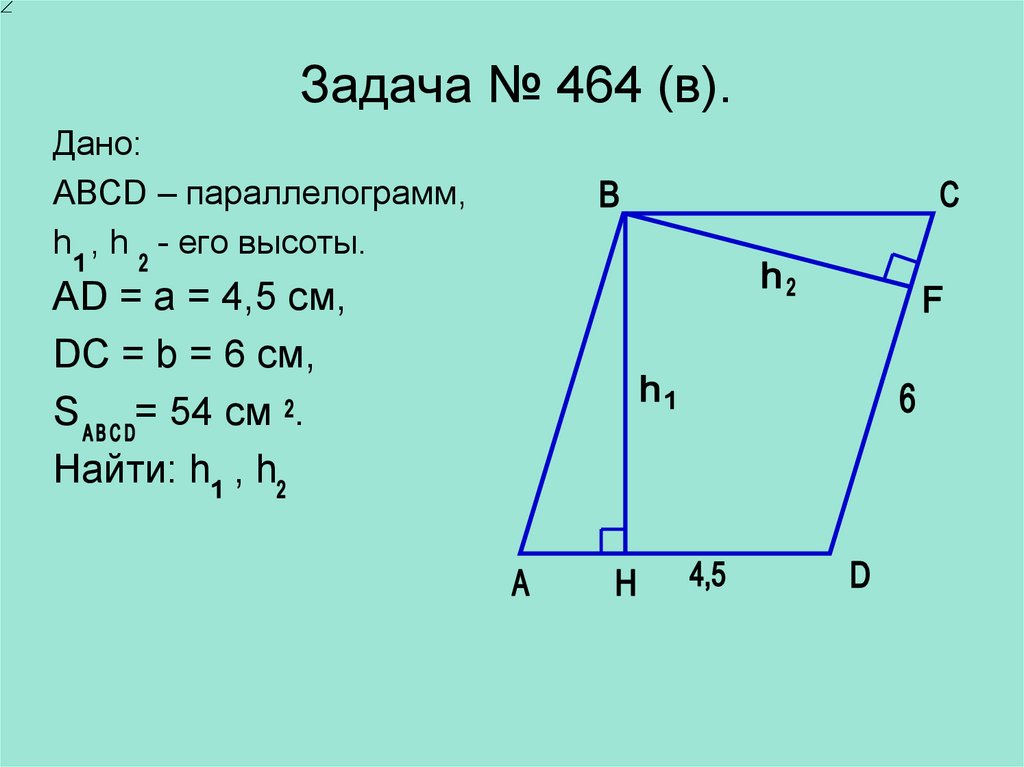
Следует отметить, что при выполнении одного условия фигура принадлежит к классу параллелограммов.
Свойства фигуры
Свойства — утверждения, доказанные математиками. Они применяются для доказательств теорем, решения диофантовых (линейных) систем уравнений на нахождение двух неизвестных величин, вычисления параметров фигуры, а также для проектирования деталей. Для этих целей можно применять такие утверждения:
После свойств математики рекомендуют ознакомиться с некоторыми теоремами, позволяющими выводить формулу площади параллелограмма.
Теоремы о площади
Формулы площади — базовые соотношения, позволяющие найти другие параметры параллелограмма. Однако начинающему математику рекомендуется посмотреть, каким образом они доказываются. В отличие от прямоугольника величина рассчитывается немного иначе. Формулы — математическая запись определенной теоремы про площадь. Их всего три:
Однако для удобства доказательства утверждений следует ввести обозначения основных параметров фигуры:
Следует отметить, что специалисты при решении любой задачи или доказательстве геометрических тождеств рекомендуют использовать сокращенные записи. Этот подход является признаком мастерства и правилом хорошего тона в точных науках.
Сторона и высота
Первую теорему можно сформулировать следующим образом: площадь параллелограмма равна произведению большей стороны на значение высоты. Доказывается утверждение довольно просто по такому алгоритму:

Следует отметить, что высоты, проведенные из вершин тупого и острого углов (h2 и h3), равны между собой. Их можно обозначить для удобства одной литерой H.
Стороны и острый угол
Следующая теорема имеет такую формулировку: при известных сторонах параллелограмма и размерности угла между ними его площадь эквивалентна произведению первых двух на синус третьего, то есть S=k*l*sin (∠v). Доказывается утверждение по такой методике:
Утверждение доказано. Следует отметить, что в геометрии очень часто одна теорема используется для доказательства другой.
Величины диагоналей
Третья теорема определения величины площади параллелограмма через диагонали имеет следующую формулировку: размерность эквивалентна произведению диагоналей на острый угол между ними (S=F*f*sin (∠z)). Доказывается утверждение по такому алгоритму:
 (2))].
(2))].Следует отметить, что из этих соотношений можно найти стороны, высоту и углы. Кроме того, последнее соотношение можно записать в другом виде: P=2[k+H/sin (z)]=2[l+H/cos (v)]. Эти формулы строятся на основании теорем о площади параллелограмма, в которых стороны и другие параметры выражаются через S треугольников. Специалисты рекомендуют после изученного материала переходить к рассмотрению других соотношений.
Другие параметры
Определение сторон и диагоналей осуществляется посредством следствий из теорем. Математики рекомендуют воспользоваться готовыми формулами, но не стоит забывать и о тренировках. Последние реализуются при помощи самостоятельного выражения одной величины через другую. Стороны можно найти, когда известны следующие параметры:
 (½).
(½).Для практического применения знаний специалисты рекомендуют переходить к заданиям по геометрии.
Пример решения
Для закрепления теоретических знаний рекомендуется постоянно решать задачи. Условие одной из них имеет следующий вид:
Необходимо найти площадь (S), высоту (H). Вычисляются необходимые параметры по следующему алгоритму:
Задачу можно решать при помощи других соотношений. Однако это приведет к увеличению количества вычислений, в результате которых могут возникнуть ошибки.
Таким образом, для нахождения площади параллелограмма нужно знать признаки фигуры, свойства, теоремы, формулы и соотношения, а также чаще решать различные задачи.
Как найти площадь параллелограмма. Как найти площадь параллелограмма, треугольника, трапеции
Формула для площади параллелограмма
Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону.
Доказательство
Если параллелограмм — прямоугольник, то равенство выполнено по теореме о площади прямоугольника. Далее считаем, что углы параллелограмма не прямые.
Пусть в параллелограмме $ABCD$ угол $\angle BAD$ острый и $AD > AB$. Иначе переименуем вершины. Тогда высота $BH$ из вершины $B$ на прямую $AD$ падает на сторону $AD$, так как катет $AH$ короче гипотенузы $AB$, а $AB
Иначе переименуем вершины. Тогда высота $BH$ из вершины $B$ на прямую $AD$ падает на сторону $AD$, так как катет $AH$ короче гипотенузы $AB$, а $AB
Сравним площадь параллелограмма $ABCD$ и площадь прямоугольника $HBCK$. Площадь параллелограмма больше на площадь $\triangle ABH$, но меньше на на площадь $\triangle DCK$. Так как эти треугольники равны, то и их площади равны. Значит, площадь параллелограмма равна площади прямоугольника со сторонами длиной в сторону и высоту параллелограмма.
Формула для площади параллелограмма через стороны и синус
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними.
Доказательство
Высота параллелограмма $ABCD$, опущенная на сторону $AB$ равна произведению отрезка $BC$ на синус угла $\angle ABC$. Осталось применить предыдущее утверждение.
Формула для площади параллелограмма через диагонали
Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.
Доказательство
Пусть диагонали параллелограмма $ABCD$ пересекаются в точке $O$ под углом $\alpha$. \circ — \angle AOD$. Значит, синусы углов при пересечении диагоналей равны $\sin \alpha$.
\circ — \angle AOD$. Значит, синусы углов при пересечении диагоналей равны $\sin \alpha$.
$S_{ABCD}=S_{\triangle AOB} + S_{\triangle BOC} + S_{\triangle COD} + S_{\triangle AOD}$
по аксиоме измерения площади. Применяем формулу площади треугольника $S_{ABC} = \dfrac{1}{2} \cdot AB \cdot BC \sin \angle ABC$ для этих треугольников и углов при пересечении диагоналей. Стороны каждого равны половинам диагоналей, синусы также равны. Следовательно, площади всех четырёх треугольников равны $S = \dfrac{1}{2} \cdot \dfrac{AC}{2} \cdot \dfrac{BD}{2} \cdot \sin \alpha = \dfrac{AC \cdot BD}{8} \sin \alpha$. Суммируя всё вышесказанное, получаем
$S_{ABCD} = 4S = 4 \cdot \dfrac{AC \cdot BD}{8} \sin \alpha = \dfrac{AC \cdot BD \cdot \sin \alpha}{2}$
Как в евклидовой геометрии точка и прямая — главные элементы теории плоскостей, так и параллелограмм является одной из ключевых фигур выпуклых четырехугольников. Из него, как нитки из клубка, втекают понятия «прямоугольника», «квадрата», «ромба» и других геометрических величин.
Вконтакте
Определение параллелограмма
Выпуклый четырехугольник, состоящий из отрезков, каждая пара из которых параллельна, известен в геометрии как параллелограмм.
Как выглядит классический параллелограмм изображает четырехугольник ABCD. Стороны называются основаниями (AB, BC, CD и AD), перпендикуляр, проведенный из любой вершины на противоположную этой вершине сторону, — высотой (BE и BF), линии AC и BD — диагоналями.
Внимание! Квадрат, ромб и прямоугольник — это частные случаи параллелограмма.
Стороны и углы: особенности соотношения
Ключевые свойства, по большому счету, предопределены самим обозначением , их доказывает теорема. Эти характеристики следующие:
- Стороны, которые являются противоположными, — попарно одинаковые.
- Углы, расположенные противоположно друг другу — попарно равны.
Доказательство: рассмотрим ∆ABC и ∆ADC, которые получаются вследствие разделения четырехугольника ABCD прямой AC. ∠BCA=∠CAD и ∠BAC=∠ACD, поскольку AC для них общая (вертикальные углы для BC||AD и AB||CD, соответственно). Из этого следует: ∆ABC = ∆ADC (второй признак равенства треугольников).
∠BCA=∠CAD и ∠BAC=∠ACD, поскольку AC для них общая (вертикальные углы для BC||AD и AB||CD, соответственно). Из этого следует: ∆ABC = ∆ADC (второй признак равенства треугольников).
Отрезки AB и BC в ∆ABC попарно соответствуют линиям CD и AD в ∆ADC, что означает их тождество: AB = CD, BC = AD. Таким образом, ∠B соответствует ∠D и они равны. Так как ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, которые так же попарно одинаковые, то ∠A = ∠C. Свойство доказано.
Характеристики диагоналей фигуры
Основной признак этих линий параллелограмма: точка пересечения разделяет их пополам.
Доказательство: пусть т. Е — это точка пересечения диагоналей AC и BD фигуры ABCD. Они образуют два соизмеримых треугольника — ∆ABE и ∆CDE.
AB=CD, так как они противоположные. Согласно прямых и секущей, ∠ABE = ∠CDE и ∠BAE = ∠DCE.
По второму признаку равенства ∆ABE = ∆CDE. Это означает, что элементы ∆ABE и ∆CDE: AE = CE, BE = DE и при этом они соразмерные части AC и BD. Свойство доказано.
Особенности смежных углов
У смежных сторон сумма углов равна 180° , поскольку они лежат по одну сторону параллельных линий и секущей. Для четырехугольника ABCD:
Для четырехугольника ABCD:
∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º
Свойства биссектрисы:
- , опущенные на одну сторону, являются перпендикулярными;
- противолежащие вершины имеют параллельные биссектрисы;
- треугольник, полученный проведением биссектрисы, будет равнобедренным.
Определение характерных черт параллелограмма по теореме
Признаки этой фигуры вытекают из ее основной теоремы, которая гласит следующее: четырехугольник считается параллелограммом в том случае, если его диагонали пересекаются, а эта точка разделяет их на равные отрезки.
Доказательство: пусть в т. Е прямые AC и BD четырехугольника ABCD пересекаются. Так как ∠AED = ∠BEC, а AE+CE=AC BE+DE=BD, то ∆AED = ∆BEC (по первому признаку равенства треугольников). То есть ∠EAD = ∠ECB. Они также являются внутренними перекрестными углами секущей AC для прямых AD и BC. Таким образом, по определению параллельности — AD || BC. Аналогичное свойство линий BC и CD выводится также.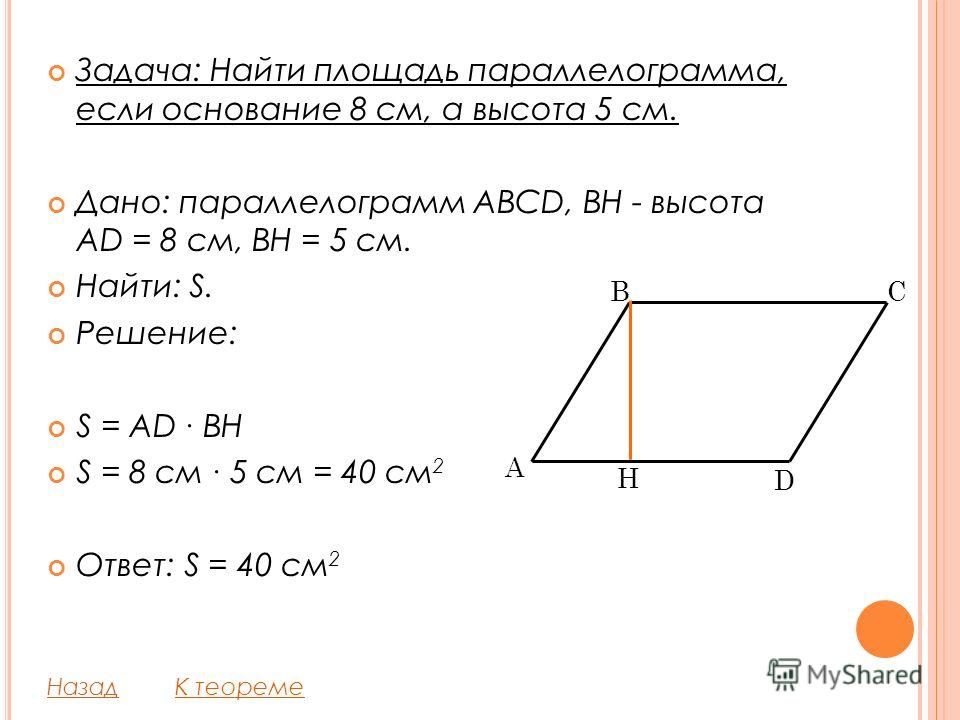 Теорема доказана.
Теорема доказана.
Вычисление площади фигуры
Площадь этой фигуры находится несколькими методами, одним из самых простых: умножения высоты и основания, к которому она проведена.
Доказательство: проведем перпендикуляры BE и CF из вершин B и C. ∆ABE и ∆DCF — равные, поскольку AB = CD и BE = CF. ABCD — равновеликий с прямоугольником EBCF, так как они состоят и соразмерных фигур: S ABE и S EBCD , а также S DCF и S EBCD . Из этого следует, что площадь этой геометрической фигуры находится так же как и прямоугольника:
S ABCD = S EBCF = BE×BC=BE×AD.
Для определения общей формулы площади параллелограмма обозначим высоту как hb , а сторону — b . Соответственно:
Другие способы нахождения площади
Вычисления площади через стороны параллелограмма и угол , который они образуют, — второй известный метод.
,
Sпр-ма — площадь;
a и b — его стороны
α — угол между отрезками a и b.
Этот способ практически основывается на первом, но в случае, если неизвестна. всегда отрезает прямоугольный треугольник, параметры которого находятся тригонометрическими тождествами, то есть . Преобразуя соотношение, получаем . В уравнении первого способа заменяем высоту этим произведением и получаем доказательство справедливости этой формулы.
всегда отрезает прямоугольный треугольник, параметры которого находятся тригонометрическими тождествами, то есть . Преобразуя соотношение, получаем . В уравнении первого способа заменяем высоту этим произведением и получаем доказательство справедливости этой формулы.
Через диагонали параллелограмма и угол, который они создают при пересечении, также можно найти площадь.
Доказательство: AC и BD пересекаясь, образуют четыре треугольника: ABE, BEC, CDE и AED. Их сумма равна площади этого четырехугольника.
Площадь каждого из этих ∆ можно найти за выражением , где a=BE, b=AE, ∠γ =∠AEB. Поскольку , то в расчетах используется единое значение синуса. То есть . Поскольку AE+CE=AC= d 1 и BE+DE=BD= d 2 , формула площади сводится до:
.
Применение в векторной алгебре
Особенности составляющих частей этого четырехугольника нашли применение в векторной алгебре, а именно: сложении двух векторов. Правило параллелограмма утверждает, что если заданные векторы и не коллинеарны, то их сумма будет равна диагонали этой фигуры, основания которой соответствуют этим векторам.
Доказательство: из произвольно выбранного начала — т. о. — строим векторы и . Далее строим параллелограмм ОАСВ, где отрезки OA и OB — стороны. Таким образом, ОС лежит на векторе или сумме .
Формулы для вычисления параметров параллелограмма
Тождества приведены при следующих условиях:
- a и b, α — стороны и угол между ними;
- d 1 и d 2 , γ — диагонали и в точке их пересечения;
- h a и h b — высоты, опущенные на стороны a и b;
| Параметр | Формула |
| Нахождение сторон | |
| по диагоналям и косинусу угла между ними | |
| по диагоналям и стороне | |
| через высоту и противоположную вершину | |
| Нахождение длины диагоналей | |
| по сторонам и величине вершины между ними | |
| по сторонам и одной из диагоналей | ВыводПараллелограмм как одна из ключевых фигур геометрии находит применение в жизни, например, в строительстве при подсчете площади участка или других измерений. |
Параллелограмм – это четырехугольник, у которого стороны попарно параллельны.
В этой фигуре противоположные стороны и углы равны между собой. Диагонали параллелограмма пересекаются в одной точке и делятся ей пополам. Формулы площади параллелограмма позволяют найти значение через стороны, высоту и диагонали. Параллелограмм также может быть представлен в частных случаях. Ими считаются прямоугольник, квадрат и ромб.
Для начала рассмотрим пример расчета площади параллелограмма по высоте и стороне, к которой она опущена.
Этот случай считается классическим и не требует дополнительного разбирательства. Лучше рассмотрим формулу вычисления площади через две стороны и угол между ними. Этот же способ применяется в расчете . Если даны стороны и угол между ними, то площадь рассчитывается так:
Допустим, дан параллелограмм со сторонами a
= 4 см, b
= 6 см. Угол между ними α
= 30°. Найдем площадь:
Угол между ними α
= 30°. Найдем площадь:
Площадь параллелограмма через диагонали
Формула площади параллелограмма через диагонали позволяет быстро найти значение.
Для вычислений понадобится величина угла, расположенного между диагоналями.
Рассмотрим пример расчета площади параллелограмма через диагонали. Пусть дан параллелограмм с диагоналями D
= 7 см, d
= 5 см. Угол, лежащий между ними α
=30°. Подставим данные в формулу:
Пример расчета площади параллелограмма через диагональ дал нам прекрасный результат – 8,75.
Зная формулу площади параллелограмма через диагональ можно решать множество интересных задач. Давайте рассмотрим одну из них.
Задача: Дан параллелограмм с площадью 92 кв. см. Точка F
расположена на середине его стороны ВС
. Давайте найдем площадь трапеции ADFB
, которая будет лежать в нашем параллелограмме. Для начала нарисуем все, что получили по условиям.
Приступаем к решению:
По нашим условиям ah
=92, а соответственно, площадь нашей трапеции будет равняться
Что такое параллелограмм? Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.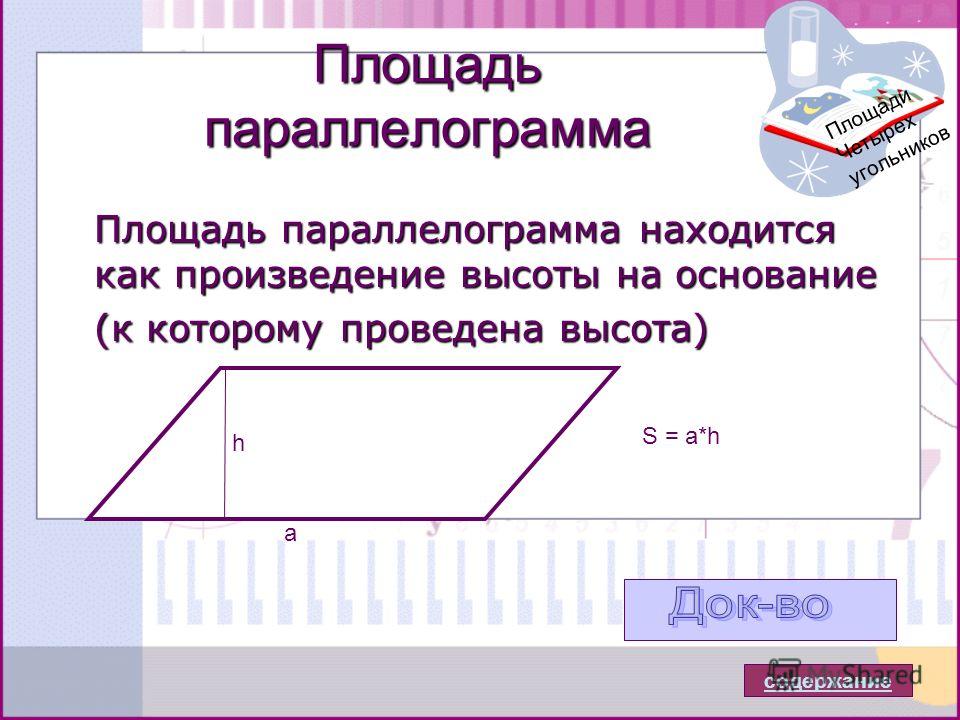
1. Площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = a \cdot h_{a}\]
где:
a – сторона параллелограмма,
h a – высота, проведенная к этой стороне.
2. Если известны длины двух смежных сторон параллелограмма и угол между ними, то площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = a \cdot b \cdot sin(\alpha) \]
3. Если заданы диагонали параллелограмма и известен угол между ними, то площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = \frac{1}{2} \cdot d_{1} \cdot d_{2} \cdot sin(\alpha) \]
Свойства параллелограмма
В параллелограмме противоположные стороны равны: \(AB = CD \) , \(BC = AD \)
В параллелограмме противоположные углы равны: \(\angle A = \angle C \) , \(\angle B = \angle D \)
Диагонали параллелограмма в точке пересечения делятся пополам \(AO = OC \) , \(BO = OD \)
Диагональ параллелограмма делит его на два равных треугольника.
Сумма углов параллелограмма, прилежащих к одной стороне равна 180 o:
\(\angle A + \angle B = 180^{o} \), \(\angle B + \angle C = 180^{o}\)
\(\angle C + \angle D = 180^{o} \), \(\angle D + \angle A = 180^{o}\)
Диагонали и стороны параллелограмма связаны следующим соотношением:
\(d_{1}^{2} + d_{2}^2 = 2a^{2} + 2b^{2} \)
В параллелограмме угол между высотами равен его острому углу: \(\angle K B H =\angle A \)
.
Биссектрисы углов, прилежащих к одной стороне параллелограмма, взаимно перпендикулярны.
Биссектрисы двух противоположных углов параллелограмма параллельны.
Признаки параллелограмма
Четырехугольник будет параллелограммом, если:
\(AB = CD \) и \(AB || CD \)
\(AB = CD \) и \(BC = AD \)
\(AO = OC \) и \(BO = OD \)
\(\angle A = \angle C \) и \(\angle B = \angle D \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Прежде чем узнать, как найти площадь параллелограмма, нам необходимо вспомнить, что такое параллелограмм и что называется его высотой. Параллелограмм – четырехугольник, противолежащие стороны которого попарно параллельны (лежат на параллельных прямых). Перпендикуляр, проведенный из произвольной точки противоположной стороны к прямой, содержащей эту сторону называется высотой параллелограмма.
Квадрат, прямоугольник и ромб – это частные случаи параллелограмма.
Площадь параллелограмма обозначается как (S).
Формулы нахождения площади параллелограмма
S=a*h , где а – это основание, h – это высота, которая проведена к основанию.
S=a*b*sinα , где a и b – это основания, а α — угол между основаниями а и b.
S =p*r , где р – это полупериметр, r – это радиус окружности, которая вписана в параллелограмм.
Площадь параллелограмма, который образован векторами a и b равна модулю произведения заданных векторов, а именно:
Рассмотрим пример №1: Дан параллелограмм, сторона которого равна 7 см, а высота 3 см. Как найти площадь параллелограмма, формула для решения нам необходима.
Таким образом, S= 7×3. S=21. Ответ: 21 см 2 .
Рассмотрим пример №2: Даны основания 6 и 7 см, а также дан угол между основаниями 60 градусов. Как найти площадь параллелограмма? Формула, используемая для решения:
Таким образом, сначала найдем синус угла. Синус 60 = 0,5, соответственно S = 6*7*0,5=21 Ответ: 21 см 2 .
Надеюсь, что эти примеры Вам помогут при решении задач. И помните, главное – это знание формул и внимательность
И помните, главное – это знание формул и внимательность
Площадь параллелограмма: формула и расчеты
Площадь параллелограмма: определение и формула
[Нажмите здесь, чтобы просмотреть примеры вопросов]
соответственно равны.
- Площадь параллелограмма относится к числу квадратных единиц, которые могут поместиться в параллелограмме, и измеряется в квадратных единицах (м 2 , см 2 и т. д.).
- Площадь параллелограмма равна произведению его основания на высоту.
- Основание параллелограмма перпендикулярно его высоте, однако внешняя сторона параллелограмма не перпендикулярна основанию.
Математическая формула площади параллелограмма:
Площадь параллелограмма = b x h
, где0006
b = основание параллелограмма
h = высота параллелограмма
Поскольку прямоугольник имеет такие же свойства, как и параллелограмм, площадь прямоугольника также равна площади параллелограмма.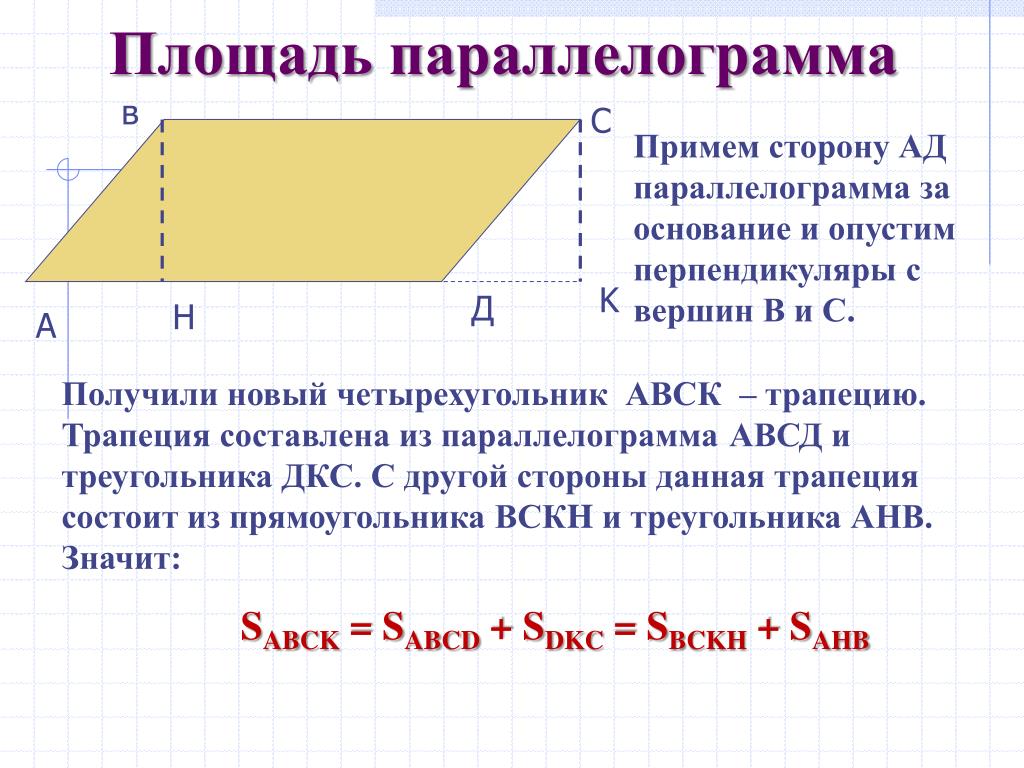
Читайте также
Как вычислить площадь параллелограмма?
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Существует три метода вычисления площади параллелограмма:
- Используя основание и высоту
- Используя две диагонали и угол их пересечения
- Используя длину параллельных сторон и угол между ними.
Площадь параллелограмма с использованием основания и высоты
Площадь параллелограмма можно найти, умножив основание и высоту параллелограмма. Формула может быть представлена следующим образом:
Площадь параллелограмма = b x h
, где
b = основание параллелограмма
h = высота параллелограмма Вычислите площадь параллелограмма, если основание 5 см, а высота 3 см.
Солн: Площадь параллелограммы — базовая x высота
= 5 x 3 см 2
= 15 см 2
область с учебными заведениями с диагентами и диагнолами и их диагенсом и диагнозом
.
 0061
0061Площадь параллелограмма можно вычислить, используя две диагонали и угол их пересечения . Формула может быть указана как:
Площадь параллелограммы = ½ x D 1 x D 2 SIN (Y)
, где
D 1 = первый диагонал параллелеграммы
D 2 2 = первый диагонал параллелеграммы
- Площадь параллелограмма вычисляется как площадь, заключенная в его четырех сторонах.
- Площадь параллелограмма = основание (b) * высота (h).
- Площадь параллелограмма с диагоналями и пересекающимся углом определяется как: ½ x d 9*}\vec{b}\)|
- Прямоугольник
- Ромб
- Квадрат
- Найдите основание и высоту перпендикуляра параллелограмма .
- Запишите формулу площади параллелограмма .
- Подставить данные значения и вычислить .
- Запишите свой окончательный ответ в единицах, возведенных в квадрат .
- Площадь
- Площадь круга
- Площадь четырехугольника
- Площадь трапеции
- Площадь равностороннего треугольника
- Площадь сложных фигур
- Pi r в квадрате
- Площадь ромба
- Площадь прямоугольного треугольника
- Площадь равнобедренного треугольника
- Площадь треугольника 1 0 90 90 out area
- Площадь прямоугольника
- Определите основание и высоту перпендикуляра параллелограмма .

- Использование неправильных единиц измерения для ответа
- Забыв преобразовать меры в общую единицу измерения
- Вычислять и сравнивать площади параллелограммов, используя стандартные единицы
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Площадь параллелограмма, определение, формула, примеры
Параллелограмм — одна из многих геометрических фигур. Это четырехугольник, у которого противоположные стороны равны и параллельны. Знание площади и периметра таких фигур крайне важно для всех изучающих геометрию.
 Площадь параллелограмма – это пространство, которое он окружает.
Он рассчитывается путем умножения длины на высоту.
Все студенты могут проверить все о площади параллелограмма здесь, в этой статье. Присоединяйтесь к онлайн-школе Safalta School и подготовьтесь к экзаменам на совет директоров под руководством наших опытных преподавателей.
Наша онлайн-школа призвана помочь учащимся подготовиться к экзаменам на совет директоров, обеспечив учащимся концептуальную ясность по всем предметам и возможность набрать максимальные баллы на экзаменах.
Площадь параллелограмма – это пространство, которое он окружает.
Он рассчитывается путем умножения длины на высоту.
Все студенты могут проверить все о площади параллелограмма здесь, в этой статье. Присоединяйтесь к онлайн-школе Safalta School и подготовьтесь к экзаменам на совет директоров под руководством наших опытных преподавателей.
Наша онлайн-школа призвана помочь учащимся подготовиться к экзаменам на совет директоров, обеспечив учащимся концептуальную ясность по всем предметам и возможность набрать максимальные баллы на экзаменах.Также проверьте,
Содержание
Конвертер см в дюймы (см в дюймы)
Формула процентов , Шаги для расчета процентов .1. Что такое площадь параллелограмма?
2. Формула площади параллелограмма
3. Вычисление площади параллелограмма
i) Площадь параллелограмма с использованием сторон
ii) Площадь параллелограмма без высоты
iii) Площадь параллелограмма с использованием 9096
Площадь параллелограмма — это область в заданном двумерном пространстве, которую он описывает.
 Параллелограмм — это особый тип четырехугольника с четырьмя сторонами, две из которых параллельны.
Параллелограмм — это особый тип четырехугольника с четырьмя сторонами, две из которых параллельны.Бесплатные демонстрационные занятия
Зарегистрируйтесь здесь, чтобы получить бесплатные демонстрационные занятия
Выберите курсExcel (10 часов)Цифровой маркетингГрафический дизайнПрограмма предпринимательстваОбработка и анализ данныхОблачные вычисленияCUET 2023UPSSSC PETОборонаSSCUP PoliceSchoolКурс навыков интервьюирования SBI CLERKCTETIBPS PO
Пожалуйста, заполните имя
Пожалуйста, введите только 10-значный номер мобильного телефона
Пожалуйста, выберите курс
Пожалуйста, заполните адрес электронной почты
Параллелограмм имеет противоположные стороны одинаковой длины и противоположные углы одинаковой величины. Площадь прямоугольника равна площади параллелограмма, потому что свойства прямоугольника и параллелограмма идентичны.
Чтобы найти площадь параллелограмма, умножьте основание перпендикуляра на его высоту.
 Следует отметить, что основание и высота параллелограмма перпендикулярны друг другу, тогда как боковая сторона параллелограмма не перпендикулярна основанию.
Таким образом, пунктирная линия изображает высоту.
Следует отметить, что основание и высота параллелограмма перпендикулярны друг другу, тогда как боковая сторона параллелограмма не перпендикулярна основанию.
Таким образом, пунктирная линия изображает высоту.Следовательно,
Площадь = b × h Квадратные единицы Где «b» — основание, а «h» — высота параллелограмма.
Давайте изучим вывод площади параллелограмма в следующем разделе.
Связанные ссылки-
- Объем сферы
- Конвертер см в дюймы (см в дюймы)
- Преобразование римских цифр
Площадь параллелограмма можно рассчитать, используя его основание и высоту.
Кроме того, можно вычислить площадь параллелограмма, если известны две его диагонали и любой из их пересекающихся углов, или если известна длина параллельных сторон и любой из углов между сторонами.
 Следовательно, есть три метода получения площади параллелограмма:
Следовательно, есть три метода получения площади параллелограмма:- Если известны основание и высота параллелограмма
- Если высота не указана
- Когда даны диагонали
Площадь параллелограмма с использованием сторонПредположим, что a и b — это набор параллельных сторон параллелограмма, а h — его высота, тогда, исходя из длины сторон и высоты, формула для его площади выглядит следующим образом: определяется как:
Площадь = Основание × Высота
A = b × h [кв.единица]
Пример: Если основание параллелограмма равно 5 см, а высота 3 см, то найти его площадь.
Решение: Дано, длина основания = 5 см, высота = 3 см
По формуле Площадь = 5 × 3 = 15 см2
Площадь параллелограмма без высотыЕсли высота параллелограмма нам неизвестна, то мы можем использовать понятие тригонометрии здесь, чтобы найти его площадь.

Площадь = ab sin (x)
Где a и b — длины параллельных сторон, а x — угол между сторонами параллелограмма.
Пример. Угол между любыми двумя сторонами параллелограмма равен 90 градусов. Если длины двух параллельных сторон равны 3 см и 4 см соответственно, то найдите площадь.
Решение: Пусть a = 3 см и b=4 см А = 12 × 1 = 12 кв.см.
Примечание: Если угол между сторонами параллелограмма равен 90 градусов, то это прямоугольник.
Вы также можете прочитать-
- Периметр прямоугольника
- Площадь квадрата
- Площадь прямоугольника
Площадь параллелограмма с использованием диагоналейПлощадь любого параллелограмма также можно вычислить, используя длины его диагоналей. Как известно, у параллелограмма есть две диагонали, которые пересекаются друг с другом.
 Предположим, диагонали пересекаются друг с другом под углом y, тогда площадь параллелограмма равна:
Предположим, диагонали пересекаются друг с другом под углом y, тогда площадь параллелограмма равна:Площадь = ½ × d1 × d2 sin (y)
Проверьте приведенную ниже таблицу, чтобы получить сводные формулы площади параллелограмма.
Все формулы для расчета площади параллелограмма Использование базы и высоты А = б × ч Использование тригонометрии А = абс синус (х) Использование диагоналей А = ½ × d1 × d2 sin (y) Где,
- b = основание параллелограмма (AB)
- h = высота параллелограмма
- а = сторона параллелограмма (AD)
- x = любой угол между сторонами параллелограмма (∠DAB или ∠ADC)
- d1 = диагональ параллелограмма (p)
- d2 = диагональ параллелограмма (q)
- y = любой угол между точками пересечения диагоналей (∠DOA или ∠DOC)
Подробнее
Источник: Safalta.
 com
com
Решенные примеры параллелограммаВопрос 1: Найдите площадь параллелограмма с основанием 4 см и высотой 5 см.
Решение:
Дано:
Основание, b = 4 см
h = 5 см
Мы знаем, что
Площадь параллелограмма = 5 = b×h 5 40 × 6
кв.см
Следовательно, площадь параллелограмма = 20 см кв.
Вопрос 2: Найдите площадь параллелограмма, ширина которого 8 см, а высота 11 см.
Решение:
, дано,
B = 8 см
H = 11 см
Площадь параллелограммы
= B × H
= 8 × 11 см квадрат
= 88 см квадрат.
Параллелограмм — геометрическая фигура, четыре стороны которой образованы двумя парами параллельных прямых. В параллелограмме противоположные стороны равны по длине и противоположные углы равны по размеру.
Площадь любого параллелограмма можно рассчитать по следующей формуле:
Площадь = основание × высота
Следует отметить, что основание и высота параллелограмма должны быть перпендикулярны.

Чтобы найти периметр параллелограмма, сложите все его стороны. Следующая формула дает периметр любого параллелограмма:
Периметр = 2 (a + b)
Площадь перпендикуляра с высотой 5 см и основанием 4 см будет;
А = b × ч
Или, A = 4 × 5 = 20 см кв.
блог область параллелограмм площадь параллелограмма
Как найти площадь параллелограмма
, опубликованная на по математике с мамой
Как найти область параллелограммыПример Videooquestionslessless
Share At Google Classroom
.
- Площадь прямоугольника равна длине × ширине, что также может быть записано как основание × высота.
- Параллелограмм — это просто переставленный прямоугольник.
- Мы можем видеть, что, взяв треугольник из одной стороны прямоугольника и переместив его на другую сторону, мы получим параллелограмм.

- Площадь осталась прежней, поэтому площадь параллелограмма равна основанию × высоте.
- Основание — это расстояние по основанию параллелограмма.
- Высота — это расстояние по вертикали непосредственно от основания до вершины параллелограмма.
- Размеры высоты и основания должны быть под прямым углом друг к другу.
- Технически мы говорим, что площадь параллелограмма равна основанию × перпендикулярной высоте, что означает, что высота и основание находятся под прямым углом друг к другу.
Площадь параллелограмма равна основанию × перпендикулярной высоте.
- Площадь параллелограмма равна основанию × высоте.
- Основание – это расстояние по низу, равное 11 см.
- Высота — это расстояние от низа до верха параллелограмма, равное 6 см.
- Площадь 11 см × 6 см = 66 см 2 .
- Единицами площади являются см 2 , потому что мы умножили см на см.
Площадь параллелограмма Рабочие листы и ответы
Как найти площадь параллелограмма
Чтобы найти площадь параллелограмма, умножьте его основание на высоту.
 Основание — это длина одной стороны, а высота — прямое расстояние между основанием и стороной, противоположной ей. Основание и высота должны быть под прямым углом друг к другу. г.
Основание — это длина одной стороны, а высота — прямое расстояние между основанием и стороной, противоположной ей. Основание и высота должны быть под прямым углом друг к другу. г.Площадь параллелограмма вычисляется путем умножения основания на перпендикулярную ему высоту. Перпендикулярная высота говорит нам, что основание и высота должны быть под прямым углом друг к другу.
Вот пример вычисления площади параллелограмма.
Площадь параллелограмма равна основанию на высоту. Основание и высота выбраны как две длины, которые находятся под прямым углом друг к другу.
Основанием параллелограмма является длина внешней стороны, которая проходит по основанию. Здесь основание равно 11 см.
Высота параллелограмма — это длина между основанием и стороной, противоположной основанию. Высота этого экземпляра 6 см.
Площадь 11 см х 6 см = 66 см 2 .
Площадь всегда записывается в единицах, возведенных в квадрат.
 Так как длина основания и высота были измерены в сантиметрах, площадь измеряется в сантиметрах в квадрате, см 2 .
Так как длина основания и высота были измерены в сантиметрах, площадь измеряется в сантиметрах в квадрате, см 2 .Вот еще один пример нахождения площади параллелограмма, основание которого не лежит на основании параллелограмма.
Мы не знаем длину самой нижней стороны этой фигуры.
Основание выбирается по известной длине внешней стороны. Основание в этом примере равно 10 см. Мы выбираем его, даже если он не находится в нижней части параллелограмма.
Тогда высота представляет собой длину между этой стороной основания и стороной, противоположной основанию. Высота 8 см.
Площадь параллелограмма равна основанию на высоту.
Площадь 10 см х 8 см = 80 см 2 .
Если параллелограмм лежит на боку, мы можем представить, что он вращается, чтобы увидеть, каково будет его основание.
Теперь нам легче увидеть основание и высоту.
Какая формула площади параллелограмма?
Формула площади параллелограмма: A = b x h, где b — длина основания, а h — высота перпендикуляра.
 Эту формулу можно записать проще как A = bh.
Эту формулу можно записать проще как A = bh. Вот пример использования формулы площади параллелограмма.
Основание 5 м, высота 8 м.
А = б х ч.
b = 5 и h = 8, поэтому A = 5 x 8 = 40.
Следовательно, площадь этого параллелограмма равна 40 м 2 . Поскольку мы измеряли стороны в метрах, площадь измеряется в метрах в квадрате.
Вот еще один пример использования формулы для нахождения площади параллелограмма.
Основание 3 мм. Высота перпендикуляра к этому основанию равна 7 мм. Расстояние от основания до вершины параллелограмма равно 7 мм.
А = чч. Это означает, что мы умножаем b и h вместе.
А = 3 мм x 7 мм = 21 мм 2 .
Это означает, что площадь этого параллелограмма равна 21 мм 2 .
Почему площадь основания параллелограмма равна высоте?
Площадь параллелограмма равна основанию, умноженному на высоту, потому что его можно перестроить в прямоугольник той же площади.
 Прямоугольник — это особый вид параллелограмма. Площадь прямоугольника равна основанию, умноженному на высоту, поэтому площадь параллелограмма также равна основанию, умноженному на высоту. г.
Прямоугольник — это особый вид параллелограмма. Площадь прямоугольника равна основанию, умноженному на высоту, поэтому площадь параллелограмма также равна основанию, умноженному на высоту. г.Площадь прямоугольника находится путем умножения основания на его высоту.
Каждый параллелограмм можно переставить так, чтобы получился прямоугольник. Начнем с перемещения этого отмеченного треугольника на правую сторону.
Теперь у нас есть прямоугольник.
Площадь прямоугольника записывается как длина х ширина или основание х высота.
Следовательно, площадь параллелограмма также равна основанию на высоту.
Важно отметить, что основание и высота прямоугольника пересекаются под прямым углом, поэтому основание и высота параллелограмма также должны пересекаться под прямым углом, чтобы использовать формулу площади параллелограмма.
Прямоугольник Тип параллелограмма
Прямоугольник — это тип параллелограмма, который имеет четыре прямых угла.
 Параллелограмм – это фигура с четырьмя сторонами и двумя парами параллельных сторон. Прямоугольник соответствует этому определению, поэтому он также является типом параллелограмма.
Параллелограмм – это фигура с четырьмя сторонами и двумя парами параллельных сторон. Прямоугольник соответствует этому определению, поэтому он также является типом параллелограмма. Параллелограмм — это тип четырехугольника, что означает, что он имеет четыре стороны.
Параллелограмм называется параллелограммом, потому что у него две пары параллельных сторон.
Прямоугольник — это особый тип параллелограмма, потому что он имеет четыре стороны и две пары параллельных сторон.
Теперь попробуйте наш урок на Площадь составной фигуры , где мы учимся находить площадь внутри фигуры, состоящей из более чем одного прямоугольника.
Видео-вопрос: нахождение площади параллелограмма с помощью тригонометрической формулы площади треугольников
𝐴𝐵𝐶𝐷 — параллелограмм, где 𝐴𝐵 = 41 см, 𝐵𝐶 = 27 см и 𝑚∠𝐵 = 159°. Найдите площадь 𝐴𝐵𝐶𝐷, давая ответ с точностью до ближайшего квадратного сантиметра.

Video Transcript
𝐴𝐵𝐶𝐷 — параллелограмм, где 𝐴𝐵 равно 41 сантиметру, 𝐵𝐶 равно 27 сантиметрам, а мера угла 𝐵 составляет 159 градусов. Найдите площадь 𝐴𝐵𝐶𝐷, давая ответ с точностью до ближайшего квадратного сантиметра.
Начнем с наброска этого параллелограмм. Нам дана мера одного угол, угол 𝐵, который равен 159 градусам. И нам даны длины две стороны параллелограмма, заключающие этот угол. Итак, эта часть параллелограмма будет выглядеть так. Конечно, две другие стороны каждый параллелограмм параллелен одной из сторон, которые мы уже нарисовали. И они такой же длины, как их противоположная сторона. Таким образом, мы можем завершить параллелограмм.
Теперь нас просят найти площадь этого параллелограмма. Обычно мы использовали формулу основание, умноженное на перпендикулярную высоту.
 Но нам не дали
перпендикулярная высота этого параллелограмма. Мы могли бы решить это, используя
тригонометрия, но есть и другой метод, который мы можем использовать. Напомним, что диагонали
параллелограмма каждая делит параллелограмм на две конгруэнтные
треугольники. Если мы хотим, мы можем доказать это, используя
условие конгруэнтности сторона-сторона-сторона или SSS.
Но нам не дали
перпендикулярная высота этого параллелограмма. Мы могли бы решить это, используя
тригонометрия, но есть и другой метод, который мы можем использовать. Напомним, что диагонали
параллелограмма каждая делит параллелограмм на две конгруэнтные
треугольники. Если мы хотим, мы можем доказать это, используя
условие конгруэнтности сторона-сторона-сторона или SSS.В треугольниках 𝐴𝐵𝐶 и 𝐴𝐷𝐶 стороны 𝐴𝐵 и 𝐶𝐷 имеют одинаковую длину, потому что они являются противоположными сторонами в Оригинальный параллелограмм. По той же причине стороны 𝐴𝐷 и 𝐶𝐵 также имеют одинаковую длину. 𝐴𝐶 — это общая сторона двух треугольники. Итак, мы показали, что два треугольники равны по условию сторона-сторона-сторона. Так как два треугольника равны, их площади равны. И, следовательно, площадь параллелограмм в два раза больше площади каждого треугольника.

Затем мы вспоминаем тригонометрический формула площади треугольника. В треугольнике 𝐴𝐵𝐶, где прописные буквы 𝐴, 𝐵 и 𝐶 обозначают меры трех углов в треугольник и строчные буквы 𝑎, 𝑏 и 𝑐 обозначают длины трех противоположные стороны, то тригонометрическая формула площади треугольника равна половине 𝑎𝑏 грех 𝐶. Здесь 𝑎 и 𝑏 представляют длины любых двух сторон треугольника, а 𝐶 представляет собой меру их включенный угол. Это угол между двумя стороны, длину которых мы используем.
Если мы рассмотрим треугольник 𝐴𝐵𝐶 в наша фигура тогда, мы знаем длины двух сторон 𝐴𝐵 и 𝐵𝐶. Им 41 и 27 сантиметров, соответственно. И мы знаем меру их включенный угол; это 159 градусов. Таким образом, заменив 41 и 27 на две длины сторон в тригонометрической формуле и 159 градусов для меры их угол между ними, мы имеем, что площадь треугольника 𝐴𝐵𝐶 равна половине умножения на 41 умножить на 27 умножить на грех 159градусов.

D 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 . = вторая диагональ параллелограмма
y = угол между диагоналями
| Пример Вопрос: Вычислите площадь параллелограмма с длинами диагоналей 15,6 см и 17,2 см соответственно. Угол пересечения равен 120 0 . Soln: Площадь параллелограмма с диагоналями и углом пересечения = ½ x d 1 x d 2 sin(y) Следовательно, подставляя, получаем 907,6 x 1 sin5,5. (120)= ½ x 15,6 x 17,2 x \(\frac{ \sqrt{3}}{2} \) = 232,37 см 2 |
Площадь параллелограмма = ab sin(x)
, где
a = Сторона 1 параллелограмма
b = сторона 2 параллелограмма
x = угол между сторонами a и b Если угол между двумя сторонами параллелограмма равен 90 0 , а длина двух параллельных сторон равна 4 см и 3 см соответственно. Вычислите площадь параллелограмма.
Soln: Площадь параллелограмма, высота которого неизвестна = ab sin(x)
Следовательно, замена, которую мы получаем,
Площадь параллелограммы = 3 x 4 x sin (90)
= 12 sin (90)
= 12 x 1
12 см 2
2 Читайте такжеПлощадь параллелограмма в векторной форме
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Когда стороны параллелограмма представлены в векторной форме , мы можем вычислить площадь параллелограмма с помощью его диагоналей.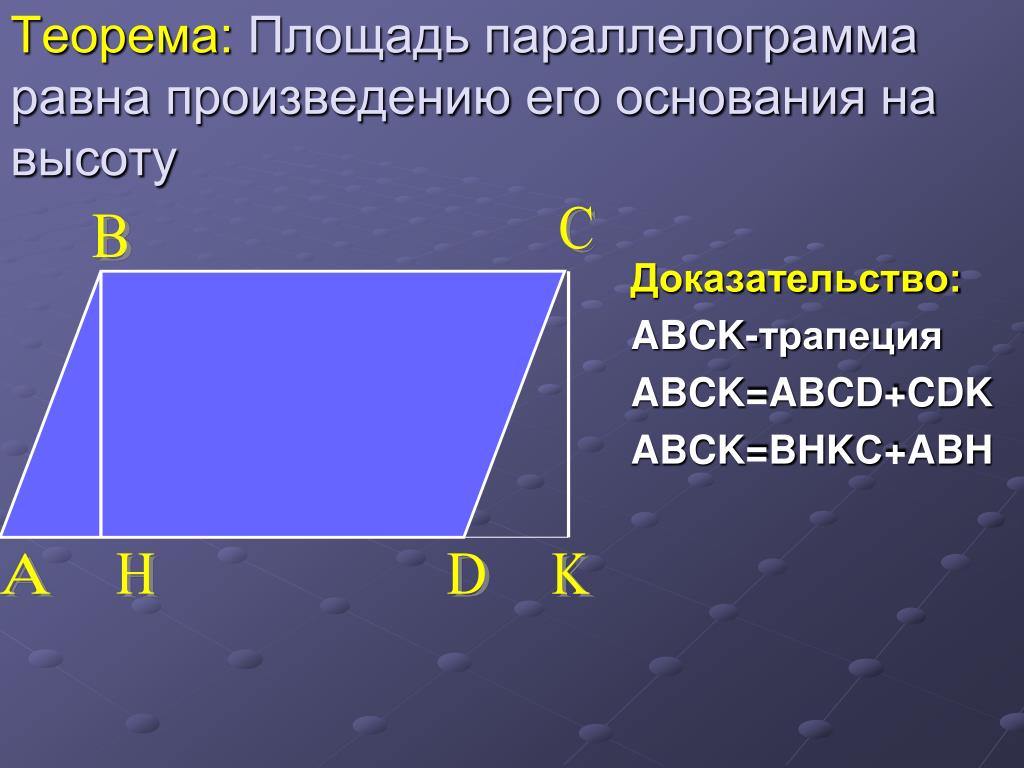 Учитывая, что есть две стороны как вектор a и вектор b параллелограмма, тогда результирующие вектор является диагональю параллелограмма.
Учитывая, что есть две стороны как вектор a и вектор b параллелограмма, тогда результирующие вектор является диагональю параллелограмма.
Площадь параллелограмма = | \(\vec{a}\times\vec{b}\)|
Чтобы найти площадь параллелограмма относительно диагоналей, предположим, что d 1 и d 2 равны в векторной форме, поэтому мы можем написать:
\(\vec{a} + \ vec{b} = \vec{d_1}\)
\(\vec{b} + (\vec{-a}) = \vec{d_2}\)
Или
\(\vec{b} — \vec{a} = \vec{d_2}\)
\(\Rightarrow\) \(\vec{d_1} * \vec{d_2} = (\vec{a} + \vec{b})( \vec{b} — \vec{a})\)
= \(\vec{a} * (\vec{b} — \vec{a}) + \vec{b} * (\vec{b} — \vec{a})\)
= \ (\vec{a} * \vec{b} — \vec{a} * \vec{a} + \vec{b}* \vec{b} — \vec{b} * \vec{a}\)
Так как\(\vec{a} * \vec{a} = 0\) и \(\vec{b} * \vec{b} = 0\)
\(\Rightarrow\) \(\vec {a} * \vec{b} = \vec{-b} * \vec{a}\)
Так как \(\vec{a} * \vec{b} = \vec{-b} * \vec {a}\)
\(\vec{d_1} + \vec{d_2} = \vec{a} * \vec{b} — (-(\vec{a} * \vec{b}))\ )
= \(2(\vec{a} * \vec{b})\)
Следовательно,
, когда диагонали заданы в векторной форме, площадь параллелограмма можно определить как: \(\frac{1}{2}|(\vec{d_1} * \vec{d_2})|\ ) где
\(\vec{d_1}\) и \(\vec{d_2}\) — диагонали.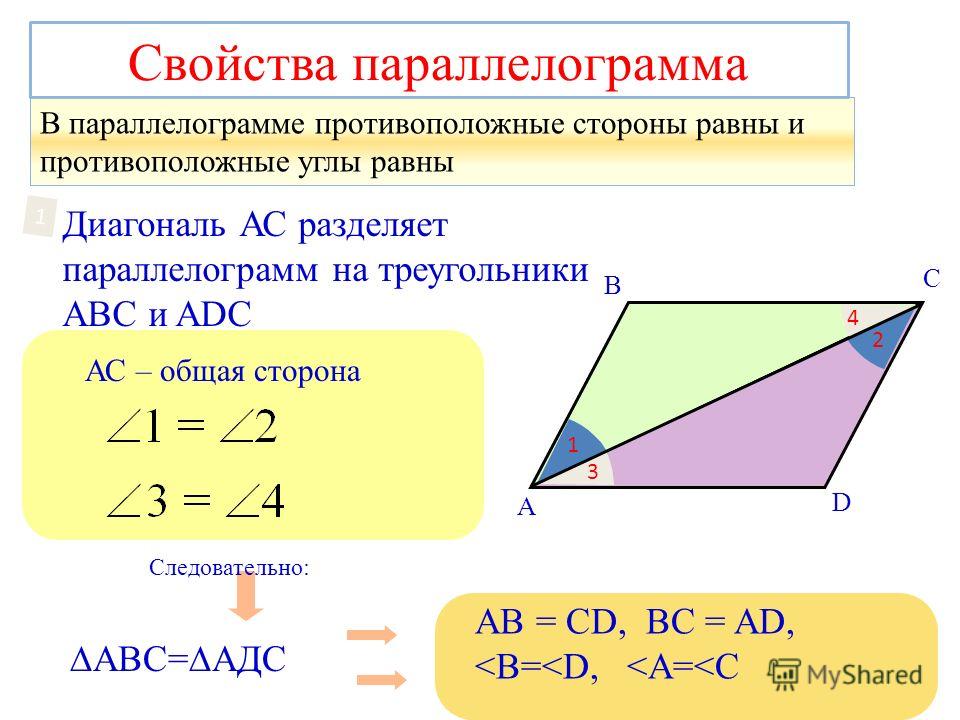
Что нужно помнить
Подробнее
Примеры вопросов
Вопросы 1. Площадь игровой площадки в форме параллелограмма равна 2500 в 2 , а одна из ее сторон равна 250 м. Найдите соответствующую высоту, используя формулу площади параллелограмма. (2 балла)
Ответ. Площадь игровой площадки = 2500 дюймов 2
Стороны игровой площадки = 250 дюймов
Соответствующая высота = 2500/250 = 10 дюймов
Следовательно, соответствующая высота параллелограмма = 10 дюймов.
Вопрос 2. Какие существуют типы параллелограмма? (2 балла)
Ответ.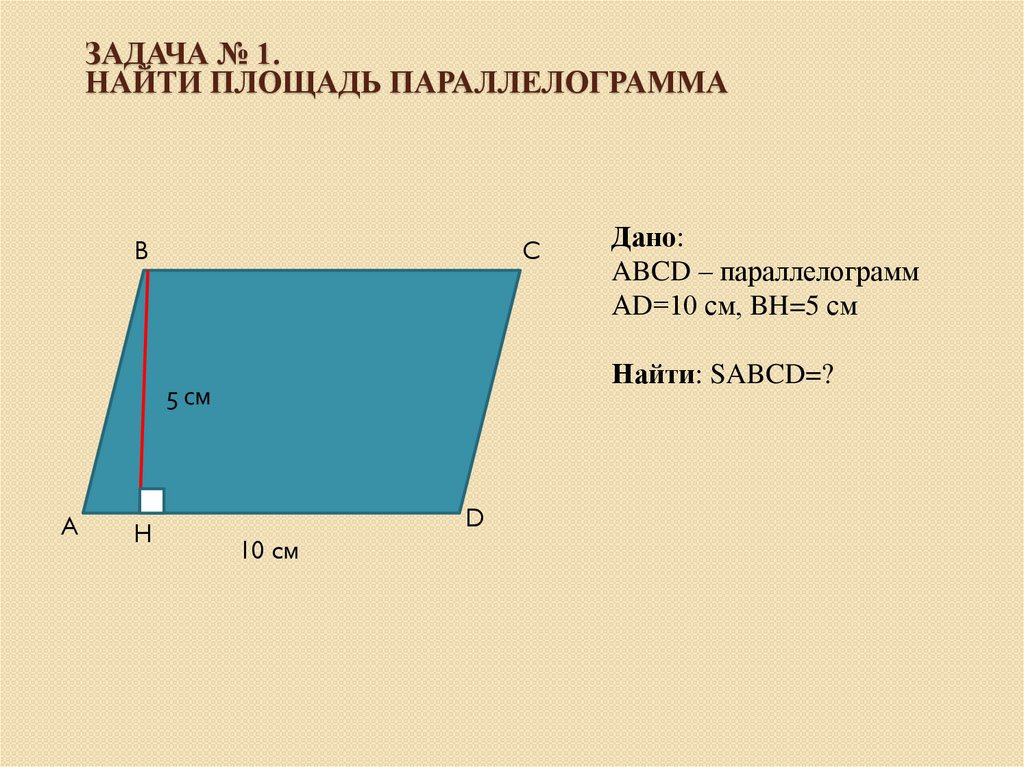 Существуют следующие типы параллелограмма:
Существуют следующие типы параллелограмма:
Вопрос 3. Какие существуют методы расчета площади параллелограмма? (3 балла)
Отв. Существует три метода вычисления площади параллелограмма. Это: 9где
h = высота параллелограмма
d 1 = первая диагональ параллелограмма
d 2 = вторая диагональ параллелограмма
y = угол между диагоналями
a = Сторона 1 параллелограмма
b = Сторона 2 параллелограмма
x = Угол между сторонами ‘a’ и ‘b’
Вопрос 4. Чему будет равна площадь параллелограмма, если его основание а высота 4см и 8см соответственно? (2 балла)
Ответ. Здесь b = 4 см и h = 8 см
Как известно,
Площадь параллелограмма = b x h
= 4 x 8
= 32 кв. см
Вопрос 5. Найдите площадь параллелограмма, если длина его смежных сторон равна 20 см и 25 см, а угол между соседними сторонами равен 34°. (3 балла)
(3 балла)
Ответ. Здесь a = 20 см, b = 25 см, x = 34°
Как известно,
Площадь параллелограмма = ab sin(x)
= 20 x 25 x sin(34°)
= 500 x 0,5591
= 279,595 кв. см
Вопрос 6. Найдите высоту и основание параллелограмма, если площадь параллелограмма 500 кв. см, а его высота в два раза больше основания. (3 балла)
Отв. Учитывая площадь параллелограмма, a = 500 кв. см
Высота, h = удвоенное основание
H = 2B
по площади формулы параллелограммы:
Область = B * H
500 = B * 2B
2B 2 = 500
B 2 = 250
B = 15.8 см
Следовательно, высота, h = 2 * b = 31,6 см
Вопрос 7. Найдите основание и высоту параллелограмма, если основание в три раза больше его высоты, а площадь равна 192 см 2 . (3 балла)
Отв. Примем высоту параллелограмма = h см
основание = 3h см
площадь параллелограмма = 192 см 2
площадь = основание * высота
Следовательно, 192 = 3h * h
\(\Rightarrow\) 9 0 9 0 6 9 011 2 2
\(\Стрелка вправо\) h 2 = 64
\(\Стрелка вправо\) h = 8 см
Поскольку высота равна 8 см, следовательно, основание = 3 * h
\(\Стрелка вправо\) 3 * 8
\(\Rightarrow\) 24 см
Вопрос 8. Найдите площадь параллелограмма, если две параллельные прямые равны 80 см и 40 см соответственно, а угол между ними равен 56 или . (3 балла)
Найдите площадь параллелограмма, если две параллельные прямые равны 80 см и 40 см соответственно, а угол между ними равен 56 или . (3 балла)
Отв. Возьмем a = 80 см
b = 40 см
Угол между a и b = 56 o .
Площадь = абс синус (\(\alpha\))
Замена,
A = 80 * 40 синус (56)
A = 3200 синус 56
A = 2652,9 кв.см.
Ques 9. Вычислите площадь параллелограмма, диагонали которого равны 18 см и 15 см, а угол пересечения диагоналей равен 43 o . (3 балла)
Ответ. Пусть D 1 = 18 см
D 2 = 15 см
\ (\ beta \) = 43 o
a = ½* D 1 * D 2 Sine \ ( \ beta \)
= ½ * 18 * 15 SINE (43 O )
= 135Sine 43 O
= 92,07 см 2
Площадь Паарллелограммы = 92,07 см 2 .
Ques 10.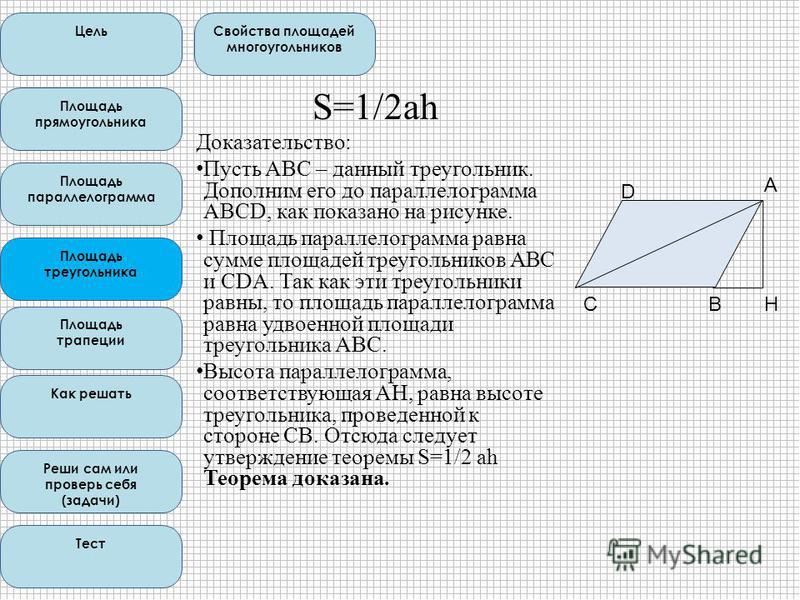 Параллелограмм с двумя параллельными сторонами 30 см и 40 см с углом между двумя сторонами 36 или . Найдите высоту параллелограмма, если его основание равно 40 см. (3 балла)
Параллелограмм с двумя параллельными сторонами 30 см и 40 см с углом между двумя сторонами 36 или . Найдите высоту параллелограмма, если его основание равно 40 см. (3 балла)
Отв. Aera = ab sine (\(\alpha\)) = bh
30 * 40 sine (36) = 40 * h
1200 sine (36) = 40 * h
Разделите обе части на 40
h = ( 1200/40) синус 36
= 30 синус 36
h = 17,63 см
Следовательно, высота параллелограмма = 17,63 см.
Прочтите также
Также проверьте
Площадь параллелограмма – объяснение и примеры
Как следует из названия, параллелограмм представляет собой четырехугольник, образованный двумя парами параллельных прямых . Он отличается от прямоугольника мерой углов при углах. У параллелограмма противоположные стороны равны по длине и противоположные углы равны по размеру, а у прямоугольника все углы равны 90 градусов.
В этой статье вы узнаете, как вычислить площадь параллелограмма, используя формулу площади параллелограмма.
Чтобы узнать, чем его площадь отличается от площади других четырехугольников и многоугольников, посетите предыдущие статьи.
Как найти площадь параллелограмма?
Площадь параллелограмма – это пространство, ограниченное двумя парами параллельных прямых. Прямоугольник и параллелограмм имеют схожие свойства, поэтому площадь параллелограмма равна площади прямоугольника.
Площадь параллелограмма Формула
Рассмотрим параллелограмм ABCD показан ниже. Площадь параллелограмма – это пространство, ограниченное сторонами AD, DC, CB, и AB.
Площадь состояний формулы параллелограмма;
Площадь параллелограмма = основание x высота
A = (b * h) кв. единицы
Где b = основание параллелограмма и,
h = высота или высота параллелограмма.
Высота или высота – это перпендикулярная линия (обычно пунктирная), проведенная из вершины параллелограмма к любому из оснований.
Пример 1
Вычислите площадь параллелограмма, основание которого равно 10 сантиметрам, а высота 8 сантиметрам.
Раствор
A = (b * h) кв. единицы.
A = (10 * 8)
A = 80 см 2
А = (b * h) кв. единицы.
= (24 * 13) квадратных дюймов.
= 312 квадратных дюймов.
Пример 3
Если основание параллелограмма в 4 раза больше его высоты, а площадь равна 676 см², найдите основание и высоту параллелограмма.
Решение
Пусть высота параллелограмма = x
и основание = 4x
Но площадь параллелограмма = b * h
676 см² = (4x * x) кв. ед.
676 = 4x 2
Разделите обе части на 4, чтобы получить
169 = x 2
Найдя квадратный корень из обеих сторон, мы получим
x = 13.
Подставим.
Основание = 4 * 13 = 52 см
Высота = 13 см.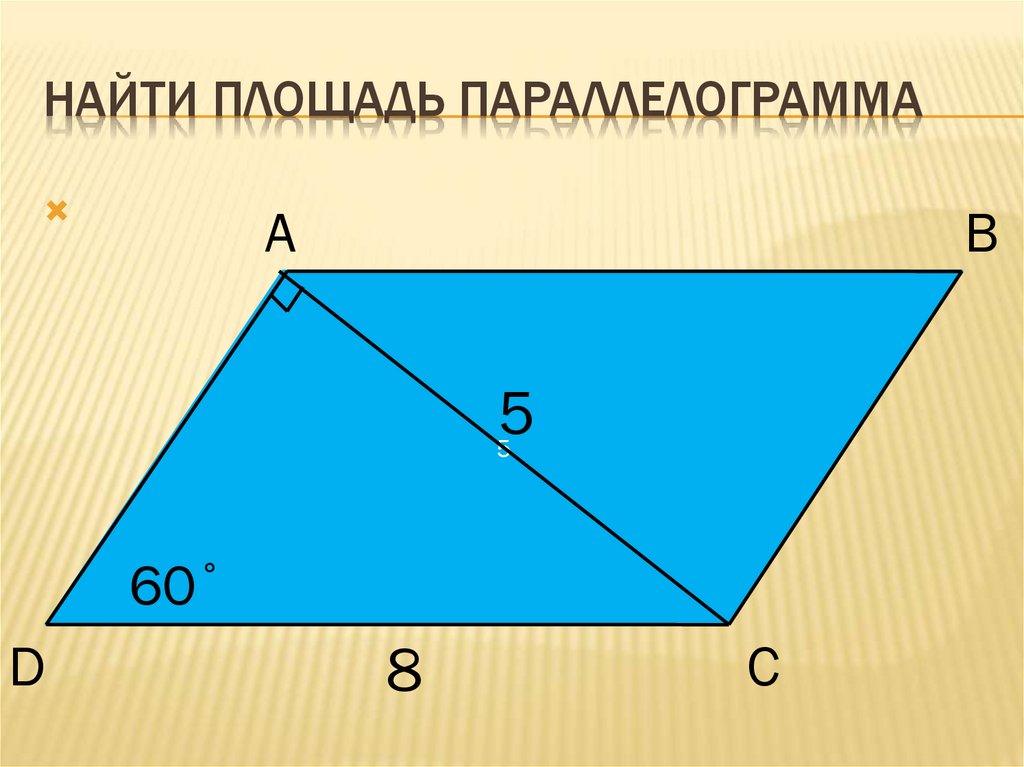
Следовательно, основание и высота параллелограмма равны 52 см и 13 см соответственно.
Помимо формулы площади параллелограмма, существуют и другие формулы для вычисления площади параллелограмма.
Давайте посмотрим.
Как найти площадь параллелограмма без высоты?
Если высота параллелограмма нам неизвестна, мы можем использовать понятие тригонометрии, чтобы найти его площадь.
Площадь = абсинус (α) = абсинус (β)
Где a и b — длины параллельных сторон, а β или α — угол между сторонами параллелограмма.
Пример 4
Найдите площадь параллелограмма, если две его параллельные стороны равны 80 см и 40 см, а угол между ними равен 56 градусов.
Решение
Пусть a = 80 см и b = 40 см.
Угол между a и b = 56 градусов.
Площадь = абсинус (α)
Замена.
A = 80 × 40 синусов (56)
A = 3200 синусов 56
A = 2652,9 кв. см.
см.
Пример 5
Вычислите углы между двумя сторонами параллелограмма, если его стороны равны 5 м и 9 м, а площадь параллелограмма равна 42,8 м 2 .
Раствор
Площадь параллелограмма = AB SINE (α)
42,8 M 2 = 9 * 5 SINE (α)
42,8 = 45 SINE (α)
Дирация оба боли на 45,
6 = 45 SINE (α).
0,95111 = SIN (α)
α = SINE -1 0,95111
α = 72 °
, но β + α = 180 °
β = 180 ° -72 °
= 108 °
- . углы между двумя параллельными сторонами параллелограмма равны; 108° и 72°.
Пример 6
Вычислите высоту параллелограмма, параллельные стороны которого равны 30 см и 40 см, а угол между этими двумя сторонами равен 36 градусам. Примите основание параллелограмма равным 40 см.
Решение
Площадь = ab синус (α) = bh
30 * 40 синус (36) = 40 * h
1200 синус (36) = 40 * h.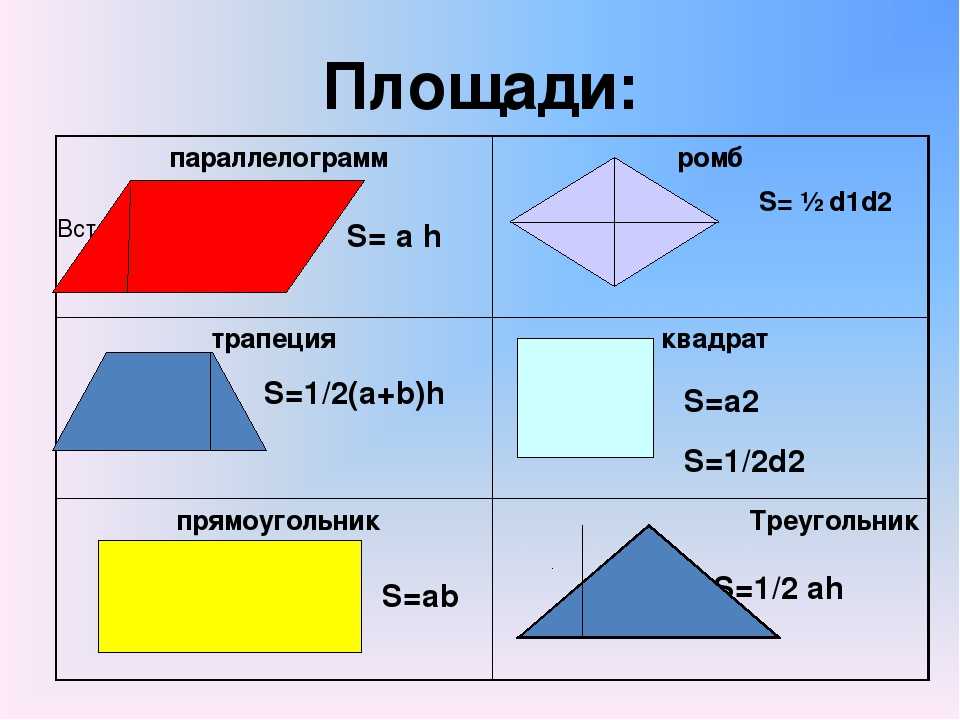
Разделить обе стороны на 40.
h = (1200/40) синус 36
= 30 синус 36
h = 17,63 см
Итак, высота параллелограмма 17,63 см.
Как найти площадь параллелограмма по диагоналям?
Предположим, что d 1 и d 2 являются диагоналями параллелограмма ABCD, тогда площадь параллелограмма определяется как β) = ½ × d 1 × d 2 синус (α)
Где β или α — угол пересечения диагоналей d 1 и д 2 .
Пример 7
Вычислите площадь параллелограмма, диагонали которого равны 18 см и 15 см, а угол пересечения диагоналей равен 43°.
Раствор
Пусть d 1 = 18 см и d 2 = 15 см.
β = 43°.
A = ½ × d 1 × d 2 синус (β)
= ½ × 18 × 15 синус (43°)
= 135sine 43°
= 92,07 см 2
Следовательно, площадь параллелограмма равна 92,07 см 2 .
Площадь параллелограмма – шаги, примеры и рабочий лист
Введение
Чему равна площадь параллелограмма?
Как найти площадь параллелограмма
Площадь рабочего листа параллелограмма
Распространенные заблуждения
Практика Область параллелограмма вопросы
Площадь параллелограмма GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Еженедельные онлайн-уроки повторения математики GCSE теперь доступны
Узнать больше
Введение
Чему равна площадь параллелограмма?
Как найти площадь параллелограмма
Площадь рабочего листа параллелограмма
Распространенные заблуждения
Практика Область параллелограмма вопросы
Площадь параллелограмма GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы научимся находить площадь параллелограмма, включая вопросы о сложной площади, вопросы с недостающими длинами сторон и вопросы, связанные с преобразованием единиц измерения. 9{2} и др.)
9{2} и др.)
Параллелограмм представляет собой четырехугольник (четырехгранный) с 2 парами параллельных сторон . Параллельные стороны равны , а противоположных углов равны . внутренних углов параллелограмма в сумме дают 360°.
Площадь параллелограмма вычисляется как умножение основания параллелограмма на его перпендикулярную высоту .
Площадь параллелограмма формула:
\[\begin{выровнено} \text {Площадь} _{\text {параллелограмм}}&=\text {база} \times \text {перпендикулярная высота} \\ \text {Площадь} _{\text {параллелограмм}}&=b \times h \end{aligned}\]
Давайте посмотрим, почему это работает:
Если мы отрежем треугольник на одном конце параллелограмма и присоединим его к другому, мы получим прямоугольник. Формула площади прямоугольника: длина х ширина (или в данном случае основание х высота).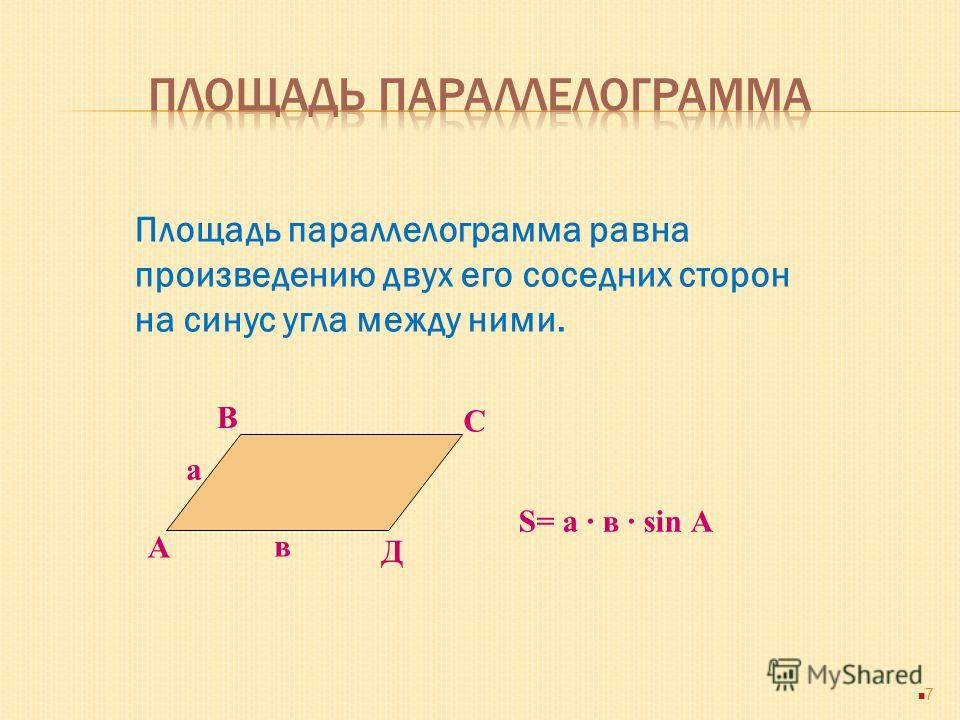
Наш окончательный ответ должен быть в единицах, возведенных в квадрат 9{2} ) и т.д.
Какова площадь параллелограмма?
Параллелограмм
Параллелограмм — это двумерная фигура, противоположные стороны которой параллельны и равны по длине. Диагонали параллелограмма делят пополам. Мы можем классифицировать их как четырехугольники, потому что у них 4 стороны.
Нам нужно определить три специальных типа параллелограммов.
Параллелограмм, у которого все стороны равны, это ромб .
Параллелограмм, у которого все углы прямые, а диагонали равны, называется прямоугольником .
Параллелограмм, у которого все стороны равны, все углы равны 90 градусов, а диагонали равны , представляет собой квадрат .
Параллелограмм, по сути, представляет собой наклонный прямоугольник, поэтому мы можем использовать те же вычисления для нахождения площади параллелограмма, что и для вычисления площади прямоугольника, если вы используете перпендикулярную высоту, а не наклонную длину.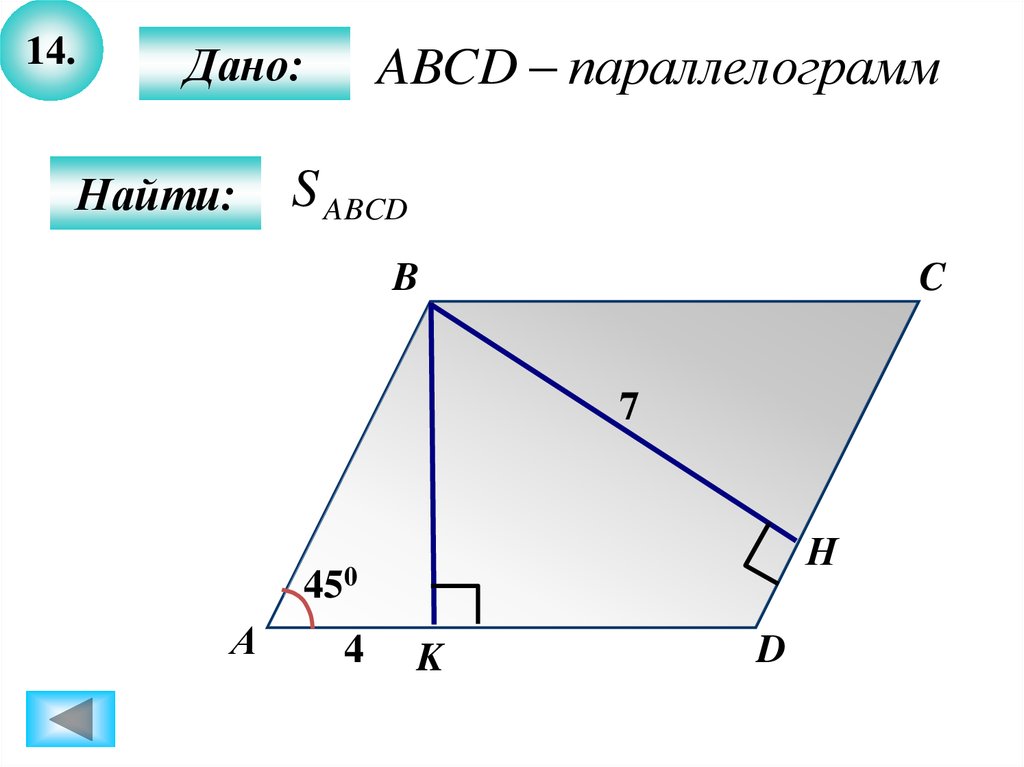
Напр.
Вычислите площадь параллелограмма.
Площадь = 10 x 6 = 60
Ниже мы рассмотрим параллелограммы подробнее.
Как найти площадь параллелограмма
Чтобы найти площадь параллелограмма:
Как найти площадь параллелограмма
Площадь листа параллелограмма
Получите бесплатно площадь листа параллелограмма из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксПлощадь рабочего листа параллелограмма
Получите бесплатную площадь рабочего листа параллелограмма из 20+ вопросов и ответов.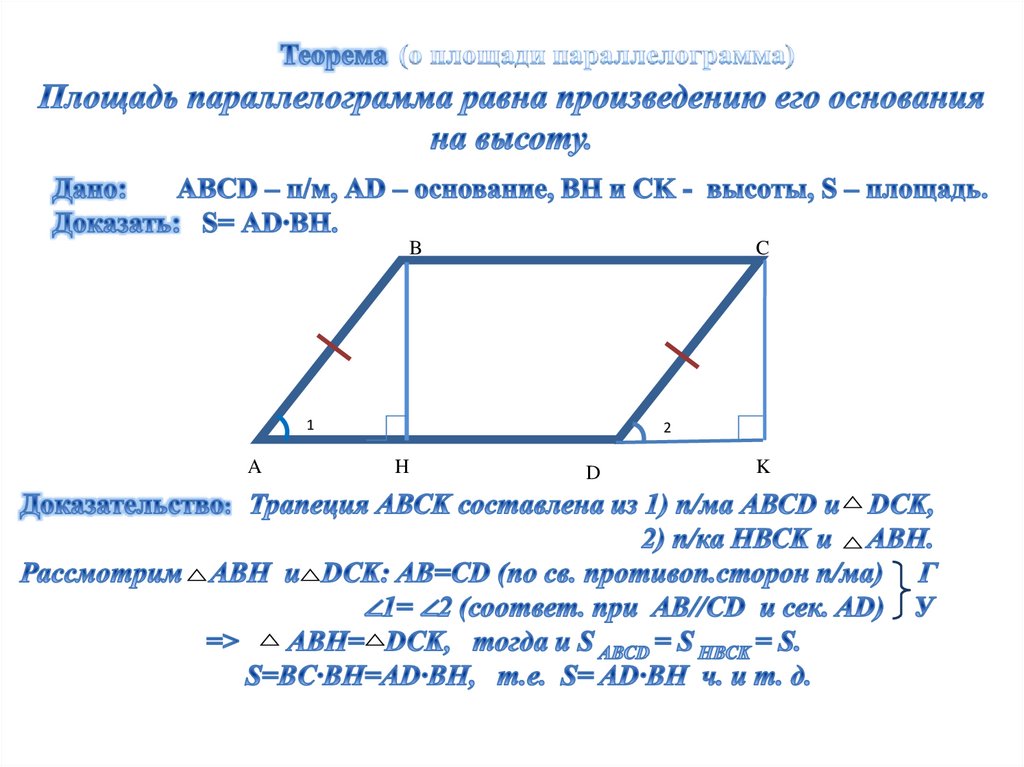 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Связанные уроки по области
Площадь параллелограмма является частью нашей серии уроков для поддержки пересмотра области . Возможно, вам будет полезно начать с основного урока, чтобы получить краткое изложение того, чего ожидать, или использовать пошаговые руководства ниже для получения более подробной информации по отдельным темам. Другие уроки этой серии включают:
Площадь параллелограмма примеры
Пример 1: нахождение площади по основанию и высоте перпендикуляра
Найдите площадь параллелограмма ниже:
Основание = 10 м
Высота перпендикуляра = 6 м
2 Запишите формулу площади параллелограмма .
\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота }
3 Подставьте данные значения и вычислите .
\[\begin{выровнено} \text {Площадь} _{\text {параллелограмм}}&=\text {Основание} \times \text {Перпендикулярная высота} \\ &=10 \умножить на 6\\ &=60 \конец{выровнено}\] 9{2}
Пример 2: нахождение площади параллелограмма, требующее преобразования единиц измерения
Найдите площадь параллелограмма ниже:
Определите высоту основания и перпендикуляра параллелограмма.
У нас есть две разные единицы измерения высоты основания и перпендикуляра, поэтому нам нужно изменить единицы измерения на общую единицу измерения.
Переведем обе меры в метры.
В метре 100 см, поэтому, если мы разделим основание на 100, получим 8 м
Основание = 8 м
Высота по перпендикуляру = 6 м
ПРИМЕЧАНИЕ: Важно отметить, что 6,3 м — это длина диагонали, а , а не — высота по перпендикуляру.
Запишите формулу площади параллелограмма.
\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота }
Подставьте данные значения и вычислите.
\ начало {выровнено} \text { Площадь }_{ \text { параллелограмм }}&=\text { Основание } \times \text { Перпендикулярная высота }\\ &=8\times6\\ &=48\ \end{выровнено} 9{2} . Сколько будет стоить нанесение логотипа?
Определите основание и перпендикулярную высоту параллелограмма .
Основание = 4 м
Высота перпендикуляра = 2 м (8\div4 параллелограмма)
Запишите формулу площади параллелограмма .
\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота }
Так как в логотипе 4 одинаковых параллелограмма, нам нужно умножить площадь на 4 . 9{2} нам нужно разделить 2,5 на 32 .
32 \дел 2,5=12,8 банок
Так как вы не можете купить 0,8 баночки, нужно округлить количество банок до 13 .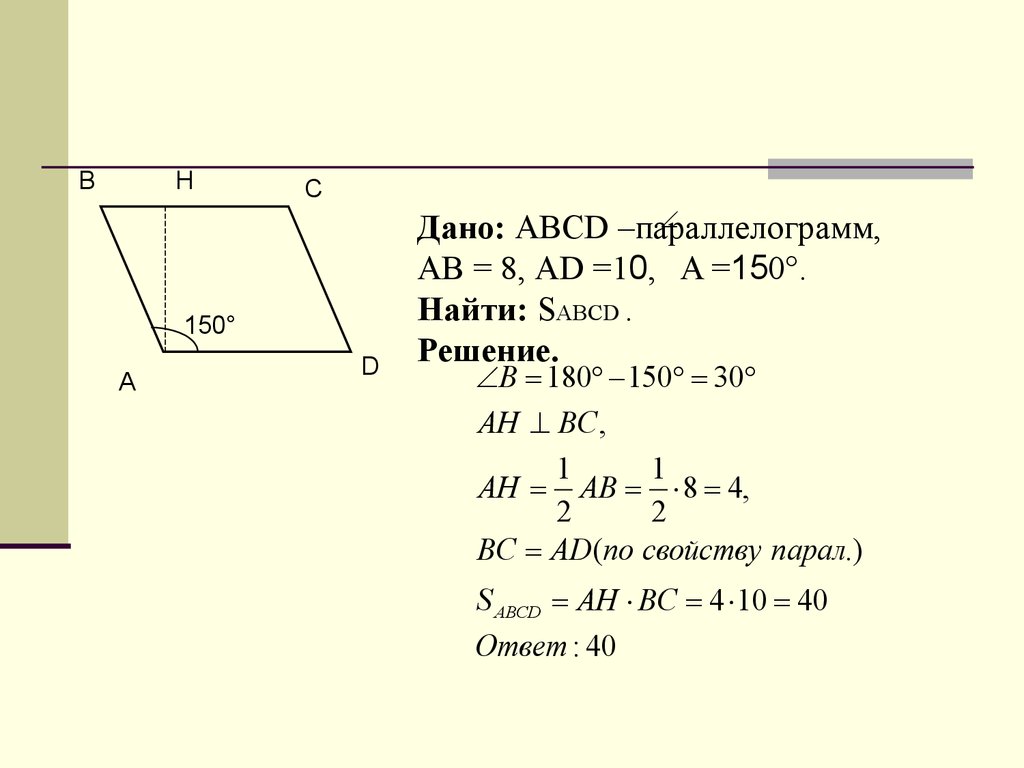
Каждая банка стоит 1,20 фунта стерлингов, поэтому 13 х 1,2 = 15,60 фунтов стерлингов
Таким образом, общая стоимость нанесения логотипа составляет 15,60 фунтов стерлингов .
Пример 4: расчет длины основания по площади
Найдите длину основания параллелограмма ниже:
Определите высоту основания и перпендикуляра параллелограмма 9{2} , который мы можем использовать для вычисления базы.
Запишите формулу площади параллелограмма .
\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота }
Подставьте данные значения и вычислите .
\[\begin{выровнено} \text { Площадь }_{ \text { параллелограмм }} &=\text { Основание } \times \text { Перпендикуляр Высота } \\ 242 &=\текст {база} \times 11 \\ \text { База } &=\frac{242}{11} \\ \текст { База } &=22 \конец{выровнено}\]
Запишите свой окончательный ответ.
Длина основания = 22 см
Пример 5: составная площадь
Вычислите площадь заштрихованной области ниже:
Определите высоту основания и перпендикуляра параллелограмма . {2}: 9{2}
{2}: 9{2}
Запишите формулу площади параллелограмма .
\text { Площадь }_{ \text { параллелограмм }}=\text { Основание } \times \text { Перпендикулярная высота }
Подставьте данные значения и вычислите .
\text {Площадь} _{\text {Параллелограмм}}=\text {Основание} \times \text {Перпендикулярная высота}
\[\begin{align} &14=2(2 х+3) \\ &14=4 х+6 \\ &4 х=8 \\ &х=2 \end{aligned}\]
Запишите свой окончательный ответ .
x=2
Распространенные заблуждения
Распространенная ошибка — забыть включить квадратные единицы измерения при вычислении площади.
Прежде чем использовать формулу для вычисления площади параллелограмма, мы должны убедиться, что используемые единицы измерения одинаковы.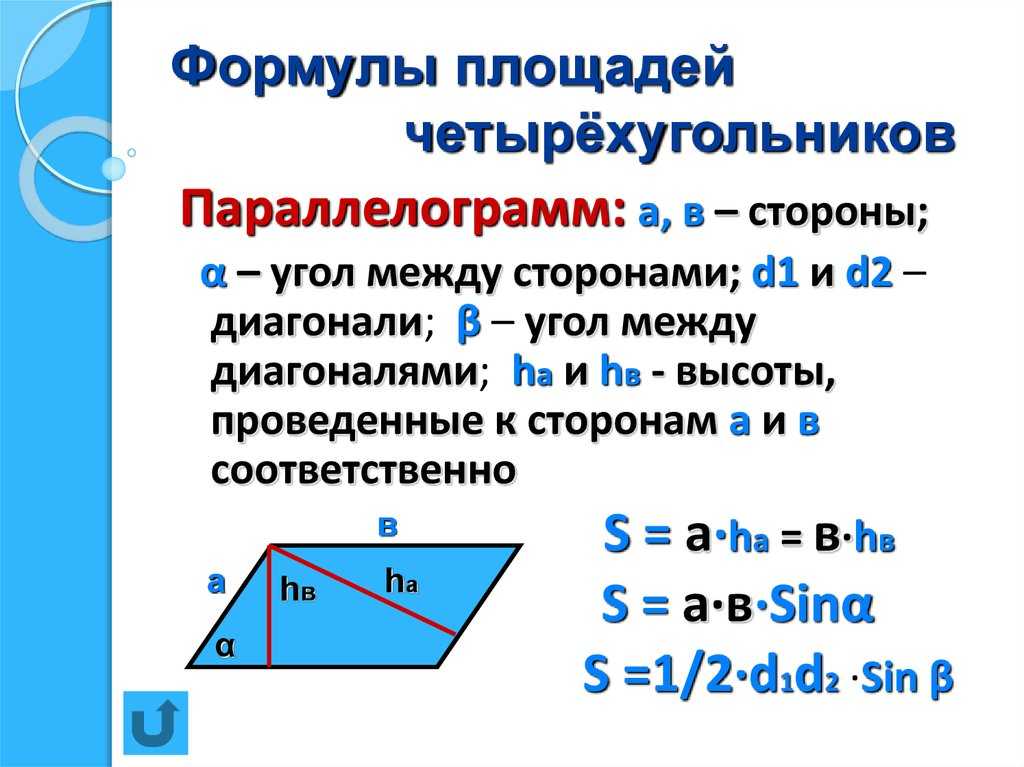 Если даны разные единицы измерения (например, длина = 4 м и ширина = 3 см), мы должны преобразовать их обе в сантиметры или обе в м. 9{2}
Если даны разные единицы измерения (например, длина = 4 м и ширина = 3 см), мы должны преобразовать их обе в сантиметры или обе в м. 9{2}
Преобразование всех мер в см. Сначала найдите площадь параллелограмма, умножив основание на высоту. Добавьте площадь прямоугольника, которая рассчитывается путем умножения длины и ширины.
Умножьте основание на высоту перпендикуляра. Не забудьте умножить два на оба члена. Измените уравнение, чтобы вычислить x . Подставьте значение x обратно в 4x-11, чтобы вычислить базовую длину.
Площадь параллелограмма GCSE вопросы 9{2}
(1)
(б)
78,25\дел3 = 26,08 рулонов травы
(1)
27\х14,5
(1)
391,50 фунтов стерлингов
(1)
3. Рассчитайте значение x на диаграмме ниже:
(4 балла)
Показ Ответ
6 \ Time (3X -9).
(1)
18х-54=36
(1)
Свидетельство перестановки уравнения для решения x
(1)
х = 5
(1)
Учебный контрольный список
Теперь вы научились:

 А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
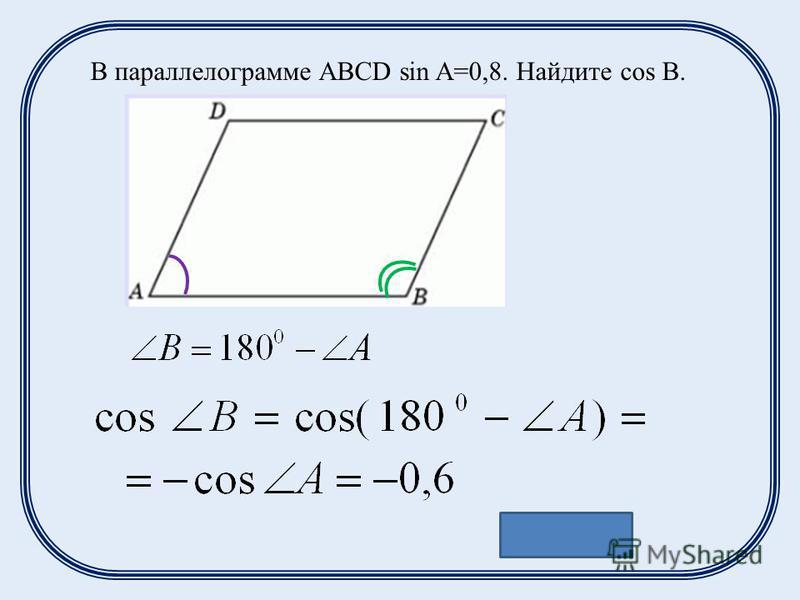
 Поэтому знания об отличительных признаках и способах вычисления различных его параметров могут пригодится в любой момент жизни.
Поэтому знания об отличительных признаках и способах вычисления различных его параметров могут пригодится в любой момент жизни.
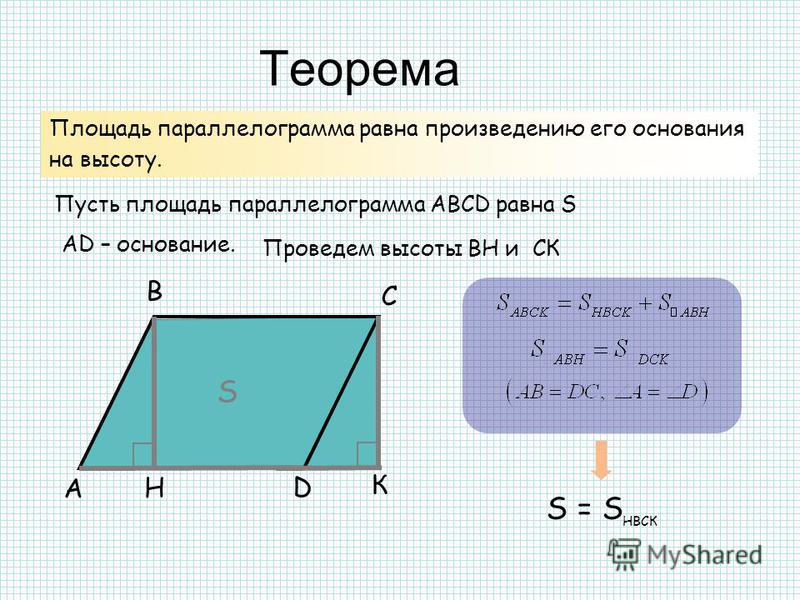
 Площадь параллелограмма – это пространство, которое он окружает.
Он рассчитывается путем умножения длины на высоту.
Все студенты могут проверить все о площади параллелограмма здесь, в этой статье. Присоединяйтесь к онлайн-школе Safalta School и подготовьтесь к экзаменам на совет директоров под руководством наших опытных преподавателей.
Наша онлайн-школа призвана помочь учащимся подготовиться к экзаменам на совет директоров, обеспечив учащимся концептуальную ясность по всем предметам и возможность набрать максимальные баллы на экзаменах.
Площадь параллелограмма – это пространство, которое он окружает.
Он рассчитывается путем умножения длины на высоту.
Все студенты могут проверить все о площади параллелограмма здесь, в этой статье. Присоединяйтесь к онлайн-школе Safalta School и подготовьтесь к экзаменам на совет директоров под руководством наших опытных преподавателей.
Наша онлайн-школа призвана помочь учащимся подготовиться к экзаменам на совет директоров, обеспечив учащимся концептуальную ясность по всем предметам и возможность набрать максимальные баллы на экзаменах. Параллелограмм — это особый тип четырехугольника с четырьмя сторонами, две из которых параллельны.
Параллелограмм — это особый тип четырехугольника с четырьмя сторонами, две из которых параллельны. Следует отметить, что основание и высота параллелограмма перпендикулярны друг другу, тогда как боковая сторона параллелограмма не перпендикулярна основанию.
Таким образом, пунктирная линия изображает высоту.
Следует отметить, что основание и высота параллелограмма перпендикулярны друг другу, тогда как боковая сторона параллелограмма не перпендикулярна основанию.
Таким образом, пунктирная линия изображает высоту. Следовательно, есть три метода получения площади параллелограмма:
Следовательно, есть три метода получения площади параллелограмма: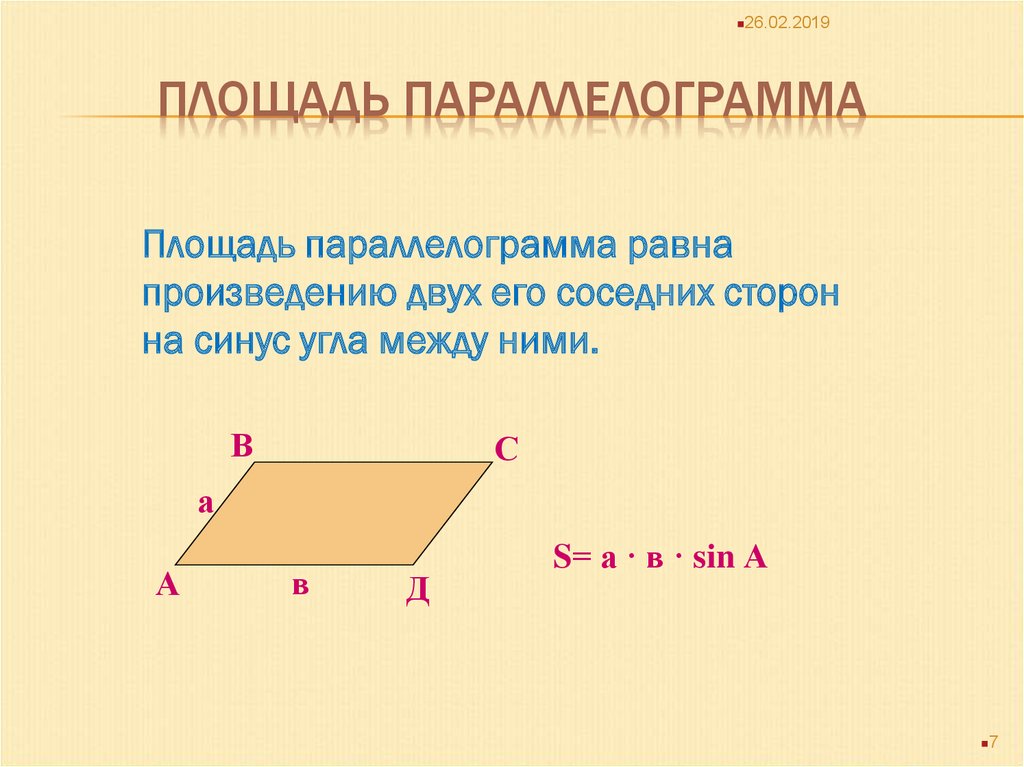
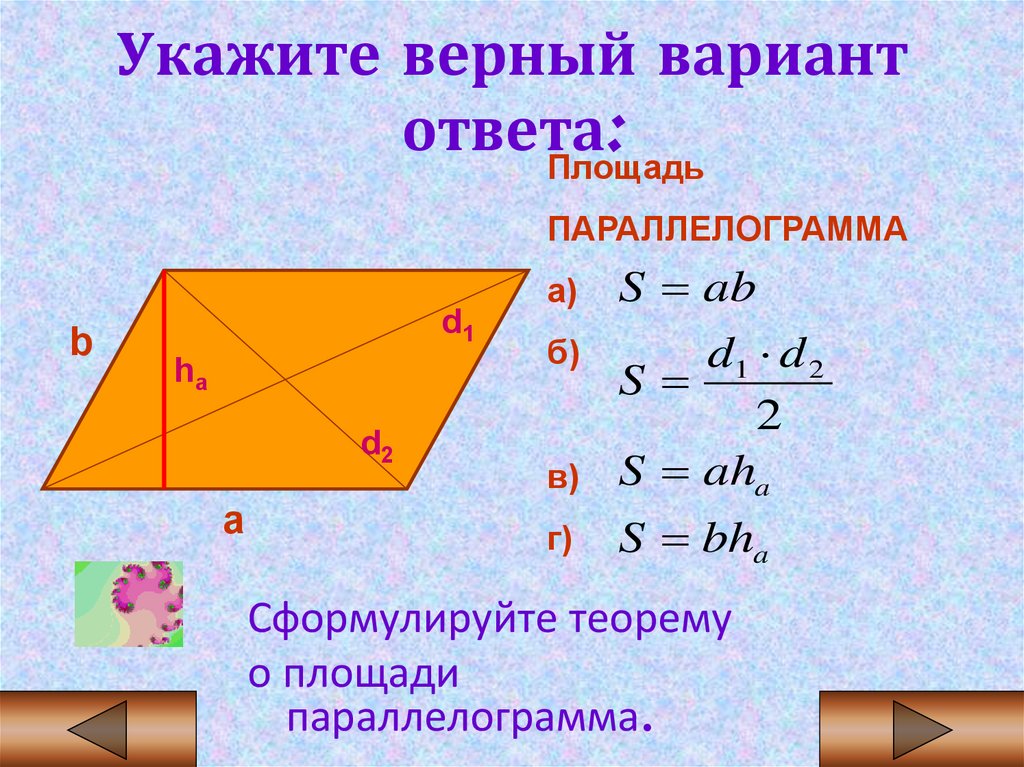 Предположим, диагонали пересекаются друг с другом под углом y, тогда площадь параллелограмма равна:
Предположим, диагонали пересекаются друг с другом под углом y, тогда площадь параллелограмма равна: com
com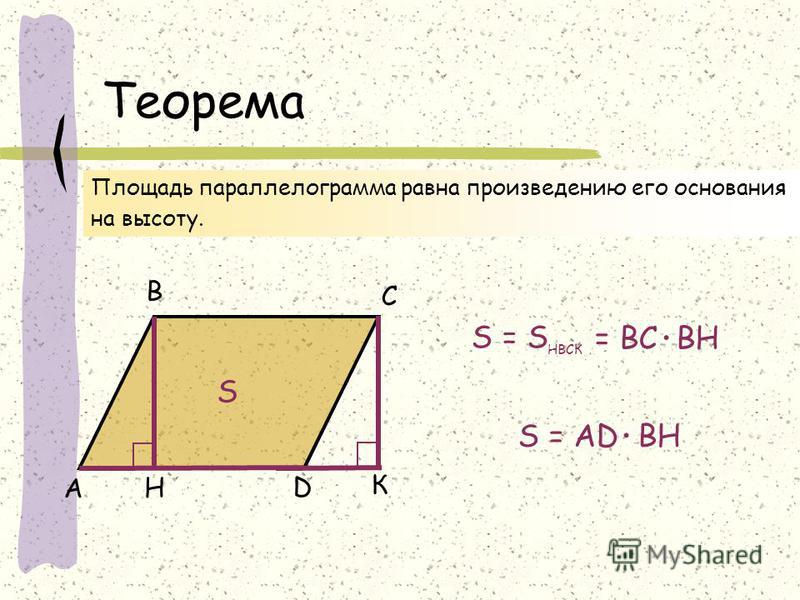

 Основание — это длина одной стороны, а высота — прямое расстояние между основанием и стороной, противоположной ей. Основание и высота должны быть под прямым углом друг к другу. г.
Основание — это длина одной стороны, а высота — прямое расстояние между основанием и стороной, противоположной ей. Основание и высота должны быть под прямым углом друг к другу. г. Так как длина основания и высота были измерены в сантиметрах, площадь измеряется в сантиметрах в квадрате, см 2 .
Так как длина основания и высота были измерены в сантиметрах, площадь измеряется в сантиметрах в квадрате, см 2 . Эту формулу можно записать проще как A = bh.
Эту формулу можно записать проще как A = bh.  Прямоугольник — это особый вид параллелограмма. Площадь прямоугольника равна основанию, умноженному на высоту, поэтому площадь параллелограмма также равна основанию, умноженному на высоту. г.
Прямоугольник — это особый вид параллелограмма. Площадь прямоугольника равна основанию, умноженному на высоту, поэтому площадь параллелограмма также равна основанию, умноженному на высоту. г. Параллелограмм – это фигура с четырьмя сторонами и двумя парами параллельных сторон. Прямоугольник соответствует этому определению, поэтому он также является типом параллелограмма.
Параллелограмм – это фигура с четырьмя сторонами и двумя парами параллельных сторон. Прямоугольник соответствует этому определению, поэтому он также является типом параллелограмма. 
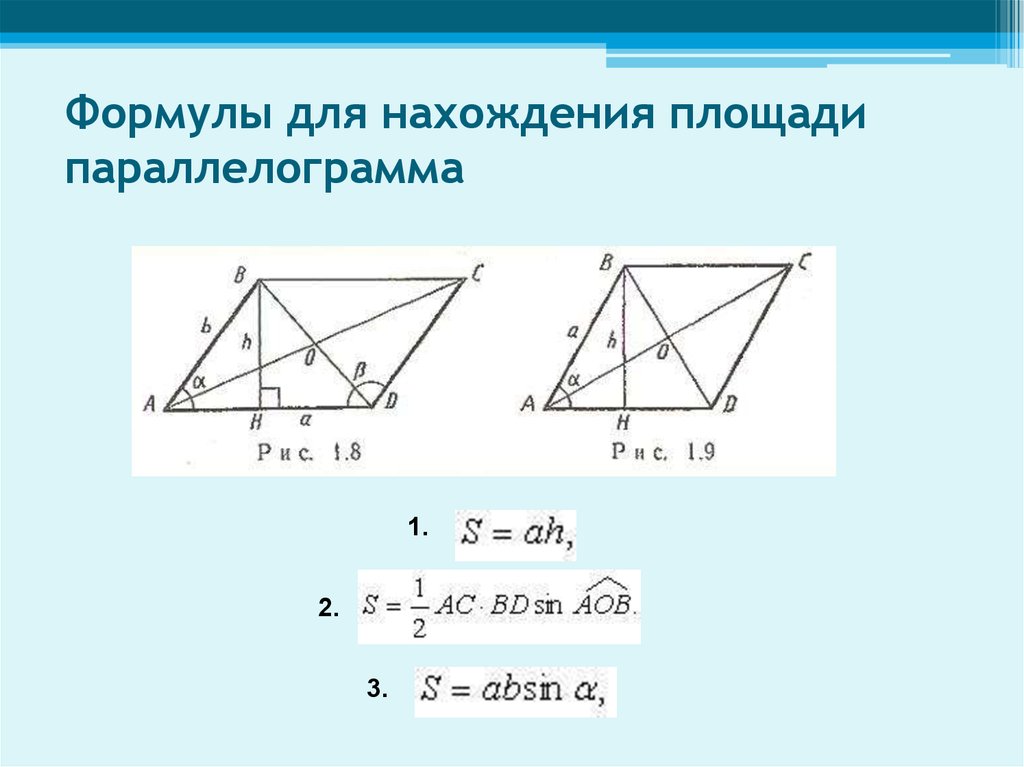 Но нам не дали
перпендикулярная высота этого параллелограмма. Мы могли бы решить это, используя
тригонометрия, но есть и другой метод, который мы можем использовать. Напомним, что диагонали
параллелограмма каждая делит параллелограмм на две конгруэнтные
треугольники. Если мы хотим, мы можем доказать это, используя
условие конгруэнтности сторона-сторона-сторона или SSS.
Но нам не дали
перпендикулярная высота этого параллелограмма. Мы могли бы решить это, используя
тригонометрия, но есть и другой метод, который мы можем использовать. Напомним, что диагонали
параллелограмма каждая делит параллелограмм на две конгруэнтные
треугольники. Если мы хотим, мы можем доказать это, используя
условие конгруэнтности сторона-сторона-сторона или SSS.