Формулы алгебраической и геометрической прогрессии: Арифметическая и геометрическая прогрессии — урок. Основной государственный экзамен (9 класс), Математика.

Произведение арифметической прогрессии. Арифметическая и геометрическая прогрессии. Связь арифметической и геометрической прогрессий.

Инструкция

Арифметическая прогрессия — это последовательность чисел вида a1, a1+d, a1+2d…, a1+(n-1)d. Число d называется шагом прогрессии .Очевидно, что общая формула произвольного n-го члена арифметической прогрессии имеет вид: An = A1+(n-1)d. Тогда зная один из членов прогрессии , первый член прогрессии и шаг прогрессии , можно определить, то есть номер члена прогресси. Очевидно, он будет определяться по формуле n = (An-A1+d)/d.

Группировка и сумма элементов

В этом разделе понятия последовательности чисел и общего термина определяются в начале. Заключительная часть посвящена реальному применению геометрических прогрессий: сложный интерес. Выведите общий термин числовой или геометрической последовательности и вычислите определенный член, известный общий термин. Признать арифметические прогрессии, получить их общий термин и найти какой-либо термин, известный первый член и разницу. Определите, является ли прогрессия геометрической или нет, найдите ее общий термин и получите любой термин, известный первому термину и причине. Найдите сумму членов убывающей геометрической прогрессии. Признайте сложный интерес как реальный случай геометрической прогрессии и решите проблемы, в которых эта концепция появляется. Признайте наличие геометрических прогрессий в реальных контекстах, таких как сложный интерес.

• Геометрические прогрессии.
• Простой интерес и сложный интерес.
• Уверенность в собственных способностях решать численные проблемы.
• Признать наличие арифметических прогрессий в реальных контекстах.

Арифметические прогрессии.

Пусть теперь известен m-ый член прогрессии и какой-то другой член прогрессии — n-ый, но n неизвестно, как и в предыдущем случае, но известно, что n и m не совпадают.Шаг прогрессии может быть вычислен по формуле: d = (An-Am)/(n-m). Тогда n = (An-Am+md)/d.

Если известна сумма нескольких элементов арифметической прогрессии , а также ее первый и последний элемент, то количество этих элементов тоже можно определить.Сумма арифметической прогрессии будет равна: S = ((A1+An)/2)n. Тогда n = 2S/(A1+An) — число чденов прогрессии . Используя тот факт, что An = A1+(n-1)d, эту формулу можно переписать в виде: n = 2S/(2A1+(n-1)d). Из этой формулы можно выразить n, решая квадратное уравнение.

Каждое из вещественных чисел называется термом последовательности. Однако не все последовательности имеют общий термин. Заметим, что каждый член последовательности такой же, как и предыдущий. Согласно определению, каждый член равен предыдущей плюс разница.

Интерполяция терминов. Интерполяционное арифметическое средство. Рассмотрим прогрессию, образованную первыми шестью кратными 5. Заметим, что сумма концов. В общем, при ограниченной арифметической прогрессии это подтверждается. При ограниченной арифметической прогрессии сумма эквидистантных членов экстремумов равна сумме экстремумов.

Арифметической последовательностью называют такой упорядоченный набор чисел, каждый член которого, кроме первого, отличается от предыдущего на одну и ту же величину. Эта постоянная величина называется разностью прогрессии или ее шагом и может быть рассчитана по известным членам арифметической прогрессии.

Инструкция

Если из условий задачи известны значения первого и второго или любой другой пары соседних членов арифметической прогрессии, для вычисления разности (d) просто отнимите от последующего члена предыдущий. Получившаяся величина может быть как положительным, так и отрицательным числом — это зависит от того, является ли прогрессия возрастающей или убывающей. В общей форме решение для произвольно взятой пары (aᵢ и aᵢ₊₁) соседних членов прогрессии запишите так: d = aᵢ₊₁ — aᵢ.

Давайте сначала рассмотрим пример. Один из способов найти сумму членов этой прогрессии состоит в том, чтобы написать сумму дважды, инвертируя термины в одну из них. Добавление двух результатов равенства. Каждый член этой последовательности равен предыдущей, умноженной на эту последовательность, является геометрической прогрессией.

Обобщение этого процесса дает общий термин. Эта проблема, состоящая из чередования нескольких терминов между двумя кубиками, называется интерполяцией. Выраженные термины называются геометрическими или пропорциональными. Обратите внимание, что в геометрической прогрессии.

Для пары членов такой прогрессии, один из которых является первым (a₁), а другой — любым другим произвольно выбранным, тоже можно составить формулу нахождения разности (d). Однако в этом случае обязательно должен быть известен порядковый номер (i) произвольного выбранного члена последовательности. Для вычисления разности сложите оба числа, а полученный результат разделите на уменьшенный на единицу порядковый номер произвольного члена. В общем виде эту формулу запишите так: d = (a₁+ aᵢ)/(i-1).

Продукт экстремальных терминов. И что произведение терминов, равноудаленных от крайностей, также. В общем, в ограниченной геометрической прогрессии он проверяется. В ограниченной геометрической прогрессии произведение терминов, равноудаленных от концов, равно произведению концов.

Умножение двух результатов равенства. Чтобы получить формулу суммы этих прогрессий, умножим на -1 числитель и знаменатель предыдущей формулы. По этой причине, чтобы найти сумму бесконечных членов убывающей геометрической прогрессии, эта формула используется. Явное применение геометрических прогрессий представляет собой сложный интерес. Давайте посмотрим на это с примером и вспомним ранее простые интересы.

Если кроме произвольного члена арифметической прогрессии с порядковым номером i известен другой ее член с порядковым номером u, измените формулу из предыдущего шага соответствующим образом. В этом случае разностью (d) прогрессии будет сумма этих двух членов, поделенная на разность их порядковых номеров: d = (aᵢ+aᵥ)/(i-v).

Формула вычисления разности (d) несколько усложнится, если в условиях задачи дано значение первого ее члена (a₁) и сумма (Sᵢ) заданного числа (i) первых членов арифметической последовательности. Для получения искомого значения разделите сумму на количество составивших ее членов, отнимите значение первого числа в последовательности, а результат удвойте. Получившуюся величину разделите на уменьшенное на единицу число членов, составивших сумму. В общем виде формулу вычисления дискриминанта запишите так: d = 2*(Sᵢ/i-a₁)/(i-1).

Отправляемся в цирк

Когда какое-либо лицо вкладывает капитал в банк в течение определенного времени, банк выплачивает проценты. В зависимости от того, периодически или периодически аннулируется интерес, интерес называется простым или сложным. До 10% через два года при простых интересах?

И сложные проценты? Давайте рассмотрим каждый случай отдельно. Вычислите член, который занимает 100-е место арифметической прогрессии, чей первый член равен 4, а разница равна. Разница двух крайностей равна 16, а сумма четвертого и тринадцатый — Рассчитать крайности. Ограниченная арифметическая прогрессия из 10 членов такова, что сумма концов равна 20, а произведение третьей и восьмой должно составлять первые 10 членов прогрессии.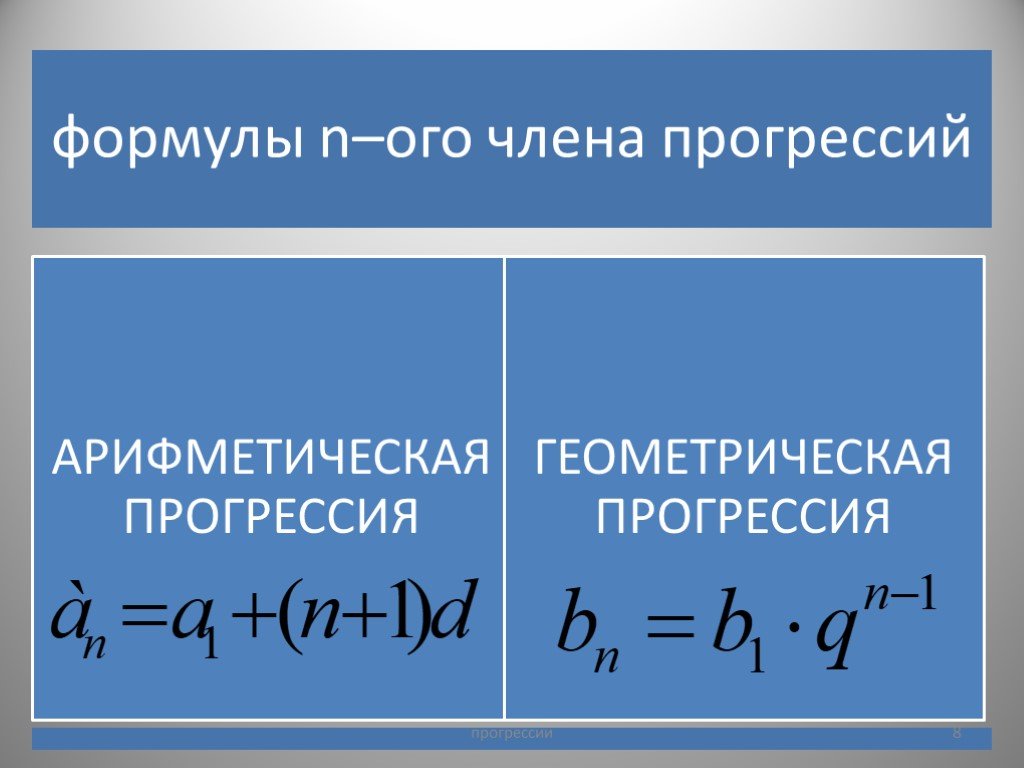 Найдите эти числа, зная, что они являются целыми числами. Вычислите три числа, зная, что они находятся в арифметической прогрессии, что их сумма равна 18 и что сумма первого и второго равна третьей, уменьшенной в двух единицах. Сумма одиннадцати первых членов арифметической прогрессии равна 176, а разница крайностей — найти члены прогрессии. Найдите четыре числа в арифметической прогрессии, шокируя их сумму, равную 22, и сумму их квадратов. Разница в арифметической прогрессии. Произведение первых четырех членов — это найти термины. Найдите первые шесть членов арифметической прогрессии, зная, что первые три складываются — 3 и последние три. В арифметической прогрессии одиннадцатый член превышает в 2 единицах до восьмого, а первый и девятый — вычисляет разницу и упомянутые термины. В арифметической прогрессии второй и третий термины складываются до 19, а пятый и седьмой члены складываются. Разница между майором и несовершеннолетним составляет 60 °. Самый старый на 6 лет старше самого молодого.

Найдите возраста четырех братьев. Лыжник начинает лыжный предсезон, делая вес в тренажерном зале в течение часа. Решите увеличить продолжительность обучения 10 минут каждый день. Сколько времени вы должны тренировать через 15 дней? Сколько времени вы потратите на обучение в течение 30-дневного месяца? В кинотеатре первый ряд сидений расходится с экрана 86 дм, а шестой — 134 дм. В каком ряду будет человек, если его расстояние от экрана составляет 230 дм? Вычислите одиннадцатый член геометрической прогрессии, первый член которой равен 1, а отношение — пятый член геометрической прогрессии — 81, а первый — вычисляет эти числа. Он определяет четыре числа в геометрической прогрессии, так что первые две суммы 0, 5 и последние два 0. Сколько членов было принято в геометрической прогрессии, зная, что первое слагаемое равно 7, последние 448 и его сумма 889? Сумма первых семи членов геометрической прогрессии разума 3: Найдите числа. Найдите первые четыре члена геометрической прогрессии, зная, что второе равно 20, а сумма первых четырех — это Халла, углы четырехугольника, если известно, что они находятся в геометрической прогрессии и что майор в 27 раз наименьший. Размеры ортоэдра находятся в геометрической прогрессии. Найдите эти цифры. Найдите четыре цифры в геометрической прогрессии, зная, что сумма первых двух равна 28 и сумма последних двух. В геометрической прогрессии первый и пятнадцатый члены равны соответственно 6 и 54. Найдите шестой термин. Геометрическая прогрессия имеет пять членов, отношение равно четвертой части первого слагаемого, а сумма первых двух членов — найти пять членов. Из длины даны два разреза, так что одна из торцевых частей имеет длину 100 м. 1 октября половина контента была опустошена; На следующий день он снова опустошил половину того, что осталось, и так каждый день. Сколько вина было принято 10 октября? Учитывая квадрат 1 м. со стороны, мы соединяем две-две середины своих сторон; Мы получаем новый квадрат, в котором мы выполняем ту же операцию, и так далее.

• Десятый член арифметической прогрессии равен 45, а разница.
• Сумма трех чисел в арифметической прогрессии равна 33 и их произведение.

Гаусс, как ребенок, делает открытие.

Арифметической прогрессией называют последовательность чисел (членов прогрессии)

В которой каждый последующий член отличается от предыдущего на сталое слагаемое, которое еще называют шагом или разницей прогрессии .

Таким образом, задавая шаг прогрессии и ее первый член можно найти любой ее элемент по формуле

Гаусс пришел из очень скромной семьи. Его отец был садовником и художником с толстой кистью. Математические навыки молодого Гаусса проявились очень скоро. Ему говорят, что однажды, в возрасте девяти лет, когда он достиг класса арифметики начальных классов, учитель попросил его и его одноклассников добавить все числа от 1 до Гаусса, чтобы подумать, И вместо того, чтобы добавлять все, один за другим, решили проблему через несколько секунд следующим образом.

То есть он обнаружил принцип формулы суммы членов арифметической прогрессии. В результате этих успехов его учителя заинтересовались им. Гаусс изучал математику и стал профессором математики в Казани, профессором астрономии и директором астрономической обсерватории в Геттингене.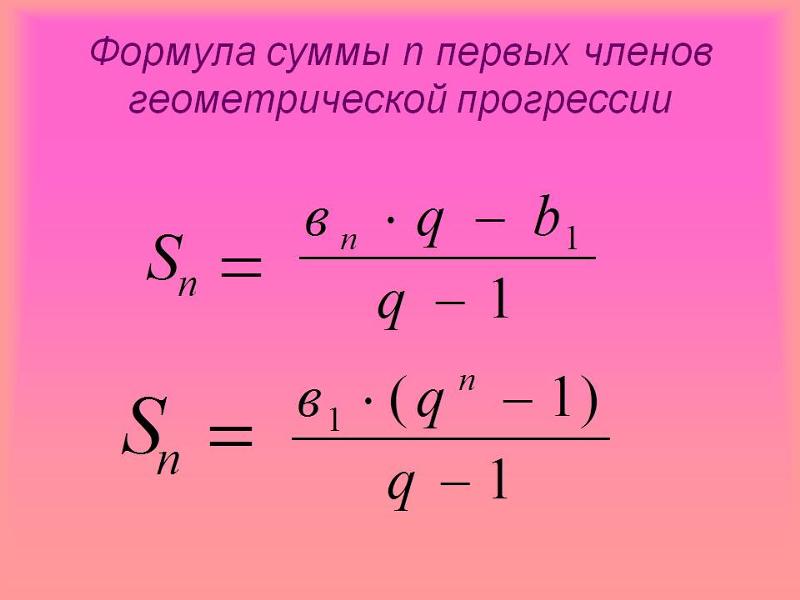

1) Каждый член арифметической прогрессии, начиная со второго номера является средним арифметическим от предыдущего и следующего члена прогрессии

Обратное утверждение также верно. Если среднее арифметическое соседних нечетных (четных) членов прогрессии равно члену, который стоит между ними, то данная последовательность чисел является арифметической прогрессией. По этим утверждением очень просто проверить любую последовательность.

Запрос изобретателя шахмат. Одна легенда гласит, что изобретатель шахмат представил свое изобретение князю Индии. Изобретатель шахмат сделал свой запрос следующим образом. «Я хочу, чтобы ты дал мне зерно пшеницы на первый квадрат на доске, два на второй, четыре на третий, восемь на четвертый, шестнадцать на пятый и т.д. до коробки 64».

Неожиданностью стало то, что секретарь князя подсчитал количество пшеницы, представленное просьбой изобретателя, потому что вся посевная пшеница была недостаточной для получения пшеницы, которую просил изобретатель.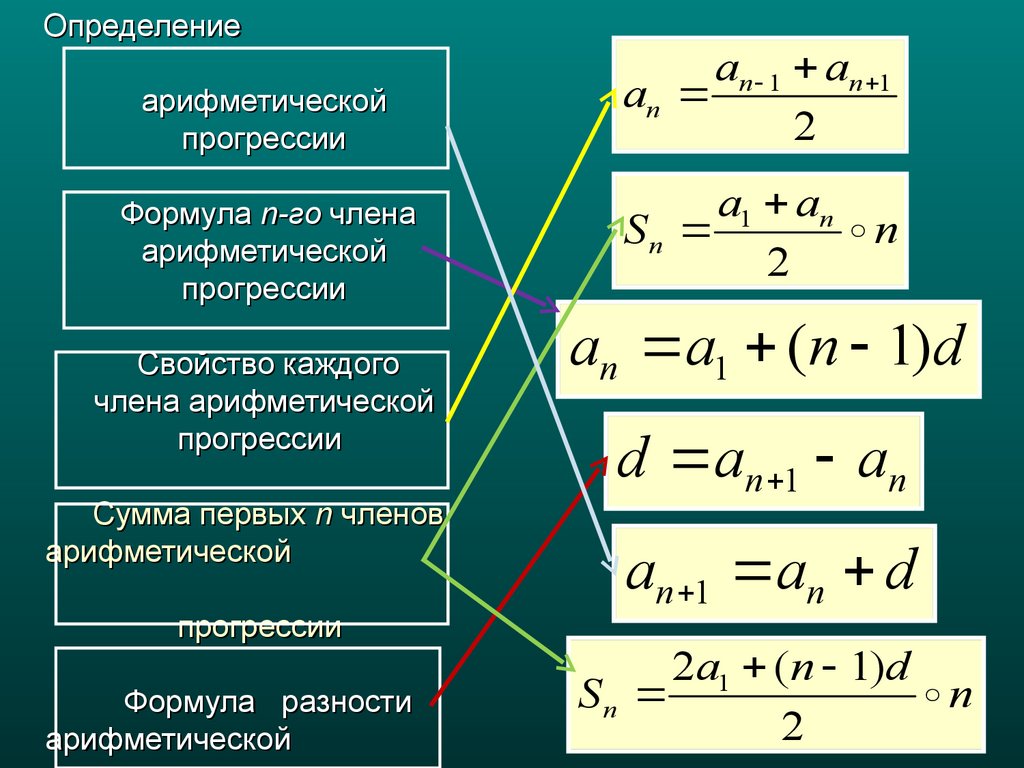 Сколько триллионов пшеницы он просил?

Также по свойству арифметической прогрессии, приведенную выше формулу можно обобщить до следующей

В этом легко убедиться, если расписать слагаемые справа от знака равенства

Ее часто применяют на практике для упрощения вычислений в задачах.

2) Сумма n первых членов арифметической прогрессии вычисляется по формуле

Запомните хорошо формулу суммы арифметической прогрессии, она незаменима при вычислениях и довольно часто встречается в простых жизненных ситуациях.

Используйте калькулятор, чтобы найти общее количество зерен пшеницы. Редакция Сантильяна. . Цель состоит в том, чтобы найти формулу, которая позволяет вычислить сумму первых членов арифметической прогрессии, не вычисляя их. Сумма первых шести терминов — это площадь, ограниченная красным многоугольником, который по конструкции совпадает с площадью белого полигона, и оба они составляют половину площади всего прямоугольника.

Факт получения прямоугольника отражает нам важное свойство арифметических прогрессий. Отмечается, что основание прямоугольника имеет в качестве своей длины сумму первого и шестого членов, совпадающих с суммой пятой и второй, и с суммой третьего и четвертого; И эти три пары терминов равноудалены от первого и шестого концов.

3) Если нужно найти не всю сумму, а часть последовательности начиная с k -го ее члена, то в Вам пригодится следующая формула суммы

4) Практический интерес представляет отыскание суммы n членов арифметической прогрессии начиная с k -го номера. Для этого используйте формулу

На этом теоретический материал заканчивается и переходим к решению распространенных на практике задач.

Таким образом, площадь прямоугольника равна. Таким образом, сумма первых шести условий. Мы хотим рассчитать сумму первых тысяч натуральных чисел, кратных пяти. Внизу мы напишем, какую переменную мы добавляем и из какого термина, в то время как наверху мы напишем последний добавляемый термин.

Ранее мы писали. Также добавьте термины справа от знака =. Указанная сумма слева от знака = представляет собой сумму всех членов, кроме первой. То, что у вас есть в круглой скобке справа от знака =, является суммой всех членов, кроме последней. Вышеуказанная сумма может быть написана. Сумма членов геометрической прогрессии равна последнему члену соотношением минус первое, деленное на отношение меньше.

Пример 1. Найти сороковой член арифметической прогрессии 4;7;…

Решение:

Согласно условию имеем

Определим шаг прогрессии

По известной формуле находим сороковой член прогрессии

Пример2. Арифметическая прогрессия задана третьим и седьмым ее членом . Найти первый член прогрессии и сумму десяти.

Решение:

Распишем заданные элементы прогрессии по формулам

Иногда лучше использовать формулу сложения в функции первого термина и причины. Для этого в формуле добавления замените значение. Чтобы рассчитать отношение, мы делим значение члена на один из предыдущих. Прогресс со всеми семью условиями будет. Сумма всех этих условий.

Примеры заданий на сумму арифметической прогрессии

Решение: Мы знаем значение суммы, отношение и первый член, применяя формулу сложения и подставляя ее значения. Знаменатель 2 будет передаваться путем умножения на другую сторону знака =. Мы остаемся в качестве последнего равенства. Если формула: мы изменим порядок, в котором мы разместили значения числителя, а знаменатель не изменит результат. Такое же, как.

От второго уравнения вычтем первое, в результате найдем шаг прогрессии

Найденное значение подставляем в любое из уравнений для отыскания первого члена арифметической прогрессии

Вычисляем сумму первых десяти членов прогрессии

Не применяя сложных вычислений ми нашли все искомые величины.

Пример 3. Арифметическую прогрессию задано знаменателем и одним из ее членов . Найти первый член прогрессии, сумму 50 ее членов начиная с 50 и сумму 100 первых.

Алгебраическая прогрессия: формулы и примеры решений

В данной статье будет рассмотрена алгебраическая прогрессия, формулы, необходимые для решения задач с ее участием, а также некоторые примеры их использования. Для полноты информации кратко будет сказано о другом виде прогрессии — геометрической.

Понятие об алгебраической прогрессии

Всякий ряд чисел, который упорядочен согласно некоторому закону, может называться прогрессией. Наиболее популярными и применяемыми для решения практических задач являются два вида таких рядов: алгебраическая и геометрическая прогрессия. Рассмотрим подробнее первую из них.

Алгебраическую чаще называют арифметической прогрессией. Математически она означает следующее:

an = an-1 + d

То есть речь идет о такой числовой последовательности, в которой любой ее член отличается от предыдущего или последующего на одинаковое число d. Это число носит название разности (его можно определить, найдя разность двух соседних элементов прогрессии).

Согласно такому определению, рассматриваемая прогрессия имеет начало, но не имеет конца. Начинается она всегда с члена a1 (любое действительное число), а затем продолжается путем суммирования этого члена с разностью d. Соответственно, она может быть бесконечно возрастающей (d > 0) или убывающей (d

Формула для нахождения произвольного члена

Как было пояснено выше, рассматриваемый вид прогрессии однозначно определяется ее первым элементом и разностью, однако это правило распространяется на любые другие величины. Например, знание двух произвольных элементов или одного элемента и суммы некоторого числа членов также однозначно определяет прогрессию.

Для вычисления n-го элемента можно с успехом пользоваться следующей формулой:

an = a1 + (n — 1) * d

Очевидность справедливости этого выражения не вызывает сомнения, и его может проверить каждый, подставляя малые значения n.

Формула для восстановления прогрессии по двум известным элементам

В школьном курсе алгебры такие задачи являются типичными на прогрессию: известно два элемента an и am, причем n > m, необходимо на них построить всю прогрессию.

Решается эта проблема с использованием формулы для n-го члена. Выпишем два соответствующих выражения:

an = a1 + (n — 1) * d;am = a1 + (m — 1) * d

Найдем разность между первым и вторым (знак равенства при этом сохраняется):

an — am = (n — m) * d =>d = (an — am) / (n — m)

Мы видим, как легко можно найти разность прогрессии, если известны два ее члена: для этого необходимо из большего по порядку вычесть меньшее, а затем полученную разность поделить на разность их порядковых номеров.

Как только найдена разность, вычислить первый член не представит никакого труда (для этого следует воспользоваться любым из двух первых выражений).

Сумма прогрессии алгебраической

Еще одной серией типичных задач на прогрессию является нахождение суммы их членов. Ниже приводится соответствующая формула суммы прогрессии алгебраической:

Sn = ∑i=1n (ai) = n * (a1 + an) / 2

То есть для определения суммы первых слагаемых n следует вычислить сумму всего двух из них (первого и n-ного), умножить ее на количество членов n и поделить результат пополам.

Математическое доказательство этого выражения мы опустим, однако логическое доказательство все же приведем. Можно заметить, что ввиду свойства рассматриваемого типа прогрессии всегда выполняется следующее равенство:

a1 + an = a2 + an-1

Действительно, второй член больше первого на d, но на столько же предпоследний (an-1) меньше последнего (an). В случае парного числа элементов мы получаем ровно половину таких сумм от всего числа элементов (n / 2), откуда и следует приведенная формула для Sn.

Принято считать, что отмеченную особенность арифметической прогрессии впервые установил Карл Гаусс, известный математик конца XVIII — первой половины XIX века, когда он в уме за несколько секунд посчитал сумму натуральных чисел от единицы до 100.

Примеры решения задач

Рассмотрим два примера алгебраической прогрессии.

1. Известно, что 9-й член равен 7, а 21-й равен 51. Необходимо найти первые 5 членов этой арифметической прогрессии.

Условие задачи позволяет сразу же рассчитать разность d, применяя формулу с an и am, которая записана выше. Имеем:

d = (an — am) / (n — m) = (51 — 7) / (21 — 9) = 3,667

При получении разности d мы выполнили округление до 3 знака после запятой.

Теперь можно рассчитать первый элемент ряда. Для этого воспользуемся данными для 9 члена:

a9 = a1 + d * 8 => a1 = a9 — d * 8 = 7 — 3,667 * 8 = -22,336

Для решения задачи осталось сделать последний шаг: последовательно добавить 4 раза величину d к первому элементу. Получаем:

a1 = -22,336;a2 = -22,336 + 3,667 = -18,669;a3 = -18,669 + 3,667 = -15,002;a4 = -15,002 + 3,667 = -11,335;a5 = -11,335 + 3,667 = -7,668

Напомним, что все рассчитанные значения справедливы до третьего знака после запятой.

2. Рабочие складывали спиленные стволы деревьев в виде пирамиды. Известно, что они сложили всего 33 бревна, причем до завершения пирамиды им не хватило всего 3 бревна. Следует определить, сколько рядов бревен сложили рабочие.

Ответ на этот вопрос заключается в решении алгебраической прогрессии, но для того, чтобы к нему приступать, необходимо внимательно разобраться с данным условием.

Во-первых, поскольку бревна складываются в пирамиду, значит, в каждом предыдущем ряду было на одно бревно больше, то есть d = 1. Во-вторых, если известно, что не хватило до завершения пирамиды всего 3 бревна, тогда два верхних ряда остались пустыми:

a1 = 1, a2 = a1 + d = 2, a1 + a2 = 3

Учтем эти три бревна, добавив их к 33 уже сложенным, и определим неизвестное число рядов n, пользуясь формулами для суммы и n-го члена:

Sn = n * (a1 + an) / 2; an = a1 + d * (n — 1) =>Sn = n * (a1 + a1 + d * (n — 1)) /2 = (2 * a1 — d) / 2 * n + d * n2 / 2

Подставляем в последнее равенство известные данные и решаем полученное квадратное уравнение относительно n:

36 = 0,5 * n + 0,5 * n2 илиn2 + n — 72 = 0Дискриминант: D = 1 — 4 * 1 * (-72) = 289Корни: n = (-1 ± 17) / 2 = (8; -9)

Отрицательное значение отбросим сразу, поскольку оно противоречит условию задачи. Таким образом, 8 рядов пирамиды будут содержать 36 бревен. Так как рабочие не завершили два верхних ряда, значит, всего они сложили 6 рядов бревен.

Несколько слов о прогрессии геометрической

Алгебраическая и геометрическая прогрессии, как правило, рассматриваются в рамках одной темы, поэтому полезно дать понятие и о втором типе упорядоченного числового ряда. Итак, прогрессия геометрическая представляет собой ряд чисел, которые подчиняются закону:

an = an-1 * r

То есть в отличие от арифметической, здесь для получения всех элементов необходимо не прибавлять одно число, а умножать на него (r называется знаменателем).

Из определения понятно, что геометрическая прогрессия растет (уменьшается) гораздо быстрее, чем арифметическая.

Применяется она часто в геометрии, например при вычислении площадей фигур с помощью их разбиения на отдельные элементы (метод деления пополам).

Объяснение урока: Приложения геометрических последовательностей и рядов

В этом объяснении мы узнаем, как решать реальные приложения геометрические последовательности и ряды, где мы найдем знаменатель, 𝑛th явная формула термина, порядок и значение конкретного члена последовательности, а также сумма заданного числа слагаемых.

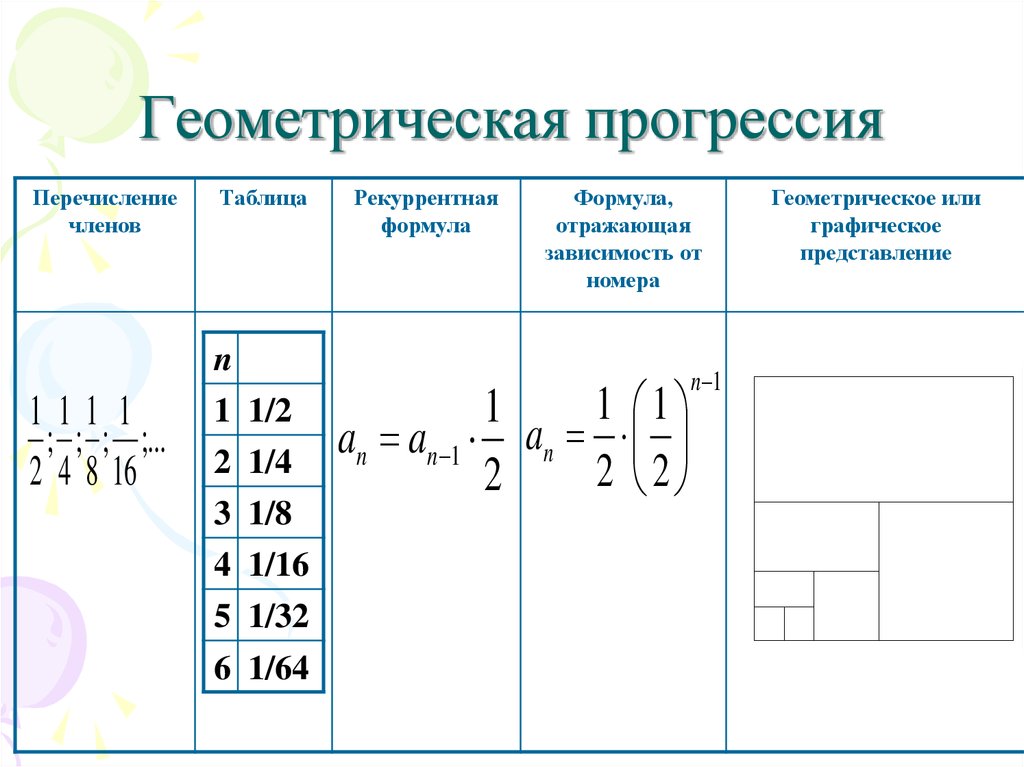
Рассмотрим последовательность, в которой каждый член находится путем умножения предыдущего термин константой. Например, последовательность 2,6,18,54,162,486,….

Мы называем этот постоянный множитель обыкновенным отношением. Другой способ описать последовательности означало бы, что каждый член последовательности равен предыдущему срок, умноженный на обыкновенный коэффициент.

Это известно как геометрическая последовательность, в данном случае с первым членом, равным 2 и обычное отношение 3. Если бы наша последовательность состояла, скажем, из шесть терминов выше (или даже любое конкретное количество терминов), то мы называем это конечная геометрическая последовательность, поскольку она имеет конечное число членов. Если последовательность всегда следовала этому шаблону, как подразумевает многоточие в конце, то мы называем это бесконечной геометрической последовательностью.

Определение: Геометрическая последовательность

Геометрическая последовательность — это последовательность, имеющая общее отношение 𝑟, между сроками подряд. Первый член обозначается 𝑇 или 𝑇, второй член 𝑇, третий член 𝑇 и так далее. 𝑛-й член обозначается 𝑇.

Каждый член находится путем умножения предыдущего члена на обыкновенное отношение: 𝑇=𝑇,𝑇=𝑇×𝑟,𝑇=𝑇×𝑟,…,𝑇=𝑇×𝑟.

Это также можно выразить как первый член, умноженный на степени обычное соотношение: 𝑇=𝑇,𝑇=𝑇𝑟,𝑇=𝑇𝑟,… такой, что 𝑛-й член определяется формулой 𝑇=𝑇𝑟.

Возвращаясь к нашей исходной геометрической последовательности выше, если мы знаем числа в последовательности, мы можем вычислить обыкновенное отношение, разделив значение одного термин на значение предыдущего термина. Поскольку соотношение является общим для всех последовательных пар терминов, не имеет значения, какую пару мы выберем для нашего расчет.

Отношение первых двух членов равно 6÷2=3, отношение вторых двух членов 18÷6=3, и так далее.

Определение: обыкновенное отношение

Поскольку мы умножаем один член на обыкновенное отношение, чтобы получить следующий член, мы можем выразить это в общем виде как 𝑇=𝑇×𝑟, и разделив обе части уравнения на 𝑇, мы получили 𝑟=𝑇𝑇. 

Альтернативно, с определением, что любой термин является результатом умножения предыдущего члена по обыкновенному соотношению, находим, что 𝑟=𝑇𝑇.

Сумма членов последовательности называется рядом. Учитывая геометрическую последовательность (2,6,18,54,162,486,1458,4374,13122,39366,…), соответствующий геометрический ряд может быть представлен следующим образом: 2+6+18+54+162+486+1458+4374+13122+39366+⋯.

В этом случае, сложив первые 10 членов ряда, мы можем видим, что сумма этих членов равна 59‎ ‎048.

Теперь выведем формулу суммы первых 𝑛 термины геометрической прогрессии.

Рассмотрим геометрическую прогрессию с первым членом 𝑇 и обыкновенное отношение 𝑟. Первые члены 𝑛 могут быть записывается как 𝑇,𝑇𝑟,𝑇𝑟,…,𝑇𝑟, поэтому сумма первых 𝑛 члены геометрической прогрессии можно записать следующим образом:

𝑆 = 𝑇+𝑇𝑟+𝑇𝑟+⋯+𝑇𝑟+𝑇𝑟.

(1)

Если мы умножаем обе стороны нашего уравнения на 𝑟, мы

𝑟𝑆 = 𝑇𝑟+𝑇𝑟+𝑇𝑟+⋯+𝑇𝑟+𝑇𝑟. 

(2)

Когда мы вычитаем термины в уравнении (2) из членов уравнения (1), все, кроме членов 𝑇 и 𝑇𝑟 отменяет: 𝑆 = 𝑇+𝑇𝑟+𝑇𝑟+⋯+𝑇𝑟+𝑇𝑟, 𝑟𝑆 = 𝑇𝑟+𝑇𝑟+𝑇𝑟+⋯+𝑇𝑟+𝑇𝑟.

Итак, 𝑆−𝑟𝑆=𝑇−𝑇𝑟.

Факторинг 𝑆 с правой стороны и 𝑇 с левой стороны позволит нам создать уравнение для 𝑆: 𝑆(1−𝑟)=𝑇(1−𝑟)𝑆=𝑇(1−𝑟)1−𝑟.

В качестве альтернативы мы могли бы вычесть (1) из уравнение (2) для получения формулы 𝑆=𝑇(𝑟−1)𝑟−1.

Определение: Сумма конечной геометрической последовательности

Сумма первых 𝑛 членов геометрической последовательности, с первым членом 𝑇 и обыкновенным отношением 𝑟, обозначается 𝑆: 𝑆=𝑇(1−𝑟)1−𝑟𝑆=𝑇(𝑟−1)𝑟−1.или

Как правило, мы используем первую версию, когда 𝑟1 и второй, когда 𝑟>1.

Если 𝑟=1, все члены геометрической последовательности равны то же самое, поэтому нам просто нужно умножить первый член на число терминов: 𝑆=𝑇×𝑛.

Теперь мы рассмотрим, как мы можем применить некоторые из приведенных выше формул для решения реальные задачи, связанные с геометрическими последовательностями и рядами.

Пример 1. Решение прикладной задачи с использованием геометрических последовательностей

Амира пришла в компанию с начальной зарплатой 28 000 долларов США. Она получает Повышение заработной платы на 2,5% после каждого полного год в работе.

1. Всего Амира зарабатывает более 𝑛 лет представляет собой геометрический ряд. Каково общее соотношение?
2. Напишите формулу для 𝑆, общей суммы в долларов, что Амира зарабатывает в 𝑛 лет в компании.
3. через 20 лет с компанией Амира уходит. Используйте свою формулу для расчета общая сумма, которую она заработала там.
4. Объясните, почему фактическая сумма, которую она заработала, будет отличаться от сумма рассчитывается по формуле.

1. Она потратила часть денег в 20 лет.
2. Стоимость доллар меняется со временем.
3. При необходимости новая годовая зарплата будет округлена.
4. Фактическая сумма будет иметь другой процент по сравнению с сумма, рассчитанная по формуле.
5. Фактическая сумма будет иметь другое начальное значение по сравнению с к сумме, рассчитанной по формуле.

Ответ

Этот вопрос состоит из четырех частей, над которыми мы будем работать индивидуально.

Часть 1

Нам известно, что у Амиры начальная зарплата $28‎ ‎000 и что она получает зарплату увеличение на 2,5% после каждого полного год в работе. Этой информации достаточно, чтобы определить, что сумма она зарабатывает в 𝑛 лет будет геометрическая прогрессия. В первой части этого вопроса нам предлагается вычислить обыкновенное отношение этого ряда.

Когда мы говорим о соотношении геометрического ряда, мы имеем в виду отношение геометрической последовательности, из которой состоит этот ряд.

Любую геометрическую последовательность можно записать в виде 𝑇,𝑇𝑟,𝑇𝑟,…,𝑇𝑟, где 𝑇 — первый член, а 𝑟 — обыкновенное отношение. Мы можем рассчитать обыкновенное отношение, вычислив частное двух последовательных членов: 𝑟=𝑇𝑇.

Мы знаем, что в год  1, Амира заработает 28 000 долларов. В год 2, у нее будет повышение зарплаты на 2,5%. Поэтому мы можем подсчитайте сумму денег, которую Амира зарабатывает в год 2, рассчитав 2,5% от 28‎ ‎‎$ а затем добавить это значение.

Альтернативным методом здесь может быть использование метода умножения. Поскольку зарплата Амиры увеличивается на 2,5%, нам нужно умножить ее зарплату на 1,025.

В году 2, она заработает 28 000 × 1,025 = 28 700 долларов.

Этого достаточно, чтобы найти знаменатель, так как мы видим, что первый член 𝑇=28000$ и обыкновенное отношение 𝑟=1,025.

Мы могли бы, однако, продолжить эту модель, чтобы показать, сколько денег Амира зарабатывает в год 3, год 4, и так далее:

• Year1=$28000
• Year2=$28000×1.025
• Year3=$28000×1.025×1.025=$28000×1.025
• Year4=$28000×1.025×1.025×1.025=$28000×1.025
• …

Это означает, что в 𝑛 год Амира заработает $28000×1,025, так как показатель степени или степень всегда будет на 1 меньше числа годы.

Это связано с нашим общим выражением для 𝑛-го члена геометрическая последовательность 𝑇=𝑇𝑟.

Обычное отношение последовательности равно 1,025.

Часть 2

Во второй части вопроса нам нужно написать формулу для 𝑆, общая сумма долларов что Амира зарабатывает в 𝑛 лет в компании.

Мы знаем, что сумма первых 𝑛 членов геометрическую серию, обозначаемую 𝑆, можно найти, используя следующая формула: 𝑆=𝑇(𝑟−1)𝑟−1.

Замена 𝑇=28000 и 𝑟=1,025, имеем 𝑆=28000(1,025−1)1,025−1𝑆=28000(1,025−1)0,025𝑆=1120000(1,025−1).

Формула 𝑆, общая сумма долларов, которые Амира зарабатывает в 𝑛 лет в компании составляет 𝑆=1120000(1,025−1).

Часть 3

Чтобы рассчитать сумму денег, которую заработает Амира спустя 20 лет на компании, нам нужно подставить 𝑛=20 в наш предыдущий ответ: 𝑆=11200001,025−1𝑆=715250,41.

Когда Амира покидает компанию после 20 лет ей будет заработал $715‎ ‎250,41, до ближайшего цент.

Часть 4

Заключительная часть вопроса спрашивает нас, почему фактическая сумма, которую она заработала будет отличаться от суммы, рассчитанной по формуле. Есть пять возможных вариантов ответа на эту часть вопроса.

Это интересная задача, и мы рассмотрим каждый вариант по одному вовремя.

Хотя это правда, что Амира, вероятно, потратила часть своего деньги в 20-летнем период, это не повлияет на сумму денег, которую она заработала, только на сумму денег, которые она оставила. Следовательно, вариант А не является правильным ответом.

Верно, что значение доллар бы изменился со временем; однако, поскольку Амире всегда платили долларов за этот период стоимость доллар не повлияет на сумму, которую зарабатывает Амира. Вариант Б тоже неверный.

Третий вариант представляет собой интересную проблему, с которой мы сталкиваемся регулярно по математике: когда округлять ответы. Когда мы используем формулу для расчета общей суммы, которую заработала Амира, мы используем точные значения для годы 1–20 и округлить ответ только в конце. Однако в действительности, зарплата будет округляться в каждом год. Например, в год 4, Амира заработала 28000$ × 1,025=30152,9$375. Это было бы округлить до ближайшего цент, так На самом деле Амира заработала 30 152,94 доллара. В результате, сложив эти округленные значения, мы получим немного другое значение, чем при использовании формулы. Это верно для любой проблемы, когда операции с валютой, так как эти значения должны быть округлены до двух знаков после запятой.

Варианты D и E предполагают, что будет другой процент и другое начальное значение; однако ни одно из этих утверждений не верно так как процент прибавки к зарплате всегда 2,5% а стартовая зарплата всегда составляет 28 000 долларов. Следовательно, оба эти ответа неверны.

Фактическая сумма заработка Амиры будет отличаться от суммы рассчитывается по формуле, так как при необходимости новый годовой оклад будет округлен. Правильный ответ — вариант C.

Пример 2. Моделирование реальной задачи с использованием геометрической последовательности и ее использование для решения проблемы

Добыча золотого рудника 2‎ ‎257 кг в первый год но производство снижалось на 14% ежегодно. Найдите сумму золота, произведенного в третьем год и Всего за все 3 года. Дайте ответы ближайшему килограмм.

Ответ

Нам нужно рассчитать количество золота, произведенного в 3-й год и общий объем производства по всем три года. Один из способов сделать это означало бы напрямую найти эти значения из информации, указанной в вопрос.

Нам сказали, что количество золота, произведенного в первый год составляет 2‎ ‎257 кг.

Во второй год, есть снижение на 14%. Мы могли бы вычислить 14% от 2‎ ‎257 кг а затем вычесть это значение из 2‎ ‎257 кг. Альтернативно, мы могли бы умножить 2‎ ‎257 кг по (1−0,14), как 14% записанный в виде десятичной дроби, равен 0,14. Это дает нам множитель, равный 0,86.

Эти методы действительно работают только тогда, когда нам нужно вычислить небольшое количество годы.

Если нам нужно рассчитать более длительный период времени, мы можем использовать наши знания геометрических последовательностей. Мы знаем, что любая геометрическая прогрессия имеет первый член 𝑇 и обыкновенное отношение 𝑟.

Количество золота, добытого рудником, образует такую ​​последовательность, где 𝑇=2257 и 𝑟=0,86. Мы знаем, что обыкновенное отношение 𝑟 равно 0,86, так как это константа, на которую мы умножаем каждый член, чтобы получить следующий член.

Общий член геометрической последовательности, 𝑇, можно рассчитать по формуле 𝑇=𝑇𝑟. Подставляя в наши значения, мы имеем 𝑇=2257(0,86)=2257(0,86)=1669,2772. 

Мы снова видим, что количество золота, произведенного в третий год равен 1‎ ‎669 кг, округлить до ближайшего килограмм.

Сумма первых 𝑛 членов геометрической прогрессии 𝑆 можно рассчитать по формуле 𝑆=𝑇(1−𝑟)1−𝑟. Подставляя в наши значения, мы имеем 𝑆=22571−0,861−0,86𝑆=22571−0,860,14𝑆=5867,2972.

Общее количество золота, произведенного по всем три года равен 5‎ ‎867 кг, округлить до ближайшего килограмм.

В следующем примере мы рассмотрим ситуацию, когда денежная сумма вкладываются на сберегательный счет, где начисляется годовая процентная ставка ежемесячно.

Пример 3. Решение финансовой проблемы, когда проценты ежемесячно начисляются с использованием Геометрические последовательности

Самех экономит 20 долларов каждый месяц на счете с годовой процентной ставкой 4% начисляется ежемесячно.

1. Сколько будет на счету Самеха после 4 года регулярной экономии? Дайте ответ ближайшему цент.
2. Если бы проценты начислялись ежеквартально, сколько было бы в аккаунт через 4 года?

Ответ

Этот вопрос состоит из двух частей, каждую из которых можно смоделировать с помощью геометрические последовательности.

Часть 1

Во-первых, у нас есть счет, на который выплачивается годовая процентная ставка Ежемесячно начисляется 4%, поэтому месячная ставка может быть рассчитывается путем деления 4% на 12: месячная процентная ставка = 0,0412 = 1300.

Таким образом, множитель будет равен 1+1300=301300, значит обыкновенное отношение 𝑟=301300.

Самех экономит 20 долларов каждый месяц, поэтому первый член геометрической прогрессии 𝑇=$20.

За четыре года период, будет 4×12=48 ежемесячных платежей, что означает в нашей геометрической последовательности 48 членов, поэтому 𝑛=48.

Сумма первых 𝑛 членов геометрической прогрессии, 𝑆, можно рассчитать по формуле 𝑆=𝑇(𝑟−1)𝑟−1. Подставляя в наши значения, мы имеем 𝑆=20−1−1𝑆=1039,1920….

Округлив это число до двух знаков после запятой, можно сделать вывод, что существует 1‎ ‎039,19 долларов СШАв Самехе счет после 4 года.

Часть 2

Во-вторых, у нас есть счет, на который выплачивается годовая процентная ставка 4% начисляется ежеквартально, поэтому квартальная ставка может быть рассчитывается путем деления 4% на 4: квартальная процентная ставка = 0,044 = 1100.

Таким образом, множитель будет равен 1+1100=101100, поэтому обыкновенное отношение 𝑟=101100.

Самех экономит 20 долларов каждый месяц, таким образом, каждый квартал он будет экономить 3 × 20 долларов = 60 долларов; следовательно, первый срок геометрическая последовательность 𝑇=60$.

За четыре года период будет 16 ежеквартальных платежей, что означает, что в нашем геометрическая последовательность, поэтому 𝑛=16.

Сумма первых 𝑛 членов геометрической прогрессии, 𝑆, можно рассчитать по формуле 𝑆=𝑇(𝑟−1)𝑟−1. Подставляя в наши значения, мы имеем 𝑆=60−1−1𝑆=1035,4718….

Округлив это число до двух знаков после запятой, можно сделать вывод, что существует 1 ‎ 035,47 доллара США в магазине Sameh’s счет через 4 года.

Таким образом, мы можем заключить, что если проценты начисляются ежемесячно а не ежеквартально, тогда Самех будет получать больше процентов через четырехлетний срок.

В нашем последнем примере мы решим еще одну реальную задачу, включающую геометрические последовательности.

Пример 4. Решение физической задачи, связанной с объемом, с использованием геометрических последовательностей

Резервуар для воды 1‎ ‎778 литров воды. Объем воды уменьшился на 14, 28 и 56 литров в течение следующего три дня соответственно. Через какое время танк быть пустым, учитывая, что объем воды уменьшается по той же схеме?

Ответ

Заметим, что значения 14,28,56,… образуют геометрическую прогрессию с первым членом 𝑇=14 и обыкновенное отношение 𝑟=2. Чтобы проверить это, мы разделим каждый член на член перед Это: 56÷28=28÷14=2.

Сумма первых 𝑛 членов геометрической прогрессии, 𝑆, можно рассчитать по формуле 𝑆=𝑇(𝑟−1)𝑟−1.

Так как общее количество воды в баке равно 1‎ ‎778 литров, тогда 𝑆=1778 и мы хотим рассчитать период времени, 𝑛, в дней.

Подставляя наши значения имеем 1778=14(2−1)2−11778=14(2−1)(14)127=2−1(1)128=2 так что 𝑛 это целочисленное значение.

На самом деле 2 равно 128, поэтому 𝑛=7.

Обратите внимание, что это также можно решить с помощью логарифмов, хотя это выходит за рамки этого пояснителя.

Таким образом, резервуар для воды будет пуст после 7 дней.

Мы можем проверить этот ответ, посчитав количество воды в баке в конце каждого дня, вычитая 14,28,56,… индивидуально.

Конец дня 1: 1778-14=1764

Конец дня 2: 1764-28=1736

Конец дня 3: 1736-56=1680

Конец дня 4: 1680-112=15068

Конец дня 5: 1568-224=1344

Конец дня 6: 1344-448=896

Конец дня 7: 896-896=0

Это подтверждает, что резервуар для воды будет пуст после 7 дней.

Мы закончим это объяснение повторением некоторых ключевых моментов.

Ключевые моменты

• Многие реальные задачи связаны с геометрическими последовательностями и рядами. Последующий определения могут помочь нам решить эти проблемы.
• Конечная геометрическая последовательность имеет вид 𝑇,𝑇𝑟,𝑇𝑟,…,𝑇𝑟, где 𝑇 — первый член, 𝑟 — знаменатель, а 𝑛 — количество членов в последовательности.
• 𝑛-й член геометрической последовательности равен 𝑇=𝑇𝑟.
• Обычное отношение 𝑟 геометрической прогрессии, 𝑛-й член 𝑇 определяется как 𝑟=𝑇𝑇 или 𝑟=𝑇𝑇.
• Сумма членов последовательности называется рядом.
• Сумма первых 𝑛 членов геометрической прогрессии, с первым членом 𝑇 и обыкновенным отношением 𝑟, обозначается 𝑆, где 𝑆=𝑇(1−𝑟)1−𝑟𝑆=𝑇(𝑟−1)𝑟−1.или

Арифметические и геометрические ряды — IB Math Stuff

Определения

Ряд — Ряд образуется суммой или добавлением терминов в последовательности. Например, арифметический ряд образуется путем суммирования членов арифметической последовательности.

Последовательность:	(1) \begin{equation} 3, 5, 7, 9,… \end{equation}
Серия :	(2) \begin{equation} 3+5+7+9+. .. \end{equation}

n ^th Частичная сумма — определяется как сумма от члена 1 ^st до члена n ^th в последовательности. Например, частичная сумма 5 ^th ряда выше будет:

(3)

\begin{equation} 3+5+7+9+11=35 \end{equation}

Обозначение частичных сумм

Существует два варианта. Тот, который довольно прост для понимания и наиболее часто используется в математике SL. Второй более сложный, страшный и используется лишь изредка в SL.

Первое обозначение: Частичное число n ^th может быть обозначено как $S_n$, где n сообщает читателю, сколько членов нужно суммировать. Например, используя арифметический ряд $3+5+7+9+…$, частичная сумма 5 ^th будет:

(4)

\begin{equation} S_5 = 3+5+7+9+11 = 35 \end{equation}

Стоит отметить, что «частичная сумма n ^th » обычно относится к фактическому результату сложения, а не к утверждению, показывающему все сложение.

Второе обозначение: Это обозначение часто называют «обозначением суммирования» и включает в себя номер термина, с которого мы начинаем, номер термина, которым мы заканчиваем, и детали того, что мы суммируем. Например:

Это обозначение позволяет нам начать суммирование с любого члена, который мы пожелаем. В следующем примере суммирование начинается с термина 5 ^th и продолжается до термина 7 ^th .

Часть «уравнения» в нотации суммирования работает путем простой замены значений на n в уравнение, выполнение арифметических действий приводит к одному из членов ряда.

Суммирование арифметического ряда

Приложив немного смекалки и наблюдательности, можно составить два уравнения, которые позволят легко вычислить арифметический ряд:

(5)

\begin{align} S_n=\frac{n}{2} (u_1 + u_n) \end{align}

Эта формула требует, чтобы вы знали первый и последний член ряда. Второе уравнение, показанное ниже, позволяет вам вычислить сумму, не зная конечного члена, который вы будете суммировать (умно!). Следующее уравнение позволяет вычислить сумму, если известны первый член и общая разность.

(6)

\begin{align} S_n=\frac{n}{2}(2u_1 +(n-1)d) \end{align}

Это уравнение получается из предыдущего уравнения при замене $u_n = u_1 + (n-1)d$ составляется и алгебраический экспресс упрощается.

Примеры

Пример 1 Найти 12 ^-й частичную сумму для $4,5+6+7,5+…$

+ Показать Решение

Пример 2 Найти $5+ для $S_ + -1 + -4$

+ Показать решение

9n)}{1-r} \end{align}

Где r — знаменатель, а $u_1$ — первый член ряда.

Примеры

Пример 1 Найти $S_{20}$ для $\frac{1}{2}+1+2+4+8+…$

+ Показать Решение

Пример 2 Найти для $18+30+50+… $ найти n , когда $S_n \ приблизительно 443 088$

+ Показать решение

Еще несколько определений

Бесконечный ряд — ряд, который имеет бесконечное количество членов . Я бы привел пример, но это займет время, чтобы записать…

Расходящийся бесконечный ряд — ряд, в котором при добавлении всего бесконечного числа членов получается положительная или отрицательная бесконечность. Если это звучит как: «Да, разве это не всегда происходит?» взгляните на следующее определение.

Сходящийся бесконечный ряд — ряд, в котором при добавлении всего бесконечного числа членов получается конечное (или не бесконечное) число. Как это возможно спросите вы? Попробуйте сложить приведенный ниже ряд на калькуляторе.

(19)

\begin{align} 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+… \end {align}

Добавляйте все больше и больше терминов в этот ряд, и он будет «сходиться» или приближаться к 2, но никогда не достигнет этого, потому что вам придется буквально добавлять бесконечное количество терминов.