3 способа решить любую 10 задачу ЕГЭ с графиком функций
В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.
Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.
1 способ – находим формулу по точкам
Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.
Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:
Алгоритм:
1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:
2. Подставляем эти координаты в «полуфабрикат» функции. Вместо \(f(x)\)– координату игрек, вместо \(x\) – икс. Получается система.
3. Решаем эту систему и получаем готовую формулу.
4. Готово, функция найдена, можно переходить ко второму этапу – вычислению \(f(-8)\). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.
Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:
2 способ – преобразование графиков функций
Этот способ сильно быстрее первого, но требует больше знаний.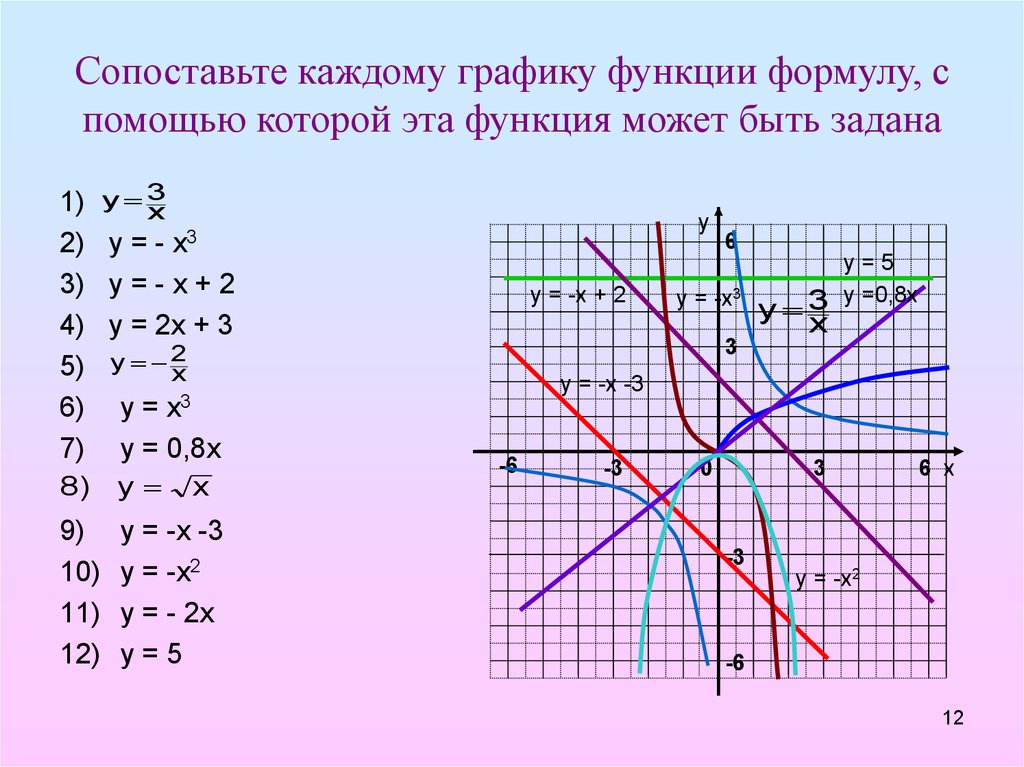
Вот как выглядит применение этого способа:
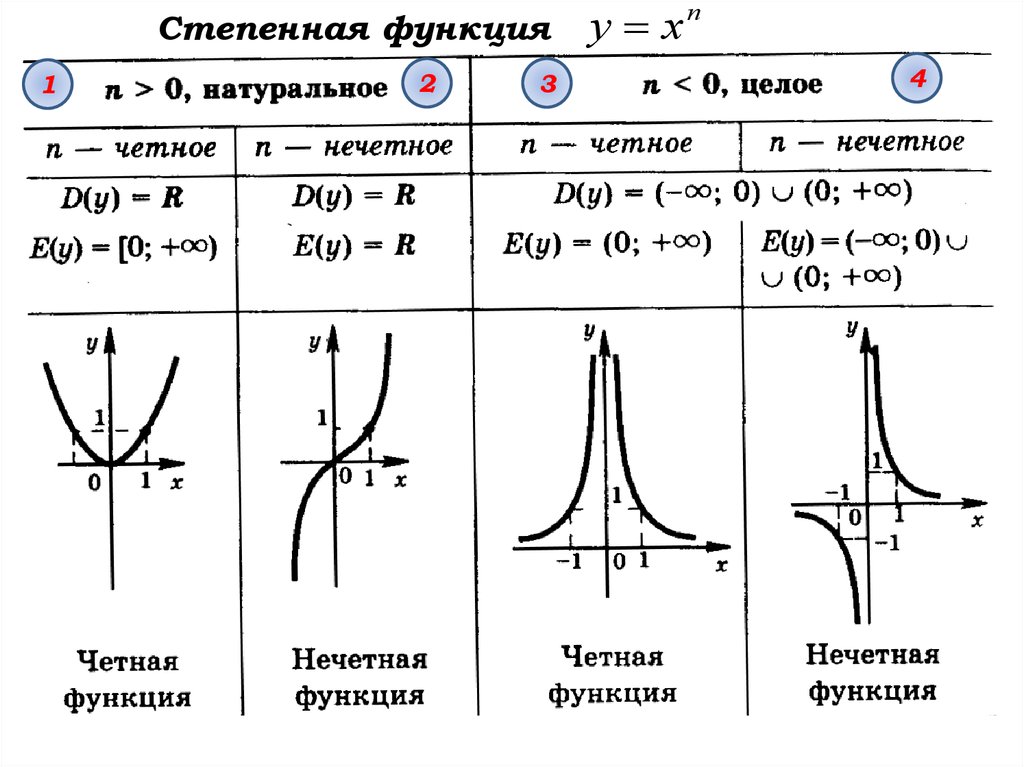
Для использования этого способа надо знать, как выглядят изначальные функции:
И понимать, как меняются функции от преобразований:
Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:
Пример:
3 способ – гибридный
Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку \((0;1)\), а любая логарифмическая — через точку \((1;0)\).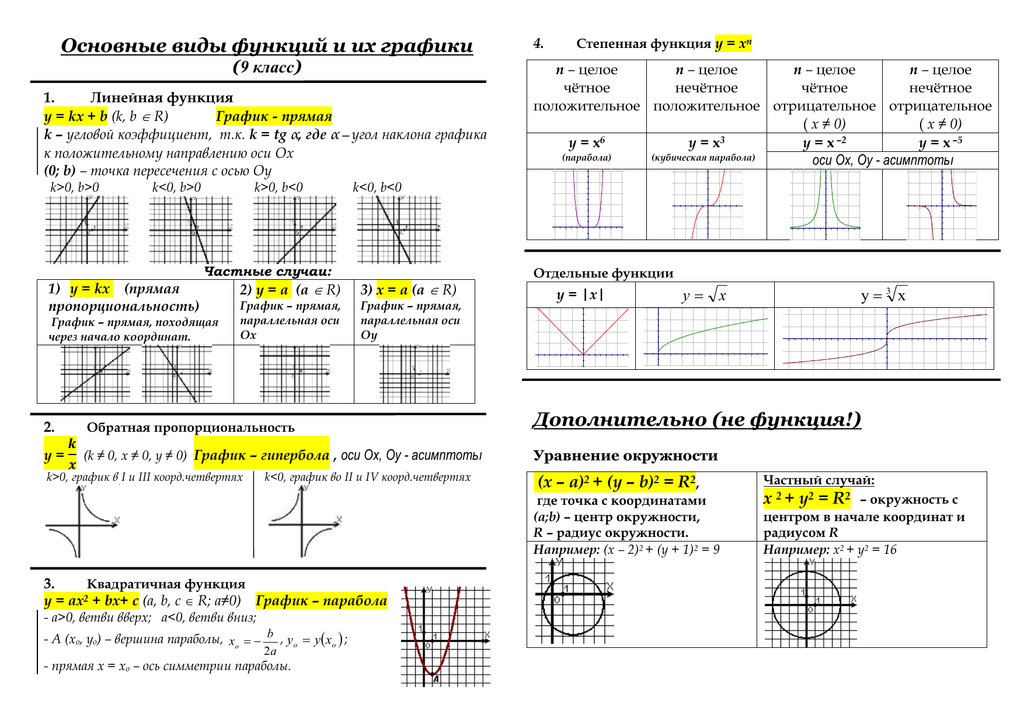
По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).
Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.
Как отвечать на вопросы в задаче, когда уже определили функцию
— Если просят найти \(f\)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:
— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения \(f(x)=\) *любое число*».
— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения \(A\)(*любое число*;*другое число*) и \(B(x_0;y_0)\) и просят найти \(x_0\).
Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения \(A\)(*любое число*;*другое число*) и \(B(x_0;y_0)\) и просят найти \(x_0\).
Пример:
— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти \(y_0\) точки пересечения двух функций.
Пример:
— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:
Установление соответствия между графиком функции и ее формулой. Подготовка к ОГЭ | План-конспект занятия по алгебре (8 класс) по теме:
Название работы | Установление соответствия между графиком функции и его формулой. |
Класс | 8-9класс |
Предметная область | Математика |
Цель | К концу занятия учащиеся смогут: 1. Различать графики параболы. гиперболы и прямой; различать формулы обратной пропорциональности, линейной функции и квадратичной функции; 2. Устанавливать соответствие между формулой функции и ее графиком; 3. Устанавливать взаимосвязь между знаками коэффициентов функции и ее графиком |
Аннотация | Краткое описание работы. К экзамену в 9 классе нужно начинать подготовку с младших классов. В 8 классе уже изучены практически все функции, которые выносятся на экзамен. Поэтому данный материал целесообразно использовать с восьмиклассниками. |
Тема: Установление соответствия между графиком функции и его формулой.
Учебно-тренировочное занятие для подготовки к ОГЭ.
Цель: К концу занятия учащиеся смогут:
1. Различать графики параболы. гиперболы и прямой; различать формулы обратной пропорциональности, линейной функции и квадратичной функции;
2. Устанавливать соответствие между формулой функции и ее графиком;
3. Устанавливать взаимосвязь между знаками коэффициентов функции и ее графиком
Метапредметные результаты: работают со справочным материалом; устанавливают соответствие, осуществляют контроль и оценку своих знаний и умений, сверяют свое решение с предложенным эталоном.
Оборудование: ПК, презентация, интерактивная доска, система для голосования, справочные материалы, тренировочные задания,[1] файл для работы с системой голосования
Этап урока | Деятельность учителя | Деятельность ученика | |
1. Орг момент | Приветствует учащихся, проверяет готовность учащихся к уроку | Включаются в ритм урока | |
2. Актуализация знаний | Слайд 1 . Предлагает учащимся выполнить задание.: Установите соответствие между формулой и названием графика | Учащиеся выполняют задание на соответствие в тетрадях. | |
| А) Прямая; Б) Ветвь параболы; В) Гипербола; Г) Парабола; Д) Прямая, проходящая через начало координат | ||
Показывает эталон выполнения задания, предлагает оценить выполнение задания и выставить себе баллы. | Учащиеся осуществляют самопроверку выполнения задания и выставляют по 1 баллу за каждое правильно установленное соответствие | ||
2) Предлагает учащимся записать название каждой из предложенных шести функций. После выполнения показывает правильные ответы на задание(слайд 2) | Учащиеся осуществляют самопроверку выполнения задания и выставляют по 1 баллу за каждое правильное название функции | ||
3. Первичная рефлексия и постановка целей на урок | Учащимся предлагается заполнить таблицу. (слайд 3)Если учащийся согласен с утверждением, то ставит «+», если не согласен, то ставит «-« | Проводят первичную рефлексию собственных знаний и умений , заполняют таблицу, расставляя «+» и «-« Формулируют тему и цель урока | |
Исходя из заполненной таблицы, учащимся предлагается сформулировать тему и цель урока | |||
4. | 1) На уроке используется система для голосования с функцией мгновенного ответа. Файл Учитель предлагает задания №1-№6 (если нет системы для голосования, то можно использовать слайдовую презентацию слайды№5-10. )
После выполнения каждого задания организуется обсуждение. Учащимся предлагается обосновать выбор своего ответа. 2) прежде чем решать задание №7, предлагает учащимся в справочных материалах. Лист 3. Разобрать пример из табл№3., а затем выполнить задание №7. Слайд №11. | Учащиеся читают задание, решают его . При решении используют справочный материал, имеющийся на партах. Вводят свои ответы, используя пульты системы голосования. На экране выводится таблица ответов., где видны результаты ответов каждого учащегося. Обосновывают свой ответ и сверяют свой ответ с названным эталоном, оценивают и корректируют свое решение, ставят баллы за правильные ответы | |
За аргументированное объяснение материала учитель может добавить учащимся баллы на свое усмотрение | Учащиеся работают с текстом справочных материалов в паре. | ||
5.Самостоятельная работа в парах | Учитель предлагает учащимся в паре решить 4 задачи (Тренировочные задания)самостоятельно и сверить свои ответы с ответами, лежащими на столе учителя. | Решают задания, обсуждая решение в паре. Выставляют баллы за верные ответы | |
6. Итог урока и рефлексия | Предлагает посчитать баллы, которые были набраны в ходе урока и выставить себе оценки по следующим критериям. После этого возвращаемся к таблице заполненной в начале урока и заполнить ее на конец урока, расставив «+» и «-« Организует обсуждение достигнутых целей | Считают баллы, выставляют оценки, заполняют таблицу рефлексии. Высказывают свое мнение о достижении поставленной на урок цели | |
Интернет- ресурсы
Тренировочные задания и задания к уроку взяты с сайта
1. http://opengia.ru/subjects/mathematics-9/topics/1
http://opengia.ru/subjects/mathematics-9/topics/1
— Как найти формулу функции по ее графику?
Наилучший способ решения такого рода проблем моделирования данных — использование теоретико-информационных подходов.
Колмогоровская сложность
Самый простой и полностью общий способ — найти пару (программа, ввод) с наименьшей общей длиной на фиксированном языке программирования общего назначения, который при запуске выводит данные точно так, как они есть. Это называется колмогоровской сложностью. Конечно, это зависит от выбранного языка программирования, и ясно, что если вы сначала посмотрите на данные, вы можете создать язык, специально адаптированный к ним (см. Code Golf SE для некоторых вопиющих примеров). Это не разрешено; вы должны сначала выбрать язык раз и навсегда, и использовать его для каждой последующей задачи, в которой вы хотите измерить сложность данных. Кроме того, язык должен быть полным по Тьюрингу. Подходят распространенные языки, такие как C++14 или Java 7. Длина программы и входной строки всегда измеряется в битах.
Длина программы и входной строки всегда измеряется в битах.
Пусть $K_L(x)$ — колмогоровская сложность строки $x$ над полным по Тьюрингу языком программирования $L$.
Почему это сработает? Можно легко доказать, что для полных по Тьюрингу языков $L,M$ существует некоторое $c$ такое, что для любой строки $x$ имеем $|K_L(x)-K_M(x)| \ле с$. Таким образом, для любого класса струн колмогоровская сложность будет асимптотически правильной, если длина строки стремится к $\infty$. Например, колмогоровская сложность строки $x_n$, состоящей ровно из $n$ нулей, будет отличаться от $\log_2(n)$ не более чем на $c$ для некоторой константы $c$, не зависящей от $n$. Таким образом, при $n \to \infty$ имеем $K_L(x_n) \in θ(\log(n))$.
Поскольку выбранный нами язык не влияет на асимптотическую колмогоровскую сложность, он является объективной мерой сложности для достаточно больших выборок, а использование общего языка, такого как C/C++ или Java, делает невозможным переоснащение.
Пригодность колмогоровской сложности
Для точных данных колмогоровская сложность фиксирует именно количество содержащейся в них информации (с точностью до константы, как указано выше). Однако можно доказать, что не существует полного по Тьюрингу языка $L$ и программы $P$, таких что $P(x) = K_L(x)$ для любой строки $x$. Таким образом, вы не можете надеяться определить колмогоровскую сложность в целом, не говоря уже о том, чтобы найти пару (программа, вход), которая свидетельствует о сложности!
Однако можно доказать, что не существует полного по Тьюрингу языка $L$ и программы $P$, таких что $P(x) = K_L(x)$ для любой строки $x$. Таким образом, вы не можете надеяться определить колмогоровскую сложность в целом, не говоря уже о том, чтобы найти пару (программа, вход), которая свидетельствует о сложности!
Что вы все еще можете сделать, так это найти верхнюю границу, что, по сути, и делают алгоритмы сжатия. Для любой строки $x$ общая длина строки, в которую сжимается $x$, и алгоритм декомпрессии (написанный в $L$) является верхней границей истинной колмогоровской сложности $K_L(x)$.
Тем не менее, большинство научных экспериментов не дают точных данных, поэтому бессмысленно просить программу, точно воспроизводящую измерения, поскольку они и без того неточны и неточны. Но те же самые идеи все еще применимы. Нам просто нужно приспособиться к шуму.
Колмогоровская сложность по модулю шума
Если данные представляют собой список пар $(x_k,y_k)_{k\in\{1.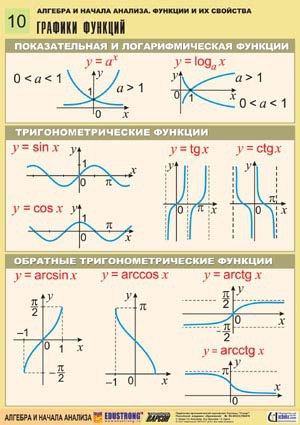 .n\}}$, как во многих эмпирических экспериментах, и мы знаем, что шум является однородным по всему списку, мы можем смоделировать данные как $N(P(x_k))=y_k$, где программа $P$ — это фактическая функция, которую мы ищем, а $N$ — это случайная программа, которая моделирует зашумленный канал, который добавляет шум. $N$ написан на полном по Тьюрингу языке, которому дополнительно разрешено вызывать функцию, возвращающую равномерно случайный бит (который не зависит от результатов предыдущего вызова). 9n \log_2(\mathbb{P}(N(P(x_k))=y_k))$. Интуитивно это длина описания тренда и источника шума плюс средняя информация в самом шуме. Это так, что если нет значимого отображения тренда $x$ в $y$, то сложность по модулю шума будет просто количеством битов, необходимых для определения шума. С другой стороны, если есть тренд, то он будет захвачен коротким $P$, и будет оптимальным $N$, поскольку он должен быть достаточно шумным, чтобы учесть расхождения, но не более необходимого. Кроме того, $N$ зафиксирует фактическое распределение шума, если выборка достаточно велика.
.n\}}$, как во многих эмпирических экспериментах, и мы знаем, что шум является однородным по всему списку, мы можем смоделировать данные как $N(P(x_k))=y_k$, где программа $P$ — это фактическая функция, которую мы ищем, а $N$ — это случайная программа, которая моделирует зашумленный канал, который добавляет шум. $N$ написан на полном по Тьюрингу языке, которому дополнительно разрешено вызывать функцию, возвращающую равномерно случайный бит (который не зависит от результатов предыдущего вызова). 9n \log_2(\mathbb{P}(N(P(x_k))=y_k))$. Интуитивно это длина описания тренда и источника шума плюс средняя информация в самом шуме. Это так, что если нет значимого отображения тренда $x$ в $y$, то сложность по модулю шума будет просто количеством битов, необходимых для определения шума. С другой стороны, если есть тренд, то он будет захвачен коротким $P$, и будет оптимальным $N$, поскольку он должен быть достаточно шумным, чтобы учесть расхождения, но не более необходимого. Кроме того, $N$ зафиксирует фактическое распределение шума, если выборка достаточно велика.
Опять же, невозможно детерминистически найти $P,N$, но мы можем найти верхнюю границу. Кроме того, это дает возможность сравнить приближений неизвестной функции с зашумленной выборкой точек. Если у нас есть 2 полинома, один с низкой степенью и простыми коэффициентами, который подходит достаточно близко, а другой с очень высокой степенью и сложными коэффициентами, но проходит через все точки с разрешением выборки, вы можете быть уверены, что полином низкой степени будет иметь меньшая сложность по модулю шума. Точно так же вы можете попробовать столько приближений, сколько захотите, и просто выбрать то, которое имеет наименьшую сложность по модулю шума.
Это также позволяет вам использовать свою интуицию, чтобы направлять свои попытки. Для реальных измерений они, как правило, страдают от гауссовского шума, поэтому вы можете попробовать $N$ как обычную случайную величину с различными дисперсиями (среднее значение уже захвачено $P$).
При использовании этого метода невозможно получить избыточное соответствие, что является важным свойством, которое вы ищете.
Линейные уравнения и функции. Функции и их графики
Функция, функция, какая у тебя функция? Вы личный тренер, известный шпион, дверной косяк или что-то совсем другое? Мы думаем, что это последний.
Функция принимает некоторые входные данные, обычно называемые x , в уравнение f ( x ). Затем x проходит через уравнение, и в конце мы получаем некоторый результат, обычно известный как y . Обратите внимание, что y и f ( x ) на самом деле одно и то же. Может быть, и — знаменитый шпион?
Мы называем x независимой переменной , а y зависимая переменная . Так что у x хорошая работа, а y все еще живет дома. Все возможные значения x- — это домен , а все возможные значения y- — диапазон .
Пример задачи
Найдите домен и область значений y = 3 x – 4, где 0 ≤ x < 4. – 4, ничего не говоря, мы бы сказали, что домен – это все действительные числа. Это исключает воображаемые, фальшивые, бредовые и позерские числа.
– 4, ничего не говоря, мы бы сказали, что домен – это все действительные числа. Это исключает воображаемые, фальшивые, бредовые и позерские числа.
В этом случае, однако, мы не можем выбрать любое x , которое нам нравится под солнцем. В задаче сказано, что 0 ≤ x < 4. Это означает, что наша область ограничена всеми действительными числами от 0 до 4, включая 0, но не 4 (из-за линии под голодным ртом Pacman).
Теперь диапазон. Диапазон — все возможные значения и . В нашем уравнении y = 3 x – 4 значения y- – это то, что мы получаем, когда подставляем x- значений, которые мы знаем. Давайте составим таблицу, чтобы зафиксировать диапазон.
Диапазон этой функции: -4 ≤ y < 8. Обратите внимание, что y меньше 8, потому что x не может равняться 4, поэтому y никогда не может точно равняться 8.
В этом случае диапазон прост; мы могли бы посмотреть наименьшее и наибольшее значения x , и они дают нам наименьшее и наибольшее значения y .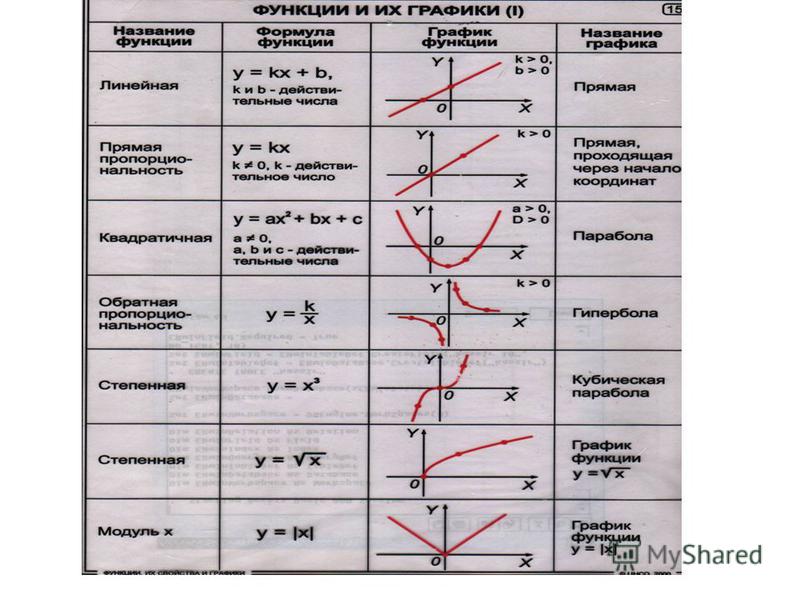 Что, если бы у нас было что-то вроде y = — x 2 , где -2 < x < 2?
Что, если бы у нас было что-то вроде y = — x 2 , где -2 < x < 2?
Здесь, если мы просто подставим x = -2 и 2, мы получим y = -4 для них обоих. Однако мы знаем, что y не всегда находится на уровне -4. Мы должны проверить x = 0, чтобы обнаружить, что там y = 0, что дает нам диапазон -4 < y < 0. Каждый раз, когда график может наклониться или опуститься, проверьте различные числа, чтобы найти правильный диапазон.
Теперь давайте на секунду поговорим о графических функциях. На самом деле, давайте поговорим и построим график одновременно. Только не просите нас тоже жевать жвачку.
Пример задачи
График y = 3 x – 4, где 0 ≤ x < 4.
О, это снова вы. Вы собираетесь повторять вещь , не так ли?
Это нормально, потому что это означает, что мы уже проделали большую часть работы. Нам известен домен и диапазон, и мы подключили несколько точек.
Начните с рисования координатной плоскости . x -ось лежит на спине, лежа, а y -ось стоит по стойке смирно. Они встречаются посередине в точке начала координат . Не пытайтесь слишком сильно визуализировать это; на самом деле это не так больно, как кажется. Мы надеемся.
Мы используем числа на осях, чтобы нанести точки и провести линию. Делаем заказанных пар , которые выглядят так: ( х , и ). И x всегда вызывает дробовик, поэтому y никогда не будет первым.
Начиная с исходной точки (0, 0), положительные значения x перемещаются вправо, а положительные значения y перемещаются вверх. Переместите оба числа вместе, чтобы построить каждую точку из нашей таблицы.
Видишь, как красиво они выстроились? Почему они не могли так красиво выглядеть на своих школьных фотографиях? Что ж, давайте проведем через них линию, пока они сидят на месте.
Здесь у нас ограниченный домен, поэтому мы рисуем только линию, где функция действительно существует. Несуществующие линии на удивление легко рисовать, так что следите за ними.
Вертикальность
В функциях есть кое-что очень важное. На самом деле, это настолько важно, что мы поместим его в отдельную строку:
На каждые x приходится только одно y . Другими словами, каждый вход имеет только один выход. Один х 9Входит 0048, выходит один и .
Если уравнение нарушает этот принцип, оно не является функцией. К счастью, нам не нужно подключаться и проверять каждое значение x-, чтобы увидеть, есть ли среди них общее значение y-. Это было бы утомительно и ужасно. Вместо этого мы можем использовать тест вертикальной линии . Какое имя, а?
Возьмем, к примеру, эти графики. Тест именно на то, на что он похож: рисование вертикальных линий поверх графика. Если любая вертикальная линия может пройти через график более одного раза, то уравнение имеет вид 9.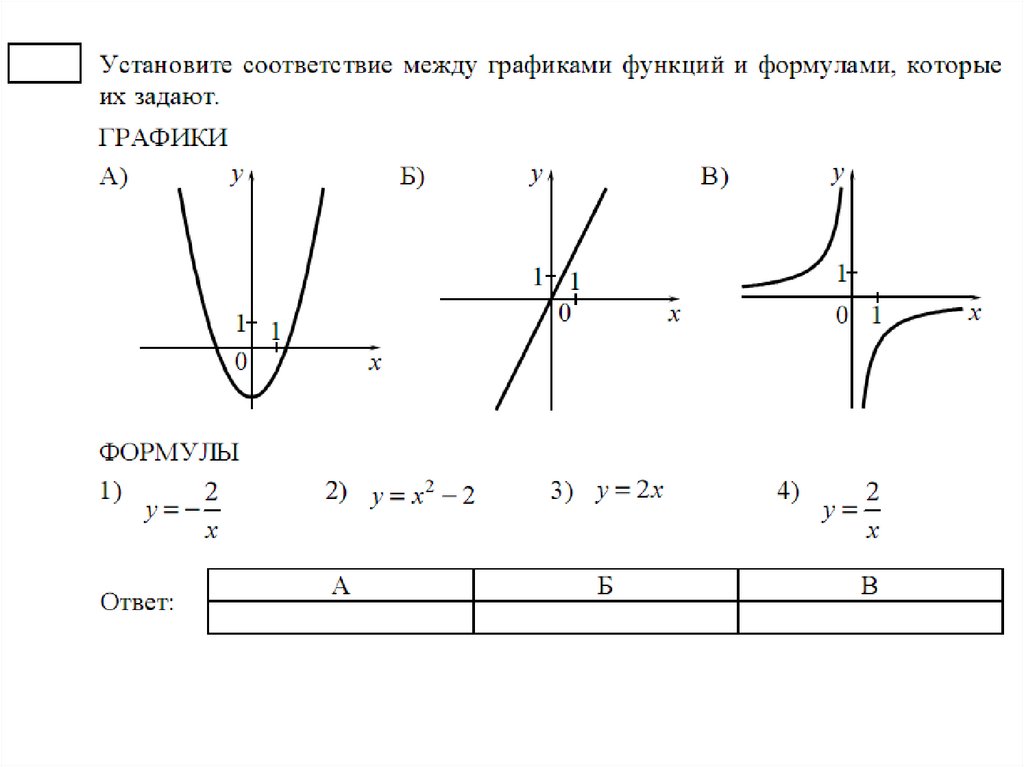

 Учебно-тренировочное занятие для подготовки к ОГЭ
Учебно-тренировочное занятие для подготовки к ОГЭ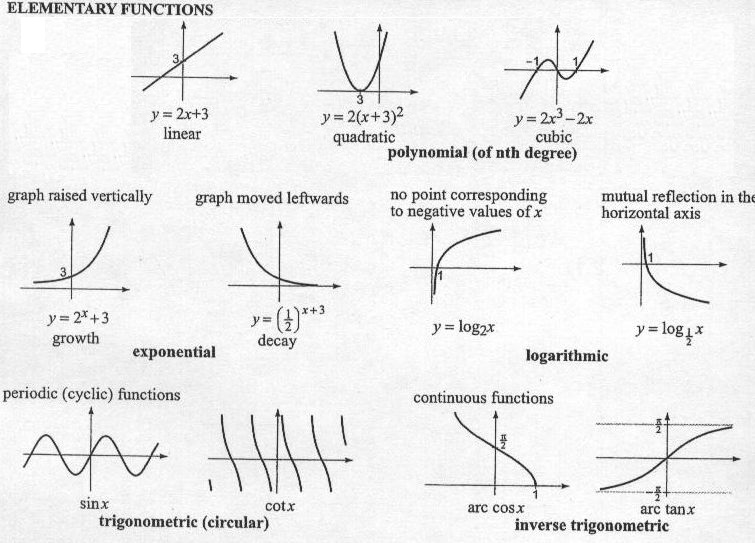 В демоверсии — это задание №5.На уроке используется система для голосования в режиме обучения, для этого используется функция мгновенного вопроса. Учащиеся учатся работать со справочными материалами. Все решенные задания оцениваются определенным количеством баллов и суммируются. В конце занятия подводится итог.
В демоверсии — это задание №5.На уроке используется система для голосования в режиме обучения, для этого используется функция мгновенного вопроса. Учащиеся учатся работать со справочными материалами. Все решенные задания оцениваются определенным количеством баллов и суммируются. В конце занятия подводится итог.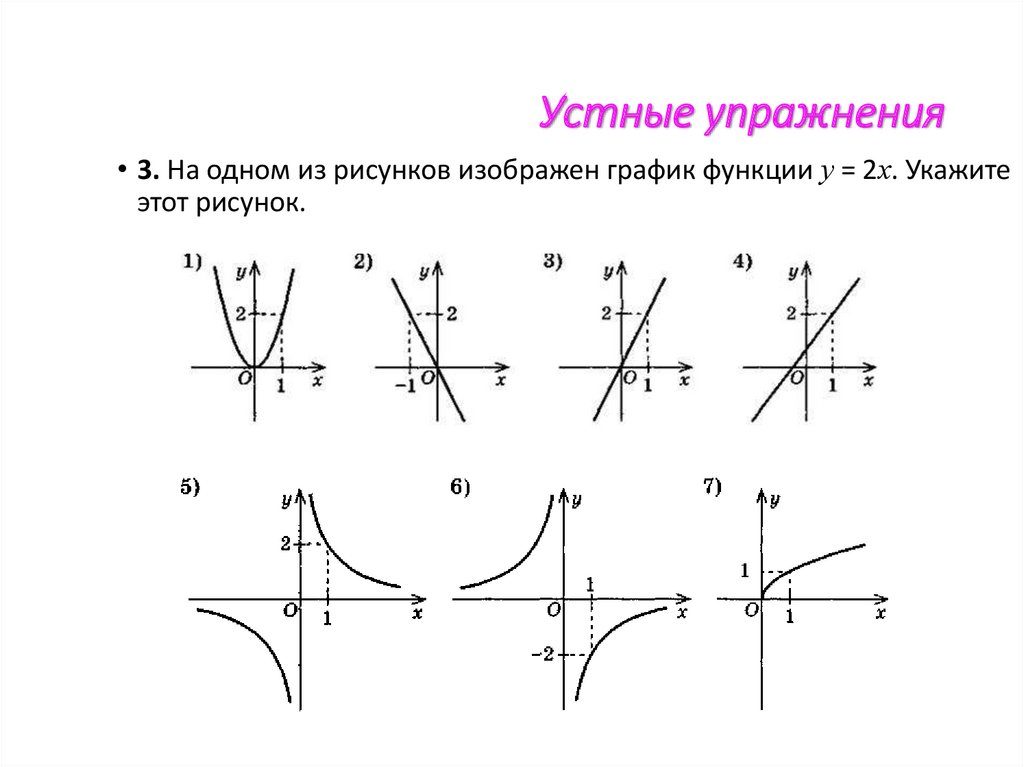
 Отработка умений
Отработка умений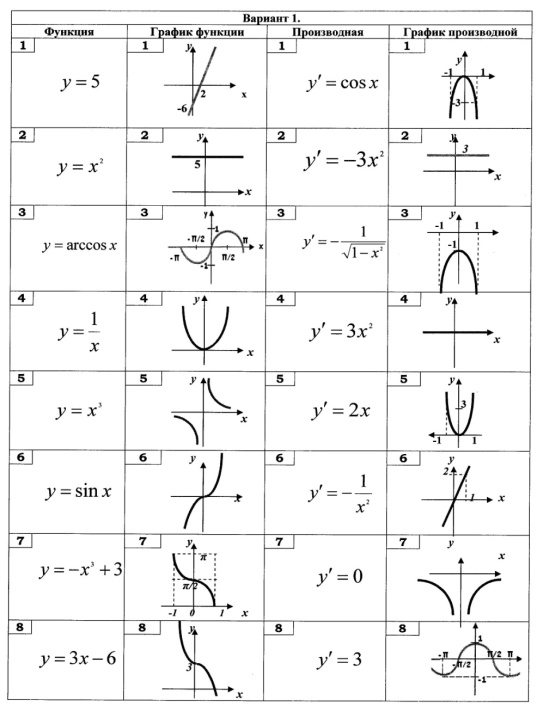 Обсуждают предложенное решение, определяют какой способ лучше. Решают задание №7. Сверяют свое решение с решениями товарищей
Обсуждают предложенное решение, определяют какой способ лучше. Решают задание №7. Сверяют свое решение с решениями товарищей