Формулы для параллелепипеда: Параллелепипед. Прямоугольный параллелепипед. Объем параллелепипеда

свойства, формулы и задачи репетитора по математике — Колпаков Александр Николаевич

Параллелепипедом называется четырехугольная призма, в основаниях которой лежат параллелограммы. Высотой параллелепипеда называют расстояние между плоскостями его основаниями. На рисунке высота показана отрезком . Различают два вида параллелепипедов: прямой и наклонный. Как правило, репетитор по математике сначала дает соответствующие определения для призмы, а затем переносит их на параллелепипед. Мы сделаем также.

Напомню, что призма называется прямой, если ее боковые ребра перпендикулярны основаниям, если перпендикулярности нет – призму называют наклонной. Эту терминологию наследует и параллелепипед. Прямой параллелепипед – ни что иное, как разновидность прямой призмы, боковое ребро которой совпадает с высотой. Сохраняются определения таких понятий, как грань, ребро и вершина, являющиеся общими для всего семейства многогранников. Появляются понятие противоположные грани. У параллелепипеда 3 пары противоположных граней, 8 вершин ти 12 ребер.

Диагональ параллелепипеда (диагональ призмы) — отрезок, соединяющий две вершины многогранника и не лежащий ни в одной из его граней.

Диагональное сечение – сечение параллелепипеда, проходящее через его диагональ и диагональ его основания.

Свойства наклонного параллелепипеда:
1) Все его грани – параллелограммы, а противоположные грани — равные параллелограммы.
2) Диагонали параллелепипеда пересекаются в одной точке и делятся в этой точки пополам.
3) Каждый параллелепипед состоит из шести равных по объему треугольных пирамид. Чтобы показать их ученику репетитор по математике должен отрезать от параллелепепеда половинку его диагональным сечением и разбить ее отдельно на 3 пирамиды. Их основания должны лежать в разных гранях исходного паралеллепипеда. Репетитор математики найдет применение этого свойства в аналитической геометрии. Оно используется для вывода объема пирамиды через смешанное произведение векторов.

Формулы объема параллелепипеда:
1) , где — площадь основания, h – высота.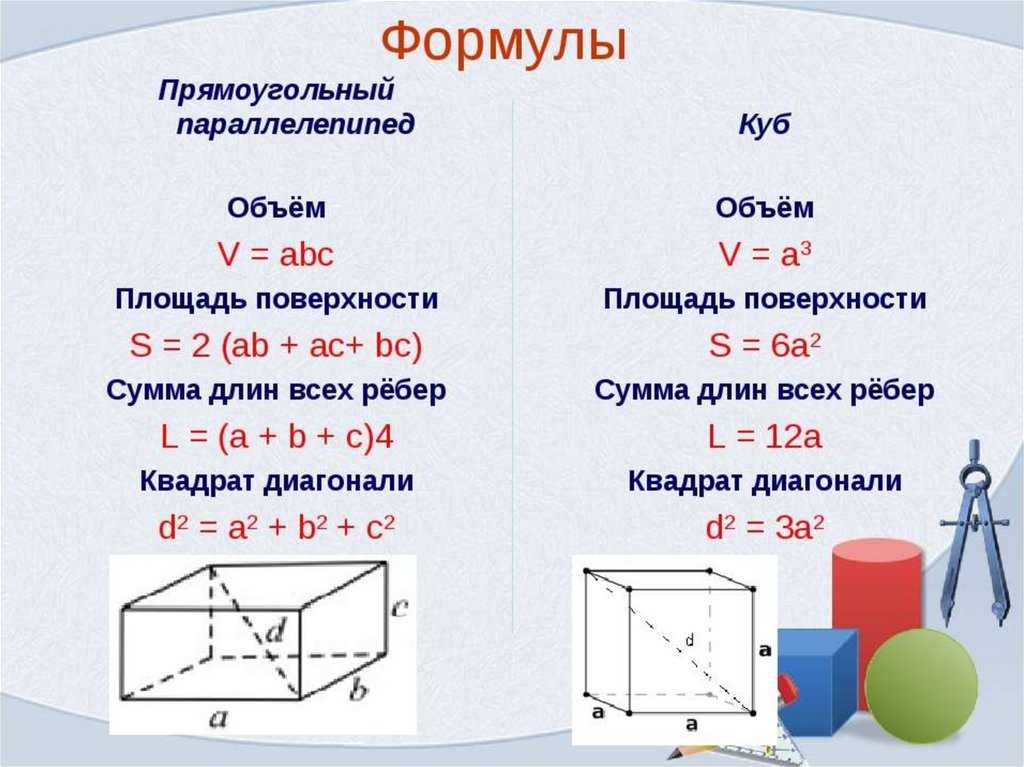
2) Объем параллелепипеда равен произведению площади поперечного сечения на боковое ребро .
Репетитору по математике: Как известно, формула является общей для всех призм и если репетитор уже доказал ее, нет смысла повторять тоже самое для параллелепипеда. Однако в работе со учеником среднего уровня (слабому формула не пригодиться) преподавателю желательно действовать с точностью до наоборот. Призму оставить в покое, а для параллелепипеда провести аккуратное доказательство.
3) , где –объем одной из шести треугольных пирамиды из которых состоит параллелепипед.
4) Если , то

Площадью боковой поверхности параллелепипеда называется сумма площадей всех его граней:
Полная поверхность параллелепипеда – это сумма площадей всех его граней, то есть площадь + две площади основания: .

О работе репетитора с наклонным параллелепипедом:
Задачами на наклонный параллелепипед репетитор по математике занимается не часто. Вероятность их появления на ЕГЭ достаточно мала, а дидактика неприлично бедная. Более-менее приличная задача на объем наклонного параллелепипеда вызывает серьезные проблемы, связанные с пределением расположения точки Н — основания его высоты. В этом случае репетитору по математике можно посоветовать обрезать параллелепипед до одной из шести его пирамид (о которых идет речь в свойстве №3), попробовать найти ее объем и умножить его на 6.

Если боковое ребро параллелепипеда имеет равные углы со сторонами основания, то Н лежит на биссектрисе угла A основания ABCD. И если, например, ABCD — ромб, то

Задачи репетитора по математике:
1) Грани параллелепипеда равные роибы со стороной 2см и острым углом . Найти объем параллелепипеда.

2) В наклонном параллелепипеде боковое ребро равно 5см. Сечение, перпендикулярное ему, является четырехугольником со взаимно перпендикулярными диагоналями, имеющими длины 6см и 8 см. Вычислить объем паралеллепипеда.
3) В наклонном параллелепипеде известно, что , а в онованием ABCD является ромб со стороной 2см и уголом . 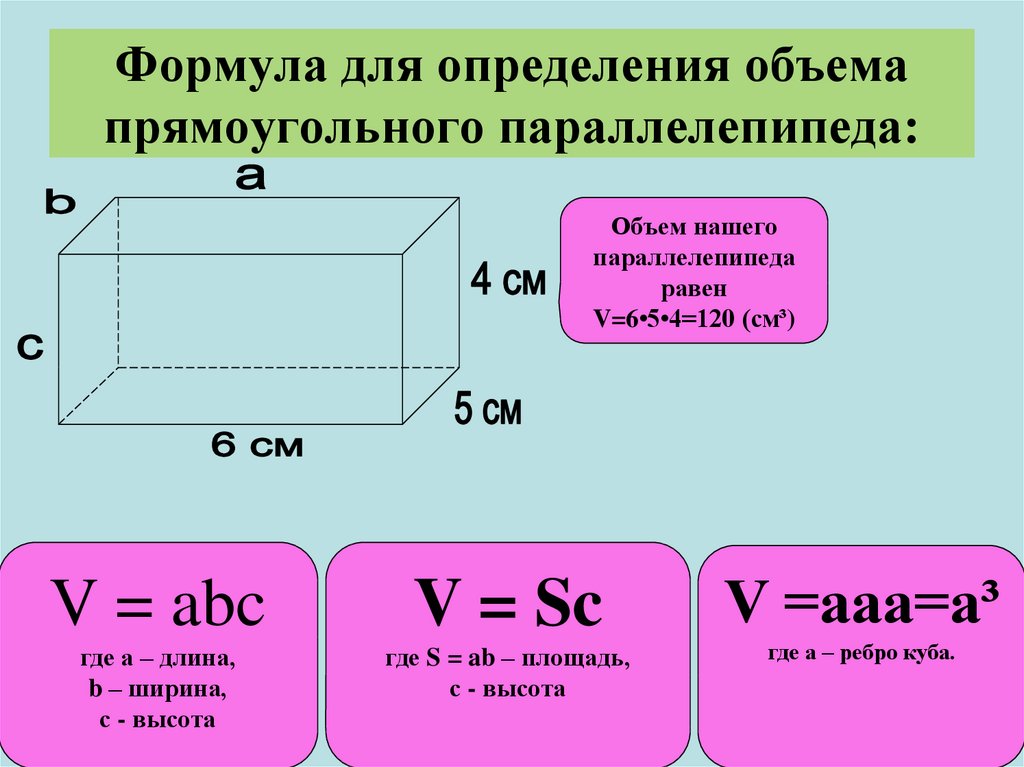Определите объем параллелепипеда.

Репетитор по математике, Александр Колпаков

5 класс. Математика. Формулы. — Объем прямоугольного параллелепипеда.

Комментарии преподавателя

 

Введение:

Как вы ду­ма­е­те, что тя­же­лее: 1 кг пуха или 1 кг гвоз­дей? А что за­ни­ма­ет боль­ше места? Вот об этом мы се­год­ня будем го­во­рить. Будем раз­би­рать­ся, в чем же раз­ни­ца между объ­е­мом и мас­сой.

Определение объема

Объем – это то, сколь­ко места в про­стран­стве за­ни­ма­ет объ­ект, а масса – это то, сколь­ко он весит. Вот литр – это объем или масса? И как он свя­зан с ки­ло­грам­мом? В ма­га­зине мо­ло­ко про­да­ет­ся в лит­ро­вых бу­тыл­ках, вода про­да­ет­ся 1,5-2-лит­ро­вых бу­тыл­ках, сме­та­на про­да­ет­ся в бан­ках по 250 грамм. А что такое 0,33 л?

Измерение объема

Итак, да­вай­те возь­мем весы, бу­тыл­ку и на­льем в нее 600 грамм масла. Потом возь­мем дру­гую такую же бу­тыл­ку и на­льем в нее 600 грамм воды.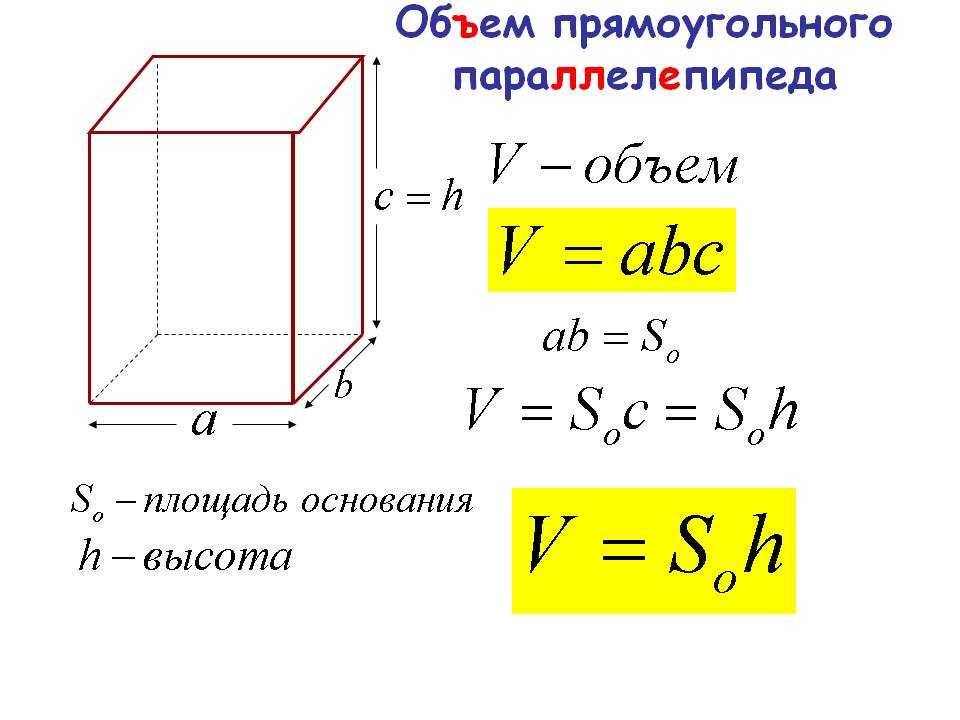 А те­перь мы возь­мем тесто для блин­чи­ков и на­льем в такую же бу­тыл­ку 600 грамм. По­смот­ри­те, мы везде на­ли­ва­ли 600 грамм – одну и ту же массу, а уро­вень жид­ко­стей по­лу­чил­ся раз­ный, но масса не из­ме­ни­лась (см. рис. 1).

Рис. 1. Срав­не­ние уров­ней жид­ко­стей: масла, воды и теста для блин­чи­ков 

Что же ме­ня­лось? Ме­ня­лось ко­ли­че­ство за­ни­ма­е­мо­го места. Как раз это – ко­ли­че­ство за­ни­ма­е­мо­го места – на­зы­ва­ют объ­е­мом. Масса у нас везде была одна и та же, а объем по­лу­чил­ся раз­ный.

Так что же такое, спро­си­те вы, литр? Возь­мем колбу и на­льем в нее 1 кг воды. Так вот, 1 кг воды, то есть то место, ко­то­рое за­ни­ма­ет 1 кг воды, до­го­во­ри­лись на­зы­вать лит­ром.

Да­вай­те еще раз сфор­му­ли­ру­ем. Объем – это число, по­ка­зы­ва­ю­щее, сколь­ко места в про­стран­стве за­ни­ма­ет объ­ект. А чем же, кроме лит­ров, ме­ря­ют объ­ект? Так же, как и у длины, и у пло­ща­ди су­ще­ству­ет много раз­ных спе­ци­аль­ных ве­ли­чин из­ме­ре­ния.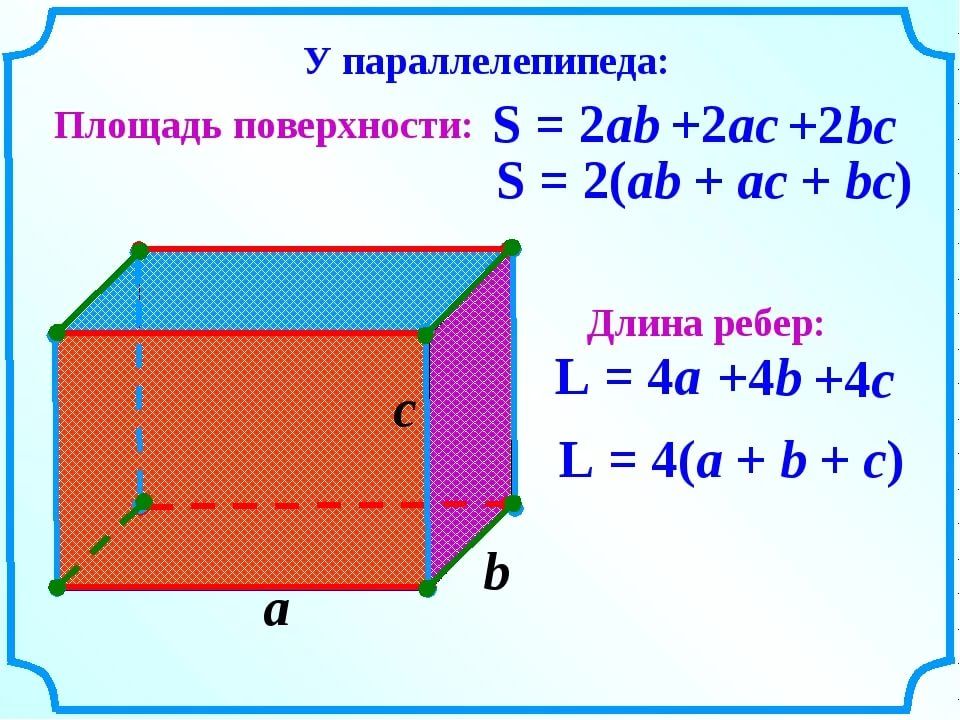 На­при­мер, бар­рель. Бар­рель – это ко­ли­че­ство нефти, ко­то­рое по­ме­ща­ет­ся в бочку, опре­де­лен­но­го раз­ме­ра (см. рис. 2).

Рис. 2. Бар­рель

Или есть такая ве­ли­чи­на как гал­лон. Гал­лон – это ве­ли­чи­на, ко­то­рой поль­зу­ют­ся для из­ме­ре­ния в Ан­глии и в Аме­ри­ке. Но обыч­но объ­е­мы ме­ря­ют ку­би­че­ски­ми де­ци­мет­ра­ми, ку­би­че­ски­ми сан­ти­мет­ра­ми, ку­би­че­ски­ми мет­ра­ми. А как же со­от­но­сит­ся литр с ку­би­че­ским де­ци­мет­ром или мет­ром? На самом деле литр – это один ку­би­че­ский де­ци­метр (см. рис. 3). 

Рис. 3. Литр – ку­би­че­ский де­ци­метр

То есть внутрь этого ку­би­ка по­ме­ща­ет­ся ровно 1 кг воды. Дело не в том, какой формы ко­роб­ка, а сколь­ко туда по­ме­ща­ет­ся. Да­вай­те по­про­бу­ем в ку­би­че­ский де­ци­метр на­сы­пать муки. Или можно пе­ре­сы­пать муку в пакет – и все равно по­лу­чит­ся 1 литр (или 1 ку­би­че­ский де­ци­метр). То, что там внут­ри, будет литр или ку­би­че­ский де­ци­метр, по­то­му что не важно, какой формы, – важно, сколь­ко за­ни­ма­ет места.

Объем прямоугольного параллелепипеда

Очень по­хо­же об­сто­ят дела с объ­е­мом пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да.

Объем куба со сто­ро­ной 1 еди­ни­ца – это 1 ку­би­че­ская еди­ни­ца. Опять же, ис­ход­ные ли­ней­ные ве­ли­чи­ны могут быть лю­бы­ми: мил­ли­мет­ры, сан­ти­мет­ры, дюймы.

На­при­мер, 1 см3 – это объем куба со сто­ро­ной 1 см, а 1 км3 – это объем куба со сто­ро­ной 1 км.

Най­дем объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да со сто­ро­на­ми 7 см, 5 см, 4 см. (Рис. 7.) 

Рис. 7. Пря­мо­уголь­ный па­рал­ле­ле­пи­пед

Ре­ше­ние

Объем на­ше­го пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да – это ко­ли­че­ство еди­нич­ных кубов, по­ме­ща­ю­щих­ся в него.

Уло­жим на дно ряд еди­нич­ных ку­би­ков со сто­ро­ной 1 см вдоль длин­ной сто­ро­ны. По­ме­сти­лось 7 штук. Уже по опыту ра­бо­ты с пря­мо­уголь­ни­ком мы знаем, что на дно по­ме­стит­ся всего 5 таких рядов, по 7 штук в каж­дом. То есть всего:

На­зо­вем это слой.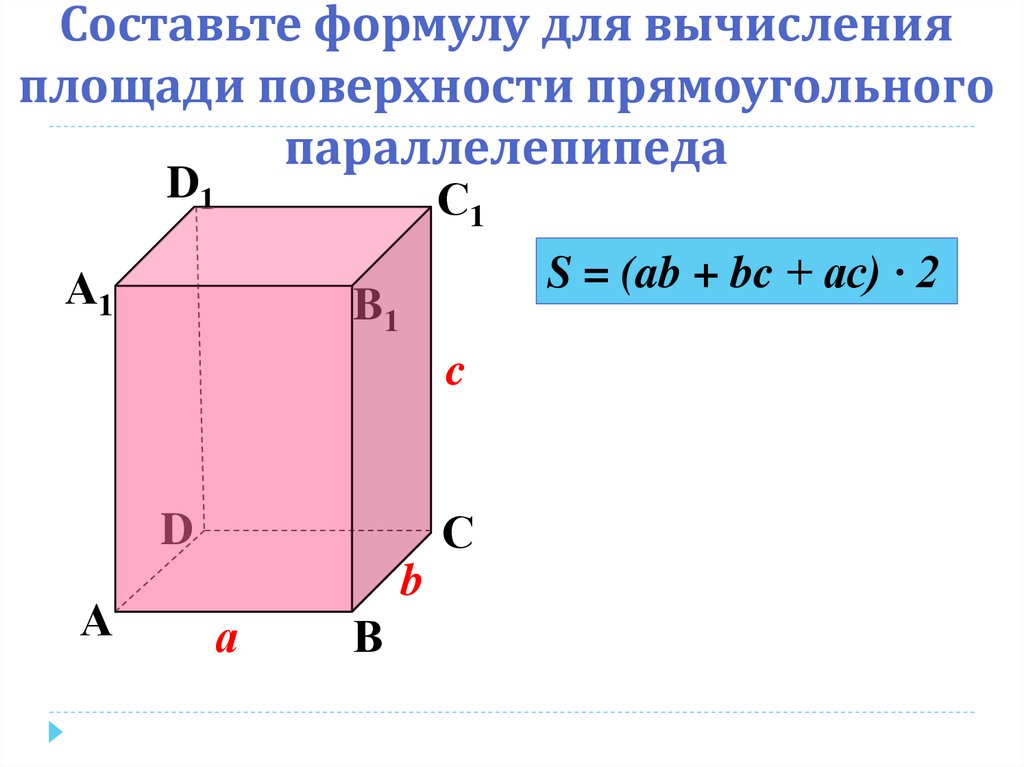 Сколь­ко таких слоев мы можем уло­жить друг на друга?

Это за­ви­сит от вы­со­ты. Она равна 4 см. Зна­чит, укла­ды­ва­ет­ся 4 слоя в каж­дом по 35 штук. Всего:

А от­ку­да у нас по­яви­лось число 35? Это 75. То есть ко­ли­че­ство ку­би­ков мы по­лу­чи­ли пе­ре­мно­же­ни­ем длин всех трех сто­рон.

Но это и есть объем на­ше­го пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да.

Ответ: 140  

Те­перь мы можем за­пи­сать фор­му­лу и в общем виде. (Рис. 8.) 

Рис. 8. Объем па­рал­ле­ле­пи­пе­да

Объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да со сто­ро­на­ми , ,  равен про­из­ве­де­нию всех трех сто­рон.

Если длины сто­рон даны в сан­ти­мет­рах, то объем по­лу­чит­ся в ку­би­че­ских сан­ти­мет­рах (см3).

Если в мет­рах, то объем в ку­би­че­ских мет­рах (м3).

Ана­ло­гич­но объем может быть из­ме­рен в ку­би­че­ских мил­ли­мет­рах, ки­ло­мет­рах и т. д.

Задача 1

Стек­лян­ный куб со сто­ро­ной 1 м на­пол­нен водой це­ли­ком. Ка­ко­ва масса воды? (Рис. 9.)

Рис. 9. Куб

Ре­ше­ние

Куб яв­ля­ет­ся еди­нич­ным. Сто­ро­на – 1 м. Объем – 1 м3.

Если мы знаем, сколь­ко весит 1 ку­би­че­ский метр воды (со­кра­щен­но го­во­рят ку­бо­метр), то за­да­ча ре­ше­на.

Но если мы этого не знаем, то нетруд­но по­счи­тать.

Длина сто­ро­ны .

По­счи­та­ем объем в дм3.

Но 1 дм3 имеет от­дель­ное на­зва­ние, 1 литр. То есть у нас 1000 лит­ров воды.

Нам всем из­вест­но, что масса од­но­го литра воды равна 1 кг. То есть у нас 1000 кг воды, или 1 тонна.

По­нят­но, что такой куб, на­пол­нен­ный водой, не под силу пе­ре­дви­нуть ни од­но­му обыч­но­му че­ло­ве­ку.

Ответ: 1 т.

Задача 2

Рис. 10. Хо­ло­диль­ник

Хо­ло­диль­ник имеет вы­со­ту 2 метра, ши­ри­ну 60 см и глу­би­ну 50 см. Найти его объем.

Ре­ше­ние

Пре­жде чем мы вос­поль­зу­ем­ся фор­му­лой объ­е­ма – про­из­ве­де­ние длин всех сто­рон – необ­хо­ди­мо пе­ре­ве­сти длины в оди­на­ко­вые еди­ни­цы из­ме­ре­ния.

Мы можем пе­ре­ве­сти все в метры или все в сан­ти­мет­ры.

Со­от­вет­ствен­но, и объем мы по­лу­чим или в ку­би­че­ских мет­рах, или ку­би­че­ских сан­ти­мет­рах.

Сде­ла­ем и так, и так.

Ответ:  или 

Думаю, вы со­гла­си­тесь, что в ку­би­че­ских мет­рах объем более по­ня­тен.

Че­ло­век на глаз плохо от­ли­ча­ет число с пятью ну­ля­ми от числа с ше­стью ну­ля­ми, а ведь одно в 10 раз боль­ше, чем дру­гое.

Перевод единиц объема

Часто нам нужно пе­ре­ве­сти одну еди­ни­цу объ­е­ма в дру­гую. На­при­мер, ку­бо­мет­ры в ку­би­че­ские де­ци­мет­ры. Тя­же­ло за­пом­нить все эти со­от­но­ше­ния. Но этого и не нужно де­лать. До­ста­точ­но по­нять общий прин­цип.

На­при­мер, сколь­ко ку­би­че­ских сан­ти­мет­ров в ку­би­че­ском метре?

Да­вай­те по­смот­рим, сколь­ко ку­би­ков со сто­ро­ной 1 сан­ти­метр по­ме­стит­ся в куб со сто­ро­ной 1 м. (Рис. 11.)

Рис. 11. Куб

В один ряд укла­ды­ва­ет­ся 100 штук (ведь в одном метре 100 см).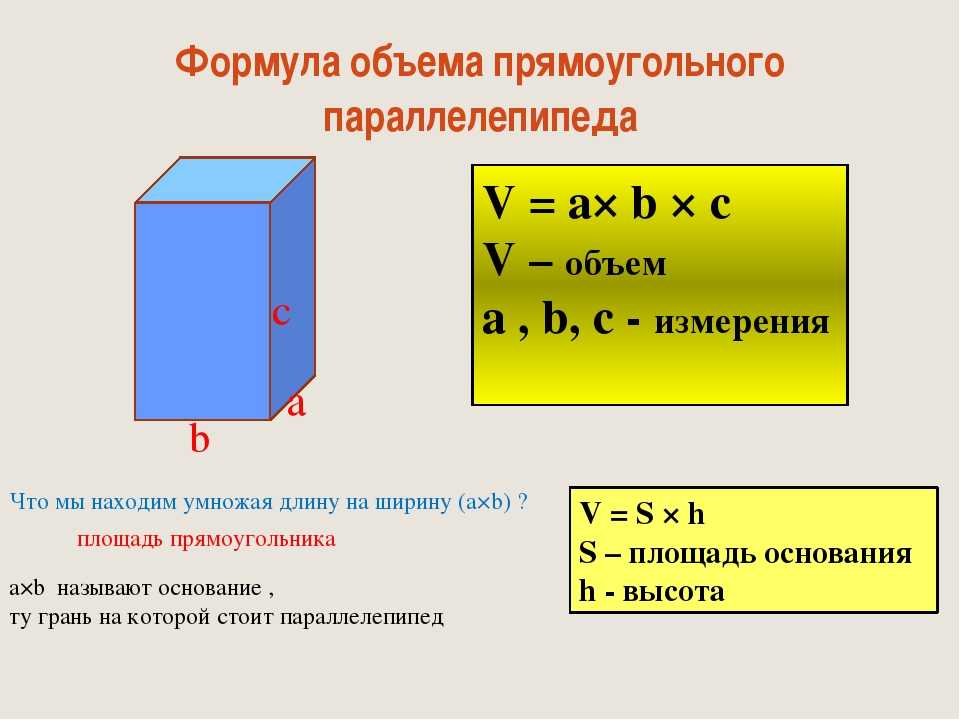

В один слой укла­ды­ва­ет­ся 100 рядов или  ку­би­ков.

Всего по­ме­ща­ет­ся 100 слоев.

Всего 

Таким об­ра­зом, 

То есть если ли­ней­ные ве­ли­чи­ны свя­за­ны со­от­но­ше­ни­ем «в одном метре 100 см», то чтобы по­лу­чить со­от­но­ше­ние для ку­би­че­ских ве­ли­чин, нужно воз­ве­сти 100 в 3 сте­пень (). И не нужно каж­дый раз чер­тить кубы.

За­од­но мы уви­де­ли со­от­но­ше­ние и для еди­ниц пло­ща­ди. В одном квад­рат­ном метре  квад­рат­ных сан­ти­мет­ров. В одном слое у нас было 10 000 ку­би­ков.

Сколь­ко в одном ку­би­че­ском ки­ло­мет­ре ку­би­че­ских мет­ров?

Ответ: 1 млрд м3.

Каж­дый ку­бо­метр воды весит 1 т. Зна­чит, ку­би­че­ский ки­ло­метр воды весит 1 млрд тонн. Та­ки­ми еди­ни­ца­ми поль­зу­ют­ся при из­ме­ре­нии ко­ли­че­ства воды в морях и оке­а­нах.

Ка­ко­ва масса од­но­го ку­би­че­ско­го сан­ти­мет­ра воды?

Мы знаем массу од­но­го литра, это 1 кг, но 1 литр – это ку­би­че­ский де­ци­метр.

Так как , то . Но это зна­чит, что 1  весит:

Для одной ты­сяч­ной су­ще­ству­ет при­став­ка «мил­ли-» (пом­ним, что мил­ли­метр – это одна ты­сяч­ная метра), эту при­став­ку ис­поль­зу­ют и здесь.

То есть иными сло­ва­ми мы можем ска­зать, что один мил­ли­литр воды имеет массу 1 г.

 

Источник видео: http://www.youtube.com/watch?v=4suTtsj23t4

Источники конспекта:

 http://interneturok.ru/ru/school/matematika/5-klass/bplowadi-i-obyomyb/ob-yomy-ob-yomy-pryamougolnogo-parallelepipeda?konspekt&chapter_id=767

http://interneturok.ru/ru/school/matematika/5-klass/bplowadi-i-obyomyb/ob-yom?konspekt&chapter_id=767

Источник теста: http://alfusja-bahova.ucoz.ru/index/test_28_obem_prjamougolnogo_parallelepipeda_edinicy_obema/0-110

Объем параллелепипеда

Дом Математика Объем параллелепипеда

Параллелепипед — это многогранник с шестью гранями, каждая грань которого является параллелограммом.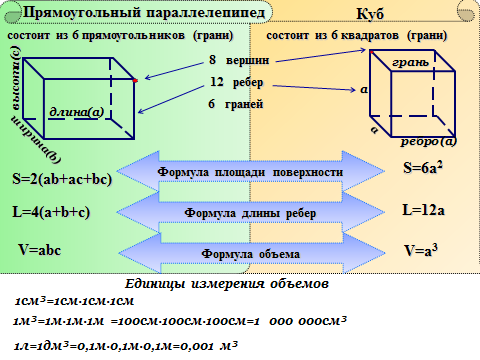

В основном они образованы шестью сторонами параллелограмма, что приводит к образованию трехмерной фигуры или призмы. Частные случаи параллелограмма могут быть кубом, параллелограммом или ромбом в зависимости от длины сторон. В этой статье мы выводим формулу параллелепипеда, используя некоторые основные векторные умножения.

Параллелепипед

Вывод формулы объема параллелепипеда

Рассчитаем формулу объема параллелепипеда, как показано на рисунке ниже.

Формула объема параллелепипеда

Стороны параллелепипеда представлены векторами a, b и c.

Объем любого четырехугольника можно вычислить, умножив площадь основания на высоту. Здесь базовая площадь будет векторным произведением двух векторов b и c. Направление b x c будет перпендикулярно базовой плоскости. Высота будет |a| |cos Ф|. Таким образом, объем параллелепипеда можно рассчитать как |( b x c ). а|.

Формула объема параллелепипеда

Объем параллелепипеда ,

 V = |bxc||c||cos ϕ|

   = |( b x c ). а|

Разница между объемом параллелепипеда и параллелограмма

Параллелограмм является двумерным четырехугольником, поэтому у него нет объема. Но у него есть площадь по формуле b*h, где b — ширина, а h — высота параллелограмма. С другой стороны, параллелепипед представляет собой трехмерный многогранник, поэтому у него есть объем и площадь поверхности. Площадь поверхности параллелепипеда можно рассчитать как сумму всех шести параллелограммов.

Real-life examples of a parallelopiped

• Eraser
• Blocks of stone
• Cubes
• Cuboids
• Rhomboids

See Also

Area of ​​a sector formula
Perimeter of a sector- Формула
Периметр прямоугольного треугольника
Каждый квадрат является прямоугольником
Ортоцентр треугольника

• БИРКИ
• класс 12

Предыдущая статья7 Различия между равноденствием и солнцестоянием

Следующая статьяБензол

Поиск

DewWool Видео дня

Счастливого Рождества и счастливого Нового года

Комикс дня

Почему бриллианты такие дорогие? Оправдана ли цена? Нажмите на изображение, чтобы прочитать больше.

Викторина дня DewWool

Поддержите нас

Мы хотим сделать науку интересной и в то же время бесплатной! Ваш вклад в эту страницу поможет нам донести качественный контент до детей, которые больше всего в нем нуждаются. Если вам нравится, что мы делаем, и вы хотите поддержать нас, вы можете посетить нашу страницу пожертвований ko-fi на www.ko-fi.com/dewwool.

Категории

• Анимация
• Биология
• Блог
• Химия
  • Органическая химия
• Комикс
• Математика
• Физика
  • Оптика и акустика
• Викторина
• Без категории
• рабочих листов

Архивы

Архивы Выбрать месяц Декабрь 2022 Ноябрь 2022 Октябрь 2022 Август 2022 Июль 2022 Июнь 2022 Май 2022 Апрель 2022 Март 2022 Январь 2022 Декабрь 2021 Ноябрь 2021 Октябрь 2021 Сентябрь 2021 Август 2021 Июль 2021 Июнь 2021 Май 2021 Ноябрь 2021 Апрель 2021 Декабрь 2021 Февраль 2020 Октябрь 2020 Сентябрь 2020 Август 2020 Июль 2020 Июнь 2020 Май 2020 Март 2020

Последние сообщения

Гравитационные комиксы

админ — 20 декабря 2022 0

Гравитация — это универсальная сила, с которой объекты притягиваются друг к другу. В нашей Вселенной есть много событий, которые регулируются гравитацией. Здесь…

10 Различия между вращением и оборотом

админ —

9 декабря 2022 0

Гравитационное притяжение Солнца удерживает Землю и другие планеты на их орбитах вокруг звезды. Как солнце притягивает землю…

15 Использование центрифуг

админ — 6 декабря 2022 0

Центрифуга — это устройство, которое использует свою центробежную силу для разделения всех компонентов, присутствующих в жидкости, путем вращения этой конкретной жидкости…

Вычисление объема прямоугольника

Объемный прямоугольник, расчет онлайн

Суммарно:

Онлайн-калькулятор позволяет рассчитать объем прямоугольника по его длине, ширине и высоте.

volume_rectangle онлайн

---

Описание:

Калькулятор способен рассчитать онлайн объем прямоугольного параллелепипеда другими словами рассчитать объем прямоугольного кубоида . Объем прямоугольного параллелепипеда определяется формулой `(L*l*h)`, где L представляет собой длину, ширину с одной стороны и h высота. Калькулятор объема поддерживает числовые, а также буквенные выражения.

Калькулятор объема умеет вычислять объем прямоугольного параллелепипеда , по переменным числовой, возвращаются точные и приблизительные результаты.

Таким образом, вычисляет объем прямоугольного параллелепипеда , длина которого равна 3, ширина равна 2, и высота 4 выполняется путем ввода следующей формулы объем_прямоугольник(`3;2;4`).

Калькулятор объема может выполнять символьные вычисления или буквальные вычисления. Например, чтобы вычислить объем прямоугольного параллелепипеда длины x, ширины x+1 и высоты x/2, введите следующую формулу volume_rectangle(`x;1+x;x/2`) , после вычисления возвращается результат.

Синтаксис:

объем_прямоугольник(длина;ширина;высота)

---

Примеры:

объем_прямоугольник(`3;2;4`), возвращает 24 также

Список связанных калькуляторов:

• Площадь квадрата : area_square. Онлайн-калькулятор площади, который может рассчитать площадь квадрата по длине стороны.
• Площадь круга : area_circle. Онлайн-калькулятор площади, который может рассчитать площадь круга по его радиусу или по диаметру.
• Площадь прямоугольника : area_rectangle. Онлайн-калькулятор площади, который может рассчитать площадь прямоугольника по его длине и ширине.
• Найти уравнение прямой линии из двух точек: уравнение_прямой_линии. Калькулятор уравнения прямой позволяет рассчитать уравнение прямой по координатам двух точек с пошаговым расчетом.
• Калькулятор периметра: периметр. Онлайн-калькулятор периметра, который вычисляет периметр прямоугольника, периметр квадрата, периметр треугольника или периметр круга.
• Периметр квадрата: perimeter_square. Онлайн-калькулятор позволяет рассчитать периметр квадрата по длине стороны.
• Периметр круга: perimeter_circle. Онлайн-калькулятор, вычисляющий периметр круга по его радиусу.
• Периметр прямоугольника : perimeter_rectangle.

  No related posts.