Калькулятор вычисления объема и площади геометрических фигур
Весь осязаемый мир представляет собой объемные геометрические фигуры и их сочетания. Определение объемов и площадей поверхностей тел может понадобиться не только при решении школьных задач, но также в быту или профессиональной деятельности. Простые объемные тела разделяются на две категории.
Тела вращения
Первая категория — это тела вращения. Такие объемные фигуры образуются путем вращения плоской фигуры вокруг одной из сторон или путем движения образующей кривой вдоль направляющей. Наш каталог предлагает калькуляторы, при помощи которых можно рассчитать параметры следующих тел вращения.
Конус
Конус — фигура, которая создается путем вращения прямоугольного треугольника вокруг одного из катетов. Также конус формируется путем движения образующего луча вдоль направляющей окружности, при этом начало луча остается неподвижным. Для определения площади поверхности конуса используется простая формула:
S = pi × R × (R + l),
где R — радиус основания, l — образующая конуса.
Для подсчета объема конической фигуры используется следующее соотношение:
V = (pi × R2 × h)/3,
где h — высота конуса.
Конусы широко встречаются в быту, производстве или науке. Например, коническую форму имеют вафельные рожки для мороженного, абажуры для светильников, пожарные ведра или воронки. В природе конус также распространен: горы, вулканы, сосновые шишки или шляпки грибов имеют форму данного тела.
Цилиндр
Цилиндр — тело вращения, которое образуется путем вращения прямоугольника вокруг одной из сторон. Также цилиндр формируется путем движения образующей прямой по направляющей кривой, которая в случае цилиндра может быть окружностью, эллипсом, параболой или гиперболой. Такие «экзотические» цилиндры носят соответствующие названия эллиптических, параболических и гиперболических фигур, однако в реальной жизни наибольшее распространение получил прямой круговой цилиндр. Для определения площади поверхности такого цилиндра используется формула:
S = 2 pi × R × (R + h),
где R — радиус основания, h — высота цилиндра.
Для вычисления объема цилиндра геометры применяют следующее соотношение:
V = pi × R2 × h.
Цилиндр легко встретить в реальной жизни: это и цистерны, и поршни двигателей, и колонны, и трубы газопроводов. Цилиндры широко используются в производстве, поэтому многим инженерам приходится вычислять площади поверхностей или объемы цилиндрических объектов.
Шар
Шар — тело вращения, созданное путем вращения круга около своей оси. Сфера — это поверхность, сформированная путем вращения окружности или полуокружности вокруг своей оси. Таким образом, шар — это пространство, ограниченное сферой. Площадь сферы вычисляется по формуле:
S = 4 pi × R2,
где R — радиус сферы.
Для подсчета объема шара используется следующее выражение:
V = 4/3 pi × R3.
Шар — идеальная фигура, поэтому в природе она встречается довольно часто. К примеру, сферическую форму принимают капли дождя, снежные комья, планеты, звезды, а также ягоды или кроны деревьев. В человеческой повседневности форму шара имеют спортивные мячи, пушечные ядра, подшипники или бусины.
В человеческой повседневности форму шара имеют спортивные мячи, пушечные ядра, подшипники или бусины.
Многогранники
Вторя категория — многогранники. Многогранник или полиэдр — это объемное тело, каждая грань которого является многоугольником. Существует огромное множество многогранников: к ним относятся призмы, пирамиды, параллелепипеды, а также платоновы тела — полиэдры, гранями которых являются правильные многоугольники. В нашем каталоге вы найдете инструменты для определения площадей поверхностей и объемов следующих многогранников.
Призма
Призма — это полиэдр, который состоит из двух n-угольных оснований, параллельных друг другу и n боковых граней, формирующих боковую поверхность призмы. Грань призмы — это всегда параллелограмм. Простыми словами, если в основании фигуры лежит квадрат, то призма считается четырехугольной, но при этом шестигранной: четыре грани составляют боковую поверхность, а две — поверхность оснований. Если в основании лежит пентагон — то призма пятиугольная и семигранная, а если додекагон — то фигура 12-угольная и 14-гранная. Если в основании призмы положить полигон, количество сторон которого стремится к бесконечности, то основание превратится в круг, а призма — в цилиндр. Для определения площади боковой поверхности призматической фигуры используется выражение:
Если в основании призмы положить полигон, количество сторон которого стремится к бесконечности, то основание превратится в круг, а призма — в цилиндр. Для определения площади боковой поверхности призматической фигуры используется выражение:
Sb = n × a × h,
где a — сторона параллелограмма, n — количество граней, h — его высота.
Площадь поверхности основания призмы зависит от многоугольника и в общем виде для правильных полигонов рассчитывается как:
So = n/4 × a2 × ctg(pi/n),
где n — количество сторон фигуры, a — длина стороны.
Полная же площадь поверхности определяется как:
S = 2 So + Sb.
Объем призмы вычисляется по следующей формуле:
V = So х h.
Призма — наиболее распространенный в человеческой повседневности полиэдр. Форму призмы имеет огромное число предметов вокруг вас: это системный блок компьютера, сабвуфер, стол, шкаф, комната и здание. Если выйти на улицу, то вы увидите царство призм. Именно поэтому инструмент для определения объемов и площадей поверхности призматических фигур всегда актуален.
Пирамида
Пирамида — это полиэдр, который составлен из n-угольного основания и n боковых граней, формирующих боковую поверхность пирамидальной фигуры. Грань пирамиды — это всегда треугольник. Вид полиэдра определяется в зависимости от того, какой полигон выступает в роли фундамента пирамиды. Следовательно, пирамиды бывают треугольные, четырехугольные, пятиугольные или n-угольные. Площадь боковой порвехности пирамиды рассчитывается согласно выражению:
Sb = 0,5 P х h,
где h — высота пирамиды, P — периметр полигона, лежащего в основании.
Площадь фундамента рассчитывается по общей формуле для любого правильного полигона:
So = n/4 × a2 × ctg(pi/n),
где a — длина стороны, n — количество сторон.
Полная площадь поверхности пирамиды определяется как:
S = So + Sb.
Для определения объема пирамиды используется формула:
V = (So х h)/3,
где h — высота фигуры.
Пирамида — довольно распространенная фигура и широко используется в архитектуре. Всем известно о величественных пирамидах в Египте или колоссальных сооружениях в Южной Америке. Современные архитекторы также активно используют пирамиды при проектировании торговых комплексов, музеев или выставочных галерей. Кроме того, пирамидальные фигуры часто встречаются в производстве и машиностроении.
Всем известно о величественных пирамидах в Египте или колоссальных сооружениях в Южной Америке. Современные архитекторы также активно используют пирамиды при проектировании торговых комплексов, музеев или выставочных галерей. Кроме того, пирамидальные фигуры часто встречаются в производстве и машиностроении.
Параллелепипед
Параллелепипед — это гексаэдр с попарно параллельными гранями. Если ребра такого шестигранника равны, то параллелепипед превращается в куб. Параллелепипед — это частный случай прямой четырехугольной призмы, поэтому формулы для расчета площади и объема фигуры выводятся из соотношений для призмы с n = 4. Таким образом, для расчета площади поверхности гексаэдра используется формула:
S = 4 (a × h) + 2 (a × b),
где a, b — стороны основания параллелепипеда, h — высота фигуры.
Объем полиэдра определяется как:
V = a × b × h.
Параллелепипед, так же как и призма, постоянно встречается в реальности. Форму такого гексаэдра имеет множество вещей вокруг нас: шлакоблоки, бетонные плиты, грузовые контейнеры или картонные коробки. Формулы для расчета атрибутов параллелепипеда, несомненно, пригодятся вам не только для решения школьных задач, но и в бытовых вопросах.
Формулы для расчета атрибутов параллелепипеда, несомненно, пригодятся вам не только для решения школьных задач, но и в бытовых вопросах.
Примеры использования
Наш калькулятор позволяет рассчитать объем или площадь поверхности любого из заданных геометрических тел. Рассмотрим пару примеров.
Заливка бетона
К примеру, вы решили построить летний коттедж, а для каждого дома необходим фундамент. Вы выбрали плитный фундамент — монолитную плиту, которую заливают под всей площадью будущего жилища. Вам требуется узнать, сколько бетона понадобится для обустройства такого фундамента. Плитное основание представляет собой обычный параллелепипед, следовательно, вам понадобится определить объем шестигранника. Пусть вы хотите построить дом с размерами 6 на 9 метров, а толщина фундамента согласно техническим требованиям должна составлять 15 см. Приведем все параметры в одни единицы измерения и воспользуемся калькулятором для расчета объема параллелепипеда.
V = 8,1
Таким образом, нам потребуется заказать 8,1 кубометров бетонной смеси.
Пошив мячей
Допустим, вы открыли производство по производству волейбольных мячей, и вам требуется узнать, сколько материала уходит на пошив одного мяча. Согласно данным из Википедии, стандартный волейбольный мяч имеет длину окружности l = 67 см, следовательно, радиус такого мячика составит 10,6 см. Зная радиус, вы без проблем можете определить, сколько синтетической кожи понадобится для создания одного изделия
S = 0,141
Это означает, что для обшивки одного мяча вам понадобится 0,141 квадратных метров кожи.
Заключение
Объемные фигуры постоянно вращаются вокруг нас, поэтому задача определения площадей поверхностей и объемов многогранников остается актуальной задачей. Используйте наш каталог онлайн-калькуляторов и выполняйте необходимые расчеты для решения бытовых или производственных задач.
Геометрический калькулятор для ОС Андроид
Советы и секреты начинающим
Популярное
- 👀 196970
Кракозябры (иероглифы) при копировании с PDF документа
👀 165920
Не работают нижние сенсорные кнопки?
👀 143344
Excel не печатает часть таблицы .
 ..
.. 👀 127523
Неправильная нумерация страниц в Microsoft Office Word
👀 89207
Быстро пишем в Ворде знак С ° (Градус Цельсия)
👀 66978
Как создать кроссворд? Онлайн сервисы для создания кроссвордов.
👀 61298
Как изменить приложение по умолчанию на Android?
JM Инструменты Просмотров: 1041
- Тип программы: APK
- Поддерживаемые ОС: Android 4.2 и выше
- Лицензия: Бесплатная
- Язык интерфейса: Английский, русский
Считайте площади, периметры и объемы геометрических фигур, установив на свой девайс геометрический калькулятор. В приложении содержатся все необходимые формулы на каждый расчет, который необходимо провести.
Для удобства программа содержит в себе обычный калькулятор.
Список расчетов для каждой геометрической фигуры, которые реализованы в калькуляторе:
-
1.
 Расчет площади и периметра квадрата через сторону или диагональ.
Расчет площади и периметра квадрата через сторону или диагональ. - 2. Расчет площади и периметра прямоугольника через сторону или диагональ.
- 3. Расчет площади, периметра, сторон и углов различных треугольников.
- 4. Расчет площади и периметра параллелограмма.
- 5. Расчет площади и периметра трапеции.
- 6. Расчет площади четырехугольника.
- 7. Расчет площади и периметра различных многоугольников.
- 8. Расчет площади и периметра ромба.
- 9. Расчет площади окружности через радиус и диаметр.
- 10. Расчет площади кольца.
- 11. Площадь сектора окружности.
- 12. Площадь сектора кольца.
- 13. Площадь эллипса.
- 14. Объем и площадь поверхности куба.
- 15. Расчет объема и площади поверхности параллелепипеда.
-
16. Объем и площадь полной и боковой поверхности цилиндра.

- 17. Объем полого цилиндра (трубы).
- 18. Объем пирамиды пяти видов.
- 19. Объем усеченной пирамиды.
- 20. Объем конуса.
- 21. Объем усеченного конуса.
- 22. Объем шара, площадь поверхности шара.
- 23. Объем сектора шара и площадь поверхности.
- 24. Объем шарового сегмента.
Страница программы в маркете
Добавить комментарий
- Вперед
+ онлайн-решатель с бесплатными простыми шагами
Калькулятор геометрической последовательности позволяет вычислить обыкновенное отношение между последовательностью чисел.
Калькулятор геометрической последовательности — это мощный инструмент, который имеет различные приложения. Существенным применением Калькулятора геометрической последовательности является нахождение прогрессирующего интереса к сберегательному счету. Другие мощные приложения можно найти в биологии и физике. 9{th}$ срок (Xk) , позиция (Xj) срок и позиция (Xk) срок. Калькулятор геометрической последовательности затем вычисляет обыкновенное отношение между этой последовательностью и предоставляет результаты.
Другие мощные приложения можно найти в биологии и физике. 9{th}$ срок (Xk) , позиция (Xj) срок и позиция (Xk) срок. Калькулятор геометрической последовательности затем вычисляет обыкновенное отношение между этой последовательностью и предоставляет результаты.
Как пользоваться калькулятором геометрической последовательности?
Вы можете использовать калькулятор геометрической последовательности , введя математические значения в соответствующие поля и нажав кнопку «Отправить». 9{th} $ условия вместе с их позициями, чтобы найти обыкновенное отношение между каждым числом в последовательности. Обычное отношение отображается в отдельном окне вместе с уравнением, используемым для получения отношения. Используемое уравнение выглядит следующим образом:
\[ r = \frac {X_{n}}{X_{n-1}} \]
Чтобы полностью понять концепцию этого калькулятора, давайте сначала рассмотрим некоторые важные понятия, связанные с работой калькулятора.
Что такое геометрическая последовательность? 9{n-1} \]
Чуть позже мы обсудим вывод этого уравнения.
Во-первых, важно понимать, что, несмотря на постоянное умножение чисел в геометрической прогрессии, оно отличается от факториала. Однако у них есть сходство, например соотношение чисел для их GCM (наибольший общий множитель) и LCM (наименьший общий множитель).
Это означает, что GCF является наименьшим значением в последовательности. Напротив, LCM представляет собой самое высокое значение в ряду.
Что такое геометрическая прогрессия?
Геометрическая прогрессия представляет собой группу чисел, связанных общим отношением, как упоминалось ранее. Обычное отношение является определяющей функцией, отвечающей за соединение этих чисел в последовательность.
Начальный номер последовательности и обыкновенное отношение используются для получения рекурсивных и явных формул.
Теперь давайте составим уравнение, которое можно использовать для описания геометрической прогрессии 9{n-1} \]
$n$ — позиция термина в последовательности.
Обычно геометрическая последовательность записывается, начиная с начального числа и продолжая в порядке возрастания. Это поможет вам рассчитать ряд гораздо проще.
Существует несколько способов представления информации в математике. Точно так же мы рассмотрим рекурсивные и явные формулы, используемые для нахождения геометрических последовательностей .
Типы геометрической прогрессии 9{k}}) = a(\frac{1}{1-r}) \]
Свойства геометрической последовательности
Вот некоторые свойства геометрической последовательности :
- Новый ряд дает геометрическую прогрессию с тем же знаменателем , когда каждый член геометрической прогрессии умножается или делится на одну и ту же ненулевую величину.
- Обратные выражения также образуют геометрическую прогрессию в геометрической прогрессии. В конечной геометрической прогрессии 9{2} = ак $.
- Новый ряд также имеет геометрическую прогрессию, когда члены существующего ряда выбираются через равные промежутки времени.

- Когда в геометрической прогрессии есть ненулевые неотрицательные члены, логарифмирование каждого члена создает арифметическую прогрессию и наоборот.
Явная формула, используемая в геометрической последовательности
Явная формула Формулы используются для определения информации в геометрической последовательности. Вывод явной формулы показан выше. Мы можем заменить значения и еще больше упростить формулу, чтобы создать общее уравнение. 9{n-1} \]
где,
\[n \in \mathbb{N} \]
Где $ n \in N $ означает n = 1,2,3,4,5,….
Теперь давайте рассмотрим рекурсивную формулу для геометрической прогрессии.
Рекурсивная формула, используемая в геометрической последовательности
Рекурсивная формула — это еще один способ представления информации в геометрической последовательности. Есть две основные части рекурсивной формулы. Обе эти части передают разную информацию о геометрических последовательностях.
В первой части объясняется, как вычислить обыкновенное отношение между числами. Вторая часть описывает первый член геометрической прогрессии. Мы можем рассчитать общее отношение, объединив эти две части информации.
Следующее уравнение является рекурсивной формулой:
\[ a_{n} = a_{n-1} \ * \ r \]
ai = x
Здесь x представляет любое явное число, которое может использоваться. Уравнение похоже на явное 9Формула 0038, которую мы рассмотрели ранее.
Что такое обычное отношение в геометрической прогрессии?
обыкновенный коэффициент — это число, умноженное или разделенное через промежутки между числами в геометрической прогрессии. Это обыкновенное отношение , потому что ответ всегда будет одним и тем же, если вы разделите две последовательные цифры. Неважно, где вы выбираете термины — они должны быть рядом друг с другом.
Обычно мы представляем общую прогрессию как a1, (a1r), (a2r), (a3r),… здесь a1 — первый член, (a1r) — второй член и так далее. Обычное отношение обозначается r.
Обычное отношение обозначается r.
Глядя на приведенное выше представление общей прогрессии, мы можем вывести следующее уравнение для обыкновенного отношения .
\[ r = \frac {a_{n}}{a_{n-1}} \]
Арифметические и геометрические последовательности
Арифметическая последовательность — это последовательность, в которой разница между двумя последовательными числами равна одинаковый. Это просто означает, что последнее число в ряду умножается на заданное целое число, чтобы определить следующее число.
Вот пример представления арифметических последовательностей:
a, a+d, a + 2d , a + 3d, a + 4d,…
Здесь $a$ – первый член, а d – общая разница между терминами.
Напротив, геометрические последовательности — это числа, имеющие общее отношение между каждым значением. Общее отношение одинаково для каждого последующего значения. Следующее число в последовательности вычисляется путем умножения обыкновенного отношения на член. 9{3},… \]
9{3},… \]
Здесь a — первое слагаемое, r — отношение между последовательностями.
В следующей таблице описаны различия между геометрическими и арифметическими последовательностями.
Пример:
5, 10, 15, 20,…
Пример:
2, 4, 8, 16,…
. Жизнь?
Геометрические последовательности широко используются в нескольких приложениях, и одно из распространенных приложений геометрических последовательностей в реальной жизни — расчет процентных ставок.
При вычислении термина в ряду математики умножают начальное значение последовательности на коэффициент, умноженный на единицу ниже номера члена. Заемщик может определить из последовательности, какую сумму его банк ожидает от него погасить, используя простые проценты. 9{3} +… \]
Биологи также используют геометрическую последовательность . Они могут рассчитать рост популяции бактерий в чашке Петри, используя геометрических последовательностей. Морские биологи также могут использовать геометрические последовательности для аппроксимации роста популяции рыб в пруду с помощью геометрических последовательностей .
Физики также используют геометрические последовательности для расчета периода полураспада радиоактивного изотопа. Геометрические последовательности также используются в нескольких физических экспериментах и уравнениях.
Геометрическая последовательность — очень универсальный математический закон, который используется в различных областях по всему миру.
История калькуляторов геометрических последовательностей
Геометрические последовательности впервые были использованы 2500 лет назад греческими математиками. Математики считали, что ходить с места на место утомительно. Зенон Элейский указал на парадокс, предположив, что нужно преодолеть половину расстояния, чтобы добраться до пункта назначения.
Пройдя половину расстояния, ему снова придется пройти половину расстояния. Этот парадокс будет продолжаться до тех пор, пока не будет достигнута бесконечность. Однако позже этот парадокс был признан ошибочным.
В 300 г. до н. э. Евклид Александрийский написал свою книгу «Элементы геометрии». Книга содержала первую интерпретацию геометрических последовательностей. Позже текст был расшифрован, и были извлечены уравнения Евклида для геометрических последовательностей . Различные математики еще больше упростили эти уравнения.
В 287 г. до н. э. Архимед Сиракузский использовал геометрические последовательности для вычисления площади параболы, заключенной в прямые линии. Реализация Архимедом геометрических последовательностей позволила ему разбить область на бесконечное количество треугольников. Сегодня площадь параболы можно легко вычислить с помощью интегрирования.
Реализация Архимедом геометрических последовательностей позволила ему разбить область на бесконечное количество треугольников. Сегодня площадь параболы можно легко вычислить с помощью интегрирования.
В 1323 году Николь Орем доказала, что ряд $ \frac{1}{2} + \frac{2}{4} + \frac{3}{8} + .., $ объединяется в 2. Николь вывела это доказательство с использованием геометрических последовательностей.
Геометрические последовательности использовались на протяжении всей истории и доказали свою значимость при получении новых доказательств. Мы обсуждали важность и происхождение геометрических последовательностей на протяжении многих лет.
Решенные примеры
Калькулятор геометрической последовательности может легко вычислить обыкновенное отношение между двумя последовательными числами. Вот несколько решенных примеров, в которых используется калькулятор геометрической последовательности .
Пример 1
Учащемуся средней школы предъявляют геометрическую последовательность из 2, 6, 18, 54, 162,….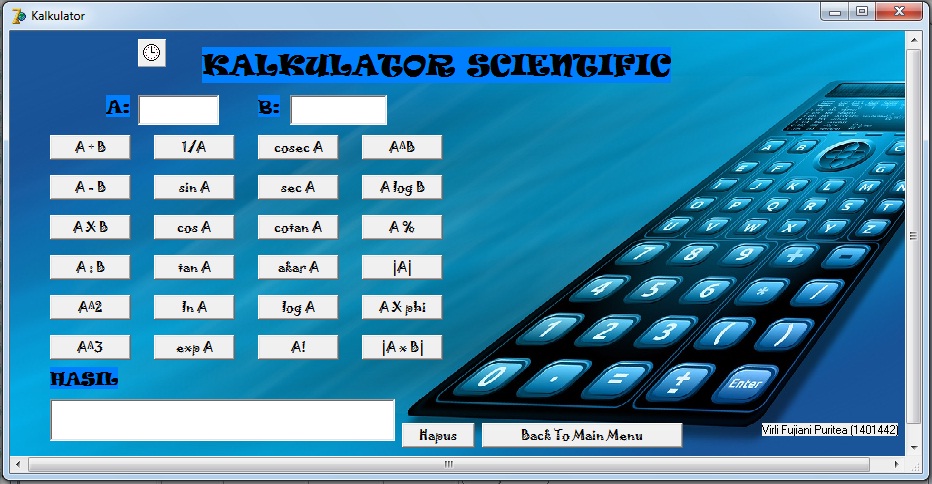 От него требуется найти знаменатель $r$. Рассчитайте c общее отношение , используя предоставленную геометрическую последовательность.
От него требуется найти знаменатель $r$. Рассчитайте c общее отношение , используя предоставленную геометрическую последовательность.
Решение
Чтобы решить эту задачу, мы можем использовать калькулятор геометрической последовательности. Сначала мы выбираем любые два последовательных значения из предоставленной геометрической последовательности. Выбираем значения 6 и 18. Позиции этих термов 1 и 2.
Введите числа из геометрической последовательности в поля Xk и Xj , затем добавьте положение каждого члена в соответствующие поля.
Нажмите кнопку «Отправить», и вам будет представлен обыкновенный коэффициент . Результаты можно увидеть ниже:
Ввод:
\[ \sqrt[2-1]{\frac{18}{16}} \]
Точный результат:
3
Имя номера:
три
Пример 2
Экспериментируя, физик наткнулся на геометрическую последовательность 3840, 960, 240, 60, 15,… . Чтобы завершить свой эксперимент, физик выводит соотношение, обычное для чисел в геометрической последовательности . Используя Калькулятор геометрической последовательности , найдите это соотношение.
Чтобы завершить свой эксперимент, физик выводит соотношение, обычное для чисел в геометрической последовательности . Используя Калькулятор геометрической последовательности , найдите это соотношение.
Решение
Для решения этой задачи нам необходимо использовать Калькулятор геометрической последовательности . Во-первых, нам нужно выбрать два числа рядом друг с другом из предоставленной геометрической последовательности. Предположим, мы выбираем числа 960 и 240. Затем мы записываем положения термов, т.е. 2 и 3 соответственно.
Затем мы вводим выбранные нами номера и добавляем их в поля Xk и Xj . После добавления чисел мы вводим позиции терминов. Наконец, после всех этих шагов, мы нажимаем кнопку «Отправить», и наше соотношение отображается в новом окне.
Результаты показаны ниже:
Ввод:
\[ \sqrt[3-2]{\frac{240}{960}} \]
Точный результат:
\[ \frac{1}{4} \]
Пример 3
Студент колледжа получил задание найти обыкновенное отношение следующей геометрической последовательности .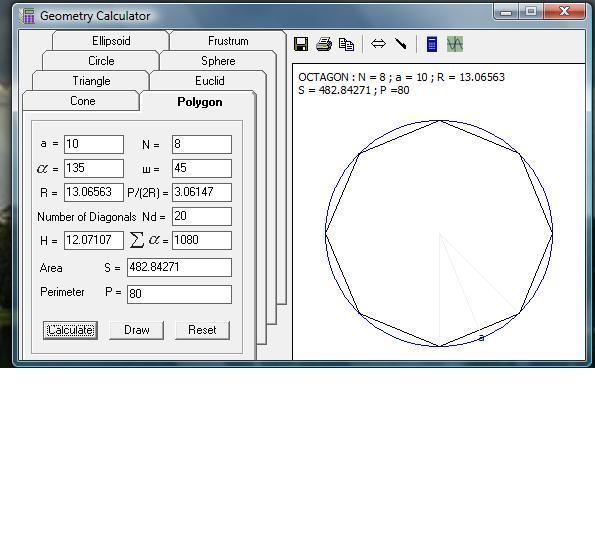
10,20,30,40,50,…
Используя Калькулятор геометрической последовательности , найдите обыкновенное отношение последовательности.
Решение
Для решения этой задачи мы воспользуемся Калькулятором геометрической последовательности . Сначала мы выбираем два числа из последовательности. Выбираем 30 и 40, имея в виду, что числа должны идти подряд. Нам также необходимо знать положения этих терминов, т.е. 3 и 4.
После сбора всех данных геометрической последовательности мы сначала подставляем пары чисел в поля Xk и Xj . Затем мы добавляем положение терминов в соответствующих полях. Чтобы узнать результат, нажимаем кнопку «Отправить». В нашем калькуляторе геометрической последовательности открывается новое окно с результатами. Вы можете посмотреть на результаты ниже.
Ввод:
\[ \sqrt[4-3]{\frac{40}{30}} \]
Точный результат:
\[ \frac{1}{4} \]
Пример 4
Студент-биолог экспериментирует с определенным типом бактерий. Студент смотрит на растущую популяцию бактерий в чашке Петри и генерирует геометрическую последовательность из 2,4,16, 32, 64,…. Найдите обыкновенное отношение , используя предоставленную геометрическую последовательность .
Студент смотрит на растущую популяцию бактерий в чашке Петри и генерирует геометрическую последовательность из 2,4,16, 32, 64,…. Найдите обыкновенное отношение , используя предоставленную геометрическую последовательность .
Решение
Используя наш Калькулятор геометрической последовательности , мы можем легко найти знаменатель геометрической последовательности. Сначала мы выбираем пару чисел, которые следуют друг за другом. В этом примере мы выбираем 32 и 64. После выбора пары мы выясняем их позиции, а именно 4 и 5.
Как только мы собрали необходимую информацию, мы можем начать вводить значения в Калькулятор геометрической последовательности . Сначала мы добавляем парные числа в поля Xk и Xj , затем добавляем позиции термов в соответствующие поля. Наконец, мы нажимаем кнопку «Отправить», которая отображает результаты в новом окне. Результаты можно увидеть ниже.
Ввод:
\[ \sqrt[5-4]{\frac{64}{32}} \]
Точный результат:
9Пример 5 Профессор хочет найти обыкновенное отношение , которое может относиться ко всей последовательности. Вычислите обыкновенное отношение геометрической последовательности , приведенной выше.
Вычислите обыкновенное отношение геометрической последовательности , приведенной выше.Решение
Использование нашего надежного калькулятора геометрических последовательностей , мы можем легко решить эту проблему. Сначала мы выбираем два числа из геометрической последовательности; эти числа должны быть последовательными. Мы выбираем 20 и 100. После выбора этих значений мы находим позиции этих терминов, а именно 2 и 3.
Теперь мы открываем первые два числа в поля Xk и Xj . Впоследствии мы добавляем позиции терминов в соответствующие поля. После ввода всех необходимых данных в наш калькулятор геометрической последовательности , мы нажимаем кнопку «Отправить». Появится новое окно, показывающее результаты калькулятора. Результаты показаны ниже.
Ввод:
\ [\ sqrt [2-3] {\ frac {100} {20}} \]
Точный результат:
5
Numb Список калькуляторов
Онлайн-калькулятор: Объем геометрических фигур
Учеба Математика
Вычисляет объем геометрических фигур: куб, призма, пирамида, усеченный конус, цилиндр, сфера, эллипсоид.
Эта статья содержит сборник калькуляторов для расчета объема геометрических фигур. Первоисточник расчетных формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.
Объем куба
Размеры куба
Формула:
Объем куба
Сторона (H)
Длина стороны
Точность вычисления после десятичной точки:
900 5
Том
Том прямоугольной призмы
Прямоугольные размеры призмы
Формула:
Объем прямоугольной призмы
Ширина (W)
Высота (H)
31 3131.
Знаки после запятой: 5
Объем
Объем пирамиды
Размеры пирамиды
Формула:
Объем пирамиды
Площадь основания (Sb)
Площадь основания пирамиды.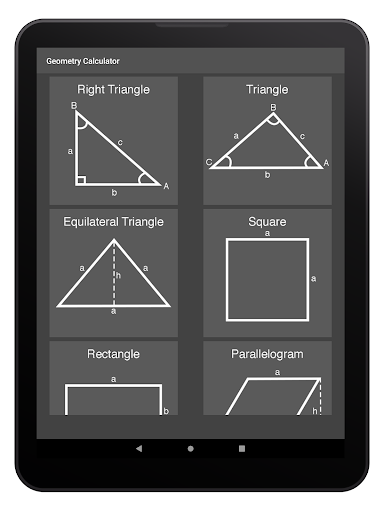

 Расчет площади и периметра квадрата через сторону или диагональ.
Расчет площади и периметра квадрата через сторону или диагональ.
