Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | |||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Решение тригонометрических неравенств: sin x > a, sin x< a, sin x ≥ a, sin x ≤ a; cos x > a, cos x< a, cos x ≥ a, cos x ≤ a; tg x > a, tg x< a, tg x ≥ a, tg x≤a; ctg x > a, ctg x< a, ctg x ≥ a, ctg x≤a Поделиться:
| ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator | ||||||
10.2.1. Решение тригонометрических неравенств. Часть 1.
Главная » 10 класс. Алгебра. » 10.2.1. Решение тригонометрических неравенств. Часть 1
На этом и последующих занятиях мы будем решать графическим способом тригонометрические неравенства одного какого-то вида. Сегодня мы решим три тригонометрических неравенства вида sint . Вот они:
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=sint и y=a.
3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается ниже прямой у=а.
Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду.
Решим первое неравенство
Для построения графика функции y=sinx выберем единичный отрезок, равный двум клеткам. Тогда по горизонтальной оси Ох значение π (≈3,14) составит шесть клеток. Рассчитываем остальные значения аргументов (в клетках).
Вот как будет выглядеть координатная плоскость.
Эти точки мы взяли из таблицы значений синуса. Также используем свойство нечетности функции y=sinx (sin (-x)=-sinx), периодичность синуса (наименьший период Т=2π) и известное равенство: sin (π-x)=sinx.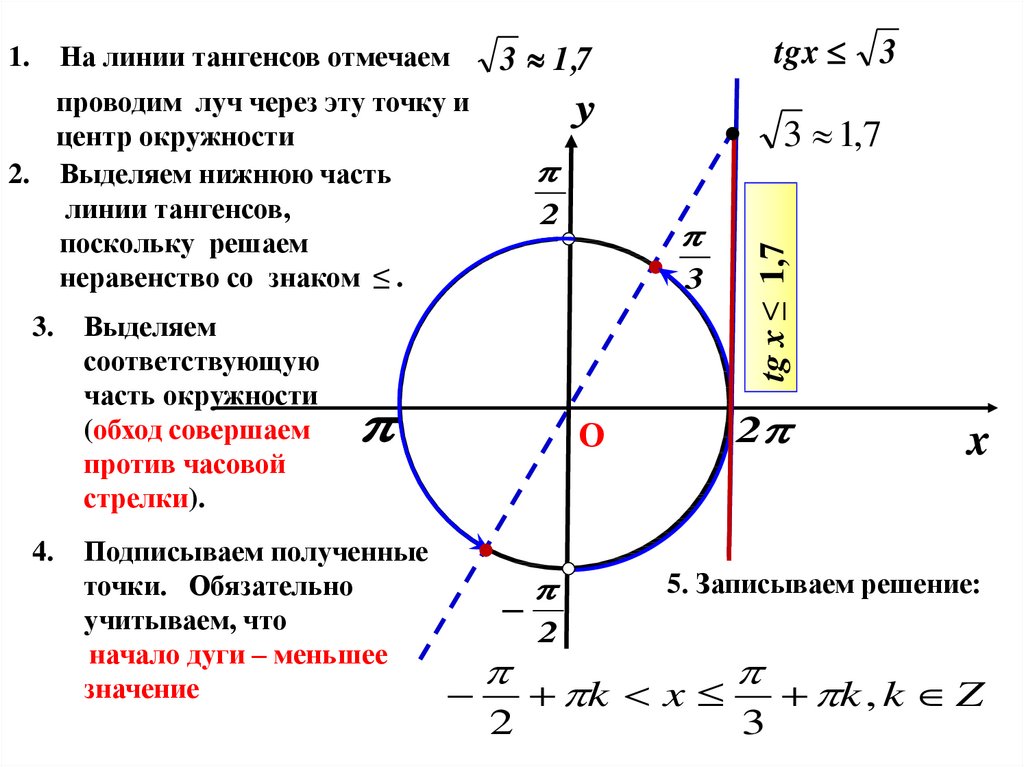
Проводим синусоиду
. Проводим прямую.
Теперь нам предстоит определить такие две точки пересечения синусоиды и прямой, между которыми синусоида располагается ниже, чем прямая. Крайняя точка справа определена, абсцисса ближайшей искомой отстоит от начала отсчета влево на 8 клеток. Построим ее и определим.
Между этими (выделенными) значениями аргумента и находится та часть синусоиды, которая лежит ниже данной прямой, а значит, промежуток между этими выделенными точками удовлетворяет данному неравенству. Учтем период синуса, запишем результат в виде двойного неравенства, а ответ в виде числового промежутка.
Решим второе неравенство
Синусоиду строим так же, а прямая будет параллельна оси Оt и отстоять от нее на 1 клетку вниз.
Определяем промежуток, внутри которого точки синусоиды лежат ниже прямой.
Записываем промежуток значений введенной переменной t. Возвращаемся к первоначальному значению аргумента (2х).
Все части двойного неравенства делим на 2 и определяем промежуток значений х. Записываем ответ в виде числового промежутка.
Аналогично решаем и третье неравенство
В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения
Ответ запишем в виде числового промежутка.
Смотрите видео: 10.2.1. Решение тригонометрических неравенств вида: sinx
И, напоследок: знаете ли вы, что математика — это определения, правила и ФОРМУЛЫ?!
Конечно, знаете! И самые любознательные, изучив эту статью и просмотрев видео, воскликнули: «Как долго и сложно! А нет ли формулы, позволяющей решать такие неравенства безо всяких графиков и окружностей?» Да, разумеется, есть!
ДЛЯ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА: sint (-1≤а≤1) справедлива формула:
— π — arcsin a + 2πn
Примените ее к рассмотренным примерам и вы получите ответ гораздо быстрее!
Вывод: УЧИТЕ ФОРМУЛЫ, ДРУЗЬЯ!
2x$, общее решение $x=2n\pi\pm\arccos(1-\sqrt{3})$ включает решения обоих уравнений $\displaystyle 2\cos\frac{x}{2}=-\cos x$ и $\displaystyle 2\cos\frac{x}{2}=\cos x$.
Примечание 2:
Для неравенства, поскольку $\displaystyle 2\cos\frac{x}{2}+\cos x$ имеет период $4\pi$, мы можем рассматривать те $x\in[0 только ,4\pi]$.
(a) Когда $x\in[0,\frac{\pi}{2}]$, $\cos\frac{x}{2}>0$ и $-\cos x\le0$. Неравенство не имеет решения.
(b) При $x\in[\frac{\pi}{2},\pi]$, $\cos\frac{x}{2}\ge0$ и $-\cos x\ge0$. Итак, $2\cos\frac{x}{2}\le-\cos x$ можно записать как 92x-2\cosx-2&\ge0\\ \cos x&\le 1-\sqrt{3}\\ 3\pi\le x &\le 4\pi-\arccos(1-\sqrt{3}) \end{align}
(h) Когда $x\in[\frac{7\pi}{2},4\pi]$, $\cos\frac{x}{2}>0$ и $- \cos х\le0$. Неравенство не имеет решения.
Объединяя результаты во всех случаях, $\displaystyle \arccos(1-\sqrt{3})\le x\le 4\pi-\arccos(1-\sqrt{3})$.
Общее решение: $\displaystyle x\in\bigcup_{n\in\mathbb{Z}}\left[4n\pi+\arccos(1-\sqrt{3}),4(n+1)\pi -\arccos(1-\sqrt{3})\right]$.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ | Тригонометрический
Пример: зубной гигиенист
Найденные 7 бесплатных книг (S)
Решение тригонометрического неравенства WWW.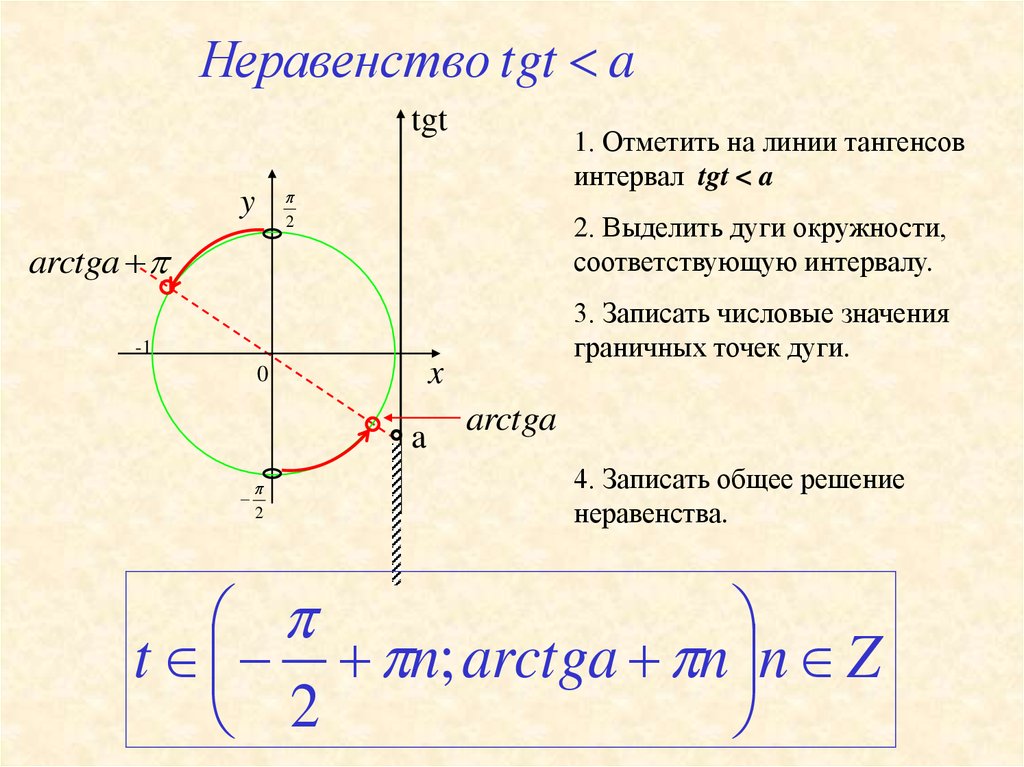
Mathematicsmagazine.com 9003 WWW.Mathematicsmagazine.com 9003 WWW.Mathematicsmagazine.com 9003 WWW.MATHEMATICSMAGAZINE.com 9003 . Нги Х. Нгуен ОПРЕДЕЛЕНИЕ. Тригонометрическое неравенство — это неравенство в стандартной форме: R(x) > …
Решение, Неравенства, Тригонометрические, Решение тригонометрических неравенств
Учебные услуги — кампус Mission del Pasowww.epcc.edu
Сохранено C: формулы тригонометрии {веб-страница} microsoftword и PDF веб-сайт: www.mathgraphs.com Примечание: sin и cos являются дополнительными углами, так же как tan и cot и sec и cos, а сумма дополнительных углов составляет 90 градусов.
Услуги, Учебные пособия, Учебные услуги, Тригонометрия
Тригонометрические функции — Математические ресурсыwww.mathcentre.ac.uk
Тригонометрические функции mc-TY-trig-2009-1 Синус, косинус и тангенс угла определяются в терминах тригонометрии , но они также могут быть выражены в виде функций.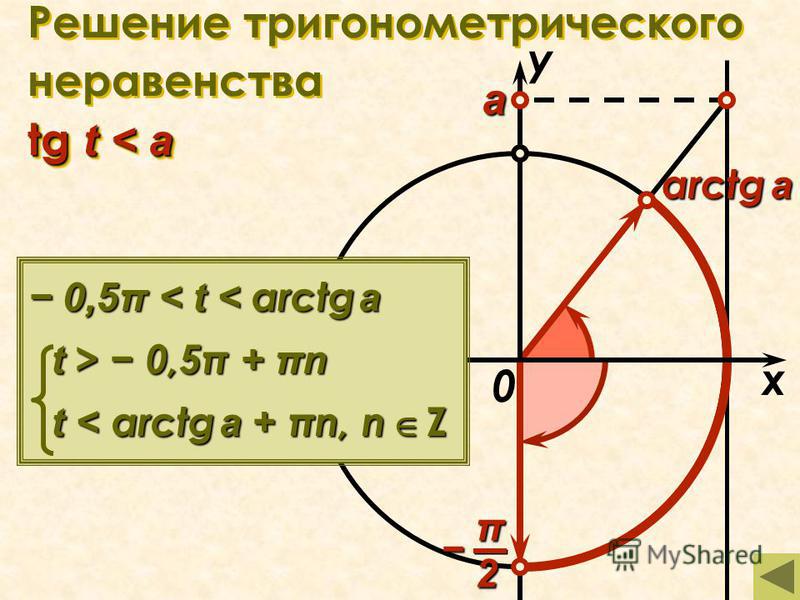
Функции, тригонометрические, тригонометрические функции
Тригонометрические уравнения — Математические ресурсыwww.mathcentre.ac.uk
1. Введение В этом модуле рассматривается решение тригонометрических уравнений . Для решения этих уравнений мы будем широко использовать графики функций синуса, косинуса и тангенса.
Уравнения, тригонометрические, тригонометрические уравнения
ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА Взаимные тождества Мощность …www.sosmath.com
c 2012 Math Medics LLC. Все права защищены. ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА Взаимные тождества SINU = 1 CSCU COSU = 1 SECU TANU = 1 COTU COTU = 1 TANU CSCU = 1 SINU
Взаимные, тригонометрические, идентификаторы, тригонометрические идентичности Относительные идентификации
TRIG Cheat Sheet — LAMAR Unialive.