Решение системы линейных уравнений с двумя неизвестными
Решить {$ main.types[data.type] $}
Введите уравнение* x +=
Введите уравнение* x2 +* x +=
Введите уравнения* x +* y +=
* x +* y +=
Введите уравнения* x +* y +* z =
* x +* y +* z =
* x +* y +* z =
{$ error $}!
Результаты расчёта
| A-1 | {$ result.IA[0][0]|number $} | {$ result.IA[0][1]|number $} | {$ result.IA[0][2]|number $} | * | {$ result.B[0][0]|number $} | = | {$ result.x|number $} |
| {$ result.IA[1][0]|number $} | {$ result.IA[1][1]|number $} | {$ result.IA[1][2]|number $} | {$ result.B[1][0]|number $} | {$ result.y|number $} | |||
| {$ result.IA[2][0]|number $} | {$ result.IA[2][1]|number $} | {$ result.IA[2][2]|number $} | {$ result. | {$ result.z|number $} |
- x = {$ result.x|number $}
- y = {$ result.y|number $}
- z = {$ result.z|number $}
Результаты расчёта
- x1 = {$ main.FormatResult(result.x1) $}
- x2 = {$ main.FormatResult(result.x2) $}
- x3 = {$ main.FormatResult(result.x3) $}
- x4 = {$ main.FormatResult(result.x4) $}
Значение дискриминанта: b2 − 4 * a * c = {$ result.d|number $}
Система линейных уравнений — это объединение нескольких линейных равенств, каждое из которых содержит по 2 неизвестных. Решением системы уравнений называется процесс поиска таких значений неизвестных, при которых выражение превращается в верное числовое равенство.
Линейные уравнения
Линейное уравнение с двумя переменными — это выражение вида:
ax + by + c = 0,
где x и y — неизвестные корни.
Это общий вид равенства, позволяющий идентифицировать его как линейное, так как очевидно, что неизвестные икс и игрек стоят в первой степени. Если переменные имеют отличную от единицы степень или сами являются показателями степеней, то такие равенства считаются нелинейными. Система двух линейных уравнений — это классический математический объект, с которым мы впервые встречаемся в шестом классе школы.
Система линейных уравнений
Система линейных алгебраических уравнений или СЛАУ — это совокупность n-ного количества равенств, содержащих k-ое количество неизвестных. В школьной алгебре существует негласное правило, что количество уравнений равно количеству неизвестных, то есть СЛАУ с двумя переменными всегда состоят из двух равенств. Высшая математика может преподносить и другие варианты, однако в школьных примерах это правило действует неукоснительно, и наш калькулятор построен по этому принципу: 2 уравнения и 2 переменных. Выглядит это следующим образом:
Выглядит это следующим образом:
- ax + by + c = 0
- dx + fy + g = 0
Под буквами a, b, c, d, f, g скрываются коэффициенты уравнения. Именно их следует вбивать в ячейки калькулятора для решения СЛАУ при помощи нашей программы. Важно учесть, что школьные уравнения обычно представляются в виде:
ax + by = с,
поэтому для корректного ввода данных требуется перенести свободный коэффициент в левую часть равенства с заменой знака на противоположный. Итак, у нас есть СЛАУ с двумя неизвестными. Пусть это будет:
- 3x − y = 14
- 5x + y = 10
Требуется найти такие значения икса и игрека, при которых уравнения превратятся в числовые тождества. При решении системы равенств возможны три варианта развития событий:
- СЛАУ совместна, определена и имеет всего 1 решение;
- система несовместна и решений нет;
- СЛАУ совместна, но неопределена, поэтому существует бесконечное множество решений.
Существует 3 простых способа поиска корней СЛАУ.
Метод подстановки
Это всем известный школьный метод, согласно которому мы выражаем одну переменную через другую, после чего заменяем вторую переменную в другом уравнении и получаем банальное линейное равенство. Посмотрим на второе уравнение нашей СЛАУ:
5x + y = 10
Мы можем спокойно перенести иксы вправо с заменой знака и выразить игрек через икс:
y = 10 − 5x
Теперь подставим это значение игрека в наше первое уравнение и решим его:
- 3x − (10 − 5x) = 14
- 3x + 5x = 14 + 10
- 8x = 24
- x = 3
Теперь вернемся ко второму уравнению и подставим числовое значение икса.
- 5x + y = 10;
- 5 × 3 + y = 10;
- y = 10 − 15;
- y = −5.
Таким образом, x = 3, y = −5 — это корни системы уравнений.
Метод сложения
Данный способ предлагает умножить обе части выражений на такие коэффициенты, чтобы при сложении двух уравнений произошло взаимное уничтожение одной из переменных. После чего метод повторяет алгоритм школьного способа подстановки. Посмотрим на нашу систему:
Посмотрим на нашу систему:
- 3x − y = 14
- 5x + y = 10
Очевидно, что игреки имеют разные знаки, поэтому при сложении двух уравнений они взаимно уничтожатся, а в результате получим:
- 8x = 24
- x = 3
Далее алгоритм полностью повторяет школьный метод. Нам повезло, что в условии игреки изначально имели коэффициент 1 с противоположными знаками. Рассмотрим пример, когда это не так. Для этого обратим внимание на иксы и попробуем от них избавиться.
- 3x — y = 14
- 5x + y = 10
Для ликвидации иксов нам потребуется найти наименьшее общее кратное коэффициентов при иксах — НОК (3,5) = 15. Следовательно, нам потребуется умножить первое уравнение на 5, а второе на минус 3. Тогда в каждом равенстве мы получим коэффициент при иксе равный 15, но с разными знаками.
- 15x − 5y = 70,
- −15x − 3y = −30.
Теперь сложим эти уравнения и решим полученное равенство:
- −8y = 40;
- y = −5.
Как видим, результат идентичен полученным корням при расчете школьным методом.
Графический метод
Суть данного способа заключается в построении графиков функции уравнений на декартовой плоскости. Так как уравнения линейны, то график их функций − это всегда прямая линия. Точка пересечения прямых и будет решением СЛАУ. Если система несовместна и не имеет корней, то прямые уравнений будут параллельны, а если СЛАУ обладает бесконечным множеством решений, то графики будут совпадать и сливаться в одну прямую.
Использование СЛАУ
Системы линейных уравнений находят широкое применение во многих науках. Такие объекты встречаются в физике, экономике, электротехнике, метрологии, компьютерных играх или криптографии — везде, где используется математический аппарат. И если говорить о математике, то системы линейных уравнений используются для определения кривой регрессии в методе наименьших квадратов, в расчете собственных векторов матриц, сингулярном разложении или методе главных компонент.
Калькулятор решения СЛАУ
Наша программа решает системы линейных уравнений графическим способом. Калькулятор отрисовывает прямые, заданные линейными функциями и отыскивает их точку пересечения. Координаты этой точки вида (x; y) и есть корни системы уравнений. Для решений СЛАУ вам потребуется только ввести коэффициенты равенств в соответствующие ячейки.
Калькулятор отрисовывает прямые, заданные линейными функциями и отыскивает их точку пересечения. Координаты этой точки вида (x; y) и есть корни системы уравнений. Для решений СЛАУ вам потребуется только ввести коэффициенты равенств в соответствующие ячейки.
Заключение
Системы линейных уравнений — наборы равенств, которые широко используются во всех областях науки. Для развязывания СЛАУ используйте наш калькулятор, который наглядно представит графическое решение системы уравнений.
Решение систем линейных уравнений способом сложения калькулятор. Решение систем уравнений способом сложения
Методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ , где в одном из уравнений есть лишь одна переменная.
Для решения системы способом почленного сложения (вычитания) следуйте следующим шагам:
1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.
2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.
Решение системы — это точки пересечения графиков функции.
Рассмотрим на примерах.
Пример 1.
Дана система:
Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (-1 и 1). В таком случае уравнения легко сложить почленно:
Действия, которые обведены красным цветом, выполняем в уме.
Результатом почленного сложения стало исчезновение переменной y . Именно в этом и В этом, собственно, и заключается смысл метода — избавиться от 1-ой из переменных.
-4 — y + 5 = 0 → y = 1,
В виде системы решение выглядит где-то так:
Ответ: x = -4 , y = 1.
Пример 2.
Дана система:
В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус — когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях . А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.
А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.
Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:
Нужно подобрать число, которое можно поделить и на 3 и на 4 , при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное . Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .
Следующий шаг:
1-е уравнение умножаем на ,
3-е уравнение умножаем на ,
Очень часто ученики затрудняются с выбором способа решения систем уравнений.
В данной статье мы рассмотрим один из способов решения систем – способ подстановки.
Если находят общее решение двух уравнений, то говорят, что эти уравнения образуют систему. В системе уравнений каждое неизвестное обозначает одно и то же число во всех уравнениях. Чтобы показать, что данные уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурной скобкой, например
Замечаем, что при х = 15 , а у = 5 оба уравнения системы верны.
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как же решать системы способом подстановки? Если коэффициенты при каком – нибудь неизвестном в обоих уравнениях равны по абсолютной величине (если же не равны, то уравниваем), то, складывая оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Затем решаем это уравнение. Определяем одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или во второе). Находим другое неизвестное. Давайте рассмотрим на примерах применение этого способа.
Пример 1. Решите систему уравнений
Здесь коэффициенты при у по абсолютному значению равны между собой, но противоположны по знаку. Давайте попробуем почленно сложить уравнения системы.
Полученное значение х=4, подставляем в какое–нибудь уравнение системы (например в первое) и находим значение у:
2 *4 +у = 11, у = 11 – 8, у = 3.
Наша система имеет решение х = 4, у = 3. Или же ответ можно записать в круглых скобках, как координаты точки, на первом месте х, на втором у.
Ответ: (4; 3)
Пример 2 . Решить систему уравнений
Уравняем коэффициенты при переменной х, для этого умножим первое уравнение на 3, а второе на (-2), получим
Будьте внимательны при сложении уравнений
Тогда у = — 2. Подставим в первое уравнение вместо у число (-2), получим
4х + 3(-2) = — 4. Решаем это уравнение 4х = — 4 + 6, 4х = 2, х = ½.
Пример 3. Решите систему уравнений
Умножим первое уравнение на (-2)
Решаем систему
получаем 0 = — 13.
Система решений не имеет, так ка 0 не равен (-13).
Ответ: решений нет.
Пример 4. Решите систему уравнений
Замечаем, что все коэффициенты второго уравнения делятся на 3,
давайте разделим второе уравнение на три и мы получаем систему, которая состоит из двух одинаковых уравнений.
Эта система имеет бесконечно много решений, так как первое и второе уравнения одинаковы (мы получили всего одно уравнение с двумя переменными). Как же представить решение этой системы? Давайте выразим переменную у из уравнения х + у = 5. Получим у = 5 – х.
Тогда ответ запишется так: (х; 5-х), х – любое число.
Мы рассмотрели решение систем уравнений способом сложения. Если остались вопросы или что – то непонятно запишитесь на урок и мы с вами устраним все проблемы.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
Получили линейное уравнение с одной переменной.
Решили систему уравнений?
Решение системы — пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Значит найденное значение х можно подставить в…
любое уравнение системы.
Мы познакомились с новым методом — методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х — число ног у овец
2у — число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612. blogspot.ru/2011/06/blog-post_25.html
blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6.
Рефлексия.
Я за свою работу на уроке ставлю оценку — …
6. Использованные ресурсы-интернет:
сервисы Google для образования
Учитель математики Соколова Н. Н.
Метод алгебраического сложения
Решить систему уравнений с двумя неизвестными можно различными способами — графическим методом или методом замены переменной.
В этом уроке познакомимся с ещё одним способом решения систем, который Вам наверняка понравится — это способ алгебраического сложения.
А откуда вообще взялась идея — что-то складывать в системах? При решении систем главной проблемой является наличие двух переменных, ведь решать уравнения с двумя переменными мы не умеем. Значит, надо каким-либо законным способом исключить одну из них. И такими законными способами являются математические правила и свойства.
Одно из таких свойств звучит так: сумма противоположных чисел равна нулю. Значит, если при одной из переменных будут противоположные коэффициенты, то их сумма будет равна нулю и нам удастся исключить эту переменную из уравнения. Понятно, что складывать только слагаемые с нужной нам переменной мы не имеем право. Складывать надо уравнения целиком, т.е. по отдельности складывают подобные слагаемые в левой части, затем в правой. В результате мы получим новое уравнение, содержащее только одну переменную. Давайте рассмотрим сказанное на конкретных примерах.
Мы видим, что в первом уравнении есть переменная у, а во втором противоположное число -у. Значит, это уравнение можно решить методом сложения.
Одно из уравнений оставляют в том виде, каком оно есть. Любое, какое Вам больше нравится.
А вот второе уравнение будет получено сложением этих двух уравнений почленно. Т.е. 3х сложим с 2х, у сложим с -у, 8 сложим с 7.
Получим систему уравнений
Второе уравнение этой системы представляет собой простое уравнение с одной переменной. Из него находим х = 3. Подставив найденное значение в первое уравнение, находим у = -1.
Из него находим х = 3. Подставив найденное значение в первое уравнение, находим у = -1.
Ответ: (3; — 1).
Образец оформления:
Решить методом алгебраического сложения систему уравнений
В данной системе нет переменных с противоположными коэффициентами. Но мы знаем, что обе части уравнения можно умножать на одно и то же число. Давайте умножим первое уравнение системы на 2.
Тогда первое уравнение примет вид:
Теперь видим, что при переменной х есть противоположные коэффициенты. Значит, поступим так же, как и в первом примере: одно из уравнений оставим в неизменном виде. Например, 2у + 2х = 10. А второе получим сложением.
Теперь у нас система уравнений:
Легко находим из второго уравнения у = 1, а затем из первого уравнения х = 4.
Образец оформления:
Давайте подведём итоги:
Мы научились решать системы двух линейных уравнений с двумя неизвестными методом алгебраического сложения. Таким образом, нам теперь известны три основных метода решения таких систем: графический, метод замены переменной и метод сложения. Практически любую систему можно решить с помощью этих способов. В более сложных случаях применяют комбинацию этих приёмов.
Практически любую систему можно решить с помощью этих способов. В более сложных случаях применяют комбинацию этих приёмов.
Список использованной литературы:
- Мордкович А.Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007.
- Мордкович А.Г., Алгебра 7 класс в 2 частях, Часть 2, Задачник для общеобразовательных учреждений/ [А.Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
- Е.Е. Тульчинская, Алгебра 7 класс. Блиц опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008.
- Александрова Л.А., Алгебра 7 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011.
- Александрова Л.А. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений, под редакцией А.
 Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010.
Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010.
Этим видео я начинаю цикл уроков, посвящённых системам уравнений. Сегодня мы поговорим о решении систем линейных уравнений методом сложения — это один из самых простых способов, но одновременно и один из самых эффективных.
Способ сложения состоит из трёх простых шагов:
- Посмотреть на систему и выбрать переменную, у которой в каждом уравнении стоят одинаковые (либо противоположные) коэффициенты;
- Выполнить алгебраическое вычитание (для противоположных чисел — сложение) уравнений друг из друга, после чего привести подобные слагаемые;
- Решить новое уравнение, получившееся после второго шага.
Если всё сделать правильно, то на выходе мы получим одно-единственное уравнение с одной переменной — решить его не составит труда. Затем останется лишь подставить найденный корень в исходную система и получить окончательный ответ.
Однако на практике всё не так просто.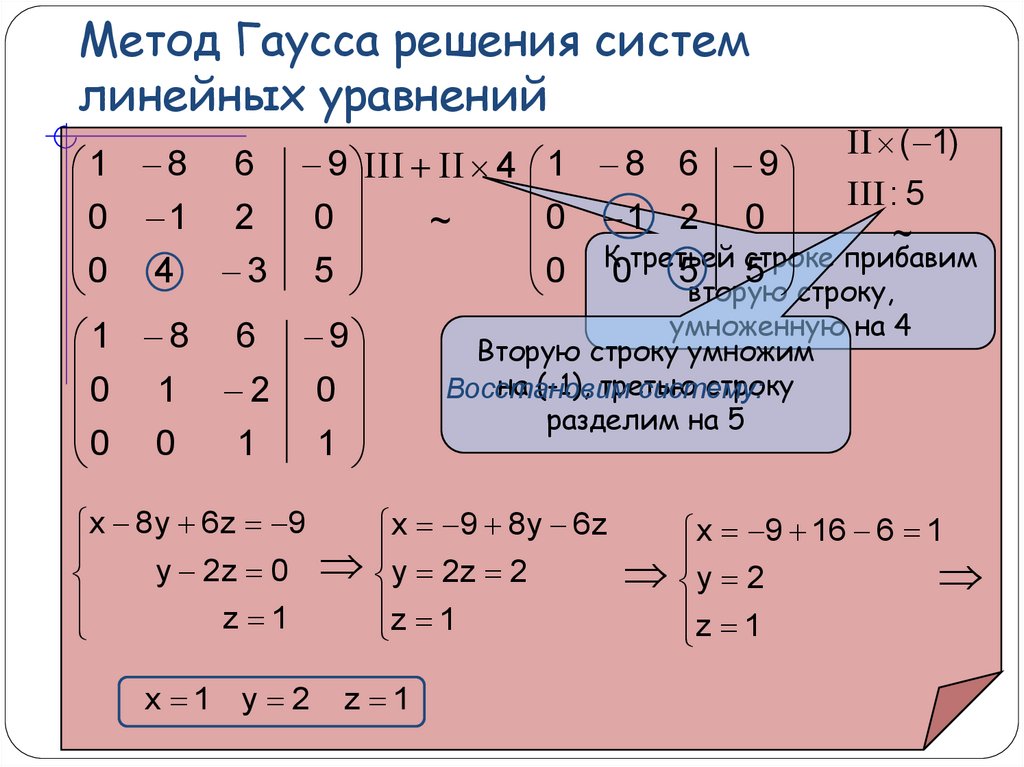 Причин тому несколько:
Причин тому несколько:
- Решение уравнений способом сложения подразумевает, что во всех строчках должны присутствовать переменные с одинаковыми/противоположными коэффициентами. А что делать, если это требование не выполняется?
- Далеко не всегда после сложения/вычитания уравнений указанным способом мы получим красивую конструкцию, которая легко решается. Возможно ли как-то упростить выкладки и ускорить вычисления?
Чтобы получить ответ на эти вопросы, а заодно разобраться с несколькими дополнительными тонкостями, на которых «заваливаются» многие ученики, смотрите мой видеоурок:
Этим уроком мы начинаем цикл лекций, посвященный системам уравнений. А начнем мы из самых простых из них, а именно из те, которые содержат два уравнения и две переменных. Каждое из них будет являться линейным.
Системы — это материал 7-го класса, но этот урок также будет полезен старшеклассникам, которые хотят освежить свои знания в этой теме.
Вообще, существует два метода решения подобных систем:
- Метод сложения;
- Метод выражения одной переменной через другую.

Сегодня мы займемся именно первым методом — будем применять способ вычитания и сложения. Но для этого нужно понимать следующий факт: как только у вас есть два или более уравнений, вы вправе взять любые два из них и сложить друг с другом. Складываются они почленно, т.е. «иксы» складываются с «иксами» и приводятся подобные, «игреки» с «игреками» — вновь приводятся подобные, а то, что стоит справа от знака равенства, также складывается друг с другом, и там тоже приводятся подобные.
Результатами подобных махинаций будет новое уравнение, которое, если и имеет корни, то они обязательно будут находиться среди корней исходного уравнения. Поэтому наша задача — сделать вычитание или сложение таким образом, чтобы или $x$, или $y$ исчез.
Как этого добиться и каким инструментом для этого пользоваться — об этом мы сейчас и поговорим.
Решение легких задач с применением способа сложения
Итак, учимся применять метод сложения на примере двух простейших выражений.
Задача № 1
\[\left\{ \begin{align}& 5x-4y=22 \\& 7x+4y=2 \\\end{align} \right. \]
\]
Заметим, что у $y$ коэффициент в первом уравнении $-4$, а во втором — $+4$. Они взаимно противоположны, поэтому логично предположить, что если мы их сложим, то в полученной сумме «игреки» взаимно уничтожатся. Складываем и получаем:
Решаем простейшую конструкцию:
Прекрасно, мы нашли «икс». Что теперь с ним делать? Мы вправе подставить его в любое из уравнений. Подставим в первое:
\[-4y=12\left| :\left(-4 \right) \right.\]
Ответ: $\left(2;-3 \right)$.
Задача № 2
\[\left\{ \begin{align}& -6x+y=21 \\& 6x-11y=-51 \\\end{align} \right.\]
Здесь полностью аналогичная ситуация, только уже с «иксами». Сложим их:
Мы получили простейшее линейное уравнение, давайте решим его:
Теперь давайте найдем $x$:
Ответ: $\left(-3;3 \right)$.
Важные моменты
Итак, только что мы решили две простейших системы линейных уравнений методом сложения. Еще раз ключевые моменты:
- Если есть противоположные коэффициенты при одной из переменных, то необходимо сложить все переменные в уравнении.
 В этом случае одна из них уничтожится.
В этом случае одна из них уничтожится. - Найденную переменную подставляем в любое из уравнений системы, чтобы найти вторую.
- Окончательную запись ответа можно представить по-разному. Например, так — $x=…,y=…$, или в виде координаты точек — $\left(…;… \right)$. Второй вариант предпочтительней. Главное помнить, что первой координатой идет $x$, а второй — $y$.
- Правило записывать ответ в виде координат точки применимо не всегда. Например, его нельзя использовать, когда в роли переменных выступают не $x$ и $y$, а, к примеру, $a$ и $b$.
В следующих задачах мы рассмотрим прием вычитания, когда коэффициенты не противоположны.
Решение легких задач с применением метода вычитания
Задача № 1
\[\left\{ \begin{align}& 10x-3y=5 \\& -6x-3y=-27 \\\end{align} \right.\]
Заметим, что противоположных коэффициентов здесь нет, однако есть одинаковые. Поэтому вычитаем из первого уравнения второе:
Теперь подставляем значение $x$ в любое из уравнений системы. Давайте в первое:
Давайте в первое:
Ответ: $\left(2;5 \right)$.
Задача № 2
\[\left\{ \begin{align}& 5x+4y=-22 \\& 5x-2y=-4 \\\end{align} \right.\]
Мы снова видим одинаковый коэффициент $5$ при $x$ в первом и во втором уравнении. Поэтому логично предположить, что нужно из первого уравнения вычесть второе:
Одну переменную мы вычислили. Теперь давайте найдем вторую, например, подставив значение $y$ во вторую конструкцию:
Ответ: $\left(-3;-2 \right)$.
Нюансы решения
Итак, что мы видим? По существу, схема ничем не отличается от решения предыдущих систем. Отличие только в том, что мы уравнения не складываем, а вычитаем. Мы проводим алгебраическое вычитание.
Другими словами, как только вы видите систему, состоящую из двух уравнений с двумя неизвестными, первое, на что вам необходимо посмотреть — это на коэффициенты. Если они где-либо одинаковые, уравнения вычитаются, а если они противоположные — применяется метод сложения. Всегда это делается для того, чтобы одна из них исчезла, и в итогом уравнении, которая осталась после вычитания, осталась бы только одна переменная.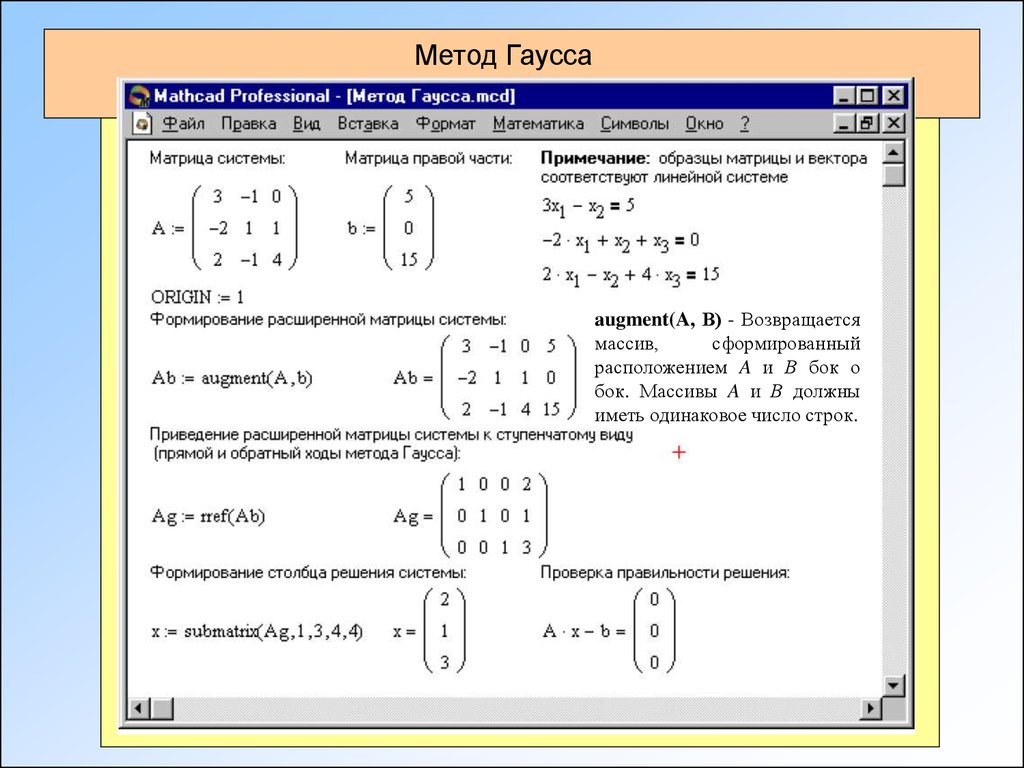
Разумеется, это еще не все. Сейчас мы рассмотрим системы, в которых уравнения вообще несогласованны. Т.е. нет в них таких переменных, которые были бы либо одинаковые, либо противоположные. В этом случае для решения таких систем применяется дополнительный прием, а именно домножение каждого из уравнений на специальный коэффициент. Как найти его и как решать вообще такие системы, сейчас мы об этом и поговорим.
Решение задач методом домножения на коэффициент
Пример № 1
\[\left\{ \begin{align}& 5x-9y=38 \\& 3x+2y=8 \\\end{align} \right.\]
Мы видим, что ни при $x$, ни при $y$ коэффициенты не только не взаимно противоположны, но и вообще никак не соотносятся с другим уравнением. Эти коэффициенты никак не исчезнут, даже если мы сложим или вычтем уравнения друг из друга. Поэтому необходимо применить домножение. Давайте попытаемся избавиться от переменной $y$. Для этого мы домножим первое уравнение на коэффициент при $y$ из второго уравнения, а второе уравнение — при $y$ из первого уравнения, при этом не трогая знак. Умножаем и получаем новую систему:
Умножаем и получаем новую систему:
\[\left\{ \begin{align}& 10x-18y=76 \\& 27x+18y=72 \\\end{align} \right.\]
Смотрим на нее: при $y$ противоположные коэффициенты. В такой ситуации необходимо применять метод сложения. Сложим:
Теперь необходимо найти $y$. Для этого подставим $x$ в первое выражение:
\[-9y=18\left| :\left(-9 \right) \right.\]
Ответ: $\left(4;-2 \right)$.
Пример № 2
\[\left\{ \begin{align}& 11x+4y=-18 \\& 13x-6y=-32 \\\end{align} \right.\]
Вновь коэффициенты ни при одной из переменных не согласованы. Домножим на коэффициенты при $y$:
\[\left\{ \begin{align}& 11x+4y=-18\left| 6 \right. \\& 13x-6y=-32\left| 4 \right. \\\end{align} \right.\]
\[\left\{ \begin{align}& 66x+24y=-108 \\& 52x-24y=-128 \\\end{align} \right.\]
Наша новая система равносильна предыдущей, однако коэффициенты при $y$ являются взаимно противоположными, и поэтому здесь легко применить метод сложения:
Теперь найдем $y$, подставив $x$ в первое уравнение:
Ответ: $\left(-2;1 \right)$.
Нюансы решения
Ключевое правило здесь следующее: всегда умножаем лишь на положительные числа — это избавит вас от глупых и обидных ошибок, связанных с изменением знаков. А вообще, схема решения довольно проста:
- Смотрим на систему и анализируем каждое уравнение.
- Если мы видим, что ни при $y$, ни при $x$ коэффициенты не согласованы, т.е. они не являются ни равными, ни противоположными, то делаем следующее: выбираем переменную, от которой нужно избавиться, а затем смотрим на коэффициенты при этих уравнениях. Если первое уравнение домножим на коэффициент из второго, а второе, соответственное, домножим на коэффициент из первого, то в итоге мы получим систему, которая полностью равносильна предыдущей, и коэффициенты при $y$ будут согласованы. Все наши действия или преобразования направлены лишь на то, чтобы получить одну переменную в одном уравнении.
- Находим одну переменную.
- Подставляем найденную переменную в одно из двух уравнений системы и находим вторую.

- Записываем ответ в виде координаты точек, если у нас переменные $x$ и $y$.
Но даже в таком нехитром алгоритме есть свои тонкости, например, коэффициенты при $x$ или $y$ могут быть дробями и прочими «некрасивыми» числами. Эти случаи мы сейчас рассмотрим отдельно, потому что в них можно действовать несколько иначе, чем по стандартному алгоритму.
Решение задач с дробными числами
Пример № 1
\[\left\{ \begin{align}& 4m-3n=32 \\& 0,8m+2,5n=-6 \\\end{align} \right.\]
Для начала заметим, что во втором уравнении присутствуют дроби. Но заметим, что можно разделить $4$ на $0,8$. Получим $5$. Давайте второе уравнение домножим на $5$:
\[\left\{ \begin{align}& 4m-3n=32 \\& 4m+12,5m=-30 \\\end{align} \right.\]
Вычитаем уравнения друг из друга:
$n$ мы нашли, теперь посчитаем $m$:
Ответ: $n=-4;m=5$
Пример № 2
\[\left\{ \begin{align}& 2,5p+1,5k=-13\left| 4 \right. \\& 2p-5k=2\left| 5 \right. \\\end{align} \right. \]
\]
Здесь, как и в предыдущей системе, присутствуют дробные коэффициенты, однако ни при одной из переменных коэффициенты в целое число раз друг в друга не укладываются. Поэтому используем стандартный алгоритм. Избавится от $p$:
\[\left\{ \begin{align}& 5p+3k=-26 \\& 5p-12,5k=5 \\\end{align} \right.\]
Применяем метод вычитания:
Давайте найдем $p$, подставив $k$ во вторую конструкцию:
Ответ: $p=-4;k=-2$.
Нюансы решения
Вот и вся оптимизация. В первом уравнении мы не стали домножать вообще ни на что, а второе уравнение домножили на $5$. В итоге мы получили согласованное и даже одинаковое уравнение при первой переменной. Во второй системе мы действовали по стандартному алгоритму.
Но как найти числа, на которые необходимо домножать уравнения? Ведь если домножать на дробные числа, мы получим новые дроби. Поэтому дроби необходимо домножить на число, которое бы дало новое целое число, а уже после этого домножать переменные на коэффициенты, следуя стандартному алгоритму.
В заключение хотел бы обратить ваше внимание на формат записи ответа. Как я уже и говорил, поскольку здесь у нас тут не $x$ и $y$, а другие значения, мы пользуемся нестандартной записью вида:
Решение сложных систем уравнений
В качестве заключительного аккорда к сегодняшнему видеоуроку давайте рассмотрим пару действительно сложных систем. Их сложность будет состоять в том, что в них и слева, и справа будут стоять переменные. Поэтому для их решения нам придется применять предварительную обработку.
Система № 1
\[\left\{ \begin{align}& 3\left(2x-y \right)+5=-2\left(x+3y \right)+4 \\& 6\left(y+1 \right)-1=5\left(2x-1 \right)+8 \\\end{align} \right.\]
Каждое уравнение несет в себе определенную сложность. Поэтому с каждым выражением давайте поступим как с обычной линейной конструкцией.
Итого мы получим окончательную систему, которая равносильна исходной:
\[\left\{ \begin{align}& 8x+3y=-1 \\& -10x+6y=-2 \\\end{align} \right.\]
Посмотрим на коэффициенты при $y$: $3$ укладывается в $6$ два раза, поэтому домножим первое уравнение на $2$:
\[\left\{ \begin{align}& 16x+6y=-2 \\& -10+6y=-2 \\\end{align} \right. \]
\]
Коэффициенты при $y$ теперь равны, поэтому вычитаем из первого уравнения второе: $$
Теперь найдем $y$:
Ответ: $\left(0;-\frac{1}{3} \right)$
Система № 2
\[\left\{ \begin{align}& 4\left(a-3b \right)-2a=3\left(b+4 \right)-11 \\& -3\left(b-2a \right)-12=2\left(a-5 \right)+b \\\end{align} \right.\]
Преобразуем первое выражение:
Разбираемся со вторым:
\[-3\left(b-2a \right)-12=2\left(a-5 \right)+b\]
\[-3b+6a-12=2a-10+b\]
\[-3b+6a-2a-b=-10+12\]
Итого, наша первоначальная система примет такой вид:
\[\left\{ \begin{align}& 2a-15b=1 \\& 4a-4b=2 \\\end{align} \right.\]
Посмотрев на коэффициенты при $a$, мы видим, что первое уравнение нужно домножить на $2$:
\[\left\{ \begin{align}& 4a-30b=2 \\& 4a-4b=2 \\\end{align} \right.\]
Вычитаем из первой конструкции вторую:
Теперь найдем $a$:
Ответ: $\left(a=\frac{1}{2};b=0 \right)$.
Вот и все. Надеюсь, этот видеоурок поможет вам разобраться в этой нелегкой теме, а именно в решении систем простых линейных уравнений. Дальше еще будет много уроков, посвященных этой теме: мы разберем более сложные примеры, где переменных будет больше, а сами уравнения уже будут нелинейными. До новых встреч!
Дальше еще будет много уроков, посвященных этой теме: мы разберем более сложные примеры, где переменных будет больше, а сами уравнения уже будут нелинейными. До новых встреч!
Калькулятор системы уравнений
Существует множество различных способов решения системы линейных уравнений. Кратко опишем несколько наиболее распространенных способов.
1. Подстановка
Первый метод, которому обучают студентов, и наиболее универсальный метод , работает путем выбора одного из уравнений, выбора одной из переменных в нем и превращения этой переменной в предмет этого уравнение . Затем мы используем это преобразованное уравнение и заменяем его каждый раз, когда эта переменная появляется в других уравнениях. Таким образом, эти другие уравнения теперь имеют на одну переменную меньше , что облегчает их решение.
Например, если у нас есть уравнение 2x + 3y = 6 и мы хотим получить из него x , то мы начинаем с , избавляясь от всего, что не содержит x слева- ручная сторона . Для этого нам нужно вычесть
Для этого нам нужно вычесть 3y с обеих сторон (потому что это выражение у нас слева). Это означает, что слева будет 2x + 3y - 3y , что равно просто 9.0019 2x , а справа будет 6-3y . Другими словами, мы преобразовали наше уравнение в 2x = 6 - 3y .
Так как мы хотим получить х , а не 2х , нам еще нужно избавиться от 2 . Для этого делим обе части на 2. Таким образом, слева получается (2x) / 2 , что равно x , а справа (6 - 3y) / 2 , что равно 3-1,5 года . В итоге мы получили x = 3 - 1,5y , и мы можем использовать эту новую формулу для замены 3 - 1,5y дюймов на каждые x в других уравнениях.
2. Исключение переменных
Решение систем уравнений методом исключения означает, что мы пытаемся уменьшить количество переменных в некоторых уравнениях, чтобы облегчить их решение .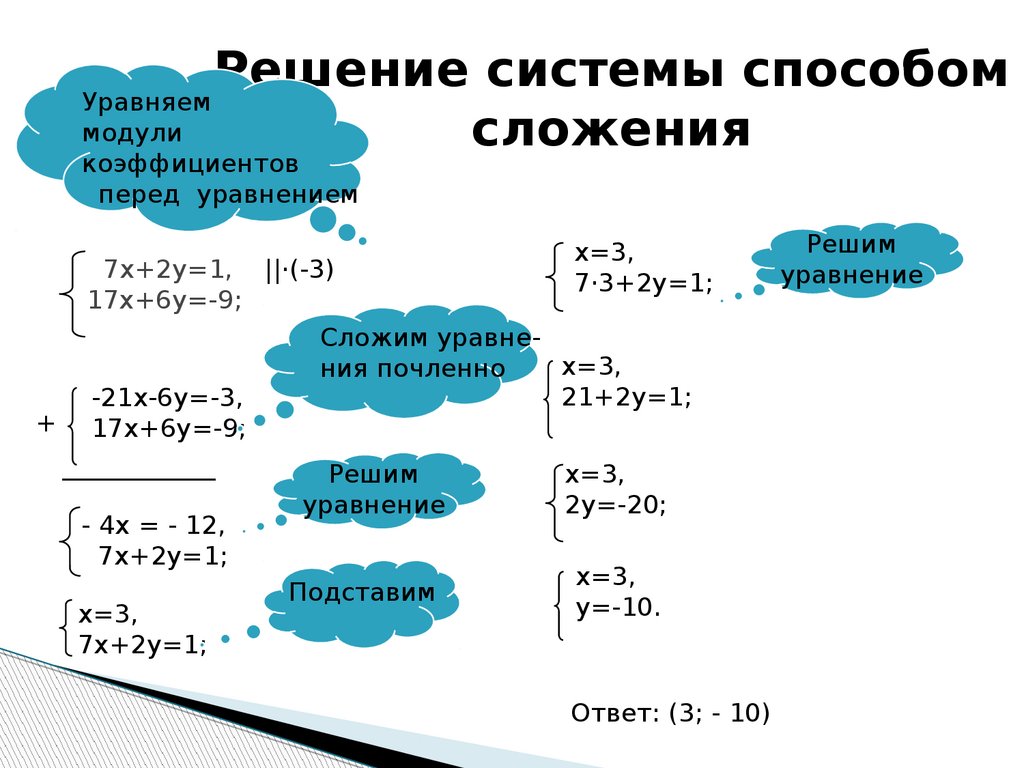 Для этого мы начнем с преобразования двух уравнений, чтобы они выглядели похожими. Чтобы быть точным, мы хотим сделать коэффициент (число рядом с переменной) одного из уравнений переменными противоположность коэффициента той же переменной в другом уравнении . Затем мы складываем два уравнения, чтобы получить новое, в котором нет этой переменной, и поэтому его легче вычислить.
Для этого мы начнем с преобразования двух уравнений, чтобы они выглядели похожими. Чтобы быть точным, мы хотим сделать коэффициент (число рядом с переменной) одного из уравнений переменными противоположность коэффициента той же переменной в другом уравнении . Затем мы складываем два уравнения, чтобы получить новое, в котором нет этой переменной, и поэтому его легче вычислить.
Например, если у нас есть система уравнений,
2x + 3y = 6 и
4x - y = 3 ,
, то мы можем попытаться сделать коэффициент х в первое уравнение должно быть противоположным коэффициенту во втором уравнении. В нашем случае это означает, что мы хотим преобразовать 2 в противоположность 4 , что равно -4 . Для этого нам нужно умножить обе части первого уравнения на -2 , так как 2 × (-2) = -4 . Это изменяет первое уравнение на
2x × (-2) + 3y × (-2) = 6 × (-2) ,
, что равно:
-4x - 6y = -12 .
Теперь мы можем добавить это уравнение ко второму ( 4x - y = 3 ), добавив левую часть к левой и правую к правой. Это дает
4x - y + (-4x - 6y) = 3 + (-12) ,
что равно:
-7y = -9 .
Мы получили новое уравнение всего с одной переменной, а это значит, что мы можем легко решить y . Затем мы можем подставить это число в любое из исходных уравнений, чтобы получить x .
3. Метод исключения Гаусса
Это метод, используемый нашим калькулятором системы уравнений. Названный в честь немецкого математика Иоганна Гаусса, он является алгоритмическим расширением метода исключения, представленного выше. В случае всего двух уравнений это точно то же самое. Однако решение систем уравнений путем регулярного исключения становится все сложнее и сложнее с увеличением количества уравнений и переменных. Вот здесь и приходит на помощь метод исключения Гаусса.
Допустим, у нас есть четыре уравнения с четырьмя переменными . Чтобы найти решение нашей системы, мы хотим попытаться получить значения наших переменных одно за другим, последовательно исключая все остальные. Для этого возьмем первое уравнение и первую из переменных . Мы используем его коэффициент, чтобы исключить все вхождения этой конкретной переменной в другие три уравнения , точно так же, как мы делали это при обычном исключении. Таким образом, у нас осталось первое уравнение таким же, как и было, и три уравнения, теперь каждое с только три переменные .
Теперь мы смотрим на первое уравнение, ставим ему «большой палец вверх» и оставляем его как есть до самого конца . Повторяем процесс для остальных трех уравнений. Другими словами, мы берем вторую переменную и ее коэффициент из второго уравнения , чтобы исключить все вхождения этой переменной в последние два уравнения. Это оставляет нам первое уравнение с четырьмя переменными, второе с тремя и последние два с 9 переменными.0003 только две переменные .
Это оставляет нам первое уравнение с четырьмя переменными, второе с тремя и последние два с 9 переменными.0003 только две переменные .
Затем мы объявляем второе уравнение красивым и красивым и оставляем его таким. Мы переходим к двум оставшимся уравнениям и берем третью переменную и ее коэффициент в третьем уравнении, чтобы исключить эту переменную из четвертого равенства.
В итоге получаем систему из четырех уравнений, в которой первое имеет четыре переменных, второе — три, третье — две, а последнее — только одну . Это означает, что мы можем легко получить значение четвертой переменной из четвертого уравнения (поскольку в нем нет других переменных). Затем мы подставляем это значение в третье уравнение и получаем значение третьей переменной (поскольку у нее больше нет других переменных) и так далее.
4. Графическое представление
Пожалуй, наименее используемый метод, но тем не менее метод. Он берет каждое уравнение в нашей системе и переводит их в функцию . Точки на графике такой функции соответствуют координатам, удовлетворяющим этому уравнению. Поэтому, если мы хотим решить систему линейных уравнений, то достаточно найти всех точек пересечения прямой на графике , т. е. координаты, удовлетворяющие всем уравнениям.
Точки на графике такой функции соответствуют координатам, удовлетворяющим этому уравнению. Поэтому, если мы хотим решить систему линейных уравнений, то достаточно найти всех точек пересечения прямой на графике , т. е. координаты, удовлетворяющие всем уравнениям.
Однако это может быть непросто. Если у нас есть только два уравнения и две переменные, то функции представляют собой линии на двумерной плоскости. Поэтому нам просто нужно найти точку, где эти две линии пересекают .
Для трех переменных функции теперь находятся в трехмерном пространстве, а уже не линии, а плоскости . Это означает, что нам нужно было бы нарисовать три плоскости (что само по себе сложно), а затем найти, где эти плоскости пересекаются. И, если вы думаете, что это сложно, попробуйте представить четыре переменные и четыре измерения . Если это приходит к вам естественным образом, пожалуйста, свяжитесь с нами, и мы направим вас в ближайший нобелевский проект или к неврологу для тщательной проверки головы.
🙋 Описывая их с помощью формы наклон-пересечение , можно легко найти пересечение между двумя линиями. Подробнее об этом читайте в нашем калькуляторе формы пересечения наклона.
5. Правило Крамера
Достаточно простой и очень простой способ решения системы линейных уравнений. Однако это так требуют хорошего понимания матриц и их определителей . В качестве ободрения отметим, что он не нуждается ни в какой подстановке, ни в игре с уравнениями, это просто старая добрая базовая арифметика . Например, для системы из трех уравнений с тремя переменными мы подставляем коэффициенты из этих уравнений, чтобы сформировать четыре матрицы размером три на три, и вычисляем их определители (что такое определитель?). Мы заканчиваем делением соответствующих значений, которые мы только что получили, чтобы получить окончательное решение.
Решение систем линейных уравнений методом исключения и замены
Система линейных уравнений представляет собой набор из двух или более линейных уравнений.
Мы можем решить систему уравнений алгебраически (путем исключения или замены) или
, построив график
.
Решить систему уравнений алгебраически — все равно, что разгадать загадку. Каждое линейное уравнение дает подсказку, необходимую для решения загадочных значений каждой переменной.
Точно так же, как ответ на загадку должен согласовываться с каждой подсказкой, значения каждой переменной в системе уравнений должны согласовываться с каждым уравнением в системе.
Это означает, что как только мы найдем значения, которые делают каждое уравнение в системе одновременно верным, мы получим наше решение.
Рассмотрим следующую систему уравнений:
x+yx+3y=6=16
Наша загадка: если
и
, чему равны
и
?
Мы можем решить систему уравнений методом исключения-замены:
Исключить x и найти y:
x+y=6−(x+3y=16)
−2y
=−10
y
=
5
Подставьте y и найдите x, используя одно из уравнений системы:
x+y=6x+5=6x=1 9 0005
Тайна раскрыта!
Обычно мы видим системы линейных уравнений с одним решением, но они также могут не иметь решений или иметь бесконечное число решений в зависимости от того, если и как пересекаются линии уравнений.

 Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010.
Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010.
 В этом случае одна из них уничтожится.
В этом случае одна из них уничтожится.