Все формулы площади трапеции для решения задач по геометрии
Нахождение площади трапеции является одним из основных действий, которое позволяет решать множество задач геометрии. Также в КИМ по математике ОГЭ и ЕГЭ есть множество задач, для решения которых необходимо знать, как искать площадь этой геометрической фигуры. В данной статье будут рассмотрены все формулы площади трапеции.
Что собой представляет данная фигура?
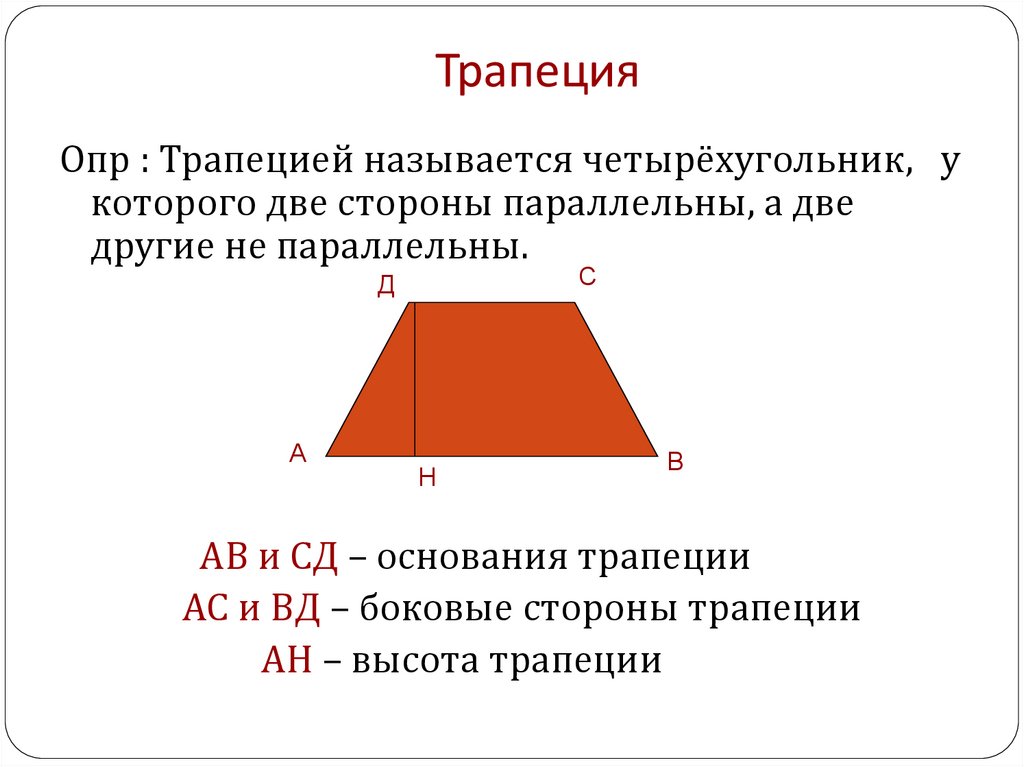
Прежде чем рассматривать все формулы площади трапеции, необходимо знать, что это такое, потому что без четкого определения невозможно грамотно пользоваться формулами и свойствами данной фигуры. Трапеция — четырехугольник, две стороны которого расположены напротив друг друга, и если продолжить их до бесконечных прямых, то они никогда не пересекутся (данные стороны являются основаниями фигуры). Две другие стороны могут обладать тупыми и острыми углами и называются боковыми (при этом, если боковые стороны ее одинаковы, а углы при основании попарно равны друг другу, то такая трапеция называется равнобокой).
Все формулы площади этого четырехугольника рассмотрены далее.
Все формулы площади трапеции
В геометрии существует множество формул нахождения площадей фигур, что является как плюсом, так и минусом. Как же найти площадь трапеции?
- Через диагонали и вертикальный угол. Для этого умножьте половину произведения диагоналей на угол между ними.
- Площадь трапеции через основание и высоту. Половину суммы оснований умножьте на высоту трапеции, проведенную к одному из оснований.
- При помощи всех сторон. Сумму оснований поделите пополам и умножьте на корень. Под корнем: сторона в квадрате минус дробь, в числителе которой — разница оснований в квадрате плюс разница боковых сторон, каждая из которых в квадрате, а в знаменателе — разница оснований, умноженная на два.
- Через высоту и медиану. Сумму оснований трапеции поделите пополам и умножьте на высоту, проведенную к основанию фигуры.
- Для равнобедренной трапеции также существует своя формула нахождения площади.
Чтобы найти площадь данной фигуры, умножьте квадрат радиуса на четыре и поделите на синус угла альфа.
Чтобы найти площадь данной фигуры, умножьте квадрат радиуса на четыре и поделите на синус угла альфа.Свойства биссектрисы трапеции
Как и биссектриса равнобедренного треугольника, проведенная к основанию, прямая, делящая угол пополам, данной фигуры обладает своими свойствами, которые пригодятся при решении задач по геометрии.
- Биссектрисы при сторонах, не параллельных друг другу, являются перпендикулярами (из этого свойства следует, что они образуют прямоугольный треугольник, гипотенузой которого является боковая сторона данной фигуры).
- Точка их пересечения при стороне, которая является основанием данной фигуры, принадлежит другому основанию (из данного свойства следует, что такими прямыми тупых углов при основании образуется равнобедренный треугольник).
- Биссектриса отсекает от основания отрезок такой же длины, что и боковая сторона (из этого свойства следует, что она образует с основанием равнобедренный треугольник, боковая сторона и основание трапеции будут являться боковыми сторонами, а биссектриса — основанием равнобедренного треугольника).
Заключение
В данной статье были предложены все формулы площади трапеции. Большинство из них не рассматривается в учебниках геометрии, но при этом все они необходимы для успешного решения задач.
Геометрия: свойства трапеции — intmag24.ru
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
При этом трапеция обладает всеми свойствами четырехугольника. Поэтому запоминать надо свойства, которые характерны для трапеции.
Определения для трапеции:
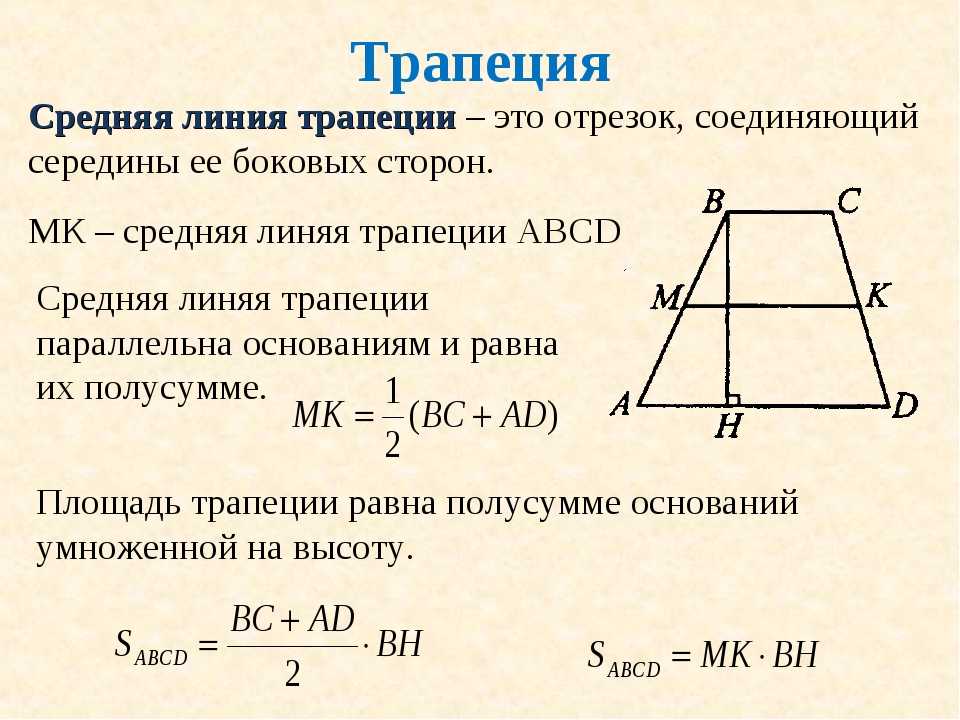
Параллельные стороны называются основаниями трапеции (BC и AD), непараллельные – боковыми сторонами (AB и CD).
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средняя линия трапеции — отрезок, который соединяет середины боковых сторон данной трапеции (на рис.
MN). Средняя линия трапеции параллельна её основаниям и равна их полусумме. Средняя линия параллельна основаниям. Её длина находится по формуле: MN=(AD+BC)/2
M – середина AB, N – середина CD,
AD||BC, MN||AD, MN||BC,
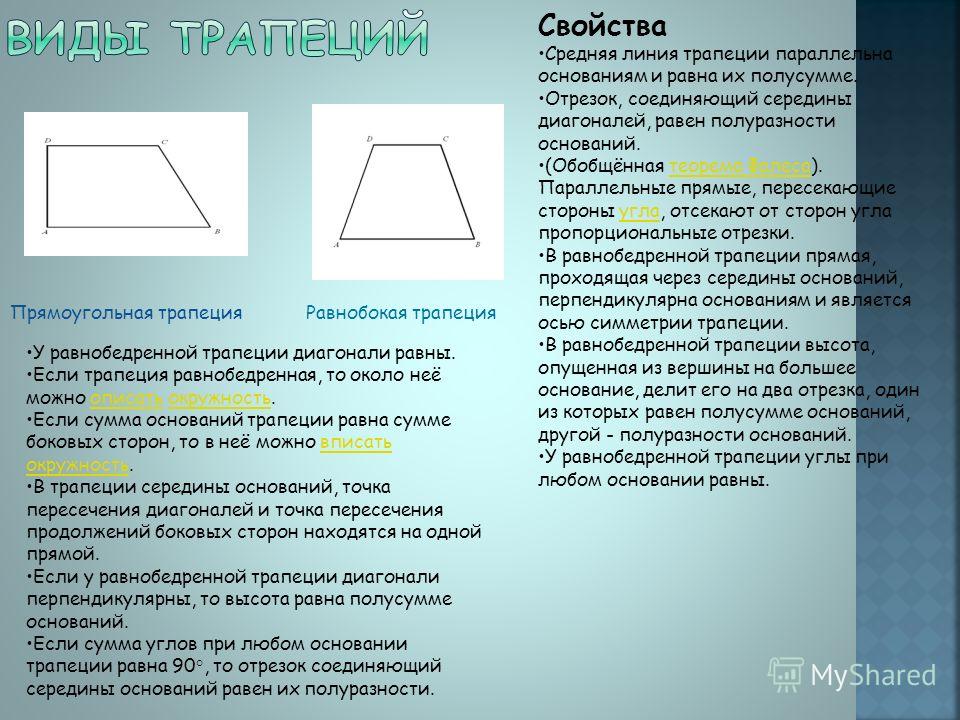
Равнобедренная (равнобокая) трапеция – трапеция, у которой боковые стороны равны (AB=CD).
В равнобедренной трапеции:
— углы при основании равны,
— проекции боковых сторон на основание равны: AE=FD,
— диагонали равны.
Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Свойства углов трапеции
- Свойства углов четырехугольника
- Сумма углов трапеции равна 360°
- Сумма внешних углов трапеции , взятых по одному при каждой вершине, равна 360°.
- Каждый угол трапеции всегда меньше суммы трёх остальных углов.
- Свойства углов трапеции
1.
Сумма углов, прилежащих к боковой стороне, равна 180°: ∠A+∠B=180°, ∠C+∠D=180°
2. Каждая диагональ трапеции образует с её основаниями равные углы.
3. Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне: AB=BE.
4. Биссектрисы смежных углов трапеции пересекаются под прямым углом.
Свойства сторон трапеции
- Свойства сторон трапеции (как у четырехугольника)
- Каждая сторона четырехугольника меньше суммы всех его других сторон.
- Сумма диагоналей меньше его периметра.
- Диагонали трапеции (как у четырехугольника)
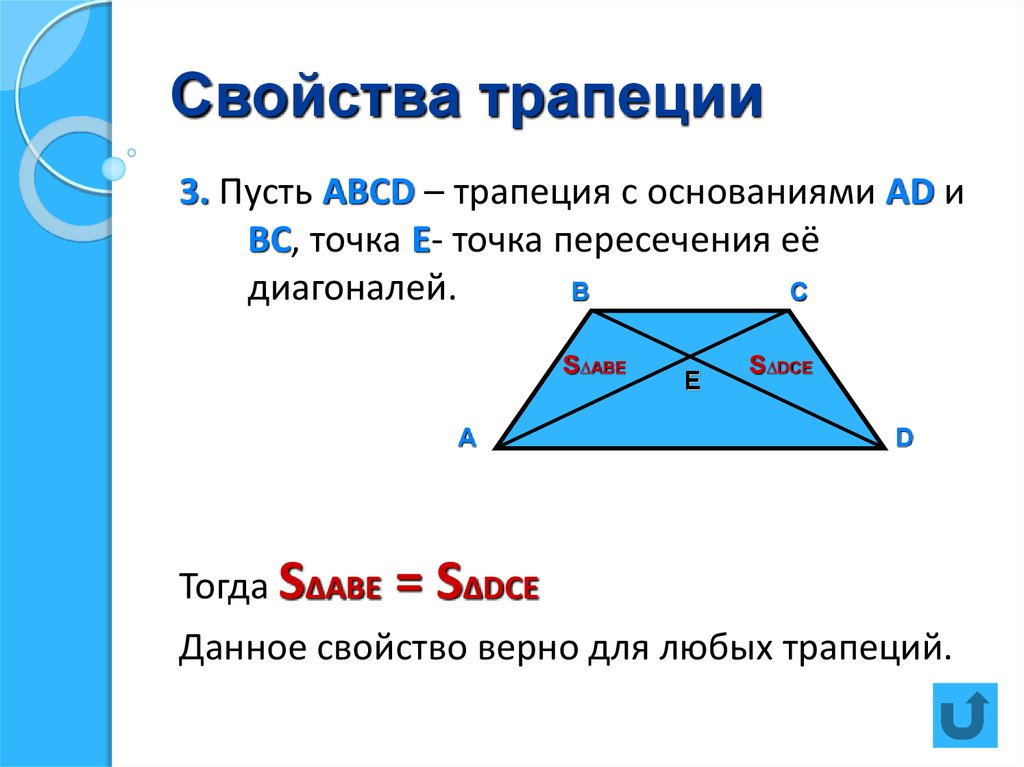
- Диагонали пересекаются в одной точке.
- Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
При пересечении диагоналей трапеции и продолжений её боковых сторон образуются подобные треугольники, прилежащие к основаниям.
Трапеция и окружность
В трапецию можно вписать окружность, если сумма её оснований равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.Радиус вписанной окружности:
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной. Центр описанной около трапеции окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон.
AB=CD ⇒ ∠ABC=∠DCB, ∠BAD=∠CDA;
AB=CD ⇒ AC=BD;
AB=CD ⇒ ABCD вписанная
Основные формулы:
Периметр трапеции
равен сумме длин всех его сторон:Площадь трапеции можно найти по двум формулам:
1.
Половине произведения суммы её оснований на высоту трапеции.
2. Половине произведения её диагоналей на синус угла между ними.
Стороны и диагональ равнобокой трапеции: Расшифровка:
a,b — основания,
c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая),
d1, d2 –диагонали,
P-периметр,
S-площадь,
h -высота, проведенная к противоположной стороне
Скачать программы, которые формируют задания на нахождение периметра и площади геометрических фигур, а также неизвестных характеристик (сторон, диагоналей и др.), в том числе для: квадрата, прямоугольника, треугольника, трапеции и другие. |
Геометрические свойства трапеции | calcresource
Геометрия
Трапеция — это четырехугольник, по крайней мере, с двумя параллельными сторонами.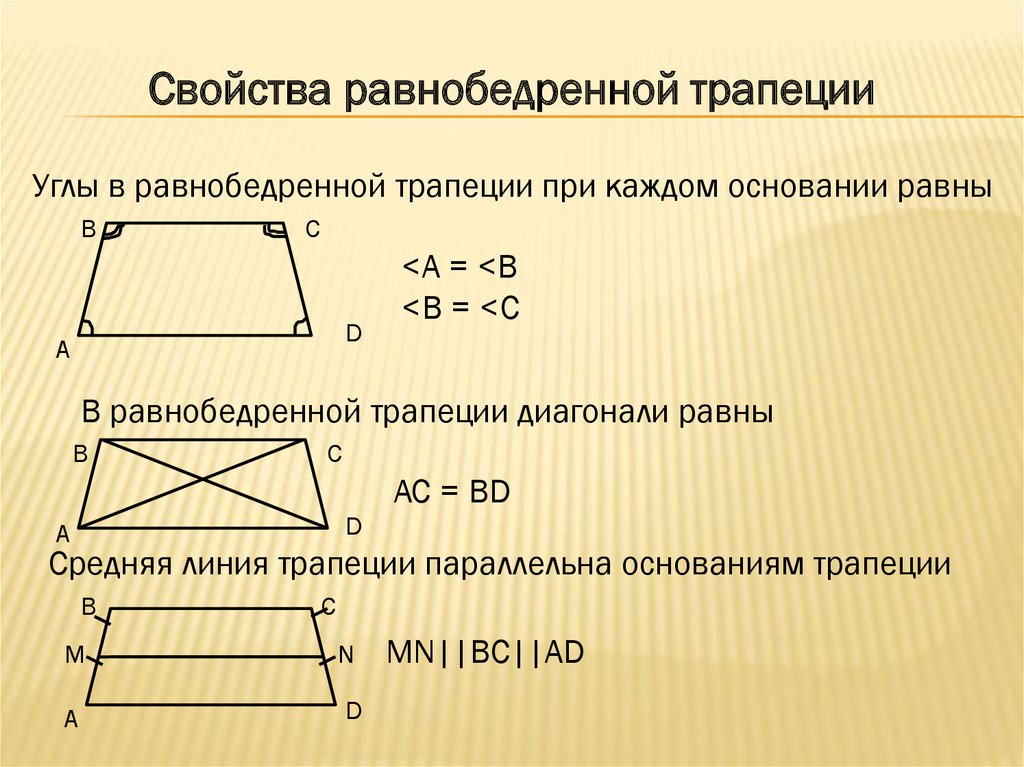
Используются определения, показанные на следующем рисунке:
Площадь трапеции определяется по формуле:
A = h\frac{a+b}{2}
где a, b длины двух оснований и h высота.
Периметр трапеции — это просто сумма длин всех сторон:
P = a+b+c+d
92}Центроид
Координаты центра тяжести относительно нижней левой вершины основания, x c и y c (см. рисунок ниже) могут быть рассчитаны с использованием первых моментов площади трех подобластей A ,ДО Н.Э.
Для x c , учитывая первые моменты площади относительно середины части B, находим:
\begin{split} & A\left(x_{c}-a_1-\frac{b} {2}\right) = \frac{a_1 h}{2}\left(-\frac{b}{2}-\frac{a_1}{3}\right) + \frac{a_2 h}{2} \left(\frac{b}{2}+\frac{a_2}{3}\right) \Rightarrow \\ \\ & x_{c} = a_1 +\frac{b}{2} + \frac{h \left(a_2-a_1\right)\left(\frac{3}{2}b+a_1+a_2 \right)}{6A} \end{split} 92\left(2b + a\right)}{6A} \\ \\ \end{split}
Приведенные выше формулы справедливы, даже когда α 1 или α 2 отрицательны, что происходит, когда углы φ 1 или φ 2 , тупые.
Использование свойств трапеций
Сделать 4 минуты чтения 3 минуты видео
Использование свойств трапеций
это не так. Параллельные стороны называются основаниями. Мы называем длину меньшего основания \(b,\), а длину большего основания \(B.\). Высота \(h,\) трапеции — это расстояние между двумя основаниями, как показано на рисунок ниже.
Трапеция имеет большее основание \(B,\) и меньшее основание \(b.\) Высота \(h\) — это расстояние между основаниями.
Формула для площади трапеции :
\({\text{Площадь}}_{\text{трапеция}}=\frac{1}{2}h\left(b+B\ справа)\)
Разделение трапеции на два треугольника может помочь нам понять формулу. Площадь трапеции равна сумме площадей двух треугольников. См. рисунок ниже.
Разделение трапеции на два треугольника может помочь вам понять формулу ее площади.
Высота трапеции также является высотой каждого из двух треугольников. См. рисунок ниже.
Формула площади трапеции:
Если мы распределим, мы получим,
Определение: свойства трапеций
- Трапеция имеет четыре стороны, как показано выше.
- Две его стороны параллельны, а две стороны нет.
- Площадь \(A,\) трапеции равна \(\text{A}=\frac{1}{2}h\left(b+B\right)\).
Пример
Найдите площадь трапеции, высота которой 6 дюймов, а основания равны \(14\) и \(11\) дюймов.
Решение
” Step 3 says, “Name. Choose a variable to represent it.” The word “name” is in bold. Beside this it says, “let A equal the area.” Step 4 says, “Translate. Write the appropriate formula. Substitute.” The word “translate” is in bold. Beside this is A equals one-half times h times parentheses little b plus big B. Below this is A equals one-half times 6 in times parentheses 11 in plus 14 in. Step 5 says, “Solve the equation.” The word “solve” is in bold. Beside this is A equals one-half times 6 times 25, then A equals 3 times 25, then A equals 75 square inches. Step 6 says, “Check,” in bold. Beside this is written, “Is this answer reasonable?”» data-label=»»>
Запишите соответствующую формулу.
Замена.
Если вокруг трапеции начертить прямоугольник с таким же большим основанием \(B\) и высотой \(h,\), то его площадь должна быть больше площади трапеции.
Если мы нарисуем прямоугольник внутри трапеции с таким же малым основанием \(b\) и высотой \(h,\), его площадь должна быть меньше площади трапеции.
Площадь большего прямоугольника составляет \(84\) квадратных дюймов, а площадь меньшего прямоугольника составляет \(66\) квадратных дюймов. Таким образом, имеет смысл, что площадь трапеции находится между \(84\) и \(66\) квадратных дюймов
Шаг 7.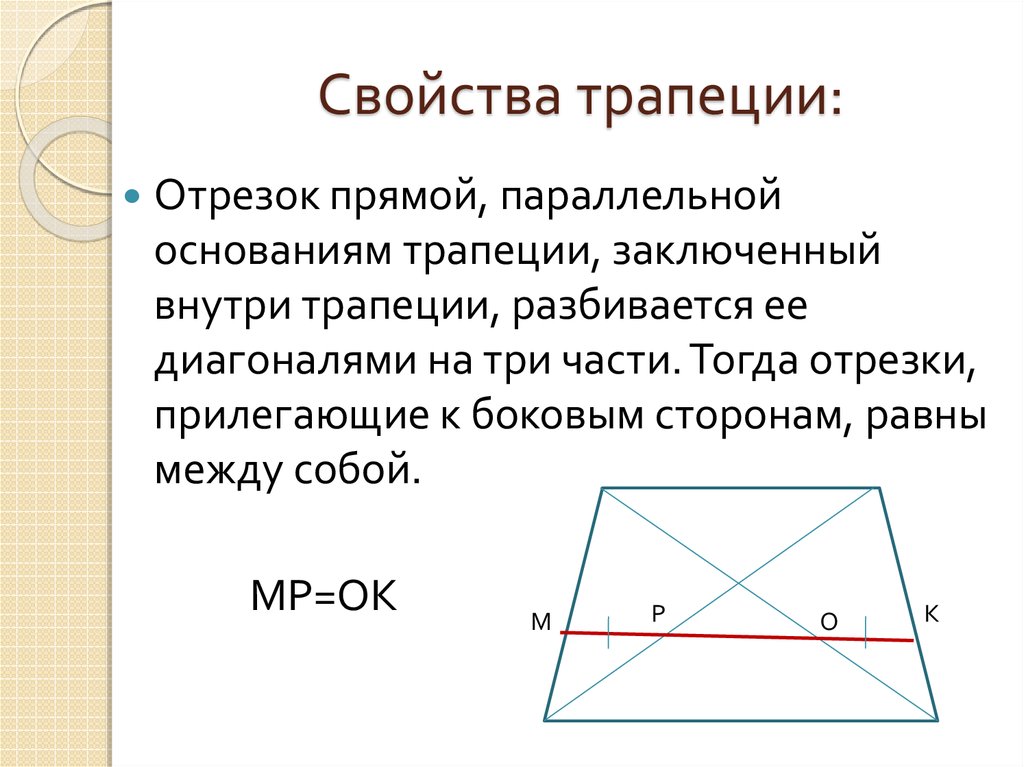
Ответьте на вопрос. Площадь трапеции равна \(75\) квадратных дюймов.
Пример
Найдите площадь трапеции, высота которой равна \(5\) футов, а основания равны \(10,3\) и \(13,7\) футов.
Решение
Below this is A equals one-half times 5 ft times parentheses 10.3 ft plus 13.7 ft. Step 5 says, “Solve the equation.” The word “solve” is in bold. Beside this is A equals one-half times 5 times 24, then A equals 12 times 5, then A equals 60 square feet. Step 6 says, “Check,” in bold. Beside this is written, “Is this answer reasonable? The area of the trapezoid should be less than the area of a rectangle with base 13.7 and height 5, but more than the area of a rectangle with base 10.3 and height 5.”» data-label=»»>
Запишите соответствующую формулу.
Замена.
Площадь трапеции должна быть меньше площади прямоугольника с основанием 13,7 и высотой 5, но больше площади прямоугольника с основанием 10,3 и высотой 5,
Пример
У Винни есть сад в форме трапеции. Трапеция имеет высоту \(3,4\) ярда, а основания — \(8,2\) и \(5,6\) ярда. Сколько квадратных метров будет доступно для посадки?
Решение
6 yd., the larger base at the bottom is labeled 8.2 yd., the height is shown by a dotted line and is labeled 3.4 yd. Step 2 says, “Identify what you are looking for.” The word “identify” is in bold. Beside this it says, “the area of a trapezoid.” Step 3 says, “Name. Choose a variable to represent it.” The word “name” is in bold. Beside this it says, “let A equal the area.” Step 4 says, “Translate. Write the appropriate formula. Substitute.” The word “translate” is in bold. Beside this is A equals one-half times h times parentheses little b plus big B. Below this is A equals one-half times 3.4 yd. times parentheses 5.6 yd. plus 8.2 yd. Step 5 says, “Solve the equation.” The word “solve” is in bold. Beside this is A equals one-half times 3.4 times 13.8, then A equals 23.46 square yards. Step 6 says, “Check,” in bold. Beside this is written, “Is this answer reasonable? Yes. The area of the trapezoid is less than the area of a rectangle with a base of 8.2 yd. and height 3.4 yd., but more than the area of a rectangle with base 5.
6 yd. and height 3.4 yd.”» data-label=»»>
Запишите соответствующую формулу.
Замена.
Да. Площадь трапеции меньше площади прямоугольника с основанием 8,2 ярда и высотой 3,4 ярда, но больше площади прямоугольника с основанием 5,6 ярда и высотой 3,4 ярда.
