Формулы гиперболы параболы и прямой: Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.

гипербола и парабола (основные формулы)

Высшая математика / Практикум по аналитической геометрии

06.02.201525.11.2015

1. Гипербола

Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, равная 2а (рис.1). Каноническое уравнение гиперболы имеет вид

Координаты фокусов гиперболы: F(c;0) и F₁(-c;0). Расстояние между фокусами равно 2с.
Точки пересечения гиперболы с осью абсцисс А(а;0) и A₁(—а;0) называются действительными вершинами.

Рис.2

Отрезок АА₁ = 2а называется действительной осью гиперболы. Точки В (0;b) и В₁(0;—b) называются мнимыми вершинами гиперболы, а отрезок ВВ₁ = 2b называется мнимой осью гиперболы.
Эксцентриситет гиперболы

Расстояния r и r₁ точки М(x;у) гиперболы до ее фокусов называются фокальными радиусами этой точки и определяются формулами:

если точка М лежит на правой ветви;

если точка М лежит на левой ветви.
Две прямые PQ и P₁Q₁ параллельные мнимой оси гиперболы и
отстоящие от нее на расстоянии a/e, называются директрисами гиперболы. Их уравнения:

или

Отношение расстояний любой точки гиперболы до фокуса и соответствующей директрисы есть величина постоянная, равная эксцентриситету гиперболы

Прямые RS и R₁S₁ определяемые уравнениями

называются асимптотами гиперболы.
Уравнение гиперболы с осями, параллельными координатным осям, имеет вид:

где x₀, у₀ — координаты центра гиперболы. Две гиперболы, выраженные уравнениями


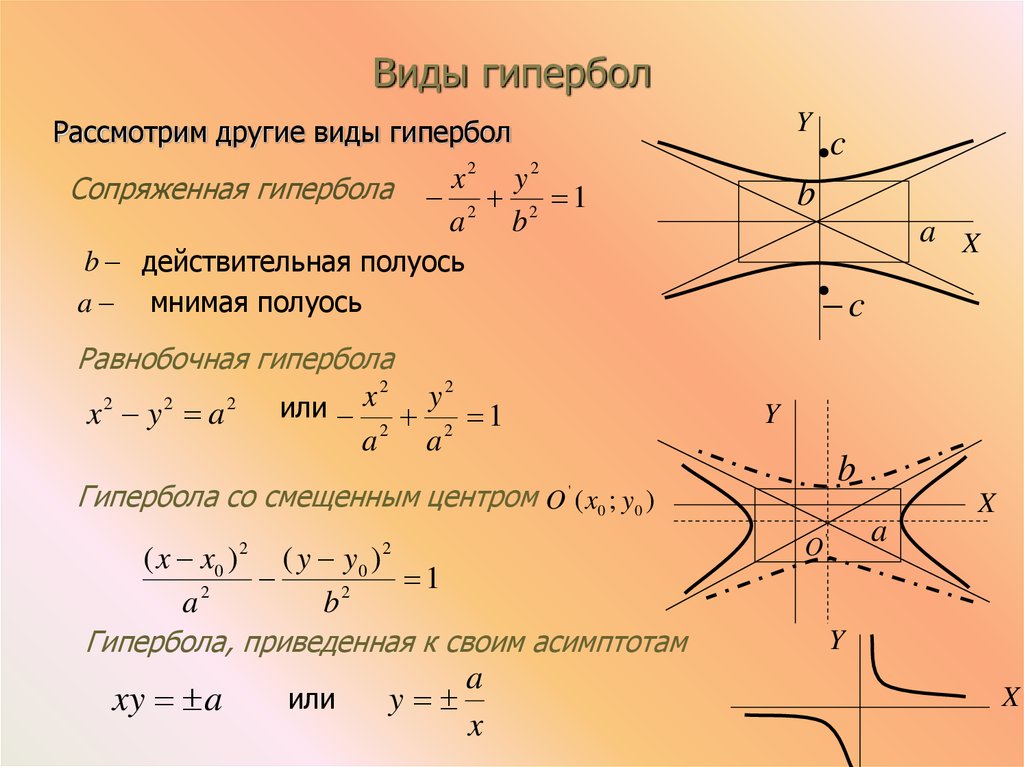
называются сопряженными (рис.3). Они имеют общие асимптоты.

Рис. 3.                                        Рис. 4.

Если оси гиперболы равны, т. е. a = b, то гипербола называется равнобочной или равносторонней (рис.4). Ее уравнение имеет вид

ее асимптотами служат биссектрисы координатных углов. Если за оси координат принять асимптоты равносторонней гиперболы, то ее уравнение примет вид

2.

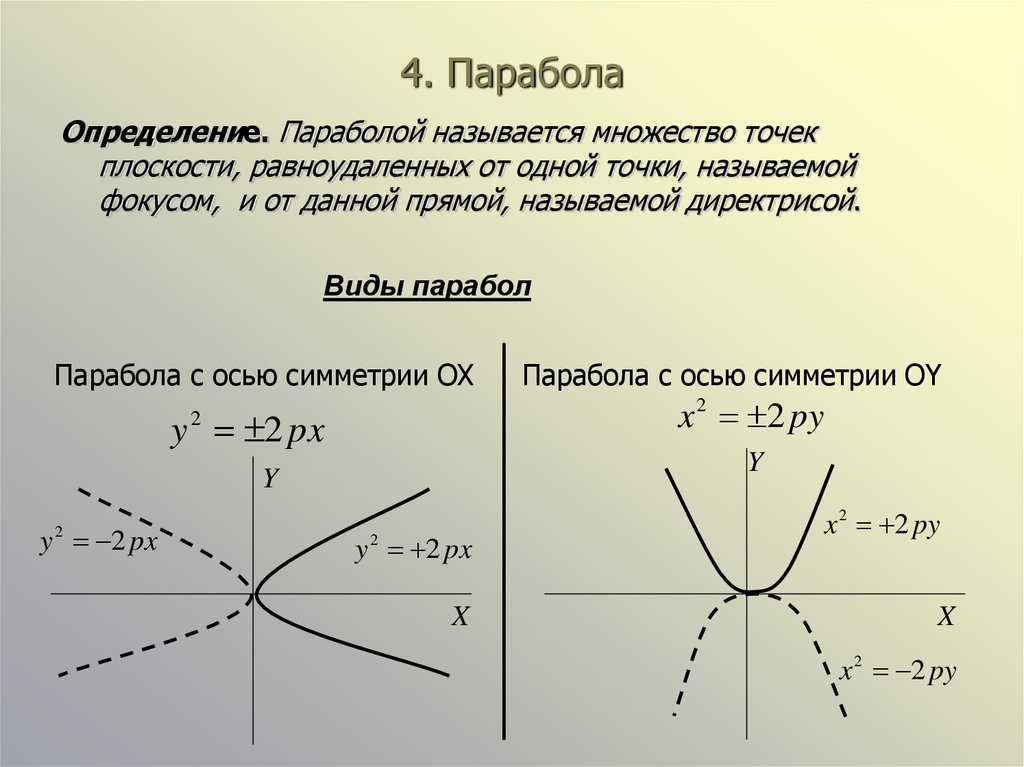
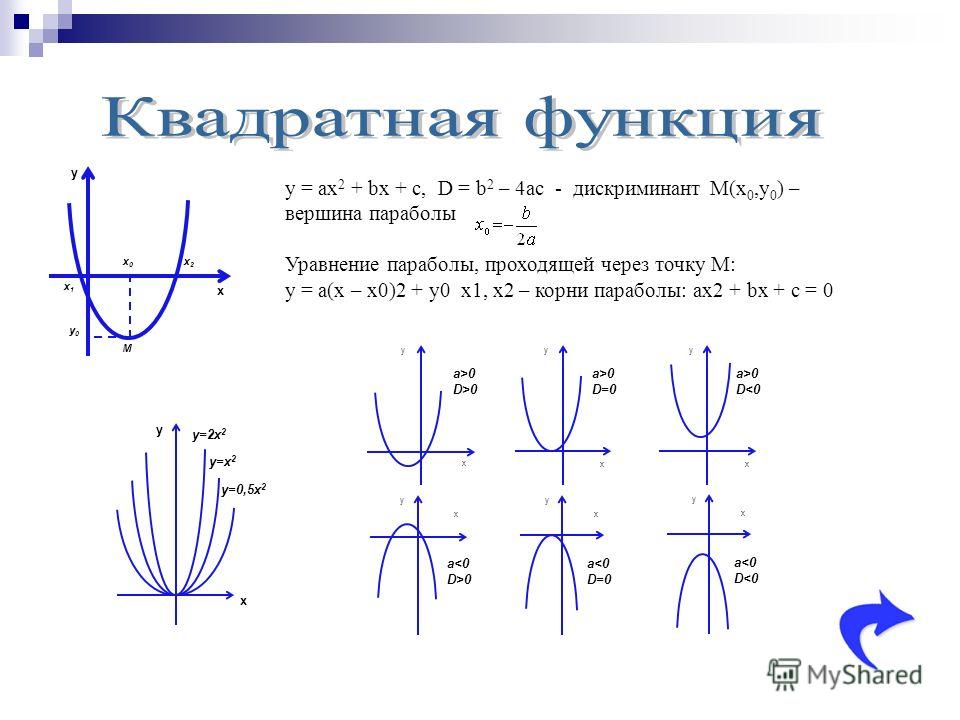Парабола

Параболой называется геометрическое место точек плоскости, равноудаленных oт данной точки — фокуса и данной прямой — директрисы (рис.5).
Каноническое уравнение параболы имеет вид

где Р — есть расстояние от фокуса до директрисы. Вершина параболы находится в начале координат, осью симметрии служит ось абсцисс.
Координаты фокуса F(p/2;0). Уравнение директрисы PQ параболы имеет вид

Фокальный радиус точки М(х;у) параболы равен:

Эксцентриситет параболы считается равным единице, е=1. Если осью симметрии параболы служит ось ординат (рис.6). то уравнение параболы имеет вид:


Рис. 3.                                        Рис. 4.
Уравнение директрисы в этом случае

Уравнение параболы с осью симметрии, параллельной одной из координатных осей, имеет вид:

или

где (x₀; y₀) — координаты вершины параболы.

3. Уравнения эллипса, гиперболы и параболы в полярных координатах

Уравнения эллипса, гиперболы и параболы в полярных координатах имеют один и тот же вид:

где е — эксцентриситет кривой.
Если е<1, то кривая, определяемая уравнением (27), есть эллипс; если е>1, то кривая — гипербола и если е=1, то кривая — парабола.
р — фокальный параметр для эллипса и гиперболы находится по формуле

Для параболы р имеет то же значение, что и в уравнении

у² = 2рх.

При этом полюс расположен для эллипса в левом фокусе, для гиперболы — в правом фокусе.

Тегиасимптоты гиперболывершина параболыгиперболагипербола онлайндиректриса параболыканоническая гиперболаканоническое уравнение гиперболыканоническое уравнение параболыпараболапарабола онлайнпарабола формулауравнение гиперболыуравнение параболыфокус параболыфокусы гиперболы

19. Гипербола и парабола. Уравнение плоскости и прямой в пространстве.

Гиперболой называется множество всех точек плоскости, разность расстояний каждой из которых до двух данных точек и (называемых фокусами гиперболы) есть величина постоянная, равная 2a.

Пусть М(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы или , т.е.

.

После упрощений получим каноническое уравнение гиперболы.

Каноническое уравнение гиперболы имеет вид , где .

Подобно эллипсу гипербола симметрична относительно обеих осей координат. Она состоит из двух частей, которые называются ее ветвями. Гипербола пересекает ось Ox в двух точках, называемых вершинами гиперболы, отрезок между вершинами называется вещественной осью гиперболы.

Прямые называются асимптотами гиперболы.

Эксцентриситетом гиперболы называется отношение .

При построении гиперболы целесообразно сначала построить основной прямоугольник гиперболы со сторонами 2a и 2b, параллельными координатным осям, и с центром в начале координат, провести прямые, проходящие через противоположные вершины этого прямоугольника, – асимптоты гиперболы и отметить вершины и гиперболы.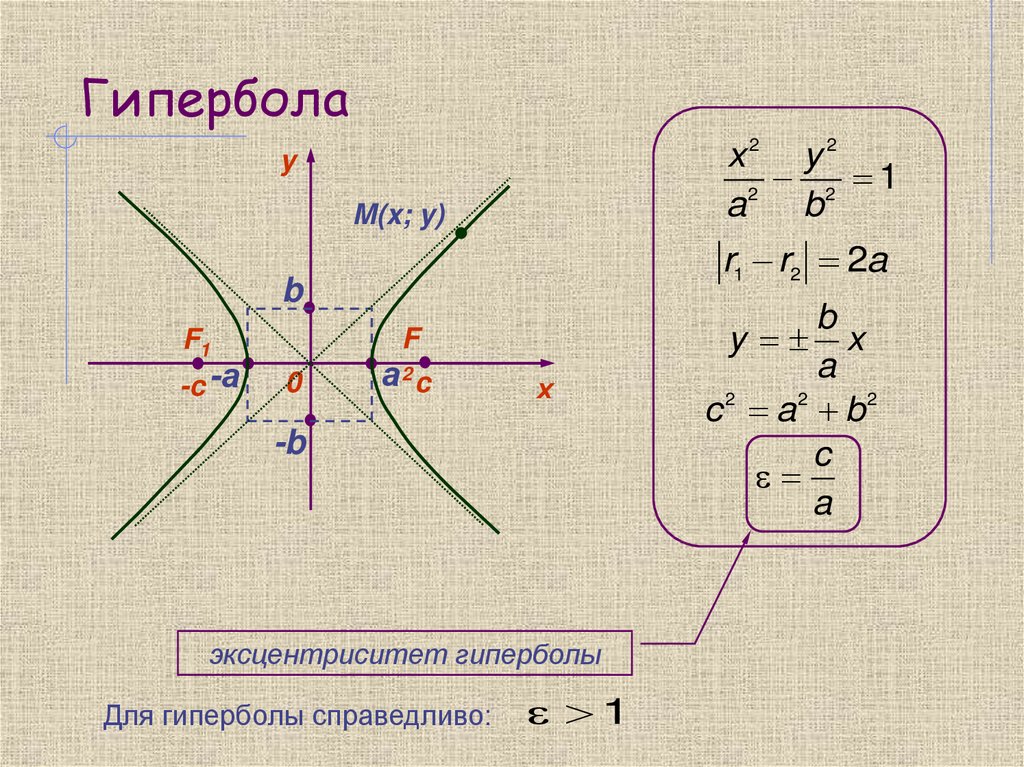

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки F, называемой фокусом, и данной прямой l, называемой директрисой.

Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p

(p > 0).

В выбранной системе фокус F имеет координаты , а уравнение директрисы имеет вид .

Уравнение называется каноническим уравнением параболы.

Вершиной параболы называется точка пересечения параболы с ее осью симметрии.

К параболам относятся также кривые, заданные уравнениями:

, .

Уравнение плоскости в пространстве.

Уравнение = 0 определяет в пространстве некоторую поверхность.

Пусть дана точка М₀ = (x₀, y₀, z₀) и ненулевой вектор (A,B,C).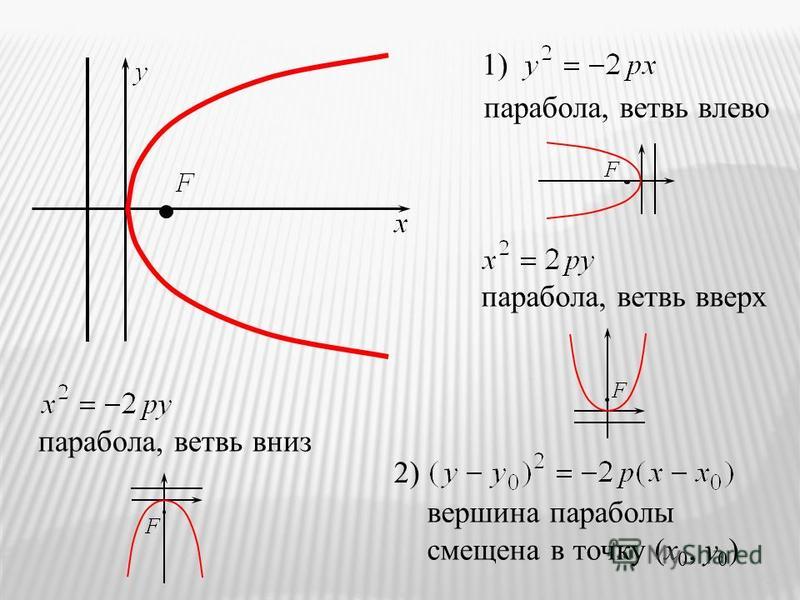 Построим в декартовой системе координат плоскость, проходящую через точку М₀, перпендикулярно к вектору (этот вектор называют

нормальным вектором или нормалью плоскости).

Рассмотри произвольную точку этой плоскости. Так как вектор лежит на плоскости, то он перпендикулярен к вектору .

Следовательно, их скалярное произведение равно нулю: .

Преобразуем в координатную форму:

(1)

Введя обозначение , уравнение (1) можно переписать в виде:

(2)

Уравнение (2) называется общим уравнением плоскости.

Определение. Общее уравнение называется полным, если все его коэффициенты отличны от нуля. Если хотя бы один из указанных коэффициентов равен нулю, то уравнение называется неполным.

Уравнение , где , , называется уравнением плоскости в «отрезках».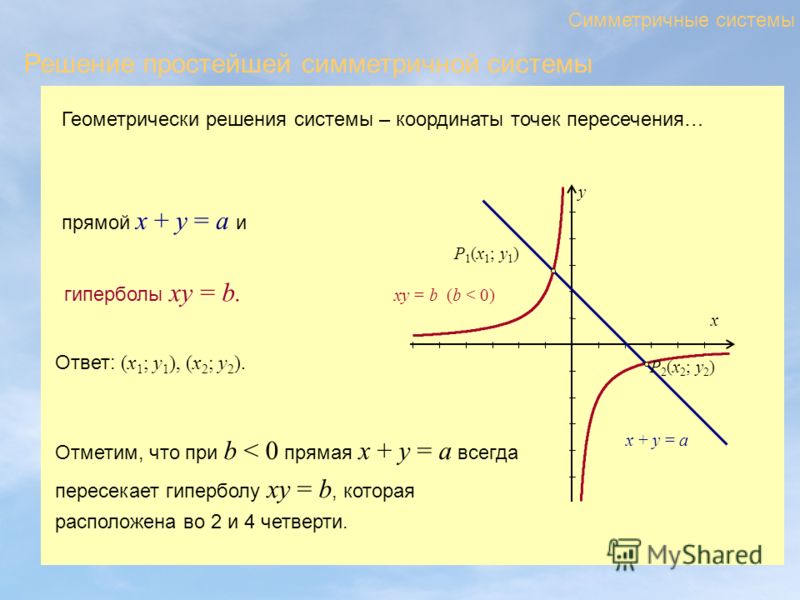

Виды неполных уравнений:

1) D = 0. Плоскость проходит через начало координат.

2) A = 0. Плоскость параллельно оси Ox (аналогично для других коэффициентов).

3) A = 0, B = 0. Плоскость параллельна координатной плоскости xOy.

4) A = 0, B = 0, С = 0. Плоскость представляет собой координатную плоскость.

Уравнение прямой в пространстве.

Рассмотрим систему уравнений:

(1)

Каждое из уравнений системы определяет плоскость. Если плоскости не параллельны, то система (1) определяет прямую как линию пересечения этих плоскостей. Уравнения (1) называются общим уравнением прямой.

Уравнение прямой в пространстве, проходящей через две данные точки

Каноническое уравнение прямой

где (х₀; у₀; z₀) – точка прямой,

(k; l; m) – направляющий вектор.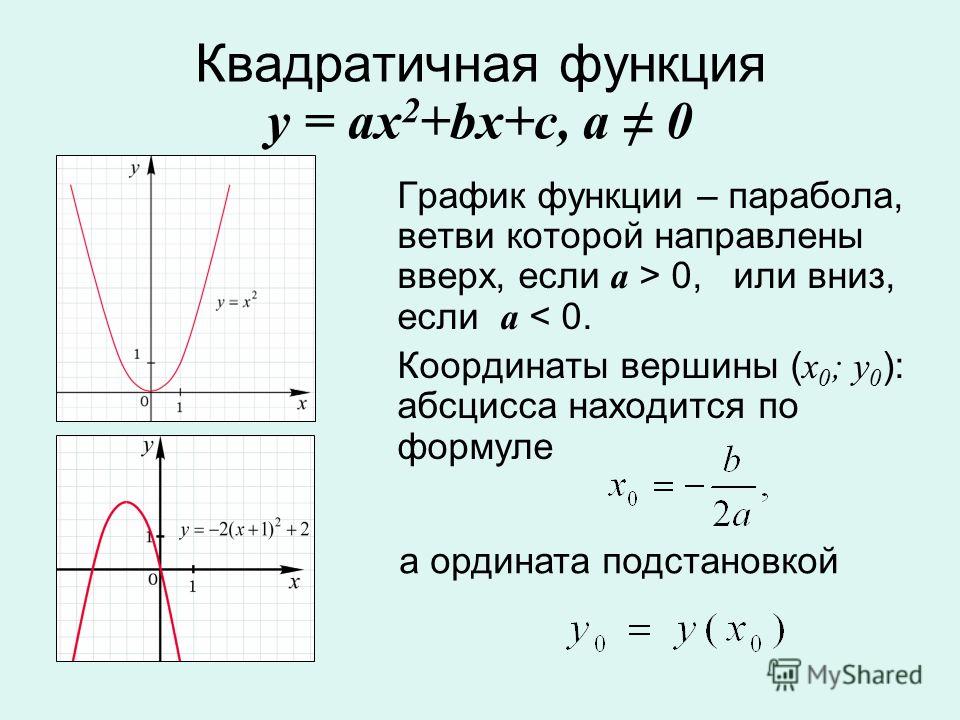

Коническое сечение – определение, формулы, уравнения, примеры

Конические сечения или сечения конуса – это кривые, полученные пересечением плоскости и конуса. Есть три основных сечения конуса или конических сечения : парабола, гипербола и эллипс (окружность — это особый вид эллипса). Конус с двумя одинаковыми покровами используется для изготовления конических профилей .

Все сечения конуса или конические сечения имеют различную форму, но у них есть некоторые общие свойства, о которых мы узнаем в следующих разделах. Давайте проверим формулы конического сечения, уравнения конуса и его параметры, с примерами, часто задаваемыми вопросами.

1.	Что такое коническое сечение?
2.	Параметры конического сечения
3.	Термины, относящиеся к коническому сечению
4.	Круг — коническое сечение
5.	Парабола — коническое сечение
6.	Эллипс — коническая секция
7.	Гипербола — коническое сечение
8.	Формулы конического сечения — стандартные формы
11.	Часто задаваемые вопросы о коническом сечении

Что такое коническое сечение?

Конические сечения — это кривые, полученные при разрезании конуса плоскостью. Конус обычно имеет две одинаковые конические формы, известные как покровы. Мы можем получить различные формы в зависимости от угла среза между плоскостью и конусом и его покровом. Разрезав конус плоскостью под разными углами, получим следующие фигуры:

• Круг
• Парабола
• Эллипс
• Гипербола

Эллипс – это коническое сечение, которое образуется при пересечении плоскости с конусом под углом. Окружность — это особый тип эллипса, у которого секущая плоскость параллельна основанию конуса.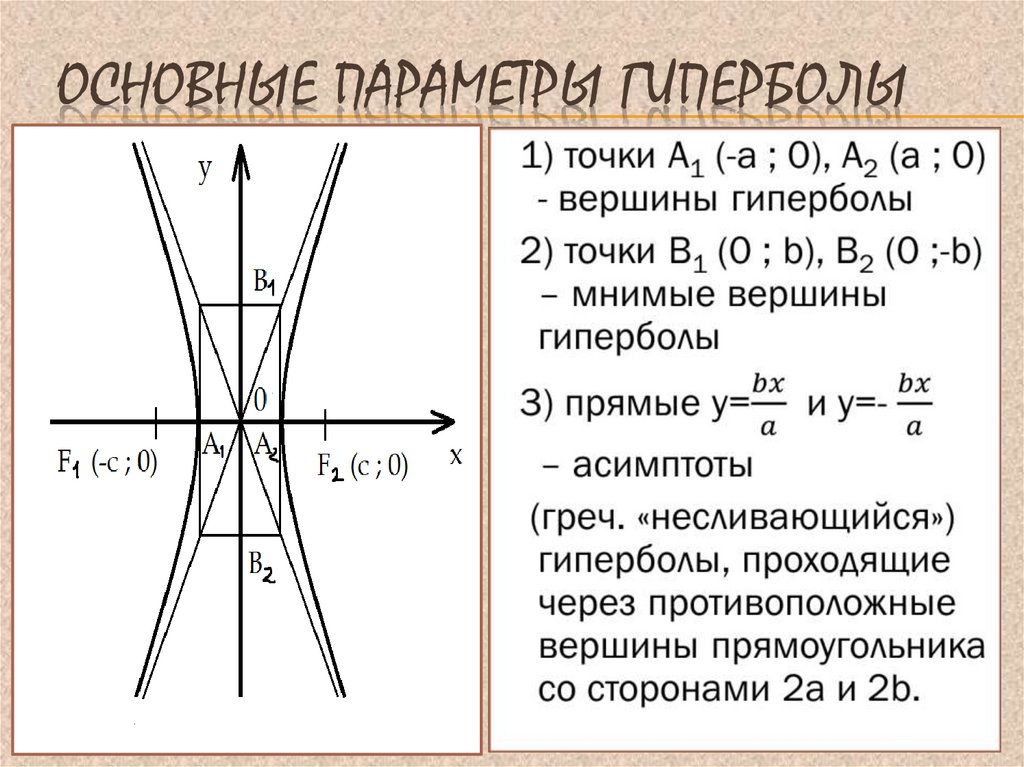 Гипербола образуется, когда интересующая плоскость параллельна оси конуса и пересекается с обеими сторонами двойного конуса. Когда пересекающая плоскость пересекает поверхность конуса под углом, мы получаем коническое сечение, называемое параболой.

Параметры конического сечения

Фокус, директриса и эксцентриситет являются тремя важными характеристиками или параметрами, определяющими конику. Различными коническими фигурами являются круг, эллипс, парабола и гипербола. И форма и ориентация этих фигур полностью основана на этих трех важных характеристиках. Узнаем подробно о каждом из них.

Фокус

Фокус или фокусы (множественное число) конического сечения – это точка (точки), вокруг которых создается коническое сечение. Они специально определены для каждого типа конического сечения. У параболы один фокус, а у эллипса и гиперболы два фокуса. Для эллипса сумма расстояний точки эллипса от двух фокусов постоянна. Окружность, являющаяся частным случаем эллипса, имеет оба фокуса в одном и том же месте, а расстояние от всех точек до фокуса постоянно. Для параболы она является предельным случаем эллипса и имеет один фокус на расстоянии от вершины, а другой — на бесконечности. Гипербола имеет два фокуса, и абсолютная разность расстояния точки гиперболы от двух фокусов постоянна.

Директриса

Директриса — это линия, используемая для определения конических сечений. Директриса – это линия, проведенная перпендикулярно оси упомянутой коники. Каждая точка на конике определяется отношением ее расстояния от директрисы и фокусов. Направляющая параллельна сопряженной оси и широкой прямой кишке коники. У круга нет направляющей. Парабола имеет 1 директрису, эллипс и гипербола имеют по 2 директрисы.

Эксцентриситет

Эксцентриситет конического сечения – это постоянное отношение расстояния точки на коническом сечении от фокуса и директрисы. Эксцентриситет используется для однозначного определения формы конического сечения. Это неотрицательное действительное число. Эксцентриситет обозначается буквой «e». Если два конических сечения имеют одинаковый эксцентриситет, они будут подобны.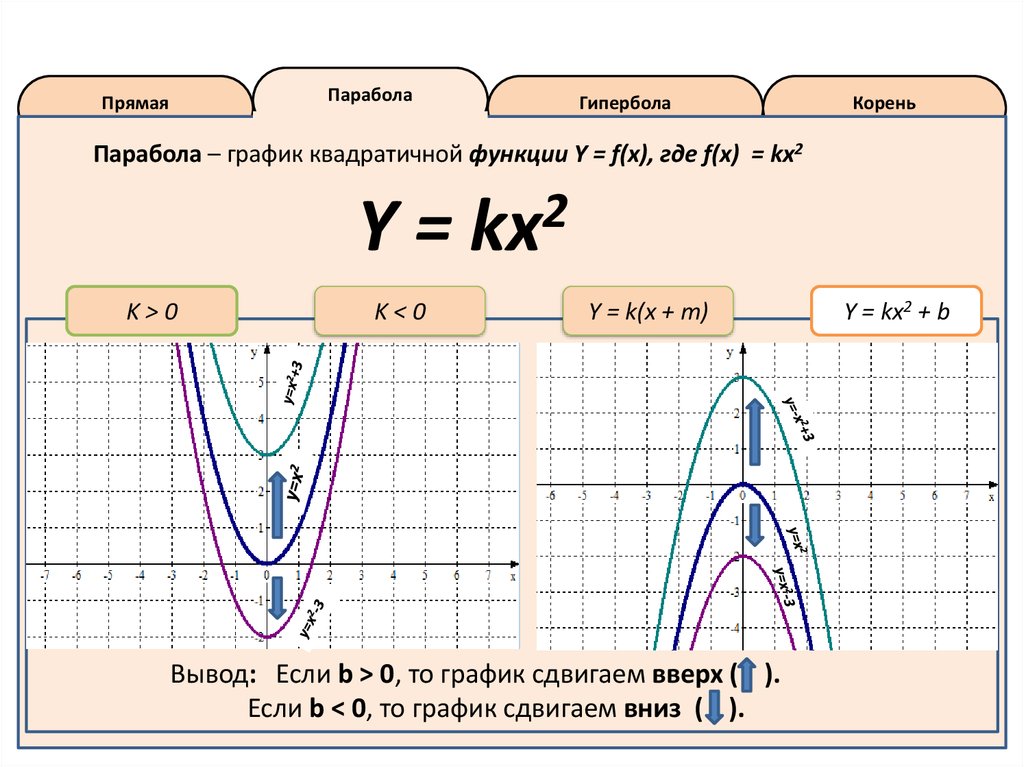 По мере увеличения эксцентриситета коническое сечение все больше и больше отклоняется от формы круга. Значение e для различных конических сечений следующее.

• Для круга, e = 0.
• Для эллипса 0 ≤ e < 1
• Для параболы e = 1
• Для гиперболы e > 1    

Помимо этих трех параметров, конические сечения имеют еще несколько параметров, таких как главная ось, широкая прямая кишка, большая и малая оси, фокальный параметр и т. д. Давайте кратко узнаем о каждом из этих параметров, связанных с коническим сечением. Ниже приведены детали параметров конического сечения.

• Главная ось: Ось, проходящая через центр и фокусы коники, является ее главной осью и также называется большой осью коники.
• Сопряженная ось: Ось, проведенная перпендикулярно главной оси и проходящая через центр коники, является сопряженной осью. Сопряженная ось также является его малой осью.
• Центр: Точка пересечения главной оси и сопряженной оси коники называется центром коники.
• Вершина: Точка на оси, где коника пересекает ось, называется вершиной коники.
• Фокусная хорда: Фокусная хорда конического сечения — это хорда, проходящая через фокус конического сечения. Фокусная хорда пересекает коническое сечение в двух различных точках.
• Фокусное расстояние: Расстояние точки \((x_1, y_1)\) на конике от любого из фокусов является фокусным расстоянием. Для эллипса, гиперболы у нас есть два фокуса, и, следовательно, у нас есть два фокусных расстояния.
• Latus Rectum: Это фокальная хорда, перпендикулярная оси конуса. Длина широкой прямой кишки для параболы LL’ = 4а. А длина прямой кишки для эллипса и гиперболы равна 2b ² /a.

• Касательная: Касательная — это линия, касающаяся коники снаружи в одной точке на конике. Точка, в которой касательная касается коники, называется точкой касания. Также из внешней точки к конике можно провести около двух касательных.

• Нормаль: Линия, проведенная перпендикулярно касательной и проходящая через точку касания и фокус коники, называется нормалью. У нас может быть одна нормаль для каждой из касательных к конике.

• Хорда контакта: Хорда, проведенная для соединения точки касания, проведенная из внешней точки к конике, называется хордой контакта.

• Полюс и поляра: Для точки, которая называется полюсом и лежит вне конического сечения, геометрическое место точек пересечения касательных, проведенных на концах хорд, проведенных из этой точки, называется полярной .

• Вспомогательная окружность: Окружность, проведенная по большой оси эллипса в качестве его диаметра, называется вспомогательной окружностью. Коническое уравнение эллипса: x ² /a ² + y ² /b ² = 1, а уравнение вспомогательной окружности: x ² + y ² = a ² .
• Окружность директора: Геометрическое место точки пересечения касательных перпендикуляров, проведенных к эллипсу, называется окружностью директора. Для эллипса (x ² /a ² + y ² /b ² = 1) уравнение окружности директора имеет вид x ² + y ² = a
6 2 ²

• Асимптоты: Пара прямых, проведенных параллельно гиперболе и предположительно касающихся гиперболы на бесконечности. Уравнения асимптот гиперболы имеют вид y = bx/a и y = -bx/a соответственно. А для гиперболы, имеющей коническое уравнение x ² /a ² — y ² /b ² = 1, уравнение пары асимптот гиперболы имеет вид \(\dfrac{x}{ а} ±  \dfrac{y}{b} = 0\).

 

Круг — коническое сечение

Окружность представляет собой особый тип эллипса, у которого секущая плоскость параллельна основанию конуса.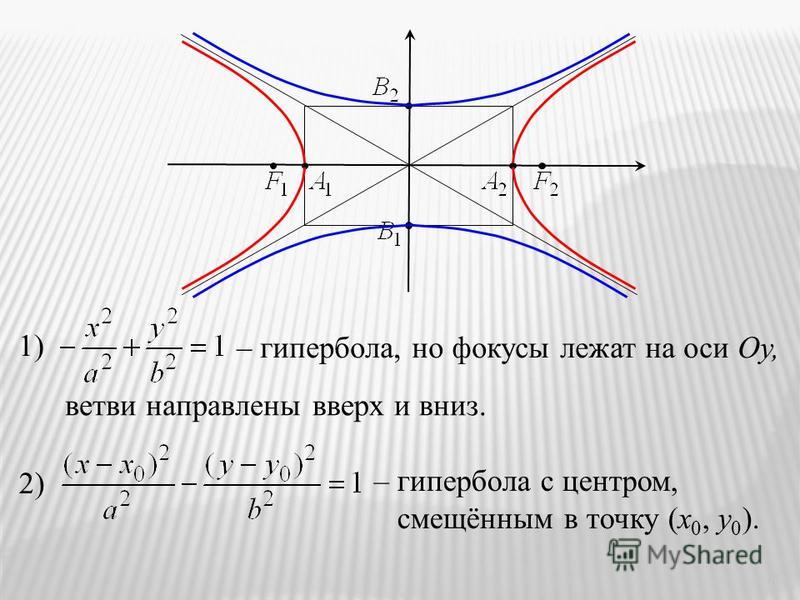 Круг имеет фокус, известный как центр круга. Геометрическое место точек на окружности находится на фиксированном расстоянии от фокуса или центра окружности и называется радиусом окружности. Значение эксцентриситета (e) для окружности равно e = 0. У окружности нет направляющей. Общая форма уравнения окружности с центром в точке (h, k) и радиусом r:

(x−h) ² + (y−k) ² = r ²

 

Парабола — коническое сечение

Когда пересекающая плоскость находится под углом к ​​поверхности конуса, мы получаем коническое сечение, называемое параболой. Представляет собой U-образное коническое сечение. Значение эксцентриситета (e) для параболы равно e = 1. Это асимметричная открытая плоская кривая, образованная пересечением конуса с плоскостью, параллельной его стороне. График квадратичной функции представляет собой параболу, линейно-симметричную кривую, форма которой подобна графику y = x ² . График параболы либо открывается вверх, как y = x ² , либо открывается вниз, как график y = -x ² . Путь снаряда под действием силы тяжести идеально следует кривой этой формы.

 

Эллипс — коническое сечение

Эллипс – это коническое сечение, которое образуется при пересечении плоскости с конусом под углом. Эллипс имеет 2 фокуса, большую ось и малую ось. Значение эксцентриситета (e) для эллипса равно e < 1. Эллипс имеет 2 направляющие. Общая форма уравнения эллипса с центром в (h, k) и длиной большой и малой осей как «2a» и «2b» соответственно. Большая ось эллипса параллельна оси x. Формула конического сечения эллипса выглядит следующим образом.

(x−h) ² /a ² + (y−k) ² /b ² = 1

места a и b в приведенной выше формуле.

Гипербола — коническое сечение

Гипербола образуется, когда интересующая плоскость параллельна оси конуса и пересекается с обеими сторонами двойного конуса. Значение эксцентриситета (e) для гиперболы равно e > 1. Два несвязанных участка гиперболы называются ветвями. Они являются зеркальным отражением друг друга, и их противоположные по диагонали плечи приближаются к пределу линии.

Гипербола является примером конического сечения, которое можно изобразить на плоскости, пересекающей двойной конус, образованный двумя покровами. Общая форма уравнения гиперболы с центром (h, k) выглядит следующим образом.

(x−h) ² /a ² — (y−k) ² /b ² = 1

Формулы конического сечения — стандартные формы

Формулы конического сечения представляют стандартные формы окружности, параболы, эллипса, гиперболы. Для эллипсов и гипербол стандартная форма имеет ось x в качестве главной оси и начало координат (0,0) в качестве центра. Вершины (±a, 0) и фокусы (±c, 0)., и определяется уравнениями c ² = a ² − b ² для эллипса и c ² = a ² + b ² для гиперболы. Для круга c = 0, поэтому a ² = b ² . Для параболы стандартная форма имеет фокус на оси x в точке (a, 0), а направляющая — это линия с уравнением x = -a.

• Круг: x ² +y ² = a ²
• Парабола: y ² = 4ax, когда a>0
• Эллипс: х ² /а ² + у ² /б ² = 1
• Гипербола: x ² /a ² – y ² /b ² = 1

 

Связанные темы

Ознакомьтесь со статьями ниже, чтобы узнать больше о темах, связанных с пересечением двух линий.

• Линии
• Параллельные линии
• Уравнение прямой
• Форма пересечения наклона линии
• Калькулятор точки пересечения

 

1. Пример 1: Каким будет уравнение для гиперболы с центром в точке (2, 3), вершиной в точке (0, 3) и фокусом в точке (5, 3).

   Решение:

   Как мы видим, для гиперболы все три точки, т. е. центр, вершина и фокус, лежат на одной прямой y = 3. = 2, c = 3

   Отсюда

   b ² = c ² — a ² = 9 – 4 = 5.

   Подставляя уравнение гиперболического сечения:

   (x−h) ^{2 2 /a (у-к) 2 /б 2 = 1}

   Получаем, Ответ: Уравнение гиперболы будет (x−2) ² /4 — (y−3) ² /5 = 1.

2. Пример 2. Если для эллипса фокус лежит в точке (3, 0), вершина лежит в точке (4, 0), а ее центр лежит в точке (0, 0). Найдите уравнение эллипса.

   Решение:

   Из данных точек мы видим, что

   C = 3 и A = 4.

   с использованием B ² = A ² — C ²

   Мы получаем:

   b ² = 16 – 9 = 7

   Подставляя уравнение конического сечения эллипса:

   x ² /A ² + Y ² /B ² = 1

   x ² /16 + y ² /7 = 1

   Ответ: Уравнение olsssse of ellips is ellips is ellips stipsse of elpsse stipsse of elpsse stipsse of elpsse stipsse of elpsse of elpsse 2 /16 + у ² /7 = 1.

перейти к слайдуперейти к слайду

 

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о коническом сечении

Что такое коническое сечение в геометрии?

Коническое сечение представляет собой геометрическое представление параболы, эллипса, гиперболы в двумерной системе координат. Эти конические получаются из простого конуса и получаются путем разрезания конуса на разные участки.

Что такое парабола в коническом сечении?

Когда пересекающая плоскость находится под углом к ​​поверхности конуса, мы получаем коническое сечение, называемое параболой. Представляет собой U-образное коническое сечение. Значение эксцентриситета (e) для параболы равно e = 1. Это симметричная открытая плоская кривая, образованная пересечением конуса с плоскостью, параллельной его стороне. Путь снаряда под действием силы тяжести идеально следует кривой этой формы.

Стандартная форма уравнения параболы с осью вдоль оси x и вершиной в начале координат: y ² = 4ax.

Что такое круг в коническом сечении?

Окружность — это особый тип эллипса, в котором секущая плоскость параллельна основанию конуса. Круг имеет фокус, известный как центр круга. Геометрическое место точек на окружности имеет фиксированное расстояние от фокуса или центра окружности, и это фиксированное расстояние называется радиусом окружности. Значение эксцентриситета (e) для окружности равно e = 0. У окружности нет направляющей. Общая форма уравнения окружности с центром в точке (h, k) и радиусом r выглядит следующим образом.

(x−h) ² + (y−k) ² = r ²

Что такое гипербола в коническом сечении?

Гипербола образуется, когда интересующая плоскость параллельна оси конуса и пересекается с обеими сторонами двойного конуса. Гипербола представляет собой геометрическое место точки, разность расстояний от которой до двух фокусов является постоянной величиной. Эксцентриситет (e) для гиперболы имеет значение больше 1. (e > 1)

Общая форма уравнения гиперболы с (h, k) в качестве центра, осью x в качестве большой оси и ось Y в качестве малой оси выглядит следующим образом.

(x−h) ² /a ² — (y−k) ² /b ² = 1

Что такое эллипс в коническом сечении?

Эллипс – это коническое сечение, которое образуется при пересечении плоскости с конусом под углом. Эллипс имеет 2 фокуса, большую ось и малую ось. Значение эксцентриситета (e) для эллипса равно e < 1. Эллипс имеет 2 направляющие. Общая форма уравнения эллипса с центром в (h, k) и длиной большой и малой осей как «2a» и «2b» соответственно. Большая ось эллипса параллельна оси x.

(x−h) ² /a ² + (y−k) ² /b ² = 1

Что такое эксцентриситет конического сечения?

Эксцентриситет конического сечения представляет собой постоянное отношение расстояния точки на коническом сечении от фокуса и директрисы. Эксцентриситет используется для однозначного определения формы конического сечения. Это неотрицательное действительное число, которое лежит между 0 и 1. Значения эксцентриситета для различных коник следующие.

• Для круга, e = 0.
• Для эллипса 0 ≤ e < 1
• Для параболы e = 1
• Для гиперболы e > 1

Каковы применения конического сечения?

Вот несколько реальных применений конических сечений, которые мы могли видеть или знать.

• Планеты движутся вокруг Солнца по эллиптическим траекториям в одном фокусе.
• Зеркала, используемые для направления световых лучей в фокус параболы, являются параболическими.
• Параболические зеркала в солнечных печах фокусируют лучи света для обогрева.
• Звуковые волны фокусируются на параболических микрофонах.
• Автомобильные фары и прожекторы спроектированы по принципу параболы.
• Путь, пройденный предметами, подброшенными в воздух, является параболическим.
• Гиперболы используются в системах дальней навигации под названием LORAN.
В телескопах
• используются параболические зеркала.

Знать формулы конического сечения здесь

Парабола Эллипс и гипербола подпадают под тему конического сечения. Коническое сечение — это геометрическое место точки, которая имеет фиксированное отношение от конкретной точки. Коническое сечение — это геометрическое место точки, которая продвигается таким образом, что ее мера от фиксированной точки всегда имеет постоянное отношение к ее перпендикулярному расстоянию от фиксированного положения, причем все они существуют в одной и той же плоскости. узнайте о важной терминологии, концепциях и формулах, касающихся конического сечения, за которыми следуют парабола, эллипс и гипербола.

Фокус

Неподвижная точка называется фокусом конического сечения.

Направляющая

Неподвижная прямая обозначается как направляющая конического сечения.

Эксцентриситет

Фиксированное отношение расстояния точки, лежащей на конике от фокуса, к ее перпендикулярному расстоянию от директрисы называется эксцентриситетом конического сечения и обозначается e.

Значение эксцентриситета следующее:

Для эллипса: e < 1

Для параболы: e = 1

Для гиперболы: e > 1

Для окружности: e = 0

Для пары прямых: e = ∞

Если вы освоили параболу, эллипс и гиперболу, вы также можете подробно узнать о Sequence и Series здесь!

Ось

Прямая линия, проходящая через фокус и перпендикулярная директрисе, обозначается как ось конического сечения.

Вершина

Точка пересечения конического сечения и его оси называется вершиной конического сечения. 92 – ab\) > 0, a + b = 0, e = 1/2 Прямоугольная гипербола

Зная терминологию, давайте перейдем к нашей первой важной теме — параболе.

Парабола

Парабола определяется как геометрическое место точки, равноудаленной от фиксированной точки, называемой фокусом, и от фиксированной прямой линии, называемой директрисой.

О стандартных формах параболы

Проверьте стандартные формы уравнения параболы ниже: 92 = – 4ay\) Eccentricity e = 1 e = 1 e = 1 e = 1 Coordinates of Vertex (0, 0) (0, 0) (0, 0) (0, 0) Координаты фокуса (а, 0) (-а, 0) (0, 4, а) 9001 -a) Уравнение директрисы x = – a x = a y = – a 93\)

Эллипс

Эллипс определяется как геометрическое место точки, движущейся по плоскости так, что отношение ее расстояния от установленной точки (фокуса) до фиксированного прямого положения (директрисы) постоянно и меньше чем единица, т. е. эксцентриситет e < 1.

Основная ось: Это линия, соединяющая две фокусные точки/фокусы эллипса/гиперболы. Его середина называется центром кривой.

Большая ось: Большая ось определяется как линия, соединяющая две вершины эллипса, начинающаяся с одной стороны эллипса, проходящая через центр, и заканчивающаяся на другой стороне. Большую ось также называют самым длинным диаметром.

Малая ось: Определяется как кратчайшая хорда эллипса или кратчайший диаметр.

Это еще один термин, относящийся к оси, то есть большая полуось , которая составляет половину большой оси, и малая полуось , которая определяется как половина малой оси.

Факт: Окружность — это Эллипс, при условии, что оба фокуса/фокуса находятся в одной и той же точке (т.е. в центре). Другими словами, окружность можно назвать «частным случаем» эллипса. 92}=1\) Координаты центра (0, 0) (0, 0) Координаты вершин (a, 0) и (-a, 0) 0 (0, а) и (0, – а) Координаты очагов (а. е., 0) и (-а.е., 0) (0, а.е.) и (0, -а.е.) Длина большой оси 2a 2a Длина малой оси 2b 2b 92}=1\) Координаты центра (0, 0) (0, 0) Координаты вершин (a, 0) и (-a, 0) 0 (0, а) и (0, – а) Координаты очагов (а.е., 0) и (-а.е., 0) (0, а.е.) и (0, -а.е.) Длина поперечной оси 2a 2a Длина сопряженной оси 2b 2b 92}}\)

Тема сосредоточена на теоретической концепции, теперь хорошо знакомой с теорией, вы можете перейти к числовым значениям для большей практики.

Применение Conics в реальной жизни

• Планеты вращаются вокруг Солнца по эллиптическим траекториям в одном фокусе.
• Зеркала, используемые для фокусировки световых лучей в точке, являются параболическими.
• Трасса, проходимая объектом, запущенным в воздух и вытянутой дугой пуска ракеты, является параболической.
• Телескопы используют параболические зеркала.
• Спутниковые системы, радиосистемы используют гиперболические функции.
• Линзы, оптические стекла и мониторы имеют форму гиперболы.
• Параболические зеркала используются в солнечных печах для фокусировки световых лучей для обогрева.
• Звуковые волны фокусируются на параболических микрофонах.
• Автомобильные фары, прожекторы, Автомобильные фары сконструированы по принципу параболы.
• Электроны в атомах движутся вокруг ядра по эллиптической орбите.
• Гиперболы используются в системах дальней навигации под названием ЛОРАН.
• Параболические лампы на маяках обеспечивают хорошую фокусировку луча, чтобы моряки могли наблюдать за ними на расстоянии.
• Спутниковая антенна, используемая в спутниках, представляет собой параболическую конструкцию, обеспечивающую фокусировку и отражение радиоволн.

Следите за обновлениями в приложении Testbook или посетите веб-сайт Testbook, чтобы узнать больше об обновлениях по подобным темам из математики, естественных наук и многих других предметов, а также можете проверить серию тестов, доступных для проверки ваших знаний о различных экзаменах.

Парабола, эллипс и гипербола. Часто задаваемые вопросы

В.1 Классификация параболы, эллипса и гиперболы на основе эксцентриситета.

Ответ 1 Значение эксцентриситета параболы, эллипса и гиперболы следующее;
Для эллипса: e < 1
Для параболы: e = 1
Для гиперболы: e > 1

Q.2 Определите вершину в коническом сечении.

Ответ 2 Точка пересечения конического сечения и его оси называется вершиной конического сечения.

Q.3 Укажите стандартные формы параболы.

Ответ 3 Стандартные формы параболы следующие:
Форма y2 = 4ax:
В этой форме фокус параболы лежит на положительной стороне оси X.
Форма y2 = – 4ax:
В этой форме фокус параболы лежит на отрицательной стороне оси X.
Форма x2 = 4ay:
В этой форме фокус параболы лежит на положительной стороне оси Y.
Форма x2 = – 4ay:
В этой форме фокус параболы лежит на отрицательной стороне оси Y.

Q.4 Как определить большую и малую оси эллипса?

Ответ 4 Большая ось определяется как линия, соединяющая две вершины эллипса, начинающаяся с одной стороны эллипса, проходящая через центр, и заканчивающаяся на другой стороне. Большую ось также называют самым длинным диаметром. тогда как малая ось определяется как кратчайшая хорда эллипса или кратчайший диаметр.

Q.5 Является ли круг эллипсом?

Ответ 5 Круг представляет собой эллипс с условием, что оба фокуса/фокуса находятся в одной и той же точке (т.е. в центре). Другими словами, окружность можно назвать «частным случаем» эллипса.

Q.